正交实验的设计(四因素三水平最新版

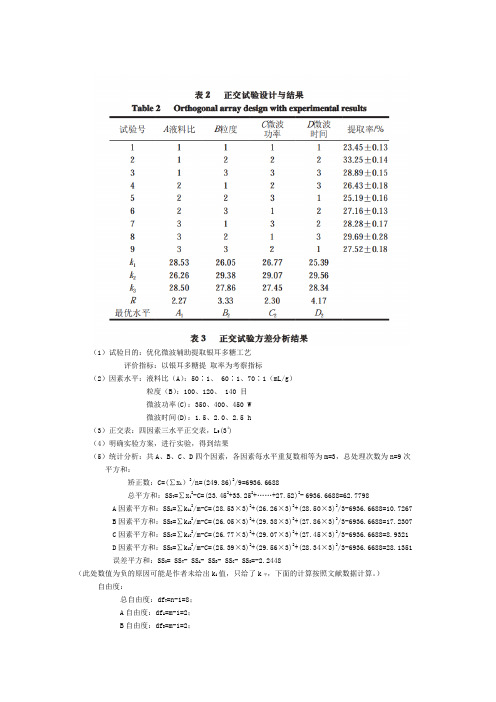
（1）试验目的：优化微波辅助提取银耳多糖工艺评价指标：以银耳多糖提取率为考察指标（2）因素水平：液料比（A）：50∶1、 60∶1、70∶1（mL/g）粒度（B）：100、120、 140 目微波功率(C)：350、400、450 W微波时间(D)：1.5、2.0、2.5 h（3）正交表：四因素三水平正交表，L9(34)（4）明确实验方案，进行实验，得到结果（5）统计分析：共A、B、C、D四个因素，各因素每水平重复数相等为m=3，总处理次数为n=9次平方和：矫正数：C=(∑x i）2/n=(249.86)2/9=6936.6688总平方和：SS T=∑x i2-C=(23.452+33.252+……+27.52)2-6936.6688=62.7798 A因素平方和：SS A=∑k iA2/m-C=(28.53×3)2+(26.26×3)2+(28.50×3)2/3-6936.6688=10.7267B因素平方和：SS B=∑k iB2/m-C=(26.05×3)2+(29.38×3)2+(27.86×3)2/3-6936.6688=17.2307C因素平方和：SS C=∑k iC2/m-C=(26.77×3)2+(29.07×3)2+(27.45×3)2/3-6936.6688=8.9321D因素平方和：SS D=∑k iD2/m-C=(25.39×3)2+(29.56×3)2+(28.34×3)2/3-6936.6688=28.1351误差平方和：SS0= SS T- SS A- SS B- SS C- SS D=-2.2448（此处数值为负的原因可能是作者未给出k i值，只给了k平，下面的计算按照文献数据计算。

）自由度：总自由度：df T=n-1=8；A自由度：df A=m-1=2；B自由度：df B=m-1=2；C自由度：df C=m-1=2；D自由度：df D=m-1=2；方差分析表：均方=平方和/自由度；F值=各因素离差平方和/误差离差平方和（文献使用各因素均方/误差均方）；在F分布表中查处相应的临界值Fα比较，判断各因素显著性大小。

四因素三水平（l9）正交实验方案excel表摘要：1.介绍四因素三水平正交实验方案2.解释Excel表在实验方案中的应用3.详细步骤：创建Excel表、输入数据、设置参数、分析结果4.分析结果的解释与实用性正文：在我们的实验研究中，常常需要考虑多个因素对实验结果的影响。

四因素三水平正交实验方案就是一个很好的方法，它可以同时考察四个因素在不同水平下的影响，从而帮助我们找到关键因素并优化实验方案。

在这个基础上，Excel表格的应用使得数据分析变得更加简便和高效。

首先，我们需要在Excel中创建一个表格，按照实验要求输入四因素三水平的数据。

在表格中，可以将因素名称设为列标题，水平编号设为行标题。

例如，我们可以将因素A、B、C、D分别命名为“因素A”、“因素B”、“因素C”和“因素D”。

接下来，我们需要设置Excel表格的参数。

在“数据”菜单中，点击“数据分析”，然后选择“回归”选项。

在弹出的对话框中，分别设置“因变量区域”和“自变量区域”。

在此示例中，我们可以将实验结果数据设为因变量，因素水平数据设为自变量。

设置完毕后，点击“确定”。

在分析结果中，我们可以看到每个因素对实验结果的影响程度。

Excel会自动计算各因素的F值、P值和平方和，帮助我们判断因素是否显著。

同时，还可以通过直观地观察回归系数来判断因素之间的交互作用。

根据分析结果，我们可以对实验方案进行优化，以提高实验效果。

最后，根据实验目的和实际情况，我们可以将分析结果整理成报告，为后续实验提供参考。

在撰写报告时，注意突出可读性和实用性，使得实验数据和分析结论更加易于理解和应用。

总之，通过四因素三水平正交实验方案和Excel表格的应用，我们可以高效地分析多个因素对实验结果的影响，从而为优化实验方案提供有力支持。

2. 必做题：2.1 质量控制方向课程设计题目：细纱机的主要零件是机梁，在细纱机中起着支撑延伸装置、导纱板升降装置、钢板升降装置，纱架等部件的作用，其质量将直接影响细纱机装配质量。

解决问题的重要性：机梁自身的结构长向薄壁形，其长厚比例达130：1，极易产生加工变形，而技术精度要求高，其中主要的技术特性值平面度要求仅仅为0.15mm。

加工工艺难度比较高。

机梁的数量大，每台细纱机有28根，每年需要67000根，机梁的好坏将直接影响该厂的经济效益，而现在的机梁波动比较大，返修率比较高。

因此提高机梁一次合格率有重要意义。

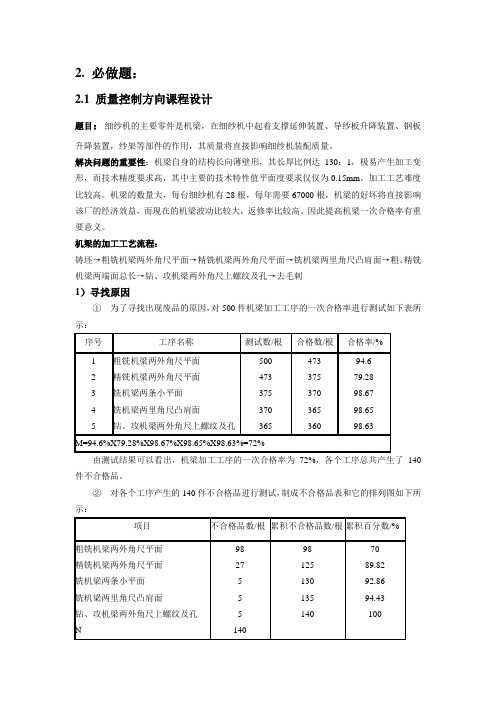
机梁的加工工艺流程：铸坯→粗铣机梁两外角尺平面→精铣机梁两外角尺平面→铣机梁两里角尺凸肩面→粗、精铣机梁两端面总长→钻、攻机梁两外角尺上螺纹及孔→去毛刺1）寻找原因1 为了寻找出现废品的原因，对500件机梁加工工序的一次合格率进行测试如下表所示：由测试结果可以看出，机梁加工工序的一次合格率为72%，各个工序总共产生了140件不合格品。

2 对各个工序产生的140件不合格品进行测试，制成不合格品表和它的排列图如下所示：项目不合格品数/根累积不合格品数/根累积百分数/%粗铣机梁两外角尺平面精铣机梁两外角尺平面铣机梁两条小平面铣机梁两里角尺凸肩面钻、攻机梁两外角尺上螺纹及孔N 9827555140981251301351407089.8292.8694.43100从不合格品表和排列图可以得出结论：粗铣机梁两外角尺平面为出现不合格品最多的工序，则下一步要解决的问题就是分析这道工序出现不合格品的主要原因。

3 取118件由粗铣机梁两外角尺平面工序所造成的不合格品进行检测，制成不合格品表和它的排列图如下所示：项目不合格品数量/根累积不合格品数/根累积百分数/%平面度0.15mm垂直度0.16mm直线度0.04mm表面粗糙度Ra<2.5μm 厚度超差其他881575218810311011511711874.5887.2993.2297.4699.15100从不合格品表和排列图可以得出结论：平面度是影响粗铣机梁两外角尺质量的A类因素即为主要因素。

2. 必做题：2.1 质量控制方向课程设计题目：细纱机的主要零件是机梁，在细纱机中起着支撑延伸装置、导纱板升降装置、钢板升降装置，纱架等部件的作用，其质量将直接影响细纱机装配质量。

解决问题的重要性：机梁自身的结构长向薄壁形，其长厚比例达130：1，极易产生加工变形，而技术精度要求高，其中主要的技术特性值平面度要求仅仅为0.15mm。

加工工艺难度比较高。

机梁的数量大，每台细纱机有28根，每年需要67000根，机梁的好坏将直接影响该厂的经济效益，而现在的机梁波动比较大，返修率比较高。

因此提高机梁一次合格率有重要意义。

机梁的加工工艺流程：铸坯→粗铣机梁两外角尺平面→精铣机梁两外角尺平面→铣机梁两里角尺凸肩面→粗、精铣机梁两端面总长→钻、攻机梁两外角尺上螺纹及孔→去毛刺1）寻找原因①为了寻找出现废品的原因，对500件机梁加工工序的一次合格率进行测试如下表所示：序号工序名称测试数/根合格数/根合格率/%1 2 3 4 5 粗铣机梁两外角尺平面精铣机梁两外角尺平面铣机梁两条小平面铣机梁两里角尺凸肩面钻、攻机梁两外角尺上螺纹及孔50047337537036547337537036536094.679.2898.6798.6598.63M=94.6%X79.28%X98.67%X98.65%X98.63%=72%由测试结果可以看出，机梁加工工序的一次合格率为72%，各个工序总共产生了140件不合格品。

②对各个工序产生的140件不合格品进行测试，制成不合格品表和它的排列图如下所示：项目不合格品数/根累积不合格品数/根累积百分数/%粗铣机梁两外角尺平面精铣机梁两外角尺平面铣机梁两条小平面铣机梁两里角尺凸肩面钻、攻机梁两外角尺上螺纹及孔N 9827555140981251301351407089.8292.8694.43100从不合格品表和排列图可以得出结论：粗铣机梁两外角尺平面为出现不合格品最多的工序，则下一步要解决的问题就是分析这道工序出现不合格品的主要原因。

三因数四水平正交表是一种正交表，用于多因素多水平的试验设计。

这种正交表将试验因素分为三组，每组因素都有四个水平，从而可以全面地研究各因素之间的交互作用和主效应。

三因数四水平正交表通常使用拉丁方的形式进行设计，即将三个因素安排在一个3x3的方阵中，每个因素占据一行或一列。

每个因素有四个水平，分别用1、2、3、4表示。

通过使用三因数四水平正交表，可以进行多因素多水平的试验，以确定各因素对试验结果的影响程度和交互作用。

这种试验设计可以大大减少试验次数，提高试验效率，同时得到较为准确的结果。

需要注意的是，在使用三因数四水平正交表时，应确保各因素的水平之间具有均衡性，以保证试验结果的可靠性和准确性。

同时，还需要根据实际情况选择合适的试验设计和数据分析方法，以得到最佳的试验效果。

四因素三水平正交表设计在科学研究和工程领域，实验设计是一项至关重要的工作。

它可以帮助研究人员更有效地分析和理解各种因素对特定结果的影响。

在本文中，我们将讨论一种常用的实验设计方法——四因素三水平正交表设计。

四因素三水平正交表设计是一种实验设计方法，旨在帮助研究人员同时考虑多个因素对结果的影响。

在这种设计中，有四个因素，每个因素有三个水平。

正交表的设计可以确保每个因素的每个水平都能够平衡地与其他因素的水平组合，从而减少实验误差，提高实验效率。

首先，让我们来看看四因素三水平正交表设计的优点。

首先，它可以帮助研究人员在较少的实验次数内获得更多的信息。

通过合理地选择因素和水平，并使用正交表设计，研究人员可以在相对较短的时间内获得全面的实验数据。

其次，正交表设计可以帮助研究人员减少实验误差，提高实验结果的可靠性和可重复性。

最后，正交表设计还可以帮助研究人员更好地理解各个因素之间的相互作用，从而为进一步的研究和实验奠定基础。

然而，四因素三水平正交表设计也存在一些局限性。

首先，正交表设计要求研究人员提前确定各个因素和水平的选择，这可能会限制实验的灵活性。

其次，正交表设计要求实验过程中的因素水平之间相互独立，这在实际操作中可能不太容易实现。

最后，正交表设计可能需要更多的实验次数来获得全面的数据，这可能会增加实验成本和时间。

总的来说，四因素三水平正交表设计是一种非常有用的实验设计方法，可以帮助研究人员更好地理解多个因素对结果的影响。

然而，研究人员在使用正交表设计时需要仔细考虑其优点和局限性，以便更好地应用于实际研究中。

希望本文可以为读者提供一些关于四因素三水平正交表设计的基本了解，并为实验设计提供一些参考和启发。