信息论信道容量总结
- 格式:ppt
- 大小:9.04 MB
- 文档页数:10


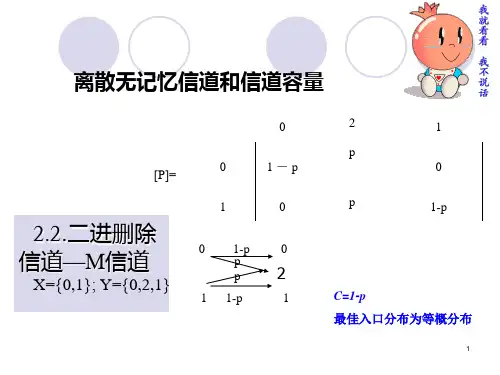



信道容量是信道的一个参数,反映了信道所能传输的最大信息量,其大小与信源无关。
对不同的输入概率分布,互信息一定存在最大值。
我们将这个最大值定义为信道的容量。
一但转移概率矩阵确定以后,信道容量也完全确定了。
尽管信道容量的定义涉及到输入概率分布,但信道容量的数值与输入概率分布无关。
我们将不同的输入概率分布称为试验信源,对不同的试验信源,互信息也不同。
其中必有一个试验信源使互信息达到最大。
这个最大值就是信道容量。
信道容量有时也表示为单位时间内可传输的二进制位的位数(称信道的数据传输速率,位速率),以位/秒(b/s)形式予以表示,简记为bps。
通信的目的是为了获得信息,为度量信息的多少(信息量),我们用到了熵这个概念。
在信号通过信道传输的过程中,我们涉及到了两个熵,发射端处信源熵——即发端信源的不确定度,接收端处在接收信号条件下的发端信源熵——即在接收信号条件下发端信源的不确定度。
接收到了信号,不确定度小了,我们也就在一定程度上消除了发端信源的不确定性,也就是在一定程度上获得了发端信源的信息,这部分信息的获取是通过信道传输信号带来的。
如果在通信的过程中熵不能够减小(不确定度减小)的话,也就没有通信的必要了。
最理想的情况就是在接收信号条件下信源熵变为0(不确定度完全消失),这时,发端信息完全得到。
通信信道,发端X,收端Y。
从信息传输的角度看,通过信道传输了I(X;Y)=H(X)-H(X|Y) ,( 接收Y前后对于X的不确定度的变化)。
I该值与两个概率有关,p(x),p(y|x),特定信道转移概率一定,那么在所有p(x) 分布中,max I(X;Y)就是该信道的信道容量C(互信息的上凸性)。
入与输出的互信息量的最大值,这一最大取值由输入信号的概率分布决定。
[3]X代表已传送信号的随机变量空间,Y代表已收到信号的随机变量空间。
代表已知X的情况下Y的条件机率。
我们先把通道的统计特性当作已知,p Y | X(y | x)就是通道的统计特性。


![信息论与编码[第三章离散信道及其信道容量]山东大学期末考试知识点复习](https://uimg.taocdn.com/b3091d87a0116c175f0e48d8.webp)
第三章离散信道及其信道容量3.1.1 信道的分类在信息论中,信道是传输信息的通道,是信息传输系统的重要组成部分之一。
信道的分类有:按照信道输入端或输出端的个数可分为单用户信道和多用户信道。
按照信道输出端有无信号反馈到输入端可分为有反馈信道和无反馈信道。
按照信道的统计参数是否随时间变化可分为时变参数信道和固定参数信道。
按照信道输入/输出信号取值幅度集合以及取值时间集合的离散性和连续性可分为离散信道(数字信道)和波形信道(模拟信道)。
按照信道输入/输出信号取值幅度集合的离散性和连续性(取值时间是离散的)可分为离散信道和连续信道。
按照信道输入/输出信号在取值时刻上是否有依赖关系可分为有记忆信道和无记忆信道。
按照信道输入信号与输出信号之间是否统计依赖关系可分为有噪信道和无噪(无干扰)信道。
3.1.2 离散信道的数字模型1.一般离散信道(多维离散信道)一般离散信道输入/输出信号取值幅度和取值时刻都是离散的平稳随机矢量。
其数学模型可用离散型概率空间[X,P(y|x),Y]来描述。
其中X=(X1X2…X N)为输入信号,Y= (Y1Y2…Y N)为输出信号。
X中X i∈A={a1,a2,…,a r},Y中Y i∈B={b1,b2,…,b s}。
又P(y|x)(x∈X,y∈Y)是信道的传递概率(转移概率),反映输入和输出信号之间统计依赖关系,并满足概率空间[X,P(y|x),Y]也可用图来描述。
2.基本离散信道(单符号离散信道)单符号离散信道是离散信道中最基本的信道,其信道输入/输出信号都是取值离散的单个随机变量。
数学模型是概率空间[X,P(y|x),Y],(或[X,P(b j|a i),Y]),其中X∈A={a1,a2,…,a r},Y∈B={b1,b2,…,b s),P(y|x)=P(b j|a i)(i=1,2,…,r;j=1,2,…,s)并满足概率空间[X,P(y|x),Y]也可用图来描述,如图3.1所示。


通信基础知识|信道容量写在前面:关于信道容量相关的定义与理论,最经典的是与AWGN信道相关的香农公式,随着移动通信系统的发展,通信信道越来越复杂,在香农公式研究的基础上实际上又有很多展开的研究,包括平坦衰落信道、频率选择性等信道的容量、又包括收发端是否已知信道信息条件下的容量。
本篇文章将相关的资料加以记录整理,供个人学习使用。
1 相关定义•香农容量(各态历经容量、遍历容量):系统无误传输(误码率为0)下,能够实现的最大传输速率;香农定义该容量为在某种输入分布\(p_X(x)\)下,信息传递能够获得的最大平均互信息\(I(X;Y)\),也即\(C_{\rmergodic}=\max_{p_X(x)}I(X;Y)\);如果信道衰落变化很快,在一个编码块内,所有的信息会经历所有可能的衰落,那么此时通常用各态历经容量来定义capacity,为每种可能衰落下,信道容量的统计平均值•中断容量:系统在某个可接受的中断概率下的最大传输速率(注意信噪比越小,中断概率越大,于是可接受的最大中断概率对应着一个最小的信噪比),有\(P_{\rm outage}=P(\gamma<\gamma_{\min})\);如果信道衰落变化较慢,在一个编码块内,信息经历相同的衰落,而不同编码块内信息经历不同的衰落,此时通常用中断容量来讨论capacity2 影响信道容量的因素•信道种类:AWGN信道、平坦衰落信道、频率选择性衰落信道、时间选择性衰落信道等•信道信息对于收发端是否已知:收发端已知信道衰落分布信息CDI、接收端已知信道实时的状态信息CSIR、收发端都已知信道实时的状态信息CSIRT3 SISO信道容量AWGN信道:最简单的加性高斯白噪声AWGN信道的(香农)信道容量,即是经典的香农公式:\(C=B\log(1+\frac{S}{N})\),其推导见通信基础知识 | 信息熵与香农公式,注意两个条件:高斯分布的信源熵最大、信号与噪声不相关平坦衰落信道:对于平坦衰落信道模型\(y=hx+n\)来说,信道的抽头系数可以写为\(\sqrt{g[i]}\),其中\(g[i]\)为每时刻的功率增益系数,信噪比此时考虑信道的衰落作用,为\(\gamma=\frac{S|h|^2}{N}\)•CDI:求解困难•CSIR:经过衰落的信道\(h\)的作用,相比AWGN信道,平坦衰落信道的信噪比会随之随机下降o各态历经容量:\(C_{\rmergodic}=B\int_0^{\infty}\log(1+\gamma)p(\gamma)d\gamma\),由于平坦衰落信道中的信噪比\(\gamma\)相比AWGN信道都是下降的,不难判断有\(C_{\rm fading}<C_{\rm AWGN}\)o中断容量:\(C_{\rmoutage}=B\log(1+\gamma_{\min})\),平均正确接受的信息速率为\(C_{\rm right}=(1-P_{\rmoutage})B\log(1+\gamma_{\min})\)•CSIRT:根据香农公式,信道容量与接收信号功率、噪声功率、信号带宽相关。
信道容量是信道的一个参数,反映了信道所能传输的最大信息量,其大小与信源无关。
对不同的输入概率分布,互信息一定存在最大值。
我们将这个最大值定义为信道的容量。
一但转移概率矩阵确定以后,信道容量也完全确定了。
尽管信道容量的定义涉及到输入概率分布,但信道容量的数值与输入概率分布无关。
我们将不同的输入概率分布称为试验信源,对不同的试验信源,互信息也不同。
其中必有一个试验信源使互信息达到最大。
这个最大值就是信道容量。
信道容量有时也表示为单位时间内可传输的二进制位的位数(称信道的数据传输速率,位速率),以位/秒(b/s)形式予以表示,简记为bps。
通信的目的是为了获得信息,为度量信息的多少(信息量),我们用到了熵这个概念。
在信号通过信道传输的过程中,我们涉及到了两个熵,发射端处信源熵——即发端信源的不确定度,接收端处在接收信号条件下的发端信源熵——即在接收信号条件下发端信源的不确定度。
接收到了信号,不确定度小了,我们也就在一定程度上消除了发端信源的不确定性,也就是在一定程度上获得了发端信源的信息,这部分信息的获取是通过信道传输信号带来的。
如果在通信的过程中熵不能够减小(不确定度减小)的话,也就没有通信的必要了。
最理想的情况就是在接收信号条件下信源熵变为0(不确定度完全消失),这时,发端信息完全得到。
通信信道,发端X,收端Y。
从信息传输的角度看,通过信道传输了I(X;Y)=H(X)-H(X|Y) ,( 接收Y前后对于X的不确定度的变化)。
I该值与两个概率有关,p(x),p(y|x),特定信道转移概率一定,那么在所有p(x) 分布中,max I(X;Y)就是该信道的信道容量C(互信息的上凸性)。
入与输出的互信息量的最大值,这一最大取值由输入信号的概率分布决定。
[3]X代表已传送信号的随机变量空间,Y代表已收到信号的随机变量空间。
代表已知X的情况下Y的条件机率。
我们先把通道的统计特性当作已知,p Y | X(y | x)就是通道的统计特性。