最新§1-4 图的基本回路数和基本割集数
- 格式：ppt
- 大小：691.50 KB
- 文档页数：3
下载文档原格式
合集下载
通路数和回路数的计算
通路数和回路数的计算通路数和回路数是图论中的重要概念，用于描述图中的路径和环的数量。
本文将介绍通路数和回路数的计算方法，并给出一些示例。
一、通路数的计算方法通路是指图中两个不同顶点之间的路径。
通路数是指从一个顶点到另一个顶点的所有通路的数量。
对于有向图和无向图，通路数的计算方法略有不同。
1. 有向图的通路数计算方法：对于有向图，通路数的计算可以通过邻接矩阵的幂运算来实现。
设邻接矩阵为A，其中A[i][j]=1表示存在一条从顶点i到顶点j的边，A[i][j]=0表示不存在边。
通路数矩阵C的元素C[i][j]表示从顶点i 到顶点j的通路数，则有C=A^k，其中k为通路的最大长度。
通过矩阵乘法的迭代计算，可以得到通路数矩阵C。
2. 无向图的通路数计算方法：对于无向图，通路数的计算可以通过邻接矩阵的幂运算和矩阵的迹来实现。
设邻接矩阵为A，其中A[i][j]=1表示存在一条连接顶点i 和顶点j的边，A[i][j]=0表示不存在边。
通路数的计算可以通过计算矩阵A的幂运算的迹来实现，即通路数等于矩阵A的幂运算后的迹。
二、回路数的计算方法回路是指图中起点和终点相同的路径，也称为环。
回路数是指图中所有回路的数量。
对于有向图和无向图，回路数的计算方法略有不同。
1. 有向图的回路数计算方法：对于有向图，回路数的计算可以通过邻接矩阵的迹和行列式来实现。
设邻接矩阵为A，其中A[i][j]=1表示存在一条从顶点i到顶点j的边，A[i][j]=0表示不存在边。
回路数的计算可以通过计算矩阵A的迹和行列式的差值来实现，即回路数等于矩阵A的迹减去行列式的值。
2. 无向图的回路数计算方法：对于无向图，回路数的计算可以通过邻接矩阵的迹和行列式来实现。
设邻接矩阵为A，其中A[i][j]=1表示存在一条连接顶点i和顶点j 的边，A[i][j]=0表示不存在边。
回路数的计算可以通过计算矩阵A 的迹和行列式的和值来实现，即回路数等于矩阵A的迹加上行列式的值。
关联矩阵、回路矩阵、割集矩阵
如果把Aa的任一行划去，剩下的(n-1) ×b矩阵用A表示，并称为降阶关联矩阵。
被划去的行对应的结点可以当作参考结点。
01
02
03
04
05
3、降阶关联矩阵
123456
Aa=
1 2 3 4
-1 0 +1 0
-1 0 0 +1
+1 -1 0 0
0 -1 +1 0
0 0 +1 -1
0 +1 0 -1
降阶关联矩阵
Q =
1 2 3
123456
3
4
5
2
6
1
①
②
③
④
-1
-1
0
-1
0
1
-1
-1
1
0
0
0
1
0
0
1
1
0
3
2
1
4
5
1
4
2
6
1
选支路3、5、6为树支
Q1
Q2
Q3
2、基本割集矩阵
如果选一组单树支割集为一组独立割集，这种割集矩阵就称为基本割集矩阵，用Qf表示。 写Qf时，注意安排其行列次序如下： 把(n-1)条树支依次排列在对应于Qf的第1到第(n-1) 列，然后再排列连支； 取每一单树支割集的序号与相应树支所在列的序号相同， 且选割集方向与相应树支方向一致， 则Qf有如下形式
因此有
Bu =0
3
4
5
2
6
1
①
②
③
④
Bu=
1 0 0
0 1 0
1 1 0
0 0 1
-1 0 -1
被划去的行对应的结点可以当作参考结点。
01
02
03
04
05
3、降阶关联矩阵
123456
Aa=
1 2 3 4
-1 0 +1 0
-1 0 0 +1
+1 -1 0 0
0 -1 +1 0
0 0 +1 -1
0 +1 0 -1
降阶关联矩阵
Q =
1 2 3
123456
3
4
5
2
6
1
①
②
③
④
-1
-1
0
-1
0
1
-1
-1
1
0
0
0
1
0
0
1
1
0
3
2
1
4
5
1
4
2
6
1
选支路3、5、6为树支
Q1
Q2
Q3
2、基本割集矩阵
如果选一组单树支割集为一组独立割集，这种割集矩阵就称为基本割集矩阵，用Qf表示。 写Qf时，注意安排其行列次序如下： 把(n-1)条树支依次排列在对应于Qf的第1到第(n-1) 列，然后再排列连支； 取每一单树支割集的序号与相应树支所在列的序号相同， 且选割集方向与相应树支方向一致， 则Qf有如下形式
因此有
Bu =0
3
4
5
2
6
1
①
②
③
④
Bu=
1 0 0
0 1 0
1 1 0
0 0 1
-1 0 -1
网络图论
电路理论
主讲 骆建
第三章 电路方程法 （网络分析的一般方法）
（电路分析方法之二）
主讲
开课单位：电气与电子工程学院电工教学基地
骆建
1
2
第三章
网络分析的一般方法
3.1 网络图论的基本概念 3.2 有向图的矩阵表示
了解支路电流分析法 重点掌握回路（电流）分析法 重点掌握节点（电压）分析法
3.3 KCL与KVL方程的矩阵表示 3.4 支路电流分析法 3.5 节点电压分析法 3.6 回路电流分析法
6
支路j属于网孔i ，方向与i一致 支路j属于网孔i ，方向与i相反 支路j不属于网孔i
Bf = 1L F
(b-n+1) 单位矩阵 树支对应的 子矩阵
2、内网孔是一组独立回路
31 32
3-2-5 有向图矩阵间的关系 1.A与Bf（或M)的关系 要求:各矩阵序号相同的列对应同一支路 则： ABfT=0 支 节 1 A= 2 3 或
支 节 1 1 1 Aa= 2 -1 3 0 4 0
2 0 -1 1 0
3 0 0 1 -1 1 1 -1 0
4 -1 0 0 1 2 0 -1 1
5 0 1 0 -1 3 0 0 1
6 1 0 -1 0 4 -1 0 0 5 6 0 1 1 0 0 -1
Aa={aij}n b
节点数 支路数
aij
Ub=AT Un
1 1 0 0 0 -1 -1 2 0 1 0 -1 -1 0 3 0 0 1 1 1 1
• 独立、完备的节点电压变量Un 。
39
u2 u4 0 u6 0 u1 = 0 u3 u5 和
6 Q3: { 1 , 5 ,3 , 6 }
4 保留4支路，图不连通的。
主讲 骆建
第三章 电路方程法 （网络分析的一般方法）
（电路分析方法之二）
主讲
开课单位：电气与电子工程学院电工教学基地
骆建
1
2
第三章
网络分析的一般方法
3.1 网络图论的基本概念 3.2 有向图的矩阵表示
了解支路电流分析法 重点掌握回路（电流）分析法 重点掌握节点（电压）分析法
3.3 KCL与KVL方程的矩阵表示 3.4 支路电流分析法 3.5 节点电压分析法 3.6 回路电流分析法
6
支路j属于网孔i ，方向与i一致 支路j属于网孔i ，方向与i相反 支路j不属于网孔i
Bf = 1L F
(b-n+1) 单位矩阵 树支对应的 子矩阵
2、内网孔是一组独立回路
31 32
3-2-5 有向图矩阵间的关系 1.A与Bf（或M)的关系 要求:各矩阵序号相同的列对应同一支路 则： ABfT=0 支 节 1 A= 2 3 或
支 节 1 1 1 Aa= 2 -1 3 0 4 0
2 0 -1 1 0
3 0 0 1 -1 1 1 -1 0
4 -1 0 0 1 2 0 -1 1
5 0 1 0 -1 3 0 0 1
6 1 0 -1 0 4 -1 0 0 5 6 0 1 1 0 0 -1
Aa={aij}n b
节点数 支路数
aij
Ub=AT Un
1 1 0 0 0 -1 -1 2 0 1 0 -1 -1 0 3 0 0 1 1 1 1
• 独立、完备的节点电压变量Un 。
39
u2 u4 0 u6 0 u1 = 0 u3 u5 和
6 Q3: { 1 , 5 ,3 , 6 }
4 保留4支路，图不连通的。
割集
§15.1 割集
一、割集
1、定义 连通图G的一个割集是G的一个支路集合，把
这些支路移去将使G分离为两个部分，但是如果少 移去一条支路，图仍将是连通的。
a
b
e
d
c
f
a
b
e
d
c
f
(b,d,e,f)是割集
a
c f
a
b
a
b
e
e
d
c
d
c
f
f
f
(a,b,c,d,e)不是割集
移去割集支路，G 被分离成三部分
a
b
e
d
c
f
(a,d,f) 是割集
b e
c
2、割集的确定
可以用在连通图G上作闭合面的方法判断确定
一个割集。
如果在G上作一个闭合面，使其包围G的某些结点，
于是，若把与此闭合面相切的所有支路全部移去，G
将被分离为两个部分，则这样一组支路便构成一个割
集。
a
d
b e
c f
Q1
a
b
e
d
c
f
d
c
f
(a,b,e) 为割集
分支路， 而树T本身是连通的且又不包含回路。 2、树支：
树中包含的支路。
树支数为n-1。 3、连支：
树支之外的其他支路。 连支数为b-(n-1)=b-n+1
例：基本割集组的确定
a
b
e
d
c
f
选择a,e,c为树 树支用实线表示 连支用虚线表示
每个基本割集中只有一个树支和相 应闭合面相切割。
a d
Q1
b e
对于一个具有n个结点和b条支路的连通图，独立的 KCL方程有(n-1)个,独立割集数将有(n-1)个. 2、一组独立割集的确定
一、割集
1、定义 连通图G的一个割集是G的一个支路集合，把
这些支路移去将使G分离为两个部分，但是如果少 移去一条支路，图仍将是连通的。
a
b
e
d
c
f
a
b
e
d
c
f
(b,d,e,f)是割集
a
c f
a
b
a
b
e
e
d
c
d
c
f
f
f
(a,b,c,d,e)不是割集
移去割集支路，G 被分离成三部分
a
b
e
d
c
f
(a,d,f) 是割集
b e
c
2、割集的确定
可以用在连通图G上作闭合面的方法判断确定
一个割集。
如果在G上作一个闭合面，使其包围G的某些结点，
于是，若把与此闭合面相切的所有支路全部移去，G
将被分离为两个部分，则这样一组支路便构成一个割
集。
a
d
b e
c f
Q1
a
b
e
d
c
f
d
c
f
(a,b,e) 为割集
分支路， 而树T本身是连通的且又不包含回路。 2、树支：
树中包含的支路。
树支数为n-1。 3、连支：
树支之外的其他支路。 连支数为b-(n-1)=b-n+1
例：基本割集组的确定
a
b
e
d
c
f
选择a,e,c为树 树支用实线表示 连支用虚线表示
每个基本割集中只有一个树支和相 应闭合面相切割。
a d
Q1
b e
对于一个具有n个结点和b条支路的连通图，独立的 KCL方程有(n-1)个,独立割集数将有(n-1)个. 2、一组独立割集的确定
如何确定电路阶数,图,割集课件
1 5 2 6 有向图 4 3
n5
抛开元 件性质
1 5
b 8
3 8
R3
2
7
4
6
元件的串联及并联 组合作为一条支路
一个元件作 为一条支路
n4 b6
返 回
上 页
下 页
结论 电路的图是用以表示电路几何结构的图
形，图中的支路和结点与电路的支路和结点一一对 应。 ⑴图的定义(Graph) G={支路，结点}
支路数＝树支数＋连支数 ＝结点数－1＋基本回路数
b n l 1
返 回 上 页 下 页
例 图示为电路的图，画出三种可能的树及其对
应的基本回路。 1 4 8 3 5 6 7 2 8 5 6 7 4 8 3 6
4 8 3 2
注意
网孔为基本回路。
返 回
上 页
下 页
15.1 割集
割集Q
连通图G中支路的集合，具有下述性质： • 把Q中全部支路移去，图分成二个分离部分。 • 任意放回Q 中一条支路，仍构成连通图。
明确 ①对应一个图有很多的树
②树支的数目是一定的
bt n 1
连支数：
bl b bt b (n 1)
返 回 上 页 下 页
②回路(Loop) 1 7 3 5 8 4
2
6
L是连通图的一个子图，构成一 条闭合路径，并满足：(1)连通， (2)每个结点关联2条支路。 不 回路 1 2 是 2 3 回 7 5 路 8 4 5
返 回 上 页 下 页
注意
③对应一组线性独立的KCL方程的割集称为独 立割集 ，基本割集是独立割集，但独立割集 不一定是单树支割集。
返 回
上 页
下 页
n5
抛开元 件性质
1 5
b 8
3 8
R3
2
7
4
6
元件的串联及并联 组合作为一条支路
一个元件作 为一条支路
n4 b6
返 回
上 页
下 页
结论 电路的图是用以表示电路几何结构的图
形，图中的支路和结点与电路的支路和结点一一对 应。 ⑴图的定义(Graph) G={支路，结点}
支路数＝树支数＋连支数 ＝结点数－1＋基本回路数
b n l 1
返 回 上 页 下 页
例 图示为电路的图，画出三种可能的树及其对
应的基本回路。 1 4 8 3 5 6 7 2 8 5 6 7 4 8 3 6
4 8 3 2
注意
网孔为基本回路。
返 回
上 页
下 页
15.1 割集
割集Q
连通图G中支路的集合，具有下述性质： • 把Q中全部支路移去，图分成二个分离部分。 • 任意放回Q 中一条支路，仍构成连通图。
明确 ①对应一个图有很多的树
②树支的数目是一定的
bt n 1
连支数：
bl b bt b (n 1)
返 回 上 页 下 页
②回路(Loop) 1 7 3 5 8 4
2
6
L是连通图的一个子图，构成一 条闭合路径，并满足：(1)连通， (2)每个结点关联2条支路。 不 回路 1 2 是 2 3 回 7 5 路 8 4 5
返 回 上 页 下 页
注意
③对应一组线性独立的KCL方程的割集称为独 立割集 ，基本割集是独立割集，但独立割集 不一定是单树支割集。
返 回
上 页
下 页
《图论》第7章-回路矩阵与割集矩阵
1 aj 在si 中且方向一致
sij = -1 aj 在si 中且方向相反 0 其他
若S1、S2、… 、Sk 包含了中所有割集，称S为G的完全割
集矩阵，记为 Se 。
[基本割集矩阵] 由G的所有基本割集构成的割集矩阵成为G的基
本割集矩阵,记为 Sf 。
19
7.3 割集矩阵
[定理7-3-1] 有向连通图 G=(V, A)，n =|V|，m =|A|，则其任意基
故 B11+ B12 C12T=0
即 B11= -B12 C12T 故 Bk =( -B12 C12T , B12) = B12 ( -C12T , I )
而 r(Bk ) = n-1，故 r(B12 ) = n-1，即 | B12 | 0
由[定理3-2-5]知此时B12各列对应的弧构成G的一棵树。 也即 C12各列对应的弧构成G的一棵树。 8
16
7.2 割集
[定理7-2-3] 设T是连通图G的一棵生成树，e 是T的一条弦，C 是由 e 确定的 T+e 中的基本回路。则 e 包含在由C中除 e 外的每条边确定的基本割集中，而不在其他的基本割集中。 [证明] ① 设 bC且 be，S是 b 确定的基本割集。由[定理7-2-2] C和S除了b外应该还有一条公共边。S 除了b以外其它边都 是T的余树边，而C中只有 e 是T的余树边，所以此公共边 只能是e，也即e包含在S中。② 若e被包含在一个由T的树 枝 h 确定的基本割集 S 中，由[定理7-2-2] C和 S 除了e 外 应该还有一条公共边。 C 除了e以外其它边都是T的树枝， 而S中只有 h 是T的树枝，所以此公共边只能是 h，也即 h 理7-2-4] 设T是连通图G的一棵生成树，b 是T的一条树枝，S 是由 b 确定的G的基本割集。则 b 包含在由S中除 b 外的每
电路原理习题集(下册)
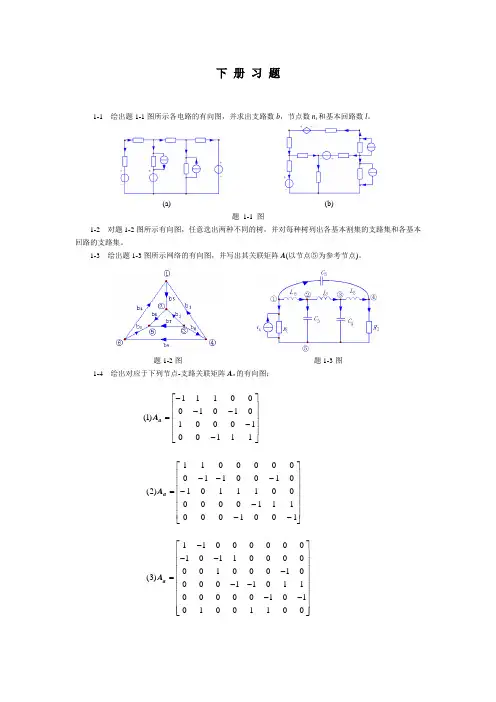
下 册 习 题1-1 绘出题1-1图所示各电路的有向图，并求出支路数b ，节点数n t 和基本回路数l 。
(a) (b)题 1-1 图 1-2 对题1-2图所示有向图，任意选出两种不同的树，并对每种树列出各基本割集的支路集和各基本回路的支路集。
1-3 绘出题1-3图所示网络的有向图，并写出其关联矩阵A (以节点⑤为参考节点)。
题1-2图 题1-3图1-4 绘出对应于下列节点-支路关联矩阵A a 的有向图：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----=11100100010101000111)1(a A ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------=10010001110000001110101001100000011)2(a A()3110000001011000000100010000110110000010101001100A a =--------⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥1-5 题1-5(a)、(b)图表示同一有向图的两种不同的树，图中粗线为树支。
试在该图上表示出各基本回路和基本割集，并写出基本回路矩阵B 和基本割集矩阵Q 。
1-6 应用题1-5写出的矩阵B 和矩阵Q 验证公式QB T =0。
1-7 对于某一有向图中的一个指定的树，其基本割集矩阵为 Q =---⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥100111001001110010101试写出对应于该有向图中同一树的基本回路矩阵B 。
1-8 对于某一有向图中的一个指定的树，其基本回路矩阵为B =---⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥101100110010011001 试写出对应于该有向图中同一树的基本割集矩阵Q 。
1-9 对题1-8-1图所示有向图，试选一树使得对应于此树的每一个基本回路是图中的一个网孔，并写出基本回路矩阵B 。
1-10 证明题1-10图中的图G 1和G 2都是图G 的对偶图。
(a)(b)题 1-10 图题 1-5 图（c ）2-1 写出题2-1图所示正弦交流网络的支路阻抗矩阵和用支路阻抗矩阵表示的支路方程的矩阵形式(电源角频率为ω)。
最新如何确定电路阶数,图,割集课件
返回 上页 下页
树
不 是 树 树支：构成树的支路 连支：属于G而不属于T的支路
明确 ①对应一个图有很多的树
②树支的数目是一定的 bt n1
连支数： b l b b t b (n 1 )
返回 上页 下页
②回路(Loop)
L是连通图的一个子图，构成一条 闭合路径，并满足：(1)连通，(2)
1 23 75
当一个割集的所有支路都连接在同一个结点
上，则割集的KCL方程变为结点上的KCL方
程。
返回 上页 下页
注意
③对应一组线性独立的KCL方程的割集称为独 立割集 ，基本割集是独立割集，但独立割集 不一定是单树支割集。
返回 上页 下页
图G的任意两结点间至少有一条路 径时称为连通图，非连通图至少存 在两个分离部分。
返回 上页 下页
(4)子图
若图G1中所有支路和结点都是图 G中的支路和结点，则称G1是G 的子图。
①树(Tree)
注：树是连 接全部节点 所需最少支 路的集合
T是连通图的一个子图且满足下 列条件： a. 连通 b.包含所有结点 c. 不含闭合路径
• 把Q中全部支路移去，图分成二个分离部分。 • 任意放回Q 中一条支路，仍构成连通图。
ห้องสมุดไป่ตู้
164
9
3
7
28 5
割集：(1 9 6) (2 8 9) (3 6 8) (4 6 7) (5 7 8)
问题
(3 6 5 8 7) , (3 6 2 8)是割集吗？
返回 上页 下页
基本割集
借助于“树确立一个独立“割集”
⑴图的定义(Graph)
G={支路，结点}
①图中的结点和支路各自是一个整体。 ②移去图中的支路，与它所联接的结点依然
树
不 是 树 树支：构成树的支路 连支：属于G而不属于T的支路
明确 ①对应一个图有很多的树
②树支的数目是一定的 bt n1
连支数： b l b b t b (n 1 )
返回 上页 下页
②回路(Loop)
L是连通图的一个子图，构成一条 闭合路径，并满足：(1)连通，(2)
1 23 75
当一个割集的所有支路都连接在同一个结点
上，则割集的KCL方程变为结点上的KCL方
程。
返回 上页 下页
注意
③对应一组线性独立的KCL方程的割集称为独 立割集 ，基本割集是独立割集，但独立割集 不一定是单树支割集。
返回 上页 下页
图G的任意两结点间至少有一条路 径时称为连通图，非连通图至少存 在两个分离部分。
返回 上页 下页
(4)子图
若图G1中所有支路和结点都是图 G中的支路和结点，则称G1是G 的子图。
①树(Tree)
注：树是连 接全部节点 所需最少支 路的集合
T是连通图的一个子图且满足下 列条件： a. 连通 b.包含所有结点 c. 不含闭合路径
• 把Q中全部支路移去，图分成二个分离部分。 • 任意放回Q 中一条支路，仍构成连通图。
ห้องสมุดไป่ตู้
164
9
3
7
28 5
割集：(1 9 6) (2 8 9) (3 6 8) (4 6 7) (5 7 8)
问题
(3 6 5 8 7) , (3 6 2 8)是割集吗？
返回 上页 下页
基本割集
借助于“树确立一个独立“割集”
⑴图的定义(Graph)
G={支路，结点}
①图中的结点和支路各自是一个整体。 ②移去图中的支路，与它所联接的结点依然
电路原理12.1.1割集 - 割集
2. 由某个树支 bt 确定的基本割集应包含那些连支，每个这种连支 构成的单连支回路中包含该树支 bt 。
返回 上页 下页
②
②
1
2
①5
③
43 ④6
Q2：{ 2，3，6 }
1
2
①5
③
43 ④6
Q3：{ 1，4，6}
②
1
①
③
3
④
②
1
2
①5
③
43 ④6
Q4：{ 1，5，2 }
返回 上页 下页
电路方程的矩阵形式
单树支割集(基本割集) 对一个连通图，若任选一个树，则对应的连支集合不能构成一个
割集(将所有连支移去后所得的图还是连通的)，故每一割集应至少包
12
4
3
{1，2，3，4}
割集
4 保留4支路，图不连通。
返回 上页 下页
电路方程的矩阵形式
同一个树的基本回路和基本割集关系
②
1
2
①5
③
43 ④6
基本回路 {1，2，3，4} {1，4，5}
{1，2，6}
基本割集 {1，5，3，6} {2，3，6} {3，4，5}
1. 由某个连支 bl 确定的单连支回路应包含那些树支，每个这种树 支所构成的基本割集中含有 bl 。
独立割集 单树支割集
独立割集
返回 上页 下页
电路方程的矩阵形式
应注意的是，割集是有方向的(移去割集的所有支路，图G 被分 离为两部分后，从其中的一部分指向另一部分的方向，即为割集的 方向，每个割集只有两个可能的方向)。若是基本割集，一般选取树 支的方向为割集的方向。
1
3
2
4
返回 上页 下页
②
②
1
2
①5
③
43 ④6
Q2：{ 2，3，6 }
1
2
①5
③
43 ④6
Q3：{ 1，4，6}
②
1
①
③
3
④
②
1
2
①5
③
43 ④6
Q4：{ 1，5，2 }
返回 上页 下页
电路方程的矩阵形式
单树支割集(基本割集) 对一个连通图，若任选一个树，则对应的连支集合不能构成一个
割集(将所有连支移去后所得的图还是连通的)，故每一割集应至少包
12
4
3
{1，2，3，4}
割集
4 保留4支路，图不连通。
返回 上页 下页
电路方程的矩阵形式
同一个树的基本回路和基本割集关系
②
1
2
①5
③
43 ④6
基本回路 {1，2，3，4} {1，4，5}
{1，2，6}
基本割集 {1，5，3，6} {2，3，6} {3，4，5}
1. 由某个连支 bl 确定的单连支回路应包含那些树支，每个这种树 支所构成的基本割集中含有 bl 。
独立割集 单树支割集
独立割集
返回 上页 下页
电路方程的矩阵形式
应注意的是，割集是有方向的(移去割集的所有支路，图G 被分 离为两部分后，从其中的一部分指向另一部分的方向，即为割集的 方向，每个割集只有两个可能的方向)。若是基本割集，一般选取树 支的方向为割集的方向。
1
3
2
4
第15章电路方程的矩阵形式
矩阵形式的KCL：[ Q ][i ]=0
it Ql il
[1
Ql
] iilt
0
回路矩阵表示时 BTt il it
Ql BtT
４
５
３
２
６
1
割集支 4
C1 1
Q= C2 0
C3 0
56123
0 0 -1 -1 0
1 0 1 1 -1
0 1 0 -1 1
Qt
Ql
回支 4 5 6 1 2 3
1 1 -1 0 1 0 0 B = 2 1 -1 1 0 1 0 = [ Bt 1 ]
6
2 13
1
3
基本回路数=连支数=b-(n-1)
3.割集Q (Cut set )
Q是连通图G中支路的集合，具有下述性质： (1)把Q中全部支路移去，图分成二个分离部分。 (2)任意放回Q 中一条支路，仍构成连通图。
6
12
5
4
3
{2,4,5,6} 12
3
{2,3,6}
1 5•
4
{1,3,5,6}是否割集？
•
Idk gkj Uej gkj (U j Usj )
•
•
•
•
•
•
Ik Yk (Uk Usk ) gkj (U j Usj ) Isk
•
(2) I dk 为 CCCS
•
•
设 I dk kj I ej
•
•
•
I ej
Yj
(U
j
Usj
)
•
•
•
•
•
•
Ik Yk (Uk Usk ) kjYj (U j Usj ) Isk
§1-4 图的基本回路数和基本割集数
平面图(planar graph)：
凡是能在一个平面上绘出，而又不致有两条支路 在一个非节点处交叉的图，称为平面图。 一个平面图的网孔数m等于图的基本回路数l 。
为什么要研究图的基本割集数目和基本回路数目？
返回
§1-4 图的基本回路数和基本割集数
一个节点数为nt=n+1，支路数为b的连通图G， 无论如何选树，恒具有n个基本割集和b-n个基本回 路。
基本割集数等于树支数
把n+1个节点全部连通以构成一种树时，至少 需要n条支路。 基本回路数等于连支数 连支数等于全部支路数b减去树支数n。
对于具有nt个节点、b条支路、s个分离部分 的非连通图，在每一分离部分中选一树，则总树 支数(即基本割集数)为nt-s，总连支数(即基本回 路数)为b-(nt-s)=b-nt+s。
流体网络题库
第一章流体网络的基本概念与拓扑关系 名词解释:1.流体网络: 无论是矿井的通风系统（包括有风流流动的井巷通道、调节风量分配用的构筑物、作为通风动力的风机等等），还是城市集中供热系统（包括输送管路、各种调节阀门、作为动力的泵站等等），以及城市煤气输送系统、自来水供应系统、集中空调系统等各种有流体流动的管路系统，它们都有一共同的特点，那就是它们都是由输送流体的管路、各种调节设施及动力设施构成，流体管路连接在一起形成流体网络。
2. 分支: 抛开流体网络的各种属性，只考虑流体管路的几何连接拓扑关系。
为此，将管路称之为分支。
3. 节点: 三条以上分支的连接点称之为节点；有时为研究问题方便，将管路的某种属性的交变点也称为节点，也就是说两条物理属性不同的分支的交点也称之为节点；还有一类分支，其一端与其他分支相连接，而另一端是自由的，不与任何分支相连接，将这类端点也称为节点。
4. 图:将流体网络中的节点和分支的集合称为图，记为),(E V G = ，式中，V 表示节点的集合，{}m v v v V ,,,21 = ，m 为节点数，V m =；E 表示分支集合，{}n e e e E ,,,21 = ，n为分支数，E n =5.有向图: 分支ke 对应着的两个节点分别为iv 和jv 。
当流体流动的方向是ji v v →，此时将分支ke 写成()j i k v v e ,=，图G 称为有向图6. 无向图:当流体流动方向尚未确定，或者流体流动方向与我们所研究的问题无关时，网络分支ke 即可写成ji k v v e ,=，也可写成ij k v v e ,=，图G 称为无向图。
7. 关联: 在图),(E V G = 中，如果节点i v 是分支k e 的一个节点，则称分支k e 和节点i v 相关联。
8. 邻接:对于节点iv 和jv ，若Ev v j i ∈,，则称iv 和jv 是邻接的。
9．子图； 对图()E V G ,= 和()E V G ''=', 来说，若有V V ⊆' 和E E ⊆' ，则称图G ' 是G 的一个子图。
电路分析中回路分析法和割集分析法(精品课件)
23
以上谈到的是用“ 笔”算方法分析电路时遇到的几 个问题，假若用计算机程序来分析电路，就不必考虑这些 问题了，只要将电路元件连接关系和参数的有关数据告诉 计算机，计算机就能够自动建立电路方程，并求解得到你 所需要的各种计算结果。当你用“ 笔”算分析电路遇到 困难时和深入研究某些比较复杂电路的特性时，建议用本 教材提供的计算机程序，可以为你节省大量时间。
17
当电路由独立电流源和压控电阻元件组成时，将压控元 件的VCR方程{i=f(u)}代入KCL方程中，将支路电流转换 为支路电压，从而得到用b个支路电压表示的n-1个KCL方 程。这些方程再加上原来的b-n+1个KVL方程，就构成以b 个支路电压作为变量的支路电压法方程。
18
由于b个支路电压中，只有n-1个独立的电压变量，其 它的支路电压是这些独立电压的线性组合。假如将这种线 性组合关系代入到支路电压方程组中，就得到以n-1个独 立电压为变量的KCL方程(结点方程或割集方程)。假如采 用连通电路的n-1个结点电压作为变量，就得到结点电压 方程；假如采用n-1个树支电压作为变量，就得到割集方 程。
i1的回路方程
8
图3－21
用观察法列出电流i1的回路方程
(5 3 1)i1 (1 3)i3 (5 3)i4 20V
代入i3=2A, i4=1A，求得电流i1
i1
20V 8V 8V 5 3 1
4A
根据支路电流与回路电流的关系可以求得其它支路电流
i2 i1 i4 3A i5 i1 i3 2A i6 i1 i3 i4 1A9
2
KCL可以用割集来陈述：在集总参数电路中，任一时刻， 与任一割集相关的全部支路电流的代数和为零。
例如，按照图示割集可以写出以下KCL方程
以上谈到的是用“ 笔”算方法分析电路时遇到的几 个问题，假若用计算机程序来分析电路，就不必考虑这些 问题了，只要将电路元件连接关系和参数的有关数据告诉 计算机，计算机就能够自动建立电路方程，并求解得到你 所需要的各种计算结果。当你用“ 笔”算分析电路遇到 困难时和深入研究某些比较复杂电路的特性时，建议用本 教材提供的计算机程序，可以为你节省大量时间。
17
当电路由独立电流源和压控电阻元件组成时，将压控元 件的VCR方程{i=f(u)}代入KCL方程中，将支路电流转换 为支路电压，从而得到用b个支路电压表示的n-1个KCL方 程。这些方程再加上原来的b-n+1个KVL方程，就构成以b 个支路电压作为变量的支路电压法方程。
18
由于b个支路电压中，只有n-1个独立的电压变量，其 它的支路电压是这些独立电压的线性组合。假如将这种线 性组合关系代入到支路电压方程组中，就得到以n-1个独 立电压为变量的KCL方程(结点方程或割集方程)。假如采 用连通电路的n-1个结点电压作为变量，就得到结点电压 方程；假如采用n-1个树支电压作为变量，就得到割集方 程。
i1的回路方程
8
图3－21
用观察法列出电流i1的回路方程
(5 3 1)i1 (1 3)i3 (5 3)i4 20V
代入i3=2A, i4=1A，求得电流i1
i1
20V 8V 8V 5 3 1
4A
根据支路电流与回路电流的关系可以求得其它支路电流
i2 i1 i4 3A i5 i1 i3 2A i6 i1 i3 i4 1A9
2
KCL可以用割集来陈述：在集总参数电路中，任一时刻， 与任一割集相关的全部支路电流的代数和为零。
例如，按照图示割集可以写出以下KCL方程
大学电路第十五章割集
例 选 2、5、6为树，连支顺序为1、 3 、 4 。
支1 3 回 1 [Bf] = 2 3 1 0 0 1 0 0
②
４ 2６ 3 ③ ５ ２ 1 ④ 1
返 回 上 页 下 页
0 -1 -1 0 0 1 0 1 1 0 -1 1
Bl
Bt
= [1 Bt ]
3. 回路矩阵[B]的作用
①用回路矩阵[B]表示矩阵形式的KVL方程；
一.复合支路
反映元件性质的支路电压和支路电流关 系的矩阵形式是网络矩阵分析法的基础。
. . .
I k I ek
Zk (Yk)
.
-
U Sk
+
I Sk
+
.
Uk
-
规定标准 支路
返 回
上 页
下 页
.
.
.
I k I ek
Zk (Yk)
.
-
U Sk
+
I Sk
+
.
复合支路特点
Uk
-
①支路的独立电压源和独立电流源的方向与支 路电压、电流的方向相反； ②支路电压与支路电流的方向关联； ③支路的阻抗（或导纳）只能是单一的电阻、 电容、电感，而不能是它们的组合。
设
[u ] [u1 u3 u4 u2 u5 u6 ]
ul
ut u
u 3 u 4 u 2 u 5 u 6
1
l个独立 KVL方程
1 0 0 -1 -1 0 [ B ][ u ]= 0 1 0 1 0 1 0 0 1 0 -1 1
u1 u 2 u5 u3 u 2 u 6 0 u 4 u5 u 6
大学电路第十五章割集
②
矩阵形式的KCL： [ B ]T[ il ]=[ i ]
返 回 上 页 下 页
三. 割集矩阵[Q]
1. 独立割集矩阵：描述割集与支路关联关系的矩阵。 支路b
[Q]=
割 集 数
注意
每一行对应一个基本割集, 每一列对应一条支路.
(n-1)b
矩阵Q的每一个元素定义为：
qij
1 支路 j 在割集 i 中，且与割集方向一致； -1 支路 j 在割集 i中，且与割集方向相反； 0 支路 j 不在割集 i 中。
设
[u ] [u1 u3 u4 u2 u5 u6 ]
ul
ut u
u 3 u 4 u 2 u 5 u 6
1
l个独立 KVL方程
1 0 0 -1 -1 0 [ B ][ u ]= 0 1 0 1 0 1 0 0 1 0 -1 1
u1 u 2 u5 u3 u 2 u 6 0 u 4 u5 u 6
特点
①每一列只有两个非零元素，一个是+1，一个 是-1，Aa的每一列元素之和为零。 ②矩阵中任一行可以从其他n-1行中导出，即只 有n-1行是独立的。
返 回 上 页 下 页
结 1 Aa= 2 3 4
支
1 -1 0 1 0
2 3 -1 1 0 -1 0 0 1 0
4 0 -1 1 0
5 0 0 1 -1
i1 i 2 1 2 3 i 4 6 0 3 3 i 4 1 4 5 i 5 i 6
i i i i i i i i i
矩阵形式的KCL: [ A ][ i ]= 0
大学电路第十五章割集
②
矩阵形式的KCL： [ B ]T[ il ]=[ i ]
返 回 上 页 下 页
三. 割集矩阵[Q]
1. 独立割集矩阵：描述割集与支路关联关系的矩阵。 支路b
[Q]=
割 集 数
注意
每一行对应一个基本割集, 每一列对应一条支路.
(n-1)b
矩阵Q的每一个元素定义为：
qij
1 支路 j 在割集 i 中，且与割集方向一致； -1 支路 j 在割集 i中，且与割集方向相反； 0 支路 j 不在割集 i 中。
U U ...... Ub 1 2
T
支路电流列向量
T
U
支路电压列向量
T
U s1 U s2 ......U sb Us
电压源的电压列向量 电流源的电流列向量 阻抗矩阵
图的矩阵表示
图的矩阵表示是指用矩阵描述图的拓扑性质。 有三种矩阵形式： 结点 回路 割集 支路 支路 支路 关联矩阵 回路矩阵 割集矩阵
返 回
上 页
下 页
一. 关联矩阵A
1. 关联矩阵Aa:描述结点和支路的关联情况的矩阵。 n个结点b条支路的图用nb的矩阵描述： 支路b 结 点 n
注意
每一行对应一个结点， 每一列对应一条支路。
例 选 2、5、6为树，连支顺序为1、 3 、 4 。
支1 3 回 1 [Bf] = 2 3 1 0 0 1 0 0
②
４ 2６ 3 ③ ５ ２ 1 ④ 1
返 回 上 页 下 页
0 -1 -1 0 0 1 0 1 1 0 -1 1
Bl
Bt
= [1 Bt ]
3. 回路矩阵[B]的作用
①用回路矩阵[B]表示矩阵形式的KVL方程；