2021届高三第一次模拟考试卷 理科数学(一) 学生版

卜人入州八九几市潮王学校2021年第一次高考模拟统一考试数学试题〔理科〕第一卷〔一共60分〕一、选择题：本大题一一共12个小题,每一小题5分,一共60分.在每一小题给出的四个选项里面，只有一项为哪一项哪一项符合题目要求的.，集合，那么〔〕A. B. C. D.【答案】D【解析】【分析】可解出集合A，B，然后进展交集的运算即可．【详解】A＝{x|﹣2＜x＜4}，B＝{x|x＞﹣1}；∴A∩B＝{x|﹣1＜x＜4}．应选：D．【点睛】此题考察描绘法的定义，分式不等式的解法，对数函数的定义域，以及交集的运算，属于根底题．2.为复数，那么是为实数的〔〕A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】【分析】根据充分条件和必要条件的定义结合复数的运算进展判断即可．【详解】令z＝a+bi，∵〔a+bi〕•〔2﹣i〕＝2a+b+〔2b﹣a〕i，∴z•〔2﹣i〕为实数⇔a＝2b，又z＝2+i⇔，∵⇒a＝2b，a＝2b推不出，∴是a＝2b充分不必要条件，即z＝2+i是z•〔2﹣i〕为实数的充分不必要条件．应选：A．【点睛】此题主要考察充分条件和必要条件的判断，根据复数的运算是解决此题的关键．sin x＜0，且sin〔cos x〕＞0，那么角是〔〕A.第一象限角B.第二象限角C.第三象限角D.第四象限角【答案】D【解析】【分析】根据三角函数角的范围和符号之间的关系进展判断即可．【详解】∵﹣1≤cos x≤1，且sin〔cos x〕＞0，∴0＜cos x≤1，又sin x＜0，∴角x为第四象限角，应选：D．【点睛】此题主要考察三角函数中角的象限确实定，根据三角函数值的符号去判断象限是解决此题的关键．的左、右焦点为，以为圆心，为半径的圆与双曲线在第一象限的交点为，且轴，那么该双曲线的离心率为〔〕A. B. C. D.【答案】C【解析】【分析】利用条件列出a，b，c关系，然后求解离心率即可．【详解】由题意可得：2c，∴b2＝2ac，∴c2﹣2ac﹣a2＝0，即e2﹣2e﹣1＝0，解得e．应选：C．【点睛】此题考察双曲线的简单性质的应用，考察计算才能．5.执行如以下图所示的程序框图，输出S的值是〔〕A. B. C. D.【答案】A【解析】【分析】由中的程序可知：该程序的功能是利用循环构造计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【详解】模拟程序的运行，可得：当k＝1时，不满足k>6，执行循环体得S=0+cos=，k=2，不满足k>6，执行循环体得S=+cos=+，k=3，不满足k>6，执行循环体得S=++cos=+，k=4，不满足k>6，执行循环体得S=++cos=+，k=5，不满足k>6，执行循环体得S=+cos=，k=6，不满足k>6，执行循环体得S=0+cos=，k=7，满足k>6，退出循环，输出S=-1，应选：A．【点睛】此题考察了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是根底题．6.河图是上古时代HY传说中伏羲通过黄河中浮出龙马身上的图案，与自己的观察，画出的“八卦〞，而龙马身上的图案就叫做“河图〞。

2021年高三数学第一次模拟试卷（理科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

第Ⅰ卷（选择题共50分）参考公式：如果事件A、B互斥，那么P（A＋B）＝P（A）＋P（B）．如果事件A、B相互独立，那么P（A·B）＝P（A）·P（B）．柱体（棱柱、圆柱）的体积公式．其中S表示柱体的底面积，h表示柱体的高．一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，n（ C ）A．B．C．D．解：．2．设函数f（x）＝2－x，函数g（x）的图象与f（x）的图象关于直线y＝x对称，函数h（x）的图象由g（x）的图象向右平移1个单位得到，则h（x）为（ A ）A．－log2（x－1）B．－log2（x＋1）ABCDE C．log2（－x－1）D．log2（－x＋1）3．已知E是正方形ABCD的边AB的中点，将△ADE和△BCE分别沿DE、EC向上折起，使A、B两点重合于P，则二面角D－PE－C的大小是（ C ）A．B．C．60°D．90°4．已知F1、F2为椭圆的两个焦点，过F1作倾斜角为的弦AB（ B ）A．B．C．D．－15．设a、b、c是△ABC的三个内角A、B、C所对的边，且lgsin A、lgsin B、lgsin C成等差数列，那么直线与直线的位置关系是( D )A．平行B．垂直C．相交但不垂直D．重合6．在△ABC中，若a＝7，b＝8，，则最大角的余弦值为（ B ）A．B．C．D．－7．设随机变量ξ的分布列为P（ξ＝i）＝，i＝1，2，…，n，则常数k的值为（C ）A．1 B．C．D．8．在的展开式中，含x4项的系数为（ A ）A．－40 B．32 C．36 D．409．已知向量，，若正数k和t使与，垂直，则k的最小值是（ D ）A．0 B．1 C．－2 D．2解：，，，化简得，∴≥2．10．已知方程（a＞0）的两根为，，且，均在区间（－，）内，则的值为（B）A．B．－2 C．D．－2或解：由=(4a)2－4(3a+1)>0得a>1或a<－(舍去)tanα、tanβ是方程的两根tanα+tanβ=－4a<0, tanαtanβ=3a+1>0又α、β∈(－,) α、β∈(－,0), α+β∈(－,0)tan(α+β)=== =tan=-2或tan=(舍去)第Ⅱ卷（非选择题共100分）二、填空题：本大题共6小题，每小题4分，共24分．把答案填在题中横线上．11．若n是奇数，则＋＝______－2______．12．已知a、b为不垂直的异面直线，是一个平面，则a、b在上的射影有可能是①两条平行直线②两条互相垂直的直线③同一条直线④一条直线及其外一点在上面结论中，正确结论的编号是①②④．（写出所有正确结论的编号）13．函数的值域为_________（0，］____________．解：设，∴t的最小值为8．∴y的最大值为．14．已知圆与抛物线（p＞0）的准线相切，则p＝________．解：圆的方程化为：，∴切线为x＝－1或x＝－3．∴p＝2或6．15．从1，2，3，……，100这100个数中，任取两个数，使其和能被4 整除的取法（不计顺序）有______1225______种（用数字作答）．解：将这100 个数分成4组：①被4整除的A＝｛4，8，12……｝，②被4除余1的B＝｛5，9，13……｝，被4除余2的C＝｛6，10，14……｝，被4除余3的D＝｛7，11，15……｝．从A里取2个符合，从B、D各取一个符合，从C里取2个符合．∴共有＝1225．16．已知A＝｛x｜x2－2x－3＞0｝，B＝｛x｜x2＋ax＋b≤0｝，若A∪B＝R，A∩B＝（3，4］，则ab＝______12______．解：由A＝（－∞，－1）∪（3，＋∞），A∪B＝R，A∩B＝（3，4］，∴B＝［－1，4］，即－1，4是方程x2＋ax＋b＝0的两个根．∴a＝－3，b＝－4．三、解答题：本大题共6小题，共76分．解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）射击比赛中每人射4次，每次一发．规定全部不中得0分，只中一发得15分，中两发得30分，中三发得55分，中四发得100分．某人每次射击的命中率为，求他得分的数学期望．解：设ξ为此人命中目标的次数，则ξ服从二项分布．设η为此人的分数，则η为与ξ相关的随机变量，η的可能取值为0，15，30，55，100．∴P（η＝0）＝P（ξ＝0）＝；………………………………2分P（η＝15）＝P（ξ＝1）＝；……………………………4分P（η＝30）＝P（ξ＝2）＝；…………………………6分P（η＝55）＝P（ξ＝3）＝；……………………………8分P（η＝100）＝P（ξ＝4）＝；………………………………10分∴E η＝1824321601530551008181818181⨯+⨯+⨯+⨯+⨯＝≈51.85．…… 12分18．（本小题满分12分）如图，直三棱柱ABC －A 1B 1C 1的底面ABC 为等腰直角三角形，∠ACB ＝90°，AC ＝1，点C 到AB 1的距离为CE ＝，D 为AB 的中点． （Ⅰ）求证：AB 1⊥平面CED ；（Ⅱ）求异面直线AB 1与CD 之间的距离；（Ⅲ）求二面角B 1—AC —B 的平面角． 解：（Ⅰ）∵D 是AB 中点，△ABC 为等腰直角三角形，∠ABC ＝90°，∴CD ⊥AB 又AA 1⊥平面ABC ，∴CD ⊥AA 1 ．∴CD ⊥平面A 1B 1BA ．∴CD ⊥AB 1，又CE ⊥AB 1．∴AB 1⊥平面CDE ． ……………………………………………………… 4分 （Ⅱ）由CD ⊥平面A 1B 1BA ， ∴CD ⊥DE ．∵AB 1⊥平面CDE ， ∴DE ⊥AB 1 ．∴DE 是异面直线AB 1与CD 的公垂线段． …………………………… 6分 ∵CE ＝，AC ＝1， ∴CD ＝．∴． ……………………………………… 8分 （Ⅲ）连结B 1C ，易证B 1C ⊥AC ，又BC ⊥AC ，∴∠B 1CB 是二面角B 1—AC —B 的平面角． …………………………… 10分 在Rt △CEA 中，CE ＝，BC ＝AC ＝1， ∴∠B 1AC ＝60°． ∴， ∴． ∴ ．∴． ………………………………………………… 12分 19．（本小题满分12分） 函数的最小值为（a ∈R ）． （Ⅰ）求的表达式；（Ⅱ）若，求a 及此时的最大值． 解：（Ⅰ）＝，设＝，∈［－1，1］…2分A BC A 1 B 1 C 1E D①当＜－1，即a ＜－2时， ； ②当－1≤≤1，即－2≤a ≤2时， ； ③当＞1，即a ＞2时， ．综上可得：21,2()21,22214,2a ag a a a a a <-⎧⎪⎪=----≤≤⎨⎪->⎪⎩ ． ………………………… 8分 （Ⅱ）当a ＜－2时，；当a ＞2时，，得，矛盾； 当－2≤a ≤2时，，则a ＝－3（舍）或a ＝－1． … 10分 ∴当a ＝－1时，2211()2cos 2cos 12(cos )22f x x x x =++=++． 当cos x ＝1时，有最大值为5． …………………………………………… 12分 20．（本小题满分12分）已知函数在区间（－2，1）内当x ＝－1时取得极小值，x ＝时取得极大值． （Ⅰ）求函数的解析式；（Ⅱ）求函数在x ＝－2时的对应点的切线方程； （Ⅲ）求函数在［－2，1］上的最大值与最小值． 解：（Ⅰ）； ……………………………………… 2分∵当x ＝－1时取得极小值，x ＝时取得极大值； ∴－1，是方程的两个根．∴． …………………………………………………… 4分 ∴． ………………………………………… 5分（Ⅱ）当x ＝－2时，，即点（－2，2）在曲线上， ………… 7分又切线的斜率为 ， ………………………………… 9分 ∴切线方程为． ……………………………………… 10分 （Ⅲ）∵32221(2)2,(1),(),(1)23272f f f f -=-=-==， ∴在［－2，1］上的最大值为2，最小值为－． ………… 12分21．（本小题满分14分）已知双曲线C 1的中心在原点，实轴在x 轴上．实轴长与虚轴长的积是2，且一焦点到其相应准线的距离为． （Ⅰ）求双曲线C 1的方程； （Ⅱ）求以双曲线C 1的实轴与虚轴分别为短轴和长轴的椭圆C 2的方程； （Ⅲ）求证：当与直线平行的直线m 被椭圆C 2截取的弦最长时，该直线m 被双曲线C 1截取的弦最短，并求该最短弦长． 解：（Ⅰ） ，设F （c ，0），准线， ，……………………………………………………………2分 ∴ ，即 ．……………………………………………4分 （Ⅱ）． ………………………………………………………6分（Ⅲ）将直线与椭圆方程联立得0125142222=-++⇒⎩⎨⎧=++=m mx x y x m x y ， 则，弦长5102]2016[252]544254[22221≤+-=--=m m m T ． 当且仅当m ＝0时取等号．……………………………………………………9分将直线与双曲线方程联立得0123142222=---⇒⎩⎨⎧=-+=m mx x y x mx y ， 则．弦长362]1216[92]34494[22222≥+=++=m m m T ， 当且仅当m ＝0时取等号 ．………………………………………………12分综上当m ＝0时直线被椭圆C 2截取的弦最长同时，该直线被双曲线C 1截取的弦最短，最短弦长为． ……………………………………………………………14分 22．（本小题满分14分）已知点B 1（1，y 1），B 2（2，y 2），…，B n （n ，y n ），…（n ∈N *）顺次为直线y ＝＋上的点，点A 1（x 1，0），A 2（x 2，0），…，A n （x n ，0）顺次为x 轴上的点，其中x 1＝a （0＜a ＜1）．对于任意n ∈N *，点A n 、B n 、A n +1构成以B n 为顶点的等腰三角形．（Ⅰ）求数列｛y n ｝的通项公式，并证明它为等差数列； （Ⅱ）求证：x n +2－x n 是常数，并求数列｛x n ｝的通项公式；（Ⅲ）上述等腰△A n B n A n +1中是否可能存在直角三角形，若可能，求出此时a 的值；若不可能，请说明理由．解：（Ⅰ）y n＝n+，y n+1－y n＝，∴数列｛y n｝是等差数列，…………………………………………………………4分（Ⅱ）由题意得，＝n，∴x n＋x n+1＝2n，①x n+1＋x n+2＝2（n＋1），②①、②相减，得x n+2－x n＝2，∴x1，x3，x5，…，x2n－1，…成等差数列；x2，x4，x6，…，x2n，…成等差数列，…………………………………………8分∴x2n－1＝x1＋2（n－1）＝2n＋a－2，x2n＝x2＋（n－1）·2＝（2－a）＋（n－1）·2＝2n－a，∴x n＝……………………………………………………10分（Ⅲ）当n为奇数时，A n（n＋a－1，0），A n+1（n＋1－a，0）所以｜A n A n+1｜＝2（1－a）；当n为偶数时，A n（n－a，0），A n+1（n＋a，0），所以｜A n A n－1｜＝2a，作B n C n⊥x轴于C n ，则｜B n C n｜＝n＋．要使等腰三角形A n B n A n+1为直角三角形，必须且只须｜A n A n+1｜＝2｜B n C n｜．…12分所以，当n为奇数时，有2（1－a）＝2（n＋），即12a＝11－3n，当n＝1时，a＝；当n＝3时，a＝；当n≥5时，方程12a＝11－3n无解．当n为偶数时，12a＝3n＋1，同理可求得a＝．综上，当a＝，或a＝或a＝时，存在直角三角形．………………………14分36656 8F30 輰H! \?*20305 4F51 佑H23515 5BDB 寛22537 5809 堉38889 97E9 韩28873 70C9 烉34508 86CC 蛌。

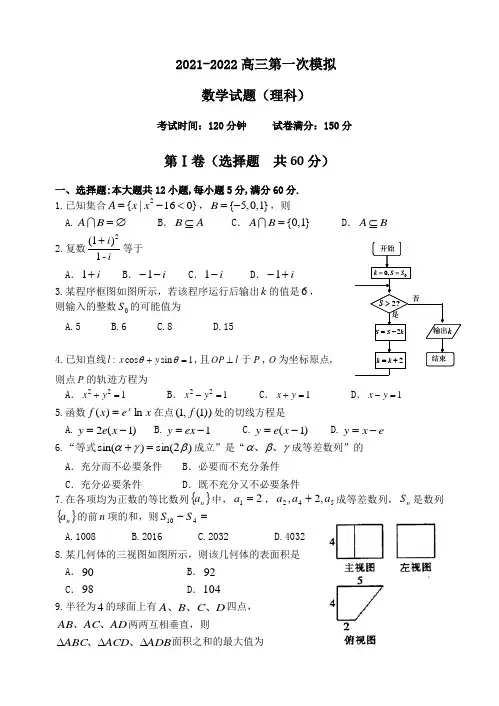
开始结束输出是否,0S S k ==?2>S kS S 2-=2+=k k k2021-2022高三第一次模拟数学试题（理科）考试时间：120分钟 试卷满分：150分第Ⅰ卷（选择题 共60分）一、选择题:本大题共12小题,每小题5分,满分60分. 1.已知集合2{|160}A x x =-<，{5,0,1}B =-，则 A.AB =∅ B ．B A ⊆C ．{0,1}A B =D ．A B ⊆2.复数ii -1)1(2+等于A ．i +1B ．i --1C ．i -1D ．i +-1 3.某程序框图如图所示，若该程序运行后输出k 的值是6， 则输入的整数0S 的可能值为A.5B.6C.8D.154.已知直线1sin cos :=+θθy x l ,且l OP ⊥于P ,O 为坐标原点, 则点P 的轨迹方程为A ．122=+y xB ．122=-y xC ．1=+y xD ．1=-y x5.函数x e x f xln )(=在点))1(,1(f 处的切线方程是A.)1(2-=x e yB.1-=ex yC.)1(-=x e yD.e x y -= 6.“等式)2sin()sin(βγα=+成立”是“γβα、、成等差数列”的 A ．充分而不必要条件 B ．必要而不充分条件C ．充分必要条件D ．既不充分又不必要条件7.在各项均为正数的等比数列{}n a 中，21=a ，542,2,a a a +成等差数列，n S 是数列{}n a 的前n 项的和，则=-410S SA.1008B.2016C.2032D.4032 8.某几何体的三视图如图所示，则该几何体的表面积是 A ．90 B ．92 C ．98 D ．104 9.半径为4的球面上有D C B A 、、、四点，AD AC AB 、、两两互相垂直，则ADB ACD ABC ∆∆∆、、面积之和的最大值为A ．8B ．16C ．32 D.6410.设等差数列{}n a 的前n 项和为n S ，若0,0109<>S S ，则993322122,2,2aa a a ，中最大的是A ．12a B ．552aC ．662aD ．992a11.已知函数)()(()(321x x x x x x x f ---=）（其中321x x x <<），)12sin(3)(++=x x x g ，且函数)(x f 的两个极值点为）（，βαβα<．设2,23221xx x x +=+=μλ，则A ．)()()()(μβλαg g g g <<<B ．)()()()(μβαλg g g g <<<C ．)()()()(βμαλg g g g <<<D ．)()()()(βμλαg g g g <<<12.设双曲线)0,0(12222>>=-b a by a x 的右焦点为F ，过点F 作x 轴的垂线交两渐近线于点B A ,两点，且与双曲线在第一象限的交点为P ，设O 为坐标原点，若)R OB OA OP ∈+=μλμλ，（，8522=+μλ，则双曲线的离心率为（ ）A ．332B ．553C ．223D ．89第Ⅱ卷（非选择题共90分）二.填空题：本大题共4小题，每小题5分．13.若n S 是数列{}n a 的前n 项的和，且762++-=n n S n ，则数列{}n a 的最大项的值为___________.14.设221(32)=⎰-a x x dx ,则二项式261()-ax x展开式中的第4项为___________.15. 已知正方形ABCD 的边长为2，点E 为AB 的中点．以A 为圆心，AE 为半径，作弧交AD 于点F ，若P 为劣弧EF 上的动点，则PC PD 的最小值为___________.16.已知函数xx a x f 22)(1+=+在]3,21[-上单调递增，则实数a 的取值范围_________.三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17．（本题满分12分）已知函数))(12(sin 2)62sin(3)(2R x x x x f ∈-+-=ππ（I ）求函数)(x f 的最小正周期；（Ⅱ）求使函数)(x f 取得最大值的x 的集合．18.（本小题满分12分）如图，在四棱锥ABCD P -中，底面ABCD 是菱形，︒=∠60DAB ，,1,==⊥AD PD ABCD PD 平面 点,E F 分别为AB 和PD 中点.(Ⅰ)求证：直线PEC AF 平面//； (Ⅱ)求PC 与平面PAB 所成角的正弦值.19.（本小题满分12分）某网站用“10分制”调查一社区人们的治安满意度．现从调查人群中随机抽取16名，以下茎叶图记录了他们的治安满意度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）．（I ）若治安满意度不低于9.5分，则称该人的治安满意度为“极安全”，求从这16人中随机选取3人，至多有1人是“极安全”的概率； （II ）以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选3人，记X 表示抽到“极安全”的人数，求X 的分布列及数学期望．20.（本小题满分12分）如图，已知直线1:+=my x l 过椭圆1:2222=+by a x C 的右焦点F ，抛物线：y x 342=的焦点为椭圆C 的上顶点，且直线l 交椭圆C 于B A 、两点，点B F A 、、在直线4=x g ：上的射影依次为点E K D 、、．FE BDCAP（Ⅰ）求椭圆C 的方程；（Ⅱ）若直线l 交y 轴于点M ，且BF MB AF MA 21λλ==，，当m 变化时，探求21λλ+的值是否为定值？若是，求出21λλ+的值，否则，说明理由.21.（本小题满分12分）设x m =和x n =是函数21()ln (2)2f x x x a x =+-+的两个极值点,其中 m n <,a R ∈.(Ⅰ) 求()()f m f n +的取值范围; (Ⅱ) 若12a e e≥+-,求()()f n f m -的最大值.22.（本小题满分10分）选修4－1：几何证明选讲 如图所示，已知⊙O 的半径长为4，两条弦BD AC ,相交于点E ，若34=BD ，DE BE >，E为AC 的中点，AE AB 2=.(Ⅰ) 求证：AC 平分BCD ∠； (Ⅱ)求ADB ∠的度数.23．（本小题满分10分）选修4－4：坐标系与参数方程已知曲线1C 的参数方程为⎩⎨⎧==θθsin 3cos 2y x （其中θ为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线2C 的极坐标方程为01sin cos =+-θρθρ.(Ⅰ) 分别写出曲线1C 与曲线2C 的普通方程；(Ⅱ)若曲线1C 与曲线2C 交于B A ,两点，求线段AB 的长.24.（本小题满分10分） 选修4－5：不等式选讲 已知函数|12|)(-=x x f . (Ⅰ)求不等式2)(<x f 的解集；(Ⅱ)若函数)1()()(-+=x f x f x g 的最小值为a ，且)0,0(>>=+n m a n m ，求nn m m 1222+++的最小值. .ABCDEO2021-2022高三第一次模拟数学（理科）答案一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项符合题目要求.1.C2.D3.C4.A5.C6.B7.B8.D9.C 10.B 11.D 12.A 二.填空题：本大题共4小题，每小题5分．13.12 14.31280-x 15.525- 16.[﹣1，1]三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17.(Ⅰ) f(x)=3sin(2x －π6)+1－cos2(x －π12)= 2[32sin2(x －π12)－12 cos2(x －π12)]+1 =2sin[2(x －π12)－π6]+1= 2sin(2x －π3) +1∴ T=2π2=π(Ⅱ)当f(x)取最大值时, sin(2x －π3)=1,有 2x －π3 =2k π+π2即x=k π+ 5π12(k ∈Z)∴所求x 的集合为{x ∈R|x= k π+ 5π12 , (k ∈Z)}.18.解：(Ⅰ)证明：作FM ∥CD 交PC 于M . ∵点F 为PD 中点，∴CD FM 21=. …………2分 ∵21=k ，∴FM AB AE ==21， ∴AEMF 为平行四边形，∴AF ∥EM ， ……4分 ∵AF PEC EM PEC ⊄⊂平面，平面， ∴直线AF //平面PEC . ……………6分 (Ⅱ)60DAB ∠=，DE DC ∴⊥.MFBACDP如图所示，建立坐标系，则P (0,0,1),C (0,1,0),E (32,0,0),A (32，12-，0)，31(,,0)22B ， ∴31,,122AP ⎛⎫=- ⎪ ⎪⎝⎭，()0,1,0AB =. …8分设平面PAB 的一个法向量为(),,n x y z =.∵0n AB ⋅=，0n AP ⋅=，∴⎪⎩⎪⎨⎧==++-02123y z y x ，取1x =，则32z =， ∴平面PAB 的一个法向量为3(1,0,)2n =. …………………………10分 设向量n PC θ与所成角为，∵(0,1,1)PC =-，∴3422cos 14724n PC n PCθ-⋅===-⨯， ∴P C 平面PAB 所成角的正弦值为4214. .…………………………12分 19.FEBACDyz x P20.解：（Ⅰ）易知椭圆右焦点F（1，0），∴c=1，抛物线的焦点坐标，∴∴b2=3 ∴a2=b2+c2=4∴椭圆C的方程（Ⅱ）易知m≠0，且l与y轴交于，设直线l交椭圆于A（x1，y1），B（x2，y2）由∴△=（6m）2+36（3m2+4）=144（m2+1）＞0∴又由∴同理∴∵∴所以，当m变化时，λ1+λ2的值为定值；（Ⅲ）证明：由（Ⅱ）知A（x1，y1），B（x2，y2），∴D（4，y1），E（4，y2）方法1）∵当时，==∴点在直线l AE上，同理可证，点也在直线l BD上；∴当m变化时，AE与BD相交于定点方法2）∵=∴k EN =k AN ∴A 、N 、E 三点共线， 同理可得B 、N 、D 也三点共线； ∴当m 变化时，AE 与BD 相交于定点．解:函数()f x 的定义域为(0,)+∞,21(2)1()(2)x a x f x x a x x-++'=+-+=.依题意,方程2(2)10x a x -++=有两个不等的正根m ,n (其中m n <).故2(2)40020a a a ⎧+->⇒>⎨+>⎩, 并且 2,1m n a mn +=+=.所以,221()()ln ()(2)()2f m f n mn m n a m n +=++-++2211[()2](2)()(2)1322m n mn a m n a =+--++=-+-<- 故()()f m f n +的取值范围是(,3)-∞-(Ⅱ)解:当12a e e≥+-时,21(2)2a e e +≥++.若设(1)nt t m =>,则222()11(2)()22m n a m n t e mn t e ++=+==++≥++.于是有 111()(1)0t e t e t e t e te +≥+⇒--≥⇒≥222211()()ln ()(2)()ln ()()()22n n f n f m n m a n m n m n m n m m m -=+--+-=+--+-2222111ln ()ln ()ln ()22211ln ()2n n n m n n m n m m m mn m m n t t t-=--=-=--=-- 构造函数11()ln ()2g t t t t =--(其中t e ≥),则222111(1)()(1)022t g t t t t-'=-+=-<. 所以()g t 在[,)e +∞上单调递减,1()()122e g t g e e≤=-+.故()()f n f m -的最大值是1122e e-+22.（本小题满分10分）解：（1）由E 为AC 的中点，AE AB 2=得AB ACAE AB ==2 又CAB BAE ∠=∠ ABE ∆∴∽ACB ∆ ACB ABE ∠=∠∴ 又ABE ACD ∠=∠ ACB ACD ∠=∠∴故AC 平分BCD ∠………………5分（2）连接OA ，由点A 是弧BAD 的中点，则BD OA ⊥，设垂足为点F ，则点F 为弦BD 的中点，32=BF 连接OB ，则2)32(42222=-=-=BF OB OF ，224=-=-=OF OA AF ，60,2142cos =∠===∠∴AOB OB OF AOB 3021=∠=∠∴AOB ADB ………………10分23.（本小题满分10分）解：（1）曲线1C 134:22=+y x ，………………2分 曲线2C ：01=+-y x ………………4分（2）联立⎪⎩⎪⎨⎧=+=+-1340122y x y x ，得08872=-+x x ， 设),(),,(2211y x B y x A ，则78,782121-=-=+x x x x 于是7244)(2112122121=-+⋅=-+=x x x x x x AB . 故线段AB 的长为724.………………10分 24.（本小题满分10分） 解：（1）由2)(<x f 知2|12|<-x ，于是2122<-<-x ，解得2321<<-x ，故不等式2)(<x f 的解集为⎪⎭⎫ ⎝⎛-23,21；……………………3分 （2）由条件得2|)32(12||32||12|)(=---≥-+-=x x x x x g ，当且仅当⎥⎦⎤⎢⎣⎡∈23,21x 时，其最小值2=a ，即2=+n m …………………6分又()()223212*********+≥⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛++=+n m m n n m n m n m ，…………8分 所以n n m m 1222+++()22321212++≥+++=n m n m 2227+=， 故nn m m 1222+++的最小值为2227+，此时222,224-=-=n m .……10分。

[新高考]2021届新高三第一次模拟测试理科数学 （一）注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．若复数的实部与虚部分别为，，则（ ）A ．B ．C ．D ．2．设集合，，则（ ）A ．B ．C ．D ．3．若函数的图象经过抛物线的焦点，则（ ）A ．B ．C ．D ．4．已知两个单位向量，的夹角为，则下列向量是单位向量的是（ ）A ．B ．C ．D ．5．的内角，，的对边分别为，，，已知，则（ ）A ．B ．C ．D ．6．设，满足约束条件，则的取值范围为（ ）A ．B ．C ．D ．7．设是一个各位数字都不是且没有重复数字的两位数，将组成的个数字按从小到大排成的两位数记为，按从大到小排成的两位数记为(例如，则，)，执行如图所示的程序框图，若输入的，则输出的（ ）A ．B ．C ．D ．8．已知，则曲线在点处的切线方程为（ ）A ．B ．C ．D ．9．（ ）A ．B ．C ．D ．10．《镜花缘》是清代文人李汝珍创作的长篇小说，书中有这样一个情节:一座楼阁到处挂满了五彩缤纷的大小灯球，灯球有两种，一种是大灯下缀个小灯，另一种是大灯下缀个小灯，大灯共个，小灯共个若在这座楼阁的灯球中，随机选取两个灯球，则至少有一个灯球是大灯下缀个小灯的概率为（ ）A ．B ．C ．D ．此卷只装订不密封班级 姓名 准考证号 考场号 座位号11．在正四棱柱中，为侧棱上一点，，，且异面直线与所成角的余弦值为，则（）A．B．C．D．12．设是双曲线的右焦点，为坐标原点过作的一条渐近线的垂线，垂足为，若的内切圆与轴切于点，且，则的离心率为（）A．B．C．D．第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．13．的展开式中的系数为．14．已知函数，若，，则．15．如图，一几何体由一个圆锥与半球组合而成，且圆锥的体积与半球的体积相等，则该圆锥的母线与底面所成角的正切值为．16．已知函数是上的奇函数，函数，若对恒成立，则的取值范围为．三、解答题：本大题共6个大题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（12分）设为数列的前项和，已知，，其中是不为的常数，且，，成等比数列．（1）求的通项公式；（2）若，求．18．（12分）下图是某超市一周百事可乐与可口可乐的销量(单位：罐)的雷达图．（1）分别计算一周百事可乐与可口可乐的销量的平均数，从计算结果看，哪种可乐的销量更好；（2）从周一开始的连续三周该超市推出买一罐可乐(仅限百事可乐或可口可乐)获得一次抽奖机会的活动，中奖率为，中奖可获得元的红包，以雷达图中一周的销量代替每周的销量．①活动期间，一位顾客买了罐百事可乐，他恰好获得元红包的概率；②在这连续三周的活动中，求该超市需要投入红包总金额的数学期望．19．（12分）在直角坐标系中，已知，，且，记动点的轨迹为．（1）求的方程；（2）若过点的直线与交于，两点，且，求直线的斜率．20．（12分）如图，在四面体中，，平面平面，，且．（1）证明：平面；（2）设为棱的中点，当四面体的体积取得最大值时，求二面角的余弦值．21．（12分）已知函数．（1）讨论的单调性；（2）若在上存在最大值，证明：．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．22．（10分）【选修4-4：坐标系与参数方程】在极坐标系中，曲线的极坐标方程为，曲线与曲线关于极点对称．（1）以极点为坐标原点，极轴为轴的正半轴建立直角坐标系，求曲线的直角坐标方程；（2）设为曲线上一动点，记到直线与直线的距离分别为，，求的最小值．23．（10分）【选修4-5：不等式选讲】已知函数，且不等式的解集为．（1）求，；（2）若，证明：．理科数学（一）答案注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2021年高三模拟试卷一数学理试题一、选择题：本大题共8个小题；每小题5分，共40分．在每小题给出的四个选项中，有且只有一项是符合题目要求的1．（5分）已知集合A={（x，y）|x+y=0，x，y∈R}，B={（x，y）|x﹣y=0，x，y∈R}，则集合A∩B的元素个数是（）A．0B．1C．2D．3考点：交集及其运算．专题：数形结合．分析：集合的交集问题转化为直线x+y=0和x﹣y=0的交点问题，作出直线x+y=0和x﹣y=0，观察它们的图象的交点情况即可．解答：解：集合的交集问题转化为直线x+y=0和x﹣y=0的交点问题，作出直线x+y=0和x﹣y=0，观察它们的图象的交点只有一个．故选B．点评：本题主要考查交集及其运算，属于基础题．2．（5分）（xx•山东）在△ABC中，角A、B、C的对边分别为a、b、c，已知A=，a=，b=1，则c=（）A．1B．2C．﹣1 D．考点：正弦定理的应用；余弦定理的应用．专题：计算题．分析：方法一：可根据余弦定理直接求，但要注意边一定大于0；方法二：可根据正弦定理求出sinB，进而求出c，要注意判断角的范围．解答：解：解法一：（余弦定理）由a2=b2+c2﹣2bccosA得：3=1+c2﹣2c×1×cos=1+c2﹣c，∴c2﹣c﹣2=0，∴c=2或﹣1（舍）．解法二：（正弦定理）由=，得：=，∴sinB=，∵b＜a，∴B=，从而C=，∴c2=a2+b2=4，∴c=2．点评：本题主要考查正弦定理和余弦定理的应用．在解三角形时一般就用这两个定理，要熟练掌握．3．（5分）设随机变量ξ服从标准正态分布N（0，1），在某项测量中，已知ξ在（﹣∞，﹣1.96]内取值的概率为0.025，则P（|ξ|≤1.29═（）A．0.025 B．0.050 C．0.950 D．0.975考点：正态分布曲线的特点及曲线所表示的意义．专题：概率与统计．分析：解法一：根据变量符合正态分布，且对称轴是x=0，得到P（|ξ|＜1.96）=P（﹣1.96＜ξ＜1.96），应用所给的ξ在（﹣∞，﹣1.96]内取值的概率为0.025，条件得到结果，解法二：本题也可以这样解根据曲线的对称轴是直线x=0，得到一系列对称关系，代入条件得到结果．解答：解：解法一：∵ξ～N（0，1）∴P（|ξ|＜1.96）=P（﹣1.96＜ξ＜1.96）=Φ（1.96）﹣Φ（﹣1.96）=1﹣2Φ（﹣1.96）=0.950解法二：因为曲线的对称轴是直线x=0，所以由图知P（ξ＞1.96）=P（ξ≤﹣1.96）=Φ（﹣1.96）=0.025 ∴P（|ξ|＜1.96）=1﹣0.25﹣0.25=0.950故选C．点评：本题考查正态曲线的特点及曲线所表示的意义，主要考查对称性，是一个数形结合的问题，是一个遇到一定要得分数的题目．4．（5分）（xx•山东）已知圆的方程为x2+y2﹣6x﹣8y=0，设该圆过点（3，5）的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积为（）A．10 B．20 C．30 D．40考点：直线与圆相交的性质．专题：压轴题．分析：根据题意可知，过（3，5）的最长弦为直径，最短弦为过（3，5）且垂直于该直径的弦，分别求出两个量，然后利用对角线垂直的四边形的面积等于对角线乘积的一半求出即可．解答：解：圆的标准方程为（x﹣3）2+（y﹣4）2=52，由题意得最长的弦|AC|=2×5=10，根据勾股定理得最短的弦|BD|=2=4，且AC⊥BD，四边形ABCD的面积S=|AC|•|BD|=×10×4=20．故选B点评：考查学生灵活运用垂径定理解决数学问题的能力，掌握对角线垂直的四边形的面积计算方法为对角线乘积的一半．5．（5分）（xx•广州二模）现有4种不同颜色要对如图所示的四个部分进行着色，要求有公共边界的两块不能用同一种颜色，则不同的着色方法共有（）A．24种B．30种C．36种D．48种考点：计数原理的应用．专题：计算题．分析：需要先给最上面一块着色，有4种结果，再给中间左边一块着色，有3种结果，再给中间右边一块着色有2种结果，左后给下面一块着色，有2种结果，相乘得到结果．解答：解：由题意知本题是一个分步计数问题，需要先给最上面一块着色，有4种结果，再给中间左边一块着色，有3种结果，再给中间右边一块着色有2种结果，左后给下面一块着色，有2种结果，根据分步计数原理知共有4×3×2×2=48种结果，故选D．点评：本题考查分步计数原理，这种问题解题的关键是看清题目中出现的结果，几个环节所包含的事件数在计算时要做到不重不漏．6．（5分）（xx•天河区一模）如果一个水平放置的图形的斜二测直观图是一个底面为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是（）A．2+ B．C．D．1+考点：斜二测法画直观图．专题：计算题；作图题．分析：原图为直角梯形，上底为1，高为2，下底为1+，利用梯形面积公式求解即可．也可利用原图和直观图的面积关系求解．解答：解：恢复后的原图形为一直角梯形，上底为1，高为2，下底为1+，S=（1++1）×2=2+．故选A点评：本题考查水平放置的平面图形的直观图斜二测画法，属基础知识的考查．7．（5分）设函数f（x）=x|x|+bx+c（x∈R）给出下列4个命题①当b=0时，f（x）=0只有一个实数根；②当c=0时，y=f（x）是偶函数；③函数y=f（x）的图象关于点（0，c）对称；④当b≠0，c≠0时，方程f（x）=0有两个不等实数根．上述命题中，所有正确命题的个数是（）A．0B．1C．2D．3考点：命题的真假判断与应用．专题：压轴题；阅读型．分析：对于①当b=0时，f（x）=x|x|+c=0，因y=x|x|与y=﹣c只有一个交点，故可判断；②当c=0时，f（x）=x|x|+bx，可判断函数为奇函数；③y=f（x）的图象可由奇函数f（x）=x|x|+bx向上或向下移|c|，y=f（x）的图象与y轴交点为（0，c），故函数y=f （x）的图象关于点（0，c）对称，故可判断；④当b≠0，c≠0时，f（x）=x|x|+x+1只有一个实数根．解答：解：①当b=0时，f（x）=x|x|+c=0，因y=x|x|与y=﹣c只有一个交点，故①正确；②当c=0时，f（x）=x|x|+bx，f（﹣x）=﹣f（x），故y=f（x）是奇函数；③y=f（x）的图象可由奇函数f（x）=x|x|+bx向上或向下移|c|，y=f（x）的图象与y 轴交点为（0，c），故函数y=f（x）的图象关于点（0，c）对称，故③正确；④当b≠0，c≠0时，f（x）=x|x|+x+1只有一个实数根．故选C．点评：本题的考点是命题的真假判断与应用．主要考查函数性质的判断，关键是正确理解函数．8．（5分）（xx•东莞市二模）如图，已知A（4，0）、B（0，4），从点P（2，0）射出的光线经直线AB反向后再射到直线OB上，最后经直线OB反射后又回到P点，则光线所经过的路程是（）A．2B．6C．3D．2考点：与直线关于点、直线对称的直线方程．专题：压轴题；数形结合；转化思想．分析：设点P关于y轴的对称点P′，点P关于直线AB：x+y﹣4=0的对称点P″，由对称特点可求P′和P″的坐标，在利用入射光线上的点关于反射轴的对称点在反射光线所在的直线上，光线所经过的路程|P′P″|．解答：解：点P关于y轴的对称点P′坐标是（﹣2，0），设点P关于直线AB：x+y﹣4=0的对称点P″（a，b）∴⇒∴光线所经过的路程|P′P″|=2．故选A．点评：本题考查求一个点关于直线的对称点的方法（利用垂直及中点在轴上），入射光线上的点关于反射轴的对称点在反射光线所在的直线上，把光线走过的路程转化为|P′P″|的长度．二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．本大题分为必做题和选做题两部分．（一）必做题：第9、10、11、12、13题为必做题，每道试题考生都必须作答．（二）选做题：第14、15题为选做题，考生只能选做一题，两题全答的，只计算前一题的得分．9．（5分）利用计算机计算，某同学编写的右边程序语句中，①处应填k＞99（或k≥100）．考点：伪代码．专题：等差数列与等比数列．分析：计算，利用直到型循环结构，最后计算的是，由此可得结论．解答：解：计算，利用直到型循环结构，最后计算的是∴①处应填k＞99（或k≥100）故答案为：k＞99（或k≥100）点评：本题考查伪代码，考查学生分析解决问题的能力，属于基础题．10．（5分）．考点：定积分的简单应用．专题：计算题．分析：由于，第一个积分根据积分所表示的几何意义是以（0，0）为圆心，1为半径第一、二象限内圆弧与坐标轴围成的面积，只需求出圆的面积乘以二分之一即可，第二个积分利用公式进行计算即可．解答：解：由于，表示的几何意义是：以（0，0）为圆心，1为半径第一，二象限内圆弧与坐标轴围成的面积=π×1=，又==0，∴原式=．故答案为：．点评：本题主要考查了定积分，定积分运算是求导的逆运算，解题的关键是求原函数，也可利用几何意义进行求解，属于基础题．11．（5分）（xx•南京一模）如图，在正方形ABCD中，已知AB=2，M为BC的中点，若N为正方形内（含边界）任意一点，则的最大值是6．考点：平面向量数量积的运算．专题：计算题；压轴题；数形结合．分析：在平面内建立合适的坐标系，将向量的数量积用坐标表示，再利用线性规划解决问题．解答：解：以A为坐标原点，以AD方向为x轴正方向，以AB方向为y轴负方向建立坐标系，则=（1，﹣2）设N点坐标为（x，y），则=（x，y），则0≤x≤2，﹣2≤y≤0 令Z==x﹣2y，将A，B，C，D四点坐标依次代入得：Z A=0，Z B=4，Z C=6，Z D=2故Z=的最大值为6故答案为：6点评：向量的主要功能就是数形结合，将几何问题转化为代数问题，但关键是建立合适的坐标系，将向量用坐标表示，再将数量积运算转化为方程或函数问题．12．（5分）在平面内有n（n∈N+，n≥3）条直线，其中任何两条不平行，任何三条不过同一点，若这n条直线把平面分成f（n）个平面区域．则f（5）的值是16；f（n）﹣f（n﹣1）=n﹣1．考点：进行简单的合情推理．分析：先求出几个特殊的值，再分析前k条直线与第k+1条直线，把平面分成的区域之间的关系，归纳出关系式f（k+1）﹣f（k）=k+1，再根据数列求和求出f（n）的关系式，问题解决．解答：解：一条直线（k=1）把平面分成了2部分，记为f（1）=2，f（2）=4，f（3）=7，…设前k条直线把平面分成了f（k）部分，第k+1条直线与原有的k条直线有k个交点，这k个交点将第k+1条直线分为k+1段，这k+1段将平面上原来的f（k）部分的每一部分分成了2个部分，共2（k+1）部分，相当于增加了k+1个部分，∴第k+1条直线将平面分成了f（k+1）部分，则f（k+1）﹣f（k）=k+1，令k=1，2，3，…．n得f（2）﹣f（1）=2，f（3）﹣f（2）=3，…，f（n）﹣f（n=1）=n，把这n﹣1个等式累加，得f（n）=2+部分．所以f（5）=16，f（n）﹣f（n﹣1）=n﹣1故答案为：16，n﹣1点评：本题主要考查了归纳推理，以及数列递推式，属于基础题．所谓归纳推理，就是从个别性知识推出一般性结论的推理．13．（5分）有以下四个命题：①两直线m，n与平面α所成的角相等的充要条件是m∥n；②若p：∀x∈R，sinx≤1，则￢P：∃x∈R，sinx＞1；③不等式10x＞x2在（0，+∞）上恒成立；④设有四个函数，其中在R上是增函数的函数有3个．其中真命题的序号是②③．（漏填、多填或错填均不得分）考点：全称命题；命题的真假判断与应用．专题：阅读型．分析：①通过举特殊情形，m，n与平面α均平行，且相交时，判断错误②根据特称命题的否定判断③根据指数函数和幂函数的增长快慢判断④根据幂函数的图象与性质判断解答：解：①当两直线m，n与平面α均平行，且相交时，所成的角相等，均为0度，显然错误②若p：∀x∈R，sinx≤1，则￢P：∃x∈R，sinx＞1 正确③根据特称命题的否定判断，可知③正确④根据幂函数的图象与性质，只有R上是增函数故答案为：②③点评：本题考查命题的真假，用到了线面角、函数的图象与性质等知识．14．（5分）（xx•惠州一模）在极坐标系中，过点作圆ρ=4sinθ的切线，则切线的极坐标方程是ρcosθ=2．考点：极坐标系．专题：计算题；转化思想．分析：求出极坐标的直角坐标，极坐标方程的直角坐标方程，然后求出切线方程，转化为极坐标方程即可．解答：解：的直角坐标为：（2，2），圆ρ=4sinθ的直角坐标方程为：x2+y2﹣4y=0；显然，圆心坐标（0，2），半径为：2；所以过（2，2）与圆相切的直线方程为：x=2，所以切线的极坐标方程是：ρcosθ=2 故答案为：ρcosθ=2点评：本题是基础题，考查极坐标与直角坐标方程的互化，考查计算能力，转化思想．15．（xx•茂名一模）如图，⊙O的直径AB=6cm，P是AB延长线上的一点，过p点作⊙O 的切线，切点为C，连接AC，若∠CPA=30°，PC=cm．考点：圆的切线的性质定理的证明．专题：计算题；压轴题．分析：在圆中线段利用由切线定理求得∠OCP=Rt∠，进而利用直角三角形PCO中的线段，结合解直角三角形求得PC即可．解答：解：连接OC，PC是⊙O的切线，∴∠OCP=90°∵∠CPA=30°，OC==3，∴tan30°=，即PC=．故填：．点评：此题考查的是直角三角形的性质、与圆有关的比例线段以及切线定理，属于基础题．三、解答题:本大题6小题，满分80分，解答须写出文字说明、证明过程和演算步骤16．（12分）已知函数f（x）=Asin（ωx+ϕ）（x∈R，A＞0，ω＞0，|ϕ|＜）的部分图象如图所示，（Ⅰ）试确定f（x）的解析式；（Ⅱ）若=，求cos（﹣α）的值．考点：由y=Asin（ωx+φ）的部分图象确定其解析式；三角函数的恒等变换及化简求值．专题：计算题；图表型．分析：（Ⅰ）先根据图象得到A=2，=﹣=，求出ω；再把点P（，2）代入结合|ϕ|＜即可求出φ，进而得到f（x）的解析式；（Ⅱ）先根据f（）=，得到sin（+）=；再结合cos（﹣a）=cos[π﹣2（+）]=﹣cos2（+）以及二倍角的余弦公式即可解题．解答：解：（Ⅰ）由图象可知A=2，=﹣=，∴T=2，ω==π将点P（，2）代入y=2sin（ωx+ϕ），得sin（+ϕ）=1，又|ϕ|＜，所以ϕ=．故所求解析式为f（x）=2sin（πx+）（x∈R）6分（Ⅱ）∵f（）=，∴2sin（+）=，即，sin（+）=∴cos（﹣a）=cos[π﹣2（+）]=﹣cos2（+）=2sin2（+）﹣1=﹣…12分．点评：本题主要考查由y=Asin（ωx+φ）的部分图象确定其解析式以及三角函数的恒等变换及化简求值．解决第二问的关键在于得到cos（﹣a）=cos[π﹣2（+）]=﹣cos2（+）．17．（12分）用射击的方法引爆装有汽油的大汽油罐，已知只有5发子弹备用，且首次命中只能使汽油流出，再次命中才能引爆成功（可以是两次不连续的命中），每次射击命中率都是，每次命中与否互相独立．（1）求油罐被引爆的概率．（2）如果引爆或子弹打光则停止射击，设射击次数为ξ，求ξ的分布列及ξ的数学期望．考点：离散型随机变量及其分布列；离散型随机变量的期望与方差．专题：概率与统计．分析：（1）设“油罐被引爆”为事件A，先求其对立事件的概率，利用即可得出；（2）利用独立事件和互斥事件的概率计算公式、随机变量的数学期望即可得出．解答：解：（1）设“油罐被引爆”为事件A，其对立事件为，则==，∴==．即油罐被引爆的概率为．（2）射击次数ξ的可能取值为2，3，4，5．则P（ξ=2）=，P（ξ=3）==，P（ξ=4）==，P（ξ=5）=或P（ξ=4）=1﹣P（ξ=2）﹣P（ξ=3）﹣P（ξ=4）=．故ξ的分布列为：故Eξ==．点评：熟练掌握独立事件的概率关系、独立事件和互斥事件的概率计算公式、随机变量的数学期望是解题的关键．18．（14分）（xx•广州一模）如图2所示，在边长为12的正方形AA'A'1A1中，点B，C在线段AA'上，且AB=3，BC=4，作BB1∥AA1，分别交A1A'1、AA'1于点B1、P，作CC1∥AA1，分别交A1A'1、AA'1于点C1、Q，将该正方形沿BB1、CC1折叠，使得A'A1′与AA1重合，构成如图3所示的三棱柱ABC﹣A1B1C1．（1）在三棱柱ABC﹣A1B1C1中，求证：AB⊥平面BCC1B1．（2）求平面APQ将三棱柱ABC﹣A1B1C1分成上、下两部分几何体的体积之比．（3）在三棱柱ABC﹣A1B1C1中，求直线AP与直线A1Q所成角的余弦值．考点：棱柱、棱锥、棱台的体积；异面直线及其所成的角；直线与平面垂直的判定．专题：证明题；综合题；转化思想．分析：（1）在三棱柱ABC﹣A1B1C1中，证明AB垂直平面BCC1B1内的两条相交直线BC、BB1即可．（2）说明AB为四棱锥A﹣BCQP的高，求出梯形BCQP的面积，即可求出平面APQ 将三棱柱ABC﹣A1B1C1分成上部分的体积；同理求出下部分几何体的体积，即可得到它们之比．（3）AB，BC，BB1两两互相垂直．以B为原点，建立如图所示的空间直角坐标系B ﹣xyz，求出，，利求直线AP与直线A1Q所成角的余弦值．解答：解：（1）证明：在正方形AA'A'1A1中，∵A'C=AA'﹣AB﹣BC=5，∴三棱柱ABC﹣A1B1C1的底面三角形ABC的边AC=5．∵AB=3，BC=4，∴AB2+BC2=AC2，则AB⊥BC．∵四边形AA'A'1A1为正方形，AA1∥BB1，∴AB⊥BB1，而BC∩BB1=B，∴AB⊥平面BCC1B1．（2）解：∵AB⊥平面BCC1B1，∴AB为四棱锥A﹣BCQP的高．∵四边形BCQP为直角梯形，且BP=AB=3，CQ=AB+BC=7，∴梯形BCQP的面积为，∴四棱锥A﹣BCQP的体积，由（1）知B1B⊥AB，B1B⊥BC，且AB∩BC=B，∴B1B⊥平面ABC．∴三棱柱ABC﹣A1B1C1为直棱柱，∴三棱柱ABC﹣A1B1C1的体积为．故平面APQ将三棱柱ABC﹣A1B1C1分成上、下两部分的体积之比为．（3）解：由（1）、（2）可知，AB，BC，BB1两两互相垂直．以B为原点，建立如图所示的空间直角坐标系B﹣xyz，则A（3，0，0），A1（3，0，12），P（0，0，3），Q（0，4，7），∴，，∴，∵异面直线所成角的范围为，∴直线AP与A1Q所成角的余弦值为．点评：本小题主要考查空间几何体中线面的位置关系，面积与体积，空间向量等基础知识，考查空间想象能力和运算求解能力．19．（14分）（xx•广州二模）已知函数，g（x）=x+lnx，其中a＞0．（Ⅰ）若x=1是函数h（x）=f（x）+g（x）的极值点，求实数a的值；（Ⅱ）是否存在正实数a，使对任意的x1，x2∈[1，e]（e为自然对数的底数）都有f（x1）≥g （x2）成立，若存在，求出实数a的取值范围；若不存在，说明理由．考点：函数在某点取得极值的条件；利用导数求闭区间上函数的最值．专计算题；分类讨论．题：分析：（1）利用函数极值点的导数等于0，且此点的左侧和右侧导数的符号相反，求得实数a的值．（2）问题等价于对任意的x1，x2∈[1，e]时，都有[f（x）]min≥[g（x）]max，分类讨论，利用导数的符号判断函数的单调性，由单调性求出函数f（x）的最小值及g（x）]的最大值，根据它们之间的关系求出实数a的取值范围．解答：（1）解：∵，其定义域为（0，+∞），∴．∵x=1是函数h（x）的极值点，∴h'（1）=0，即3﹣a2=0，∵a＞0，∴．经检验，当时，x=1是函数h（x）的极值点，∴．（2）解：假设存在实数a，对任意的x1，x2∈[1，e]都有f（x1）≥g（x2）成立，等价于对任意的x1，x2∈[1，e]时，都有[f（x）]min≥[g（x）]max，当x∈[1，e]时，．∴函数g（x）=x+lnx在[1，e]上是增函数．∴[g（x）]max=g（e）=e+1．∵，且x∈[1，e]，a＞0，①当0＜a＜1且x∈[1，e]时，，∴函数在[1，e]上是增函数．∴[f（x）]min=f（1）=1+a2．由1+a2≥e+1，得a≥，又0＜a＜1，∴a 不合题意．②当1≤a≤e时，若1≤x＜a，则，若a＜x≤e，则．∴函数在[1，a）上是减函数，在（a，e]上是增函数．∴[f（x）]min=f（a）=2a.2a≥e+1，得a≥，1≤a≤e，∴≤a≤e．③当a＞e且x∈[1，e]时，，∴函数在[1，e]上是减函数．∴．由≥e+1，得a≥，又a＞e，∴a＞e．综上所述，存在正实数a的取值范围为．点评：本题考查函数在某点存在极值的条件，利用导数求函数在闭区间上的最值．20．（14分）（xx•潮州二模）已知数列{a n}满足：a1=1，a2=，且a n+2=．（I）求证：数列为等差数列；（II）求数列{a n}的通项公式；（III）求下表中前n行所有数的和S n．考点：等差关系的确定；数列的求和．专题：压轴题．分析：（1）把所给的递推式整理，构造要求的数列形式，仿写一个递推式，用数列的后一项去减前一项，合并同类项，发现满足等差中项公式，得到结论．（2）写出（1）中的数列通项，用叠乘的方法把其他项都约去，得到第n项和第一项，因第一项可求出结果，所以得到通项公式．（3）根据表中构造的新数列，由它的特点写出第n行的各数之和，代入所求数列的通项，整理出组合数形式，用二项式定理的各项系数之间的关系，得到第n行的各数之和，于是构造一个新数列用等比数列前n项和公式求解．解答：解：（I）∵==，∴，∴数列满足等差中项公式为等差数列．（II）由（I）得故当n≥2时，即又当n=1时，满足上式所以通项公式为．（III）∵∴第n行各数之和∴表中前n行所有数的和S n=（22﹣2）+（23﹣2）++（2n+1﹣2）=（22+23++2n+1）﹣2n==2n+2﹣2n﹣4点评：有关数列的试题经常是综合题，经常把数列知识和指数函数、对数函数和不等式的知识综合起来，试题也常把等差数列、等比数列，求极限和数学归纳法综合在一起．探索性问题是高考的热点，常在数列解答题中出现．21．（14分）（xx•深圳一模）已知点H（﹣3，0），点P在y轴上，点Q在x轴的正半轴上，点M在直线PQ上，且满足，．（Ⅰ）当点P在y轴上移动时，求点M的轨迹C；（Ⅱ）过定点D（m，0）（m＞0）作直线l交轨迹C于A、B两点，E是D点关于坐标原点O的对称点，求证：∠AED=∠BED；（Ⅲ）在（Ⅱ）中，是否存在垂直于x轴的直线l'被以AD为直径的圆截得的弦长恒为定值？若存在求出l'的方程；若不存在，请说明理由．考点：直线与圆锥曲线的关系；轨迹方程．专题：综合题．分析：（I）设M（x，y），P（0，y'），Q（x'，0）则可得，，由代入整理可求点M的轨迹C；（II）要证明∠AED=∠BED，根据直线的倾斜角与斜率的关系，只要证K AE=﹣K BE 即可；分两种情况讨论：（1）当直线l垂直于x轴时，根据抛物线的对称性，有∠AED=∠BED；（2）当直线l与x轴不垂直时，利用直线的斜率进行转换即得；（III）假设存在满足条件的直线，根据垂径定理得性质可知，要使弦长为定值，则只要圆心到直线的距离为定值即可．解答：解：（Ⅰ）设M（x，y），P（0，y'），Q（x'，0）（x'＞0）∵，．∴且（3，y'）•（x，y﹣y'）=0…（2分）∴．…（3分）∴y2=4x（x＞0）…（4分）∴动点M的轨迹C是以O（0，0）为顶点，以（1，0）为焦点的抛物线（除去原点）．…（5分）（Ⅱ）：（1）当直线l垂直于x轴时，根据抛物线的对称性，有∠AED=∠BED；…（6分）（2）当直线l与x轴不垂直时，依题意，可设直线l的方程为y=k（x﹣m）（k≠0，m ＞0），A（x1，y1），B（x2，y2），则A，B两点的坐标满足方程组消去x并整理，得ky2﹣4y﹣4km=0∴…（7分）设直线AE和BE的斜率分别为k1、k2，则k1+k2=====…（9分）∴tan∠AED+tan（180°﹣∠BED）=0∴tan∠AED=tan∠BED∵，∴∠AED=∠BED．综合（1）、（2）可知∠AED=∠BED．…（10分）（Ⅲ）假设存在满足条件的直线l'，其方程为x=a，AD的中点为O'，l'与AD为直径的圆相交于点F、G，FG的中点为H，则O'H⊥FG，O'点的坐标为．∵=，∴|FH|2=|O'F|2﹣|O'H|2==（a﹣m+1）x1+a（m﹣a）…（12分）∴|FG|2=（2|FH|）2=4[（a﹣m+1）x1+a（m﹣a）]令a﹣m+1=0，得a=m﹣1此时，|FG|2=4（m﹣1）∴当m﹣1＞0，即m＞1时，（定值）∴当m＞1时，满足条件的直线l'存在，其方程为x=m﹣1；当0＜m≤1时，满足条件的直线l'不存在．…（14分）点评：本题以向量得数量积得坐标表示为载体考查了圆锥曲线得求解及直线与圆、圆锥曲线的位置关系得求解．属于综合试题．36505 8E99 躙fBHIEk36951 9057 遗26320 66D0 曐25342 62FE 拾20793 5139 儹20346 4F7A 佺F 33826 8422 萢。

2021年陕西省西安市高考数学第一次质检试卷（理科）（一模）一、选择题（共12小题）.1．已知集合M＝{x|x2﹣3x﹣10＜0}，，则（∁R N）∩M为（）A．{x|3＜x＜5}B．{x|x＜﹣3或x＞5}C．{x|﹣3≤x≤﹣2}D．{x|﹣3＜x＜5} 2．i（2+3i）＝（）A．3﹣2i B．3+2i C．﹣3﹣2i D．﹣3+2i3．已知点A（﹣2，3）在抛物线y2＝2px的准线上，则p＝（）A．1B．2C．4D．84．已知首项为最小正整数，公差不为零的等差数列{a n}中，a2，a8，a12依次成等比数列，则a4的值是（）A．B．C．﹣26D．585．从点P（m，3）向圆（x﹣2）2+y2＝1引切线，则切线长的最小值（）A．B．5C．D．6．某三棱锥的三视图如图所示，则该三棱锥的体积是（）A．6B．8C．12D．247．已知函数f（x）＝sin（2x+φ）其中φ∈（0，2π），若对于一切x∈R恒成立，则f（x）的单调递增区间是（）A．B．C．D．8．已知定义域为R的函数f（x）满足f（x+2）＝f（x），且当0≤x≤1时，f（x）＝lg（x2+2），则f（﹣2021）＝（）A．﹣lg3B．lg9C．lg3D．09．直线y＝kx+1与曲线f（x）＝alnx+b相切于点P（1，2），则2a+b＝（）A．4B．3C．2D．110．设图F1、F2分别为双曲线的左、右焦点，双曲线上存在一点P使得|PF1|+|PF2|＝3b，|PF1|•|PF2|＝ab，则该双曲线的离心率为（）A ．B ．C ．D．311．天干地支纪年法（简称干支纪年法）是中国历法上自古以来就一直使用的纪年方法．天干有十，即：甲、乙，丙、丁、戊、己、庚，辛，壬、癸；地支有十二，即：子、丑、寅、卯、辰，巳、午，未、申、酉、戌、亥．干支纪年法中，天干地支对应的规律如表：天干甲乙丙丁戊己庚辛壬癸甲乙丙…地支子丑寅卯辰巳午未申酉戌亥子…干支纪年甲子年乙丑年丙寅年丁卯年戊辰年己巳年庚午年辛未年壬申年癸酉年甲戌年乙亥年丙子年…2049年是新中国成立100周年．这一百年，中国逐步实现中华民族的伟大复兴．使用干支纪年法，2049年是己巳年，则2058年是（）年．A．己巳B．甲申C．戊寅D．丙戌12．已知正方体的外接球与内切球上各有一个动点M、N，若线段MN 的最小值为，则下列结论不正确的是（）A．正方体的外接球的表面积为12πB ．正方体的内切球的体积为C．正方体的棱长为2D．线段MN 的最大值为二、填空题（共4小题）.13．已知向量，，若，则k ＝．14．在（x﹣）6展开式中，常数项为．（用数值表示）15．已知实数x，y满足约束条件，则z＝3x+2y的最大值．16．已知数列{a n}的前n项和为S n，满足a1＝+1，则数列{a n}的前16项和S16＝．三、解答题（第17～21题为必考题，每个试题考生都必须作答．第22，23题为选考题，考生根据要求作答．）（一）必考题：共60分．17．在△ABC中，角A、B、C所对的边分别为a、b、c，a＝2．（1）若，求角B；（2）若c＝2b，当角B最大时，求△ABC的面积．18．为了推进分级诊疗，实现“基层首诊，双向转诊，急慢分治、上下联动”的诊疗模式，某地区自2016年起全面推行家庭医生签约服务．已知该地区居民约为2000万．从1岁到101岁的居民年龄结构的频率分布直方图如图甲所示．为了解各年龄段居民签约家庭医生的情况，现调查了1000名年满18周岁以上的居民，各年龄段被访者签约率如图乙所示．（1）估计该地区年龄在71～80岁且已签约家庭医生的居民人数；（2）若以图中年龄在71～80岁居民签约率作为此地区该年龄段每个居民签约家庭医生的概率，则从该地区年龄在71～80岁居民中随机抽取三人，以已签约家庭医生的居民为变量X，求这三人中恰有二人已签约家庭医生的概率；并求变量X的数学期望和方差．19．如图，AB是半圆O的直径，C是半圆O上除A，B外的一个动点，DC垂直于半圆O 所在的平面，DC∥EB，DC＝EB＝1，AB＝4．（1）证明：平面ADE⊥平面ACD；（2）当C点为半圆的中点时，求二面角D﹣AE﹣B的余弦值．20．已知椭圆离心率为，点A，B，D，E分别是C的左，右，上，下顶点，且四边形ADBE的面积为．（1）求椭圆C的标准方程；（2）已知F是C的右焦点，过F的直线交椭圆C于P，Q两点，记直线AP，BQ的交点为T，求证：点T横坐标为定值．21．已知函数f（x）＝e x（x+a），其中e是自然对数的底数，a∈R．（1）求函数f（x）的单调区间；（2）设g（x）＝f（x﹣a）﹣x2，讨论函数g（x）零点的个数，并说明理由．（二）选考题：共10．请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，已知圆C 的极坐标方程为ρ2+12ρcosθ+11＝0．（1）求圆心C的直角坐标；（2）若直线l的参数方程是（t为参数），l与C交于A，B两点，，求l的斜率．[选修4-5：不等式选讲]23．已知函数f（x）＝x2+1，g（x）＝|x﹣a|﹣|2x﹣1|，a≥．（1）当a＝时，解不等式g（x2）＜﹣；（2）对任意x1，x2∈R．若不等式f（x1）≥g（x2）恒成立，求实数a的取值范围．参考答案一、选择题（共12小题）.1．已知集合M＝{x|x2﹣3x﹣10＜0}，，则（∁R N）∩M为（）A．{x|3＜x＜5}B．{x|x＜﹣3或x＞5}C．{x|﹣3≤x≤﹣2}D．{x|﹣3＜x＜5}解：∵集合M＝{x|x2﹣3x﹣10＜0}＝{x|﹣2＜x＜5}，＝{x|﹣3≤x≤3}，∴∁R N＝{x|x＜﹣3或x＞3}，∴（∁R N）∩M＝{x|3＜x＜5}．故选：A．2．i（2+3i）＝（）A．3﹣2i B．3+2i C．﹣3﹣2i D．﹣3+2i解：i（2+3i）＝2i+3i2＝﹣3+2i．故选：D．3．已知点A（﹣2，3）在抛物线y2＝2px的准线上，则p＝（）A．1B．2C．4D．8解：由已知得，抛物线y2＝2px的准线方程为，且过点A（﹣2，3），故，p＝4．故选：C．4．已知首项为最小正整数，公差不为零的等差数列{a n}中，a2，a8，a12依次成等比数列，则a4的值是（）A．B．C．﹣26D．58解：设公差不为零的等差数列{a n}的公差为d（d≠0），∵a2，a8，a12依次成等比数列，∴a82＝a2a12，即（a1+7d）2＝（a1+d）（a1+11d），可得19d2＝﹣a1d，∵d≠0，∴a1＝﹣19d，又由已知可得a1＝1，在，因此，，故选：A．5．从点P（m，3）向圆（x﹣2）2+y2＝1引切线，则切线长的最小值（）A．B．5C．D．解：设切线长为d，由题设条件可得：d2＝（m﹣2）2+（3﹣0）2﹣1＝（m﹣2）2+8≥8，∴，当且仅当m＝2时取“＝“，故选：D．6．某三棱锥的三视图如图所示，则该三棱锥的体积是（）A．6B．8C．12D．24解：根据几何体的三视图转换为几何体为：如图所示：所以，由于锥体的高为4，故．故选：B．7．已知函数f（x）＝sin（2x+φ）其中φ∈（0，2π），若对于一切x∈R恒成立，则f（x）的单调递增区间是（）A．B．C．D．解：函数f（x）＝sin（2x+φ），其中φ∈（0，2π），若对于一切x∈R 恒成立，则2×+φ＝2kπ+，k∈Z，所以φ＝2kπ+，k∈Z，由于φ∈（0，2π），所以φ＝，即f（x）＝sin（2x+），令2kπ﹣≤2x+≤2kπ+，k∈Z，解得kπ﹣≤x≤kπ+，k∈Z，即f（x）的单调递增区间是．故选：B．8．已知定义域为R的函数f（x）满足f（x+2）＝f（x），且当0≤x≤1时，f（x）＝lg（x2+2），则f（﹣2021）＝（）A．﹣lg3B．lg9C．lg3D．0解：根据题意，定义域为R的函数f（x）满足f（x+2）＝f（x），则f（x）是周期为2的周期函数，则有f（﹣2021）＝f（1﹣2×1011）＝f（1），又由当0≤x≤1时，f（x）＝lg（x2+2），则f（1）＝lg3，则f（﹣2021）＝f（1）＝lg3，故选：C．9．直线y＝kx+1与曲线f（x）＝alnx+b相切于点P（1，2），则2a+b＝（）A．4B．3C．2D．1解：直线y＝kx+1与曲线f（x）＝alnx+b相切于点P（1，2），可得k+1＝2，即k＝1，f（1）＝b＝2，f（x）的导数为f′（x ）＝，即有a＝1，则2a+b＝2+2＝4．故选：A．10．设图F1、F2分别为双曲线的左、右焦点，双曲线上存在一点P使得|PF1|+|PF2|＝3b，|PF1|•|PF2|＝ab，则该双曲线的离心率为（）A ．B ．C ．D．3解：由双曲线的定义得：|PF1|﹣|PF2|＝2a，（不妨设该点在右支上）又|PF1|+|PF2|＝3b ，所以，两式相乘得．结合c2＝a2+b2得．故e ＝．故选：B．11．天干地支纪年法（简称干支纪年法）是中国历法上自古以来就一直使用的纪年方法．天干有十，即：甲、乙，丙、丁、戊、己、庚，辛，壬、癸；地支有十二，即：子、丑、寅、卯、辰，巳、午，未、申、酉、戌、亥．干支纪年法中，天干地支对应的规律如表：天干甲乙丙丁戊己庚辛壬癸甲乙丙…地支子丑寅卯辰巳午未申酉戌亥子…干支纪年甲子年乙丑年丙寅年丁卯年戊辰年己巳年庚午年辛未年壬申年癸酉年甲戌年乙亥年丙子年…2049年是新中国成立100周年．这一百年，中国逐步实现中华民族的伟大复兴．使用干支纪年法，2049年是己巳年，则2058年是（）年．A．己巳B．甲申C．戊寅D．丙戌解：根据题意，列表如下：2049年是己巳年，往后数9年，可得2058年是戊寅．故选：C．12．已知正方体的外接球与内切球上各有一个动点M、N，若线段MN的最小值为，则下列结论不正确的是（）A．正方体的外接球的表面积为12πB．正方体的内切球的体积为C．正方体的棱长为2D．线段MN的最大值为解：设正方体的棱长为a，则正方体外接球半径为体对角线长的一半，即，内切球半径为棱长的一半，即．∵M、N分别为外接球和内切球上动点，∴，解得：a＝2．即正方体惨长为2，C正确；∴正方体外接球表面积为，A正确；内切球体积为，B正确；线段MN的最大值为，D错误．故选：D．二、填空题：本题共4小题，每小题5分，共20分．13．已知向量，，若，则k＝12．解：根据题意，向量，，则，若，则有，解得k＝12，故答案为：12．14．在（x﹣）6展开式中，常数项为﹣20．（用数值表示）解：二项式（x﹣）6＝[x+（﹣x﹣1）]6，其展开式的通项公式为：T r+1＝•x6﹣r•（﹣x﹣1）r＝（﹣1）r••x6﹣2r，当6﹣2r＝0时，得r＝3，所以展开式的常数项为：T4＝（﹣1）3•＝﹣20．故答案为：﹣20．15．已知实数x，y满足约束条件，则z＝3x+2y的最大值9．解：由约束条件直线可行域如图，令t＝x+2y，由图可知，当直线t＝x+2y过A时，t有最大值为t＝2，此时z＝3x+2y的最大值为9．故答案为：9．16．已知数列{a n}的前n项和为S n，满足a1＝+1，则数列{a n}的前16项和S16＝84．解：2（S n+2+S n）＝4S n+1+1，化为，即，∵，∴{a n}为等差数列，公差，∴．故答案为：84．三、解答题（共7．解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22，23题为选考题，考生根据要求作答．）（一）必考题：共60分．17．在△ABC中，角A、B、C所对的边分别为a、b、c，a＝2．（1）若，求角B；（2）若c＝2b，当角B最大时，求△ABC的面积．解：（1）因为，所以＝＝，整理可得a2+c2﹣b2＝ac，可得cos B＝＝＝，因为B∈（0，π），可得B＝．（2）在△ABC中，b2＝a2+c2﹣2ac cos B，c＝2b，所以cos B＝≥，当且仅当b＝时取等号，此时B＝，C＝，所以△ABC的面积S＝ab＝＝．18．为了推进分级诊疗，实现“基层首诊，双向转诊，急慢分治、上下联动”的诊疗模式，某地区自2016年起全面推行家庭医生签约服务．已知该地区居民约为2000万．从1岁到101岁的居民年龄结构的频率分布直方图如图甲所示．为了解各年龄段居民签约家庭医生的情况，现调查了1000名年满18周岁以上的居民，各年龄段被访者签约率如图乙所示．（1）估计该地区年龄在71～80岁且已签约家庭医生的居民人数；（2）若以图中年龄在71～80岁居民签约率作为此地区该年龄段每个居民签约家庭医生的概率，则从该地区年龄在71～80岁居民中随机抽取三人，以已签约家庭医生的居民为变量X，求这三人中恰有二人已签约家庭医生的概率；并求变量X的数学期望和方差．解：（1）由题知该地区居民约为2000万，由图1知，该地区年龄在71～80岁的居民人数为0.004×10×2000＝80万．由图2知．年龄在71～80岁的居民签概率为0.7．所以该地区年龄在71～80岁且已签约家庭医生的居民人数为80×0.7＝56万．（2）由题知此地区年龄段在71～80的每个居民签约家庭医生的概率为P＝0.7，且每个居民之间是否签约是独立的，所以设“从该地区年龄在71～80岁居民中随机抽取三人”为事件B，随机变量为X，这三人中恰有二人已签约庭医生的概率为：．数学期望E（X）＝3×0.7＝2.1，方差D（X）＝3×0.7×0.3＝0.63．19．如图，AB是半圆O的直径，C是半圆O上除A，B外的一个动点，DC垂直于半圆O 所在的平面，DC∥EB，DC＝EB＝1，AB＝4．（1）证明：平面ADE⊥平面ACD；（2）当C点为半圆的中点时，求二面角D﹣AE﹣B的余弦值．【解答】（1）证明：∵AB是圆O的直径，∴AC⊥BC，∵DC⊥平面ABC，BC⊂平面ABC，∴DC⊥BC，又DC∩AC＝C，∴BC⊥平面ACD，∵DC∥EB，DC＝EB，∴四边形DCBE是平行四边形，∴DE∥BC，∴DE⊥平面ACD，又DE⊂平面ADE，∴平面ACD⊥平面ADE．（2）当C点为半圆的中点时，AC＝BC＝2，以C为原点，以CA，CB，CD为坐标轴建立空间坐标系如图所示：则D（0，0，1），E（0，2，1），A（2，0，0），B（0，2，0），∴＝（﹣2，2，0），＝（0，0，1），＝（0，2，0），＝（2，0，﹣1），设平面DAE的法向量为＝（x1，y1，z1），平面ABE的法向量为＝（x2，y2，z2），则，，即，，令x1＝1得＝（1，0，2），令x2＝1得＝（1，1，0）．∴cos＜＞＝＝＝．∵二面角D﹣AE﹣B是钝二面角，∴二面角D﹣AE﹣B的余弦值为﹣．20．已知椭圆离心率为，点A，B，D，E分别是C的左，右，上，下顶点，且四边形ADBE的面积为．（1）求椭圆C的标准方程；（2）已知F是C的右焦点，过F的直线交椭圆C于P，Q两点，记直线AP，BQ的交点为T，求证：点T横坐标为定值．解：（1）设椭圆C的半焦距为c，根据题意，，解得，所以椭圆的方程为+＝1．（2）证明：由（1）知A（﹣3，0），B（3，0），F（2，0），设T（x0，y0），P（x1，y1），Q（x2，y2），由k TA＝k PA，得＝，k TB＝k QB，得＝，两式相除得＝•，又+＝1，故﹣1＝﹣•＝﹣，故＝﹣，于是＝•＝﹣•，由于直线PQ经过点F，故设直线PQ的方程为x＝my+2，联立椭圆的方程可得（5m2+9）y2+20my﹣25＝0，所以，所以＝﹣•＝﹣•＝﹣•＝﹣•＝，解得x0＝，所以点T横坐标为定值．21．已知函数f（x）＝e x（x+a），其中e是自然对数的底数，a∈R．（1）求函数f（x）的单调区间；（2）设g（x）＝f（x﹣a）﹣x2，讨论函数g（x）零点的个数，并说明理由．解：（1）因为f（x）＝e x（x+a），所以f'（x）＝e x（x+a+1）．………………………………………………………………（1分）由f'（x）＞0，得x＞﹣a﹣1；由f'（x）＜0，得x＜﹣a﹣1．………………………………………………………………所以f（x）的增区间是（﹣a﹣1，+∞），减区间是（﹣∞，﹣a﹣1）．………………………（2）因为g（x）＝f（x﹣a）﹣x2＝xe x﹣a﹣x2＝x（e x﹣a﹣x）．由g（x）＝0，得x＝0或e x﹣a﹣x＝0．………………………………………………………………………设h（x）＝e x﹣a﹣x，又h（0）＝e﹣a≠0，即x＝0不是h（x）的零点，故只需再讨论函数h（x）零点的个数．因为h'（x）＝e x﹣a﹣1，所以当x∈（﹣∞，a）时，h'（x）＜0，h（x）单调递减；当x∈（a，+∞）时，h'（x）＞0，h（x）单调递增．…………………………………………所以当x＝a时，h（x）取得最小值h（a）＝1﹣a．………………………………………①当h（a）＞0，即a＜1时，h（x）＞0，h（x）无零点；…………………………………②当h（a）＝0，即a＝1时，h（x）有唯一零点；…………………………………………③当h（a）＜0，即a＞1时，因为h（0）＝e﹣a＞0，所以h（x）在（﹣∞，a）上有且只有一个零点．……………………………………………令x＝2a，则h（2a）＝e a﹣2a．设φ（a）＝h（2a）＝e a﹣2a（a＞1），则φ'（a）＝e a﹣2＞0，所以φ（a）在（1，+∞）上单调递增，所以，∀a∈（1，+∞），都有φ（a）≥φ（1）＝e﹣2＞0．所以h（2a）＝φ（a）＝e a﹣2a＞0．………………………………………………………所以h（x）在（a，+∞）上有且只有一个零点．所以当a＞1时，h（x）有两个零点．………………………………………………………综上所述，当a＜1时，g（x）有一个零点；当a＝1时，g（x）有两个零点；当a＞1时，g（x）有三个零点．……………………………………………………………（二）选考题：共10．请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，已知圆C 的极坐标方程为ρ2+12ρcosθ+11＝0．（1）求圆心C的直角坐标；（2）若直线l的参数方程是（t为参数），l与C交于A，B两点，，求l的斜率．解：（1）将x＝ρcosθ，y＝ρsinθ，x2+y2＝ρ2代入ρ2+12ρcosθ+11＝0，得x2+y2+12x+11＝0，即（x+6）2+y2＝25，所以圆C的圆心坐标为（﹣6，0）；（2）在极坐标系中，直线l的极坐标方程为θ＝α（ρ∈R）．设A，B所对应的极径分别为ρ1，ρ2，将l的极坐标方程代入C的极坐标方程得ρ2+12ρcosα+11＝0．于是ρ1+ρ2＝﹣12cosα，ρ1ρ2＝11，，由，得，，tanα＝＝±＝，所以l的斜率为或．[选修4-5：不等式选讲]23．已知函数f（x）＝x2+1，g（x）＝|x﹣a|﹣|2x﹣1|，a≥．（1）当a＝时，解不等式g（x2）＜﹣；（2）对任意x1，x2∈R．若不等式f（x1）≥g（x2）恒成立，求实数a的取值范围．解：（1）当时，，不等式g（x2）＜﹣，即，即，解得x2＞4或x2＜﹣3（舍去），由x2＞4，解得x＜﹣2或x＞2，所以不等式的解集是（﹣∞，﹣2）∪（2，+∞）．（2）由题意知，只需满足f（x）mix≥g（x）max即可，因为f（x）＝x2+1，所以f（x）min＝1，依题意，当时，g（x）＝，得f（x）min≥g（x）max，得，即，所以，即a的取值范围是[，]．。

2021年高考数学第一次适应性试卷（理科）（一模）一、选择题（每题5分）.1．已知集合A＝{x|x2＞4），B＝{﹣1，0，1，2，3}，则（∁R A）∩B＝（）A．{﹣2，3}B．{﹣1，0}C．{﹣1，0，1}D．{﹣1，0，1，2}2．复数z＝的虚部是（）A．i B．C．﹣i D．﹣3．若，则＝（）A．B．C．D．4．（+2）5的展开式中，x2的系数是（）A．4B．8C．10D．205．已知直线l，两个不同的平面α和β．下列说法正确的是（）A．若l⊥α，α⊥β，则l∥βB．若l∥α，α⊥β，则l⊥βC．若l∥α，l∥β，则α∥βD．若l⊂α，α∥β，则l∥β6．记S n为等差数列{a n}的前n项和，若a3＝2，S4＝7，则数列{a n}的通项公式a n＝（）A．n﹣1B．C．2n﹣4D．（n﹣1）（n﹣2）7．过点P（2，2）的直线l1与圆（x﹣1）2+y2＝1相切，则直线l1的方程为（）A．3x﹣4y+2＝0B．4x﹣3y﹣2＝0C．3x﹣4y+2＝0或x＝2D．4x﹣3y﹣2＝0或x＝28．已知函数f（x）＝，则其大致图象为（）A．B．C．D．9．春天是鲜花的季节，水仙花就是其中最迷人的代表，数学上有个水仙花数，它是这样定义的：“水仙花数”是指一个三位数，它的各位数字的立方和等于其本身．三位的水仙花数共有4个，其中仅有1个在区间（150，160）内，我们姑且称它为“水仙四妹”，则在集合{142，147，152，154，157，“水仙四妹”}，共6个整数中，任意取其中3个整数，则这3个整数中含有“水仙四妹”，且其余两个整数至少有一个比“水仙四妹”小的概率是（）A．B．C．D．10．已知抛物线C：x2＝2py（p＞0）的焦点在直线x+y﹣1＝0上，又经过抛物线C的焦点且倾斜角为60°的直线交抛物线C于A、B两点，则|AB|＝（）A．12B．14C．16D．1811．已知双曲线E：＝1（a＞0，b＞0）的左焦点为F1，过点F1的直线与两条渐近线的交点分别为M、N两点（点F1位于点M与点N之间），且，又过点F1作F1P⊥OM于P（点O为坐标原点），且|ON|＝OP|，则双曲线E的离心率e＝（）A．B．C．D．12．设a＝，b＝，c＝，则a，b，c的大小顺序为（）A．a＜c＜b B．c＜a＜b C．a＜b＜c D．b＜a＜c二、填空题（共4小题）.13．已知向量＝（﹣2，1），＝（x，4），若⊥，则x＝．14．记S n为递增等比数列{a n}的前n项和，若a2＝2，a4＝a3+4，则S10的值为．15．函数f（x）＝sin（ωx﹣）（ω＞0）的图象向右平移个单位长度后得到函数g（x）的图象，且g（x）的图象的一条对称轴是直线x ＝﹣，则ω的最小值为．16．已知母线长为6的圆锥的顶点为S，点A、B为圆锥的底面圆周上两动点，当SA与SB 所夹的角最大时，锐角△SAB的面积为8，则此时圆锥的体积为．三、解答题：共70分。

绝密★启用前2021届高三第一次模拟考试数学试题(理科)本试卷分第Ⅰ卷和第II 卷两部分，满分150分，时间120分钟第Ⅰ卷一、选择题：本大题12小题，每小题5分，共60分，在每小题给出的四个选项中只有一项是符合题目要求的。

1．设集合{}512|≥-=x x A ，集合⎭⎬⎫⎩⎨⎧-==x x y x B 7cos |，则B A 等于（ ） A ．()3,7 B ．[]3,7 C ．(]3,7 D ．[)3,72．已知i 为虚数单位，a 为实数，复数(2)(1)z a i i =-+在复平面内对应的点为M ，则“21=a ”是“点M 在第四象限”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条3．设等比数列{}n a 的前n 项和为n S ，满足0,1n a q >>，且352620,64a a a a +==，则6S =（）A ．63B ．48C ．42D ．36 4．已知58cos 3sin =+x x ，则=-)6cos(x π（）A ．－35B ．35C ．－45D ．455．已知命题p :函数21()sin 2f x x =-的最小正周期为π；命题q ：若函数)1(+x f 为偶函数，则)(x f 关于1=x 对称.则下列命题是真命题的是（）A ．q p ∧B ．q p ∨C ．()()p q ⌝∧⌝D ．()p q ∨⌝6．已知实数{},8,7,6,5,4,3,2,1∈x ，执行如图所示的程序框图，则输出的x 不小于．．．121的概率为（ ）A ．34B ．85 C ．87 D ．21 否开始n=1输入xn= n +1x= 3x +1输入x 输出结束是3?n ≤7．已知⎰-=20)cos (πdx x a ，则912ax ax ⎛⎫+ ⎪⎝⎭展开式中，3x 项的系数为（） A ．638B ．6316C ．221-D ．638-8．甲乙两人从4门课程中各选修两门，则甲乙所选的课程中至少有1门不相同．．．的选法共有（） A ．30种 B ．36种 C ．60种 D ．72种9．已知F 是双曲线)0,0(12222>>=-b a b y a x 的左焦点，过F 作倾斜角为o 60的直线l ，直线l 与双曲线交于点A 与y 轴交于点B 且FB FA 31=，则该双曲线的离心率等于（） A ．15+B ．217+C ．15-D ．217- 10．已知方程sin xk x=在(0,)+∞有两个不同的解,αβ（αβ<），则下面结论正确的是（） A ．1tan()41πααα++=- B ．1tan()41πααα-+=+C ．1tan()41πβββ++=-D ．1tan()41πβββ-+=+ 11．设函数)(x f 是定义在)0,(-∞上的可导函数，其导函数为)(x f '，且有0)()(3>'+x f x x f ，则不等式0)3(27)2015()2015(3>-+++f x f x 的解集（）A ．)2015,2018(--B ．)2016,(--∞C ．)2015,2016(--D ．)2012,(--∞12．设函数⎩⎨⎧>≤=0,log 0,2)(2x x x x f x ，若对任意给定的),1(+∞∈t ，都存在唯一的R x ∈，满足at t a x f f +=222))((，则正实数．．．a 的最小值是（）A ．2B ．21C ．41D ．81第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分 13．已知2a =，3b =，,a b 的夹角为60°，则2a b -=．14．设实数,x y 满足,102,1,x y y x x ≤⎧⎪≤-⎨⎪≥⎩则124y xz ⎛⎫=⨯ ⎪⎝⎭的最大值为．15．棱锥的三视图如上图所示，且三个三角形均为直角三角形，则yx 11+的最小值为． 16．球O 为边长为4的正方体1111D C B A ABCD -的内切球，P为球O 的球面上动点，M 为11C B 中点，DP BM ⊥，则点P 的轨迹周长为．三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分12分）已知公比为负值的等比数列{}n a 中，154a a =，41a =-． （Ⅰ）求数列{}n a 的通项公式； （Ⅱ）设()11112231n n n n b n n +++=++⋅⋅⋅+⨯⨯+，求数列{}n n a b +的前n 项和n S ． 18．(本小题满分12分）湖南卫视“我是歌手”这个节目深受广大观众喜爱，节目每周直播一次，在某周比赛中歌手甲、乙、丙竞演完毕，现场的某4位大众评审对这3位歌手进行投票，每位大众评审只能投一票且把票投给任一歌手是等可能的，求： （Ⅰ）恰有2人把票投给歌手甲的概率；（Ⅱ）投票结束后得票歌手的个数ζ的分布列与期望． 19．(本小题满分12分）在如图所示的几何体中，AE ⊥平面ABC ，CD ∥AE ，F 是BE 的中点，AC BC =1=，90ACB ∠=︒，22AECD ．（Ⅰ）证明 DF ⊥平面ABE ；（Ⅱ）求二面角A BD E --的余弦值的大小． 20．（小题满分12）椭圆C 的方程为22221 (0)x ya b a b +=>>，1F 、2F 分别是它的左、右焦点，已知椭圆C 过点(0, 1)，且离心率22e =． （Ⅰ）求椭圆C 的方程；（Ⅱ）如图，设椭圆的左、右顶点分别为A 、B ，直线l的方程为4x =，P 是椭圆上异于A 、B 的任意一点，直线PA 、PB 分别交直线l 于D 、E 两点，求12F D F E ⋅的值；（Ⅲ）过点(1 0)Q ，任意作直线m （与x 轴不垂直）与椭圆C 交于M 、N 两点，与l 交于R 点，RM xMQ =，RN yNQ =． 求证：4450x y ++=．21．（本大题满分12分）已知函数2()(0)f x x ax a =-≠，()ln g x x =，()f x 图象与x 轴异于原点的交点M 处F ED CBAm QE DR PF 2F 1yxONMBA的切线为1l ，(1)g x -与x 轴的交点N 处的切线为2l ，并且1l 与2l 平行． （Ⅰ）求(2)f 的值；（Ⅱ）已知实数R t ∈，求[]ln ,1,u x x x e =∈的取值范围及函数[][()+],1,y f xg x t x e =∈的最小值；（Ⅲ）令()()'()F x g x g x =+，给定1212,(1,),x x x x ∈+∞<，对于两个大于1的正数βα,，存在实数m 满足：21)1(x m mx -+=α，21)1(mx x m +-=β，并且使得不等式12|()()||()()|F F F x F x αβ-<-恒成立，求实数m 的取值范围.．22．(本小题满分10分）选修4—1：几何证明选讲如图，ABC ∆内接于直径为BC 的圆O ，过点A 作圆O 的切线交CB 的延长线于点P ，BAC ∠的平分线分别交BC 和圆O 于点 E D 、，若102==PB PA ．（Ⅰ）求证：AB AC 2=； （Ⅱ）求DE AD ⋅的值．23．(本小题满分10分）选修4—4：坐标系与参数方程已知曲线C 的极坐标方程是θρcos 4=．以极点为平面直角坐标系的原点，极轴为x 轴的正半轴，建立平面直角坐标系，直线l 的参数方程是t t y t x (sin cos 1⎩⎨⎧=+=αα是参数)． （Ⅰ）将曲线C 的极坐标方程化为直角坐标方程；（Ⅱ）若直线l 与曲线C 相交于A 、B 两点，且14=AB ，求直线的倾斜角α的值．24.（本小题满分10分）选修4—5：不等式选讲设函数()f x x a =-．（Ⅰ）当2a =时，解不等式()41f x x ≥--； （Ⅱ）若()1f x ≤的解集为[]0,2，()110,02a m n m n+=>>，求证：24m n +≥．PABCD 22题图O鹰潭市2021届高三第一次模拟考试数学(理科)答案一、选择题：1—5 DAADB 6 —10 BCABC 11—12 AB二、填空题：1313 14．2115．510216．π558三、解答题：17．解：（Ⅰ）因为数列{}n a 是等比数列，所以42351==a a a ，则23-=a 或2，因为数列{}n a 的公比为负值，所以23=a ，故2134-==a a q ，则8231==q a a ，故111)21(8---==n n n q a a 即数列{}n a 的通项公式为1)21(8--=n n a ……………………………………6分（Ⅱ）由条件知，)1(1321211+++⋅⋅⋅⋅+⨯++⨯+=n n n n n b n ))1(1321211)(1(++⋅⋅⋅⋅+⨯+⨯+=n n n)1113121211)(1(+-+⋅⋅⋅⋅+-+-+=n n nn n n =+-+=)111)(1(………………9分则n b a n n n +-=+-1)21(8故)(21n n a a a S +⋅⋅⋅⋅++=)(21n b b b +⋅⋅⋅⋅+++⎥⎦⎤⎢⎣⎡--=n )21(1316)1(21++n n 。

2021年高三数学第一次模拟试题理（含解析）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．A等于（）1．（5分）（xx•乐山一模）设全集U={x丨x＞0}，集合A={x丨x＞2}，则∁UA．{x|0＜x＜2}B．{x|x＜2}C．{x|x≤2}D．{x|0＜x≤2}补集及其运算考点：专题：计算题．分析：直接利用补集的定义，求出A的补集即可．解答：解：因为U={x丨x＞0}，集合A={x丨x＞2}，则∁U A={x丨0＜x≤2}，故选D．点评：本题考查补集的运算，补集的定义，考查基本知识的应用．2．（5分）（xx•乐山一模）已知点A（﹣1，0）、B（1，3），向量=（2k﹣1，2），若⊥，则实数k的值为（）A．﹣2 B．﹣1 C．1D．2考点：数量积判断两个平面向量的垂直关系．专题：常规题型；计算题．分析：先用B的坐标减去A即得的坐标，再利用两个向量垂直，数量积等于0求出实数k的值．解答：解：∵=（2，3），向量a=（2k﹣1，2），∵⊥，∴•=（2，3）•（2k﹣1，2）=2（2k﹣1）+6=0，∴k=﹣1，故选 B．点评：本题考查利用两个向量的数量积判断2个向量垂直的方法，两个向量垂直，数量积等于0．3．（5分）（xx•乐山一模）“a＞1”是“函数f（x）=a x﹣1﹣2（a＞0且a≠1）在区间[1，2]上存在零点”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：探究型．分析：先判断函数f（x）在区间[1，2]上存在零点的条件，然后判断a＞l与条件之间的关系，判断是充分条件还是必要条件．解答：解：要使函数f（x）=a x﹣1﹣2（a＞0且a≠1）在区间[1，2]上存在零点，则有f（1）f（2）≤0，即﹣1×（a﹣2）≤0，解得a≥2．所以a＞1推不出a≥2，但a≥2⇒a＞1，所以“a＞1”是“函数f（x）=a x﹣1﹣2（a＞0且a≠1）在区间[1，2]上存在零点”的必要不充分条件，故选B．点评：本题考查了充分条件和必要条件的判断．要求掌握判断充分条件和必要条件的方法：①若p⇒q为真命题且q⇒p为假命题，则命题p是命题q的充分不必要条件；②若p⇒q为假命题且q⇒p为真命题，则命题p是命题q的必要不充分条件；③若p⇒q为真命题且q⇒p为真命题，则命题p是命题q的充要条件；④若p⇒q为假命题且q⇒p为假命题，则命题p是命题q的即不充分也不必要条件．4．（5分）（xx•乐山一模）下图给出4个幂函数的图象，则图象与函数的大致对应是（）A．①，②y=x2，③，④y=x﹣1B．①y=x3，②y=x2，③，④y=x﹣1C．①y=x2，②y=x3，③，④y=x﹣1D．①，②，③y=x2，④y=x﹣1考点：幂函数图象及其与指数的关系．专题：综合题．分析：通过②的图象的对称性判断出②对应的函数是偶函数；①对应的幂指数大于1，通过排除法得到选项．解答：解：②的图象关于y轴对称，②应为偶函数，故排除选项C，D①由图象知，在第一象限内，图象下凸，递增的较快，所以幂函数的指数大于1，故排除A故选B点评：本题考查幂函数的性质、考查幂函数的图象取决于幂指数．5．（5分）（xx•乐山一模）一个体积为12的正三棱柱的三视图如图所示，则这个三棱柱的侧视图的面积为（）A．6B．8C．8D．12考点：由三视图求面积、体积．专题：计算题．分析：此几何体是一个正三棱柱，正视图即内侧面，底面正三角形的高是，由正三角形的性质可以求出其边长，由于本题中体积已知，故可设出棱柱的高，利用体积公式建立起关于高的方程求高，再由正方形的面积公式求侧视图的面积即可．解答：解：设棱柱的高为h，由左视图知，底面正三角形的高是，由正三角形的性质知，其边长是4，故底面三角形的面积是 =4由于其体积为，故有h×=，得h=3由三视图的定义知，侧视图的宽即此三棱柱的高，故侧视图的宽是3，其面积为3×=故选A点评：本题考点是简单空间图形的三视图，考查根据作三视图的规则几何体的直观图的能力以及利用体积公式建立方程求参数的能力，三视图的投影规则是：“主视、俯视长对正；主视、左视高平齐，左视、俯视宽相等”．6．（5分）（xx•乐山一模）已知锐角θ的终边上有一点P（sin10°，1+sin80°），则锐角θ=（）A．85°B．65°C．10°D．5°考点：任意角的三角函数的定义．专题：三角函数的求值．分析：由任意角的正切函数的定义可得 tanθ=，利用同角三角函数的基本关系、两角和的正切公式化简为tan85°，由此求得锐角θ的值．解答：解：∵已知锐角θ的终边上有一点P（sin10°，1+sin80°），由任意角的正切函数的定义可得tanθ======tan（45°+40°）=tan85°，∴锐角θ=85°，故选A．点评：本题主要考查任意角的正切函数的定义，同角三角函数的基本关系、两角和的正切公式的应用，根据三角函数的值求角，属于中档题．7．（5分）（xx•乐山一模）如图，梯形ABCD中，AB∥CD，且AB=2CD，对角线AC、DB相交于点O，若，，则=（）A．B．C．D．考点：向量加减混合运算及其几何意义．专题：计算题．分析：先证明△DOC∽△BOA，然后根据AB=2CD得到AO与AD的比例关系，最后转化成用基底表示即可．解答：解：∵AB∥CD，AB=2CD，∴△DOC∽△BOA且AO=2OC则=2=而=+=+=∴==（）=故选D．点评：本题主要考查了向量加减混合运算及其几何意义，解题的关键是弄清AO与AD的比例关系，属于基础题．8．（5分）（xx•乐山一模）直线y=5与y=﹣1在区间[0，]截曲线y=msinx+n（m，n＞0）所得的弦长相等且不为零，则下列正确的是（）A．m≤B．m≤3，n=2 C．m＞D．m＞3，n=2考点：由y=Asin（ωx+φ）的部分图象确定其解析式．专题：计算题．分析：由于曲线y=msinx+n（m，n＞0）的周期T=，依题意，可求得n=2，m＞3．解答：解：∵曲线y=msinx+n（m，n＞0）的周期T=，直线y=5与y=﹣1在区间[0，]截曲线y=msinx+n（m，n＞0）所得的弦长相等且不为零，∴n==2；m+2＞5，∴m＞3．故选D．点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，求得n=2是关键，也是难点，考查理解与应用能力，属于中档题．9．（5分）（xx•乐山一模）在数列{a n}中，a1=2，na n+1=（n+1）a n+2（n∈N*），则a10为（）A．34 B．36 C．38 D．40考点：数列递推式．专题：计算题．分析：先根据地推关系得到，再由可求出a10的值．解答：解：∵na n+1=（n+1）a n+2∴∴=2[（）+（）+…+（1﹣）]+2=a10=38故选C．点评：本题主要考查数列的递推关系式，考查综合观察和转化能力．10．（5分）（xx•乐山一模）函数f（x）=，满足f（1）+f（a）=2，则a的所有可能值为（）A．1或B．﹣C．1D．1或﹣或考点：运用诱导公式化简求值．专题：计算题．分析：依题意，可求得f（1），由f（1）+f（a）=2可得f（a），利用f（x）=，即可求得a的所有可能值．解答：解：∵f（x）=，∴f（1）=e0=1，又f（1）+f（a）=2，∴f（a）=1；∴当﹣1＜a＜0时，f（a）=2sinπa2=1，∴a2=或a2=，∴a=﹣或a=﹣；当a≥0时，e a﹣1=1，∴a=1．综上所述，a=﹣或a=﹣或a=1．故选D点评：本题考查函数解析式的应用，考查分析、运算能力，属于中档题．11．（5分）（xx•乐山一模）函数f（x）=﹣（cosx）1g|x|的部分图象是（）A．B．C．D．考点：函数的图象．专题：计算题；函数的性质及应用．分析：先利用函数f（x）=﹣（cosx）1g|x|的奇偶性进行排除，再对x→0+时的函数符号判断即可．解答：解：∵f（x）=﹣（cosx）1g|x|，∴f（﹣x）=﹣[cos（﹣x）]1g|﹣x|=﹣（cosx）1g|x|=f（x）（x≠0），∴函数f（x）=﹣（cosx）1g|x|为偶函数，故其图象关于y轴对称，可排除B，D；又当x→0+时，cosx＞0，1g|x|＜0，∴当x→0+时，f（x）=﹣（cosx）1g|x|＞0，故可排除C；故选A．点评：本题考查函数的图象，着重考查函数的奇偶性与单调性，属于基础题．12．（5分）（xx•重庆）把函数f（x）=x3﹣3x的图象C1向右平移u个单位长度，再向下平移v个单位长度后得到图象C2、若对任意的u＞0，曲线C1与C2至多只有一个交点，则v的最小值为（）A．2B．4C．6D．8考点：函数单调性的性质；函数的图象；函数的零点与方程根的关系．专题：计算题；压轴题．分析：由平移规律得出平移后的曲线对应的解析式，因两曲线有交点，故相应方程有根，对方程（x ﹣u）3﹣3（x﹣u）﹣v=x3﹣3x，进行变形，得出v关于u 的不等式，转化成恒成立的问题求参数v的范围．解答：解：根据题意曲线C的解析式为y=（x﹣u）3﹣3（x﹣u）﹣v，由题意，方程（x﹣u）3﹣3（x﹣u）﹣v=x3﹣3x至多有一个根，即3ux2﹣3xu2+（u3﹣3u+v）=0至多有一个根，故有△=9u4﹣12u（u3﹣3u+v）≤0对任意的u＞0恒成立整理得对任意u＞0恒成立，令，则由此知函数g（u）在（0，2）上为增函数，在（2，+∞）上为减函数，所以当u=2时，函数g（u）取最大值，即为4，于是v≥4；故选B．点评：考查据题意进行转化的能力，以及观察变形的能力，解本题过程中，把一个变量表示成另一个变量的函数，依据不等式恒成立的问题转化求求函数的最值来求出参数的范围，题型新颖．二、填空题：本大题共4小题；每小题4分，共16分，把答案填在题中横线上．13．（4分）（xx•乐山一模）复数z满足等式（2一i）•z=i，则复数z在复平面内对应的点的坐标为．考点：复数的代数表示法及其几何意义．专题：计算题．分析：将所给的式子变形表示出复数z，再分子分母同乘以2+i进行化简，整理出实部和虚部，再写出复平面内对应的定的坐标．解答：解：由（2一i）•z=i得，z====，则复数z在复平面内对应的点的坐标为，故答案为：．点评：本题考查了复数的除法运算和复数的几何意义，对于除法运算需要分子分母同乘以分母的共轭复数再进行化简．14．（4分）（xx•乐山一模）已知命题p：“∃x∈[1，2]，使x2﹣a＜0成立”，若￢p是真命题，则实数a的取值范围是a≤1．考点：特称命题；命题的否定．专题：计算题．分析：由已知，∀x∈[1，2]，x2﹣a≥0，为真命题，即x2≥a在x∈[1，2]恒成立，只须a≤（x2）min=解答：解：由已知￢p：∀x∈[1，2]，x2﹣a≥0，为真命题．即x2≥a在x∈[1，2]恒成立，只须a≤（x2）min=1即可故答案为：a≤1点评：本题考查命题真假，求参数取值范围，考查转化，逻辑思维能力．15．（4分）（xx•乐山一模）如图，已知直线l过点A（0，4），交函数y=2x的图象于点C，交x轴于点B，若AC：CB=2：3，则点B的横坐标为 3.16 ．（结果精确到0.01，参考数据lg2=0.3010，lg3=0.4771）考点：指数式与对数式的互化．专题：计算题．分析：设点B为（a，0），由于点A（0，4）以及AC：CB=2：3，可得点C的坐标，再代入函数y=2x 的解析式，解出即可．解答：解：设点B为（a，0），由已知直线l过点A（0，4），且直线AB交函数y=2x的图象于点C，AC：CB=2：3，则点C的坐标为，由于点C在函数y=2x的图象上，则，即得=2+log23﹣log25=又由lg2=0.3010，lg3=0.4771，则a≈3.16．故答案为 3.16．点评：本题考查方程的零点与方程根的关系，用待定系数法求点B的横坐标的值．在解答的过程当中充分体现了问题转化的能力以及运算的能力．值得同学们体会反思．16．（4分）（xx•乐山一模）已知函数f（x）=x3+ax2+bx+c在x=x1处取得极大值，在x=x2处取得极小值，且满足x1∈（0，1），x2∈（1，2），则的取值范围是．考点：函数在某点取得极值的条件．专题：导数的综合应用．分析：求导数，利用导函数f′（x）=x2+ax+b的图象开口朝上且x1∈（0，1），x2∈（1，2），得a，b的约束条件，据线性规划求出最值．解答：解：∵函数f（x）=x3+ax2+bx+c在x=x1处取得极大值，在x=x2处取得极小值，∴x1，x2是导函数f′（x）=x2+ax+b的两根由于导函数f′（x）=x2+ax+b的图象开口朝上且x1∈（0，1），x2∈（1，2），∴满足条件的约束条件的可行域如图所示：令Z=，则其几何意义是区域内的点与（0，3）连线的斜率，∴由，可得a=﹣3，b=2∴∈（）∵=，∴=时，的最小值为，=3时，=∴的取值范围是，故答案为：点评：本题考查学生利用导数研究函数极值的能力，以及会进行简单的线性规划的能力，解题时要认真审题，仔细解答．三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或推演步骤17．（12分）（xx•乐山一模）已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜）的图象（部分）如图所示．（1）求函数f（x）的解析式；（2）在△ABC中，a，b，c分别是角A，B，C的对边，且a=l，b+c=2，f（A）=1，求△ABC的面积．考点：余弦定理；由y=Asin（ωx+φ）的部分图象确定其解析式．专题：计算题；三角函数的图像与性质．分析：（1）根据函数的最大值得出A=2，由函数的周期T=4（﹣）=π算出ω=2，得函数表达式为f（x）=2sin（2x+φ）．最后根据当x=时函数取得最大值，解出φ=，从而得出函数f（x）的解析式；（2）由（1）的函数解析式结合f（A）=1解出A=，利用余弦定理结合题中数据算出bc=3（2﹣），再根据正弦定理的面积公式即可算出△ABC的面积．解答：解：（1）∵函数的最大值为2，∴A=2又∵函数的周期T=4（﹣）=π，∴ω==2，得函数表达式为f（x）=2sin（2x+φ）∵f（）=2为函数的最大值，∴2×+φ=+2π（k∈Z）结合|φ|＜，取k=0得φ=∴函数f（x）的解析式为f（x）=2sin（2x+）（2）由（1）得f（A）=2sin（2A+）=1，∵A∈（0，π），∴2A+=，得A=根据余弦定理，得a2=b2+c2﹣2bccosA=（b+c）2﹣2bc（1+cos），即1=22﹣2bc（1+cos），解之得bc==3（2﹣）因此，△ABC的面积S=bcsinA=3（2﹣）×sin=点评：本题给出三角函数的部分图象，求函数的表达式，并依此求三角形ABC的面积，着重考查了三角函数的图象与性质、三角形的面积公式和余弦定理等知识，属于中档题．18．（12分）（xx•乐山一模）已知函数是奇函数．（1）求m的值；（2）请讨论它的单调性，并给予证明．考点：函数奇偶性的判断；函数单调性的判断与证明．专题：计算题；证明题．分析：（1）由函数奇偶性的定义可知，f（﹣x）+f（x）=0，将f（x）的解析式代入求解m即可．（2）先求出f（x）的定义域，因为函数是奇函数，故只要先判断f（x）在（0，1）内的单调性即可，可由单调性的定义直接判断．解答：解：（1）∵f（x）是奇函数，∴f（﹣x）+f（x）=0；即，解得：m=1，其中m=﹣1（舍）；经验证当m=1时，确是奇函数．（2）先研究f（x）在（0，1）内的单调性，任取x1、x2∈（0，1），且设x1＜x2，则，，得f（x1）﹣f（x2）＞0，即f（x）在（0，1）内单调递减；由于f（x）是奇函数，其图象关于原点对称，所以函数f（x）在（﹣1，0）内单调递减．点评：本题考查函数单调性的判断和证明及已知奇偶性求参数和奇偶性的应用问题，属基本题型的考查．19．（12分）（xx•乐山一模）济南高新区引进一高科技企业，投入资金720万元建设基本设施，第一年各种运营费用120万元，以后每年增加40万元；每年企业销售收入500万元，设f（n）表示前n年的纯收入．（f（n）=前n年的总收入﹣前n年的总支出﹣投资额）（Ⅰ）从第几年开始获取纯利润？（Ⅱ）若干年后，该企业为开发新产品，有两种处理方案：①年平均利润最大时，以480万元出售该企业；②纯利润最大时，以160万元出售该企业；问哪种方案最合算？考点：数列的应用．专题：综合题．分析：（Ⅰ）根据第一年各种运营费用120万元，以后每年增加40万元，可知每年的运营费用是以120为首项，40为公差的等差数列，利用f（n）=前n年的总收入﹣前n年的总支出﹣投资额，可确立函数的解析式，进而可建立不等式，从而可求从第几年开始获取纯利润．（Ⅱ）①求出年平均利润，利用基本不等式，可求此方案获利最大值的时间；②f（n）=﹣20n2+400n﹣720=﹣20（n﹣10）2+1280，利用配方法，求此方案获利最大值的时间，比较即可得出结论．解答：解：由题意知每年的运营费用是以120为首项，40为公差的等差数列．设纯利润与年数的关系为f（n），设．﹣﹣﹣﹣﹣﹣（3分）（Ⅰ）获取纯利润就是要求f（n）＞0，故有﹣20n2+400n﹣720＞0，解得2＜n＜18．又n∈N*，知从第三年开始获取纯利润．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（5分）（Ⅱ）①年平均利润，当且仅当n=6时取等号．故此方案获利6×160+480=1440（万元），此时n=6．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（7分）②f（n）=﹣20n2+400n﹣720=﹣20（n﹣10）2+1280，当n=10时，f（n）max=1280．故此方案共获利1280+160=1440（万元）．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（9分）比较两种方案，在同等数额获利的基础上，第①种方案只需6年，第②种方案需要10年，故选择第①种方案．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）点评：本题考查数列模型，考查基本不等式的运用，考查二次函数最值的研究，解题的关键是建立数列模型，选择适当的方法求最值．20．（12分）（xx•乐山一模）已知某几何体的直观图和三视图如图所示，其正视图为矩形，左视图为等腰直角三角形，俯视图为直角梯形．（Ⅰ）证明：BN⊥平面C1NB1；（Ⅱ）求平面CNB1与平面C1NB1所成角的余弦值；考点：用空间向量求平面间的夹角；由三视图求面积、体积；直线与平面垂直的判定．专题：综合题．分析：（Ⅰ）根据题意，可得BA，BC，BB1两两垂直，以BA，BB1，BC分别为x，y，z轴建立空间直角坐标系，用坐标表示点、向量，利用数量积证明NB⊥NB1，BN⊥B1C1，即可证明BN⊥平面C1NB1．（Ⅱ）是平面C1B1N的一个法向量，求出平面NCB1的一个法向量，利用向量的数量积，可求二面角C﹣NB1﹣C1的余弦值．解答：（Ⅰ）证明：∵该几何体的正视图为矩形，左视图为等腰直角三角形，俯视图为直角梯形，∴BA，BC，BB1两两垂直．以BA，BB1，BC分别为x，y，z轴建立空间直角坐标系如图．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（2分）则B（0，0，0），N（4，4，0），B1（0，8，0），C1（0，8，4），C（0，0，4）．∴，．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）∴NB⊥NB1，BN⊥B1C1．又NB1与B1C1相交于B1，∴BN⊥平面C1NB1．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）（Ⅱ）解：∵BN⊥平面C1NB1，∴是平面C1B1N的一个法向量，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（8分）设为平面NCB1的一个法向量，则，∴所以可取．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（10分）则cos==∴所求二面角C﹣NB1﹣C1的余弦值为．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（12分）点评：本题考查线面垂直，考查面面角，解题的关键是构建空间直角坐标系，确定平面的法向量．21．（12分）（xx•乐山一模）已知数列{a n}是等差数列，a5=5，若（6﹣a1）=a2+a3，且A、B、C三点共线（O为该直线外一点）；点列（n，b n）在函数x的反函数的图象上．（1）求a n和b n；（2）记数列C n=a n b n+b n（n∈N*），若{C n}的前n项和为T n，求使不等式成立的最小自然数n的值．考点：数列与向量的综合；数列与不等式的综合．专题：等差数列与等比数列．分析：（1）利用三点共线的结论，可得6﹣a1=a2+a3，结合a5=5，求出首项与公差，可求a n；利用点列（n，b n）在函数x的反函数的图象上，可求b n；（2）确定数列的通项，利用错位相减法求和，即可求得结论．解答：解：（1）设数列{a n}的公差为d，则∵（6﹣a1）=a2+a3，且A、B、C三点共线，∴由三点共线的条件，可得6﹣a1=a2+a3，∴a1+d=2，∵a5=5，∴a1+4d=5，∴d=1，a1=1，∴a n=n；∵点列（n，b n）在函数x的反函数的图象上∴；（2）C n=a n b n+b n=，∴T n=，∴T n=两式相减，可得T n==∴T n=∴3﹣T n=∴等价于∴n＞6∴使不等式成立的最小自然数n的值为7．点评：本题考查数列的通项与求和，考查数列与不等式的联系，确定数列的通项，正确求和是关键．22．（14分）（xx•乐山一模）已知函数f（x）=e x﹣kx，（1）若k=e，试确定函数f（x）的单调区间；（2）若k＞0，且对于任意x∈R，f（|x|）＞0恒成立，试确定实数k的取值范围；（3）设函数F（x）=f（x）+f（﹣x），求证：F（1）F（2）…F（n）＞（n∈N+）．考点：利用导数研究函数的单调性；函数恒成立问题；利用导数研究函数的极值；不等式的证明．专题：计算题；压轴题．分析：（1）先确定函数的定义域然后求导数fˊ（x），在函数的定义域内解不等式fˊ（x）＞0，f′（x）＜0（2）f（|x|）是偶函数，只需研究f（x）＞0对任意x≥0成立即可，即当x≥0时f（x）min ＞0（3）观察结论，要证F（1）F（2）…F（n）＞，即证[F（1）F（2）…F（n）]2＞（e n+1+2）n，变形可得[F（1）F（n）][F（2）F（n﹣1）]…[F（n）F（1）]＞（e n+1+2）n，可证F（1）F（n）＞e n+1+2，F（2）F（n﹣1）＞e n+1+2，F（n）F（1）＞e n+1+2．问题得以解决．解答：解：（Ⅰ）由k=e得f（x）=e x﹣ex，所以f'（x）=e x﹣e．由f'（x）＞0得x＞1，故f（x）的单调递增区间是（1，+∞），由f'（x）＜0得x＜1，故f（x）的单调递减区间是（﹣∞，1）．（Ⅱ）由f（|﹣x|）=f（|x|）可知f（|x|）是偶函数．于是f（|x|）＞0对任意x∈R成立等价于f（x）＞0对任意x≥0成立．由f'（x）=e x﹣k=0得x=lnk．①当k∈（0，1]时，f'（x）=e x﹣k＞1﹣k≥0（x＞0）．此时f（x）在[0，+∞）上单调递增．故f（x）≥f（0）=1＞0，符合题意．②当k∈（1，+∞）时，lnk＞0．当x变化时f'（x），f（x）的变化情况如下表：x （0，lnk）lnk （lnk，+∞）f′（x）﹣0 +f（x）单调递减极小值单调递增由此可得，在[0，+∞）上，f（x）≥f（lnk）=k﹣klnk．依题意，k﹣klnk＞0，又k＞1，∴1＜k＜e．综合①，②得，实数k的取值范围是0＜k＜e．（Ⅲ）∵F（x）=f（x）+f（﹣x）=e x+e﹣x，∴F（x1）F（x2）=，∴F（1）F（n）＞e n+1+2，F（2）F（n﹣1）＞e n+1+2，F（n）F（1）＞e n+1+2．由此得，[F（1）F（2）F（n）]2=[F（1）F（n）][F（2）F（n﹣1）][F（n）F（1）]＞（e n+1+2）n故，n∈N*．点评：本小题主要考查函数的单调性、极值、导数、不等式等基本知识，考查运用导数研究函数性质的方法，考查分类讨论、化归以及数形结合等数学思想方法，考查分析问题、解决问题的能力．@ 21715 54D3 哓28944 7110 焐n30561 7761 睡Z33240 81D8 臘u21631 547F 呿U&27966 6D3E 派=30114 75A2 疢。

2021年高三数学上学期第一次模拟考试试题理（含解析）第Ⅰ卷(共60分)【试卷综析】本试题是一份高三一模考试的好题，涉及范围广，包括集合、不等式、简易逻辑、函数、导数、程序框图、平面向量、三角函数等高考核心考点，又涉及了集合与简易逻辑、基本函数、三角向量、导数应用的方方面面等必考解答题型。

本题难易程度设计比较合理，梯度分明；既有考查基础知识的经典题目，如17,18,19,20又有考查能力的创新题目，如21,22；从10,12,16等题能看到在创新方面的努力，从1,2,3,4,5,6,7,8,9,11,13,14,15等题可以看出考基础，考规范；从22题可以看出考融合，考拓展，考创新。

一．选择题:本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．【题文】1.若集合，且，则集合可能是A. B. C. D.【知识点】集合及其运算A1【答案解析】A 解析：，易知A对【思路点拨】转化是关键。

【题文】2.已知，则下列结论错误的是A. B. C. D.【知识点】不等式的概念与性质E1【答案解析】C 解析：由易得两边都乘，且，所以，故C错。

【思路点拨】不等式的性质要娴熟运用。

尤其倒数不等式的性质。

【题文】3.若不等式对一切实数都成立，则的取值范围为A. B. C. D.【知识点】不等式 E8【答案解析】 D 解析：显然时满足题意，故排除A、B；时，不满足题意。

故选D【思路点拨】恒成立问题是高考特别能考的问题，一定要掌握。

含参数的二次不等式恒成立主要要讨论。

【题文】4.规定，若，则函数的值域A. B． C． D．【知识点】函数及其表示B1【答案解析】A 解析：由得，【思路点拨】新定义关键是会“套”模式，套的合适，准确。

【题文】5. 设命题函数在定义域上为减函数；命题,当时, ，以下说法正确的是A.为真B.为真C.真假D.，均假【知识点】命题及其关系函数单调性不等式的性质A2 B3 E1【答案解析】 D 解析：因为的定义域是，知道假；而由，得，故也假。