空间几何体的外接球和内切球问题讲课教案

立体几何外接球、内切球问题一、教学分析：纵观近几年高考对于组合体的考查，与球相关的外接与内切问题是高考命题的热点之一.高考命题小题综合化倾向尤为明显，要求学生有较强的空间想象能力和准确的计算能力，才能顺利解答•从实际教学来看，这部分知识学生掌握较为薄弱、认识较为模糊，看到就头疼的题目•分析原因，除了这类题目的入手确实不易之外，主要是学生没有形成解题的模式和套路，以至于遇到类似的题目便产生畏惧心理.从近几年全国高考命题来看，这部分内容以选择题、填空题为主，大题很少见•此部分是重点也是一个难点，建议分两个课时，第一个课时以基础的方法为主，第二个课时在第一课时的基础上进行总结整理并拓展。

二、学情分析：学生在高一必修二教材系统的学习了立体几何，这部分内容本身对知识掌握的要求就比较高，又是难点，再加上疫情原因，很多同学不能系统了解和掌握，而一部分学生也只能解决长方体的外接球问题，稍复杂一点就不会。

三、教学目标：知识与技能：学生学会用构造法解决空间几何体的外接球、内切球问题。

过程与方法：学生建立空间感，体会转化数学思想方法。

情感、态度、价值观：完善学生知识体系，增进学生对数学的信心和兴趣。

四、教学重点：学会转化、数形结合的思想方法。

五、教学难点：构造法的要点。

六、教学过程分析问：如果是正方体，它的体对角线长和棱长什么关系2.复习圆柱的外接球问题问：一个球满足什么条件，我们把它叫做这个圆柱的外接球问：球心的位置在哪问：如果给出圆柱的底面半径和母线长，怎么求它外接球的半径问：一个球满足什么条件，我们把它叫做这个圆锥的外接球 问：球心的位置在哪 问：如果给出圆锥的底面半径和母线长，怎么求它外接球的半径 方程：先算出H其实我们一直是在求它们截面的外接圆的半径，长方体对角面矩形的 顶点都在球面上，长方体对角面长方形外接圆的直径也就是这个长方 体外接球的直径，圆柱和圆锥我们解是它们轴截面图形外接圆的半径, 把求一个空间几何体外接球半径问题转化为求一个截面图形外接圆半.复习圆锥的外接球问题O径问题的过程这就是我们所说的立体问题平面化三角形的外接圆半径除了刚才同学想到在直角三角形中用勾股定理列 方程的方法，还有什么方法回想一下解三角形那一章正弦定理：比较正弦定理，不用确定外接圆的圆心知道么）活动二:问题三棱锥的三条棱PA, PB, PC 两两垂直，PA 1, PB 2, PC 3,则其外接球的半径为问：三棱锥的的顶点和长方体的顶点之间什么关系它们的外接球是不是相同的问：球心在哪，半径怎么求（求长方体体对角线长需要长方体的长宽高，这几个量我们现在解决一个 几何体的 外接球可 能有多种 办法，让 学生发挥 想象，提 出各种方 法，通过 比较生成 对结合体 外接球问 题的认 识。

进门测1正方体中，若外接圆半径为，则该正方体外接球的表面积为（）A．B．C．D．答案C解答如图所示，为等边三角形，设的外接圆半径为，由正弦定理可得：，，设正方体边长为，则，，设外接球半径为，则，，面积，故选．2已知三棱柱的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，，，，则此球的表面积等于．答案．解答设此球半径为，三棱柱高为，则底面积，，解得，又，，，为直角三角形，的外接圆半径,，球的表面积3在三棱锥中，，，，则三棱锥的外接球的表面积为（）A．B．C．D．答案A解答在中，由余弦定理得， ，，，，≌，，，，为等边三角形，，取中点为点，连接、，如图所示，外接球球心必在过点（外接圆圆心），垂直平面的直线上，其中，，，，，，又，，平面，，设外接球半径为，，，，，，，外接球的表面积为，故选．4三棱锥中，平面且，是边长为的等边三角形，则该三棱锥外接球的表面积为（）A．B．C．D．答案C解答第面是边长为的等边三角形，设底面所截外接球的截面圆的半径为，空间几何体的外接球和内切球问题知识点梳理：，，如图所示，，，设外接球半径为，，外接球，故选．5已知三棱锥的体积为，是等腰直角三角形，其斜边，且三棱锥的外接球的球心恰好是的中点，则球的体积为.答案解答设球的半径为，球心到平面的距离为，则由是的中点得，点到平面的距离等于，所以＝＝＝，解得＝，记的中点为，则平面.在中，＝＋，即＝＋＝，所以球的体积＝＝＝.一、外接球常见模型1. 【墙角模型】三条线两个垂直，不找球心的位置即可求出球半径方法：找三条两两垂直的线段，利用公式，即，求出．2. 【对棱相等模型】三棱锥中，已知，，，则可补形为长方体，再求外接球半径．第一步：画出一个长方体，标出互为异面直线的三组面对角线；第二步：设出长方体的长宽高分别为，，列方程组：；第三步：根据墙角模型，，即．3. 【切瓜模型】两个大小圆面互相垂直且交于小圆直径，利用正弦定理解大圆三角形是通法．如图，平面平面，且(即为小圆的直径)，则球心在大圆面上，利用正弦定理即可求出外接球半径．4. 【垂面模型】三棱锥中，当一条棱垂直于某个面时，球心离底面距离为这条棱长的一半．如图平面，求外接球半径的步骤：第一步：将画在小圆面上，为小圆直径的一个端点，作小圆直径，连接，则必过球心；第二步：为的外心，所以平面，算出小圆的半径(可利用正弦定理计算)，又；第三步：利用勾股定理求三棱锥的外接球半径：①；或②．如图，的射影是的外心三棱锥的三条侧棱相等三棱锥的底面在圆锥的底上，顶点也是圆锥的顶点．求解步骤：第一步：确定球心的位置，取的外心，则三点共线；第二步：先算出小圆的半径，再算出棱锥的高(也是圆锥的高)；第三步：勾股定理：，解出．方法二：小圆直径参与构造大圆，用正弦定理求大圆直径得球的直径．5. 【汉堡模型】直棱柱的外接球、圆柱的外接球如图，直三棱柱内接于球(同时直棱柱也内接与圆柱，棱柱上下底面可以是任意三角形)．第一步：确定球心的位置，是的外心，则面；第二步：算出小圆半径，(也是圆柱的高)；第三步：勾股定理：，即．6. 【折叠模型】两个全等三角形或等腰三角形拼在一起，或菱形折叠第一步：先画出如图所示的图形，将画在小圆上，找出和的外心和；第二步：过和分别作平面和平面的垂线，两垂线的交点即为球心，连接，；第三步：解，算出，在中，勾股定理：．7. 【直角双拼模型】两直角三角形拼接在一起(斜边相同)题设：，求三棱锥外接球半径（分析：取公共的斜边的中点，连接，，则，为三棱锥外接球球心，然后在中求出半径）．二、内切球1. 正方体的中心与内切球的球心重合，若正方体的棱长为，内切球的半径为，，如下图所示：2. 正四面体的中心与内切球的球心重合，正四面体的棱长为，体高为，内切球半径为，，如下图所示：证明：正四面体的棱长为，体高为，内切球半径为．正四面体的内切球半径为，正四面体的体积，得①，在中，，即，化简得②，由①②可得．3. 空间多面体的每个面的面积为，多面体的体积为，则该多面体的内切球半径为．例如，利用等体积法求四面体的内切球半径．例题精讲：6设长方体的长、宽、高分别为，，，其顶点都在一个球面上，则该球的表面积为（ ）A ．B ．C ．D ．答案B解答由题意可知，该球为长方体的外接球，则该球的半径，则该球的表面积为，故选．7已知三棱锥的顶点都在球的表面上，若，，两两互相垂直，且，则球的体积为（ ）A．B ．C ．D ．答案C解答且，，，，取的中心连接，设球心为，球半径为，则，延长交于，则，，，在中，，，在中，，即，解得， ，故选．8四面体中，，，点是的中点，点在平面的射影恰好为的中点，则该四面体外接球的表面积为（）A．B．C．D．答案A解答，为等边三角形，又，，为等腰直角三角形，又为中点，为中点，，，点为外接圆圆心，设球心为，则面，在中，，，在中，，，设球半径为，则，又，，即，解得，，外接圆表面积，故选．9三棱锥中，平面，，，，则该三棱锥外接球的表面积为（）A．B．C．D．答案A解答将其放在长方体中如下图所示：则有，，在中，，在中，，则球的半径，表面积，故选．10已知三棱柱的个顶点都在球的球面上，若，，，，则球的半径为（）A．B．C．D．答案C解答由于三棱柱的个顶点都在球上，所以三棱柱是直三棱柱，如图，取中点，中点，连结，，则垂直底面，又，，、分别是两底面三角形外接圆的圆心，故球心在上且是的中点，四边形是平行四边形，，，又，，，，，，，，， ，， ，故选．11已知三棱锥中，，，则三棱锥的外接球的表面积为．答案．解答由题意知，是对棱相等的三棱锥，则三棱锥的六条棱可以是长方体的面对角线，如下图所示：则的外接球与长方体外接球相同，，．外12在三棱柱中，已知底面为正三角形，平面，，，则该三棱柱外接球的表面积为（）A．B．C．D．答案A解答取中点为点，连接，设的外心为，三棱柱外接球球心为，连接，，为正三角形，点为的重心，又，，， ，则 ，又平面，平面，为直角三角形， ， ，则外接球表面积 ，故选．13矩形中，，，沿将矩形折起，使面面，则四面体的外接球的体积为（）A．B．C．D．答案C解答如图所示，取中点，则中，，在中，，，即为外接球球心，半径，又，，体积，故选．14已知矩形，，，为的中点现分别沿，将，翻折，使点，重合，记为点，则几何体的外接球表面积为．答案．解答由，，为中点，可得，，，，为长方体一角，其外接球直径为其体对角线长，，，外接球表面积为．15如图，边长为的正方形中，点，分别是边，的中点，、、分别沿、、折起，使，，三点重合于点，若四面体的四个顶点在同一个球面上，则该球的半径为（）A．B．C．D．答案B解答由题意知为等腰直角三角形，即，且，，，巩固练习：平面，四面体的外接球与以四面体扩展的长方体外接球是同一个，，故选．16如果一个球的外切圆锥的高是这个球的半径的倍，则圆锥的侧面面积和球的表面积之比为（ ）A ．B ．C ．D ．答案C解答如图所示，由于球的外切圆锥的高为球半径的倍，图中为球心，，，为圆锥的高，则设，，，与相似，又，，，，圆锥侧面积为侧，球的表面积为球，圆锥的侧面面积和球的表面积之比为：侧球,故选．17已知三棱锥的所有顶点都在球的球面上，是边长为的正三角形，为球的直径，且，则此棱锥的体积为（ ）A ．B ．C ．D ．答案A 解答如图，取中点，则为外接球球心，过点作底面，由于底面三角形是正三角形，所以是底面三角形的中心，连结并延长交于点，过点作交于点，则是三棱锥的高，正三角形边长为，，，又，，，，又 ，三棱锥 ，故正确．18设三棱柱的侧棱垂直于底面，所有棱的长都为，顶点都在一个球面上，则该球的表面积为（）A．B．C．D．答案B解答由题意可知，该球的球心在两底面中心的连线的中点处，则球的半径，该球的表面积为：，故选．19已知圆锥的高为，底面圆的半径为，它的顶点和底面的圆周都在同一个球的球面上，则该球的表面积为（）A．B．C．D．答案B解答如图所示，设为球心，为底面圆心，则，，，在中，，即，解得，表面积，故选．20底面边长为的正三棱锥的内切球半径为，则其外接球的表面积为（）A．B．C．D．答案A解答由题可知：设该正三棱锥为，底面所对应的正三角形的高为，则，，，，，即，解得，，设外接球的半径为，则可建立勾股定理得，，解得，由球的的表面积得，　，故选．21在长方体中，，是的中点，则三棱锥外接球的表面积为（）A．B．C．D．答案B解答如图，取中点，中点，连接，则平面，点为的外心，三棱锥外接球圆心在上，连接，则，平面平面，，又，，，设，则，，即，解得，点与点重合，，，表故选．22已知正四棱锥的各顶点都在同一球面上，底面正方形的边长为，若该正四棱锥的体积为，则此球的体积为 （）A．B．C．D．答案C解答设正四棱锥的高为，外接球半径为，，，该棱锥底面外接圆半径，该外接球球心所在圆截面如图所示，，，，该外接球体积为，故选．23已知三棱锥中，底面，，，，，则该三棱锥的内切球的体积为．答案．解答设内切球的半径为，以球心为顶点，三棱锥的三个面作为底面把大三棱锥分为四个小三棱锥，则可由等体积法得：大的三棱锥体积等于四个小三棱锥体积之和，又底面，，，，，，，，又，，由等体积得，，，由球的体积得，　．24将棱长为的正方体木块削成一个体积最大的球，则该球的体积为（）A．B．C．D．答案A解答将正方体木块削成一个体积最大的球，即求该正方体内切球的体积，则该球的半径为，，球故选．25点，，，在同一个球面上，，，若球的表面积为，则四面体体积最大值为（）A．B．C．D．答案C解答设球的半径为，则，，又，，，为等腰直角三角形，设为斜边上的中点，则为外接圆圆心，设为球心，则面，在中，，又为定值，最大，即为到面的距离最大，延长交球于，此时最大，有，，故选．26在正四面体中，是棱的中点，是棱上一动点，的最小值为，则该正四面体的外接球面积是．答案．解答由题可得，将正四面体展开成菱形，连接，交于，如图所示，则长即为最小值，即，，为中点，，设，，由余弦定理得，，，，正四面体棱长为，将正四面体可补形为正方体，棱长为正方体面对角线，补形得正方体棱长为，其外接球半径为，其外接球表面积为．27已知在直角梯形中，，，，将直角梯形沿折叠成三棱锥，当三棱锥的体积取最大值时，其外接球的体积为．答案．解答由题意，直角梯形中，，，，如图所示，取的中点，连接，连接、交于点，，直角梯形中，，四边形是正方形，，，将其沿折叠成三棱锥如下图所示：，为点到平面的距离，当平面平面时，最大，即有最大值，连接，平面平面，，平面，平面，，在中，，，，外接球的球心在点上，半径，．外接球28三棱锥中，平面，，的面积为，则三棱锥的外接球体积的最小值为（）A．B．C．D．答案D解答如图，平面，平面，，，设，则，在中，，令的外接圆半径为，则，三棱锥外接球直径为，，当且仅当，即时，等号成立，，即三棱锥的外接球体积最小值为，故选．29三棱锥内接于半径为的球，过球心，当三棱锥体积取得最大值时，三棱锥的表面积为（）A．B．C．D．答案D解答三棱锥内接于半径为的球，过球心，如下图所示，当在点的正上方，时，三棱锥体积最大，此时，，，，与是正三角形，，，表故选．30如图，在三棱锥中，平面平面，，，现将一小球放入三棱锥内，往三棱锥内注水，当注水的体积是三棱锥的体积的时，小球恰与该三棱锥各侧面及水面相切（小球完全浮在水面上方），则小球的表面积等于．答案．解答如下图，分别取、、、中点、、、，连接，，，，，，设则，，，，，，，相似比都是，，，公共，≌，，，面，面，又，面面，，为中点，，平面平面，平面平面，，面，已证面面，面，，，，同理可得，， ，，，，，，，，即，，，即面是水面，≌，，，，面，面，，，，，，，，，同理可得，，表表 ，球 ．31已知三棱柱的侧棱垂直于底面，该棱柱的体积为，，，，若在该三棱柱内部有一个球，则此球表面积的最大值为（）A．B．C．D．答案C解答，，，可知为直角三角形，，，设内切圆半径为，可知，，，内切圆半径为，又柱体的体积为，且侧棱垂直于底面，，，，可知在该三棱柱内部有一个球的最大半径为，由球的表面积得：　，故选．32正三棱锥的高为，底面边长为，内有一个球与它的四个面都相切．(1)棱锥的表面积；(2)内切球的表面积与体积．(1)答案．解答正三棱锥的高为，底面边长为，可知底面正三角形的高为，可得侧面等腰三角形的高为，，可知表底侧 ．(2)答案表面积，体积．解答设球的半径为，以球心为顶点，棱锥的四个面为底面，把正三棱锥分为三个小三棱锥，则根据等体积得：，，由球的表面积公式得：，由球的体积公式得：．33边长为的等边的三个顶点，，都在以为球心的球面上，若球的表面积为，则三棱锥的体积为．答案．解答设球的半径为，，，连接外接圆圆心与球心，，如图所示，平面，，在等边三角形中，，，，又， ．34已知球面上有四个点，，，，球心为点，在上，若三棱锥的体积的最大值为，则该球的表面积为．答案．解答由题可得，为三棱锥外接球直径，当为等腰直角三角形，底面面积最大，面面，且等腰时，过点到平面的高最大，此时，高就是．此时，，三棱锥体积为 ，，球的表面积为．35在三棱锥中，平面，，，，，则该三棱锥的外接球表面积为．答案．解答在中，由余弦定理得，，，由正弦定理可得，外接圆直径为，平面，，三棱锥外接球半径为，，该外接球的表面积为．36已知三棱锥的所有顶点都在球的球面上，是球的直径．若平面平面，，，三棱锥的体积为，则球的表面积为．答案解答设球的半径为，是球的直径，，，三角形与三角形都是等腰直角三角形，有，且、．平面平面，，是等腰直角三角形，且面．三棱锥的体积为，，解得．球的表面积为：．37一个几何体的三视图如图所示，其中正视图是一个正三角形，俯视图是一个等腰直角三角形，则该几何体的外接球的表面积为．答案．解答由三视图可知该几何体为三棱锥，作出原图如下：其中面平面，，平面，其外接球的球心在上，设球心为，，则，解得，外接球的半径，外接球的表面积为．38如图，网格纸上小正方形的边长为，粗实线画出的是某几何体的三视图，若该几何体的顶点都在球的球画上，则球的表面积是（）A．B．C．D．答案A解答由三视图可知：该几何体为三棱锥，如图所示，则有面，，且，，，故其外接球半径，其表面积，故选．39在三棱锥中，，，，的中点为，的余弦值是，若，，，都在同一球面上，则该球的表面积是（）A．B．C．D．答案C解答根据题意作出下图，，，，又为中点，，为等边三角形，则，根据余弦定理：， ， ，，，，，，，，，面，面，面，，又，，面，又，三棱锥可看成长方体一角，外接圆半径， ， ，，球 ， ，故选．40在三棱锥中，，，，，，且三棱锥的外接球的表面积为，则（）A．B．C．D．答案B解答，，，，为，，又，，、均在面内，面，又，外接圆半径①，又外接球表面积为，，②，联立①②可得，（舍去），故选．41已知，，，是球的球面上四个不同的点，若，且平面平面，则球的表面积为（）A．B．C．D．答案A解答分别取和的外心，，分别过，作平面和平面的垂线相交于点，即为球心，取中点，连接，，则，，如图所示：，出门测（15分钟）可知，又、为三角形的外心，，四边形为正方形，且边长为，， ，球的半径为，球的表面积，故选．42已知三棱锥的所有顶点都在球的球面上，是球的直径，是等腰直角三角形，，若，三棱锥的体积是，则球的表面积为．答案．解答可将三棱锥在长方体中还原，如图所示，，，，，，三棱锥的外接球与长方体的外接球相同，，球的表面积为．43直三棱柱中，已知，，，，若三棱柱的所有顶点都在同一球面上，则该球的表面积为．答案．解答在直棱柱中，，故可将其变形为长方体，其中，、、为长方体的棱，该三棱柱外接球半径为：，该外接球表面积为．44已知圆锥的侧面展开图是一个半径为的半圆，若该圆锥的顶点及底面圆周在球的表面上，则球的体积为（）A．B．C．D．答案A解答设圆锥的高为，底面圆的半径为，，，，，球即该圆锥的外接球，设球的半径为，，，，球的体积为：，故选．45如图，虚线小方格是边长为的正方形，粗实（虚）线为某几何体的三视图，则该几何体外接球的表面积为（）A．B．C．D．答案D解答由题可得，该几何体的直观图如图所示，其中，，即为该几何体外接球直径，由三视图可得，，，该外接球的表面积为，故选．46如图，网格纸上小正方形的边长为，粗线画出的是某三棱锥的三视图，则该三棱锥的外接球的表面积为（）A．B．C．D．答案B解答由题意可知该几何体是三菱锥，把该三棱锥放入长宽高分别为，，的长方体中，则该三棱锥的外接球，即为长方形的外接球，如图所示：且外接球的直径为，所以该外接球表面记为，故选．47如图，在四面体中，平面，是边长为的等边三角形．若，则四面体外接球的表面积为．答案．解答由正弦定理可得，正的外接圆直径为，设四面体的外接球半径为，平面，，，，四面体外接球的表面积为．48某三棱锥的三视图如图所示，其侧（左）视图为直角三角形，则该三棱锥外接球的表面积为（）A．B．C．D．答案A解答该几何体的直观图如图所示：由三视图及图象可知：、、两两垂直，则三棱锥可补为以、为邻边的长方形为底面，为侧棱的长方体，其外接球半径为，外接球表面积．49中国古代数学专著《九章算术》系统地总结了战国、秦、汉时期的数学成就．书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑．如图为一个阳马与一个鳖臑的组合体，已知三棱锥为鳖臑，且平面，，，该鳖臑的外接球的表面积为，则阳马的外接球的体积为（）A．B．C．D．答案D解答由题可得，在三棱锥中，，平面，，，即、、两两垂直，三棱锥的外接球直径，设，，三棱锥的外接球表面积为，，，，在阳马四棱锥中，、、两两垂直，其外接球直径为，，，其外接球的体积为，故选．41。

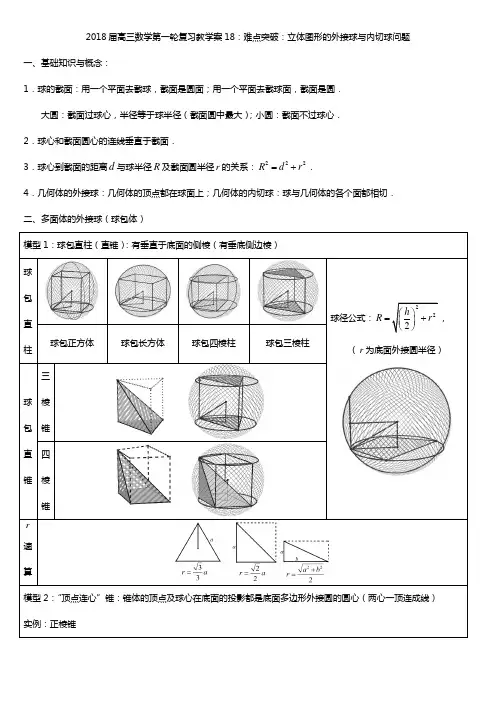
2018届高三数学第一轮复习教学案18：难点突破：立体图形的外接球与内切球问题一、基础知识与概念：1．球的截面：用一个平面去截球，截面是圆面；用一个平面去截球面，截面是圆．大圆：截面过球心，半径等于球半径（截面圆中最大）；小圆：截面不过球心．2．球心和截面圆心的连线垂直于截面．3．球心到截面的距离d与球半径R及截面圆半径r的关系：222R d r=+．4．几何体的外接球：几何体的顶点都在球面上；几何体的内切球：球与几何体的各个面都相切．二、多面体的外接球（球包体）模型1：球包直柱（直锥）：有垂直于底面的侧棱（有垂底侧边棱）球包直柱球径公式：222hR r⎛⎫=+⎪⎝⎭，（r为底面外接圆半径）球包正方体球包长方体球包四棱柱球包三棱柱球包直锥三棱锥四棱锥r速算模型2：“顶点连心”锥：锥体的顶点及球心在底面的投影都是底面多边形外接圆的圆心（两心一顶连成线）实例：正棱锥球径计算方程：()222h R r R -+=2222202h r h hR r R h+⇒-+=⇒=，（h 为棱锥的高，r 为底面外接圆半径） 特别地，（1）边长为a 正四面体的外接球半径：R =______________．（2）底面边长为a ，高为h 的正三棱锥的外接球半径：R =__________． （3）底面边长为a ，高为h 的正四棱锥的外接球半径：R =__________．例：1．（2017年全国卷III 第8题）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为A ．πB ．34πC ．2π D ．4π 【解析】模式辨识：“球包体”中的“垂底侧边棱（母线）”类型，1h =，1R =，底面半径为r ，则由222h R r⎛⎫=+ ⎪⎝⎭得：222213124r r ⎛⎫=+⇒= ⎪⎝⎭，234V r h ππ==．2．（2010年全国新课标卷第10题）设三棱柱的侧棱垂直于底面，所有棱的长都为a ，顶点都在一个球面上，则该球的表面积为A ．2a πB ．273a πC ．2113a πD ．25a π【解析】“球包体”中的“垂底侧边棱”类型，h a =，3r =，222222724312h a a a R r ⎛⎫=+=+= ⎪⎝⎭， 所以该球的表面积2227744123a a S R ππ==⨯=．答案B ． 3．（2014年全国大纲卷第8题）正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为A ．814πB ．16πC ．9πD ．274π【解析】模式辨识：“球包体”中的“顶点连心锥”，4h =，222r ==221629284h r R h ++===， 所以2818144164S R πππ==⨯=，答案：A ． 4．（2013年全国卷I 第6题）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为A ．35003cm πB ．38663cm πC ．313723cm πD ．320483cm π【解析】设水面与球的接触点（切点）为P ，球心为O ，则PO 垂直于正方体的上表面，依题意P 到正方体上表面的距离为2h =，球与正方体上表面相交圆的半径4r =，有：()2222R r R -+=，2454r R +⇒==，所以球的体积3450033V R ππ==． 三、定心大法：球心在过截面圆的圆心且垂直于截面圆所在平面的直线上．两圆定心法：如下图，过两个截面圆的圆心分别作相应截面圆的垂线，由两垂线的交点确定圆心．例2：1．已知边长为23的棱形ABCD 中，60∠=︒，现沿对角线BD 折起，使得二面角A BD C --为120︒，此时点A ，B ，C ，D 在同一个球面上，则该球的表面积为（ ）A ．20πB ．24πC ．28πD ．32π2．在矩形ABCD 中，4AB =，3BC =，沿AC 将矩形折成一个直二面角B AC D --，则四面体ABCD 的外接球的体积为___________．3．在边长为1的菱形ABCD 中，60BAD ∠=︒，沿对角线将菱形折成直二面角A BD C --，则三棱锥A BCD -的外接球的表面积为_____________． 四、正多面体的内切球（体中球）锥体的内切球：R =____________．圆锥的内切球：R =边长为a 的正方体： 2aR =等边圆柱（母线a ）：R =2a ． 边长a 的正八面体：R =五、正多面体的“切边球”（与所有的棱都相切的球）正四面体边长为a ，球半径R =正方体边长为a ，球半径R =正四面体边长为a ，球半径R =例3：1．一个球的外切正方体的全面积为6，则球的体积为_________．2．某圆锥的截面为边长为2的正三角形，则该圆锥的内切球的表面积为_______．3．（2016年全国卷III 第10题）在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球，若AB BC ⊥，6AB =，8BC =，13AA =，则V 的最大值是A ．4πB ．92πC ．6πD ．323π【解析】考查直三棱柱中截面的内切圆为球的大圆的情景，有()13681068222AA R R ++=⨯⇒=>=，故当球半径为32时球的体积最大为344273382V R πππ9==⨯=．答案B ． 练习：1．（2015年全国卷II 第9题）已知A ，B 是球O 的球面上两点，90AOB ∠=︒，C 为该球面上的动点，若三棱锥O ABC -体积的最大值为36，则球O 的表面积为A ．36πB ．64πC ．144πD ．256π2．（2016年福建漳州市5月质检）三棱锥S ABC -中，SB ⊥平面ABC ，5SB =ABC ∆3的正三角形，则三棱锥S ABC -的外接球的表面积为（）A ．3πB ．5πC ．9πD ．12π3．（2014年湖南卷）一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于（ ）A ．1B ．2C ．3D ．44．（2013年辽宁卷理10）已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上，若3AB =，4AC =，AB AC ⊥，112AA =，则球O 的半径为（）A 317B ．10C ．132D ．3105．（2012年全国新课标卷第11题）已知三棱锥S ABC -的所有顶点都在球O 的球面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =，则此棱锥的体积为A ．26B ．36C ．23D ．226．在正三棱锥P ABC -中，3PA PB PC ===，侧棱PA 与底面ABC 所成的角为60︒，则该三棱锥外接球的体积为（ ）A ．πB ．3πC ．4πD ．43π 7．已知底面边长为12的正四棱柱的各顶点均在同一个球面上，则该球的体积为（ ）A ．323πB ．4πC ．2πD ．43π 8．（2017年福建省质检）．空间四边形ABCD 的四个顶点都在同一球面上，E 、F 分别是AB 、CD 的中点，且,EF AB EF CD ⊥⊥，若8,4AB CD EF ===，则该球的半径等于A ．65216B ．28C ．652D 659．若三棱锥P ABC -的最长的棱2PA =，且各面均为直角三角形，则此三棱锥的外接球的体积是__________． 10．（2008年高考浙江卷理14）已知球O 的面上四点A 、B 、C 、D ，DA ⊥平面ABC ，AB BC ⊥，3DA AB BC ===，则球O 的体积为____________．11．（2016年东北三省三校联考）三棱柱111ABC A B C -各顶点都在一个球面上，侧棱与底面垂直，120ACB ∠=︒，23CA CB ==14AA =，则这个球的表面积为____________．12．在三棱柱111ABC A B C -中，侧棱1AA 垂直底面，90ACB ∠=︒，30BAC ∠=︒，1BC =，且三棱柱111ABC A B C -的体积为3，则三棱柱111ABC A B C -的外接球表面积为_________．13．在正三棱锥S ABC -中，M ，N 分别是棱SC 、BC 的中点，且AM MN ⊥，若侧棱23SA =，则正三棱锥S ABC -外接球的表面积是____________．14．在三棱锥A BCD -中，2AB CD ==，5AD BC ==7AC BD ==，则三棱锥A BCD -外接球的表面积为__________．15．（2017年天津卷）已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为______．16．（2017年江苏卷）如图，在圆柱12O O 内有一个球，该球与圆柱的上、下底面及母线均相切，记圆柱12O O 的体积为1V ，球O 的体积为2V ，则12V V 的值是_____________．。

空间几何体的外接球与内切球问题高考分析： 球与几何体的切接问题是近几年高考的高频考点，常以选择题和填空题的形式出现，以中档题和偏难题为主. 一、几种常见几何体的外接与内切球 1.长方体的外接球 (1)球心：体对角线的交点；(2)半径：R ＝a 2＋b 2＋c 22(a ，b ，c 为长方体的长、宽、高)．2.正方体的外接球、内切球及与各条棱相切的球 (1)外接球：球心是正方体的中心；半径R ＝32a(a 为正方体的棱长)； (2)内切球：球心是正方体的中心；半径r ＝2a(a 为正方体的棱长)；(3)与各条棱都相切的球：球心是正方体的中心；半径=2r a (a 为正方体的棱长)． 3.正四面体的外接球与内切球(1)外接球：球心是正四面体的中心；半径R (a 为正四面体的棱长)；(2)内切球：球心是正四面体的中心；半径r (a 为正四面体的棱长)．求外接球问题常用方法：1.补体法。

将几何体补形成长方体正方体等常见模型去求解2.外接球的球心都在过底面外接圆圆心的垂线上（注意球体可以滚动所以可以选择较为方便计算的那一面作为底面）3.利用外接球球心到几何体各顶点距离都等于半径4.球心与截面圆圆心的连线垂直于截面圆求外接球的关键是确定球心位置，进而计算出外接球半径。

题型一：柱体的外接球1.已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为_________．2.已知三棱柱111ABC A B C －的底面是边长为6的正三角形，侧棱垂直于底面，且该三棱柱的外接球的表面积为12 ，则该三棱柱的体积为_________．3.已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是( )A ．16πB ．20πC ．24πD ．32π4.已知圆柱的底面半径为12，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为( )A.πB.3π4 C.π2 D.π4题型二：锥体的外接球5.求棱长为1的正四面体外接球的体积为_________．6.已知正四棱锥P －ABCD 内接于一个半径为R 的球，则正四棱锥P －ABCD 体积的最大值是( )A.16R 381B.32R 381C.64R 381 D ．R 3 7.如图，在四棱锥P －ABCD 中，底面ABCD 为菱形，PB ⊥底面ABCD ，O 为对角线AC 与BD 的交点，若PB ＝1，∠APB ＝∠BAD ＝π3，则三棱锥P －AOB 的外接球的体积是_________．8.已知△ABC 是面积为的等边三角形，且其顶点都在球O 的球面上.若球O 的表面积为16π，则O 到平面ABC 的距离为（ ） A.B.C. 1D.9.已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC 的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为（ ）A. 64πB. 48πC. 36πD. 32π10.《九章算术》中对一些特殊的几何体有特定的称谓，例如：将底面为直角三角形的直三棱柱称为堑堵．将一堑堵沿其一顶点与相对的棱切开，得到一个阳马(底面是长方形，且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均是直角三角形的四面体)．在如图所示的堑堵ABC －A 1B 1C 1中，AA 1＝AC ＝5，AB ＝3，BC ＝4，则阳马C 1－ABB 1A 1的外接球的表面积是( )A ．25πB ．50πC ．100πD ．200π11.已知三棱锥P −ABC 的四个顶点在球O 的球面上，PA =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°，则球O 的体积为 A ．68πB ．64πC ．62πD ．6π12.已知正三棱锥的所有顶点都在球O 的球面上，其底面边长为3，E,F ,G 分别为为侧棱AB,AC,AD 的中点.若O 在三棱锥A -BCD 内，且三棱锥A -BCD 的体积是三棱锥O -BCD 体积的3倍，则平面EFG 截球O 所得截面的面积为微专题 球与几何体的切接问题——内切球1.半径为R 的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为_________，体积为_________．2.若正四面体的棱长为a ，则其内切球的半径为_________．3.已知正三棱锥的高为6，内切球(与四个面都相切)的表面积为16π，则其底面边长为( ) A ．18 B ．12 C ．6 3 D ．434.将半径为3，圆心角为2π3的扇形围成一个圆锥(接缝处忽略不计)，则该圆锥的内切球的体积为( )A.2π3 B.3π3 C.4π3D ．2π 5.如图，已知球O 是棱长为1的正方体ABCD －A 1B 1C 1D 1的内切球，则平面ACD 1截球O 的截面面积为( )A.66π B.π3 C.π6 D.33π题型三 最值问题6.已知底面是正六边形的六棱锥P －ABCDEF 的七个顶点均在球O 的表面上，底面正六边形的边长为1，若该六棱锥体积的最大值为3，则球O 的表面积为_________．7.四棱锥S －ABCD 的所有顶点都在同一球面上，底面ABCD 是正方形且和球心O 在同一平面内，当此四棱锥的体积取得最大值时，其表面积等于8＋83，则球O 的体积等于( )A.32π3B.322π3 C ．16π D.162π38.已知SAB 是边上为2的等边三角形，045ACB ∠=，则三棱锥体积最大时，CA = ;其外接球的表面积为。

高三数学《空间几何体的外接球》教案一、教学内容分析空间几何体的外接球问题是近几年高考的热点，这类题目对学生而言比较抽象，较难找到解题的切入点与突破口，为此，本节课将梳理有关外接球常用几种模型，总结一般题型的方法与套路，这就要求学生能够熟悉常见的模型，比如：长方体模型、柱体模型、锥体模型等，同时，希望通过本节课学生能够将空间问题转化为平面问题。

二、学生学情分析空间几何体的外接球问题是近几年高考的热点，主要以选择、填空题形式出现，考查载体主要是柱体。

锥体为主，对空间想象能力要求较高，解题的关键是找出球半径和线面的关系，这就要求学生能够熟悉常见的模型，能够将空间问题转化为平面问题。

本人任教的班级是高三8班，理科平行班级，学生基础不是很好，空间想象能力不强，因此针对本班的实际情况，我将近几年的与空间几何体外接球有关高考题进行了分类，总结出三种模型，供学生直接运用到题目中。

三、教学目标分析1、掌握空间几何体外接球的常见模型，并熟悉每种模型采用的方法。

2、培养学生的空间想象能力，将空间问题能够转化成平面问题。

四、教学设计过程回顾高考：近几年新课标全国卷空间几何体外接球试题在考查题型、考查载体、考查能力、解题方法等方面呈现怎样的特征?试题特点近几年与空间几何体外接球有关的高考题，需要学生能够确定球的半径或者确定球心的位置，其中球心的确定是关键，考查学生的空间想象能力，运用体和球之间的主要位置关系和数量关系，从而把空间问题化为平面问题，进而运用平面几何的知识寻找球半径的解法。

高三数学《空间几何体的外接球》教案2.问题设置本节课的3个例题所涉及到的函数相同,都是,这样设计的好处在于避免在函数的理解、认识上以及计算上浪费时间,将时间尽量集中在切线问题的处理方法上,凸显本节课的主题.其次,这3个例题逐步递进,难度逐渐加大.问题梯度明确,例1起点不高,学生比较容易解决,但由于审题原因,容易犯错误,例2问题不再单一,不仅要用到切线问题的处理方法,还需要用到转化与化归的思想,函数与方程思想以及数形结合思想,有一定的综合性.例3在题意的理解上,问题的处理上难度较大,在问题的解决中不仅用到了转化与化归的思想,数形结合思想,还用到了构造的思想,对学生来说是一个巨大的挑战.这样设计体现了新课程“分层推进、逐渐深化”的课程理念.有助于逐步加深学生对切线问题的认识,激发学生的学习积极性和求知欲.3.教学过程教学过程的设计经过3次大的修改.第1次修改在经过第1次试讲以后,发现的问题是时间不够,主题不鲜明,基础知识的讲解不全面.要回顾导数的几何意义,就必需复习导数的几何意义的推导,因此就得复习导数的定义.经过备课组老师的讨论,修改如下:第一个部分导数的几何意义的主要内容变为:(1)导数的定义;(2)切线的定义;(3)导数的几何意义;(4)有关切线的两点说明:第1点是切线与曲线的公共点个数问题.第2点是切线与曲线的位置关系问题.这两点以问题教学的方式进行复习.第1点是为例1,例2的讲解作好知识铺垫,第2点是为例3的讲解作好知识铺垫.第2次修改在经过第2次试讲后,发现时间还是不够,课堂节奏太快,学生思考讨论时间太少.主要原因在于讲解有关切线的两点说明这个内容所用时间大概有10来分钟,不仅没有为后面例题的讲解起到应有的帮助,而且冲淡了本节课的主题.因此第2次修改将有关切线的两点说明这个内容去掉.将第一部分的内容改为:(1)内容;(2)推导,包括3个部分:①导数的定义;②切线的定义;③两个定义的关系;(3)作用.并且明确了本节课的核心为:切线方程.主线为:切点切线方程切线问题.第3次修改在经过第3次试讲后,前面基础知识的讲解时间大概在10分钟左右,但是由于后面例题分析,引导,讲解,板书所用时间较长,因此例3没有讲完,就匆匆小结.经过备课组的讨论,对例3的讲解变为只给学生分析,引导思路.把例3的求解过程留成作业让学生课后完成.这样一来,就可以留出较多的时间让学生思考交流,以及进行课堂小结,升华本节课的内容与方法.本节课的教学设计最终完成.高三数学《空间几何体的外接球》教案4.板书设计由于例1,例2,例3所用的方法是一样的,所以在板书过程中有些内容例1写完后,例2,例3不用重新写,只需要进行个别地方的修改.例3重在分析思路,过程可用多媒体展示.这样的设计就能节约大量时间.5.课后作业课后两个题都是高考原题.实质上例2,例3就是从这两个高考题提炼出来的.这样设计在于保证例题设置不会偏离高考方向,有助于学生感受高考试题的类型和难度,更好的备战高考.。

《空间几何体的外接球》教学设计方案《《空间几何体的外接球》教学设计方案》这是优秀的教学设计文章，希望可以对您的学习工作中带来帮助！学习主题介绍学习主题名称：《空间几何体的外接球》主题内容简介：通过例题发现与探究空间几何体的外接球问题，并归纳长方体、直三棱柱、可以补形为直三棱柱的三棱锥、正棱锥的外接球的求解方法。

学习目标分析知识目标：理解空间几何体外接球的特征与性质，掌握几种常见几何体的外接球的求解方法。

能力目标：培养学生观察、分析、归纳、推理的能力；在掌握求解长方体和直三棱柱的外接球的前提下，通过方法迁移与问题化归来研究可以补形为直三棱柱的三棱锥的外接球的方法，培养学生的知识、方法迁移能力；培养学生自主探究、合作探究的能力；提高分析问题和解决问题的能力。

情感目标：培养学生善于观察，勇于探究的创新精神，提高直观想象的核心素养。

学情分析前需知识掌握情况：本节课之前，学生已经在高二时学过了立体几何，对空间几何体的结构特征、体积和面积的相关公式已经比较熟悉了。

在高三高考第一轮复习时，学生对知识的掌握有点回生，并且之前也没有全面地对各种几何体的外接球求解方法进行系统的归纳与总结。

学生直观想象以及作图能力有所欠缺，在解立体几何问题过程中经常出现方法不懂、运算出错的问题。

对微课的认识：现在的网络教学比较普遍，高三学生或多或少已经有接触过，而微课相对于网络课更简洁、更有针对性，学生对微课更有新鲜感和期待。

微课可重复播放，能帮助学困生避免似懂非懂，而又无法重构课堂老师讲解的场面，学生通过多次学习微课可以熟练掌握知识与方法，进而解决问题。

微课也有利于学生分层教学，提高教学的针对性和效率。

学生特征分析学习态度：利用微课进行辅助教学或自主学习，能给学生提供直观的画面，学生会更加感兴趣，学习也更加的专注。

学习风格：微课的画面感和动画感比较强，并且课件制作精良。

老师所制作的微课也是通过多次的演练而成，授课的过程语言简洁，分析问题精准到位，往往能激发学生的学习热情。

《空间几何体的外接球》教学设计一、课标要求三维空间是人类生存的现实空间，认识空间图形、培养和发展学生的空间想象能力、推理论证能力、运用图形语言进行交流的能力以及几何直观能力，是高中阶段数学必修系列课程的。

基本要求：1、认识柱、锥、台、球极其简单组合体的结构特征；2、了解球、棱柱、棱锥、台的表面积和体积的计算公式.二、教学分析：纵观近几年高考题，几何体的外接球问题在高考中既是考查的热点又是考查的难点。

与球有关的几何体问题能很好地考查学生的空间想象能力以及化归转化能力.本节课我们将着重研究三、教学目标1、掌握确定球心、求解半径的方法。

2、通过同类问题的变式探究，培养学生空间问题平面化、几何问题代数化的能力，深刻体会化归的数学思想；通过对问题难度的升级及总结，锻炼学生的几何直观和空间想象能力，培养学生的数学直观想象素养.四、教学重难点教学重点：会求正棱柱、正棱锥及一般三棱锥的外接球半径；教学难点：确定多面体外接球的球心并求出半径.五、教法分析本节课针对高三年级学生的认知特点，在遵循启发式教学原则的基础上，借助多媒体用讲授法、讨论法、练习法等教学方法，引导学生探索以正方体或长方体的顶点为顶点的三棱锥的结构特点，由浅入深的研究三棱锥与球相联系的桥梁。

本节课坚持以学生为主体，教学中让学生自主地“做数学”，将传统意义下的“学习”数学改变为“研究”数学。

从而，使传授知识与培养能力融为一体，在转变学习方式的同时学会数学地思考。

五、教学过程教学环节教学内容与问题设置设计意图复习回顾引入新课回顾下列知识：1.球的表面积公式：_________2.球的体积公式:______________3.长方体体对角线的求法:______________4.利用正弦定理求三角形外接圆的半径:____________5. 球的性质性质1：用一个平面去截球，截面是________；用一个平面去截球面，截线是_____。

大圆截面过________，半径等于_________；小圆截面不过______性质2: 球心和截面圆心的连线垂直于________．性质3: 球心到截面的距离 d 与球的半径R 及截面的半径r 下面的关系:____________知识准备。

空间几何体的外接球和内切球问题空间几何体的外接球和内切球问题类型1 外接球的问题1.必备知识：(1)简单多面体外接球的球心的结论.结论1：正方体或长方体的外接球的球心是其体对角线的中点.结论2：正棱柱的外接球的球心是上下底面中心的连线的中点.结论3：直三棱柱的外接球的球心是上下底面三角形外心的连线的中点.(2)构造正方体或长方体确定球心.(3)利用球心O 与截面圆圆心O 1的连线垂直于截面圆及球心O 与弦中点的连线垂直于弦的性质，确定球心.2.方法技巧：（1）几何体补成正方体或长方体.（2）轴截面法（3）空间向量法1AB DC AD BC BD AC ======例1-1、正四面体的棱长都为，求此四面体外接球和内切球的半径例1-2、四面体中，， 求此四面体外接球的表面积 例1-3．若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（ ）A.3B.6C.36D.9训练1（创新110页） 某几何体的三视图如图所示，则该几何体的外接球的表面积为( )A.25πB.26πC.32πD.36π训练2（创新110页）已知边长为2的等边三角形ABC ，D 为BC 的中点，沿AD 进行折叠，使折叠后的∠BDC ＝π2，则过A ，B ，C ，D 四点的球的表面积为( ) A.3π B.4π C.5π D.6π例2-1（创新110页）体积为3的三棱锥P －ABC 的顶点都在球O 的球面上，P A ⊥平面ABC ，P A ＝2，∠ABC ＝120°，则球O 的体积的最小值为( ) A.773π B.2873π C.19193π D.76193π 例2-1（创新109页）三棱锥P －ABC 中，平面P AC ⊥平面ABC ，AB ⊥AC ，P A ＝PC ＝AC ＝2，AB ＝4，则三棱锥P －ABC 的外接球的表面积为( )A.23πB.234πC.64πD.643π 类型2 内切球问题1.必备知识：(1)内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等.(2)正多面体的内切球和外接球的球心重合. (3)正棱锥的内切球和外接球球心都在高线上，但不一定重合.2.方法技巧：体积分割是求内切球半径的通用做法.【例3】 体积为4π3的球与正三棱柱的所有面均相切，则该棱柱的体积为________. 空间几何体的外接球和内切球问题近几年高考题1、（2019全国1卷第12题）已知三棱锥P ABC -的四个顶点在球O 的球面上，PA PB PC ==，△ABC 是边长为2的正三角形，E ，F 分别是PA ，PB 的中点，90CEF ∠=︒，则球O 的体积为（ ）A ．B ．C ． D2、（2018全国3卷第10题）．设A B C D ，，，是同一个半径为4的球的球面上四点，ABC △为等边三角形且其面积为D ABC -体积的最大值为（ ）A ．B ．C ．D ．3．（2017全国1卷第16题）如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O .D ，E ，F 为圆O 上的点，△DBC ，△ECA ，△FAB 分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ，CA ，AB 为折痕折起△DBC ，△ECA ，△FAB ，使得D ，E ，F 重合，得到三棱锥．当△ABC 的边长变化时，所得三棱锥体积(单位：cm 3)的最大值为______．4、（2017新课标全国Ⅲ理科）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（ ）A.πB.3π4 C.π2 D.π4 5、（2016年全国1卷第6题）．如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3，则它的表面积是 ( )（A ）17π （B ）18π （C ）20π （D ）28π6、（2016年全国3卷第10题）在封闭的直三棱柱ABC −A 1B 1C 1内有一个体积为V 的球，若AB ⊥BC ，AB =6，BC =8，AA 1=3，则V 的最大值是( ) (A)4π (B)9π2 (C)6π (D)32π37、（2015年全国1卷第11题）．圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20π，则r=（ ）（A ） 1 （B）2 （C ）4 （D ）88、（2015年全国2卷第9题）．已知是球的球面上两点,,为该球面上的动点.若三棱锥体积的最大值为36,则球的表面积为（ ） A ．36πB ．64πC ．144πD ．256π 7.(2014·大纲全国，8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4，底面边长为2，则该球的表面积为( )A.81π4B.16πC.9πD.27π49、（2013年课标1卷第6题）、如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为( )A 、500π3cm 3B 、866π3cm 3C 、1372π3cm 3D 、2048π3cm 310、（2012课标卷第11题）已知三棱锥S ABC -的所有顶点都在球O 的求面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =；则此棱锥的体积为（ ）()A 26 ()B 36 ()C 23 ()D 2211、（2011课标卷第15题）已知矩形的顶点都在半径为4的球的球面上，且,则棱锥的体积为 。