广东金融学院期末考试试题(B)概率论与数理统计

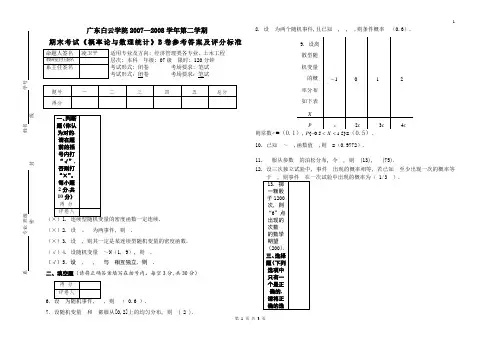
广东白云学院2007—2008学年第二学期期末考试《概率论与数理统计》B卷参考答案及评分标准适用专业及方向: 经济管理类各专业、土木工程层次: 本科年级: 07级限时: 120分钟考试形式: 闭卷考场要求: 笔试考试形式：闭卷考场要求：笔试.（×）2. 设、为两事件, 则.（×）3. 设, 则其一定是某连续型随机变量的密度函数.（√）4. 设随机变量～N（1, 9）, 则.（√）5．设, , 与相互独立, 则.二、填空题（请将正确答案填写在括号内。

每空3分,共30分）, 则（ 0.6 ）.7．设随机变量和都服从[0,2]上的均匀分布, 则( 2 ).8. 设为两个随机事件,且已知, , ,则条件概率（0.6）.则常数c=（0.1）,}5.15.0{<<-XP=（0.5）.10. 已知～,函数值,则=（0.9772）.11. 服从参数的泊松分布, 令, 则(13), (75).12. 设三次独立试验中, 事件出现的概率相等, 若已知至少出现一次的概率等1/3 ）.,则下列关系成立的是（ C ）A. B.C. D.15．同时抛掷3枚均匀的硬币, 则恰好有两枚正面朝上的概率为（ D ）A. 0.5B. 0.125C. 0.25D. 0.37516. 10张奖券中含有3张中奖的奖券,每人购买一张,则第3个购买者中奖的概率为（ B ）A. B. 0.3 C. D.17. 设连续型随机变量服从参数为的指数分布,若方差,则数学期望（ B ）A. B. C. D.18. 如果离散型随机变量相互独立,且服从参数为的泊松分布,则当充分大时,离散型随机变量（ D ）近似服从标准正态分布.A. B. C. D.19. 设连续型随机变量的概率密度为,则（ A ）A. B. C.D.四、计算题（每小题8分,共32分）(1)若事件BA,互不相容,求α; (2)若事件BA,相互独立,求α.解 (1)因为BA,互不相容,所以φ=AB, (1分)所以)()()()(BPABPBPBAP=-= (2分)而)(1)()()()(APBAPBPAPBAP-=-+=(3分)所以α=0.3 (4分)(2)因为BA,相互独立,则A与B也相互独立, (5分))())(1)(()()()()()(BPBPAPBPAPBPAPBAP+-=-+=（7分）所以α=73（8分）21. 某产品主要由三个厂家供货.甲、乙、丙三个厂家的产品分别占总数的15%,80%,5%,其次品率分别为0.02,0.01,0.03,试计算(1)从这批产品中任取一件是不合格品的概率;(2)已知从这批产品中随机地取出的一件是不合格品,问这件产品由哪个厂家生产的可能性最大?解记=A{所取一件产品是不合格品},321,,BBB分别表示”产品来自甲、乙、丙厂” (1分) 依题意有:15.0)(1=BP, 80.0)(2=BP,05.0)(3=BP02.0)(1=BAP,01.0)(2=BAP,03.0)(3=BAP (2分) (1)由全概率公式0125.0)()()(31==∑=iiiBPBAPAP (5分) (2)由贝叶斯公式24.00125.002.015.0)()()()(111=⨯==APBAPBPABP, (6分)64.00125.001.080.0)()()()(222=⨯==APBAPBPABP, (7分)12.00125.003.005.0)()()()(333=⨯==A PB A P B P A B P (8分) 22.设连续型随机变量X 的密度函数⎩⎨⎧<<=其他020)(2x Ax x ϕ,求(1)常数A ;(2))(),(X D X E .解 因为138)(202===⎰⎰∞+∞-A dx Ax dx x ϕ (2分) 所以 83=A (3分)所以 ⎪⎩⎪⎨⎧<<=其他2083)(2x xx ϕ2383)()(203===⎰⎰∞+∞-dx x dx x x X E ϕ (5分) 51283)()(20422===⎰⎰∞+∞-dx x dx x x X E ϕ (7分) 20323512)]([)()(222=⎪⎭⎫ ⎝⎛-=-=X E X E X D (8分) 23. 已知电站供电网有10000盏电灯, 夜晚每一盏灯开灯的概率都是0.7, 而假定开、关时间彼此独立, 试用切贝谢夫不等式估计夜晚同时开着的灯数在6800与7200之间的概率。

《概率分析与数理统计》期末考试试题及
解答(DOC)
概率分析与数理统计期末考试试题及解答
选择题
1. 以下哪个选项不是概率的性质？
- A. 非负性
- B. 有界性
- C. 可加性
- D. 全备性
答案：B. 有界性
2. 离散随机变量的概率分布可以通过哪个方法来表示？
- A. 概率分布函数
- B. 累积分布函数
- C. 概率密度函数
- D. 方差公式
答案：B. 累积分布函数
计算题
3. 一批产品有10% 的不合格品。

从该批产品中随机抽查5个，计算至少有一个不合格品的概率。

解答：
设事件 A 为至少有一个不合格品的概率，事件 A 的对立事件
为没有不合格品的概率。

不合格品的概率为 0.1，合格品的概率为 0.9。

则没有不合格品的概率为 (0.9)^5。

至少有一个不合格品的概率为 1 - (0.9)^5，约为 0.409。

4. 一个骰子投掷两次，计算至少一次出现的点数大于3的概率。

解答：
设事件 A 为至少一次出现的点数大于3的概率，事件 A 的对立事件为两次投掷点数都小于等于3的概率。

一个骰子点数大于3的概率为 3/6 = 1/2。

两次投掷点数都小于等于3的概率为 (1/2)^2 = 1/4。

至少一次出现的点数大于3的概率为 1 - 1/4，约为 0.75。

以上是《概率分析与数理统计》期末考试的部分试题及解答。

希望对你有帮助！。

概率论与数理统计期末试卷及答案一、是非题（共7分，每题1分）1．设A ,B ,C 为随机事件，则A 与C B A ⋃⋃是互不相容的. （ ） 2．)(x F 是正态随机变量的分布函数，则)(1)(x F x F -≠-. （ ） 3．若随机变量X 与Y 独立，它们取1与1-的概率均为5.0，则Y X =. （ ）4．等边三角形域上二维均匀分布的边缘分布仍是均匀分布. （ ） 5. 样本均值的平方2X 不是总体期望平方2μ的无偏估计. （ ） 6．在给定的置信度α-1下，被估参数的置信区间不一定惟一. （ ） 7．在参数的假设检验中，拒绝域的形式是根据备择假设1H 而确定的. （ ）二、选择题（15分，每题3分）（1）设A B ⊂，则下面正确的等式是 。

（ａ）)(1)(A P AB P -=； （ｂ）)()()(A P B P A B P -=-； （ｃ）)()|(B P A B P =； （ｄ）)()|(A P B A P =（2）离散型随机变量X 的概率分布为kA k X P λ==)(( ,2,1=k )的充要条件是 。

（ａ）1)1(-+=A λ且0>A ； （ｂ）λ-=1A 且10<<λ； （ｃ）11-=-λA 且1<λ； （ｄ）0>A 且10<<λ.（3）设10个电子管的寿命i X (10~1=i )独立同分布，且A X D i =)((10~1=i )，则10个电子管的平均寿命Y 的方差=)(Y D .（ａ）A ； （ｂ）A 1.0； （ｃ）A 2.0； （ｄ）A 10.（4）设),,,(21n X X X 为总体)1,0(~N X 的一个样本，X 为样本均值，2S 为样本方差，则有 。

（ａ）)1,0(~N X ； （ｂ）)1,0(~N X n ； （ｃ）)1(~/-n t S X ； （ｄ）)1,1(~/)1(2221--∑=n F XX n ni i.（5）设),,,(21n X X X 为总体),(2σμN (μ已知)的一个样本，X 为样本均值，则在总体方差2σ的下列估计量中，为无偏估计量的是 。

广东金融学院期末考试试题一、选择题（共40分）1.下列不属于金融机构的是：a.银行b.保险公司c.证券公司d.超市2.金融市场的主要功能不包括：a.资金融通b.风险管理c.资产评估d.产品交易3.下列哪个是金融市场中的主流市场：a.股票市场b.大宗商品市场c.期货市场d.二手车市场4.存款准备金率是指商业银行必须向央行存放的：a.存款金额b.公司资产c.存款准备金d.利润5.利率水平主要受以下哪个因素影响：a.通货膨胀预期b.股价变动c.外汇市场波动d.社会舆论6.中国人民银行是：a.国际货币基金组织b.开发性金融机构c.非营利机构d.银行业监管机构7.货币政策的目标不包括：a.维护汇率稳定b.促进经济增长c.控制通货膨胀d.增加就业岗位8.金融工具的种类不包括：a.股票b.债券c.期货d.汽车9.下列不属于金融市场参与者的是：a.个人投资者b.金融机构c.政府部门d.电商平台10.金融市场监管的机构是：a.证券监管委员会b.人民银行c.中央银行d.所有选项都对二、填空题（共30分）1.金融市场具有流动性高、风险大的特点。

2.央行通过调整存款准备金率来影响商业银行的资本金比例。

3.股票市场是进行股票买卖的主要场所。

4.金融市场的交易方式包括场内交易和场外交易。

5.货币政策的工具主要有利率和存款准备金率。

6.债券市场是进行债券买卖的主要场所。

7.金融衍生品市场是进行期货买卖的主要场所。

8.在中国，货币政策的决策权属于中国人民银行。

9.金融机构主要有银行、证券公司、保险公司等。

10.金融市场的核心是资金交换。

三、判断题（共30分）1.金融机构只包括银行和保险公司。

（错误）2.股票市场是进行股票买卖的主要场所。

（正确）3.货币政策对经济发展没有影响。

（错误）4.金融市场的功能只有融资和投资。

（错误）5.存款准备金率的调整可以影响货币供应量。

（正确）6.利率水平主要受到政府财政支出的影响。

（错误）7.股票和债券属于金融工具。

广东金融学院期末考试试题（B ）(闭卷 120分钟)一、填空题（每题3分，共24分）1. 一批零件共有100个，其中10个不合格品，从中一个一个取出，则第三次才取得不合格品的概率为 .2. 设随机变量X 的密度函数为0()00xe x p x x -⎧>=⎨≤⎩，则(2)E X += .3. 设随机变量X 服从正态分布2(10,2)N ，则35~X + .4. 设随机变量X 的二阶矩存在，且()4D X =,()1E X =则X 的变异系数()v C X = .5. 已知随机变量12,X X 相互独立，且1~(0,6)X U ，2~(1,3)X N ,则12(2)E X X -=6. 两点分布的特征函数为()t ϕ= .7. 若(,)0Cov X Y >，则称X 与Y ，若(,)0Cov X Y <，则称X 与Y .8.设X 与Y 是两个相互独立的连续随机变量，其密度函数为分别为()X p x 和()Y p y ，则其和Z X Y =+的密度函数为 .二、（6分）已知1()4P A =,1()2P B A =,1()3P A B =,求()P A B ⋃. 三、（10分）一个学生在做一道有4个选项的单项选择题时，如果他不知道问题的正确答案时，就做随机猜测，现从卷面上看题是答对了，试在以下情况下求该学生确实知道正确答案的概率.（1）该学生知道正确答案和胡乱猜测的概率都是1/2；（2）该学生知道正确答案的概率是1/5。

四、（10分）设随机变量X 的密度函数为cos 2()02A x x p x x ππ⎧≤⎪⎪=⎨⎪>⎪⎩，试求（1）系数A ；（2）X 落在区间(0,/4)π的概率。

五、（10分）设随机变量X 服从区间(0,3)上的均匀分布，（1）求52Y X =+的密度函数；（2）求(1)P Y <.六、（10分）设(,)X Y 的联合密度函数为2360,0(,)0x ye x y p x y --⎧>>=⎨⎩其他；试求（1）(,)X Y 的联合分布函数(,)F x y ；（2）(1,1)P X Y <>；（3）()P X Y >.七、（10分）若二维随机变量(,)X Y 的联合密度函数为101,(,)0x y x p x y ⎧<<<=⎨⎩其他， 试求：（1）边际密度函数()X p x ，()Y p y ；（2）(1/2)P X <.八、（10分）设二维随机变量(,)X Y 的联合密度函数为1,01(,)0y x x p x y ⎧<<<=⎨⎩其他；试求()E X ,()E Y 与(,)Cov X Y . 九、（10分）一复杂系统由100个相互独立工作的部件组成，每个部件正常工作的概率为0.9，已知整个系统中至少有85个部件正常工作，系统工作才正常，试求系统正常工作的概率。

海南师范大学物理、电子、自动化、地理、城规、计算机专业《概率论与数理统计》 2009—2010学年度第一学期期末考试（B ）卷答案与评分标准注意事项：1. 考前请将密封线内填写清楚 2. 所有答案请直接答在试卷上3．考试形式：闭卷4. 本试卷共五大题，满分100分， 考试时间100分钟一、单项选择题（本题共六小题，每小题3分，共18分。

在每小题列出的四个选项中只有一个是符合题目要求的，请将其代码填在题后的括号内。

错选或未选均无分）1、将3个不同的球随机地放入4个不同的杯中, 有一个杯子放入2个球的概率是（ B ）.. A ：324234C C ⋅; B ：324234P C ⋅ ; C ：424233P C ⋅; D ：424233C C ⋅.2、下列函数中，可看作某一随机变量X 的概率分布密度函数的是( C ) A ：;,1)(2+∞<<-∞+=x x x f B ：;,11)(2+∞<<-∞+=x xx fC ：;,)1(1)(2+∞<<-∞+=x x x f π; D ：.,)1(2)(2+∞<<-∞+=x x x f π3、己知随机变量Y X ,相互独立且都服从正态分布)4 ,2(N , 则( B ) . A ：)4 ,4(～N Y X +； B ：)8 ,4(～N Y X + ； C ：)4 ,0(～N Y X -； D ：Y X -不服从正态分布.4、己知随机变量X 服从二项分布)2.0 ,10(B , 则方差=)(X D （ D ）. A ：1； B ：0.5； C ：0.8； D ：1.6.5、己知随机变量X 的期望5)(=X E , 方差4)(=X D , 则（ A ）. A ：98}65-X {≥<P ； B ：98}65-X {≤<P ； C ：98}65-X {≥≥P ； D ：98}65-X {≤≥P .6、设4321,,,X X X X 是来自正态总体) ,(2σμN 的简单随机样本，下列四个μ的无偏估计量中,最有效的是( D ). A ：)(313211X X X ++=μ； B ：)2(413214X X X ++=μ； C ：)32(613213X X X ++=μ； D ：)(4143212X X X X +++=μ.二、填空题（将答案直接填入栝号内，本题共六小题，每小题3分，共18分）1、设B A 与为随机事件,3.0)(,5.0)(==AB P A P ，则条件概率=)(A B P ( 0.6 )2、已知随机变量X 服从区间,10]2[内的均匀分布，X 的概率分布函数为),(x F 则=)4(F （ 0.25 ）。

华中农业大学本科课程考试 参考答案与评分标准考试课程：概率论与数理统计 学年学期： 试卷类型：B 考试日期：一、单项选择题（从下列各题四个备选答案中选出一个正确答案，并将其字母代号写在该题【 】内。

答案错选或未选者，该题不得分。

每小题2分，共10分。

） 1. 设随机变量X 的概率密度)1(1)(2x x p +=π，则X Y 2=的分布密度为 . 【 b 】 (a))41(12x +π； (b) )4(22x +π； (c) )1(12x +π； (d) x arctan 1π． 2. 设随机变量序列x 1, x 2,…, x n …相互独立,并且都服从参数为1/2的指数分布,则当n 充分大时,随机变量Y n =∑=ni i x n 11的概率分布近似服从 . 【 b 】(a) N(2,4) (b) N(2,4/n) (c) N(1/2,1/4n) (d) N(2n,4n)3. 设总体X 服从正态分布),(N 2σμ，其中μ已知，2σ未知，321X ,X ,X 是总体X 的一个 简单随机样本，则下列表达式中不是统计量的是 ． 【 C 】（a ）321X X X ++； （b ）)X ,X ,X min(321； （c ）∑=σ31i 22i X ； （d ）μ+2X ．4．在假设检验问题中，检验水平α意义是 ． 【 a 】 （a ）原假设H 0成立，经检验被拒绝的概率； （b ）原假设H 0成立，经检验不能拒绝的概率； （c ）原假设H 0不成立，经检验被拒绝的概率； （d ）原假设H 0不成立，经检验不能拒绝的概率．5．在线性回归分析中，以下命题中，错误的是 . 【 d 】（a ）SSR 越大，SSE 越小； （b ）SSE 越小，回归效果越好； （c ）r 越大，回归效果越好； （d ）r 越小，SSR 越大．二、填空题（将答案写在该题横线上。

答案错选或未选者，该题不得分。

每小题2分，共10分。

)B =________________.3个,恰好抽到),(8ak ==(24)P X -<= 乙企业生产的50件产品中有四、(本题12分)设二维随机向量(,)X Y 的联合分布律为\01210.10.20.120.10.2Y X a 试求: (1) a 的值; (2)X 与Y 的边缘分布律; (3)X 与Y 是否独立?为什么?五、(本题12分) 设随机变量X 的概率密度为(),01,2,12,0,.x x f x x x ≤<⎧⎪=-≤≤⎨⎪⎩其他 求()(),E X D X一、填空题(每小题3分,共30分) 1、ABC 或AB C 2、0.6 3、2156311C C C 或411或0.3636 4、1 5、136、2014131555kX p 7、1 8、(2,1)N -二、解 设12,A A 分别表示取出的产品为甲企业和乙企业生产,B 表示取出的零件为次品,则由已知有 1212606505121101(),(),(|),(|)1101111011605505P A P A P B A P B A ======== .................. 2分 (1)由全概率公式得112261511()()(|)()(|)1151155P B P A P B A P A P B A =+=⨯+⨯= ............................................ 7分 (2)由贝叶斯公式得22251()()5115()1()115P A P B A P A B P B ⨯=== ................................................................................. 12分三、(本题12分)解 (1)由概率密度的性质知 340391()21224x f x dx kxdx dx k +∞-∞⎛⎫=+-=+= ⎪⎝⎭⎰⎰⎰故16k =. ..................................................................................................................................................... 3分 (2)当0x ≤时,()()0xF x f t dt -∞==⎰;当03x <<时, 2011()()612xxF x f t dt tdt x -∞===⎰⎰; 当34x ≤<时, 320311()()223624x x t F x f t dt tdt dt x x -∞⎛⎫==+-=-+- ⎪⎝⎭⎰⎰⎰;当4x ≥时, 34031()()2162x t F x f t dt tdt dt -∞⎛⎫==+-= ⎪⎝⎭⎰⎰⎰;故X 的分布函数为220,01,0312()123,3441,4x x x F x x x x x ≤⎧⎪⎪<<⎪=⎨⎪-+-≤<⎪⎪≥⎩.......................................................................................... 9分(3) 77151411(1)22161248P X F F ⎧⎫⎛⎫<≤=-=-=⎨⎬ ⎪⎩⎭⎝⎭....................................................................... 12分四、解 (1)由分布律的性质知 01.0.20.10.10.a +++++= 故0.3a = .................................................................................................................................................... 4分(2)(,)X Y 分别关于X 和Y 的边缘分布律为0120.40.30.3X p ........................................................................................................................ 6分120.40.6Y p .................................................................................................................................. 8分(3)由于{}0,10.1P X Y ===,{}{}010.40.40.16P X P Y ===⨯=,故 {}{}{}0,101P X Y P X P Y ==≠== 所以X 与Y 不相互独立. ............................................................................................................................ 12分 五、(本题12分) 设随机变量X 的概率密度为(),01,2,12,0,.x x f x x x ≤<⎧⎪=-≤≤⎨⎪⎩其他求()(),E X D X .解 2131223201011()()d d (2)d 1.33x E X xf x x x x x x x x x +∞-∞⎡⎤⎡⎤==+-=+-=⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰⎰ ................................ 6分122232017()()d d (2)d 6E X x f x x x x x x x +∞-∞==+-=⎰⎰⎰................................................................... 9分 221()()[()].6D XE X E X =-= ........................................................................................................ 12分一、填空题（每空3分，共45分）1、已知P(A) = 0.92, P(B) = 0.93, P(B|A ) = 0.85, 则P(A|B ) = P( A ∪B) =2、设事件A 与B 独立，A 与B 都不发生的概率为19，A 发生且B 不发生的概率与B 发生且A 不发生的概率相等，则A 发生的概率为： ；3、一间宿舍内住有6个同学，求他们之中恰好有4个人的生日在同一个月份的概率： 没有任何人的生日在同一个月份的概率4、已知随机变量X 的密度函数为：,0()1/4,020,2x Ae x x x x ϕ⎧<⎪=≤<⎨⎪≥⎩, 则常数A= ,分布函数F (x )= , 概率{0.51}P X -<<= ；5、设随机变量X~ B(2，p)、Y~ B(1，p)，若{1}5/9P X ≥=，则p = ，若X 与Y 独立，则Z=max(X,Y)的分布律： ；6、设~(200,0.01),~(4),X B Y P 且X 与Y 相互独立，则D(2X-3Y)= , 1、 (12分)设连续型随机变量X 的密度函数为：1,02()20,x x x ϕ⎧≤≤⎪=⎨⎪⎩其它求：1）{|21|2}P X -<；2）2Y X =的密度函数()Y y ϕ；3）(21)E X -；2、(12分)设随机变量(X,Y)的密度函数为1）1/4,||,02,(,)0,y x x x y ϕ<<<⎧=⎨⎩其他求边缘密度函数(),()X Y x y ϕϕ；2） 问X 与Y 是否独立？是否相关？计算Z = X + Y 的密度函数()Z z ϕ1、（10分）设某人从外地赶来参加紧急会议，他乘火车、轮船、汽车或飞机来的概率分别是3/10，1/5，1/10和2/5。