三种射线及典型题分析

三射线定理及其典型应用2015年10月21日 意琦行 数海拾贝三射线定理 如图，、、分别是从出发的三条射线，、、分别为、、，二面角（记其大小为）满足：三射线定理描述了异面共边的两个角的另外两边构成的角（空间斜角）与这两个角形成的二面角（空间正角）之间的数量关系，因此往往用来求二面角的大小或者空间斜角的大小．三射线定理中的基本图形又称为三面角．证明 如图，过射线上一点作垂直于的平面，射线、分别与该平面相交于、两点．方法一 利用空间向量根据已知，有PA PB PC P ∠APC ∠BPC ∠APB αβθA −PC −B φcos θ=cos α⋅cos β+sin α⋅sin β⋅cos φ.PC H PC PA PB M N ⋅PM −→−−−PN −→−−=(+)⋅(+)PH −→−−HM −→−−−PH −→−−HN −→−−−=P +⋅H 2HM −→−−−HN−→−−−=P +HM ⋅HN ⋅cos φ,H2又于是两边同除以得方法二 利用余弦定理在三角形和三角形中分别应用余弦定理，有两式相减得移项整理即得．三射线定理的记忆 可以借助两角差的余弦公式记忆，当时，三射线定理退化为两角和与差的余弦公式．当时，三射线定理变成著名的三余弦定理：接下来通过两道例题说明该定理在空间求角时的作用．例1 （知斜求正）如图，在直角三角形中，为直角，，，、分别是、上的点，且，，将沿折起到的位置，使．求平面与平面所成锐角的余弦值．⋅=PM ⋅PN cos θ,PM−→−−−PN −→−−PM ⋅PN cos θ=cos α⋅cos β+sin α⋅sin β⋅cos φ.MNP MNH MN 2MN 2=M +N −2⋅MP ⋅NP ⋅cos θ,P 2P 2=M +N −2⋅MH ⋅NH ⋅cos φ,H 2H 20=2P −2⋅MP ⋅NP ⋅cos θ+2⋅MH ⋅NH ⋅cos φ,H 2φ=0,πφ=π2cos θ=cos α⋅cos β.ABC C BC =3AC =6D E AC AB DE ∥BC DE =2△ADE DE △DE A 1D ⊥CD A 1CD A 1BE A 1解 这是一道由2012年高考北京卷理科数学第16题改编的习题．如图，在底面里分别延长和，交于（实际上就是在未折叠的三角形还原在直观图中），于是所求的锐角就是二面角的大小．我们可以利用三面角中解决问题．令，，，，而于是解得BCDE CD BE A ABC C −A −B A 1A −DE A 1∠AD =αA 1∠EA =βA 1∠CAB =θC −A −B =φA 1cos α=,cos β=,cos θ=,2√22√5√25√=⋅+⋅⋅cos φ,25√2√22√5√2√23√5√cos φ=.6√3事实上，取的中点，则即为二面角的平面角．例2（知正求斜）如图，在长方形中，，，为中点，为线段（端点除外）上一动点．现将沿折起，使平面与平面垂直．在平面内过点作，为垂足．设，则的取值范围是_______．解 这是2009年高考浙江卷理科数学第17题．我们可以利用三面角解决问题．令，，，且，于是可得即于是其取值范围不难求得为．接下来给出两道练习题．练习1、如图，是半径为的球的球心，点、、在球面上，、、两两垂直，、分别是大圆弧与A A 1M ∠DME C −A −B A 1ABCD AB =2BC =1E DC F EC △AFD AF ABD ABC ABD D DK ⊥AB K AK =t t A −DKF ∠DAK =α∠FAK =β∠DAF =θD −AK −F =π2cos ∠DAF =cos ∠DAK ⋅cos ∠FAK ,=⋅,DA AF AK AD DF AFAK =,AD 2DF(,1)12O 1A B C OA OB OC E F AB AC的中点，则点、在该球面上的球面距离是_______．练习2、如图，一个正四面体和一个正四棱锥的所有棱长均为，将正四面体与正四棱锥组合起来，使得正四面体的其中一个面与正四棱锥的一个侧面重合．问得到的多面体有多少个面？参考答案练习1、练习2、组合体为三棱柱，有个面．更多的内容可以参考：《每日一题[46] 三射线定理》《每日一题[154] 折叠中的二面角》《每日一题[202] 又见三射线》《每日一题[255] 代表平面—出击！》E F 1π35每日一题[46] 三射线定理2015年3月5日 意琦行 数海拾贝已知二面角为，，，，与成角，则异面直线与所成角的余弦值为________．正确答案是．事实上，我们有一般的结论（三射线定理）．如图，、、分别是从出发的三条射线，、、分别为、、，则二面角（记其大小为）满足：证明如下：过射线上一点作垂直于的平面，射线、分别与该平面相交于、两点，则α−AB −β120∘CD ⊂αCD ⊥AB EF ⊂βEF AB 30∘CD EF14PA PB PC P ∠APC ∠BPC ∠APB αβθA −PC −B φcos θ=cos α⋅cos β+sin α⋅sin β⋅cos φ.PC H PC PA PB M N −→−−−−→−−−→−−−→−−−−→−−−→−−−又于是两边同除以得在今天的这道试题中，应用三射线定理，有于是所求值为．⋅PM −→−−−PN −→−−=(+)⋅(+)PH −→−−HM −→−−−PH −→−−HN −→−−−=P +⋅H 2HM −→−−−HN −→−−−=P +HM ⋅HN ⋅cos φ,H 2⋅=PM ⋅PN cos θ,PM −→−−−PN −→−−PM ⋅PN cos θ=cos α⋅cos β+sin α⋅sin β⋅cos φ.cos θ=cos ⋅cos +sin ⋅sin ⋅cos =−,30∘90∘30∘90∘120∘1414每日一题[154] 折叠中的二面角2015年6月22日 意琦行 数海拾贝2015年高考浙江卷理科数学第8题（选择压轴题）：如图，已知三角形，是的中点，沿直线将三角形折成三角形，所成二面角的平面角为，则（）A ．B ．C ．D ．正确答案是B．得到答案是容易的，可以取以下两种极端情形进行排除：ABC D AB CD ACD CD A ′−CD −B A ′α∠DB ⩽αA ′∠DB ⩾αA ′∠CB ⩽αA ′∠CB ⩾αA′当时，显然，而，排除D；当时，显然，而，排除A、C．下面证明选项B是正确的．如图，在平面内过作线段垂直于，且，亦为的中点．设在折叠过程中，的对应点为，则根据二面角的平面角的定义有．若线段与线段重合，那么就有，命题成立；若线段不于线段重合，那么和分别位于直线两侧，于是和分别位于平面两侧．进而在三角形和三角形中，且，于是．而在三角形和三角形中，且，于是，于是命题成立．注 也可以利用三射线定理结合，有α=π∠DB =∠ADB =πA ′∠CB =∠ACB <πA ′α=0∠DB =∠DB >0A ′A ′′∠CB =∠CB >0A ′A ′′ABC D MN CD AB =MN D MN M M ′α=∠DN M ′MN AB ∠DN =∠DB M ′A ′MN AB A B MN A ′B DN M ′DB A ′DB M ′D =D M ′A ′B >B A ′M ′∠DB >∠DB A ′M ′DB M ′DN M ′DN =DB B >N M ′M ′∠DB >∠DN M ′M ′cos ∠DB =cos ∠DC cos ∠BDC +sin ∠DC sin ∠BDC cos α,A ′A ′A ′∠DC +∠BDC =πA ′1+cos ∠DB =(1+cos α)⋅sin ∠DC sin ∠BDC ,A ′A′因此考虑到余弦函数在内单调递减，于是命题成立．cos ∠DB ⩽cos α,A ′[0,π]每日一题[202] 又见三射线2015年8月9日 意琦行 数海拾贝2014年全国高中数学联赛山东省预赛第5题：已知直角三角形的两条直角边，，为斜边上一点，将将此三角形折成直二面角，当时，二面角的值为_______．正确答案是．如图，在平面内过作直二面角的棱的垂线交边于，则．于是在平面中过作二面角的棱的垂线，垂足为，连接，则为二面角的平面角，且．根据每日一题[46] 三射线定理，有于是ABC AC =2BC =3P AB CP A −CP −B AB =7√P −AC −B arctan 2√PCB P A −CP −B CP BC E EP ⊥ACP PAC P P −AC −B AC D DE ∠PDE P −AC −B tan ∠PDE =EP PDcos ∠ACB =cos ∠ACP ⋅cos ∠BCP ,+−222解得如图．因此所求二面角的值为．=cos ∠ACP ⋅sin ∠ACP ,A +B −A C 2C 2B 22⋅AC ⋅BC∠ACP =,π4P −AC −B arctan 2√每日一题[255] 代表平面—出击！2015年10月1日 意琦行 数海拾贝已知平面和相交形成的四个二面角中的其中一个为，则在空间中过某定点与这两个平面所成的线面角均为的直线条数为_______．正确答案是．解 我们知道，研究空间的角度问题时，平面与其他空间图形所成的角度往往依托其法线进行计算．换句话说，平面的法线是平面方向的代表．在这个问题中，设平面与平面过点的法线分别为、，则．而此时条件直线与两个平面所成的线面角为可以转化为直线与直线、所成的角均为．如图，平面上的两条直线（所成角为）的平分线——为互相垂直的两条直线——在运动过程中始终保持与两条直线所成的角相等，且该角的取值范围分别为以及．因此当，而与两条直线所成角均为时对应的直线为条．αβ60∘P 30∘l 3αβP m n ⟨m ,n ⟩=60∘l 30∘l m n 60∘θ[,]θ2π2[,]π−θ2π2θ=60∘60∘3下面给出一个练习题．将一个水平放置的正方形绕直线向上转动到，再将所得正方形绕直线向上转动到，则平面与平面所成二面角的正弦值是_______．（）提示 可以化为法线问题后应用三射线定理，可以参考 每日一题[46]三射线定理，以及 每日一题[202] 又见三射线定理．ABCD AB 45∘ABC 1D 1ABC 1D 1BC 145∘B A 2C 1D 2B A 2C 1D 2ABCD 3√2。

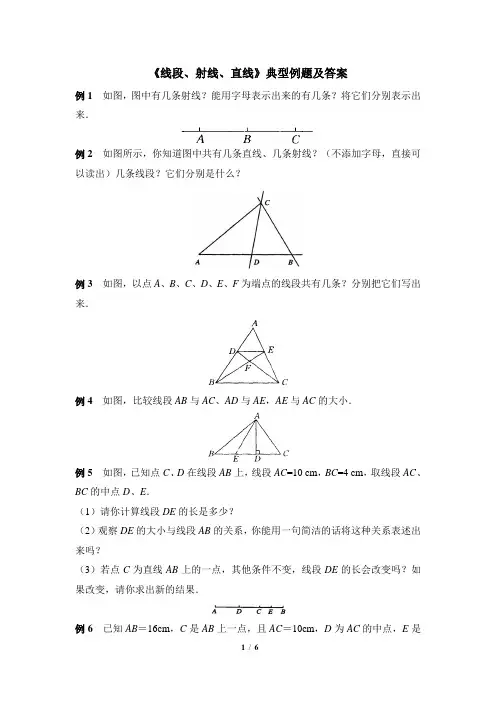
《线段、射线、直线》典型例题及答案例1 如图，图中有几条射线？能用字母表示出来的有几条？将它们分别表示出来．例2 如图所示，你知道图中共有几条直线、几条射线？（不添加字母，直接可以读出）几条线段？它们分别是什么？例3如图，以点A、B、C、D、E、F为端点的线段共有几条？分别把它们写出来．例4如图，比较线段AB与AC、AD与AE，AE与AC的大小．例5如图，已知点C、D在线段AB上，线段AC=10 cm，BC=4 cm，取线段AC、BC的中点D、E．（1）请你计算线段DE的长是多少？（2）观察DE的大小与线段AB的关系，你能用一句简洁的话将这种关系表述出来吗？（3）若点C为直线AB上的一点，其他条件不变，线段DE的长会改变吗？如果改变，请你求出新的结果．例6 已知AB＝16cm，C是AB上一点，且AC＝10cm，D为AC的中点，E是BC的中点，求线段DE的长．例7 （1）过一个已知点可以画多少条直线？（2）过两个已知点可以画多少条直线？（3）过平面上三点A、B、C中的任意两点可以画多少条直线？（4）试猜想过平面上四点A、B、C、D中的任意两点可以画多少条直线？例8 如图，A、B是两个车站，若要在公路l上修建一个加油站，如何使它到车站A、B的离和最小，请在公路l上标出点P的位置，并说明理由．AlB参考答案例1 分析：直线上的一点将直线分成两条射线，因此以A为端点的射线有两条，同样道理以B、C为端点的射线也分别有两条．因此共有6条射线，能用图中字母表示出来的有4条．解：图中共有6条射线，能用图中字母表示出来的有4条，分别为：射线AB、射线BC、射线BA、射线、CA．说明：要抓住直线上一点将直线分成两条射线，数射线时不能重复或遗漏，抓住端点和方向，表示射线时，要将端点的字母写在前面．例2 解：图中有2条直线，分别是直线BC、直线DC．图中有6条可以直接读出的射线，分别是射线CD、DC、CB、BC、AB、DB．图中有6条线段，分别是线段AD、BD、AB、CA、CD、CB．说明：（1）直线是最基本、简单、抽象的几何图形．直线到底是什么形状呢？可以借助“孙悟空的金箍棒”想象一下，直线没有端点，可以向两方无限延伸；“手电筒发出的光”给我们以射线的形象，射线有一个端点，它可以向一方无限延伸；“一枝铅笔”可以抽象成一条线段，线段有两个端点，它不可延伸，直线和射线都没有长度，线段有长度；（2）直线有两种表示方法（如图1），可以先在直线上任取两个点A、B，这条直线可记作直线AB（或直线BA），也可以用一个小写字母表示，如直线l；射线的两种表示方法分别为射线AB、射线l（如图2），要注意射线AB与射线BA表示不同的射线；线段的两种表示方法分别为线段AB（或线段BA）、线段a（如图3）；（3）数直线时应注意直线BC与直线CB是同一条直线；数射线时要注意射线的两个特征：端点与方向，所以射线AD与射线AB是相同的射线，射线AB与射线DB是不同的射线，因为它们的端点不同，射线DA与射线DB也是不同的射线，因为它们的方向不同；数线段时注意寻求规律，做到不重不漏．如线段CA、CD、CB属不同直线上的三条线段，而线段AD、BD、AB属同一条直线上的三条线段，同一条直线上的线段的数法有两种：①以始点计：AD、AB、DB；②以组成计：单个线段：AB、BC；两条线段组成的：AC．图1 图2 图3另外在同一条直线上的线段总条数s 与直线上点的个数n 之间有如下关系：2)1()1()2(321-=-+-++++=n n n n S ． 例3 分析：在一个三角形中，由于交点众多，为做到不遗漏，不重复，可以按字母的先后顺序找出图中的线段．解：图中共有14条线段，分别为线段AB 、AC 、AD 、AE 、BC 、BD 、BE 、BF 、CD 、CE 、CF 、DE 、DF 、EF ．说明：当点众多时，可以以字母的顺序寻找线段，可以避免出错．例4 分析：比较线段的长度可用度量法和重合法．解法1：用度量法，用直尺测量各线段的长度．比较得：AB ＞AC ，AD ＜AE ，AE ＝AC ．解法2：用叠合法，可用圆规截取比较得：AB ＞AC 、AD ＜AE ，AE ＝AC ．说明：比较线段的大小，就是用度量法和叠合法，但是可以根据题目的的特点选择合适的方法．例5 解：（1）∵AC =10，BC =4，∴AB =AC +BC =14又∵点D 是AC 中点，点E 是BC 中点， ∴BC EC AC DC 21,21==， ∴721)(212121==+=+=+=AB BC AC BC AC CE DC DE （cm ）． （2）由（1）知AB DE 21=，即：线段上任一点把线段分成两部分，这两部分中点间的距离等于原线段长度的一半．（3）DE 的长会改变．可分两种情形考虑：当点C 在线段AB 上时721==AB DE （cm ）． 当点C 在线段AB 外时（如图），3)410(21)(212121=-=-=-=-=BC AC BC AC CE DC DE （cm ）． ∴DE 的长为7 cm 或3 cm ．说明：（1）本题先通过特殊的数值求出线段DE 的长，在求解过程中通过观察、猜测，发现了一般性的结论，我们称之为规律．在学知识或是解题时，不要局限于问题表面，而是要多思考、多总结，从而在更深层次上认识所学内容．（2）此题通过C 点的位置由特殊到一般，由在线段上运动到在直线上运动的变化过程，只要抓住不变量，即CE DC DE ±=，就可以以不变应万变．另外随着条件的逐步开放，结论也发生了变化，有时由于C 点的位置考虑不全面，导致丢解．如果遇到没给出图形的问题，解答时一定要先画图，并全面考虑到所有可能情形．（3）利用中点的性质进行线段长度的计算是解题的关键，若C 是AB 的中点，则它的表达式为AC AB 2=或AB AC BC AB 21,2==或BC AC AB BC ==,21，不同情况下选择不同的表达式，可使书写简洁．例6 分析：根据线段中点的特点，BD CE AC DC 21,21==，而CE DC DE +=，故可根据题设解出DE 的长．解：因为D 是AC 的中点，而E 是BC 的中点，因此有：.21,21BC CE AC DC ==而AB BC AC CE DC DE =++=,． 即).cm (8162121)(212121=⨯==+=+=+=AB BC AC BC AC CE DC DE 说明：充分利用线段中点的特点，将所求线段转移到线段长度上去．例7 解：（1）过一点可以画无数条直线；（2）过两点可以画一条直线；（3）当 A 、B 、C 三点不共线时可以画三条直线，当 A 、B 、C 三点共线时只能画一条直线；（4）当 A 、B 、C 、D 四个点在同一条直线上时，只能画一条直线（如图1）；当 A 、B 、C 、D 四个点中有三个点在同一条直线上时，可以画四条直线（如图2）；当 A 、B 、C 、D 四个点中任意三点都不在同一条直线上时，可以画六条直线（如图3）．图1 图2 图3 说明：题（1）（3）和（4）中没有明确平面上三点、四点是否在一条直线上，解答时要分各种情况，即分类讨论；（2）由此题可知，过平面上三个点中的任意两点最多可以画三条直线，过平面上四个点中的任意两点最多可以画六条直线，如果过平面上n 个点中的任意两点，最多可以画多少条直线呢？分析：根据连接两点的线中，线段最短，只需在A 、B 间作一条线段、与l 的交点，便是它到A 、B 两点距离和最小的点．例8 解：连接A 、B 作线段，与l 的交点P 为所求建加油站的点．因为两点之间，线段最短．说明：利用线段公理，两点之间，线段最短．AB lC。

第四章 几何图形初步4.2 直线、射线、线段一、知识考点知识点1【直线】1、直线：把线段向两端无限延伸形成的图形叫做直线。

2、特点：是直的；无粗细之分；无端点；不可以度量；不可以比较长短，无限长。

3、基本性质：经过两点有且只有一条直线（两点确定一条直线）；4、直线有两种表示方法:（1）用直线上任意两点的大写字母,如:表示为直线AB 或直线BA 。

（2）也可以用一个小写字母表示,如:直线l5、直线和点的位置关系：（1）在直线上:点O 在直线l 上,或者说说直线l 经过点O（2）点在直线外:点P 在直线l 外,或者说说直线l 不经过点P6、交点：当两条不同的直线有一个公共点时，我们就称这两条直线相交，这个公共点叫做他们的交点。

O Pl知识点2【射线】1、射线：将线段向一个方向无限延长，就形成了射线，射线有一个端点。

2、特点：是直的,有一个端点,不可以度量,不可以比较长短,无限长。

3、射线有两种表示方法：（1）可以用两个大写英文字母表示，其中一个是射线的端点,另一个是射线上除端点外的任意的一点,端点写在前面。

(如图：可以记作射线OM,但不能记作射线MO) （2）可以用一个小写英文字母表示,比如:射线OM也可以记为射线l。

4、射线的画法：画射线一要画出射线端点，二要画出射线经过一点,并向一旁延伸的情况。

知识点3【线段】1、线段：直线上两个点和它们之间的部分叫做线段，这两个点叫做线段的端点。

2、特点：线段是直的,它有两个端点,他的长度是有限的,可以度量的,可以比较长短。

3、基本性质：(1) 线段公理：两点之间的所有连线中,线段最短（两点之间，线段最短）(2) 两点之间的距离：两点之间线段的长度，叫做这两点之间的距离。

注意：两点间的距离是指线段的长度,是一个数值,而不是指线段本身。

(3) 线段的中点到两端点的距离相等。

(4) 线段的大小关系和它们的长度的大小关系是一致的4、线段有两种表示方法：（1）可以用它的两个端点的大写英文字母来表示，如线段AB（或线段BA）（2）可以用一个小写字母来表示,如线段a5、线段的画法：用直尺和尺规作图（尺规作图）已知：线段a(如图所示),用直尺和圆规画一条线段,使它等于已知线段a第一步：任意画一条射线AC第二步：用圆规量取已知线段a的长度。

第一讲X射线荧光及其分析原理1、X 射线X 射线是一种电磁波，根据波粒二相性原理，X 射线也是一种粒子，其每个粒子根据下列公式可以找到其能量和波长的一一对应关系. E ＝hv=h c/式中h 为普朗克常数，v 为频率，c 为光速，为波长.可见其能量在0。

1 100（kev ）之间。

X 紫 可 红 微 短 长射 射 外 见线 线 线 光 外 波 波 波 波长X 射线的产生有几种1、高速电子轰击物质，产生韧致辐射和标识辐射。

其产生的韧致辐射的X 射线的能量取决于电子的能量，是一个连续的分布.而标识辐射是一种能量只与其靶材有关的X 射线。

E kev A o().()=123964λ常见的X射线光管就是采用的这种原理.其X射线能量分布如下：强度能量2、同位素X射线源。

同位素在衰变过程中,其原子核释放的能量,被原子的内层电子吸收,吸收后跳出内层轨道，形成内层轨道空位.但由于内层轨道的能级很低,外层电子前来补充，由于外层电子的能量较高，跳到内层后，会释放出光能来，这种能就是X射线.这就是我们常见的同位素X射线源。

由于电子的能级是量化的，故释放的射线的能量也是量化的,而不是连续的.强度能量3、同步辐射源。

电子在同步加速器中运动，作园周运动，有一个恒定的加速度,电子在加速运动时，会释放出X射线，所以用这种方法得到的X射线叫同步辐射X射线。

2、X射线荧光实际上，有很多办法能产生X射线，例如用质子、射线、射线等打在物质上,都可以产生X射线,而人们通常把X射线照射在物质上而产生的次级X射线叫X射线荧光（X—Ray Fluorescence），而把用来照射的X射线叫原级X射线。

所以X射线荧光仍是X射线。

3、特征X射线有人会问，为什么可以用X射线来分析物质的成分呢？这些都归功于特征X射线。

早在用电子轰击阳极靶而产生X射线时,人们就发现，有几个强度很高的X射线，其能量并没有随加速电子用的高压变化，而且不同元素的靶材，其特殊的X射线的能量也不一样，人们把它称为特征X射线，它是每种元素所特有的。

《线段、射线、直线》典型例题及解析例题1 下面是四个图形和就每一个图形给出的一句话，其中所有图形都是画在同一平面上的．①线段AB与射线MN不相交．②点M在线段AB上③直线a与直线b不相交．④延长线射线AB，则会通过点C．其中，正确语句的个数是（）A．0 B．1 C．2 D．3分析“射线MN”不仅告诉我们MN是一条射线，还表示点M是射线的端点．既然如此，图①中的射线MN就是向右无限伸展的，确定与线段AB不相交．“点M在线段AB上”与“点M在线段AB的上方”含义是不同的，语句②不正确．直线是向两个方向无限伸展的，图中③的a、b是相交的．射线AB是从点A出发且由A至B的方向无限延伸的图形，不存在延长的问题，所以语句④不对．解选B说明线段、射线、直线，以及将要学到的角、圆等图形的表示方法，是数学语言的组成部分，可谓“言简意赅”，读者一定要清楚地知道其含义，而不可只会“照葫芦画瓢”．简单明了是数学语言的特点之一，同学们要细心体会，学会使用．例题2 如图，有七个点，其中在同一条直线上，其他任何三个点都不在同一直线上，如果画过其中每两个点的直线，共计可以画多少条？分析（1）点的个数不算很多，可以通过画图来解决，不过，图形会显得比较乱，也可能导致把直线的条数查错．（2）可以先放弃题目中“在同一直线上”这个条件，使题目变得简单些，这样得出的结果肯定大于正确的结果，然后再减掉多出的部分，就能得出正确结果了．（3）如果七个点中任何三个点都不共线，那么先画经过点的直线，经过的直线，经过的直线，经过的直线，共有6条，如果画经过的直线，经过的直线，经过的直线，……，经过的直线，共计也有6条，……不过，直线与直线是同一条直线，直线与直线也是同一条直线……，这是必须考虑到的．解如果点不在同一直线上，那么可画出条直线，其中经过中某两个点的直线有条直线．实际上，由于三点共线，所以经过它们中任意两点的直线只能画出1条．因此，所求直线条数为说明如果题目中点的总个数不是7，而是8或10，其中共线的个数不是3，而是4，或者其中某三个点在同一条直线上，另外还有三个点在另外一条直线上，你也能顺利解出题目吗？例题3 当我们把一根木条用一个钉钉在墙上时，木条就会绕这个钉旋转．如果用两个钉钉在墙上时，这根木条就固定不动了，请说出道理．分析：木条这里可以理解成一条直线；钉看成是点，钉一个钉就是过一点画直线；钉两个钉就是过两点画直线．解因为过一点能画无数条直线，所以用一个钉把木条钉在墙上木条就会绕这一点旋转，就等于过一点画无数条直线；而两点确定一条直线，所以两个钉就可以在墙上固定一根木条．说明木条我们只是理解成线，实际来讲它不是线，因为在数学中的线是没有宽窄的．例4 如图中有几条射线？能用图中字母表示的射线有几条？分别表示出来.分析：直线上任一点可将直线分成两条射线，直线上有3个点可得到6条射线，但表示射线需一个端点字母和射线上另一个字母.解：图中共有射线6条；能用字母表示的射线有4条，它们是射线AB，射线BA，射线BC，射线CB.例题5 作下面线段：（1）有不在同一直线上的三点（如图所示），每两点连一条线段，问可以连几条线段；（2）有四个点，且每三点都不在同一直线上（如图所示），每两点连一条线段，问可以连几条线段；（3）用这个图形解决一个实际问题．分析（1）和（2）很容易做出，（3）我们可以把一个点看成一个足球队，两个点之间的连线就可以表示两个队之间进行的一场比赛，而线段的条数就是几个尽球队进行单循环比赛的场数．解（3）一个点可以看成一个足球队，如果三个队每两个队之间进行一场比赛，则共要进行三场比赛；如果四个队每两个队之间进行一场比赛，则需进行六场比赛．说明好多实际问题可以把它用图形来直观加以解决，这也是数学之美妙的一个方面．我们应该注意发现现实生活中的素材，提高我们解决实际问题的能力．。

重难点10 原子结构和原子核【知识梳理】一、氢原子光谱、氢原子的能级、能级公式 1．原子的核式结构（1）电子的发现：英国物理学家汤姆孙发现了电子。

（2）α粒子散射实验：1909～1911年，英国物理学家卢瑟福和他的助手进行了用α粒子轰击金箔的实验，实验发现绝大多数α粒子穿过金箔后基本上仍沿原来方向前进，但有少数α粒子发生了大角度偏转，偏转的角度甚至大于90°，也就是说它们几乎被“撞”了回来。

（3）原子的核式结构模型：在原子中心有一个很小的核，原子全部的正电荷和几乎全部质量都集中在核里，带负电的电子在核外空间绕核旋转。

2．光谱 （1）光谱用光栅或棱镜可以把光按波长展开，获得光的波长（频率）和强度分布的记录，即光谱。

（2）光谱分类有些光谱是一条条的亮线，这样的光谱叫做线状谱。

有的光谱是连在一起的光带，这样的光谱叫做连续谱。

（3）氢原子光谱的实验规律巴耳末线系是氢原子光谱在可见光区的谱线，其波长公式1λ＝R ⎝⎛⎭⎫122－1n 2，（n ＝3,4,5，…），R 是里德伯常量，R ＝1.10×107 m －1，n 为量子数。

3．玻尔理论（1）定态：原子只能处于一系列不连续的能量状态中，在这些能量状态中原子是稳定的，电子虽然绕核运动，但并不向外辐射能量。

（2）跃迁：原子从一种定态跃迁到另一种定态时，它辐射或吸收一定频率的光子，光子的能量由这两个定态的能量差决定，即hν＝E m －E n 。

（h 是普朗克常量，h ＝6.63×10－34 J·s ） （3）轨道：原子的不同能量状态跟电子在不同的圆周轨道绕核运动相对应。

原子的定态是不连续的，因此电子的可能轨道也是不连续的。

4．氢原子的能级、能级公式 （1）氢原子的能级 能级图如图所示（2）氢原子的能级和轨道半径①氢原子的能级公式：E n＝1n2E1（n＝1,2,3，…），其中E1为基态能量，其数值为E1＝－13.6 eV。

医用放射防护学考试题库及答案1、核衰变的类型主要有α，β，γ三种，其中α粒子的电离能力最强；而γ粒子的穿透能力最强。

2、1Ci = 3.7 ×1010 Bq3、放射性核素的半衰期是指放射性核素的核数或活度因衰变减少到原来一半所需要的时间。

4、放射性活度指单位时间内放射性核素发生自发核衰变的次数；其衰变规律可表示为：。

5、氢的同位素有3种。

6、放射性核素经2个半衰期后，其活度将减至原来的四分之一。

7、1Bq表示每秒一次核衰变。

8、α、β、γ射线的理化特性为_______bd_____。

（多选）A. 穿透能力α> β> γB.穿透能力α< β< γC.电离能力α< β< γD.电离能力α> β> γ9、对于一原子核，下列说法正确的是：（多选）abdA. A代表该原子核质量数B.Z代表原子核质子数C.这个核子处于稳定态D.N = A –Z10、以下关于钴的同位素，说法正确的是？（多选）bcdA. 60Co是钴的天然同位素之一B.钴的同位素可由反应堆或加速器生成C.天然界中存在的59Co是一种金属D.60Co在工业上常应用于食品等的杀菌、消毒，医疗上常应用于放射治疗11、正常本底地区，天然辐射源对成年人造成的平均年有效剂量约为___b_____。

A. 20 mSv／年；B. 2.4 mSv／年；C. 5 mSv／年12、在人工辐射源中，对人类照射剂量贡献最大的是__b______。

A. 核电；B. 医疗照射；C. 氡子体13、天然辐射源对成年人造成的平均年有效剂量当量aA. 其中2／3来自内照射B. 其中2／3来自外照射C. 其中2／3来自宇宙照射14、γ光子能量大于1.02MeV时，与物质相互作用可发生电子对生成效应。

15、带电粒子与物质作用损失能量的主要方式有：（多选）abA. 电离与激发B. 轫致辐射C. 弹性碰撞16、γ光子是通过次级效应与物质发生作用，次级效应主要的方式有以下几种？（多选）acdA. 光电效应B. 轫致辐射效应C. 康普顿效应D. 电子对效应17、1Gy = 100 rad 1R = 2.58 ×104 c/Kg18、在辐射防护上，表示辐射所致的有害效应发生几率或危害程度的物理量是（c）：A. 照射量B. 照射量率C. 吸收剂量D. 比释动能19、比释动能的SI单位是焦耳/ 千克（J ·kg-1），其专有名称为？（单选）dA. SvB. CiC. RD. Gy20、1伦琴等于多少C ·kg-1？（单选）cA. 2.55 ×10-4B. 2.55 ×10-5C. 2.58 ×10-4D. 3.87 ×10-521、描述有效剂量的专有单位为：aA. SvB. GyC. RD. Rad二、多选题1. 随机性效应的特点包括abcA. 效应严重程度与剂量大小无关B.没有阈值C.表现是诱发癌症D.严重程度与剂量大小有关E.有阈值2.关于辐射生效应影响因素的叙述，描述正确的是abcdeA.χ和g射线穿透力强，易造成皮肤和深部组织或器官的损伤。

线段、射线、直线亭湖区青墩初中王红丽教学目标：1.认识并会用数学语言表示线段、射线、直线。

2.会画出线段、射线、直线。

3.掌握并应用“两点之间的所有连线中，线段最短”。

4.通过具体情境，发展学生有条理的思考，并能正确地表述。

5.让学生们感受数学的美，培养他们用数学的眼光认识世界，感受世界。

教学准备：直尺、多媒体教学方法：启发诱导、动手操作、讨论观察、合作交流教学过程：一、情境创设：1、图片欣赏2.说说生活中的线段、射线、直线的实例。

二、学一学1、线段、射线、直线的表示方法（运用类比的方法来讲解这三种表达方式）2、探究：具备什么条件的两条射线是同一条射线？3、总结归纳4、画一画A B C D三、灵活应用活动一：自从第一次龟兔赛跑之后，小兔子一直想找个机会和小乌龟重新比赛一次。

机会终于来了,它在路上遇到了小乌龟,提出了再比赛一次的要求。

乌龟说：“好啊，不过这次是谁走的路近,谁就胜,”小兔子先选择了路线。

讨论一：⑴小兔子会选择哪条路线,为什么?⑵小白兔选择了路线②之后，小乌龟还是胜利了,你知道它是怎么走的吗?⑶小兔子还不服气，想再走一次，你们认为小兔子能走得比乌龟更近吗?为什么？归纳：两点之间所有的连线中,线段最短.⑴ 画线段AB⑵ 画射线AC⑶ 画直线AD两点之间线段的长度,叫做这两点之间的距离.讨论二：说出下列三个概念之间的区别和联系：线段、线段的长度、两点间的距离活动二★如图：已知一条直线a1、在直线a上取1个点，图中的射线有条，线段有条2、在直线a上取2个点，图中的射线有条，线段有条3、在直线a上取3个点，图中的射线有条，线段有条4、在直线a上取n个点，图中的射线有条，线段有条a四、我学习我应用此环节主要是运用今天这一节课所学习的内容来解决问题，让学生们在游戏中巩固知识。

五、课堂小结今天这节课你学到了什么？六、作业开放性作业：通过上面这个图形的展示，你还能用线段、射线或直线创造出美丽的图案吗？《直线、射线、线段》教学反思直线、射线、线段是最简单、最基本的图形，是研究复杂图形的基础。