1.6复数的极限及连续性
- 格式:doc
- 大小:217.50 KB
- 文档页数:3








3复变函数的极限连续性、导数与解析函数1、函数zw 1=把下列z 平面上的曲线映射成w 平面上的什么曲线? (1)922=+y x (2)0=+x y 【解】 曲线为 【解】 曲线为)sin (cos 3t i t z +=, it t z -=,则 则)sin (cos 311t i t z w -==, i t t z w 221+==, 即 即 ⎪⎪⎩⎪⎪⎨⎧-==.sin 31,cos 31t v t u ⎪⎪⎩⎪⎪⎨⎧==.2,2t v t u 从而 从而9122=+v u . v u =. (3)1=y (4)1)1(22=+-y x 【解】 曲线为 【解】 曲线为i t z +=, t i t z sin )cos 1(++=,则 则11122+-+==t i t t z w , t i z w tan 21211-==, 即 即⎪⎪⎩⎪⎪⎨⎧+-=+=.11,122t v t t u ⎪⎪⎩⎪⎪⎨⎧-==.tan 21,21t v u 从而 从而, 对任意的v ,有41)21(22=++v u . 21=u . ………………………………………………………………………………………………………2、已知映射3z w =, 求: (1)点i z i z i z +=-==3,1,321在w 平面上的象;【解】 i z w -=)(1; i z w 22)(2--=; i z w 8)(3=. (2)射线0,≥=x x y 在w 平面上的象;【解】 曲线为 i t z +=, 则i t t z w 33322+-==,即32t u -=, 32t v =)0(≥t从而0=+v u )0(≥v .(3)区域3arg 0π<<z 在w 平面上的象;【解】 由于3arg 0π<<z , 且3z w =, 故π<<w arg 0. ………………………………………………………………………………………………………3、证明复变函数z i z w arg ln +=在原点与负实轴上不连续.[证] 由于当0=z 时, z ln 不存在, 故函数在原点处不连续; 当0≠+=iy x z 时i z w y π+=+→||ln lim 0, i z w y π-=-→||ln lim 0故函数在负实轴上不连续.………………………………………………………………………………………………………4、利用导数的定义证明211z z -='⎪⎭⎫ ⎝⎛. [证] 由定义, 有z z z z z z ∆⎪⎭⎫ ⎝⎛-∆+='⎪⎭⎫ ⎝⎛→∆11lim 10201)(1lim z z z z z -=∆+-=→∆. ………………………………………………………………………………………………………5、指出下列函数)(z f w =的解析区域、奇点,在解析区域求其导数.(1)z i z w )3(3++=【解】 函数无奇点, 在整个复平面内处处解析,且导数为i z w ++='332.(2)112+=z w 【解】 函数的奇点为i z ±=, 除奇点外函数在整个复平面内处处解析,且导数为22)1(2+-='z z w . (3)1143++=z z w 【解】 函数有四个奇点, 分别为 )1(22i z ±=,)1(22i z ±-=. 除奇点外函数在整个复平面内处处解析,且导数为2442)1()43(+--='z z z z w . (4))0(≠-++=bc ad d c b a dcz b az w 为复常数且、、、 【解】 当0=c 时, 函数在复平面上无奇点, 处处解析, 此时da w ='; 当0≠c 时, 函数在复平面上有奇点cd z -=, 除奇点外处处解析, 此时 2)(d cz bc ad w +-='. ………………………………………………………………………………………………………。

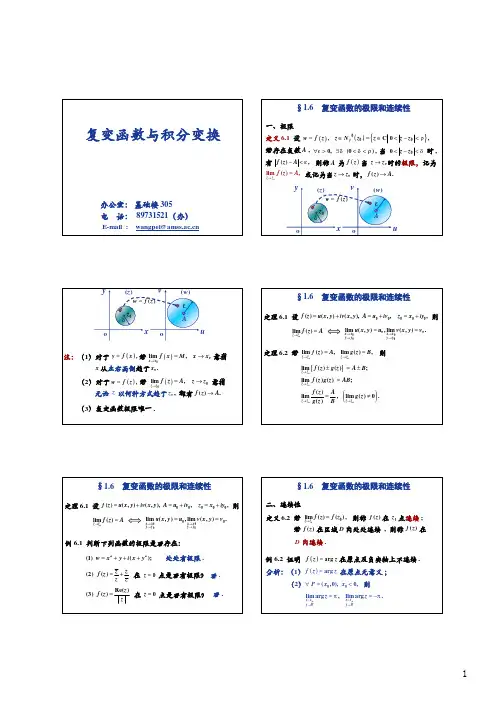

第三节复变函数的极限与连续一、复变函数的概念二、复变函数的极限三、复变函数的连续性一、复变函数的概念1. 复变函数的定义定义1.1 设E 是复平面上的点集, 若对任何z ∈E , 都存在惟一确定的复数w 和z 对应, 称在E 上确定了一个单值复变函数,用w =f (z )表示.E 称为该函数的定义域.在上述对应中, 当z ∈E 所对应的w 不止一个时, 称在E 上确定了一个多值复变函数.(){()|}() A f E f z z E w f z ==∈=称为复函的值域数.2. 复变函数与自变量之间的关系:() :w z w f z =复变函数与自变量之间的关系相当于两个实函数),,(),,(y x v v y x u u ==例3 , 2z w =函数,, iv u w iy x z +=+=令2)( iy x iv u +=+则,222xyi y x +−= : 2数对应于两个二元实变函于是函数z w =,22y x u −=.2xy v =,,z x iy w u iv =+=+因为,若记则()Re ()Im ()(,)(,).w f z f z i f z u x y iv x y ==+=+例4解,, iv u w iy x z +=+=令2)( iy x iv u +=+则,222xyi y x +−=,22y x u −=.2xy v =所以222424 4.w z z x y xy w u v =−====于是将平面上的双曲线与分别映为平面上直线和222,42w z z x y xy w =−== 设复函数试问它将平面上的双曲线 与 分别映为平面上的何种曲线?7函数w =z 2对应于两个二元实变函数: u =x 2−y 2, v =2xy 把z 平面上的两族双曲线x 2−y 2 = c 1 , 2xy = c 2 分别映射成w 平面上的两族平行直线u =c 1 , v =c 2 .101−1−1−10−8−6−4−2x 2468v =101y −10−8−6−4−2u =02468uv 1010−10−10⎯⎯→⎯=2z w θr ϕρ二、复变函数的极限1.复变函数极限的定义定义1.200000,()0,0,,0|||()|,()lim(),lim ().z z z E z z w f z E C z E C z E z z f z z z f z f z f z αεδδαεααα→∈→=⊂∈∀>∃>∈<−<−<== 设复函数在点集上有定义,为的一个聚点, 。
复变函数的极限与连续性例题和知识点总结在复变函数的学习中,极限与连续性是非常重要的概念。
理解和掌握它们对于解决许多复变函数的问题至关重要。
下面我们将通过一些例题来深入探讨复变函数的极限与连续性,并对相关知识点进行总结。
一、复变函数极限的定义设函数\(f(z)\)定义在\(z_0\)的去心邻域内,如果存在一个复数\(A\),对于任意给定的正数\(ε\),总存在正数\(δ\),使得当\(0 <|z z_0| <δ\)时,有\(|f(z) A| <ε\),则称\(A\)为\(f(z)\)当\(z\)趋于\(z_0\)时的极限,记作\(\lim_{z \to z_0} f(z) = A\)。
二、复变函数连续性的定义如果函数\(f(z)\)在\(z_0\)处满足\(\lim_{z \to z_0} f(z) = f(z_0)\),则称\(f(z)\)在\(z_0\)处连续。
三、例题分析例 1:设\(f(z) = z^2\),求\(\lim_{z \to 1 + i} f(z)\)。
解:\(\lim_{z \to 1 + i} f(z) =\lim_{z \to 1 + i} z^2 =(1 + i)^2 = 1 + 2i + i^2 = 2i\)例 2:判断函数\(f(z) =\frac{z}{|z|}\)在\(z = 0\)处的连续性。
解:当\(z\)沿实轴趋于\(0\)时,\(f(z) =\frac{x}{|x|}\),极限不存在;当\(z\)沿虚轴趋于\(0\)时,\(f(z) =\frac{iy}{|iy|}\),极限不存在。
所以\(f(z)\)在\(z = 0\)处不连续。
例 3:设\(f(z) =\begin{cases} \frac{z^2 1}{z 1},& z \neq 1 \\ 2, & z = 1 \end{cases}\),判断\(f(z)\)在\(z = 1\)处的连续性。
解:\(\lim_{z \to 1} f(z) =\lim_{z \to 1} \frac{z^2 1}{z 1} =\lim_{z \to 1} (z + 1) = 2\),且\(f(1) = 2\),所以\(f(z)\)在\(z = 1\)处连续。
复数域上的极限与连续复数域是数学中一个重要的概念,它包含了实数域的所有元素以及虚数单位i。
在复数域上,我们可以定义函数的极限和连续性,这些概念和实数域上的定义有着一定的差异。
本文将深入探讨复数域上函数的极限和连续性的性质。
复数域上函数的极限在实数域中,函数的极限可以用$\\epsilon$-$\\delta$定义来描述。
在复数域中,我们也可以采用类似的方式定义函数极限。
给定一个复数z0,如果对于任意的$\\epsilon > 0$,存在一个$\\delta > 0$,使得当$|z - z_0|<\\delta$时,$|f(z) -L|<\\epsilon$,则称函数f(z)在z0处的极限为L,记作$\\lim_{z\\to z_0} f(z) = L$。
复数域上函数的极限有着与实数域上函数的极限类似的性质,包括唯一性、局部性和代数运算规律等。
我们可以通过$\\epsilon$-$\\delta$定义来证明复数域上函数的极限存在性和性质。
复数域上函数的连续性与函数的极限类似,复数域上函数的连续性也是重要的性质之一。
一个函数在复数域上是连续的,意味着函数在整个定义域上都没有断裂或跳跃。
在复数域上,我们可以通过以下定理来描述函数的连续性:定理1:如果函数f(z)在复数域上处处可导,则f(z)在复数域上是连续的。
这个定理说明了在复数域上连续性和可导性之间的关系。
在实数域上也有类似的定理,但在复数域上要求更加严格。
复数域上函数的连续性与极限的关系在复数域上,函数的连续性与极限密切相关。
如果一个函数在某个点处连续,那么它在该点处的极限也存在且与函数在该点处的取值相等。
下面给出一个用于证明这个结论的定理:定理2:如果f(z)在复数域上是连续的,并且$\\lim_{z\\to z_0} f(z) = f(z_0)$,那么f(z)在z0处连续。
这个定理说明了连续性与极限之间的内在联系。
在复数域上,函数的连续性和极限在很大程度上决定了函数的性质。
1.6复数的极限及连续性
一.函数的极限
定义:若存在数A ,0)
0,,δρεδ
ε<≤∀>∃(()当00z z δ<-<时,有()f z A ε-<,则称A 为()f z 为0z z →时的极限,记作0
lim ()z z f z A →=或当0z z →时,()f z A →。
通俗定义:设函数0(),(,)w f z z U z ρ=∈ ,如果)()(lim 00
z f z f z z =→成立,则称)
(z f 在0z 处连续;如果)(z f 在E 中每一点连续,则称)(z f 在E 上连续。
几何意义: 当变点z 一旦进入0z 的充分小去心邻域时,它的象点()f z 就落入A 的一个预先给定的ε邻域中
注:1.意义中0z z →的方式是任意的。
与一元函数相比较要求更高。
2. A 是复数;若()f z 在z 出有极限,则极限是唯一。
二、极限的运算法则
复变函数极限与其实部和虚部极限的关系: 定理一.如果000iy x z +=,则
00
000
00,0000,lim
(,)(,)lim ()lim (,)(,)x x y y z z x x y y u x y u x y f z A u iv v x y v x y →→→→→=⎧⎪==+⇔⎨=⎪⎩
即一个复变函数的连续性等价于两个实变二元函数的连续性,给出了证明复变函数连续性的方法。
定理二.若0
lim ()lim ()z z z z f z A g z B →→==,则:
[]0
lim ()()lim ()lim ()z z z z z z f z g z f z g z A B →→→±=±=±
lim ()()lim ()lim ()z z z z z z f z g z f z g z AB →→→==
0000
lim ()()lim (lim ()0)()lim ()z z
z z z z z z f z f z A g z g z g z B
→→→→=≠= 以上定理用极限的定义去证。
例1.22()w x y i x y =+++试证在平面上处处有极限 证明:22,x y x y ++ 在平面上处处有极限 例2.()0z z f z z z z
=+→求在时的极限
证明:2222
2()
()x y f z x y -=+ 在(0,0)处的极限不存在。
例3.Re ()0z
f z z z
=→证明在时的极限不存在
()f z =
(,)(,)0,u x y v x y == , z y kx =当沿直线趋于零时
000
lim (,)x x x x y kx
y kx
u x y →→→→======
例4. () (0) 0 z
f z z z z
=≠→证明函数当时的极限不存在。
解: ,
()z x iy f z u iv =+=+令22
22
(,),x y u x y x y
-=+则222(,),xy v x y x y =+ , z y kx =当沿直线趋于零时222
022lim (,)lim
,1x x y kx
y kx
xy k
v x y x y k →→====++
三、函数的连续性
定义:若0
0lim ()()z z f z f z →=,则称()f z 在处连续;若在区域D 内处处连续,则称
()f z 在D 内连续;若0z z C ∈、,且0
0lim ()()z z f z
f z →=,则称()f z 在曲线C 上点0z 处连续。
注:三要素 由定义、有极限、极限值等于函数值。
定理三、()(,)(,)f z u x y iv x y =+在000z x iy =+处连续000000(,)(,)00(,)(,)
lim
(,)(,)lim
(,)(,)
x y x y x y x y u x y u x y v x y v x y →→=⇔
=
例1.00: () , () .f z z f z z 证明如果在连续那末在也连续
证: ()(,)(,)f z u x y iv x y =+,则()(,)(,)f z u x y iv x y =-,0 () , f z z 由在连续于是00 (,) (,) (, ), u x y v x y x y -和也在处连续0 () f z z 故在连续。
例2.2222()ln()()f z x y i x y =++-
解:22(,)ln()u x y x y =+在复平面内除原点外处处连续22(,)v x y x y =-。
在复平面处处联系。
(,) . f x y 故在复平面内除原点外处处连续 例3.证明()arg f z z =在原点及负实轴上不连续。
(1)()arg f z z = 在原点没有定义,故不连续。
00
0(2) (,0)(0),lim arg , lim arg y y x x x x P x x z z ππ
+-→→→→∀<==- 在负实轴上arg z ∴在负实轴上不连续。
定理四、连续函数的和、差、积、商 (分母不为0)仍为连续函数;连续函数的
复合函数仍为连续函数。
由以上讨论01()n n P z a a z a z ⇒=+++ 在整个复平面内连续;()
()()
P z R z Q z =在复平面内除分母为零点外处处连续。
设曲线C 为闭曲线或端点包括在内的曲线段,若()f z 在曲线C 上连续,
0M ⇒∃>在曲线上恒有()f z M ≤.。