云团扩散模型

扩散模型与生成模型详解-概述说明以及解释1.引言1.1 概述扩散模型与生成模型是两种常见的数学模型，用于描述和解释不同类型的数据和现象。

在许多领域，包括社会科学、自然科学和工程学等，这两种模型被广泛应用于数据分析、预测和决策等方面。

扩散模型是通过描述信息、物质或现象在空间和时间上的传播过程来模拟和预测其扩散的行为。

其基本思想是基于传播的概率和随机过程，通过建立数学模型来模拟和分析人群、病毒、信息等的传播行为。

扩散模型的应用非常广泛，如在流行病学中用于分析疾病传播的规律，或在社交网络中用于预测信息的传播路径和速度等。

生成模型是通过建立概率模型来模拟和生成数据。

与扩散模型不同，生成模型的目的是从已有的数据中学习其分布规律，并用于生成新的数据样本。

生成模型通常基于统计学和机器学习的方法，通过学习样本数据的概率分布来生成具有相似特性的新样本。

生成模型的应用非常广泛，如在自然语言处理中用于生成文本内容或在图像生成领域用于生成逼真的图像等。

本文将详细介绍扩散模型和生成模型的定义、常见类型及其应用领域。

首先，我们将对扩散模型进行概述，包括其基本定义和常见的扩散模型类型，以及扩散模型在疾病传播和信息传播等领域的应用。

接下来，我们将介绍生成模型的定义以及常见的生成模型类型，包括基于概率图模型的生成模型和基于深度学习的生成模型。

最后，我们将对比扩散模型和生成模型的特点和应用场景，并分析它们各自的优劣势。

同时，我们还将展望扩散模型和生成模型未来的发展趋势。

通过阅读本文，读者将对扩散模型和生成模型有一个全面的了解，并能够理解它们在实际问题中的应用价值。

1.2文章结构文章结构部分主要是对整篇文章的结构进行介绍，指出各个章节的主题和内容，以帮助读者快速了解文章的组织结构和主要内容。

在本篇文章中，共有四个主要章节，分别为引言、扩散模型、生成模型和结论。

下面将对每个章节的主题和内容进行简要介绍。

引言部分（Chapter 1）是文章的开篇部分，主要用于介绍本篇文章的背景和意义，以及引导读者进入主题。

液氯泄漏事故定量分析评价氯气中毒事件时有发生，威胁着人们的生命与财产安全。

从以往的事故案例中可以看出，发生氯气泄漏所涉及的主要方面有：疏散任务紧急、人数多、距离远，事故应急救援牵扯部门多，给毒害区域人们生活带来影响恶劣，造成的环境破坏和财产损失大。

现对项目的生产、储存单元中的氯钢瓶泄漏事故进行模拟，定量分析其对周围企业、村庄的影响。

根据事故发生泄漏的特点，选用箱模型中的重气云团盒子模型作为氯气扩散过程模拟模型。

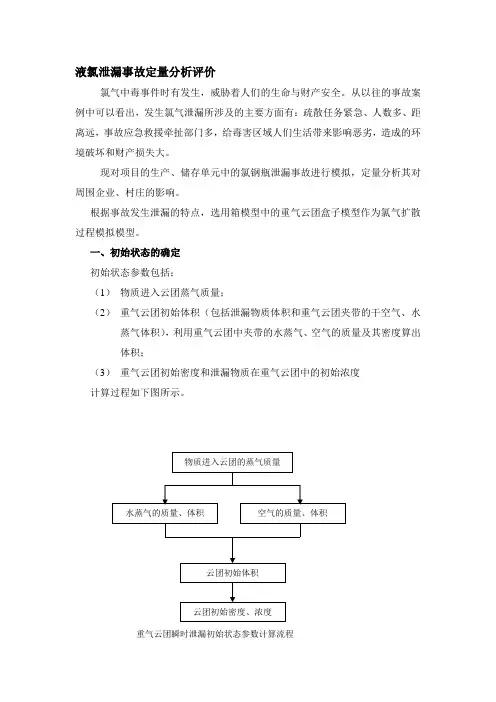
一、初始状态的确定初始状态参数包括：（1）物质进入云团蒸气质量；（2）重气云团初始体积（包括泄漏物质体积和重气云团夹带的干空气、水蒸气体积），利用重气云团中夹带的水蒸气、空气的质量及其密度算出体积；（3）重气云团初始密度和泄漏物质在重气云团中的初始浓度计算过程如下图所示。

重气云团瞬时泄漏初始状态参数计算流程1．泄漏蒸气物质氯质量计算F vap＜0.2时按下式计算m=5F vap G式中，m——泄漏物质氯进入云团的蒸气质量，kg；G——物质储存质量，取值为1000kg；F vap——闪蒸率，经计算取值0.189。

2.云团总质量计算云团的总重量由云团泄漏物质氯总量（气、液）和初始夹带的空气总量（含水蒸气）构成。

（1）空气总量计算m airo＝am F vap式中，m airo——初始重气云团中的空气质量，kg；a ——初始重气云团中泄漏物质气态含量与夹带空气质量的关系系数，泄漏物质为氯时，取值为5.5。

（2）水蒸气含量计算m wo＝m airo K wK w ＝ρw/ρaHR/100exp（14.4144－5328/ T a）式中，m wo——初始重气云团中的水蒸气量，kg；Kw——与温度、相对湿度有关的系数；ρw——水蒸气密度，kg/m3；ρa——空气密度，kg/m3；HR——相对湿度，％；Ta——气温，K。

（3）干空气质量计算m airdo＝m airo－m wo式中，m airdo——初始重气云团中干空气质量，kg；3．初始体积计算V airdo＝0.082×T o×m airdo/ m aV wo＝0.082×T o×m wo/ m w，T o≥273KρcwV co＝0.0 82×T o×m co×F vap/ m c+(1- F vap) m co/ρcw 式中，V airdo——干燥空气体积，m3；V wo——水蒸气体积，m3；V co ——泄漏物质体积，m3；m c 、mwo、ma——分别为泄漏物质液氯、水蒸气、空气的分子量；To、F vap——云团的初始温度（K）和闪蒸率；ρcw ——泄漏物质的液态密度，kg/m3，取值为1.40×103 kg/m3。

扩散模型分类在数学和物理学中，扩散模型是一种描述扩散过程的数学模型。

扩散是指物质在不同浓度区域间的自发传输。

扩散模型可以应用于多个领域，包括化学、生物学、环境科学等。

根据不同的条件和假设，扩散模型可以分为不同的分类。

本文将对扩散模型的分类进行详细的介绍。

1. 精确解与近似解扩散模型的解可以分为精确解和近似解两种。

精确解是指通过严格的数学分析和求解，得到的能够准确描述扩散过程的解。

精确解常常是基于一些理想化的假设和边界条件得出的。

而近似解则是通过采用近似方法，将扩散模型简化为更容易求解的形式得到的解。

近似解可以通过数值方法或者解析方法得到，常常适用于复杂的扩散模型。

2. 线性与非线性模型线性扩散模型是指扩散过程中物质浓度与浓度梯度之间满足线性关系的模型。

线性扩散模型通常适用于物质浓度变化较小的情况。

而非线性扩散模型则是指扩散过程中物质浓度和浓度梯度之间存在非线性关系的模型。

非线性扩散模型适用于物质浓度变化较大的情况，通常需要借助数值方法进行求解。

3. 稳态与非稳态模型扩散模型还可以根据是否考虑时间因素进行分类。

稳态模型是指扩散过程中物质浓度不随时间变化的模型。

稳态模型适用于描述无外部影响，且物质浓度分布保持不变的情况。

非稳态模型则是指扩散过程中物质浓度随时间变化的模型。

非稳态模型适用于描述外部影响较大，或者物质浓度分布随时间变化的情况。

4. 离散与连续模型扩散模型还可以分为离散模型和连续模型两种。

离散模型是指将扩散过程离散为一系列的离散点，对每个离散点进行建模和计算。

离散模型适用于描述扩散在离散介质中的传播过程。

而连续模型则是指将扩散过程看作是在连续介质中的传播，通过连续的微分方程进行描述。

连续模型适用于描述扩散在连续介质中的传播过程。

5. 空间维度的不同最后，扩散模型还可以根据空间维度的不同进行分类。

一维扩散模型是指扩散过程在一维空间中进行，常用于描述沿直线传播的扩散。

二维扩散模型是指扩散过程在二维平面中进行，常用于描述平面上的扩散。

扩散模型生成特征在数据科学和机器学习领域，特征工程是非常重要的一环。

特征工程的核心是根据原始数据提取出有意义且能够反映数据内在规律的特征，以供后续模型训练和预测使用。

扩散模型是一种常用的特征生成方法，通过对数据进行扩散操作，可以得到更加丰富的特征表示。

一、什么是扩散模型扩散模型是一种基于局部邻域的特征生成方法。

它的核心思想是通过对原始数据进行多次迭代，将每个数据点的邻域信息进行扩散，从而生成新的特征。

在扩散过程中，每个数据点会与其邻域内的数据点进行信息交流和融合，从而使得原始数据的特征得到了增强和扩展。

二、扩散模型的基本原理扩散模型的基本原理是通过局部邻域的信息交流和融合，在特征空间中生成新的特征。

具体而言，扩散模型通过迭代的方式，将每个数据点的特征与其邻域内的数据点的特征进行加权平均，得到新的特征表示。

迭代的次数越多，新特征的表达能力就越强，从而更能反映数据的内在规律。

三、扩散模型的优势扩散模型具有以下几个优势：1. 丰富特征表示：扩散模型通过迭代的方式，将每个数据点的特征与邻域内的数据点的特征进行融合，使得特征得到了扩展和增强。

这样可以提高特征的表达能力，更好地反映数据的内在规律。

2. 自适应性：扩散模型在融合特征时，会根据邻域内的数据点的相似度进行加权平均。

这样可以使得扩散模型更具有自适应性，能够更好地适应不同数据的特点。

3. 鲁棒性：扩散模型对噪声和异常值具有一定的鲁棒性。

在扩散过程中，邻域内的数据点会对特征进行平滑化处理，从而减少噪声和异常值的影响。

四、扩散模型的应用扩散模型在各个领域都有广泛的应用。

以下是几个典型的应用案例：1. 图像处理：扩散模型可以应用于图像处理领域，对图像进行特征提取和图像增强。

通过扩散模型生成的特征，可以更好地表达图像的纹理和形状等特征。

2. 文本分类：扩散模型可以应用于文本分类领域，对文本进行特征提取和分类。

通过扩散模型生成的特征，可以更好地表达文本的语义和语法等特征。

扩散模型发展及应用一、引言扩散模型是一种数学模型，用于描述某种物质或信息在空间中的扩散过程。

扩散模型的发展可以追溯到19世纪末，当时数学家们开始研究物质在空间中的传播规律。

随着科学技术的进步，扩散模型的应用范围也越来越广泛，涉及到物理、化学、生物、环境科学等多个领域。

二、扩散模型的发展历程扩散模型的发展可以分为三个阶段：基本扩散模型、复杂扩散模型和非线性扩散模型。

1.基本扩散模型基本扩散模型是最简单的扩散模型，也是最早研究的模型之一。

它假设扩散物质是均匀的，扩散速率与浓度梯度成正比。

基本扩散模型的数学表达式为Fick's law，即扩散通量等于扩散系数与浓度梯度的乘积。

这个模型主要适用于稳态扩散过程。

2.复杂扩散模型复杂扩散模型考虑了更多的因素，如非均匀性、反应速率等。

这些模型通常采用偏微分方程进行描述，求解过程较为复杂。

复杂扩散模型的应用范围更广，可以用于研究非稳态扩散过程、化学反应扩散等。

3.非线性扩散模型非线性扩散模型是近年来扩散模型研究的热点之一。

它考虑了扩散物质的非线性特性，可以描述更复杂的扩散过程。

非线性扩散模型的研究主要集中在数学上的求解方法和模拟实验上的验证。

三、扩散模型的应用领域1.物理学中的应用在物理学中，扩散模型广泛应用于研究热传导、质量传递等现象。

例如，在材料科学中，研究材料的扩散性能对于优化材料的制备过程具有重要意义。

扩散模型可以帮助科学家预测材料中各种元素的扩散行为，从而指导材料的设计和改进。

2.化学领域中的应用化学反应中的扩散过程是化学反应速率的决定因素之一。

通过建立化学反应扩散模型，可以研究不同条件下反应速率的变化规律，为化学反应的优化提供理论依据。

3.生物学中的应用在生物学中，扩散模型被广泛应用于研究生物体内物质运输的过程。

例如，在生物医学领域，研究药物在人体内的扩散过程对于合理用药具有重要意义。

扩散模型可以帮助科学家预测药物在人体内的分布情况，从而指导药物的剂量和给药方式。

扩散模型概述扩散模型是一种数学模型，用于描述物质、信息或其他现象在空间中扩散的过程。

它是一种常见的分析工具，在各个领域都有广泛应用，包括化学、生物学、物理学、经济学等。

扩散模型可以帮助我们理解和预测扩散过程的特征和行为。

基本原理在扩散模型中，我们通常将空间划分为离散的单元，如网格或格点。

每个格点上都有一定数量的物质或信息，它们可以通过相邻格点之间的转移进行扩散。

扩散速率取决于扩散现象的性质以及格点间的距离和差异。

扩散模型的基本原理可以用Fick定律来描述。

Fick定律指出，扩散通量的大小与物质浓度梯度成正比，与扩散系数成反比。

这意味着在浓度梯度较大的地方，物质的扩散速率更快；而在扩散系数较小的地方，扩散速率更慢。

数学表达在数学上，扩散模型通常使用偏微分方程来描述。

最常见的扩散模型是扩散方程，也称为热传导方程或扩散方程。

它的一般形式可以写为：∂C/∂t = D∇²C其中，C表示物质或信息的浓度，t表示时间，D表示扩散系数，∇²表示拉普拉斯算符。

这个方程说明了物质或信息浓度随时间和空间的变化情况。

解析方法扩散方程是一个非常重要的偏微分方程，它在许多问题中都有解析解。

通过求解扩散方程，我们可以得到扩散过程的精确解，进而研究其特性和行为。

对于简单的一维情况，扩散方程可以用分析方法求解。

我们可以应用变量分离、傅里叶变换等技巧，将方程化简为常微分方程，并找到相应的解析解。

数值方法然而，在许多实际问题中，扩散方程往往是复杂的，很难通过解析方法求解。

这时，我们可以使用数值方法来近似求解。

常见的数值方法包括有限差分法、有限元法和边界元法等。

这些方法将偏微分方程转化为离散的代数方程，然后通过求解代数方程组来得到数值解。

通过数值方法，我们可以模拟扩散过程的演化，研究其动态行为和稳定性。

这种基于计算机模拟的方法可以帮助我们更好地理解和预测实际问题中的扩散现象。

应用领域扩散模型在各个领域都有广泛的应用。

扩散模型损失函数推导扩散模型（Diffusion Model）是一种用于解决信息传播、疾病传播等问题的模型。

在扩散模型中，我们通常使用损失函数来衡量模型预测结果与实际数据之间的差异。

在扩散模型中，我们可以假设信息或疾病的传播是基于一定的规则，例如传播速率、传播范围等。

基于这些假设，我们可以构建一个数学模型来描述信息或疾病的传播过程。

一般来说，扩散模型可以分为离散模型和连续模型。

对于离散模型，我们可以使用损失函数来衡量模型的预测结果与实际数据之间的差异。

常用的损失函数包括平方损失（Mean Square Error，MSE）、交叉熵损失（Cross Entropy Loss）等。

以平方损失为例，假设我们的模型预测结果为y_pred，实际数据为y_true，则平方损失为：\[L(y_{true}, y_{pred}) = (y_{true} - y_{pred})^2\]损失函数越小，表示模型预测结果与实际数据之间的差异越小，模型的准确性越高。

对于连续模型，我们可以利用微分方程来描述信息或疾病的传播过程。

在连续模型中，损失函数通常是通过最小化模型预测结果与实际数据之间的差异来实现的。

常用的损失函数包括均方差损失（Mean Squared Error）、平均绝对误差（Mean Absolute Error）等。

以均方差损失为例，假设模型的预测结果为u(x, t)，实际数据为u_true(x, t)，则均方差损失为：\[L(u_{true}, u_{pred}) = \int \int (u_{true}(x, t) - u_{pred}(x, t))^2 dx dt\]通过最小化损失函数，我们可以得到最优的模型参数，从而使得模型的预测结果与实际数据最为接近。

需要注意的是，损失函数的具体形式取决于问题的特点和模型的设计。

在实际应用中，我们需要根据具体情况选择合适的损失函数，以达到最佳的模型效果。

1 云团扩散模型根据物质泄漏后所形成的气云的物理性质的不同，可以将描述气云扩散的模型分为非重气云模型和重气云模型两种[5-13]。

非重气云模型高斯模型是一种常用的非重气扩散模型，高斯烟羽(Plume model)模型又称高架点连续点源扩散模型，适用于连续源的扩散，即连续源或泄放时间大于或等于扩散时间的扩散。

高斯烟团(Puff model)模型适用于短时间泄漏的扩散，即泄放时间相对于扩散时间比较短的情形，如突发性泄放等。

若假设气体云内空间上的分布为高斯分布，则地面地处风向的烟团浓度分布算式为式中，c(x，y，H)——点(x，y，H)处浓度值，mg/m3；Q——源强，即单位时问的排放量，mg/s；u——环境平均风速，m/s；σx，σy，σz——扩散参数；H——源高(烟团高度)，m；x——下方向到泄漏原点的距离，m；y，z——侧风方向、垂直向上方向离泄漏原点的距离，m。

高斯模式的实际应用效果很大程度上依赖于如何给定模式中的一些参数，尤其要注意源强、扩散参数等的确定。

源强与污染物的物理化学属性、扩散方式、释放点的地理环境等有关。

扩散参数表征大气边界层内湍流扩散的强弱，是高斯模式的一项重要数据。

高斯扩散模式所描述的扩散过程(实质上也包含了在实际应用中对高斯模式的一些限制)主要有：1)下垫面平坦、开阔、性质均匀，平均流场稳定，不考虑风场的切变。

2)扩散过程中，污染物本身是被动、保守的，即污染物和空气无相对运动，且扩散过程中污染物无损失、无转化，污染物在地面被反射。

3)扩散在同一温度层结中发生，平均风速大于 m/s。

4)适用范围一般小于10～20 km。

重气云模型由于重气本身的特殊性，在重气扩散领域也有大量基于不同理论的模型。

鉴于重气扩散与中性或浮性气体扩散有着明显的区别，目前国内外已开发大量的不同复杂程度的重气扩散模型，如箱模型、相似模型、LTA－HGDM模型、CFD模型等。

箱(BOX)模型箱模型是指假定浓度、温度和其他场，在任何下风横截面处为矩形分布等简单形状，这里的矩形分布是指在某些空间范围内场是均匀的，而在其他地方为零。

扩散模型是一种用于描述和预测物质或信息在空间和时间中传播过程的数学模型。

它被广泛应用于各个领域，如物理学、化学、生物学、社会学和经济学等，以研究和解释各种扩散现象和现象的传播行为。

在扩散模型中，通常假设存在某种物质或信息，具有在空间中传播的趋势。

这种传播可以是通过扩散、传导、迁移、扩张或传送等方式进行。

扩散模型的目标是理解和预测这种传播现象的过程、速率和规律。

常见的扩散模型包括：1. 扩散方程模型：基于扩散方程的模型是描述物质或信息扩散过程的常见方法。

它基于扩散方程，该方程描述了物质或信息在空间和时间上的变化。

通过解析或数值方法求解扩散方程，可以得到物质或信息的扩散行为的预测结果。

2. 随机扩散模型：有些情况下，扩散过程可能受到随机因素的影响。

随机扩散模型采用随机过程和概率方法来建模扩散现象。

例如，布朗运动模型描述微粒在液体或气体中的随机运动和扩散行为。

3. 网络扩散模型：在网络科学中，扩散模型被用于研究信息在网络中的传播。

这些模型考虑了节点之间的连接和交互，并通过模拟节点之间的信息传播来预测网络中的扩散过程。

通过使用扩散模型，研究人员可以深入了解和预测各种扩散现象，如热传导、分子扩散、疾病传播、信息传播、社会影响等。

这些模型为我们理解和干预扩散过程提供了重要的工具和框架。

在计算机领域，扩散模型有多种应用。

下面是其中几个常见的应用：1. 网络传播模型：扩散模型可以用于研究信息在计算机网络中的传播过程。

例如，在社交媒体平台上，研究人员可以使用扩散模型来模拟和预测消息、观点或病毒视频等内容在用户之间的传播路径和速度。

这有助于我们理解信息的扩散规律、病毒传播方式，以及如何优化信息传播策略和社交网络的设计。

2. 数据传输和通信：在数据传输和通信领域，扩散模型可以用于研究和优化数据的传输过程。

例如，在无线传感器网络中，扩散模型可以帮助确定最佳的数据传输路径和路由策略，以最大程度地减少能量消耗和传输延迟。

此外，在蓝牙、Wi-Fi和移动通信等领域，扩散模型可以帮助优化信号传输范围和覆盖率，提高通信效率和质量。