关于FANUC宏程序椭圆参数计算
- 格式:doc
- 大小:21.00 KB
- 文档页数:1

数控车椭圆宏程序编程解析(总9页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除数控车椭圆宏程序编程解析相关知识:椭圆关于中心、坐标轴都是对称的,坐标轴是对称轴,原点是对称中心。
对称中心叫做椭圆中心。
椭圆和X轴有2两个交点,和Y轴有两个交点,这四个交点叫做椭圆顶点。
椭圆标准方程:x2 / a2 + y2 / b2 = 1 ( a为长半轴,b为短半轴,a > b > 0 )椭圆参数方程:x=a*cosM y=b*sinM ( a为长半轴,b为短半轴,a > b >0 ,M是离心角,是椭圆上任意一点到椭圆中心连线与X正半轴所成的夹角,顺时针为负,逆时针为正。
)编程思路:如N090 #101=20N100 WHILE[#101GE0]DO1N110 #102=26*SQRT[1-[#101*#101]/[20*20]]N120 G01 X[#102] Z[#101-20]N130 #101=#N140 END1将椭圆曲线分成200条线段,用直线进行拟合非圆曲线,每段直线在Z轴方向的直线与直线的间距为,如#101=#,根据曲线公式,以Z轴坐标作为自变量,X 轴坐标作为应变量,Z轴坐标每次递减,计算出对应的X坐标值。
宏程序变量如下:#101为非圆曲线公式中的Z坐标值,初始值为20#102为非圆曲线公式中的X坐标值(直径值),初始值为0G01 X[#102] Z[#101-20]建立非圆曲线在工件坐标系中的X Z坐标,系就是椭圆的中心坐标。
各种椭圆类型宏程序编制:图纸一:图纸一分析:加工本例工件时,试采用B类宏程序编写,先用封闭轮廓复合循环指令进行去除余量加工。
精加工时,同样用直线进行拟合,这里以Z坐标作为自变量,X坐标作为应变量,其加工程序如下:O0001G99 G97 G21G50 S1800G96 S120S800 M03 T0101G00 X43 Z2 M08G73 U21 W0 R19G73 P1 Q2 FN1 G00 X0 S1000G42 G01 0 F#101=25N10 #102=30*SQRT[1-[#101*#101]/[25*25]]G01 X[#102] Z[#101-25]#101=#IF[#101GE0]GOTO10G02 X35 Z-40G01 X36X40 Z-42N2 X43G70 P1 Q2G40 G00 X100 Z100 M09T0100 M05G97M30图纸二:图纸二分析:加工本例工件时,试采用B类宏程序编写,先用封闭轮廓复合循环指令进行去除余量加工。



法兰克系统椭圆球面宏程序Summary: This text synopsis introduced the set up of concept, the plait distance priniple and mathematics pattern of the great procedure a method. Also take processing oval sphere as solid instance, introduced draw up of great procedure process in detail. Finally give adoption Siemens 802 D the system draw up of procedure and procedure annotationof the process of oval sphere.Key words:Great procedure;Oval sphere;The parameter square distance;Great variable;R parameter)一、导言对于具有曲面或复杂轮廓的零件,特别是包含三维曲面的零件,采用一般手工编程困难很大,且容易出现错误,有的甚至无法编制程序。
而采用宏程序,就能很好的解决这一问题。
二、宏程序宏程序就是使用了宏变量的程序。
在一般的程序编制中,程序字中地址字符后为一常量,一个程序只能描述一个几何形状,所以缺乏灵活性和适用性。
宏程序中的地址字符后则为一变量(也称宏变量),可以根据需要通过赋值语句加以改变,使程序具用通用性。
配合循环语句、分支语句和子程序调用语句,可以编制各种复杂零件的加工程序。
三、宏程序的编制编制宏程序时必须建立被加工零件的数学模型。
也就是通过数学处理找出能够描述加工零件的数学公式。
数学处理一般有以下两个环节:一是选择插补方式;二是求出插补节点的坐标计算通式。
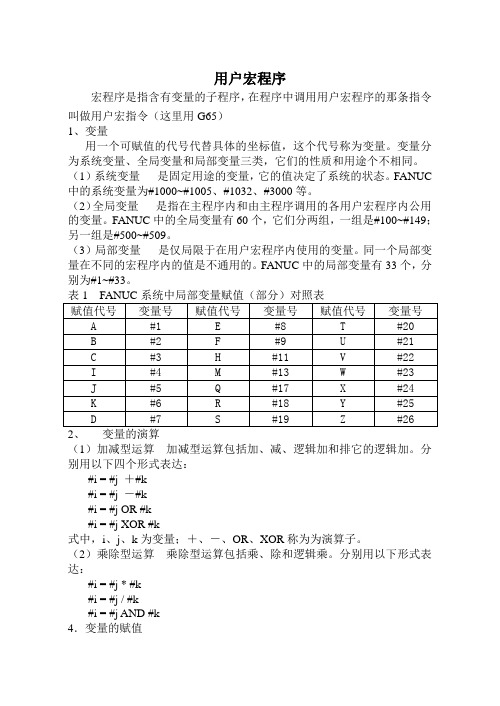
用户宏程序宏程序是指含有变量的子程序,在程序中调用用户宏程序的那条指令叫做用户宏指令(这里用G65)1、变量用一个可赋值的代号代替具体的坐标值,这个代号称为变量。
变量分为系统变量、全局变量和局部变量三类,它们的性质和用途个不相同。
(1)系统变量是固定用途的变量,它的值决定了系统的状态。
FANUC 中的系统变量为#1000~#1005、#1032、#3000等。
(2)全局变量是指在主程序内和由主程序调用的各用户宏程序内公用的变量。
FANUC中的全局变量有60个,它们分两组,一组是#100~#149;另一组是#500~#509。
(3)局部变量是仅局限于在用户宏程序内使用的变量。
同一个局部变量在不同的宏程序内的值是不通用的。
FANUC中的局部变量有33个,分别为#1~#33。
(1)加减型运算加减型运算包括加、减、逻辑加和排它的逻辑加。
分别用以下四个形式表达:#i = #j +#k#i = #j -#k#i = #j OR #k#i = #j XOR #k式中,i、j、k为变量;+、-、OR、XOR称为为演算子。
(2)乘除型运算乘除型运算包括乘、除和逻辑乘。
分别用以下形式表达:#i = #j * #k#i = #j / #k#i = #j AND #k4.变量的赋值由于系统变量的赋值情况比较复杂,这里只介绍公共变量和局部变量的赋值。
变量的赋值方式可分为直接和间接两种。
(1)直接赋值例:#1=115(表示将变量115赋值于#1变量)#100=#2(表示将变量#2的即时值赋于变量#100)(2)间接赋值间接赋值就是用演算式赋值,即把演算式内演算的结果赋给某个变量。
在演算式中有自变量代号,自变量每得到一个即时值,相应就得到一个演算结果,该结果就赋值给变量,该变量也叫应变量。
5.转向语句转向语句分为无条件转向语句和条件转向语句两种。
(1)无条件转向语句程序段格式:GOTO N ;其中N后面的数值为程序段号。
例如:GOTO 55;表示无条件转向执行N55程序段,而不论N55程序段在转向语句之前还是之后。

工业设计2020年第21期0引言椭圆轮廓的加工,是宏程序在实际加工应用中一个很典型的例子,在各类数控技能鉴定和数控技能大赛中也会经常出现。
因目前大多数的数控系统只提供直线插补、圆弧插补和螺旋插补三种插补类型。
更高档的数控系统(如FANUC16i)也仅提供双曲线、正弦曲线和样条曲线插补功能,一般都没有椭圆插补的功能。
这时就需要采用宏程序语句套用椭圆参数方程来实现椭圆轮廓的加工。
本文归纳总结了Fanuc0i系统编制椭圆轮廓宏程序几种编程思路和方法。
1椭圆轮廓宏程序编程方法加工如图1所示椭圆工件,将工件坐标系建立在工件上表面中心处,采用刀具直径为φ10mm立铣刀。
利用椭圆参数方程配合条件转移语句来编制宏程序,目前常用的几种编程方法如下:图1 椭圆工件1.1不加刀补型关于椭圆轮廓宏程序编制,人们往往有一种错误的认识,以为只要刀具中心轨迹走出的形状是椭圆,那加工出的轮廓就是椭圆,许多常见的椭圆轮廓宏程序就是在这个错误认识基础上编写的,既在整个椭圆的加工过程中不采用刀具半径补偿G41(G42),而是直接利用椭圆的长、短半轴值减去刀具的半径值来进行编程。
程序如下:O0001;(程序名)……#1=0;(椭圆起始角度)WHILE [#1LE360] DO1;(当#1小于等于360°时执行循环1)G1 X[35*COS[#1]] Y-[25*SIN[#1]] F1000;(椭圆插补)#1=#1+1;(#1角度每次递增1°)END1;(循环1结束)……M30;(程序结束)需要说明的是这种编程方法看上去非常简单易懂,而且也不会因为刀具补偿的错误应用而引起椭圆轮廓的过切。
很多编程人员也早已习惯了这种编程方法,但是这样加工出来的形状绝对不是真正意义上的椭圆,而是与椭圆轮廓等距一个刀具半径的等距曲线,如图2所示。
如果要加工一个真正意义上的椭圆是不能采用这种方法的,需要采用后两种方法。
数字1代表基准椭圆a=30mm,b=20mm;数字2代表铣刀直径;数字3代表大椭圆a=35mm,b=25mm;数字4代表正确的刀具中心运行轨迹;图2椭圆轮廓轨迹加工示意图1.2刀补加在循环外型如果第一种方法不可行,必须加上刀具半径补偿才能编制出正确的椭圆程序,那么按照常规的编程思路会将刀具半径补偿加在循环外面来进行编程,程序如下:O0002;(程序名)……G1 G41 X30 Y0 D1 F1000;(加入刀具半径补偿)#1=0;(椭圆起始角度)WHILE [#1LE360] DO1;(当#1小于等于360°时执行循环1)G1 X[30*COS[#1]] Y-[20*SIN[#1]];(椭圆插补)#1=#1+1;(#1角度每次递增1°)END1;(循环1结束)FANUC系统宏程序铣削椭圆方法研究陈行行(中国工程物理研究院机械制造工艺研究所 四川 绵阳 621999)摘 要:对于椭圆轮廓的加工,数控系统中是没有能够直接实现椭圆插补的G代码指令,这时就需要采用宏程序语句套用椭圆参数方程来实现椭圆轮廓的加工。
椭圆加工宏程序
实际应用中,还经常会遇到各种各样的椭圆形加工特征。
在现今的数控系统中,无论硬件数控系统,还是软件数控系统,其插补的基本原理是相同的,只是实现插补运算的方法有所区别。
常见的是直线插补和圆弧擂补,没有椭圆插补,手工常规编程无法编制出椭圆加工程序,常需要用电脑逐一编程,但这有时受设备和条件的限制。
这时可以采用拟合计算,用宏程序方式,手工编程即可实现,简捷高效,并且不受条件的限制。
加工如下图所示的椭圆形的半球曲面,刀具为R8的球铣刀。
利用椭圆的参数方程和圆的参数方程来编写宏程序。
椭圆的参数方程为:X=A*COS&;
Y=B*COS&;
其中,A为椭圆的长轴,B为椭圆的短轴。
编制参考宏程序如下:
%0012
#1=0
#2=20
#3=30
#4=1
#5=90
WHILE #5 GE #1 DO1
#6=#3*COS[#5*PI/180]+4
#7=#2*SIN[#5*PI/180]
G01X[#6]F800
Z[#7]
#8=360
#9=0
WHILE #9 LE #8 DO2
#10=#6*COS[#9*PI/180]
#11=#6*SIN[#9*pi/180]*2/3
G01X[#10]Y[#11]F800
#9=#9+1 (计数器)
END1
#5=#5-#4 (计数器)
END2
M99
在上例中可看出,角度每次增加的大小和最后工件的加工表面质量有较大关系,即记数器的每次变化量与加工的表面质量和效率有直接关系。
希望读者在实际应用中注意。
宏程序是数控加工专业高级工、技师和高级技师应掌握的内容。
笔者在与企业的交流中得知,有许多职工没有系统地学习过数控知识,尤其是宏程序这一块了解得很少,因此笔者特撰写本篇稿子,希望通过文中椭圆加工的宏程序能够对其他非圆曲线的编写加工起到举一反三、抛砖引玉的作用。
在数控车床上加工非圆曲线的零件是企业生产及数控大赛经常涉及到的,非圆曲线包括了椭圆、双曲线、抛物线和正弦曲线等。
如图1所示,为一典型的椭圆零件, 编程加工时可采用“四心法”和“直线逼近法”。
四心法计算编程简单,但椭圆的加工精度低。
当要求加工精度高,编程相对简单,程序量精简时,则可以采用直线逼近法。
直线逼近法加工椭圆时只要步距足够小,就能加工出标准的椭圆。
目前数控系统都还没有提供完善的非圆曲线插补功能,编程时则要采用数控系统自带的另一种编程方法:FANUC系统采用宏程序编程,SINUMERIK系统采用R参数编程,FAGOR系统采用计算机高级语言编程。
下面主要介绍F A N U C 0i-T C系统中的B类宏程序。
一、宏程序数控程序中含有变量的程序称为宏程序。
宏程序可以让用户利用数控系统提供的变量、数学运算、逻辑判断和程序循环等功能,来实现一些特殊的用法,从而使得编制同样的加工程序更加简便。
1.变量普通加工程序直接用数值指定G代码和移动距离,例如,GO1和X100. 0。
使用用户宏程序时,数值可以直接指定或用变量指定。
当用变量时,变量值可用程序或用M D I面板上的操作改变。
如:#1=#2+100或G01 X#1 F300。
(1)变量的表示及类型一般编程方法允许对变量命名,但用户宏程序不行。
变量用变量符号“#” 和后面的变量号指定。
例如:#1、#100 等。
表达式可以用于指定变量号。
此时,表达式必须封闭在括号中。
例如:#[#1+#2-12]。
变量根据变量号可以分成四种类型,如表1所示。
(2)变量的运算变量常用算术、逻辑运算和运算符(如表2和表3所示)。
用宏程序在数控车上加工椭圆数控宏程序的编制与应用是手工编程的最高形式,它具有灵活性、通用性、和加工效率高的特点。
在此,我将自己在宏程序应用中的经验总结介绍。
标签:宏程序数控机床加工在中职数控车大赛当中,各种非圆曲线加工成为比赛的重要内容,选手们一般用自动编程加工,自动编程产生的程序繁琐,难以分析和查找错误,加工时间相对较长。
而用宏程序不但简化了编程,而且效率也提高不少。
数控宏程序的编制与应用是手工编程的最高形式,它具有灵活性、通用性、和加工效率高的特点。
在此,我将自己在宏程序应用中的经验总结介绍。
一、加工工艺路线1.装夹件2毛坯,粗、精车件2左端部分至尺寸要求。
2.装夹件1毛坯一端,伸出长度60mm,平端面对刀。
3.用93°菱形外圆车刀粗、精车左端外轮廓至尺寸要求。
4.用切槽刀粗、精车40°槽,并粗车椭圆左端槽。
5.调头夹φ36×28外圆,定总长97±0.05mm,粗精加工内孔部分至尺寸要求。
6.粗车椭圆。
7.将件2旋入件1,定件2总长。
8.用93°菱形外圆刀粗车件2椭圆。
9. 用93°菱形外圆刀精车椭圆和槽。
二、工艺知识1.椭圆的加工原理宏程序其实就是根据曲线方程以变量方式进行插补编程加工零件,在X轴、Z轴构成的坐标平面上,椭圆的标准方程是:x2/b2+z2/a2=1。
其中:a为Z轴方向长半轴,b为X轴方向短半轴;a、b为常量是已知量,X、Z是未知量。
因为零件图中工件坐标系零点与椭圆中心不在同一点上,编程时需要换算两坐标系之间的关系,因此:①若以Z值为自变量时(用#1赋值),转换公式为:即:#2=24/40*SQRT[40*40-[#1+12]*[#1+12]]②若以X为自变量时(用#1赋值),转换公式为即:#2=-40+40/24*SQRT[24*24-[#1*#1]]2.加工难点分析椭圆是较难加工的部分,在FANUC-0i,G71指令中不能包含宏程序,G73指令空行程太多,因此粗加工椭圆轮廓时,常用的方法是根据椭圆的近似画法,采用两段圆弧用G71编程粗车,然后在用宏程序精车椭圆。