人教版六年级下册数学第三单元测试卷及答案

人教版六年级下册数学第三单元测试卷及答案·最新简介：人教版六年级下册数学第三单元测试试卷，主要针对第三单元所学的知识进行测验，涵盖了所学的所有知识点和必考点，同时对知识点进行了拓展，能够起到巩固知识点，拓展孩子知识应用的作用，本试卷试题结合了其他地区试卷的精华，望对老师和家长朋友有所帮助。

人教版六年级下册数学第三单元测试卷（1）1圆柱的认识圆柱的表面积一、用心思考，正确填写。

(每空1分，共10分)1．圆柱有（）条高，有（）个底面，有（）个侧面。

2．把一根长1 m，底面直径2 dm的圆柱形木料横截成2段，表面积增加了（）。

3．一个高18.84 cm的圆柱，侧面展开后是一个正方形，这个圆柱的底面直径是（）cm，底面半径是（）cm。

4．[思维发散题]一个圆柱形地窖，侧面积是113.04 m2，底面直径是12 m，这个地窖深（）m。

5．把一个长6.28 dm，宽3.14 dm的长方形纸片卷成一个圆柱，这个圆柱的侧面积是（）dm2(保留整数)，它的底面积可能是（）dm2，也可能是（）dm2。

二、仔细推敲，判断正误。

(对的画“√”，错的画“×”)(5分)1．如果一个物体上、下底面是面积相等的两个圆，那么这个物体一定是圆柱。

（）2．求做一节圆柱形通风管需要多少铁皮，就是求圆柱的侧面积。

（）3．如果两个圆柱的侧面积相等，那么这两个圆柱的底面积也相等。

（）4．(湖南娄底期末)一个长方形以它的一条边为轴，旋转一周得到的旋转体是一个圆柱体。

（）5．[易错易混题]半径为2 dm的圆柱，它的底面周长和底面面积相等。

（）2．下图中用h表示的线段中，是圆柱的高的在括号内画“√”。

(3四、认真辨析，合理选择。

(将正确答案的序号填在括号里)(8分)A. B. C.3．两个圆柱的底面半径之比是2∶3，高相等，小圆柱的体积是A. B. C.2圆柱的体积利用圆柱的体积解决问题五、认真读题，巧妙填空。

(每空2分，共8分)1．一个圆柱的体积是30cm3，底面积是5cm2，它的高是（）cm。

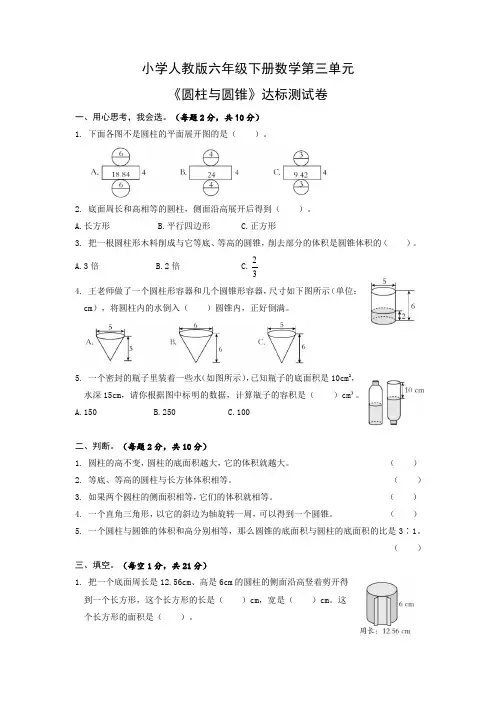
小学人教版六年级下册数学第三单元《圆柱与圆锥》达标测试卷一、用心思考，我会选。

（每题2分，共10分）1. 下面各图不是圆柱的平面展开图的是（）。

2. 底面周长和高相等的圆柱，侧面沿高展开后得到（）。

A.长方形B.平行四边形C.正方形3. 把一根圆柱形木料削成与它等底、等高的圆锥，削去部分的体积是圆锥体积的（）。

2A.3倍B.2倍C.34. 王老师做了一个圆柱形容器和几个圆锥形容器，尺寸如下图所示（单位：cm），将圆柱内的水倒入（）圆锥内，正好倒满。

5. 一个密封的瓶子里装着一些水（如图所示），已知瓶子的底面积是10cm2，水深15cm，请你根据图中标明的数据，计算瓶子的容积是（）cm³。

A.150B.250C.100二、判断。

（每题2分，共10分）1. 圆柱的高不变，圆柱的底面积越大，它的体积就越大。

（）2. 等底、等高的圆柱与长方体体积相等。

（）3. 如果两个圆柱的侧面积相等，它们的体积就相等。

（）4. 一个直角三角形，以它的斜边为轴旋转一周，可以得到一个圆锥。

（）5. 一个圆柱与圆锥的体积和高分别相等，那么圆锥的底面积与圆柱的底面积的比是3∶1。

（）三、填空。

（每空1分，共21分）1. 把一个底面周长是12.56cm、高是6cm的圆柱的侧面沿高竖着剪开得到一个长方形，这个长方形的长是（）cm，宽是（）cm。

这个长方形的面积是（）。

2. 一个圆柱高是 8cm，侧面积是100.48cm2，它的底面积是（）cm²，表面积是（）cm²。

3. 把一个圆柱的底面分成许多相等的扇形，然后竖直切开拼成一个长方体，长方体的底面积等于圆柱的（），高等于圆柱的（），因为长方体的体积=（）×（），所以圆柱的体积=（）×（）。

4. 把一个底面直径为12cm、高是20cm的圆柱，沿底面直径切割成同样大小的两半，表面积增加（）cm²，体积是（）cm³。

人教版数学6年级下册第3单元·时间：90分钟满分：100分班级__________姓名__________得分__________一．选择题（共7小题，满分21分，每小题3分）1．（3分）一个圆柱体纸筒，底面半径是1分米，高是6.28分米，这个纸筒沿高剪开，侧面展开是（ ）A．长方形B．正方形C．平行四边形D．梯形2．（3分）做一根长3米的圆柱形通风管，横截面直径是0.2米，做这根通风管至少需要材料（ ）平方米。

A．1.884B．3.768C．18.84D．37.683．（3分）下面图形以较粗的直线为轴，快速旋转后可以形成圆锥的是（ ）A．B．C．D．4．（3分）在如图中，以直线为轴旋转一周，可以得出圆柱的是（ ）A．B．C．D．5．（3分）如果一个圆柱体和一个长方体的底面周长和高分别相等，那么（ ）的体积较大。

A．圆柱体B．长方体C．一样大D．无法比较6．（3分）用一块长28.26cm，宽15.7cm的长方形铁皮做一个圆柱形容器的侧面，配（ ）的铁皮当底面更能节省材料。

A．底面半径4.5cm B．底面直径6cmC．底面直径5cm7．（3分）等底等高的圆柱与圆锥，体积之和是360cm3，圆柱的体积是（ ）cm3。

A．270B．120C．90二．填空题（共7小题，满分21分，每小题3分）8．（3分）一个圆柱体，侧面积是37.68平方分米，高是2分米，它的底面直径是 分米。

9．（3分）如果把一个圆柱的高截短4cm，它的表面积就减少125.6cm2，同时这个圆柱的体积减少 cm2。

10．（3分）一个圆柱和一个圆锥的体积和高相等。

若圆锥的底面积15厘米，那么圆柱的底面积是 厘米。

11．（3分）一个圆锥和一个圆柱的底面积及体积分别相等，圆锥的高是7.35厘米，圆柱的高是 厘米。

12．（3分）圆锥的底面直径是6厘米，高5厘米，沿底面直径把它切成两个完全相等的部分，这两部分的表面积之和与原来圆锥的表面积相比，增加了 平方厘米。

最新部编人教版小学六年级数学下册第三单元检测试卷（及答案）时间：90分钟满分：100分学校: _______姓名：________班级：________考号：________一．选择题（满分16分，每小题2分）1．圆锥是由()个面围成的立体图形．A．1B．2C．32．一个圆柱体的侧面展开是一个正方形，这个圆柱体的底面半径是5厘米，这个圆柱体的高是()厘米．A．5B．10C．15.7D．31.43．如图是一个圆柱体，如果把它的高截短4厘米，它的表面积减少50.24平方厘米．这个圆柱体的体积减少()立方厘米．A．12.56B．50.24C．200.96D．100.484．下面那个圆柱的体积与如图的圆锥的体积相等？()A．B．C．D．5．（如图所示）高度相同，底面直径不同的圆锥与圆柱，圆锥的体积()圆柱的体积．A．大于B．小于C．等于6．四个完全相同的水杯，分别往里面注水，水量如图中的涂色部分，如果再往每个水杯中分别放入大小一样的方糖，完全溶解后，()杯溶液的甜度最高．A．①号B．②号C．③号D．④号7．如图的圆柱杯子与圆锥杯子底面积相等，把圆锥装满水倒进圆柱里，至少要()杯才能把圆柱装满．A．3B．6C．9D．128．长方体、正方体、圆柱、圆锥的底面积相等，高也相等，下面说法正确的是() A．圆锥的体积是圆柱体积的3倍B．圆锥的体积是长方体体积的13C．长方体的体积比正方体的体积小D．圆柱的体积比正方体的体积大二．填空题（满分16分，每小题2分）9．把一个棱长6分米的正方体切削成一个最大的圆锥体，这个圆锥体的体积是立方分米．10．一个圆柱体和一个圆锥体体积相同，底面积也相同，如果圆柱的高是12厘米，圆锥的高是厘米，如果圆锥的高是12厘米，圆柱的高是厘米．11．一个长方体、一个圆柱体和一个圆锥体的底面积相等、体积也相等，那么圆锥的高是圆柱的，长方体高是圆锥高的．12．两个高相等，底面半径之比是1:2的圆柱与圆锥，它们的体积之比是．13．一个正方体木块的棱长是6cm，把它削成一个最大的圆柱．圆柱的体积是3cm，再把这个圆柱削成一个最大的圆锥，这个圆锥的体积是3cm．14．一个圆柱形的水桶，里面盛有12升水，正好盛满，如果把一块与水桶等底等高的圆锥形实心木块完全浸入水中，这时桶内还有升水。

人教版六年级下册数学第三单元《圆柱与圆锥》测试卷一.选择题(共6题，共12分)1.一个圆柱和一个圆锥，底面周长的比是2：3，体积比是5：6，那么这个圆柱和圆锥高的最简单的整数比是（）。

A.8：5B.5：8C.12：5D.5：122.下面的说法错误的有（）句。

①圆柱的底面积与高都扩大3倍，它的体积就扩大6倍②既是2的倍数又是5的倍数的数的特征是个位必须是0③一条线段绕着它的一个端点旋转120°，形成的图形是圆④在长方体上，我们找不到两条既不平行也不相交的线段⑤公式S梯形 =（a+b）h÷2，当a=b时，就是平行四边形的面积计算公式A.1B.2C.3D.43.下列图形绕虚线旋转一周，形成的几何体是圆锥的是（）。

A. B. C. D.4.等底等高的圆柱、正方体、长方体的体积相比较（）。

A.一样大B.长方体体积大C.圆柱体体积大D.正方体体积大5.一个圆柱体水桶的容积（）圆锥体积。

A.相等B.大于C.小于D.无法确定6.如图，圆柱体的侧面积是（）。

A.235.5cm2B.263.76cm2C.307.24cm2D.207.24cm2二.判断题(共6题，共12分)1.侧面积相等的两个圆柱，表面积也相等。

（）2.如果圆锥的底面积是圆柱底面积的3倍，则圆锥和圆柱的体积相等。

（）3.如果把一个圆柱的底面半径扩大到原来的3倍，高不变，那么他的体积就扩大到原来的9倍。

（）4.圆柱的上下两个面都是圆形，大小不一样。

（）5.把一个圆柱体削成一个最大的圆锥体，圆锥体的体积是削去部分的。

（）6.圆柱体的底面周长和高相等时，沿着它的一条高剪开，侧面展开是一个正方形。

（）三.填空题(共6题，共9分)1.一根2米长的圆柱形木材，锯成3段小圆柱后，它们的表面积总和比原来增加了12.56dm2，原来这根木材的体积是（）dm3。

2.一个圆柱的直径和高都是2dm，这个圆柱的表面积是（）平方分米。

3.从正面看到的图形是（）形，从左面看是（）形，从上面看是（）形。

人教版六年级数学下册第三单元单元测试解析及答案一、填空（没空1分.共38分）1.把圆柱的侧面沿高剪开.得到一个（）.这个（）的长等于圆柱底面的（）.宽等于圆柱的（）.所以圆柱的侧面积等于（）.2. 做一个圆柱形白铁皮通风管需要铁皮多少.就是求它的( ).字母公式( ).3. 求做一个圆柱形汽油桶需要铁皮多少.就是求它的( ).计算公式( ).4．底面周长是18.84米.高5米的圆柱.它的表面积是（）平方米.体积是（）立方米. 5．在一张长6分米.宽4分米的长方形纸上剪下最大的圆.这个圆的面积是（）平方分米.6、一圆柱和一圆锥的体积和高相等.圆锥的底面积是9平方厘米.圆柱的底面积是（）平方厘米．7．5千米60米＝（）千米. （）日＝36小时9.08平方米＝（）平方分米. （）毫升＝4.05立方分米.6.2公顷 =（）平方米8.一种商品打八折销售.“八折”表示原价的（）%.如果这种商品原价100元.现在便宜了（）元.9.有两个空的玻璃容器（如图）.再把这水倒入圆柱形容器.圆柱形容器里的水高（10.把一张边长是40厘米的正方形纸片.卷成一个最大的最大圆柱形纸筒.它的底面周长是（）厘米.高是（）厘米.11.等底等高的圆柱和圆锥的体积相和是36立方米.这个圆柱的体积是（）立方米.圆锥的体积是（）立方米.12. 体积是1 cm3的小正方体堆成一个体积是1dm3的大正方体.需要（）个小正方体.如果把这些小正方体一个挨一个排成一行.长（）米.表面积是（）13.一个棱长是a厘米的正方体.它的所有棱长之和是（）厘米.表面积是（）平方厘米.体积是（）立方厘米14.一个长方体的所有棱长之和是72厘米.它的长、宽、高的比是4∶3∶2.它的体积是（）立方厘米.15.把两个完全相同的圆柱拼在一起.高是1分米.表面积减少25.12平方厘米.原来一个柱体的体积是（）立方厘米.若将此组合圆柱削成一个最大的圆锥.圆锥的体积约是（）立方厘米（得数保留一位小数）.16.等底等高的圆柱和圆锥.圆柱的体积是圆锥的（）.圆锥的体积是圆柱的（）.圆柱的体积比圆锥大（）.圆锥的体积比圆柱小（）.【解析】4、先求半径：18.84÷3.14÷2=3m再求表面积：3.14×3×3×2+18.84×5=150.72㎡最后求体积：3.14×3×3×5=141.3立方米5、剪下最大圆直径是4分米. 3.14×（4÷2）×（4÷2）=12.56平方分米6、体积和高相等的圆柱和圆锥.圆锥底面积是圆柱底面积的三倍.圆柱的底面积：9÷3=3平方厘米9、体积和底面积相等的圆柱和圆锥.圆锥高是圆柱高的三倍.5×1/3=5/3厘米 10、底面周长等于高等于边长11、等底等高圆柱体积是圆锥体积的三倍.圆柱体积：36×3/4=27立方米.圆锥体积：36×1/4=9立方米12、拼成的长方体的长是1000厘米.宽是1厘米.高是1厘米14、棱长总和÷4=长+宽+高 72÷4=18厘米长：18×4/9=8厘米宽：18×3/9=6厘米高：18×2/9=4厘米长方体体积=长×宽×高=8×6×4=192 平方厘米15、表面积减少两个底面积.一个底面积是25.12÷2=12.56平方厘米体积V柱=S底h=12.56×10=125.6平方厘米削成的圆锥和圆柱等底等高圆锥体积是圆柱体积的1/3,125.6×1/3≈41.9立方厘米【答案】：1、长方形长方形周长高底面周长×高 . 2、侧面积S侧=Ch 3、表面积 S表=S侧+2S底 4、150.72 141.3 5、 12.56 6、37、5.06 1.5 9080 4050 62000 8、80 20 9、5/3 10、40 4011、27 9 12、 1000 10 4002平方厘米 13、12a 6a²a³ 14、19215、125.6 41.9 16、3倍 1/3 2倍 2/3【点评】：对知识进行整理.能熟练运用公式进行计算.对基础知识的理解和灵活运用能力.第1、2、3属于知识点.第11、16题进一步沟通圆柱圆锥体积之间的关系.让学生对等底等高能进一步理解和灵活运用.二、判断（每题2分.共8分）1、圆柱的底面积和高各扩大3倍.体积就扩大9倍.（）2、圆柱的体积是圆锥体积的3倍. （）3. 圆柱体的底面半径是3厘米.高是9.42厘米.它的侧面展开后是一个正方形.（）4. 半径是2分米的圆.它的周长与面积相等.（）5. 平行四边形的面积是三角形面积的2倍.（）6．圆柱体积比与它等底等高的圆锥体的体积大2倍．（）7、一个正方体与一个圆锥体的底面积和高都相等.这个正方体体积等于圆锥体积的3倍.（ ) 8．一个圆柱与一个圆锥的底面积和体积相等.那么圆锥的高是圆柱高的1/3 . ( )【解析】：2、一定要等底等高才成立.4、周长和面积表示的意义不同.不能比较大小.8、应是三倍.【答案】：1、√ 2、 × 3、 × 4、 ×5、 × 6、√ 7、√ 8、×【点评】：对易错题进行梳理.三、选择.(将正确答案的序号填在括号里)（每题2分.共20分）1．把一个圆柱削成一个最大的圆锥.削去部分的体积是圆锥体积的( )A.3倍B.2倍C.D.2．已知一个圆柱的体积是45立方厘米.则圆锥的体积是( )A.15立方厘米B.135立方厘米C.不能确定3．一个圆锥体的底面积是等高的圆柱体底面积的3倍.它们的体积( )A.相等B.圆锥体的体积大C.圆柱体的体积大4．一个圆锥体.底面半径是3米.高3.5米.体积是( )A.28.26立方米B.98.91立方米C.32.97立方米D.61.23立方米5．两个底面积和体积分别相等的圆柱和圆锥.圆柱的高一定是圆锥高的( )A.3倍B. 1/3C. 2/36．把一段圆钢切削成一个最大的圆锥体.切削掉的部分部分重8千克.这段圆钢重（）千克．A24 B16 C12 D87．一个圆柱体积比一个与它等底等高的圆锥体的体积大（）A 1/3 B1 C2倍D3倍8．一个底面直径是27厘米.高9厘米的圆锥体木块.分成形状大小完全相同的两个木块后.表面积比原来增加（）平方厘米．A81 B243 C121.5 D125.69、将圆柱的底面半径扩大2倍.高不变.则圆柱的体积增加（）倍.A、4B、7C、810、把一个圆柱体削成一个最大的圆锥体.削去部分的体积是圆锥体的（）.A、2/3B、2倍C、1/3【解析】4、V锥=S底h÷3=3.14×3×3×3.5÷3=32.97立方米 6、切掉的部分是圆钢的2/3,8÷2/3=12千克 8、表面积增加了两个三角形.三角形底是直径.高是圆锥的高.增加的面积是：27×9÷2×2=243平方厘米 9、半径扩大2倍底面积扩大4倍.体积扩大4倍【答案】：1、B 2、C 3、A 4、C 5、C 6、C 7、C 8、B 9、A 10、B【点评】：等底等高、等体积等高、等体积等面积的圆柱圆锥体积之间的关系.这部分内容.学生不易理解.容易混淆.进一步巩固.四、应用题.（第1、2、3、5题每题5分.第4题6分）1、一个圆锥形沙堆.底面半径10米.高是6米.用这堆沙在10米宽的公路铺5厘米厚的路面.能铺多少米？2、有一块正方形木料.它的棱长是5分米.把这快木料加工成一个最大的圆柱.圆柱的体积是多少？这个圆柱的体积是正方体木料的百分之几？3、一个近似于圆锥体的小麦堆.量得底面周长12.56米.高2.1米.这堆小麦的体积是多少立方米？如果每立方米小麦重800千克.这堆小麦大约有多少千克？4、我校在“创建绿色校园示范单位”活动中.打算在生物园新挖一个深1.2米.直径是深的5/6的圆柱形水池.（1）这个水池的占地面积是多少平方米？（2）如果这个水池修好后.需要用水泥把池底和侧壁粉刷.粉刷的面积有多大？（3）需要挖土多少方？5、一个装满水的圆锥形容器.底面半径是2分米.高是1.5分米.现在把容器里的水倒入一个内壁长3分米、宽2分米、高1.2分米的长方体水槽内.能盛下吗？（请通过计算说明）【解析】：1、圆锥的体积=铺成的长方体的体积长方体体积÷宽÷高=长2、加工成的最大圆柱底面直径和高都等于正方形的棱长.3、先用周长÷∏÷d.求出圆锥的半径.再通用圆锥的体积公式求出体积.4、（1）占地面积是求底面积（2）粉刷面积有2个面一个底面积＋一个侧面面积5、首先求出这两个容器的容积.再比较【答案】： 1、 1/3×（3.14×10×10）×6=628立方米5厘米=0.05米628÷10÷5=12.56米2、圆柱的体积：5÷2=2.5分米3.14×2.5×2.5×5=98.125立方分米正方体体积：5×5×5=125立方分米98.125÷125=78.5 ％3、12.56÷3.14÷2=2米1/3×3.14×2×2×2.1=8.792立方米8.792×800=7033.6千克4、（1）直径：1.2×5/6=1米半径：1÷2=0.5米（2） 3.14×0.5×0.5=0.785平方米3.14×1×1.2＋0.785=4.553平方米（3） 0.785×1.2=0.942立方米=0.942方5、圆锥的容积：1/3×(3.14×2×2)×1.5=6.28立方分米=6.28L圆柱的体积：3×2×1.2=7.2立方分米=7.2L因为7.2L＞6.28L.所以能盛下.【点评】：第1、5、小题是一个比较典型的等积变形问题.物体的形状发生变化后.体积与原来的相等.第4、小题主要考查学生利用圆柱的表面积和体积计算公式解决生活中实际问题的能力.在计算时一定要注意圆柱和圆锥体积公式的区别.。

人教版六年级下册数学第三单元测试卷一、填空题1．一个圆柱的侧面展开图恰好是一个正方形，如果这个圆柱的底面半径是4cm，那么它的高是( )；侧面积大约是( )。

（取整数）2．一个圆柱的侧面积是94.2cm2，高是5cm。

它底面的半径是( )cm，底面积是( )cm2。

3．如图，一顶厨师帽，高30cm，帽顶半径是10cm，做这样一顶帽子至少要用( )cm2的面料。

4．（如图），饮料瓶的容积是500mL，现在瓶中装有一些饮料，正放时饮料高度是20cm；倒放时，空余部分的高度是5cm，瓶中现有饮料( )mL。

5．如图，将直角三角形以一条直角边所在的直线为轴旋转一周，可以得到一个圆锥，圆锥的底面直径是( )，高是( )。

6．下图中，瓶底的面积和锥形杯口的面积相等，将瓶子中的液体倒入锥形杯子中，能倒满( )杯。

7．圆柱的底面半径是2分米，高是5分米，它的表面积是( )平方分米；体积是( )立方分米。

（ 计算时取3.14）8．圆锥和圆柱的底面积和体积分别相等，圆锥与圆柱高的比值是( )。

9．把一根长2米的圆柱形木料截成三个小圆柱，表面积增加了50.24平方厘米，这根木料原来的体积是( )。

10．用一张长为6dm，宽为2dm的长方形纸围成一个圆柱体，这个圆柱的侧面积是( )dm2。

二、判断题1．一个圆锥的高不变，半径扩大到原来的2倍，体积也扩大到原来的2倍。

( )2．以直角三角形的一条直角边为轴旋转一周，转出的几何体是圆锥。

( )3．圆锥的体积比圆柱的体积小三分之二。

( )4．等体积等高的圆柱圆锥，圆锥的底面积是圆柱的3倍。

( )5．圆柱的侧面展开是正方形时，这个圆柱的高和它的底面周长相等。

_____三、选择题1．用一个高36厘米的圆锥形容器盛满水，倒入和它等底等高的圆柱形容器中，水的高度是（）厘米．A．36 B．18 C．16 D．122．下图中，大圆锥的底面半径是小圆锥的2倍，高也是小圆锥的2倍，大圆锥的体积是小圆锥的（）倍。

人教版六年级下册第三单元《圆柱与圆锥》测试卷学校:___________姓名：___________班级：___________等级：___________一、选择题（将正确答案的序号填在括号里)（10分)1．（2分）把一个圆柱形木头截成相等的三段，表面积（）A．不变B．增加2个底面C．增加3个底面D．增加4个底面2．（2分）将一个圆柱体削制成一个圆锥体，削去部分的体积是圆柱体积的（）A．B．C．2倍D．不能确定3．（2分）下面图形中,以某一边为轴旋转一周,可以得到圆柱体的是( )。

A．B． C．D．4．（2分）一个圆柱和一个圆锥的体积和底面积相等，圆柱的高是9厘米，圆锥的高是（）A．9cm B．3cm C．27cm5．（2分）制作一个圆柱形油桶，至少需要多少平方米的材料，是求圆柱的（）。

A．侧面积B．表面积C．容积D．体积二、填空题（共22分)6．（4分）圆柱的上、下底面是两个面积相等的_____形．圆柱的侧面是一个_____，沿着高展开后可能是一个_____形，也可能是一个_____形．7．（1分）计算做一个圆柱形的烟囱要用多少铁皮，要计算圆柱的______。

8．（1分）等底和等高的圆柱和圆锥，它们的体积之比是_________。

9．（2分）如下图，把圆柱切开拼成一个长方体，已知长方体的长是3.14米，高是2米。

这个圆柱体的底面半径是________米，体积是__________立方米。

10．（1分）一个圆柱的体积比与它等底等高的圆锥的体积大50.24 dm3，已知圆锥的底面半径是20cm，圆锥的高是_________dm。

11．（1分）一个圆锥形的沙堆，底面周长是62.8平方米，高是6米，这堆沙子______立方米。

12．（3分）一个圆柱的底面半径是3cm，高是10cm，侧面积是________cm2，表面积是________cm2，体积是________cm3。

13．（2分）一个圆锥的底面面积是62.8平方分米，高是6分米，它的体积是_____立方分米，与它等底等高的圆柱体的体积是_______。

人教版数学六年级下册第三单元试卷3份含答案人教版数学六年级下册第3单元达标检测卷一、填空。

(每小题2分，共20分)1．750 cm2＝() dm2 2.05 dm3＝()L()mL 2．如图是一个圆柱的展开图，这个圆柱的表面积是()cm2，体积是() cm3。

第2题图第3题图第7题图3．如图，分别以直角三角形的两条直角边所在直线为轴旋转一周，所得到的立体图形的体积差是()cm3。

4．一个圆锥的体积是75.36 dm3，底面半径是4 dm，这个圆锥的高是() dm。

5．把一根长2 m的圆柱形木料沿横截面锯成三段，表面积增加了12.56 dm2，这根圆柱形木料的体积是() dm3。

6．把一根圆柱形木料削成一个与其等底等高的圆锥，削去部分的体积是8.4 dm3，原来圆柱形木料的体积是()dm3，削成的圆锥的体积是()dm3。

7．如图，把一个高为10 cm的圆柱切成若干等份，拼成一个近似的长方体，表面积比原来增加了80 cm2，那么圆柱的体积是()cm3。

8．一个圆柱和一个圆锥的体积相等，底面半径也相等，圆柱的高是3.6 dm，圆锥的高是()dm。

9．一个圆柱，如果高增加1 cm，那么它的侧面积就增加25.12 cm2，如果这个圆柱的高是25 cm，那么这个圆柱的体积是()cm3。

10．一个圆锥和一个圆柱的体积相等，它们底面半径的比是32，圆锥的高是16 cm，圆柱的高是()cm。

二、判断。

(对的画“√”，错的画“×”。

每小题1分，共5分)1．一个圆柱的底面周长和高相等，那么它的侧面沿高展开一定是正方形。

() 2．圆柱的体积一般比它的表面积大。

() 3．底面积相等的两个圆柱，它们的体积也相等。

() 4．圆柱的底面直径是3 cm，高是9.42 cm，侧面沿高剪开后是一个正方形。

() 5．圆柱的底面半径扩大到原来的2倍，高也扩大到原来的2倍，则圆柱的体积扩大到原来的4倍。

()三、选择。

(将正确答案的字母填在括号里。

人教版六年级下册数学第三单元《圆柱与圆锥》测试卷一.选择题(共5题, 共10分)1.一个圆柱的侧面展开图如图, 那么这个圆柱可能是下列图中的（）。

A. B. C.2.一个圆锥的体积是36立方厘米, 底面积是12平方厘米, 高是（）厘米。

A.9B.6C.33.求圆柱形罐头盒的用料就是求圆柱（）。

A.体积B.容积C.表面积4.将一个圆锥底面积扩大6倍, 高不变, 那么圆锥的体积扩大（）倍。

A.6B.3C.25.圆柱的底面直径是6分米, 高是8分米, 与它等底等高的圆锥的体积是（）立方分米。

A.113.04B.226.08C.75.36二.判断题(共5题, 共10分)1.圆锥的体积一定等于圆柱的。

（）2.一个圆锥体的底面积不变, 如果高扩大3倍, 体积也扩大3倍。

（）3.一个直角三角形, 以它的斜边为轴旋转一周, 可以生成一个圆锥。

（）4.一张长方形铁皮分别横着、竖着卷成两个圆柱, 把它们竖放在桌面上, 它们的容积完全相同。

（）5.从圆锥的顶点到底面周长任意一点的连线都是圆锥的高。

（）三.填空题(共8题, 共11分)1.一个圆柱的底面面积是25平方匣米, 高是10分米, 它的体积是（）立方厘米。

2.一个圆柱底面半径2分米, 侧面积是113.04平方分米, 这个圆柱体的高是（）分米。

3.把一个圆柱体等分成若干份, 可以拼成一个近似的长方体。

拼成的长方体的长等于圆柱的（）, 长方体的宽等于圆柱的（）, 高等于圆柱的（）。

4.一个圆柱体的侧面积为150cm2, 底面半径是4厘米, 它的体积是（）cm3。

5.一个圆柱的侧面展开图是一个正方形, 高是25.12 cm, 这个圆柱的底面半径是（）cm。

6.把一个圆锥沿底面直径纵切开, 切面是一个（）形。

7.一个圆柱的体积是100.48dm3, 它的底面半径是2dm, 高是（）dm。

8.李师傅用一张长40分米, 宽12分米的铁皮做成圆柱形铁桶, 铁桶的侧面积是（）平方分米；如果给这个铁桶再加一个底, 还需要（）平方分米的铁皮。