2017高考一轮复习教案二次函数与幂函数(后附完整答案)

第4讲二次函数与幂函数考纲展示命题探究1二次函数解析式的三种形式(1)一般式：y＝ax2＋bx＋c(a≠0)．(2)顶点式：y＝a(x－h)2＋k(a≠0)，其中(h，k)为抛物线顶点坐标．(3)两点式：y＝a(x－x1)(x－x2)(a≠0)，其中x1，x2是抛物线与x 轴交点的横坐标．2二次函数的图象与性质y min＝4ac－b24a y max＝4ac－b24a注意点解决二次函数问题应用数形结合思想二次函数、一元二次方程和一元二次不等式统称为三个“二次”．它们常结合在一起，而二次函数又是其核心．因此，利用二次函数的图象数形结合是探求这类问题的基本策略.1．思维辨析(1)形如y＝ax2＋bx＋c的函数一定是二次函数．()(2)二次函数y＝ax2＋bx＋c，x∈R，不可能是偶函数．()(3)二次函数y＝ax2＋bx＋c，x∈[m，n]的最值一定是4ac－b24a.()(4)若函数f(x)＝(k2－1)x2＋2x－3在(－∞，2)上单调递增，则k＝±22.()(5)已知f(x)＝x2－4x＋5，x∈[0,3)，则f(x)max＝f(0)＝5，f(x)min＝f(3)＝2.()答案(1)×(2)×(3)×(4)×(5)×2．已知函数f(x)＝－x2＋4x＋a，x∈[0,1]．若f(x)有最小值－2，则f(x)的最大值为()A．－1 B．0C．1 D．2答案 C解析函数f(x)＝－x2＋4x＋a的对称轴为直线x＝2，开口向下，f(x)＝－x2＋4x＋a在[0,1]上单调递增，则当x＝0时，f(x)的最小值为f(0)＝a＝－2；当x＝1时，f(x)的最大值为f(1)＝3＋a＝3－2＝1，选C.3．(1)已知关于x的不等式x2－ax＋2a>0在R上恒成立，则实数a 的取值范围是________．(2)已知f (x )＝ax 2＋bx ＋3a ＋b 是偶函数，且其定义域为[a －1,2a ]，则y ＝f (x )的值域为______．答案 (1)(0,8) (2)⎣⎢⎡⎦⎥⎤1，3127 解析 (1)由题意知，Δ＝(－a )2－8a <0，解得0<a <8. (2)∵f (x )＝ax 2＋bx ＋3a ＋b 是偶函数， ∴其定义域[a －1,2a ]关于原点对称， ∴即a －1＝－2a ，∴a ＝13， ∵f (x )＝ax 2＋bx ＋3a ＋b 是偶函数， 即f (－x )＝f (x )，∴b ＝0，∴f (x )＝13x 2＋1，x ∈⎣⎢⎡⎦⎥⎤－23，23，其值域为⎩⎨⎧⎭⎬⎫y ⎪⎪⎪1≤y ≤3127.[考法综述] 高考中以考查二次函数的图象、单调性、最值为主，有二次不等式恒成立问题以及二次方程根的分布问题等．命题法 二次函数的图象及性质的应用典例 (1)如图是二次函数y ＝ax 2＋bx ＋c 图象的一部分，图象过点A (－3,0)，对称轴为x ＝－1.给出下面四个结论：①b 2>4ac ；②2a －b ＝1；③a －b ＋c ＝0；④5a <b .其中正确的是( ) A ．②④ B ．①④ C ．②③D ．①③(2)已知对任意的a ∈[－1,1]，函数f (x )＝x 2＋(a －4)x ＋4－2a 的值总大于0，则x 的取值范围是( )A ．1<x <3B ．x <1或x >3C ．1<x <2D ．x <2或x >3[解析] (1)因为图象与x 轴有两个交点，所以b 2－4ac >0，即b 2>4ac ，①正确；对称轴为x ＝－1，即－b2a ＝－1,2a －b ＝0，②错误； 结合图象，当x ＝－1时，y >0，即a －b ＋c >0，③错误； 由对称轴为x ＝－1知，b ＝2a .又函数图象开口向下，所以a <0，所以5a <2a ，即5a <b ，④正确．(2)f (x )＝x 2＋(a －4)x ＋4－2a ＝(x －2)a ＋(x 2－4x ＋4)．记g (a )＝(x －2)a ＋(x 2－4x ＋4)，由题意可得⎩⎨⎧g (－1)>0，g (1)>0，即⎩⎨⎧g (－1)＝x 2－5x ＋6>0，g (1)＝x 2－3x ＋2>0，解得x <1或x >3.故选B.[答案] (1)B (2)B【解题法】 二次函数问题的求解策略(1)二次函数的最值问题一般先配方，通过对称轴，开口方向等特征求得，有时需要讨论，如动轴定区间问题和定轴动区间问题．(2)与二次函数图象有关的问题采用数形结合的方法，需尽量规范作图，尤其是图象的开口方向、顶点、对称轴及与两坐标轴的交点要标清楚．1.如果函数f (x )＝12(m －2)x 2＋(n －8)x ＋1(m ≥0，n ≥0)在区间⎣⎢⎡⎦⎥⎤12，2上单调递减，那么mn 的最大值为( ) A ．16 B ．18C ．25 D.812答案 B解析 由已知得f ′(x )＝(m －2)x ＋n －8，又对任意的x ∈⎣⎢⎡⎦⎥⎤12，2，f ′(x )≤0，所以⎩⎨⎧f ′⎝ ⎛⎭⎪⎫12≤0f ′(2)≤0，即⎩⎪⎨⎪⎧m ≥0，n ≥0m ＋2n ≤182m ＋n ≤12，画出该不等式组表示的平面区域如图中阴影部分所示，令mn ＝t ，则当n ＝0时，t ＝0，当n ≠0时，m ＝tn .由线性规划的相关知识知，只有当直线2m ＋n ＝12与曲线m ＝tn 相切时，t 取得最大值．由⎩⎪⎨⎪⎧－t n 2＝－126－12n ＝tn，解得n ＝6，t ＝18，所以(mn )max ＝18，选B.2．已知a ，b ，c ∈R ，函数f (x )＝ax 2＋bx ＋c .若f (0)＝f (4)>f (1)，则( )A ．a >0,4a ＋b ＝0B ．a <0,4a ＋b ＝0C ．a >0,2a ＋b ＝0D ．a <0,2a ＋b ＝0答案 A解析 由f (0)＝f (4)得f (x )＝ax 2＋bx ＋c 的对称轴为x ＝－b2a ＝2，∴4a ＋b ＝0，又f (0)>f (1)，∴f (x )先减后增，∴a >0，选A.3．两个二次函数f (x )＝ax 2＋bx ＋c 与g (x )＝bx 2＋ax ＋c 的图象可能是( )答案 D解析 函数f (x )图象的对称轴为x ＝－b2a ，函数g (x )图象的对称轴为x ＝－a 2b ，显然－b 2a 与－a2b 同号，故两个函数图象的对称轴应该在y 轴的同侧，只有D 满足．故选D.4．若函数f (x )＝cos2x ＋a sin x 在区间⎝ ⎛⎭⎪⎫π6，π2上是减函数，则a 的取值范围是________．答案 (－∞，2]解析 f (x )＝cos2x ＋a sin x ＝1－2sin 2x ＋a sin x ，令t ＝sin x ，x ∈⎝ ⎛⎭⎪⎫π6，π2，则t ∈⎝ ⎛⎭⎪⎫12，1，原函数化为y ＝－2t 2＋at ＋1，由题意及复合函数单调性的判定可知y ＝－2t 2＋at ＋1在⎝ ⎛⎭⎪⎫12，1上是减函数，结合抛物线图象可知，a 4≤12，所以a ≤2.5.已知函数f (x )＝－x 2＋2ax ＋1－a 在x ∈[0,1]时有最大值2，则a 的值为________．答案 2或－1解析 f (x )＝－(x －a )2＋a 2－a ＋1，在x ∈[0,1]时， 当a ≥1时，f (x )max ＝f (1)＝a ； 当0<a <1时，f (x )max ＝f (a )＝a 2－a ＋1； 当a ≤0时，f (x )max ＝f (0)＝1－a .根据已知条件得，⎩⎨⎧a ≥1，a ＝2或⎩⎨⎧0<a <1，a 2－a ＋1＝2或⎩⎨⎧a ≤0，1－a ＝2.解得a ＝2或a ＝－1.6．对于c >0，当非零实数a ，b 满足4a 2－2ab ＋4b 2－c ＝0且使|2a ＋b |最大时，3a －4b ＋5c 的最小值为________．答案 －2解析 设2a ＋b ＝t ，则2a ＝t －b ，由已知得关于b 的方程(t －b )2－b (t －b )＋4b 2－c ＝0有解，即6b 2－3tb ＋t 2－c ＝0有解．故Δ＝9t 2－24(t 2－c )≥0，所以t 2≤85c ，所以|t |max ＝210c 5，此时c ＝58t 2，b ＝14t ，2a ＝t －b ＝3t4，所以a ＝3t 8.故3a －4b ＋5c ＝8t －16t ＋8t 2＝8⎝ ⎛⎭⎪⎫1t 2－1t＝8⎝ ⎛⎭⎪⎫1t －122－2≥－2. 7．已知函数f (x )＝|x 2＋3x |，x ∈R .若方程f (x )－a |x －1|＝0恰有4个互异的实数根，则实数a 的取值范围为________．答案 (0,1)∪(9，＋∞)解析 在同一坐标系中分别作出函数f (x )与y ＝a |x －1|的图象，由图知，当a ＝0时，两函数的图象只有2个交点，当a <0时，两图象没有交点，故必有a >0.若曲线y ＝－x 2－3x (－3≤x ≤0)与直线y ＝－a (x －1)(x ≤1)相切，联立方程得x 2＋(3－a )x ＋a ＝0，则由Δ＝0得a ＝1(a ＝9舍去)，因此当0<a <1时，f (x )的图象与y ＝a |x －1|的图象有4个交点；若曲线y ＝x 2＋3x (x >0)与直线y ＝a (x －1)(x >1)相切，联立方程得x 2＋(3－a )x ＋a ＝0，则由Δ＝0可得a ＝9(a ＝1舍去)，因此当a >9时，f(x)的图象与y＝a|x－1|的图象有4个交点，故当方程有4个互异实数根时，实数a的取值范围是(0,1)∪(9，＋∞)．1幂函数的定义一般地，形如y＝xα(α∈R)的函数称为幂函数．2五种幂函数图象的比较3幂函数的性质比较注意点α的大小对幂函数图象的影响幂函数在第一象限的图象中，以直线x＝1为分界，当0<x<1时，α越大，图象越低(即图象越靠近x轴，可记为“指大图低”)；当x>1时，α越大，图象越高(即图象离x轴越远，不包含y＝x0).1．思维辨析(1)函数y＝2x 12是幂函数．()(2)如果幂函数的图象与坐标轴相交，则交点一定是原点．()(3)当n<0时，幂函数y＝x n是定义域上的减函数．()(4)当n>0时，幂函数y＝x n是定义域上的增函数．()(5)幂函数的图象都经过点(1,1)和点(0,0)．()答案(1)×(2)√(3)×(4)×(5)×2．当x∈(1，＋∞)时，下列函数中图象全在直线y＝x下方的增函数是()A．y＝x 12B．y＝x2C．y＝x3D．y＝x－1答案 A解析y＝x2，y＝x3在x∈(1，＋∞)时，图象不在直线y＝x下方，排除B、C，而y＝x－1是(－∞，0)，(0，＋∞)上的减函数．3．已知f (x )＝x 12，若0<a <b <1，则下列各式中正确的是( )A ．f (a )<f (b )<f ⎝ ⎛⎭⎪⎫1a <f ⎝ ⎛⎭⎪⎫1bB ．f ⎝ ⎛⎭⎪⎫1a <f ⎝ ⎛⎭⎪⎫1b <f (b )<f (a )C ．f (a )<f (b )<f ⎝ ⎛⎭⎪⎫1b <f ⎝ ⎛⎭⎪⎫1aD ．f ⎝ ⎛⎭⎪⎫1a <f (a )<f ⎝ ⎛⎭⎪⎫1b <f (b )答案 C解析 因为函数f (x )＝x 12 在(0，＋∞)上是增函数，又0<a <b <1b <1a ，故选C.[考法综述] 考查幂函数的概念、图象及性质，以及利用幂函数性质求参数范围，有时会结合指数、对数比较大小，难度不大．命题法 幂函数的图象及性质的应用典例 (1)在同一直角坐标系中，函数f (x )＝x a (x >0)，g (x )＝log a x 的图象可能是( )(2)若a ＝⎝ ⎛⎭⎪⎫12 23 ，b ＝⎝ ⎛⎭⎪⎫15 23 ，c ＝⎝ ⎛⎭⎪⎫12 13，则a ，b ，c 的大小关系是( )A ．a <b <cB ．c <a <bC ．b <c <aD ．b <a <c[解析] (1)因为a >0，所以f (x )＝x a 在(0，＋∞)上为增函数，故A 不符合；在B 中，由f (x )的图象知a >1，由g (x )的图象知0<a <1，矛盾，故B 不符合；在C 中，由f (x )的图象知0<a <1，由g (x )的图象知a >1，矛盾，故C 不符合；在D 中，由f (x )的图象知0<a <1，由g (x )的图象知0<a <1，相符．(2)因为y ＝x 23 在第一象限内是增函数，所以a ＝⎝ ⎛⎭⎪⎫12 23 >b ＝⎝ ⎛⎭⎪⎫15 23 ，因为y ＝⎝ ⎛⎭⎪⎫12x 是减函数，所以a ＝⎝ ⎛⎭⎪⎫12 23 <c ＝⎝ ⎛⎭⎪⎫12 13，所以b <a <c .[答案] (1)D (2)D【解题法】 幂函数的图象与性质问题的解题策略 (1)关于图象辨识问题，关键是熟悉各类幂函数的图象特征，如过特殊点、凹凸性等．(2)关于比较幂值大小问题，结合幂值的特点利用指数幂的运算性质化成同指数幂，选择适当的幂函数，借助其单调性进行比较或应用．1．若幂函数f (x )的图象经过点⎝⎛⎭⎪⎫3，33，则其定义域为( )A ．{x |x ∈R ，且x >0}B ．{x |x ∈R ，且x <0}C ．{x |x ∈R ，且x ≠0}D ．R答案 A解析 设f (x )＝x α，∴3α＝33，α＝－12，f (x )＝x －12， ∴其定义域为{x |x >0}，选A 项．2．下面给出4个幂函数的图象，则图象与函数的大致对应是( )A ．①y ＝x 13 ，②y ＝x 2，③y ＝x 12，④y ＝x －1 B ．①y ＝x 3，②y ＝x 2，③y ＝x 12，④y ＝x －1C ．①y ＝x 2，②y ＝x 3，③y ＝x 12，④y ＝x －1 D ．①y ＝x 13 ，②y ＝x 12，③y ＝x 2，④y ＝x －1 答案 B解析 ②的图象关于y 轴对称，②应为偶函数，故排除选项C 、D.①由图象知，在第一象限内，图象下凸，递增的较快，所以幂函数的指数大于1，故排除A.选B.3．若f (x )＝x 23 －x － 12，则满足f (x )<0的x 的取值范围是________．答案 (0,1)解析 令y 1＝x 23 ，y 2＝x － 12 ，则f (x )<0即为y 1<y 2.函数y 1＝x 23，y 2＝x － 12 的图象如图所示，由图象知：当0<x <1时，y 1<y 2，所以满足f (x )<0的x 的取值范围是(0,1)．4.已知幂函数f (x )＝(m 2－m －1)·x －5m －3在(0，＋∞)上是增函数，则m ＝________.答案 －1 解析由已知得⎩⎨⎧m 2－m －1＝1，－5m －3>0，解得m ＝－1.已知x ∈[－1,1]时，f (x )＝x 2－ax ＋a2>0恒成立，则实数a 的取值范围是( )A ．(0,2)B ．(2，＋∞)C ．(0，＋∞)D.⎝ ⎛⎭⎪⎫－23，2[错解][正解] 二次函数图象开口向上，对称轴为x ＝a2，又x ∈[－1,1]时，f (x )＝x 2－ax ＋a2>0恒成立，即f (x )最小值>0.①当a 2≤－1，即a ≤－2时，f (－1)＝1＋a ＋a 2>0，解得a >－23，与a ≤－2矛盾；②当a 2≥1，即a ≥2时，f (1)＝1－a ＋a2>0，解得a <2，与a ≥2矛盾；③当－1<a2<1，即－2<a <2时，f ⎝ ⎛⎭⎪⎫a 2＝14a 2－12a 2＋a 2>0，解得0<a <2.综上得实数a 的取值范围是(0,2)．[答案] A [心得体会]………………………………………………………………………………………………时间：60分钟基础组1.[2016·冀州中学周测]已知幂函数f (x )＝(n 2＋2n －2)x n2－3n(n ∈Z )的图象关于y 轴对称，且在(0，＋∞)上是减函数，则n 的值为( )A ．－3B ．1C ．2D ．1或2答案 B解析 由于f (x )为幂函数，所以n 2＋2n －2＝1，解得n ＝1或n ＝－3，经检验只有n ＝1适合题意，故选B.2．[2016·冀州中学热身]若函数f (x )＝x 2＋bx ＋c 的图象的顶点在第四象限，则函数f ′(x )的图象是( )答案 A解析 函数f (x )＝x 2＋bx ＋c 图象的顶点坐标为⎝ ⎛⎭⎪⎪⎫－b 2，4c －b 24，则－b 2>0.f ′(x )＝2x ＋b ，令f ′(x )＝0，得x ＝－b2>0，即导函数f ′(x )的图象与x 轴的交点位于x 轴正半轴上，且斜率为正，故选A.3．[2016·枣强中学周测]定义域为R 的函数f (x )满足f (x ＋1)＝2f (x )，且当x ∈[0,1]时，f (x )＝x 2－x ，则当x ∈[－2，－1]时，f (x )的最小值为( )A ．－116B ．－18 C ．－14 D ．0答案 A解析 设x ∈[－2，－1]，则x ＋2∈[0,1]，则f (x ＋2)＝(x ＋2)2－(x ＋2)＝x 2＋3x ＋2，又f (x ＋2)＝f [(x ＋1)＋1]＝2f (x ＋1)＝4f (x )，∴f (x )＝14(x 2＋3x ＋2)∴当x ＝－32时，取到最小值为－116.4. [2016·冀州中学预测]对任意实数a ，b 定义运算“⊗”：a ⊗b ＝⎩⎪⎨⎪⎧b ，a －b ≥1，a ，a －b <1.设f (x )＝(x 2－1)⊗(4＋x )，若函数y ＝f (x )＋k 的图象与x 轴恰有三个不同交点，则k 的取值范围是( )A ．(－2,1)B ．[0,1]C ．[－2,0)D ．[－2,1)答案 D解析 解不等式x 2－1－(4＋x )≥1，得x ≤－2或x ≥3.所以f (x )＝⎩⎨⎧x ＋4，x ∈(－∞，－2]∪[3，＋∞)，x 2－1，x ∈(－2，3).其图象如下图实线所示，由图可知，当－2≤k <1时，函数y ＝f (x )＋k 的图象与x 轴恰有三个不同交点，故选D.5．[2016·衡水中学期末]幂函数f (x )＝x α的图象过点(2,4)，那么函数f (x )的单调递增区间是( )A ．(－2，＋∞)B ．[－1，＋∞)C ．[0，＋∞)D ．(－∞，－2)答案 C解析 因为函数过点(2,4)，所以4＝2α，α＝2，故f (x )＝x 2，单调增区间为[0，＋∞)，选C.6．[2016·武邑中学期中]设函数f (x )＝ax 2＋bx ＋c (a ，b ，c ∈R )，若a ＝c ，则函数f (x )的图象不可能是( )答案 D解析 由A 、B 、C 、D 四个选项知，图象与x 轴均有交点，记两个交点的横坐标分别为x 1，x 2，若只有一个交点，则x 1＝x 2.因为a ＝c ，所以x 1x 2＝ca ＝1，比较四个选项，可知选项D 的x 1<－1，x 2<－1，所以D 不满足．故选D.7. [2016·衡水中学期中]已知函数f (x )＝a sin x －12cos2x ＋a －3a ＋12(a ∈R ，a ≠0)，若对任意x ∈R 都有f (x )≤0，则a 的取值范围是( )A.⎣⎢⎡⎭⎪⎫－32，0 B ．[－1,0)∪(0,1] C ．(0,1] D ．[1,3]答案 C解析 化简函数得f (x )＝sin 2x ＋a sin x ＋a －3a .令t ＝sin x (－1≤t ≤1)，则g (t )＝t 2＋at ＋a －3a ，问题转化为使g (t )在[－1,1]上恒有g (t )≤0，即⎩⎪⎨⎪⎧g (－1)＝1－3a ≤0，g (1)＝1＋2a －3a ≤0，解得0<a ≤1，故选C.8．[2016·枣强中学猜题]若二次函数f (x )满足f (x ＋1)－f (x )＝2x ，且f (0)＝1，则f (x )的表达式为( )A ．f (x )＝－x 2－x －1B ．f (x )＝－x 2＋x －1C ．f (x )＝x 2－x －1D ．f (x )＝x 2－x ＋1答案 D解析 设f (x )＝ax 2＋bx ＋c (a ≠0)，由题意得 故⎩⎪⎨⎪⎧2a ＝2，a ＋b ＝0，c ＝1，解得⎩⎪⎨⎪⎧a ＝1，b ＝－1，c ＝1，则f (x )＝x 2－x ＋1.故选D.9．[2016·衡水中学月考]“a ＝1”是“函数f (x )＝x 2－4ax ＋3在区间[2，＋∞)上为增函数”的( )A ．必要不充分条件B ．充分不必要条件C ．充分必要条件D ．既不充分又不必要条件答案 B解析 函数f (x )＝x 2－4ax ＋3在区间[2，＋∞)上为增函数，则满足对称轴－－4a2＝2a ≤2，即a ≤1，所以“a ＝1”是“函数f (x )＝x 2－4ax ＋3在区间[2，＋∞)上为增函数”的充分不必要条件．10．[2016·武邑中学周测]已知二次函数f (x )＝ax 2＋bx ＋c 满足条件：①f (3－x )＝f (x )；②f (1)＝0；③对任意实数x ，f (x )≥14a －12恒成立． 则其解析式为f (x )＝________. 答案 x 2－3x ＋2解析 依题意可设f (x )＝a ⎝ ⎛⎭⎪⎫x －322＋k ，由f (1)＝14a ＋k ＝0，得k ＝－14a ， 从而f (x )＝a ⎝ ⎛⎭⎪⎫x －322－a 4≥14a －12恒成立，则－a 4≥14a －12，且a >0，即14a ＋a 4－12≤0，即a 2－2a ＋14a ≤0，且a >0，∴a ＝1. 从而f (x )＝⎝ ⎛⎭⎪⎫x －322－14＝x 2－3x ＋2. 11．[2016·冀州中学月考]已知二次函数图象的对称轴为x ＝－2，截x 轴所得的弦长为4，且过点(0，－1)，求函数的解析式． 解 ∵二次函数图象的对称轴为x ＝－2，∴可设所求函数的解析式为f (x )＝a (x ＋2)2＋b .∵二次函数f (x )的图象截x 轴所得的弦长为4，∴f (x )过点(－2＋2,0)和(－2－2,0)．又二次函数f (x )的图象过点(0，－1)，∴⎩⎨⎧4a ＋b ＝02a ＋b ＝－1，解得⎩⎪⎨⎪⎧a ＝12b ＝－2.∴f (x )＝12(x ＋2)2－2.即f (x )＝12x 2＋2x －1.12．[2016·衡水中学周测]已知函数f (x )＝ax 2－2ax ＋2＋b (a ≠0)在区间[2,3]上有最大值5，最小值2.(1)求a ，b 的值；(2)若b <1，g (x )＝f (x )－2m x 在[2,4]上单调，求m 的取值范围． 解 (1)f (x )＝a (x －1)2＋2＋b －a .①当a >0时，f (x )在[2,3]上为增函数，故⎩⎨⎧ f (3)＝5，f (2)＝2，∴⎩⎨⎧ 9a －6a ＋2＋b ＝5，4a －4a ＋2＋b ＝2，∴⎩⎨⎧a ＝1，b ＝0.②当a <0时，f (x )在[2,3]上为减函数，故⎩⎨⎧f (3)＝2，f (2)＝5，∴⎩⎨⎧9a －6a ＋2＋b ＝2，4a －4a ＋2＋b ＝5，∴⎩⎨⎧a ＝－1，b ＝3.∴a ＝1，b ＝0或a ＝－1，b ＝3. (2)∵b <1，∴a ＝1，b ＝0，即f (x )＝x 2－2x ＋2，g (x )＝x 2－2x ＋2－2m x ＝x 2－(2＋2m )x ＋2. 若g (x )在[2,4]上单调，则2＋2m 2≤2或2m ＋22≥4，∴2m ≤2或2m ≥6，即m ≤1或m ≥log 26.故m 的取值范围是(－∞，1]∪[log 26，＋∞)．能力组13.[2016·枣强中学一轮检测]已知函数f (x )＝(m －1)x 2＋2mx ＋3为偶函数，则f (x )在区间(－5，－3)上( )A ．先减后增B ．先增后减C ．单调递减D ．单调递增答案 D解析 当m ＝1时，f (x )＝2x ＋3不是偶函数；当m ≠1时，f (x )为二次函数，要使其为偶函数，则其对称轴应为y 轴，故需m ＝0，此时f (x )＝－x 2＋3，其图象的开口向下，所以函数f (x )在(－5，－3)上单调递增，故选D.14．[2016·武邑中学模拟]函数f (x )＝ax 2＋ax －1在R 上恒满足f (x )<0，则a 的取值范围是( )A ．a ≤0B ．a <－4C ．－4<a <0D ．－4<a ≤0答案 D解析 当a ＝0时，f (x )＝－1在R 上恒有f (x )<0； 当a ≠0时，∵f (x )在R 上恒有f (x )<0，∴⎩⎪⎨⎪⎧a <0a 2＋4a <0，∴－4<a <0. 综上可知：－4<a ≤0.15．[2016·冀州中学预测]当0<x <1时，函数f (x )＝x ，g (x )＝x ，h (x )＝x －2的大小关系是________．答案 h (x )>g (x )>f (x )解析 如图所示为函数f (x )，g (x )，h (x )在(0,1)上的图象，由此可知，h (x )>g (x )>f (x )．16．[2016·枣强中学周测]是否存在实数a ，使函数f (x )＝x 2－2ax ＋a 的定义域为[－1,1]时，值域为[－2,2]？若存在，求a 的值；若不存在，说明理由．解 f (x )＝(x －a )2＋a －a 2.当a <－1时，f (x )在[－1,1]上为增函数，∴⎩⎨⎧f (－1)＝1＋3a ＝－2，f (1)＝1－a ＝2⇒a ＝－1(舍去)；当－1≤a ≤0时，⎩⎨⎧f (a )＝a －a 2＝－2，f (1)＝1－a ＝2⇒a ＝－1；当0<a ≤1时，⎩⎨⎧f (a )＝a －a 2＝－2，f (－1)＝1＋3a ＝2⇒a 不存在；当a >1时，f (x )在[－1,1]上为减函数，∴⎩⎨⎧f (－1)＝1＋3a ＝2，f (1)＝1－a ＝－2⇒a 不存在．综上可得a ＝－1.。

第六节二次函数与幂函数[知识能否忆起]一、常用幂函数的图象与性质函数特征性质y＝x y＝x2y＝x3y＝x12y＝x－1图象定义域R R R{x|x≥0}{x|x≠0} 值域R{y|y≥0}R{y|y≥0}{y|y≠0} 奇偶性奇偶奇非奇非偶奇单调性增(－∞，0]减(0，＋∞)增增增(－∞，0)和(0，＋∞)减公共点(1,1)二、二次函数1．二次函数的定义形如f(x)＝ax2＋bx＋c(a≠0)的函数叫做二次函数．2．二次函数解析式的三种形式(1)一般式：f(x)＝ax2＋bx＋c(a≠0)；(2)顶点式：f(x)＝a(x－m)2＋n(a≠0)；(3)零点式：f(x)＝a(x－x1)(x－x2)(a≠0)．3．二次函数的图象和性质a>0a<0 图象图象特点①对称轴：x＝－b2a；②顶点：⎝⎛⎭⎫－b2a，4ac－b24a性质定义域 x ∈R值域y ∈⎣⎡4ac －b 24a ，＋∞y ∈⎝⎛⎦⎤－∞，4ac －b 24a 奇偶性b ＝0时为偶函数，b ≠0时既非奇函数也非偶函数单调性x ∈－∞，⎦⎤－b 2a 时递减，x ∈－b2a，＋∞时递增x ∈⎝⎛⎦⎤－∞，－b2a 时递增，x ∈⎣⎡⎭⎫－b 2a ，＋∞时递减[小题能否全取]1．若f (x )既是幂函数又是二次函数，则f (x )可以是( ) A ．f (x )＝x 2－1 B ．f (x )＝5x 2 C ．f (x )＝－x 2D ．f (x )＝x 2解析：选D 形如f (x )＝x α的函数是幂函数，其中α是常数．2．(教材习题改编)设α∈⎩⎨⎧⎭⎬⎫－1，1，12，3，则使函数y ＝x α的定义域为R 且为奇函数的所有α值为( )A ．1,3B ．－1,1C ．－1,3D ．－1,1,3解析：选A 在函数y ＝x －1，y ＝x ，y ＝x 12，y ＝x 3中，只有函数y ＝x 和y ＝x 3的定义域是R ，且是奇函数，故α＝1,3.3．(教材习题改编)已知函数f (x )＝ax 2＋x ＋5的图象在x 轴上方，则a 的取值范围是( )A.⎝⎛⎭⎫0，120B.⎝⎛⎭⎫－∞，－120 C.⎝⎛⎭⎫120，＋∞D.⎝⎛⎭⎫－120，0 解析：选C 由题意知⎩⎪⎨⎪⎧ a >0，Δ<0，即⎩⎪⎨⎪⎧a >0，1－20a <0得a >120.4．(教材习题改编)已知点M ⎝⎛⎭⎫33，3在幂函数f (x )的图象上，则f (x )的表达式为________．解析：设幂函数的解析式为y ＝x α，则3＝⎝⎛⎭⎫33α，得α＝－2.故y ＝x －2. 答案：y ＝x －25．如果函数f (x )＝x 2＋(a ＋2)x ＋b (x ∈[a ，b ])的图象关于直线x ＝1对称，则函数f (x )的最小值为________．解析：由题意知⎩⎨⎧－a ＋22＝1，a ＋b ＝2，得⎩⎪⎨⎪⎧a ＝－4，b ＝6.则f (x )＝x 2－2x ＋6＝(x －1)2＋5≥5. 答案：51.幂函数图象的特点(1)幂函数的图象一定会经过第一象限，一定不会经过第四象限，是否经过第二、三象限，要看函数的奇偶性；(2)幂函数的图象最多只能经过两个象限内；(3)如果幂函数的图象与坐标轴相交，则交点一定是原点． 2．与二次函数有关的不等式恒成立问题 (1)ax 2＋bx ＋c >0，a ≠0恒成立的充要条件是⎩⎪⎨⎪⎧a >0，b 2－4ac <0.(2)ax 2＋bx ＋c <0，a ≠0恒成立的充要条件是⎩⎪⎨⎪⎧a <0，b 2－4ac <0.[注意] 当题目条件中未说明a ≠0时，就要讨论a ＝0和a ≠0两种情况．幂函数的图象与性质典题导入[例1] 已知幂函数f (x )＝(m 2－m －1)x－5m －3在(0，＋∞)上是增函数，则m ＝________.[自主解答] ∵函数f (x )＝(m 2－m －1)x －5m －3是幂函数， ∴m 2－m －1＝1，解得m ＝2或m ＝－1.当m ＝2时，－5m －3＝－13，函数y ＝x －13在(0，＋∞)上是减函数； 当m ＝－1时，－5m －3＝2，函数y ＝x 2在(0，＋∞)上是增函数． ∴m ＝－1. [答案] －1由题悟法1．幂函数y ＝x α的图象与性质由于α的值不同而比较复杂，一般从两个方面考查： (1)α的正负：α>0时，图象过原点和(1,1)，在第一象限的图象上升；α<0时，图象不过原点，在第一象限的图象下降．(2)曲线在第一象限的凹凸性：α>1时，曲线下凸； 0<α<1时，曲线上凸；α<0时，曲线下凸．2．在比较幂值的大小时，必须结合幂值的特点，选择适当的函数．借助其单调性进行比较，准确掌握各个幂函数的图象和性质是解题的关键．以题试法1．(1)如图给出4个幂函数大致的图象，则图象与函数对应正确的是( )A ．①y ＝x 13，②y ＝x 2，③y ＝x 12，④y ＝x －1B ．①y ＝x 3，②y ＝x 2，③y ＝x 12，④y ＝x －1C ．①y ＝x 2，②y ＝x 3，③y ＝x 12，④y ＝x －1D ．①y ＝x 13，②y ＝x 12，③y ＝x 2，④y ＝x －1解析：选B 由图①知，该图象对应的函数为奇函数且定义域为R ，当x >0时，图象是向下凸的，结合选项知选B.(2)(·淄博模拟)若a <0，则下列不等式成立的是( ) A ．2a >⎝⎛⎭⎫12a>(0.2)aB ．(0.2)a >⎝⎛⎭⎫12a>2aC.⎝⎛⎭⎫12a>(0.2)a>2aD ．2a >(0.2)a >⎝⎛⎭⎫12a解析：选B 若a <0，则幂函数y ＝x a 在(0，＋∞)上是减函数，所以(0.2)a >⎝⎛⎭⎫12a>0.所以(0.2)a >⎝⎛⎭⎫12a>2a .求二次函数的解析式典题导入[例2] 已知二次函数f (x )有两个零点0和－2，且它有最小值－1. (1)求f (x )解析式；(2)若g (x )与f (x )图象关于原点对称，求g (x )解析式． [自主解答] (1)由于f (x )有两个零点0和－2， 所以可设f (x )＝ax (x ＋2)(a ≠0)， 这时f (x )＝ax (x ＋2)＝a (x ＋1)2－a ， 由于f (x )有最小值－1，所以必有⎩⎪⎨⎪⎧a >0，－a ＝－1，解得a ＝1.因此f (x )的解析式是f (x )＝x (x ＋2)＝x 2＋2x .(2)设点P (x ，y )是函数g (x )图象上任一点，它关于原点对称的点P ′(－x ，－y )必在f (x )图象上，所以－y ＝(－x )2＋2(－x )， 即－y ＝x 2－2x ， y ＝－x 2＋2x ， 故g (x )＝－x 2＋2x .由题悟法求二次函数的解析式常用待定系数法．合理选择解析式的形式，并根据已知条件正确地列出含有待定系数的等式，把问题转化为方程(组)求解是解决此类问题的基本方法．以题试法2．设f (x )是定义在R 上的偶函数，当0≤x ≤2时，y ＝x ，当x >2时，y ＝f (x )的图象是顶点为P (3,4)，且过点A (2,2)的抛物线的一部分．(1)求函数f (x )在(－∞，－2)上的解析式；(2)在下面的直角坐标系中直接画出函数f (x )的草图； (3)写出函数f (x )的值域．解：(1)设顶点为P(3,4)且过点A(2,2)的抛物线的方程为y＝a(x－3)2＋4，将(2,2)代入可得a＝－2，则y＝－2(x－3)2＋4，即x>2时，f(x)＝－2x2＋12x－14.当x<－2时，即－x>2.又f(x)为偶函数，f(x)＝f(－x)＝－2×(－x)2－12x－14，即f(x)＝－2x2－12x－14.所以函数f(x)在(－∞，－2)上的解析式为f(x)＝－2x2－12x－14.(2)函数f(x)的图象如图，(3)由图象可知，函数f(x)的值域为(－∞，4]．二次函数的图象与性质典题导入[例3]已知函数f(x)＝x2＋2ax＋3，x∈[－4,6]．(1)当a＝－2时，求f(x)的最值；(2)求实数a的取值范围，使y＝f(x)在区间[－4,6]上是单调函数．[自主解答](1)当a＝－2时，f(x)＝x2－4x＋3＝(x－2)2－1，由于x∈[－4,6]．所以f(x)在[－4,2]上单调递减，在[2,6]上单调递增，故f(x)的最小值是f(2)＝－1，又f(－4)＝35，f(6)＝15，故f(x)的最大值是35.(2)由于函数f(x)的图象开口向上，对称轴是x＝－a，所以要使f(x)在[－4,6]上是单调函数，应有－a≤－4或－a≥6，即a≤－6或a≥4.故a 的取值范围为(－∞，－6]∪[4，＋∞)．本例条件不变，求当a ＝1时，f (|x |)的单调区间． 解：当a ＝1时，f (x )＝x 2＋2x ＋3，则f (|x |)＝x 2＋2|x |＋3，此时定义域为x ∈[－6,6]，且f (x )＝⎩⎪⎨⎪⎧x 2＋2x ＋3，x ∈(0，6]，x 2－2x ＋3，x ∈[－6，0]，故f (|x |)的单调递增区间是(0,6]， 单调递减区间是[－6,0]．由题悟法解决二次函数图象与性质问题时要注意：(1)抛物线的开口，对称轴位置，定义区间三者相互制约，常见的题型中这三者有两定一不定，要注意分类讨论．(2)要注意数形结合思想的应用，尤其是给定区间上二次函数最值问题的求法．以题试法3．(·泰安调研)已知函数f (x )＝－x 2＋2ax ＋1－a 在x ∈[0,1]时有最大值2，则a 的值为________．解析：f (x )＝－(x －a )2＋a 2－a ＋1， 当a >1时，y max ＝a ；当0≤a ≤1时，y max ＝a 2－a ＋1； 当a ＜0时，y max ＝1－a .根据已知条件⎩⎪⎨⎪⎧ a ＞1，a ＝2或⎩⎪⎨⎪⎧ 0≤a ≤1，a 2－a ＋1＝2或⎩⎪⎨⎪⎧a ＜0，1－a ＝2，解得a ＝2或a ＝－1. 答案：2或－1二次函数的综合问题[例4] (·衡水月考)已知函数f (x )＝x 2，g (x )＝x －1. (1)若存在x ∈R 使f (x )<b ·g (x )，求实数b 的取值范围；(2)设F (x )＝f (x )－mg (x )＋1－m －m 2，且|F (x )|在[0,1]上单调递增，求实数m 的取值范围．[自主解答] (1)∃x ∈R ，f (x )<bg (x )⇒∃x ∈R ， x 2－bx ＋b <0⇒(－b )2－4b >0⇒b <0或b >4. 故b 的取值范围为(－∞，0)∪(4，＋∞)． (2)F (x )＝x 2－mx ＋1－m 2， Δ＝m 2－4(1－m 2)＝5m 2－4. ①当Δ≤0，即－255≤m ≤255时，则必需⎩⎨⎧m2≤0，－255≤m ≤255⇒－255≤m ≤0.②当Δ>0，即m <－255或m >255时，设方程F (x )＝0的根为x 1，x 2(x 1<x 2)．若m2≥1，则x 1≤0， 即⎩⎪⎨⎪⎧ m 2≥1，F (0)＝1－m 2≤0⇒m ≥2； 若m2≤0，则x 2≤0， 即⎩⎪⎨⎪⎧m 2≤0，F (0)＝1－m 2≥0⇒－1≤m ≤－255.综上所述，m 的取值范围为[－1,0]∪[2，＋∞)．由题悟法二次函数与二次方程、二次不等式统称“三个二次”，它们之间有着密切的联系，而二次函数又是“三个二次”的核心，通过二次函数的图象贯穿为一体．因此，有关“三个二次”的问题，数形结合，密切联系图象是探求解题思路的有效方法．4．若二次函数f (x )＝ax 2＋bx ＋c (a ≠0)满足f (x ＋1)－f (x )＝2x ，且f (0)＝1. (1)求f (x )的解析式；(2)若在区间[－1,1]上，不等式f (x )>2x ＋m 恒成立，求实数m 的取值范围． 解：(1)由f (0)＝1，得c ＝1.即f (x )＝ax 2＋bx ＋1. 又f (x ＋1)－f (x )＝2x ，则a (x ＋1)2＋b (x ＋1)＋1－(ax 2＋bx ＋1)＝2x ， 即2ax ＋a ＋b ＝2x ，所以⎩⎪⎨⎪⎧ 2a ＝2，a ＋b ＝0，解得⎩⎪⎨⎪⎧a ＝1，b ＝－1.因此，f (x )＝x 2－x ＋1.(2)f (x )>2x ＋m 等价于x 2－x ＋1>2x ＋m ，即x 2－3x ＋1－m >0，要使此不等式在[－1,1]上恒成立，只需使函数g (x )＝x 2－3x ＋1－m 在[－1,1]上的最小值大于0即可．∵g (x )＝x 2－3x ＋1－m 在[－1,1]上单调递减， ∴g (x )min ＝g (1)＝－m －1， 由－m －1>0得，m <－1.因此满足条件的实数m 的取值范围是(－∞，－1)．1．已知幂函数f (x )＝x α的部分对应值如下表：x 1 12 f (x )122则不等式f (|x |)≤2的解集是(A ．{x |0<x ≤2} B ．{x |0≤x ≤4} C ．{x |－2≤x ≤2}D ．{x |－4≤x ≤4}解析：选D 由f ⎝⎛⎭⎫12＝22⇒α＝12，即f (x )＝x 12，故f (|x |)≤2⇒|x |12≤2⇒|x |≤4，故其解集为{x |－4≤x ≤4}．2．已知函数y ＝ax 2＋bx ＋c ，如果a >b >c 且a ＋b ＋c ＝0，则它的图象可能是( )解析：选D ∵a >b >c ，且a ＋b ＋c ＝0， ∴a >0，c <0.∴图象开口向上与y 轴交于负半轴．3．已知f (x )＝x 12，若0<a <b <1，则下列各式中正确的是( )A ．f (a )<f (b )<f ⎝⎛⎭⎫1a <f ⎝⎛⎭⎫1b B ．f ⎝⎛⎭⎫1a <f ⎝⎛⎭⎫1b <f (b )<f (a ) C ．f (a )<f (b )<f ⎝⎛⎭⎫1b <f ⎝⎛⎭⎫1a D ．f ⎝⎛⎭⎫1a <f (a )<f ⎝⎛⎭⎫1b <f (b ) 解析：选C 因为函数f (x )＝x 12在(0，＋∞)上是增函数，又0<a <b <1b <1a ，故f (a )<f (b )<f ⎝⎛⎭⎫1b <f ⎝⎛⎭⎫1a .4．已知f (x )＝x 2＋bx ＋c 且f (－1)＝f (3)，则( ) A ．f (－3)<c <f ⎝⎛⎭⎫52 B ．f ⎝⎛⎭⎫52<c <f (－3) C ．f ⎝⎛⎭⎫52<f (－3)<cD ．c <f ⎝⎛⎭⎫52<f (－3)解析：选D 由已知可得二次函数图象关于直线x ＝1对称，则f (－3)＝f (5)，c ＝f (0)＝f (2)，二次函数在区间(1，＋∞)上单调递增，故有f (－3)＝f (5)>f ⎝⎛⎭⎫52>f (2)＝f (0)＝c .5．设二次函数f (x )＝ax 2－2ax ＋c 在区间[0,1]上单调递减，且f (m )≤f (0)，则实数m 的取值范围是( )A ．(－∞，0]B ．[2，＋∞)C ．(－∞，0]∪[2，＋∞)D ．[0,2]解析：选D 二次函数f (x )＝ax 2－2ax ＋c 在区间[0,1]上单调递减，则a ≠0，f ′(x )＝2a (x －1)≤0，x ∈[0,1]，所以a >0，即函数图象的开口向上，对称轴是直线x ＝1. 所以f (0)＝f (2)，则当f (m )≤f (0)时，有0≤m ≤2.6．若方程x 2－2mx ＋4＝0的两根满足一根大于1，一根小于1，则m 的取值范围是( )A.⎝⎛⎭⎫－∞，－52B.⎝⎛⎭⎫52，＋∞ C ．(－∞，－2)∪(2，＋∞)D.⎝⎛⎭⎫－52，＋∞ 解析：选B 设f (x )＝x 2－2mx ＋4，则题设条件等价于f (1)<0，即1－2m ＋4<0，解得m >52. 7．对于函数y ＝x 2，y ＝x 12有下列说法：①两个函数都是幂函数；②两个函数在第一象限内都单调递增； ③它们的图象关于直线y ＝x 对称； ④两个函数都是偶函数； ⑤两个函数都经过点(0,0)、(1,1)； ⑥两个函数的图象都是抛物线型． 其中正确的有________．解析：从两个函数的定义域、奇偶性、单调性等性质去进行比较． 答案：①②⑤⑥8．(·北京西城二模)已知函数f (x )＝x 2＋bx ＋1是R 上的偶函数，则实数b ＝________，不等式f (x －1)<x 的解集为________．解析：因为f (x )＝x 2＋bx ＋1是R 上的偶函数，所以b ＝0，则f (x )＝x 2＋1，解不等式(x －1)2＋1<x ，即x 2－3x ＋2<0得1<x <2.答案：0 {x |1<x <2}9．若x ≥0，y ≥0，且x ＋2y ＝1，那么2x ＋3y 2的最小值为________． 解析：由x ≥0，y ≥0，x ＝1－2y ≥0知0≤y ≤12，令t ＝2x ＋3y 2＝3y 2－4y ＋2， 则t ＝3⎝⎛⎭⎫y －232＋23. 在⎣⎡⎦⎤0，12上递减，当y ＝12时，t 取到最小值，t min ＝34.答案：3410．如果幂函数f (x )＝x －12p 2＋p ＋32(p ∈Z)是偶函数，且在(0，＋∞)上是增函数．求p的值，并写出相应的函数f (x )的解析式．解：∵f (x )在(0，＋∞)上是增函数， ∴－12p 2＋p ＋32>0，即p 2－2p －3<0.∴－1<p <3.又∵f (x )是偶函数且p ∈Z ， ∴p ＝1，故f (x )＝x 2.11．已知二次函数f (x )的图象过点A (－1,0)、B (3,0)、C (1，－8)． (1)求f (x )的解析式；(2)求f (x )在x ∈[0,3]上的最值； (3)求不等式f (x )≥0的解集．解：(1)由题意可设f (x )＝a (x ＋1)(x －3)， 将C (1，－8)代入得－8＝a (1＋1)(1－3)，得a ＝2. 即f (x )＝2(x ＋1)(x －3)＝2x 2－4x －6. (2)f (x )＝2(x －1)2－8，当x ∈[0,3]时，由二次函数图象知， f (x )min ＝f (1)＝－8，f (x )max ＝f (3)＝0. (3)f (x )≥0的解集为{x |x ≤－1，或x ≥3}．12．已知函数f (x )＝ax 2－2ax ＋2＋b (a ≠0)，若f (x )在区间[2,3]上有最大值5，最小值2. (1)求a ，b 的值；(2)若b <1，g (x )＝f (x )－m ·x 在[2,4]上单调，求m 的取值范围． 解：(1)f (x )＝a (x －1)2＋2＋b －a . 当a >0时，f (x )在[2,3]上为增函数，故⎩⎪⎨⎪⎧ f (3)＝5，f (2)＝2，⇒⎩⎪⎨⎪⎧ 9a －6a ＋2＋b ＝5，4a －4a ＋2＋b ＝2，⇒⎩⎪⎨⎪⎧a ＝1，b ＝0. 当a <0时，f (x )在[2,3]上为减函数，故⎩⎪⎨⎪⎧ f (3)＝2，f (2)＝5，⇒⎩⎪⎨⎪⎧ 9a －6a ＋2＋b ＝2，4a －4a ＋2＋b ＝5，⇒⎩⎪⎨⎪⎧a ＝－1，b ＝3.(2)∵b <1，∴a ＝1，b ＝0，即f (x )＝x 2－2x ＋2. g (x )＝x 2－2x ＋2－mx ＝x 2－(2＋m )x ＋2， ∵g (x )在[2,4]上单调，∴2＋m 2≤2或m ＋22≥4.∴m ≤2或m ≥6.1．已知y ＝f (x )是偶函数，当x >0时，f (x )＝(x －1)2，若当x ∈⎣⎡⎦⎤－2，－12时，n ≤f (x )≤m 恒成立，则m －n 的最小值为( )A.13 B.12 C.34D ．1解析：选D 当x <0时，－x >0，f (x )＝f (－x )＝(x ＋1)2， ∵x ∈⎣⎡⎦⎤－2，－12， ∴f (x )min ＝f (－1)＝0，f (x )max ＝f (－2)＝1， ∴m ≥1，n ≤0，m －n ≥1.2．(·青岛质检)设f (x )与g (x )是定义在同一区间[a ，b ]上的两个函数，若函数y ＝f (x )－g (x )在x ∈[a ，b ]上有两个不同的零点，则称f (x )和g (x )在[a ，b ]上是“关联函数”，区间[a ，b ]称为“关联区间”．若f (x )＝x 2－3x ＋4与g (x )＝2x ＋m 在[0,3]上是“关联函数”，则m 的取值范围为________．解析：由题意知，y ＝f (x )－g (x )＝x 2－5x ＋4－m 在[0,3]上有两个不同的零点．在同一坐标系下作出函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图象如图所示，结合图象可知，当x ∈[2,3]时，y ＝x 2－5x ＋4∈⎣⎡⎦⎤－94，－2，故当m ∈⎝⎛⎦⎤－94，－2时，函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图象有两个交点．答案：⎝⎛⎦⎤－94，－2 3．(·滨州模拟)已知函数f (x )＝ax 2＋bx ＋c (a >0，b ∈R ，c ∈R)．(1)若函数f (x )的最小值是f (－1)＝0，且c ＝1，F (x )＝⎩⎪⎨⎪⎧f (x )，x >0，－f (x )，x <0，求F (2)＋F (－2)的值；(2)若a ＝1，c ＝0，且|f (x )|≤1在区间(0,1]上恒成立，试求b 的取值范围． 解：(1)由已知得c ＝1，a －b ＋c ＝0，－b2a ＝－1，解得a ＝1，b ＝2.则f (x )＝(x ＋1)2.则F (x )＝⎩⎪⎨⎪⎧(x ＋1)2，x >0，－(x ＋1)2，x <0.故F (2)＋F (－2)＝(2＋1)2＋[－(－2＋1)2]＝8.(2)由题意得f (x )＝x 2＋bx ，原命题等价于－1≤x 2＋bx ≤1在(0,1]上恒成立，即b ≤1x －x且b ≥－1x－x 在(0,1]上恒成立．又当x ∈(0,1]时，1x －x 的最小值为0，－1x －x 的最大值为－2，故－2≤b ≤0.1．比较下列各组中数值的大小． (1)30.8,30.7；(2)0.213,0.233；(3)4.125，3.8－25，(－1.4)35；(4)0.20.5,0.40.3.解：(1)函数y ＝3x 是增函数，故30.8>30.7. (2)y ＝x 3是增函数，故0.213<0.233.(3)4.125>1,0<3.8－25<1，而(－1.4)35<0，故4.125>3.8－25>(－1.4)35.(4)先比较0.20.5与0.20.3，再比较0.20.3与0.40.3，y ＝0.2x 是减函数，故0.20.5<0.20.3；y ＝x 0.3在(0，＋∞)上是增函数，故0.20.3<0.40.3.则0.20.5<0.40.3.2．设abc >0，二次函数f (x )＝ax 2＋bx ＋c 的图象可能是( )解析：选D 当－b2a <0时，ab >0，从而c >0，可排除A ，C ；当－b2a >0时，ab <0，从而c <0，可排除B ，选D.3．已知函数f (x )＝ax 2－2x ＋1. (1)试讨论函数f (x )的单调性；(2)若13≤a ≤1，且f (x )在[1,3]上的最大值为M (a )，最小值为N (a )，令g (a )＝M (a )－N (a )，求g (a )的表达式；(3)在(2)的条件下，求证：g (a )≥12.解：(1)当a ＝0时，函数f (x )＝－2x ＋1在(－∞，＋∞)上为减函数； 当a >0时，抛物线f (x )＝ax 2－2x ＋1开口向上，对称轴为x ＝1a ，故函数f (x )在⎝⎛⎦⎤－∞，1a 上为减函数，在⎣⎡⎭⎫1a ，＋∞上为增函数； 当a <0时，抛物线f (x )＝ax 2－2x ＋1开口向下，对称轴为x ＝1a ，故函数f (x )在⎝⎛⎦⎤－∞，1a 上为增函数，在⎣⎡⎭⎫1a ，＋∞上为减函数． (2)∵f (x )＝a ⎝⎛⎭⎫x －1a 2＋1－1a， 由13≤a ≤1得1≤1a ≤3，∴N (a )＝f ⎝⎛⎭⎫1a ＝1－1a . 当1≤1a <2，即12<a ≤1时，M (a )＝f (3)＝9a －5，故g (a )＝9a ＋1a－6；当2≤1a ≤3，即13≤a ≤12时，M (a )＝f (1)＝a －1，故g (a )＝a ＋1a－2.∴g (a )＝⎩⎨⎧a ＋1a－2，a ∈⎣⎡⎦⎤13，12，9a ＋1a －6，a ∈⎝⎛⎦⎤12，1.(3)证明：当a ∈⎣⎡⎦⎤13，12时，g ′(a )＝1－1a 2<0， ∴函数g (a )在⎣⎡⎦⎤13，12上为减函数； 当a ∈⎝⎛⎦⎤12，1时，g ′(a )＝9－1a 2>0， ∴函数g (a )在⎝⎛⎦⎤12，1上为增函数，∴当a ＝12时，g (a )取最小值，g (a )min ＝g ⎝⎛⎭⎫12＝12. 故g (a )≥12.。

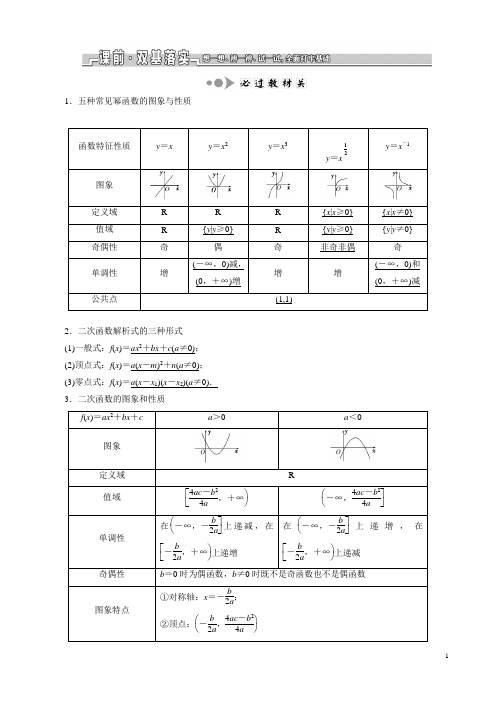
1．五种常见幂函数的图象与性质2．二次函数解析式的三种形式 (1)一般式：f (x )＝ax 2＋bx ＋c (a ≠0)； (2)顶点式：f (x )＝a (x －m )2＋n (a ≠0)； (3)零点式：f (x )＝a (x －x 1)(x －x 2)(a ≠0)． 3．二次函数的图象和性质[小题体验]1．已知幂函数y ＝f (x )的图象过点(9,3)，则函数的解析式为________________． 答案：f (x )＝x 12(x ≥0)2．(2019·天一中学高三测试)已知点P 1(x 1,2 019)和P 2(x 2,2 019)在二次函数f (x )＝ax 2＋bx ＋9的图象上，则f (x 1＋x 2)的值为________．答案：93．已知f (x )＝ax 2＋bx ＋3a ＋b 是偶函数，且其定义域为[a －1,2a ]，则y ＝f (x )的值域为________． 答案：⎣⎡⎦⎤1，31271．对于函数y ＝ax 2＋bx ＋c ，要认为它是二次函数，就必须满足a ≠0，当题目条件中未说明a ≠0时，就要讨论a ＝0和a ≠0两种情况．2．幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限，至于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图象最多只能同时出现在两个象限内；如果幂函数图象与坐标轴相交，则交点一定是原点．[小题纠偏]1．已知函数f (x )＝ax 2＋x ＋5的图象在x 轴上方，则a 的取值范围是________． 答案：⎝⎛⎭⎫120，＋∞ 2．给出下列命题： ①函数y ＝2x 是幂函数；②如果幂函数的图象与坐标轴相交，则交点一定是原点； ③当n ＜0时，幂函数y ＝x n 是定义域上的减函数；④二次函数y ＝ax 2＋bx ＋c ，x ∈[m ，n ]的最值一定是4ac －b 24a.其中正确的是________(填序号)． 答案：②考点一 幂函数的图象与性质基础送分型考点——自主练透[题组练透]1．(2018·苏州高三期中调研)已知幂函数y ＝x 2m－m 2(m ∈N *)在(0，＋∞)是增函数，则实数m 的值是________．解析：由题意知2m －m 2＞0，解得0＜m ＜2，因为m ∈N *，所以m ＝1. 答案：12．(2019·常州一中检测)已知函数f (x )＝(3－m )x 2m－5是幂函数，则f ⎝⎛⎭⎫12＝________.解析：函数f (x )＝(3－m )x 2m －5是幂函数，则3－m ＝1，解得m ＝2， ∴f (x )＝x －1，∴f ⎝⎛⎭⎫12＝2. 答案：23．若(a ＋1)12＜(3－2a )12，则实数a 的取值范围是________． 解析：易知函数y ＝x 12的定义域为[0，＋∞)，在定义域内为增函数， 所以⎩⎪⎨⎪⎧a ＋1≥0，3－2a ≥0，a ＋1＜3－2a ，解得－1≤a ＜23.答案：⎣⎡⎭⎫－1，23 [谨记通法]幂函数的指数与图象特征的关系(1)幂函数的形式是y ＝x α(α∈R)，其中只有一个参数α，因此只需一个条件即可确定其解析式． (2)若幂函数y ＝x α(α∈R)是偶函数，则α必为偶数．当α是分数时，一般将其先化为根式，再判断． (3)若幂函数y ＝x α在(0，＋∞)上单调递增，则α＞0，若在(0，＋∞)上单调递减，则α＜0. 考点二 二次函数的解析式重点保分型考点——师生共研[典例引领]已知二次函数f (x )满足f (2)＝－1，f (－1)＝－1，且f (x )的最大值是8，试确定此二次函数的解析式． 解：法一：(利用一般式) 设f (x )＝ax 2＋bx ＋c (a ≠0)．由题意得⎩⎪⎨⎪⎧4a ＋2b ＋c ＝－1，a －b ＋c ＝－1，4ac －b 24a ＝8，解得⎩⎪⎨⎪⎧a ＝－4，b ＝4，c ＝7.故所求二次函数为f (x )＝－4x 2＋4x ＋7.法二：(利用顶点式) 设f (x )＝a (x －m )2＋n .因为f (2)＝f (－1)，所以抛物线对称轴为x ＝2＋－12＝12.所以m ＝12，又根据题意函数有最大值8，所以n ＝8，所以y ＝f (x )＝a ⎝⎛⎭⎫x －122＋8.因为f (2)＝－1，所以a ⎝⎛⎭⎫2－122＋8＝－1，解得a ＝－4， 所以f (x )＝－4⎝⎛⎭⎫x －122＋8＝－4x 2＋4x ＋7. 法三：(利用零点式)由已知f (x )＋1＝0的两根为x 1＝2，x 2＝－1， 故可设f (x )＋1＝a (x －2)(x ＋1)， 即f (x )＝ax 2－ax －2a －1. 又函数有最大值y max ＝8，即4a－2a －1－a 24a＝8.解得a ＝－4或a ＝0(舍去)，故所求函数解析式为f (x )＝－4x 2＋4x ＋7.[由题悟法]求二次函数解析式的方法[即时应用]1．已知二次函数f (x )的图象的顶点坐标是(－2，－1)，且图象经过点(1,0)，则函数的解析式为f (x )＝________.解析：法一：设所求解析式为f (x )＝ax 2＋bx ＋c (a ≠0)．由已知得⎩⎨⎧－b2a＝－2，4ac －b24a＝－1，a ＋b ＋c ＝0，解得⎩⎪⎨⎪⎧a ＝19，b ＝49，c ＝－59，所以所求解析式为f (x )＝19x 2＋49x －59.法二：设所求解析式为f (x )＝ax 2＋bx ＋c (a ≠0)．由已知得⎩⎪⎨⎪⎧－b2a ＝－2，4a －2b ＋c ＝－1，a ＋b ＋c ＝0，解得⎩⎪⎨⎪⎧a ＝19，b ＝49，c ＝－59，所以所求解析式为f (x )＝19x 2＋49x －59.法三：设所求解析式为f (x )＝a (x －h )2＋k (a ≠0)． 由已知得f (x )＝a (x ＋2)2－1， 将点(1,0)代入，得a ＝19，所以f (x )＝19(x ＋2)2－1，即f (x )＝19x 2＋49x －59.答案：19x 2＋49x －592．已知二次函数f (x )的图象经过点(4,3)，它在x 轴上截得的线段长为2，并且对任意x ∈R ，都有f (2－x )＝f (2＋x )，求f (x )的解析式．解：因为f (2－x )＝f (2＋x )对x ∈R 恒成立， 所以f (x )的对称轴为x ＝2.又因为f (x )的图象被x 轴截得的线段长为2， 所以f (x )＝0的两根为1和3.设f (x )的解析式为f (x )＝a (x －1)(x －3)(a ≠0)． 又因为f (x )的图象过点(4,3)， 所以3a ＝3，a ＝1.所以所求f (x )的解析式为f (x )＝(x －1)(x －3)， 即f (x )＝x 2－4x ＋3.考点三 二次函数的图象与性质题点多变型考点——多角探明[锁定考向]高考对二次函数图象与性质的考查．常与一元二次方程、一元二次不等式等知识交汇． 常见的命题角度有： (1)二次函数的单调性问题； (2)二次函数的最值问题；(3)二次函数中恒成立问题．[题点全练]角度一：二次函数的单调性问题1．(2019·江安中学测试)已知函数f (x )＝x 2－(a －1)x ＋5在区间⎝⎛⎭⎫12，1上为增函数，则f (2)的取值范围是________．解析：函数f (x )的图象(抛物线)开口向上，对称轴为x ＝a －12，若函数f (x )在区间⎝⎛⎭⎫12，1上为增函数，则a －12≤12，解得a ≤2，所以f (2)＝4－(a －1)×2＋5≥7，即f (2)≥7.答案：[7，＋∞)角度二：二次函数的最值问题2．(1)(2019·苏州测试)已知函数f (x )＝x 2＋abx ＋a ＋2b ，若f (0)＝4，则f (1)的最大值为________． (2)已知函数f (x )＝－x 2＋2ax ＋1－a 在x ∈[0,1]时，有最大值2，则a 的值为________．解析：(1)因为f (0)＝4，所以a ＋2b ＝4，即a ＝4－2b ，所以f (1)＝ab ＋a ＋2b ＋1＝ab ＋5＝(4－2b )b ＋5＝－2b 2＋4b ＋5＝－2(b －1)2＋7，所以当b ＝1时，f (1)的最大值为7.(2)函数f (x )＝－x 2＋2ax ＋1－a ＝－(x －a )2＋a 2－a ＋1，x ∈[0,1]，对称轴方程为x ＝a . 当a ＜0时，f (x )max ＝f (0)＝1－a ， 所以1－a ＝2，所以a ＝－1.当0≤a ≤1时，f (x )max ＝f (a )＝a 2－a ＋1， 所以a 2－a ＋1＝2，即a 2－a －1＝0， 解得a ＝1±52(舍去)．当a ＞1时，f (x )max ＝f (1)＝a ，所以a ＝2. 综上可知，a ＝－1或a ＝2. 答案：(1)7 (2)－1或2 角度三：二次函数中恒成立问题3．已知函数f (x )＝x 2＋2x ＋1，f (x )＞x ＋k 在区间[－3，－1]上恒成立，则k 的取值范围为________． 解析：由题意得x 2＋x ＋1＞k 在区间[－3，－1]上恒成立． 设g (x )＝x 2＋x ＋1，x ∈[－3，－1]， ∵g (x )在[－3，－1]上单调递减， ∴g (x )min ＝g (－1)＝1.∴k ＜1.故k 的取值范围为(－∞，1)． 答案：(－∞，1)[通法在握]1．二次函数最值问题的3种类型及解题思路(1)类型：①对称轴、区间都是给定的；②对称轴动、区间固定；③对称轴定、区间变动． (2)思路：抓“三点一轴”，三点是指区间两个端点和中点，一轴指的是对称轴． 2．由不等式恒成立求参数取值范围的2大思路及1个关键 (1)思路：一是分离参数；二是不分离参数．(2)关键：两种思路都是将问题归结为求函数的最值，至于用哪种方法，关键是看参数是否已分离．这两个思路的依据是：a ≥f (x )恒成立⇔a ≥f (x )max ，a ≤f (x )恒成立⇔a ≤f (x )min .[演练冲关]已知函数f (x )＝x 2＋2ax ＋2，x ∈[－5,5]． (1)当a ＝－1时，求函数f (x )的最大值和最小值；(2)求实数a 的取值范围，使y ＝f (x )在区间[－5,5]上是单调函数．解：(1)当a ＝－1时，f (x )＝x 2－2x ＋2＝(x －1)2＋1，x ∈[－5,5]，所以当x ＝1时，f (x )取得最小值1； 当x ＝－5时，f (x )取得最大值37.(2)函数f (x )＝(x ＋a )2＋2－a 2的图象的对称轴为直线x ＝－a ，因为y ＝f (x )在区间[－5,5]上是单调函数，所以－a ≤－5或－a ≥5，即a ≤－5或a ≥5.故a 的取值范围是(－∞，－5]∪[5，＋∞)．一抓基础，多练小题做到眼疾手快1．(2018·清河中学检测)已知幂函数f (x )＝k ·x α的图象过点⎝⎛⎭⎫12，22，则k ＋α＝________.解析：由幂函数的定义知k ＝1.又f ⎝⎛⎭⎫12＝22，所以⎝⎛⎭⎫12α＝22，解得α＝12，从而k ＋α＝32. 答案：322．(2019·连云港调研)若函数f (x )＝－x 2＋2(a －1)x ＋2在(－∞，4)上为增函数，则a 的取值范围是________．解析：∵f (x )＝－x 2＋2(a －1)x ＋2的对称轴为x ＝a －1， f (x )＝－x 2＋2(a －1)x ＋2在(－∞，4)上为增函数， ∴对称轴x ＝a －1≥4，∴a ≥5. 答案：[5，＋∞)3．(2018·淮阴模拟)已知函数f (x )＝x 2－m是定义在区间[－3－m ，m 2－m ]上的奇函数，则f (m )，f (0)的大小关系为________．解析：因为函数f (x )是奇函数，所以－3－m ＋m 2－m ＝0，解得m ＝3或－1.当m ＝3时，函数f (x )＝x－1，定义域不是[－6,6]，不合题意；当m ＝－1时，函数f (x )＝x 3在定义域[－2,2]上单调递增，又m ＜0，所以f (m )＜f (0)．答案：f (m )＜f (0)4．已知函数f (x )＝x 2＋x ＋m ，若|f (x )|在区间[0,1]上单调，则实数m 的取值范围为________． 解析：因为f (x )＝x 2＋x ＋m ，且|f (x )|在区间[0,1]上单调， 所以f (x )在[0,1]上满足f (0)·f (1)≥0， 即m (1＋1＋m )≥0，解得m ≥0或m ≤－2. 答案：(－∞，－2]∪[0，＋∞)5．若二次函数f (x )＝－x 2＋4x ＋t 图象的顶点在x 轴上，则t ＝________. 解析：由于f (x )＝－x 2＋4x ＋t ＝－(x －2)2＋t ＋4图象的顶点在x 轴上， 所以f (2)＝t ＋4＝0， 所以t ＝－4. 答案：－46．(2019·杭州测试)若函数f (x )＝x 2－2x ＋1在区间[a ，a ＋2]上的最小值为4，则实数a 的取值集合为________．解析：因为函数f (x )＝x 2－2x ＋1＝(x －1)2的图象的对称轴为直线x ＝1，f (x )在区间[a ，a ＋2]上的最小值为4，所以当a ≥1时，f (x )min ＝f (a )＝(a －1)2＝4，a ＝－1(舍去)或a ＝3；当a ＋2≤1，即a ≤－1时，f (x )min ＝f (a ＋2)＝(a ＋1)2＝4，a ＝1(舍去)或a ＝－3； 当a ＜1＜a ＋2，即－1＜a ＜1时，f (x )min ＝f (1)＝0≠4. 故a 的取值集合为{－3,3}． 答案：{－3,3}二保高考，全练题型做到高考达标1．(2019·海安中学检测)已知幂函数f (x )＝x α，其中α∈⎩⎨⎧⎭⎬⎫－2，－1，12，1，2，3.则使f (x )为奇函数，且在区间(0，＋∞)上是单调增函数的α的取值集合为________．解析：若幂函数f (x )为奇函数，则α＝－1,1,3，又f (x )在区间(0，＋∞)上是单调增函数，所以α的取值集合为{1,3}．答案：{1,3}2．(2019·武汉调研)已知幂函数f (x )＝x m2－4m(m ∈Z)的图象关于y 轴对称，且在区间(0，＋∞)上为减函数，则m 的值为________．解析：∵幂函数f (x )＝x m2－4m(m ∈Z)在区间(0，＋∞)上为减函数，∴m 2－4m ＜0，解得0＜m ＜4. 又m ∈Z ，∴m ＝1或m ＝2或m ＝3.当m ＝1时，f (x )＝x －3，图象不关于y 轴对称；当m ＝2时，f (x )＝x －4，图象关于y 轴对称；当m ＝3时，f (x )＝x －3，图象不关于y 轴对称．综上，m 的值为2. 答案：23．若关于x 的不等式x 2－4x －2－a ＞0在区间(1,4)内有解，则实数a 的取值范围是________． 解析：不等式x 2－4x －2－a ＞0在区间(1,4)内有解等价于a ＜(x 2－4x －2)max ， 令f (x )＝x 2－4x －2，x ∈(1,4)， 所以f (x )＜f (4)＝－2，所以a ＜－2. 答案：(－∞，－2)4．(2018·泰州中学调研)已知f (x )是定义在R 上的奇函数，当x ＜0时，f (x )＝x 2－2x ＋1，不等式f (x 2－3)＞f (2x )的解集为________．解析：根据题意，f (x )是定义在R 上的奇函数，则有f (0)＝0，当x ＜0时，f (x )＝x 2－2x ＋1＝(x －1)2为减函数，则当x ＞0时，f (x )也为减函数，综上可得f (x )在R 上为减函数，若f (x 2－3)＞f (2x )，则有x 2－3＜2x ，解得－1＜x ＜3，即不等式f (x 2－3)＞f (2x )的解集为(－1,3)．答案：(－1,3)5．若函数f (x )＝x α2－2α－3(常数α∈Z)为偶函数，且在(0，＋∞)上是单调递减函数，则α的值为________．解析：根据幂函数的性质，要使函数f (x )为偶函数，且在(0，＋∞)上是单调递减函数，则α2－2α－3为偶数，且α2－2α－3＜0，解不等式可得－1＜α＜3.因为α∈Z ，所以α＝0,1,2.当α＝0时，α2－2α－3＝－3，不满足条件；当α＝1时，α2－2α－3＝－4，满足条件；当α＝2时，α2－2α－3＝－3，不满足条件，所以α＝1.答案：16．若函数y ＝x 2－3x －4的定义域为[0，m ]，值域为⎣⎡⎦⎤－254，－4，则m 的取值范围是________．解析：二次函数图象的对称轴为x ＝32，且f ⎝⎛⎭⎫32＝－254，f (3)＝f (0)＝－4，由图得m ∈⎣⎡⎦⎤32，3.答案：⎣⎡⎦⎤32，37．对于任意实数x ，函数f (x )＝(5－a )x 2－6x ＋a ＋5恒为正值，则a 的取值范围是________．解析：由题意可得⎩⎪⎨⎪⎧5－a ＞0，Δ＝36－45－a a ＋5＜0，解得－4＜a ＜4. 答案：(－4,4)8．(2019·南通一调)若函数f (x )＝ax 2＋20x ＋14(a ＞0)对任意实数t ，在闭区间[t －1，t ＋1]上总存在两实数x 1，x 2，使得|f (x 1)－f (x 2)|≥8成立，则实数a 的最小值为________．解析：由题意可得，当x ∈[t －1，t ＋1]时，[f (x )max －f (x )min ]min ≥8，当[t －1，t ＋1]关于对称轴对称时，f (x )max －f (x )min 取得最小值，即f (t ＋1)－f (t )＝2at ＋a ＋20≥8，f (t －1)－f (t )＝－2at ＋a －20≥8，两式相加，得a ≥8，所以实数a 的最小值为8.答案：89．已知幂函数f (x )＝x21(m m )－＋(m ∈N *)．(1)试确定该函数的定义域，并指明该函数在其定义域上的单调性．(2)若该函数f (x )的图象经过点(2，2)，试确定m 的值，并求满足条件f (2－a )＞f (a －1)的实数a 的取值范围．解：(1)因为m 2＋m ＝m (m ＋1)(m ∈N *)，而m 与m ＋1中必有一个为偶数， 所以m 2＋m 为偶数， 所以函数f (x )＝x21(m m )－＋(m ∈N *)的定义域为[0，＋∞)，并且该函数在[0，＋∞)上为增函数．(2)因为函数f (x )的图象经过点(2，2)， 所以2＝221(m m )－＋，即212＝221(m m )－＋，所以m 2＋m ＝2，解得m ＝1或m ＝－2.又因为m ∈N *，所以m ＝1，f (x )＝x 12. 又因为f (2－a )＞f (a －1)， 所以⎩⎪⎨⎪⎧2－a ≥0，a －1≥0，2－a ＞a －1，解得1≤a ＜32，故函数f (x )的图象经过点(2，2)时，m ＝1.满足条件f (2－a )＞f (a －1)的实数a 的取值范围为⎣⎡⎭⎫1，32. 10．(2019·启东检测)已知a ∈R ，函数f (x )＝x 2－2ax ＋5.(1)若a ＞1，且函数f (x )的定义域和值域均为[1，a ]，求实数a 的值； (2)若不等式x |f (x )－x 2|≤1对x ∈⎣⎡⎦⎤13，12恒成立，求实数a 的取值范围． 解：(1)因为f (x )＝x 2－2ax ＋5的图象的对称轴为x ＝a (a ＞1)， 所以f (x )在[1，a ]上为减函数， 所以f (x )的值域为[f (a )，f (1)]． 又已知值域为[1，a ]，所以⎩⎪⎨⎪⎧f a ＝a 2－2a 2＋5＝1，f 1＝1－2a ＋5＝a ，解得a ＝2.(2)由x |f (x )－x 2|≤1，得－12x 2＋52x ≤a ≤12x 2＋52x .(*)令1x＝t ，t ∈[2,3]， 则(*)可化为－12t 2＋52t ≤a ≤12t 2＋52t .记g (t )＝－12t 2＋52t ＝－12⎝⎛⎭⎫t －522＋258， 则g (t )max ＝g ⎝⎛⎭⎫52＝258，所以a ≥258； 记h (t )＝12t 2＋52t ＝12⎝⎛⎭⎫t ＋522－258， 则h (t )min ＝h (2)＝7，所以a ≤7， 综上所述，258≤a ≤7.所以实数a 的取值范围是⎣⎡⎦⎤258，7. 三上台阶，自主选做志在冲刺名校1．(2019·金陵中学期中)设f (x )与g (x )是定义在同一区间[a ，b ]上的两个函数，若函数y ＝f (x )－g (x )在[a ，b ]上有两个不同的零点，则称f (x )与g (x )在[a ，b ]上是“关联函数”，区间[a ，b ]称为f (x )与g (x )的“关联区间”．若f (x )＝13x 3－x 2－x 与g (x )＝2x ＋b 的“关联区间”是[－3,0]，则b 的取值范围是________． 解析：由题意设m (x )＝f (x )－g (x )＝13x 3－x 2－3x －b ，则m ′(x )＝x 2－2x －3，由m ′(x )＝0，得m ＝－1或m ＝3.∵f (x )与g (x )在[－3,0]上是“关联函数”，∴x ＝－1是函数m (x )在[－3,0]上的极大值，同时也是最大值．要使m (x )＝f (x )－g (x )在[－3,0]上有两个不同的零点，则⎩⎪⎨⎪⎧m 00，m －1＞0，m －30，即⎩⎪⎨⎪⎧－b ≤0，53－b ＞0，－9－b ≤0，解得0≤b ＜53，故b 的取值范围是⎣⎡⎭⎫0，53.答案：⎣⎡⎭⎫0，532．(2019·泰州中学检测)已知函数f (x )＝x 2＋(x －1)·|x －a |.(1)若a ＝－1，求满足f (x )＝1的x 的取值集合；(2)若函数f (x )在R 上单调递增，求实数a 的取值范围；(3)若a ＜1且不等式f (x )≥2x －3对一切实数x ∈R 恒成立，求a 的取值范围．解：(1)当a ＝－1时，有f (x )＝⎩⎪⎨⎪⎧ 2x 2－1，x ≥－1，1，x ＜－1.当x ≥－1时，令2x 2－1＝1，解得x ＝1或x ＝－1；当x ＜－1时，f (x )＝1恒成立，∴x 的取值集合为{x |x ≤－1或x ＝1}．(2)f (x )＝⎩⎪⎨⎪⎧ 2x 2－a ＋1x ＋a ，x ≥a ，a ＋1x －a ，x ＜a ，若f (x )在R 上单调递增，且f (x )是连续的，则有⎩⎪⎨⎪⎧a ＋14≤a ，a ＋1＞0，解得a ≥13， 即实数a 的取值范围是⎣⎡⎭⎫13，＋∞.(3)设g (x )＝f (x )－(2x －3)，则g (x )＝⎩⎪⎨⎪⎧ 2x 2－a ＋3x ＋a ＋3，x ≥a ，a －1x －a ＋3，x ＜a .若不等式g (x )≥0对一切实数x ∈R 恒成立，则当x＜a时，∵a＜1，∴g(x)单调递减，其值域为(a2－2a＋3，＋∞)．∵a2－2a＋3＝(a－1)2＋2＞2，∴g(x)≥0恒成立．当x≥a时，∵a＜1，∴a＜a＋34，∴g(x)min＝g⎝⎛⎭⎫a＋34＝a＋3－a＋328≥0，得－3≤a≤5.∵a＜1，∴－3≤a＜1，综上，a的取值范围是[－3,1)．。

专题07 二次函数与幂函数（教学案）2017年高考数学（理）一轮复习精品资料1.考查三个“二次”的联系和应用；2.以5种幂函数为载体，考查幂函数的概念、图象、性质，多以客观题的形式出现；3.和其他知识交汇，以解答题形式考查综合应用．1．一次函数与二次函数的解析式(1)一次函数：y＝kx＋b (k，b为常数，且k≠0)．(2)二次函数①一般式：f(x)＝ax2＋bx＋c_(a≠0)．②顶点式：f(x)＝a(x－m)2＋n(a≠0)．③零点式：f(x)＝a(x－x1)(x－x2)_(a≠0)．2．一次函数与二次函数的定义及性质函数一次函数二次函数解析式y＝kx＋b (k≠0)y＝ax2＋bx＋c (a≠0)图象k>0 k<0 a>0 a<0b>0b>0b<0，c>0 b>0，c<0定义域R R值域R [4ac－b24a，＋∞)(－∞，4ac－b24a]单调性在(－∞，＋∞)上是增函数在(－∞，＋∞)上是减函数在(－∞，－b2a]上是减函数；在[－b2a，＋∞)上是增函数在(－∞，－b2a]上是增函数；在[－b2a，＋∞)上是减函数函数性质y＝x y＝x2y＝x3y＝x12y＝x－1图象定义域R R R[0，＋∞){x|x∈R且x≠0}值域R[0，＋∞)R[0，＋∞){y|y∈R且y≠0}奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性增x∈时，减增增x∈(0，＋∞)时，减；x∈(－∞，0)时，减高频一求二次函数的解析式例1、已知二次函数f(x)满足f(2)＝－1，f(－1)＝－1，且f(x)的最大值是8，试确定此二次函数的解析式．方法二(利用顶点式)：设f(x)＝a(x－m)2＋n.∵f(2)＝f(－1)，∴抛物线的图象的对称轴为x＝2＋－12＝12.∴m＝12.又根据题意函数有最大值8，∴n＝8，∴y＝f(x)＝a ⎝ ⎛⎭⎪⎫x －122＋8. ∵f(2)＝－1，∴a ⎝ ⎛⎭⎪⎫2－122＋8＝－1，解得a ＝－4， ∴f(x)＝－4⎝ ⎛⎭⎪⎫x －122＋8＝－4x2＋4x ＋7. 方法三 (利用零点式)：由已知f(x)＋1＝0的两根为x1＝2，x2＝－1， 故可设f(x)＋1＝a(x －2)(x ＋1)， 即f(x)＝ax2－ax －2a －1. 又函数的最大值是8，即4a－2a －1－－a 24a＝8.解得a ＝－4，∴所求函数的解析式为f(x)＝－4x2＋4x ＋7.【感悟提升】求二次函数的解析式，关键是灵活选取二次函数解析式的形式，利用所给出的条件，根据二次函数的性质进行求解．【变式探究】(1)二次函数的图象过点(0,1)，对称轴为x ＝2，最小值为－1，则它的解析式是_____________________________．(2)若函数f(x)＝(x ＋a)(bx ＋2a)(常数a ，b∈R)是偶函数，且它的值域为(－∞，4]，则该函数的解析式f(x)＝________.答案 (1)f(x)＝12x2－2x ＋1 (2)－2x2＋4高频考点二 二次函数的图象与性质例2、已知函数f(x)＝x2＋2ax ＋3，x∈，(1)求实数a 的取值范围，使y ＝f(x)在区间上是单调函数； (2)当a ＝－1时，求f(|x|)的单调区间．解 (1)函数f(x)＝x2＋2ax ＋3的图象的对称轴为x ＝－2a2＝－a ，∴要使f(x)在上为单调函数，只需－a≤－4或－a≥6，解得a≥4或a≤－6. 故a 的取值范围是(－∞，－6]∪，∴f(|x|)在区间上为增函数． 【变式探究】(1)设函数f(x)＝ax2－2x ＋2，对于满足1<x<4的一切x 值都有f(x)>0，则实数a 的取值范围为________．(2)已知a 是实数，函数f(x)＝2ax2＋2x －3在x∈上恒小于零，则实数a 的取值范围为________．答案 (1)⎝ ⎛⎭⎪⎫12，＋∞ (2)⎝⎛⎭⎪⎫－∞，12【感悟提升】(1)二次函数最值问题解法：抓住“三点一轴”数形结合，三点是指区间两个端点和中点，一轴指的是对称轴，结合配方法，根据函数的单调性及分类讨论的思想即可完成．(2)由不等式恒成立求参数取值范围的思路及关键①一般有两个解题思路：一是分离参数；二是不分离参数．②两种思路都是将问题归结为求函数的最值，至于用哪种方法，关键是看参数是否已分离．这两个思路的依据是：a≥f(x)恒成立⇔a≥f(x)max，a≤f(x)恒成立⇔a≤f(x)min.【举一反三】 已知函数f(x)＝x2＋2ax ＋2，x∈． (1)当a ＝－1时，求函数f(x)的最大值和最小值； (2)求实数a 的取值范围，使y ＝f(x)在区间上是单调函数．高频考点三 幂函数的图象和性质例3、(1)已知幂函数f(x)＝k·xα的图象过点⎝ ⎛⎭⎪⎫12，22，则k ＋α等于( )A.12 B ．1 C.32D ．2 (2)若(2m ＋1)12>(m2＋m －1)12，则实数m 的取值范围是( ) A.⎝ ⎛⎦⎥⎤－∞，－5－12 B.⎣⎢⎡⎭⎪⎫5－12，＋∞C ．(－1,2)D.⎣⎢⎡⎭⎪⎫5－12，2答案 (1)C (2)D解析 (1)由幂函数的定义知k ＝1. 又f ⎝ ⎛⎭⎪⎫12＝22，所以⎝ ⎛⎭⎪⎫12α＝22，解得α＝12，从而k ＋α＝32. (2)因为函数y ＝x 12的定义域为上递减，∴f(x)min＝f(1)＝－2.(2)当a>0时，f(x)＝ax2－2x 图象的开口方向向上，且对称轴为x ＝1a.①当1a ≤1，即a≥1时，f(x)＝ax2－2x 图象的对称轴在内，∴f(x)在上递减，在[1a ，1]上递增．∴f(x)min＝f(1a )＝1a －2a ＝－1a.②当1a >1，即0<a<1时，f(x)＝ax2－2x 图象的对称轴在的右侧，∴f(x)在上递减．∴f(x)min＝f(1)＝a －2.【方法与技巧】 1．二次函数的三种形式(1)已知三个点的坐标时，宜用一般式．(2)已知二次函数的顶点坐标或与对称轴有关或与最大(小)值有关的量时，常使用顶点式．(3)已知二次函数与x 轴有两个交点，且横坐标已知时，选用零点式求f(x)更方便． 2．研究二次函数的性质要注意： (1)结合图象分析；(2)含参数的二次函数，要进行分类讨论． 3．利用幂函数的单调性比较幂值大小的技巧在比较幂值的大小时，必须结合幂值的特点，转化为同指数幂，再选择适当的函数，借助其单调性进行比较．【失误与防范】1．对于函数y ＝ax2＋bx ＋c ，要认为它是二次函数，就必须满足a≠0，当题目条件中未说明a≠0时，就要讨论a ＝0和a≠0两种情况．2．幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限，至于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图象最多能同时出现在两个象限内；如果幂函数图象与坐标轴相交，则交点一定是原点．1.【2016高考新课标3理数】已知432a =，254b =，1325c =，则（ ） （A ）b a c << （B ）a b c << （C ）b c a << （D ）c a b << 【答案】A【解析】因为422335244a b ==>=，1223332554c a ==>=，所以b a c <<，故选A ．1．（2014·全国卷）若函数f (x )＝cos 2x ＋a sin x 在区间⎝ ⎛⎭⎪⎫π6，π2是减函数，则a 的取值范围是________．【答案】(－∞，2]2．（2014·浙江卷）在同一直角坐标系中，函数f (x )＝x a(x >0)，g (x )＝log a x 的图像可能是( )A BC D 【答案】D【解析】只有选项D 符合，此时0<a <1，幂函数f (x )在(0，＋∞)上为增函数，且当x ∈(0，1)时，f (x )的图像在直线y ＝x 的上方，对数函数g (x )在(0，＋∞)上为减函数，故选D.3．（2013·安徽卷）“a≤0”是“函数f(x)＝|(ax －1)x|在区间(0，＋∞)内单调递增”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 【答案】C4．（2013·湖南卷）函数f(x)＝2ln x的图像与函数g(x)＝x2－4x＋5的图像的交点个数为( )A．3 B．2 C．1 D．0【答案】B【解析】法一：作出函数f(x)＝2ln x，g(x)＝x2－4x＋5的图像如图：可知，其交点个数为2，选B.法二：也可以采用数值法：x 1 2 4f(x)＝2ln x 0 2ln 2＝ln 4>1 ln 42<5g(x)＝x2－4x＋5 2 1 5可知它们有2个交点，选B.5．（2013·新课标全国卷Ⅱ] 已知函数f(x)＝x3＋ax2＋bx＋c，下列结论中错误的是( )A．x0∈R，f(x0)＝0B．函数y＝f(x)的图像是中心对称图形C．若x0是f(x)的极小值点，则f(x)在区间(－∞，x0)单调递减D．若x0是f(x)的极值点，则f′(x0)＝0【答案】C6．（2013·北京卷）函数f(x)的图像向右平移1个单位长度，所得图像与曲线y ＝e x关于y 轴对称，则f(x)＝( )A ．ex ＋1B ．ex －1C ．e－x ＋1D ．e－x －1【答案】D【解析】依题意，f(x)向右平移一个单位长度得到f(x －1)的图像，又y ＝e x的图像关于y 轴对称的图像的解析式为y ＝e －x，所以f(x －1)＝e －x，所以f(x)＝e－x －1.1．设α∈⎩⎨⎧⎭⎬⎫－2，－1，－12，12，1，2，则使f (x )＝x α为奇函数，且在(0，＋∞)上单调递减的α的值的个数是( )A ．1B ．2C ．3D ．4解析：选A 由f (x )＝x α在(0，＋∞)上单调递减，可知α<0.又因为f (x )＝x α为奇函数，所以α只能取－1.2．若函数f (x )＝(1－x 2)(x 2＋ax －5)的图象关于直线x ＝0对称，则f (x )的最大值是( )A ．－4B ．4C ．4或－4D ．不存在解析：选B 依题意，函数f (x )是偶函数，则y ＝x 2＋ax －5是偶函数，故a ＝0，f (x )＝(1－x 2)(x 2－5)＝－x 4＋6x 2－5＝－(x 2－3)2＋4，当x 2＝3时，f (x )取最大值为4.3．若幂函数y ＝(m 2－3m ＋3)·xm 2－m －2的图象不过原点，则m 的取值是( ) A ．－1≤m ≤2 B ．m ＝1或m ＝2 C ．m ＝2D ．m ＝1解析：选B 由幂函数性质可知m 2－3m ＋3＝1，∴m ＝2或m ＝1.又幂函数图象不过原点，∴m 2－m －2≤0，即－1≤m ≤2，∴m ＝2或m ＝1.4．设函数f (x )＝x 2－23x ＋60，g (x )＝f (x )＋|f (x )|，则g (1)＋g (2)＋…＋g (20)＝( ) A ．56 B ．112 C ．0D ．38解析：选B 由二次函数图象的性质得，当3≤x ≤20时，f (x )＋|f (x )|＝0，∴g (1)＋g (2)＋…＋g (20)＝g (1)＋g (2)＝112.5．若函数y ＝x 2－3x －4的定义域为，值域为⎣⎢⎡⎦⎥⎤－254，－4，则m 的取值范围是( )A ．B.⎣⎢⎡⎦⎥⎤32，4C.⎣⎢⎡⎭⎪⎫32，＋∞ D.⎣⎢⎡⎦⎥⎤32，3解析：选D 二次函数图象的对称轴为x ＝32，且f ⎝ ⎛⎭⎪⎫32＝－254，f (3)＝f (0)＝－4，由图得m ∈⎣⎢⎡⎦⎥⎤32，3.6．若函数y ＝x 2＋(a ＋2)x ＋3，x ∈的图象关于直线x ＝1对称，则b ＝________. 解析：由已知得－a ＋22＝1，解得a ＝－4.又因为a ＋b2＝1，所以b ＝2－a ＝6.答案：67．设二次函数f (x )＝ax 2＋2ax ＋1在上有最大值4，则实数a 的值为________． 解析：此函数图象的对称轴为直线x ＝－1.当a >0时，图象开口向上，所以x ＝2时取得最大值，f (2)＝4a ＋4a ＋1＝4，解得a ＝38；当a <0时，图象开口向下，所以x ＝－1时取得最大值，f (－1)＝a －2a ＋1＝4，解得a ＝－3.答案：－3或388．已知幂函数f (x )＝x 12－，若f (a ＋1)＜f (10－2a )，则a 的取值范围是________．解析：∵f (x )＝x 12－＝1x(x ＞0)，易知x ∈(0，＋∞)时为减函数，又f (a ＋1)＜f (10－2a )，∴⎩⎪⎨⎪⎧ a ＋1＞0，10－2a ＞0，a ＋1＞10－2a ，解得⎩⎪⎨⎪⎧ a ＞－1，a ＜5，a ＞3，∴3＜a ＜5.答案：(3,5) 9．已知函数f (x )＝x －2m 2＋m ＋3(m ∈Z)是偶函数，且f (x )在(0，＋∞)上单调递增．(1) 求m 的值，并确定f (x )的解析式；(2)g (x )＝log 2，求g (x )的定义域和值域．解：(1)因为f (x )在(0，＋∞)单调递增，由幂函数的性质得－2m 2＋m ＋3>0，解得－1<m <32. 因为m ∈Z，所以m ＝0或m ＝1.当m ＝0时，f (x )＝x 3不是偶函数；当m ＝1时，f (x )＝x 2是偶函数，所以m ＝1，f (x )＝x 2.10．已知函数f (x )＝ax 2＋bx ＋1(a ，b 为实数，a ≠0，x ∈R)．(1)若函数f (x )的图象过点(－2,1)，且方程f (x )＝0有且只有一个根，求f (x )的表达式；(2)在(1)的条件下，当x ∈时，g (x )＝f (x )－kx 是单调函数，求实数k 的取值范围． 解：(1)因为f (－2)＝1，即4a －2b ＋1＝1，所以b ＝2a .因为方程f (x )＝0有且只有一个根，所以Δ＝b 2－4a ＝0.所以4a 2－4a ＝0，所以a ＝1，b ＝2.所以f (x )＝(x ＋1)2. (2)g (x )＝f (x )－kx ＝x 2＋2x ＋1－kx ＝x 2－(k －2)x ＋1＝⎝ ⎛⎭⎪⎫x －k －222＋1－k －224.由g (x )的图象知，要满足题意，则k －22≥2或k －22≤－1，即k ≥6或k ≤0，∴所求实数k 的取值范围为(－∞，0]∪[6，＋∞)．。

幂函数与二次函数考纲要求 1.了解幂函数的概念；结合函数y ＝x ，y ＝x 2，y ＝x 3，y ＝x 12，y ＝1x 的图象，了解它们的变化情况；2.理解二次函数的图象和性质，能用二次函数、方程、不等式之间的关系解决简单问题. 知识梳理 1.幂函数 (1)幂函数的定义一般地，形如y ＝x α的函数称为幂函数，其中x 是自变量，α为常数. (2)常见的五种幂函数的图象(3)幂函数的性质①幂函数在(0，＋∞)上都有定义；②当α>0时，幂函数的图象都过点(1，1)和(0，0)，且在(0，＋∞)上单调递增； ③当α<0时，幂函数的图象都过点(1，1)，且在(0，＋∞)上单调递减. 2.二次函数(1)二次函数解析式的三种形式 一般式：f (x )＝ax 2＋bx ＋c (a ≠0).顶点式：f (x )＝a (x －m )2＋n (a ≠0)，顶点坐标为(m ，n ). 零点式：f (x )＝a (x －x 1)(x －x 2)(a ≠0)，x 1，x 2为f (x )的零点.(2)二次函数的图象和性质函数 y ＝ax 2＋bx ＋c (a >0)y ＝ax 2＋bx ＋c (a <0)图象 (抛物线)定义域 R值域 ⎣⎡⎭⎫4ac －b 24a ，＋∞ ⎝⎛⎦⎤－∞，4ac －b 24a对称轴 x ＝－b2a顶点 坐标 ⎝⎛⎭⎫－b 2a，4ac －b 24a奇偶性当b ＝0时是偶函数，当b ≠0时是非奇非偶函数 单调性在⎝⎛⎦⎤－∞，－b 2a 上是减函数； 在⎣⎡⎭⎫－b2a ，＋∞上是增函数 在⎝⎛⎦⎤－∞，－b2a 上是增函数； 在⎣⎡⎭⎫－b2a ，＋∞上是减函数1.二次函数的单调性、最值与抛物线的开口方向和对称轴及给定区间的范围有关.2.若f (x )＝ax 2＋bx ＋c (a ≠0)，则当⎩⎪⎨⎪⎧a >0，Δ<0时，恒有f (x )>0；当⎩⎪⎨⎪⎧a <0，Δ<0时，恒有f (x )<0.3.(1)幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限；(2)幂函数的图象过定点(1，1)，如果幂函数的图象与坐标轴相交，则交点一定是原点.诊断自测1.判断下列结论正误(在括号内打“√”或“×”) (1)函数y ＝2x 13是幂函数.( )(2)当α>0时，幂函数y ＝x α在(0，＋∞)上是增函数.( )(3)二次函数y ＝ax 2＋bx ＋c (a ≠0)的两个零点可以确定函数的解析式.( ) (4)二次函数y ＝ax 2＋bx ＋c (x ∈[a ，b ])的最值一定是4ac －b 24a.( )答案 (1)× (2)√ (3)× (4)×解析 (1)由于幂函数的解析式为f (x )＝x α，故y ＝2x 13不是幂函数，(1)错误. (3)确定二次函数的解析式需要三个独立的条件，两个零点不能确定函数的解析式. (4)对称轴x ＝－b 2a ，当－b2a 不在给定定义域内时，最值不是4ac －b 24a，故(4)错误.2.已知幂函数f (x )＝k ·x α的图象过点⎝⎛⎭⎫12，22，则k ＋α＝( )A.12B.1C.32D.2答案 C解析 因为f (x )＝k ·x α是幂函数，所以k ＝1. 又f (x )的图象过点⎝⎛⎭⎫12，22，所以⎝⎛⎭⎫12α＝22， 所以α＝12，所以k ＋α＝1＋12＝32.3.已知函数f (x )＝－2x 2＋mx ＋3(0≤m ≤4，0≤x ≤1)的最大值为4，则m 的值为________. 答案 2 2解析 f (x )＝－2x 2＋mx ＋3＝－2⎝⎛⎭⎫x －m 42＋m 28＋3，∵0≤m ≤4，∴0≤m4≤1，∴当x ＝m4时，f (x )取得最大值，∴m 28＋3＝4，解得m ＝2 2.4.(2021·全国大联考)不等式(x 2＋1)12>(3x ＋5)12的解集为( ) A.⎣⎡⎭⎫－53，－1∪(4，＋∞) B.(－1，4)C.(4，＋∞)D.(－∞，－1)∪(4，＋∞)答案 A解析 不等式(x 2＋1)12>(3x ＋5)12等价于x 2＋1>3x ＋5≥0， 解得－53≤x <－1或x >4.所以原不等式的解集为⎣⎡⎭⎫－53，－1∪(4，＋∞). 5.(2020·贵阳质检)若函数f (x )＝4x 2－kx －8在[5，8]上是单调函数，则k 的取值范围是( ) A.(－∞，40]B.[40，64]C.(－∞，40]∪[64，＋∞)D.[64，＋∞)答案 C解析 f (x )图象的对称轴x ＝k8，且f (x )在[5，8]上是单调函数， ∴k 8≥8或k8≤5，解之得k ≥64或k ≤40. 6.(2018·上海卷)已知α∈⎩⎨⎧－2，－1，－12，⎭⎬⎫12，1，2，3.若幂函数f (x )＝x α为奇函数，且在(0，＋∞)上递减，则α＝______. 答案 －1解析 由y ＝x α为奇函数，知α取－1，1，3. 又y ＝x α在(0，＋∞)上递减， ∴α<0，取α＝－1.考点一 幂函数的图象和性质1.若幂函数y ＝f (x )的图象过点(4，2)，则幂函数y ＝f (x )的大致图象是( )答案 C解析 设幂函数的解析式为y ＝x α， 因为幂函数y ＝f (x )的图象过点(4，2)， 所以2＝4α，解得α＝12.所以y ＝x ，其定义域为[0，＋∞)，且是增函数，当0<x <1时，其图象在直线y ＝x 的上方，对照选项，C 正确.2.已知函数f (x )＝(m 2－m －1)·x m 2－2m －3是幂函数，且在(0，＋∞)上递减，则实数m ＝( )A.2B.－1C.4D.2或－1答案 A解析 依幂函数定义，m 2－m －1＝1，∴m ＝2或m ＝－1， 当m ＝2时，f (x )＝x－3在(0，＋∞)上是减函数，当m ＝－1时，f (x )＝x 0＝1在(0，＋∞)上不是减函数，舍去. ∴m ＝2.3.(2021·衡水中学调研)已知点(m ，8)在幂函数f (x )＝(m －1)x n 的图象上，设a ＝f ⎝⎛⎭⎫13，b ＝f (ln π)，c ＝f (2－12)，则a ，b ，c 的大小关系是( ) A.a <c <b B.a <b <cC.b <c <aD.b <a <c答案 A解析 由于f (x )＝(m －1)x n 为幂函数， 所以m －1＝1，则m ＝2，f (x )＝x n . 又点(2，8)在函数f (x )＝x n 的图象上，所以8＝2n ，知n ＝3，故f (x )＝x 3，且在R 上是增函数， 又ln π>1>2－12＝22>13， 所以f (ln π)>f (2－12)>f ⎝⎛⎭⎫13，则b >c >a .4.(2021·郑州质检)幂函数f (x )＝(m 2－3m ＋3)x m 的图象关于y 轴对称，则实数m ＝________. 答案 2解析 由幂函数定义，知m 2－3m ＋3＝1，解得m ＝1或m ＝2， 当m ＝1时，f (x )＝x 的图象不关于y 轴对称，舍去， 当m ＝2时，f (x )＝x 2的图象关于y 轴对称， 因此m ＝2.感悟升华 1.对于幂函数图象的掌握，需记住在第一象限内三条线分第一象限为六个区域，即x ＝1，y ＝1，y ＝x 所分区域.根据α<0，0<α<1，α＝1，α>1的取值确定位置后，其余象限部分由奇偶性决定.2.在比较幂值的大小时，必须结合幂值的特点，选择适当的函数，借助其单调性进行比较.3.在区间(0，1)上，幂函数中指数越大，函数图象越靠近x 轴(简记为“指大图低”)，在区间(1，＋∞)上，幂函数中指数越大，函数图象越远离x 轴. 考点二 二次函数的解析式【例1】 已知二次函数f (x )满足f (2)＝－1，f (－1)＝－1，且f (x )的最大值是8，试确定该二次函数的解析式.解 法一 (利用“一般式”) 设f (x )＝ax 2＋bx ＋c (a ≠0).由题意得⎩⎪⎨⎪⎧4a ＋2b ＋c ＝－1，a －b ＋c ＝－1，4ac －b 24a ＝8，解得⎩⎪⎨⎪⎧a ＝－4，b ＝4，c ＝7.∴所求二次函数的解析式为f (x )＝－4x 2＋4x ＋7. 法二 (利用“顶点式”) 设f (x )＝a (x －m )2＋n (a ≠0). 因为f (2)＝f (－1)，所以抛物线的对称轴为x ＝2＋（－1）2＝12，所以m ＝12.又根据题意，函数有最大值8，所以n ＝8， 所以y ＝f (x )＝a ⎝⎛⎭⎫x －122＋8. 因为f (2)＝－1，所以a ⎝⎛⎭⎫2－122＋8＝－1，解得a ＝－4， 所以f (x )＝－4⎝⎛⎭⎫x －122＋8＝－4x 2＋4x ＋7. 法三 (利用“零点式”)由已知f (x )＋1＝0的两根为x 1＝2，x 2＝－1， 故可设f (x )＋1＝a (x －2)(x ＋1)(a ≠0)， 即f (x )＝ax 2－ax －2a －1.又函数有最大值8，即4a （－2a －1）－（－a ）24a ＝8.解得a ＝－4或a ＝0(舍).故所求函数的解析式为f (x )＝－4x 2＋4x ＋7.感悟升华 求二次函数的解析式，一般用待定系数法，其关键是根据已知条件恰当选择二次函数解析式的形式，一般选择规律如下：【训练1】 (1)已知二次函数f (x )与x 轴的两个交点坐标为(0，0)和(－2，0)，且有最小值－1，则f (x )＝________.(2)已知二次函数f (x )的图象经过点(4，3)，在x 轴上截得的线段长为2，并且对任意x ∈R ，都有f (2－x )＝f (2＋x )，则f (x )＝________. 答案 (1)x 2＋2x (2)x 2－4x ＋3解析 (1)设函数的解析式为f (x )＝ax (x ＋2)(a ≠0)， 所以f (x )＝ax 2＋2ax ， 由4a ×0－4a 24a ＝－1，得a ＝1，所以f (x )＝x 2＋2x .(2)因为f (2－x )＝f (2＋x )对x ∈R 恒成立， 所以y ＝f (x )的图象关于x ＝2对称.又y ＝f (x )的图象在x 轴上截得的线段长为2， 所以f (x )＝0的两根为2－22＝1或2＋22＝3.所以二次函数f (x )与x 轴的两交点坐标为(1，0)和(3，0). 因此设f (x )＝a (x －1)(x －3). 又点(4，3)在y ＝f (x )的图象上， 所以3a ＝3，则a ＝1.故f (x )＝(x －1)(x －3)＝x 2－4x ＋3. 考点三 二次函数的图象和性质角度1 二次函数的图象【例2】 (1)如图是二次函数y ＝ax 2＋bx ＋c (a ≠0)图象的一部分，图象过点A (－3，0)，对称轴为x ＝－1.给出下面四个结论：①b 2>4ac ；②2a －b ＝1；③a －b ＋c ＝0；④5a <b . 其中正确的是( ) A.②④B.①④C.②③D.①③(2)设函数f (x )＝x 2＋x ＋a (a >0)，若f (m )<0，则( ) A.f (m ＋1)≥0 B.f (m ＋1)≤0C.f (m ＋1)>0D.f (m ＋1)<0答案 (1)B (2)C解析 (1)因为图象与x 轴交于两点，所以b 2－4ac >0，即b 2>4ac ，①正确. 对称轴为x ＝－1，即－b2a ＝－1，2a －b ＝0，②错误.结合图象，当x ＝－1时，y >0，即a －b ＋c >0，③错误. 由对称轴为x ＝－1知，b ＝2a .根据抛物线开口向下，知a <0，所以5a <2a ， 即5a <b ，④正确.(2)因为f (x )的对称轴为x ＝－12，f (0)＝a >0，所以f (x )的大致图象如图所示.由f (m )<0，得－1<m <0，所以m ＋1>0>－12，所以f (m ＋1)>f (0)>0.感悟升华 1.研究二次函数图象应从“三点一线一开口”进行分析，“三点”中有一个点是顶点，另两个点是图象上关于对称轴对称的两个点，常取与x 轴的交点；“一线”是指对称轴这条直线；“一开口”是指抛物线的开口方向.2.求解与二次函数有关的不等式问题，可借助二次函数的图象特征，分析不等关系成立的条件.角度2 二次函数的单调性与最值【例3】 (2021·西安模拟)已知f (x )＝ax 2－2x (0≤x ≤1)，求f (x )的最小值. 解 (1)当a ＝0时，f (x )＝－2x 在[0，1]上递减， ∴f (x )min ＝f (1)＝－2.(2)当a >0时，f (x )＝ax 2－2x 图象开口方向向上，且对称轴为x ＝1a.①当1a ≤1，即a ≥1时，f (x )＝ax 2－2x 图象的对称轴在[0，1]内，∴f (x )在⎣⎡⎦⎤0，1a 上递减，在⎣⎡⎦⎤1a ，1上递增.∴f (x )min ＝f ⎝⎛⎭⎫1a ＝1a －2a ＝－1a. ②当1a >1，即0<a <1时，f (x )＝ax 2－2x 图象的对称轴在[0，1]的右侧，∴f (x )在[0，1]上递减.∴f (x )min ＝f (1)＝a －2.(3)当a <0时，f (x )＝ax 2－2x 的图象的开口方向向下，且对称轴x ＝1a <0，在y 轴的左侧，∴f (x )＝ax 2－2x 在[0，1]上递减. ∴f (x )min ＝f (1)＝a －2.综上所述，f (x )min ＝⎩⎪⎨⎪⎧a －2，a <1，－1a，a ≥1.感悟升华 (1)闭区间上二次函数最值问题的解法：抓住“三点一轴”数形结合，三点是指区间两个端点和中点，一轴指的是对称轴，结合图象，根据函数的单调性及分类讨论的思想求解.(2)二次函数在闭区间上的最值主要有三种类型：轴定区间定、轴动区间定、轴定区间动.无论哪种类型，解题的关键都是图象的对称轴与区间的位置关系，当含有参数时，要依据图象的对称轴与区间的位置关系进行分类讨论.角度3 二次函数中的恒成立问题【例4】 设函数f (x )＝mx 2－mx －1.(1)若对于一切实数x ，f (x )<0恒成立，求m 的取值范围；(2)对于x ∈[1，3]，f (x )<－m ＋5恒成立，求m 的取值范围.解 (1)要使mx 2－mx －1<0恒成立，若m ＝0，显然－1<0，满足题意；若m ≠0，得⎩⎪⎨⎪⎧m <0，Δ＝m 2＋4m <0， 即－4<m <0.∴－4<m ≤0.∴所求m 的取值范围是(－4，0].(2)法一 要使f (x )<－m ＋5在x ∈[1，3]上恒成立.就要使m ⎝⎛⎭⎫x －122＋34m －6<0在x ∈[1，3]上恒成立. 令g (x )＝m ⎝⎛⎭⎫x －122＋34m －6，x ∈[1，3]. 当m >0时，g (x )在[1，3]上是增函数，∴g (x )max ＝g (3)＝7m －6<0，∴0<m <67； 当m ＝0时，－6<0恒成立；当m <0时，g (x )在[1，3]上是减函数，∴g (x )max ＝g (1)＝m －6<0，得m <6，∴m <0.综上所述，m 的取值范围是⎝⎛⎭⎫－∞，67. 法二 当x ∈[1，3]时，f (x )<－m ＋5恒成立，即当x ∈[1，3]时，m (x 2－x ＋1)－6<0恒成立.∵x 2－x ＋1＝⎝⎛⎭⎫x －122＋34>0， 又m (x 2－x ＋1)－6<0，∴m <6x 2－x ＋1. ∵函数y ＝6x 2－x ＋1＝6⎝⎛⎭⎫x －122＋34在[1，3]上的最小值为67，∴只需m <67即可. 综上所述，m 的取值范围是⎝⎛⎭⎫－∞，67. 感悟升华 由不等式恒成立求参数取值范围的思路及关键(1)一般有两个解题思路：一是分离参数；二是不分离参数.(2)两种思路都是将问题归结为求函数的最值，至于用哪种方法，关键是看参数是否易分离.其中分离参数的依据是：a ≥f (x )恒成立⇔a ≥f (x )max ，a ≤f (x )恒成立⇔a ≤f (x )min .【训练2】 (1)(2021·长春五校联考)已知二次函数f (x )满足f (3＋x )＝f (3－x )，若f (x )在区间[3，＋∞)上单调递减，且f (m )≥f (0)恒成立，则实数m 的取值范围是( )A.(－∞，0]B.[0，6]C.[6，＋∞)D.(－∞，0]∪[6，＋∞)(2)已知函数f (x )＝x 2－x ＋1，在区间[－1，1]上f (x )>2x ＋m 恒成立，则实数m 的取值范围是________.答案 (1)B (2)(－∞，－1)解析 (1)设f (x )＝ax 2＋bx ＋c (a ，b ，c ∈R ，且a ≠0)，∵f (3＋x )＝f (3－x )，∴a (3＋x )2＋b (3＋x )＋c ＝a (3－x )2＋b (3－x )＋c ，∴x (6a ＋b )＝0，∴6a ＋b ＝0，∴f (x )＝ax 2－6ax ＋c ＝a (x －3)2－9a ＋c .又∵f (x )在区间[3，＋∞)上单调递减，∴a <0，∴f (x )的图象是以直线x ＝3为对称轴，开口向下的抛物线，∴由f(m)≥f(0)恒成立，得0≤m≤6，∴实数m的取值范围是[0，6].(2)f(x)>2x＋m等价于x2－x＋1>2x＋m，即x2－3x＋1－m>0，令g(x)＝x2－3x＋1－m，要使g(x)＝x2－3x＋1－m>0在[－1，1]上恒成立，只需使函数g(x)＝x2－3x＋1－m在[－1，1]上的最小值大于0即可.∵g(x)＝x2－3x＋1－m在[－1，1]上单调递减，∴g(x)min＝g(1)＝－m－1.由－m－1>0，得m<－1.因此满足条件的实数m的取值范围是(－∞，－1).(3)设函数f(x)＝x2－2x＋2，x∈[t，t＋1]，t∈R，求函数f(x)的最小值.解f(x)＝x2－2x＋2＝(x－1)2＋1，x∈[t，t＋1]，t∈R，函数图象的对称轴为x＝1.当t＋1≤1，即t≤0时，函数图象如图(1)所示，函数f(x)在区间[t，t＋1]上为减函数，所以最小值为f(t＋1)＝t2＋1；当t<1<t＋1，即0<t<1时，函数图象如图(2)所示，在对称轴x＝1处取得最小值，最小值为f(1)＝1；当t≥1时，函数图象如图(3)所示，函数f(x)在区间[t，t＋1]上为增函数，所以最小值为f(t)＝t2－2t＋2.综上可知，当t≤0时，f(x)min＝t2＋1，当0<t<1时，f (x )min ＝1，当t ≥1时，f (x )min ＝t 2－2t ＋2.A 级 基础巩固一、选择题1.若幂函数f (x )＝(m 2－4m ＋4)·xm 2－6m ＋8在(0，＋∞)上为增函数，则m 的值为( )A.1或3B.1C.3D.2答案 B解析 由题意得m 2－4m ＋4＝1，m 2－6m ＋8>0，解得m ＝1.2.(2021·河南名校联考)函数y ＝1－|x －x 2|的图象大致是( )答案 C解析 ∵当0≤x ≤1时，y ＝x 2－x ＋1＝⎝⎛⎭⎫x －122＋34，又当x >1或x <0时，y ＝－x 2＋x ＋1＝－⎝⎛⎭⎫x －122＋54，因此，结合图象，选项C 正确. 3.(2020·成都诊断)已知幂函数y ＝f (x )的图象过点⎝⎛⎭⎫12，22，则log 4f (2)的值为( ) A.14B.－14C.2D.－2答案 A解析 设幂函数为f (x )＝x α，由于点⎝⎛⎭⎫12，22在幂函数的图象上，所以22＝⎝⎛⎭⎫12α，解得α＝12，则f (x )＝x 12，故log 4f (2)＝log 4212＝14.4.(2021·西安检测)已知函数f (x )＝x －3，若a ＝f (0.60.6)，b ＝f (0.60.4)，c ＝f (0.40.6)，则a ，b ，c 的大小关系是( )A.a <c <bB.b <a <cC.b <c <aD.c <a <b 答案 B解析 ∵0.40.6<0.60.6<0.60.4，又y ＝f (x )＝x －3在(0，＋∞)上是减函数，∴b <a <c .5.已知在(－∞，1]上递减的函数f (x )＝x 2－2tx ＋1，且对任意的x 1，x 2∈[0，t ＋1]，总有|f (x 1)－f (x 2)|≤2，则实数t 的取值范围是( )A.[－2，2]B.[1，2]C.[2，3]D.[1，2]答案 B解析 由于f (x )＝x 2－2tx ＋1的图象的对称轴为x ＝t ，又y ＝f (x )在(－∞，1]上是减函数，所以t ≥1.则在区间[0，t ＋1]上，f (x )max ＝f (0)＝1，f (x )min ＝f (t )＝t 2－2t 2＋1＝－t 2＋1，要使对任意的x 1，x 2∈[0，t ＋1]，都有|f (x 1)－f (x 2)|≤2，只需1－(－t 2＋1)≤2，解得－2≤t ≤ 2.又t ≥1，∴1≤t ≤ 2.6.幂函数y ＝x α，当α取不同的正数时，在区间[0，1]上它们的图象是一组美丽的曲线(如图)，设点A (1，0)，B (0，1)，连接AB ，线段AB 恰好被其中的两个幂函数y ＝x a ，y ＝x b 的图象三等分，即有BM ＝MN ＝NA ，那么a －1b ＝( )A.0B.1C.12D.2 答案 A解析 BM ＝MN ＝NA ，点A (1，0)，B (0，1)，所以M ⎝⎛⎭⎫13，23，N ⎝⎛⎭⎫23，13， 将两点坐标分别代入y ＝x a ，y ＝x b ，得a ＝log 1323，b ＝log 2313，∴a －1b ＝log 1323－1log 2313＝0. 二、填空题7.已知函数f (x )为幂函数，且f (4)＝12，则当f (a )＝4f (a ＋3)时，则实数a ＝________. 答案 15解析 设f (x )＝x α，则4α＝12，所以α＝－12. 因此f (x )＝x －12，从而a －12＝4(a ＋3)－12，解得a ＝15. 8.(2021·青岛联考)已知函数f (x )＝x 2－2ax ＋b (a >1)的定义域和值域都为[1，a ]，则b ＝________.答案 5解析 f (x )＝x 2－2ax ＋b 的图象关于x ＝a 对称，所以f (x )在[1，a ]上为减函数，又f (x )的值域为[1，a ]，所以⎩⎪⎨⎪⎧f （1）＝1－2a ＋b ＝a ，f （a ）＝a 2－2a 2＋b ＝1. 消去b ，得a 2－3a ＋2＝0，解得a ＝2(a >1)，从而得b ＝3a －1＝5.9.设函数f (x )＝ax 2－2x ＋2，对于满足1＜x ＜4的一切x 的值都有f (x )＞0，则实数a 的取值范围为________.答案 ⎝⎛⎭⎫12，＋∞解析 由题意得a >2x －2x 2对1<x <4恒成立， 又2x －2x 2＝－2⎝⎛⎭⎫1x －122＋12，14<1x<1， ∴⎝⎛⎭⎫2x －2x 2max ＝12，∴a >12. 三、解答题10.已知函数f (x )＝x 2＋2ax ＋3，x ∈[－4，6].(1)当a ＝－2时，求f (x )的最值；(2)求实数a 的取值范围，使y ＝f (x )在区间[－4，6]上是单调函数.解 (1)当a ＝－2时，f (x )＝x 2－4x ＋3＝(x －2)2－1，由于x ∈[－4，6]，∴f (x )在[－4，2]上单调递减，在[2，6]上单调递增，∴f (x )的最小值是f (2)＝－1，又f (－4)＝35，f (6)＝15，故f (x )的最大值是35.(2)由于函数f (x )的图象开口向上，对称轴是x ＝－a ，所以要使f (x )在[－4，6]上是单调函数，应有－a ≤－4或－a ≥6，即a ≤－6或a ≥4，故a 的取值范围是(－∞，－6]∪[4，＋∞).11.已知二次函数f (x )＝ax 2＋bx ＋1(a ，b ∈R 且a ≠0)，x ∈R .(1)若函数f (x )的最小值为f (－1)＝0，求f (x )的解析式，并写出单调区间；(2)在(1)的条件下，f (x )>x ＋k 在区间[－3，－1]上恒成立，试求k 的取值范围.解 (1)由题意知⎩⎪⎨⎪⎧a >0，－b 2a ＝－1，f （－1）＝a －b ＋1＝0，解得⎩⎪⎨⎪⎧a ＝1，b ＝2. 所以f (x )＝x 2＋2x ＋1，由f (x )＝(x ＋1)2知，函数f (x )的单调递增区间为[－1，＋∞)，单调递减区间为(－∞，－1].(2)由题意知，x 2＋2x ＋1>x ＋k 在区间[－3，－1]上恒成立，即k <x 2＋x ＋1在区间[－3，－1]上恒成立，令g (x )＝x 2＋x ＋1，x ∈[－3，－1]，由g (x )＝⎝⎛⎭⎫x ＋122＋34知g (x )在区间[－3，－1]上是减函数，则g (x )min ＝g (－1)＝1，所以k <1， 故k 的取值范围是(－∞，1). B 级 能力提升12.(2021·江南十校调研)已知幂函数f (x )＝mx 1＋n 是定义在区间[－2，n ]上的奇函数，设a ＝f ⎝⎛⎭⎫sin 2π7，b ＝f ⎝⎛⎭⎫cos 2π7，c ＝f ⎝⎛⎭⎫tan 2π7，则( ) A.b <a <cB.c <b <aC.b <c <aD.a <b <c 答案 A解析 根据f (x )＝mx 1＋n 是幂函数，且在区间[－2，n ]上是奇函数，得m ＝1，且－2＋n ＝0，解得n ＝2，∴f (x )＝x 3，且在定义域[－2，2]上是单调增函数.又0<π4<2π7<π2，∴cos 2π7<sin 2π7<1<tan 2π7， ∴f ⎝⎛⎭⎫cos 2π7<f ⎝⎛⎭⎫sin 2π7<f ⎝⎛⎭⎫tan 2π7，即b <a <c . 13.(2019·上海春招)如图，正方形OABC 的边长为a (a >1)，函数y ＝3x 2的图象交AB 于点Q ，函数y ＝x －12的图象交BC 于点P ，则当|AQ |＋|CP |最小时，a 的值为________.答案 3解析 依题意得Q ⎝⎛⎭⎫a 3，a ，P ⎝⎛⎭⎫a ，1a ，则|AQ |＋|CP |＝a 3＋1a ＝a 3＋1a ，记a ＝t (t >1)，f (t )＝|AQ |＋|CP |，则f (t )＝t 3＋1t ，所以f (t )＝t 3＋1t ≥213， 当且仅当t 3＝1t ，即t 2＝3时取等号，此时a ＝ 3. 14.已知二次函数f (x )满足f (x ＋1)－f (x )＝2x ，且f (0)＝1.(1)求f (x )的解析式；(2)当x ∈[－1，1]时，函数y ＝f (x )的图象恒在函数y ＝2x ＋m 的图象的上方，求实数m 的取值范围.解 (1)设f (x )＝ax 2＋bx ＋c (a ≠0)，由f (x ＋1)－f (x )＝2x ，得2ax ＋a ＋b ＝2x .所以，2a ＝2且a ＋b ＝0，解得a ＝1，b ＝－1，又f (0)＝1，所以c ＝1.因此f (x )的解析式为f (x )＝x 2－x ＋1.(2)因为当x ∈[－1，1]时，y ＝f (x )的图象恒在y ＝2x ＋m 的图象上方，所以在[－1，1]上，x 2－x ＋1>2x ＋m 恒成立；即x 2－3x ＋1>m 在区间[－1，1]上恒成立.所以令g (x )＝x 2－3x ＋1＝⎝⎛⎭⎫x －322－54， 因为g (x )在[－1，1]上的最小值为g (1)＝－1，所以m <－1.故实数m 的取值范围为(－∞，－1).。

高考数学一轮复习第二章函数2.5幂函数与二次函数教学案苏教版[最新考纲] 1.(1)了解幂函数的概念；(2)结合函数y ＝x ，y ＝x 2，y ＝x 3，y ＝x12，y ＝1x的图象，了解它们的变化情况.2.理解二次函数的图象和性质，能用二次函数、方程、不等式之间的关系解决简单问题．1．幂函数 (1)幂函数的定义一般地，形如y ＝x α(α∈R )的函数称为幂函数，其中x 是自变量，α是常数． (2)常见的五种幂函数的图象和性质比较 函数y ＝x y ＝x 2 y ＝x 3y ＝x 12y ＝x －1图象性质定义域 R RR {x |x ≥0} {x |x ≠0} 值域 R {y |y ≥0} R{y |y ≥0} {y |y ≠0} 奇偶性奇函数偶函数 奇函数非奇非偶 函数奇函数单调性在R 上单 调递增 在(－∞，0]上单调递减； 在(0，＋∞) 上单调递增在R 上单调递增在[0，＋∞)上单调递增在(－∞，0)和(0，＋∞)上单调递减公共点(1,1)解析式f (x )＝ax 2＋bx ＋c(a ＞0)f (x )＝ax 2＋bx ＋c(a ＜0)图象定义域R R值域⎝⎛⎦⎥⎤－∞，4ac－b24a单调性在x∈上单调递减；在x∈⎣⎢⎡⎭⎪⎫－b2a，＋∞上单调递增在x∈⎝⎛⎦⎥⎤－∞，－b2a上单调递增；在x∈⎣⎢⎡⎭⎪⎫－b2a，＋∞上单调递减对称性函数的图象关于直线x＝－b2a对称[常用结论]1．幂函数y＝xα性质研究的方法(1)先确定幂函数的定义域(分数指数幂先转化为根式)，若对称，判定其奇偶性；(2)研究幂函数在第一象限的图象与性质：①当α＞0时，函数y＝xα恒经过(0,0)，(1,1)；在[0，＋∞)上为增函数；②当α＜0时，函数恒经过(1,1)；在(0，＋∞)上为减函数；(3)结合函数的奇偶性研究其它象限的图象．(4)当x∈(0,1)时，α越大，函数值越小；当x∈(1，＋∞)时，α越大，函数值越大．2．二次函数解析式的三种形式(1)一般式：f(x)＝ax2＋bx＋c(a≠0)；(2)顶点式：f(x)＝a(x－m)2＋n(a≠0)；(3)零点式：f(x)＝a(x－x1)(x－x2)(a≠0)．3．一元二次不等式恒成立的条件(1)ax2＋bx＋c＞0(a≠0)恒成立的充要条件是“a＞0且Δ＜0”；(2)ax2＋bx＋c＜0(a≠0)恒成立的充要条件是“a＜0且Δ＜0”．一、思考辨析(正确的打“√”，错误的打“×”)(1)函数y＝2x12是幂函数．( )(2)如果幂函数的图象与坐标轴相交，则交点一定是原点．( )(3)当α＜0时，幂函数y＝xα是定义域上的减函数．( )(4)二次函数y ＝ax 2＋bx ＋c ，x ∈[a ，b ]的最值一定是4ac －b24a.( )(5)二次函数y ＝ax 2＋bx ＋c ，x ∈R 不可能是偶函数． ( )(6)在y ＝ax 2＋bx ＋c (a ≠0)中，a 决定了图象的开口方向和在同一直角坐标系中的开口大小．( )[答案](1)× (2)√ (3)× (4)× (5)× (6)√ 二、教材改编1．已知幂函数f (x )＝k ·x α的图象过点⎝ ⎛⎭⎪⎫12，22，则k ＋α＝( )A.12 B ．1 C.32D ．2 C [因为函数f (x )＝k ·x α是幂函数，所以k ＝1，又函数f (x )的图象过点⎝ ⎛⎭⎪⎫12，22，所以⎝ ⎛⎭⎪⎫12a＝22，解得α＝12，则k ＋α＝32.] 2.如图是①y ＝x a；②y ＝x b；③y ＝x c在第一象限的图象，则a ，b ，c 的大小关系为( )A ．c ＜b ＜aB ．a ＜b ＜cC ．b ＜c ＜aD ．a ＜c ＜bD [根据幂函数的性质，可知选D.]3．已知函数f (x )＝x 2＋4ax 在区间(－∞，6)内单调递减，则a 的取值范围是( ) A ．a ≥3 B ．a ≤3 C ．a ＜－3D ．a ≤－3D [函数f (x )＝x 2＋4ax 的图象是开口向上的抛物线，其对称轴是x ＝－2a ，由函数在区间(－∞，6)内单调递减可知，区间(－∞，6)应在直线x ＝－2a 的左侧，所以－2a ≥6，解得a ≤－3，故选D.]4．函数g (x )＝x 2－2x (x ∈[0,3])的值域是________． [－1,3] [∵g (x )＝x 2－2x ＝(x －1)2－1，x ∈[0,3]， ∴当x ＝1时，g (x )min ＝g (1)＝－1，又g (0)＝0，g (3)＝9－6＝3， ∴g (x )max ＝3，即g (x )的值域为[－1,3]．]考点1 幂函数的图象及性质 幂函数的性质与图象特征的关系(1)幂函数的形式是y ＝x α(α∈R )，其中只有一个参数α，因此只需一个条件即可确定其解析式．(2)判断幂函数y ＝x α(α∈R )的奇偶性时，当α是分数时，一般将其先化为根式，再判断．(3)若幂函数y ＝x α在(0，＋∞)上单调递增，则α＞0，若在(0，＋∞)上单调递减，则α＜0.1.幂函数y ＝f (x )的图象经过点(3，3)，则f (x )是( )A ．偶函数，且在(0，＋∞)上是增函数B ．偶函数，且在(0，＋∞)上是减函数C ．奇函数，且在(0，＋∞)上是减函数D ．非奇非偶函数，且在(0，＋∞)上是增函数D [设幂函数f (x )＝x α，则f (3)＝3α＝3，解得α＝12，则f (x )＝x 12＝x ，是非奇非偶函数，且在(0，＋∞)上是增函数．]2．当x ∈(0，＋∞)时，幂函数y ＝(m 2＋m －1)x －5m －3为减函数，则实数m 的值为( )A ．－2B ．1C ．1或－2D ．m ≠－1±52B [因为函数y ＝(m 2＋m －1)x－5m －3既是幂函数又是(0，＋∞)上的减函数，所以⎩⎪⎨⎪⎧m 2＋m －1＝1，－5m －3＜0，解得m ＝1.]3．若a ＝⎝ ⎛⎭⎪⎫1223，b ＝⎝ ⎛⎭⎪⎫1523，c ＝⎝ ⎛⎭⎪⎫1213，则a ，b ，c 的大小关系是( )A ．a ＜b ＜cB ．c ＜a ＜bC ．b ＜c ＜aD ．b ＜a ＜cD [因为y ＝x23在第一象限内是增函数，所以a ＝⎝ ⎛⎭⎪⎫1223＞b ＝⎝ ⎛⎭⎪⎫1523，因为y ＝⎝ ⎛⎭⎪⎫12x 是减函数，所以a ＝⎝ ⎛⎭⎪⎫1223＜c ＝⎝ ⎛⎭⎪⎫1213，所以b ＜a ＜c .]4．若(a ＋1)12＜(3－2a )12，则实数a 的取值范围是________．⎣⎢⎡⎭⎪⎫－1，23 [易知函数y ＝x 12的定义域为[0，＋∞)，在定义域内为增函数， 所以⎩⎪⎨⎪⎧a ＋1≥0，3－2a ≥0，a ＋1＜3－2a ，解得－1≤a ＜23.]在比较幂值的大小时， 必须结合幂值的特点，选择适当的函数，借助其单调性进行比较，如T 3.考点2 求二次函数的解析式 求二次函数解析式的策略[一题多解]已知二次函数f (x )满足f (2)＝－1，f (－1)＝－1，且f (x )的最大值是8，试确定此二次函数的解析式．[解] 法一：(利用二次函数的一般式) 设f (x )＝ax 2＋bx ＋c (a ≠0)． 由题意得⎩⎪⎨⎪⎧4a ＋2b ＋c ＝－1，a －b ＋c ＝－1，4ac －b 24a ＝8，解得⎩⎪⎨⎪⎧a ＝－4，b ＝4，c ＝7.故所求二次函数为f (x )＝－4x 2＋4x ＋7. 法二：(利用二次函数的顶点式) 设f (x )＝a (x －m )2＋n .∵f (2)＝f (－1)，∴抛物线对称轴为x ＝2＋－12＝12.∴m ＝12，又根据题意函数有最大值8，∴n ＝8，∴y ＝f (x )＝a ⎝ ⎛⎭⎪⎫x －122＋8. ∵f (2)＝－1，∴a ⎝ ⎛⎭⎪⎫2－122＋8＝－1，解得a ＝－4， ∴f (x )＝－4⎝ ⎛⎭⎪⎫x －122＋8＝－4x 2＋4x ＋7.法三：(利用零点式)由已知f (x )＋1＝0的两根为x 1＝2，x 2＝－1， 故可设f (x )＋1＝a (x －2)(x ＋1)， 即f (x )＝ax 2－ax －2a －1.又函数有最大值y max ＝8，即4a －2a －1－a24a ＝8.解得a ＝－4或a ＝0(舍去)，故所求函数解析式为f (x )＝－4x 2＋4x ＋7.求二次函数的解析式常利用待定系数法，但由于条件不同，则所选用的解析式不同，其方法也不同．1.已知二次函数f (x )的图象的顶点坐标是(－2，－1)，且图象经过点(1,0)，则函数的解析式为f (x )＝________.19x 2＋49x －59[法一：(一般式)设所求解析式为f (x )＝ax 2＋bx ＋c (a ≠0)． 由已知得⎩⎪⎨⎪⎧ －b2a＝－2，4ac －b24a ＝－1，a ＋b ＋c ＝0，解得⎩⎪⎨⎪⎧a ＝19，b ＝49，c ＝－59，所以所求解析式为f (x )＝19x 2＋49x －59.法二：(顶点式)设所求解析式为f (x )＝a (x －h )2＋k . 由已知得f (x )＝a (x ＋2)2－1，将点(1,0)代入，得a ＝19，所以f (x )＝19(x ＋2)2－1，即f (x )＝19x 2＋49x －59.]2．已知二次函数f(x)的图象经过点(4,3)，它在x轴上截得的线段长为2，并且对任意x∈R，都有f(2－x)＝f(2＋x)，则函数的解析式f(x)＝________.x2－4x＋3[∵f(2－x)＝f(2＋x)对x∈R恒成立，∴f(x)的对称轴为x＝2.又∵f(x)的图象被x轴截得的线段长为2，∴f(x)＝0的两根为1和3.设f(x)的解析式为f(x)＝a(x－1)(x－3)(a≠0)．又∵f(x)的图象经过点(4,3)，∴3a＝3，a＝1.∴所求f(x)的解析式为f(x)＝(x－1)(x－3)，即f(x)＝x2－4x＋3.]考点3 二次函数的图象与性质解决二次函数图象与性质问题时应注意2点(1)抛物线的开口，对称轴位置，定义区间三者相互制约，要注意分类讨论．(2)要注意数形结合思想的应用，尤其是给定区间上的二次函数最值问题，先“定性”(作草图)，再“定量”(看图求解)．二次函数的图象已知abc＞0，则二次函数f(x)＝ax2＋bx＋c的图象可能是( )A BC DD[A项，因为a＜0，－b2a＜0，所以b＜0.又因为abc＞0，所以c＞0，而f(0)＝c＜0，故A错．B项，因为a＜0，－b2a＞0，所以b＞0.又因为abc＞0，所以c＜0，而f(0)＝c＞0，故B错．C项，因为a＞0，－b2a＜0，所以b＞0.又因为abc＞0，所以c＞0，而f(0)＝c＜0，故C错．D项，因为a＞0，－b2a＞0，所以b＜0，因为abc＞0，所以c＜0，而f(0)＝c＜0，故选D.]识别二次函数图象应学会“三看”。