2021届广东省清远市高三上学期摸底考试(11月) 数学 PDF版

2020-2021学年广东清远高三上数学月考试卷一、选择题1. 若，则在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限2. 已知全集，集合，，则( )A.）B.C.D.3. 已知，，，则，，的大小关系为( )A. B. C. D.4. “”是“直线与圆：相交”的( )A.充分不必要条件B.充要条件C.必要不充分条件D.既不充分也不必要条件5. 已知，，，则的最小值是（）A. B. C. D.6. “阿基米德多面体”是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美．如图，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形，六个面为正方形的“阿基米德多面体”．若该多面体的棱长为，则其体积为( )A. B. C. D.7. 已知函数的定义域为，是偶函数，，在上单调递减，则不等式的解集为( )A. B. C. D.8. 在平行四边形中，，若，则( ) A. B. C. D.二、多选题9. 若二项式的展开式中各项的二项式系数之和为，则（）A. B. C.第项为 D.第项为10. 已知函数，则( )A.图象的一条对称轴方程为B.图象的一个对称中心为C.将曲线上各点的横坐标缩短到原来的（纵坐标不变），再向下平移个单位长度，可得到的图象D.将的图象向右平移个单位长度，得到的曲线关于轴对称11. 为了研究某种病毒在特定环境下随时间变化的繁殖情况，得到了一些数据，绘制成散点图，发现用模型拟合比较合适．令，得到，经计算发现，满足下表：则( )A. B. C. D.12. 双曲线的左、右焦点分别为，，点为的左支上任意一点，直线是双曲线的一条渐近线，，垂足为．当的最小值为时，的中点在双曲线上，则( )A.的方程为B.的离心率为C.的渐近线方程为D.的方程为三、填空题13. 已知角终边上一点的坐标为，则________.14. 若函数的图象在点处的切线垂直于直线，则函数的最小值是________.15. 已知椭圆：的右焦点为，若点到直线的距离为，则的离心率为________.16. 在矩形中，，将沿向上折起到的位置，得到四面体当四面体的体积最大时，异面直线与所成角的余弦值为________.四、解答题17. 在①，②的面积为，③这三个条件中任选一个，补充在下面的问题中，并解答问题．问题：在中，角，，的对边分别为，，，________，且，的外接圆的半径为．求的周长．注：如果选择多个条件解答，按第一个解答计分．18. 某学校为了了解学生暑假期间学习数学的情况，抽取了人数相等的甲、乙两班进行调查，甲班同学每天学习数学的平均时间的频率分布直方图（将时间分成，，，，，共组）和乙班同学每天学习数学的平均时间的频数分布表如图所示（单位：小时）．从甲班每天学习数学的平均时间在的人中随机选出人，求人中恰有人每天学习数学的平均时间在范围内的概率；从甲、乙两个班每天学习数学平均时间不小于个小时的学生中随机抽取人进一步了解其他情况，设人中乙班学生的人数为，求的分布列和数学期望.19. 在四棱锥中，，，，，为的中点．证明：平面；若平面，且，求与平面所成角的正弦值．20. 已知数列满足，设数列的前项和为.求数列的通项公式；令求的前项和.21. 已知圆：，动圆与圆相外切，且与直线相切．求动圆圆心的轨迹的方程；已知点，，过点的直线与曲线交于两个不同的点，（与点不重合），直线，的斜率之和是否为定值？若是，求出该定值；若不是，说明理由．22. 已知函数.若只有一个极值点，求的取值范围；若函数存在两个极值点，记过点的直线的斜率为，证明：.参考答案与试题解析2020-2021学年广东清远高三上数学月考试卷一、选择题1.【答案】D【考点】复数的代数表示法及其几何意义【解析】把所给的复数先进行复数的除法运算，分子和分母同乘以分母的共轭复数，整理后得到最简形式，写出复数在复平面上对应的点的坐标，根据坐标的正负得到所在的象限．【解答】解：∵，∴在复平面对应的点的坐标是，∴它对应的点在第四象限.故选.2.【答案】C【考点】对数函数的定义域一元二次不等式的解法交、并、补集的混合运算【解析】此题暂无解析【解答】解：因为或，所以．因为，所以 .故选.3.【答案】B【考点】指数式、对数式的综合比较【解析】暂无【解答】解：因为，，，所以.故选.4.【答案】A【考点】必要条件、充分条件与充要条件的判断【解析】此题暂无解析【解答】解：∵直线与圆：相交，∴圆心到直线的距离，解得：.∵，∴ “”是“直线与圆：相交”的充分不必要条件. 故选．5.【答案】D【考点】基本不等式在最值问题中的应用【解析】【解答】解：因为，，，所以，当且仅当，即，时取等号．故选.6.【答案】D【考点】组合几何体的面积、体积问题【解析】暂无【解答】解：将该多面体放入正方体中，如图所示：因为多面体的棱长为，所以正方体的棱长为.该多面体是由棱长为的正方体沿各棱中点截去个三棱锥所得的，所以该多面体的体积为.故选.7.【答案】D【考点】奇偶性与单调性的综合【解析】暂无【解答】解：因为是偶函数，所以函数的图象关于直线对称，所以.因为在上单调递减，所以在上单调递增，所以等价于，解得.故选.8.【答案】B【考点】向量的模向量在几何中的应用【解析】暂无【解答】解：因为，所以四边形为菱形，即.因为，所以.故选. 二、多选题9.【答案】A,C【考点】二项式定理的应用二项展开式的特定项与特定系数【解析】因为二项式的展开式中所有项的二项式系数之和为，所以，所以因为二项式的展开式的通项公式为，所以【解答】解：因为二项式的展开式中所有项的二项式系数之和为，所以，所以因为二项式的展开式的通项公式为，所以.故选.10.【答案】C,D【考点】函数y=Asin（ωx+φ）的图象变换正弦函数的对称性【解析】暂无【解答】解：∵，令，，则对称轴为，，故错误；令，，则，，所以图象的对称中心为，，故错误；将曲线上各点的横坐标缩短到原来的（纵坐标不变），得到曲线的图象，再向下平移个单位长度得到曲线的图象，故正确；将的图象向右平移个单位长度，得到的曲线方程为，其为偶函数，故正确．故选.11.【答案】A,B【考点】求解线性回归方程函数模型的选择与应用【解析】此题暂无解析【解答】解：因为，，所以的中心点为，代入，得 .因为，所以，，即 .故选 .12.【答案】B,C,D【考点】双曲线的离心率双曲线的渐近线双曲线的标准方程【解析】利用双曲线的定义及焦点到渐近线的距离得，再将的中点代入双曲线得解. 【解答】解：因为，所以，因为焦点到渐近线的距离为，所以的最小值，，不妨设直线为，因为，所以点，，的中点为，将其代入双曲线方程得：，即，解得，又因为，，所以，故双曲线的方程为，故错误，正确；离心率为，故正确；渐近线方程为，故正确.故选.三、填空题13.【答案】【考点】任意角的三角函数【解析】因为所以.【解答】解：因为，，所以.故答案为：.14.【答案】【考点】利用导数研究曲线上某点切线方程利用导数研究函数的最值【解析】因为，所以，所以．因为．所以单调递减上单调递增，故函数的最小值是 . 【解答】解：因为，所以，，所以．因为，所以在上单调递减，在上单调递增，故函数的最小值是 .故答案为：.15.【答案】【考点】椭圆的离心率【解析】由题意可知，，得．因为，所以，故 .【解答】解：由题意，得，解得．又因为，所以，所以 .故答案为：.16.【答案】【考点】异面直线及其所成的角【解析】【解答】解：如图，当平面平面时，四面体的体积最大．过作于，则平面．因为，所以因为，所以或它的补角为异面直线与所成的角．因为，所以异面直线与所成角的余弦值为.故答案为：.四、解答题17.【答案】解：因为，所以.因为，所以.因为，所以.因为，所以，，因为外接圆的半径为，所以.选择①，因为，所以.因为，，所以.因为，所以，所以的周长为.选择②，因为的面积为，所以.因为，所以.因为，由，可得，即，所以，所以的周长为.选择③，因为，所以，即. 因为，，所以，因为，所以，即.因为，所以.因为，所以，即.因为，，所以，，所以的周长为．【考点】两角和与差的正弦公式余弦定理正弦定理【解析】暂无【解答】解：因为，所以.因为，所以.因为，所以.因为，所以，，因为外接圆的半径为，所以.选择①，因为，所以.因为，，所以.因为，所以，所以的周长为.选择②，因为的面积为，所以.因为，所以.因为，由，可得，即，所以，所以的周长为.选择③，因为，所以，即.因为，，所以，因为，所以，即.因为，所以.因为，所以，即.因为，，所以，，所以的周长为．18.【答案】解：因为乙班学生的总人数为，所以甲班中学习平均时间在内的人数为，甲班中学习平均时间在内的人数为．设“人中恰有人学习数学的平均时间在范围内”为事件，则．甲班学习数学平均时间在区间的人数为．由频数分布表知乙班学习数学平均时间在区间的人数为，所以两班中学习数学的平均时间不小于小时的同学共人，的所有可能取值为，，，，，，，，所以的分布列为：所以．【考点】频率分布直方图古典概型及其概率计算公式离散型随机变量的期望与方差离散型随机变量及其分布列【解析】暂无．暂无．【解答】解：因为乙班学生的总人数为，所以甲班中学习平均时间在内的人数为，甲班中学习平均时间在内的人数为．设“人中恰有人学习数学的平均时间在范围内”为事件，则．甲班学习数学平均时间在区间的人数为．由频数分布表知乙班学习数学平均时间在区间的人数为，所以两班中学习数学的平均时间不小于小时的同学共人，的所有可能取值为，，，，，，，，所以的分布列为：19.【答案】证明：设的中点为，连接，．因为为的中点，所以，且．因为，且，所以，且，所以四边形为平行四边形，所以．因为平面，平面，所以平面．解：因为，，，且，所以．如图，以为坐标原点，分别以，，的方向为轴，轴，轴的正方向建立空间直角坐标系，则，，，，，，．设平面的法向量为，则令，得．设与平面所成角为，则，即与平面所成角的正弦值为．【考点】直线与平面所成的角直线与平面平行的判定【解析】暂无．暂无．【解答】证明：设的中点为，连接，．因为为的中点，所以，且．因为，且，所以，且，所以四边形为平行四边形，所以．因为平面，平面，所以平面．解：因为，，，且，所以．如图，以为坐标原点，分别以，，的方向为轴，轴，轴的正方向建立空间直角坐标系，则，，，，，，．设平面的法向量为，则令，得．设与平面所成角为，则，即与平面所成角的正弦值为．20.【答案】解：令，设数列的前项和为，则．当时，，则；当时，．所以数列是常数列，即，故．因为，所以．所以当时，；当时，．因为当时，也符合上式，所以，所以，所以.【考点】数列递推式等差数列的通项公式数列的求和【解析】暂无．暂无．【解答】解：令，设数列的前项和为，则．当时，，则；当时，．所以数列是常数列，即，故．因为，所以．所以当时，；当时，．因为当时，也符合上式，所以，所以，所以.21.【答案】解：设到直线的距离为.∵，∴到直线的距离等于到的距离.由抛物线的定义可知，的轨迹为抛物线，∴轨迹的方程为.设直线的方程为，即.∵，与点不重合，∴ .设直线，的斜率分别为和，，点，，联立消去，得，则，，由，解得或，且.因为，同理可得，所以，所以直线，的斜率之和为定值．【考点】直线与圆的位置关系抛物线的定义轨迹方程圆锥曲线中的定点与定值问题【解析】暂无暂无【解答】解：设到直线的距离为.∵，∴到直线的距离等于到的距离.由抛物线的定义可知，的轨迹为抛物线，∴轨迹的方程为.设直线的方程为，即.∵，与点不重合，∴ .设直线，的斜率分别为和，，点，，联立消去，得，则，，由，解得或，且.因为，同理可得，所以，所以直线，的斜率之和为定值．22.【答案】解：．令，则.令，要使函数只有一个极值点，则需满足即．证明：因为，所以．因为存在两个极值点，所以解得：．设，则．要证，即证，只需证，即，即．设，则，．因为，所以，所以，即，故在上单调递减，所以．又因为，所以，即，从而得证．【考点】利用导数研究不等式恒成立问题利用导数研究函数的极值【解析】暂无．暂无．【解答】解：．令，则.令，要使函数只有一个极值点，则需满足即．证明：因为，所以．因为存在两个极值点，所以解得：．设，则．要证，即证，只需证，即，即．设，则，．因为，所以，所以，即，故在上单调递减，所以．又因为，所以，即，从而得证．。

2021年高三上学期11月摸底考试数学（理）试题含答案一、选择题（本大题共12个小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的）1、设{|{|ln(1)}A x y B x y x ====+，则（ ） A ． B ． C ． D ． 2、函数的最大值为（ ）A ．-1B ．1C ．2D ．3 3、已知，则是的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也非必要条件 4、若正实数满足，则的最小值为（ ） A ．1 B ．2 C ．3 D ．4 5、已知中，，且的面积为，则（ ） A ． B ． C ．或 D ．或 6、已知，则（ ）A ．B ．C ．D ．7、已知为由不等式组02x y x ⎧≤≤⎪≤⎨⎪≤⎩，所确定的平面区域上的动点，若点，则的最大值为（ ）A ．3B ．C ．4D ． 8、定义在R 上的偶函数满足：对且， 都有()1212[()()]0x x f x f x --<，则（ ） A ． B ． C ． D ．9、在中，若OA OB OB OC OC OA ⋅=⋅=⋅，且，则的周长为（ ） A ． B ． C ． D ．10、若变量满足，则关于的函数图象大致是（ ）11、设点P 是函数图象上异于原点的动点，且该图象在点P 处的切线的倾斜角为，则的取值范围是（ ）A ．B ．C ．D ．12、已知是等差数列的前n 项和，且，给出下列五个命题： ①；②；③；④数列中的最大项为；⑤。

其中正确命题的个数是（ ）A ．5B ．4C ．3D ．1第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上。

. 13、若，则14、在中，分别是内角的对边，若，的面积为， 则 的值为15、设是等比数列的前n 项的和，若，则的值是 16、函数()[]12sin(),2,41f x x x xπ=-∈--的所有零点之和为三、解答题：解答应写出文字说明、证明过程或演算步骤 17、（本小题满分12分）已知公差为2的等差数列的前n 项和为，且. (1) 求数列的通项公式；(2) 若为等比数列，且，记3132333log log log log n n T b b b b =++++，求的值。

清远盛兴中英文2021-2021学年度第一学期高三年级第一次月考数学（理）试题考试时刻：120分钟 总分值：150分钟一、选择题：本大题共8小题，每题5分，共40分. 在每题给出的四个选项中，只有一项符合题目要求. 1．复数iiz +=1（其中i 为虚数单位）的虚部是 （ ） 2．已知集合},1{R x x y y A ∈-==，}2{≥=x x B ，那么以下结论正确的选项是（ ）3．某学校高一、高二、高三年级的学生人数别离为9009001200、、人，现用分层抽样的方式从该校高中三个年级的学生中抽取容量为50的样本，那么应从高三年级抽取的学生人数为 ( ) 4．已知等差数列}{n a 的前n 项和为n S ，假设5418a a -=，那么=8S5．在二项式52)1(xx -的展开式中，含4x 的项的系数是（ ）6．假设某几何体的三视图如右图所示，那么此几何体的体积等于（ 7．已知y x ,都是区间]2,0[π内任取的一个实数，那么使得x y sin ≤8．设向量),(21a a a =，),(21b b b =，概念一种向量积：),(),(),(22112121b a b a b b a a b a =⊗=⊗．已知向量)4,21(=m ，)0,6(π=n ，点P 在cos y x =的图象上运动，点Q 在()y f x =的图象上运动，且知足n OP m OQ +⊗=（其中O 为坐标原点），那么()y f x =在区间]3,6[ππ上的最大值是（ ）A ．4B ．2C ．D ．二、填空题（本大题共7小题，分为必做题和选做题两部份．每题5分，总分值30分） （一）必做题：第9至13题为必做题，每道试题考生都必需作答． 9． 函数3log (32)y x =-的概念域是 .10．以抛物线x y 42=的核心为极点，极点为中心，离心率为2的双曲线方程是 .11．用数字1,2,3,4能够排成没有重复数字的四位偶数，共有____________个.12．设变量y x ,知足⎪⎩⎪⎨⎧≤+≤≥110y y x x ，那么y x +的最大值是 .13．函数)(x f 的概念域为R ，2)1(=-f ，对任意R x ∈，2)('>x f ，那么42)(+>x x f 的解集为 .（二）选做题：第14、15题为选做题，考生只选做其中一题，两题全答的，只计前一题的得分。

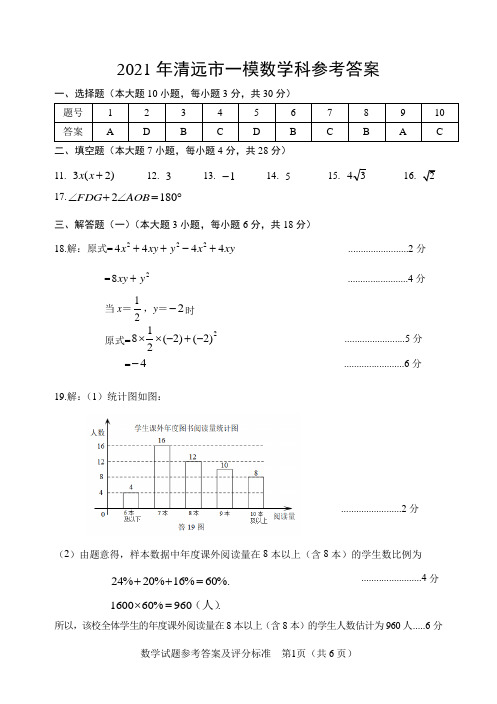
2021年清远市一模数学科参考答案一、选择题（本大题10小题，每小题3分，共30分） 二、填空题（本大题7小题，每小题4分，共28分）11. )2(3+x x 12. 3 13. 1- 14. 5 15. 34 16. 217.︒=∠+∠1802AOB FDG三、解答题（一）（本大题3小题，每小题6分，共18分）18.解：原式=xy x y xy x 4444222+-++ ........................2分 =28y xy + ........................4分当x ＝21，y ＝2-时 原式=2)2()2(218-+-⨯⨯........................5分 =4- ........................6分19.解：（1）统计图如图：........................2分（2）由题意得，样本数据中年度课外阅读量在8本以上（含8本）的学生数比例为 %.60%16%20%24=++ ........................4分 . 960%601600（人）=⨯所以，该校全体学生的年度课外阅读量在8本以上（含8本）的学生人数估计为960人.....6分题号 1 2 3 4 5 6 7 8 9 10 答案ADBCDBCBAC20. 解：（1）∵AC AB =∴ ABC ∆是等腰三角形. ........................1分 ∵ ，︒=∠70B∴ .40270180︒=⨯︒-︒=∠BAC ........................2分 又∵ D 为AB 中点,∴ AD 平分BAC ∠，即.21BAC CAD BAD ∠=∠=∠ ∴ .20︒=∠CAD ........................3分 （2）∵ ，AC NM //∴ .CAD ANM ∠=∠ ..................... 4分 又∵ ，CAD BAD ∠=∠∴ .BADANM ∠=∠ ∴ ANM ∆是等腰三角形.∴ .NM AN = ........................5分∵ 8=AB ，，3=BN ∴ BMN ∆的周长为：.11 =+=++=++AB BN MABM BN NM BM BN ........................6分 四、解答题（二）（本大题3小题，每小题8分，共24分） 21.解：（1）∵()6x y ⊗-=-，且212y x ⊗=， ∴26,2212.x y y x -=-⎧⎨+=⎩ ........................2分解得24.x y =⎧⎨=⎩， ........................4分∴x ，y 的值分别是2，4．（2）2、4为边长的等腰三角形构成腰长为4，底边为2的等腰三角形， ........................6分所求的等腰三角形面积为：122⨯ ........................8分-6，22．解：（1）连接OC ， ........................ 1分∵CD 为⊙O 的切线，∴OC ⊥CD ∵AD ⊥CD ，∴OC ∥AD ............... 2分 ∴∠1＝∠3 又∵OA ＝OC ，∴∠2＝∠3， ............... 3分 ∴∠1＝∠2∴CE ＝CB ． ............... 4分 （2）∵AB 为⊙O 的直径 ∴∠ACB ＝90°∵AC ＝25，CB ＝CE ＝5∴AB ＝2222(25)(5)5AC CB +=+=............... 5分∵∠ADC ＝∠ACB ＝90°，∠1＝∠2，∴△ADC ∽△ACB ............... 6分 ∴AD AC DCAC AB CB ==，即255255AD DC ==, ∴AD ＝4，DC ＝2 ............... 7分在Rt △DCE 中，DE ＝2222(5)21EC DC -=-=∴AE ＝AD －ED ＝4－1＝3． ............... 8分23.（1）解：设每本故事书需涨价x 元，由题意，得 .................................. 1分(5040)(50020)6000x x +--=， ................................. 2分解得 1x ＝5，2x ＝10（不合题意，舍去）． ................................. 3分 答：每本故事书需涨5元； ................................. 4分 （2）解：设每本故事书的售价为m 元， ................................ 5分则500﹣20（m ﹣50）≥300， ................................ 6分 解得，m≤60． ................................ 7分 答：每本故事书的售价应不高于60元． ................................ 8分321O EDCBA五、解答题（三）（本大题2小题，每小题10分，共20分） 24.解：（1）在矩形OABC 中，∵B 点坐标为(23)，，BC ∴边中点D 的坐标为(13)，． ........................1分 又∵反比例函数ky x=图像经过点(13)D ，， 31k ∴=， 3k ∴=． ........................2分 ∵E 点在AB 上，E ∴点的横坐标为2．又∵y= 经过点E ，E ∴点纵坐标为32．E ∴点坐标为322⎛⎫⎪⎝⎭，． ........................3分（2）由（1）得1BD =，32BE =，2CB =． FBC DEB △∽△，BD BE CF CB ∴=，即3122CF =． 43CF ∴=．53OF ∴=，即点F 的坐标为503⎛⎫⎪⎝⎭，． ........................5分 设直线FB 的解析式为1y k x b =+，而直线FB 经过(23)B ，，503F ⎛⎫ ⎪⎝⎭，． ∴13253k b b =+⎧⎪⎨=⎪⎩，．12533k b ∴==，．∴直线FB 的解析式为2533y x =+． ........................7分 x 3∵（3）131232313222AOE COD BDOE OABC S S S S =--=⨯-⨯⨯-⨯⨯=△△四边形矩形. 由题意，得12OP ·DC ＝3，DC ＝1， 6OP ∴=，∴点P 的坐标为(0，6)或(0，6-). ........................10分25.解：（1）由4212++-=x x y ，令0=y 得 04212=++-x x 即0)4)(2(=-+x x解得4,221=-=x x ，所以)0,4()0,2(B A ，- ........................1分令0=x 得4=y ，所以)4,0(C ........................2分 设直线BC 的解析式为b kx y +=，代入B 、C 坐标得⎩⎨⎧==+404b b k ，解得⎩⎨⎧=-=41b k ， 所以直线BC 的解析式为4+-=x y .........................3分 （2）方法一：如题25图①，过点P 作x 轴的垂线，交直线BC 于点H ，设点）（421,2++-x x x P ，则)4,(+-x x H ， 4)2(4)]4(421[2221222+--=+-=+--++-==-⋅=∆x xx x x x PHx x PH S C B PBC ）（ 当2=x 时，PBC S ∆取最大值为4，此时），（42P . ........................6分 方法二：设过P 点且与直线BC 平行的直线的解析式为m x y +-=，联立⎪⎩⎪⎨⎧+-=++-=mx y x x y 4212，消去y ，得042212=-++-m x x ， ∵ ∵当0)4(24=-+=∆m ，即6=m 时，PBC S ∆取最大值，此时），（42P ，PBC S ∆的最大值为4. ........................6分题25图① 题25图②（3）由（2）得），（42P ，又因为)0,4()40(B C ，，所以在PBC ∆中，︒=∠45PCB ，2=PC ，24=CB ，52=PB .............7分 由于点E 在线段AB 上，点F 在线段OC 上，要满足以A 、E 、F 为顶点的三角形与PBC∆相似，只有以下三种情况：i) 如题25图②，当︒=∠=∠45PCB EAF 时，EAF ∆∽PCB ∆，此时CBPCAF EA =，所以），（01-E ，），（20F ； ........................8分 ii) 如题25图③，当︒=∠=∠45PCB FEA 时，FEA ∆∽PCB ∆，此时CB PC EA FE =，所以），（032E ，），（320F ； ........................9分题25图③ 题25图④iii) 如题25图④，当︒=∠=∠45PCB EFA 时，EFA ∆∽PCB ∆， 此时CB PC FA EF =，所以），（031-E ，），（320F . ........................10分。

2020-2021学年广东省清远市清城中学高三数学理模拟试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 若，则双曲线的离心率的取值范围是（）A．B． C. D．(1,2)参考答案：C2. 已知关于x的方程的两根分别为，则的取值范围是A． B． C．D．参考答案：B3. 设,若,则的最大值为（）（A）（B）2 （C）（D）3参考答案：B 4. 我国南北朝数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法，其理论依据是：设实数的不足近似值和过剩近似值分别为和（，，，），则是的更为精确的不足近似值或过剩近似值．我们知道…，若令，则第一次用“调日法”后得是的更为精确的过剩近似值，即，若每次都取最简分数，那么第四次用“调日法”后可得的近似分数为（）A． B． C． D．参考答案：A试题分析：由题意：第一次用“调日法”后得是的更为精确的过剩近似值，即，第二次用“调日法”后得是的更为精确的过剩近似值，即,第三次用“调日法”后得是的更为精确的过剩近似值，即,第四次用“调日法”后得是的更为精确的过剩近似值，即,故选A.考点：合情推理.【易错点晴】本题主要考查了合情推理这个知识点,属于中档题. 本题易错的地方:没有读懂题意,题目中“第一次用“调日法”后得是的更为精确的过剩近似值”的等于，那第二次第三次第四次都是用这个公式计算的.在2016年高考考纲中增加了“数学文化”.考查了学生的读题和计算能力,属于基础题.5. 若定义在上的函数满足对任意，都有，则下列说法一定正确的是（）A．是奇函数 B．是偶函数C．是奇函数 D．是偶函数参考答案：B∵，∴∴6. 复数（）A． B． C． D．参考答案：D试题分析：，故选D.考点：复数的运算7. 已知为偶函数，当时，，则不等式的解集为（）A．B．C．D．参考答案：B略8. 已知某几何体的三视图如图所示，则该几何体的体积为A. B. C. D.参考答案：B9. 集合，则=A. B. C. D.参考答案：10. 一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是直角边长为1的等腰直角三角形，则该几何体的表面积为()A．4+ 。

2021年高三上学期摸底考试（11月）数学含答案1．已知全集，集合，则▲ ．2．已知复数满足，其中为虚数单位，则的实部为▲ ．3．函数的最小正周期为▲ ．4．右图是一个算法的流程图，则输出的值为▲ ．5．某校有足球、篮球、排球三个兴趣小组，共有成员120人，其中足球、篮球、排球的成员分别有40人、60人、20人．现用分层抽样的方法从这三个兴趣小组中抽取24人来调查活动开展情况，则在足球兴趣小组中应抽取▲ 人．6．若随机地从1，2，3，4，5五个数中选出两个数，则这两个数恰好为一奇一偶的概率为▲ ．7．设实数，满足则的最大值为▲ ．8．设是等差数列的前项和，且，，则的值为▲ ．（第49．将斜边长为的等腰直角三角形绕其斜边所在直线旋转一周，则所形成的几何体体积是▲ ．10．如图，在平面直角坐标系中，已知，，分别为 椭圆的右、下、上顶点，是椭圆 的右焦点．若，则椭圆的离心率是 ▲ ． 11．若，且，则的值 为 ▲ ． 12．已知正数，满足，则的最小值为 ▲ ． 13．已知为圆的直径，为圆的弦上一动点，，14．已知函数，．若的最大值是，则实数的取值范围是 ▲ ．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答．．．．．．．．．．，解答时应写出文字说明、证明过程或计算步骤． 15．（本小题满分14分）在中，已知角，，所对的边分别为，，，且，． （1）求角的大小； （2）若，求的长．16．（本小题满分14分）如图，在正三棱柱中，已知，分别为，的中点，点在棱上，且．求证： （1）直线∥平面； （2）直线平面．17．（本小题满分14分） 如图，在平面直角坐标系中，已知圆及点，． （1）若直线平行于，与圆相交于，两点，，求直线的方程；（2）在圆上是否存在点，使得？若存在，求点的个数；若不存在，说明理由．18．（本小题满分16分）某城市有一直角梯形绿地，其中，km ，km ．现过边界上的点处铺设一条直的灌溉水管，将绿地分成面积相等的两部分．（1）如图①，若为的中点，在边界上，求灌溉水管的长度； （2）如图②，若在边界上，求灌溉水管的最短长度．（第18题图①） （第18题图②） A BC D E A 1 B 1C 1 F（第16题） （第10题）19．（本小题满分16分）在数列中，已知，，，设为的前项和． （1）求证：数列是等差数列； （2）求；（3）是否存在正整数，，，使成等差数列？若存在，求出，，的值；若不存在，说明理由．20．（本小题满分16分）设函数，为正实数．（1）当时，求曲线在点处的切线方程； （2）求证：；（3）若函数有且只有个零点，求的值．21．[选做题]本题包括A 、B 、C 、D 四小题，请选定其中两题．．．．．．．，并在相应的答题区域内作答．．．．．．．．．．．．．解答时应写出文字说明、证明过程或演算步骤． A ．[选修4-1：几何证明选讲]（本小题满分10分）如图，是圆的直径，弦，的延长线相交于点，过作的延长线的垂线，垂足为．求证：．B ．[选修4-2：矩阵与变换]（本小题满分10分）求椭圆在矩阵对应的变换作用下所得的曲线的方程．C ．[选修4-4：坐标系与参数方程]（本小题满分10分）已知曲线的极坐标方程为，以极点为坐标原点，极轴为轴的正半轴建立平面直角坐标系，求曲线的直角坐标方程．(第21－A 题)D．[选修4 5：不等式选讲]（本小题满分10分）设，，，求证：．【必做题】第22题、第23题，每题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤．22．（本小题满分10分）如图，在四棱锥中，平面，，，，为的中点．（1）求异面直线，所成角的余弦值；（2）点在线段上，且，若直线与平面所成角的正弦值为，求的值．Array23．（本小题满分10分）设，．（1）求，，的值；（2）证明：对任意正整数，是8的倍数．参考答案与评分标准一、填空题1．2．1 3．4．23 5．8 6．7．8．81 9．10．11．12．36 13．14．二、解答题15．（1）因为，，，所以…………………………………2分，………………………………4分又，所以．……………………………………………………6分（2）因为，且，又，所以，……………………………………………8分同理可得，．…………………………………………………10分由正弦定理，得．……………………………14分16．（1）连结，因为，分别为，的中点，所以且，所以四边形是平行四边形，…………………2分A1C1所以且，又且， 所以且，所以四边形是平行四边形，…………………4分 所以，又因为，，所以直线平面．…………………………………………………7分（2）在正三棱柱中，平面，又平面，所以，又是正三角形，且为的中点，所以，……………9分 又平面，， 所以平面，又平面，所以，……………………………………11分 又，平面，，所以直线平面．…………………………………………………14分17．（1）圆的标准方程为，所以圆心，半径为．因为，，，所以直线的斜率为，设直线的方程为， ……………………………………………2分 则圆心到直线的距离为．…………………………4分 因为， 而，所以， ……………………………6分 解得或，故直线的方程为或．…………………………………8分 （2）假设圆上存在点，设，则，222222(1)(0)(1)(2)12PA PB x y x y +=++-+-+-=， 即，即， ………………………………10分 因为，……………………………………12分 所以圆与圆相交，所以点的个数为．…………………………………………………………14分 18．（1）因为，，，所以，……………………………………2分取中点，则四边形的面积为，即，解得，…………………………………………6分 所以(km)．故灌溉水管的长度为km ．……………………8分 （2）设，，在中，，所以在中，， 所以， 所以的面积为，又，所以，即．……………………12分在中，由余弦定理，得， 当且仅当时，取“”．故灌溉水管的最短长度为km ．……………………………………16分19．（1）证明：因为，所以，…………………2分又因为，所以，所以是首项为1，公差为的等差数列． …………………………4分 （2）由（1）知，所以，………6分所以12311111()(1)()(3)()(32)()3333n n S n =⋅+-⋅+-⋅++-⋅…，（第18题图②）所以23+1111111()(1)()(52)()+(32)()33333n n n S n n =⋅+-⋅+⋅⋅⋅+-⋅-⋅ ，两式相减得2312111112[()()()](32)()333333n n n S n +=-++⋯+--⋅，所以．…………………………………………………………………10分 （3）假设存在正整数，，，使成等差数列， 则，即． 由于当时，，所以数列单调递减．又，所以且至少为2，所以， ………………12分 ．①当时，，又，所以，等式不成立．…………………………………………14分②当时，，所以，所以，所以(单调递减，解唯一确定)． 综上可知，，，的值为，，． ………………………………16分20．（1）当时，，则，……………2分所以，又，所以曲线在点处的切线方程为．…………4分（2）因为，设函数，则， …………………………………………………6分所以．………………………………………………8分 （3），，令，得，因为，所以在上单调增，在上单调减．所以．………………………………………………10分 设，因为函数只有1个零点，而， 所以是函数的唯一零点． 当时，，有且只有个零点，此时，解得．…………………………………………12分 下证，当时，的零点不唯一． 若，则，此时，即，则． 由（2）知，，又函数在以和为端点的闭区间上的图象不间断， 所以在和之间存在的零点，则共有2个零点，不符合题意； 若，则，此时，即，则．同理可得，在和之间存在的零点，则共有2个零点，不符合题意． 因此，所以的值为．…………………………………………………16分21．[选做题]本题包括A 、B 、C 、D 四小题，请选定其中两题．．．．．．．，并在相应的答题区域内作答．．．．．．．．．．．．．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．A ．证明：连结，因为为圆的直径，所以，又，，则四点共圆，所以，…………………………5分 又∽，即，所以．………… 10分B ．设椭圆上的点在矩阵对应的变换作用下得到点， 则，………………………………………………5分则 代入椭圆方程，得，所以所求曲线的方程为．……………………………………………10分 C ．由得，…………………………………5分又，，所以曲线的直角坐标方程为．…………………………………10分 D ．因为，所以，故………………………………………………………5分，故．………………………………………………………………10分 22．（1）因为平面，且平面，所以，， 又因为，所以两两互相垂直． 分别以为轴建立空间直角坐标系， 则由，可得 ，，，，， 又因为为的中点，所以． 所以，，…………2分 所以 ，（2）因为，所以，则， ，，设平面的法向量为， 则 即 令，解得，，所以是平面的一个法向量．……………………………7分 因为直线与平面所成角的正弦值为，所以||4|cos ,|5||||MN MN MN ⋅〈〉===m m m ，解得，所以的值为．……………………………………………………………10分23．（1）代入求出，，．……………………………3分（2）①当时，是8的倍数，命题成立．…………………………4分 ②假设当时命题成立，即是8的倍数，那么当时，11(1)3723(372)4(71)k k k k k f k +++=+-=+-++， 因为是偶数，所以是的倍数， 又由归纳假设知是8的倍数， 所以是8的倍数，所以当时，命题也成立．根据①②知命题对任意成立．…………………………………………10分H 25939 6553 敓32637 7F7D 罽35763 8BB3 讳27641 6BF9 毹31298 7A42 穂633445 82A5 芥y36656 8F30 輰k[L。

2021年广东省清远市第三中学高三数学理模拟试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 若x，y是正数，则的最小值是（）A．3 B． C．4 D．参考答案：答案：C2. 定义在R上的函数则f(3)的值为()A.－1B.－2 C．1 D．2参考答案：B3. 已知是函数f(x)=的两个零点则（）A. B.1< C.e< D.2e<参考答案：A4. 将2本不同的数学书和1本语文书在书架上随机排成一行，则2本数学书相邻的概率为A．B．C．D．参考答案：C5. 已知集合A＝{x｜＝1}，B＝{0}，则A∪B的子集的个数为（）A．3 B．4 C．7D．8参考答案：D6. 已知圆的方程圆心坐标为(5,0)，则它的半径为（）A．3 B．C．5 D．4参考答案：D7. 函数的图像大致是（）参考答案：A试题分析：，所以函数为偶函数，所以排除C、D，令时，，所以排除B，所以答案为A.考点：函数图象.8. 的外接圆的圆心为，半径为，且，则向量在方向上的投影为A. B. C. D.参考答案：A9. 已知两点为坐标原点，点在第二象限，且，设等于A． B．２ C．1 D．参考答案：C因为所以，,，因为，所以，所以。

平方解得，选C.10. 若关于的不等式有实数解，则实数的取值范围为（）A． B． C． D．参考答案：B二、填空题:本大题共7小题,每小题4分,共28分11. 在Rt△ABC中，∠A=90°，AB=AC=2，点D为AC中点，点E满足，则= ．参考答案：﹣2【考点】平面向量数量积的运算．【分析】由已知画出图形，结合向量的加法与减法法则把用表示，展开后代值得答案．【解答】解：如图，∵，∴=，又D为AC中点，∴，则===．故答案为：﹣2．【点评】本题考查平面向量的数量积运算，考查向量的加法与减法法则，是中档题．12. 已知函数,则曲线在点处的切线倾斜角是_________。

2020-2021学年广东清远高三上数学月考试卷一、选择题1. 若集合A ={x |−2<x ≤2} ,B ={x |−1≤x <3}，则A ∪B =( ) A.(−2,2] B.(−2,3) C.[−2,3） D.(−1,2]2. 已知复数z =5i2−i +5i ，则|z|=( ) A.3√2 B.√5 C.2√5 D.5√23. 已知a =e −13，b =ln 13，c =log 1e13，则a ，b ，c 的大小关系( )A.a <c <bB.a <b <cC.b <a <cD.c <b <a4. 《周髀算经》中一个问题，从冬至之日起，小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气的日影子长依次成等差数列，若冬至、立春、春分的日影子长的和是37.5尺，芒种的日影子长为4.5尺，则冬至的日影子长为( ) A.12.5尺 B.15.5尺 C.10.5尺 D.9.5尺5. 2020年初，我国突发新冠肺炎疫情，面对“突发灾难”，举国上下齐心，在以习近平同志为核心的党中央的领导下，全党全军全国各族人民众志成城，共克时艰，疫情防控取得了阶段性成效，彰显了中国特色社会主义制度的优越性．在此疫情期间，为分担“逆行者”的后顾之忧，某教育机构团队开展“爱心辅学”活动，为抗疫前线工作者子女在线免费辅导功课．现教育机构安排了3位经验丰富的老师对小王、小李、小刘、小陈4名学生进行功课辅导，假设每位老师至少辅导一位学生，且每名学生至多一名老师辅导，则不同的分配方案共有( ) A.36种 B.12种 C.72种 D.24种6. 已知曲线f (x )=ln x +ax 在点(1,f(1))处的切线与直线y =x +1垂直，则a 的值为( )A.1B.−2C.2D.07. 点P 是双曲线C 1：x 2a 2−y 2b 2=1(a >0,b >0)与圆C 2:x 2+y 2=a 2+b 2的一个交点，且2∠PF 1F 2=∠PF 2F 1，其中F 1、F 2分别为C 1的左右焦点，则C 1的离心率为( ) A.√3+1 B.√3+12C.√5−1D.√5+128. 设f(x)是定义在R 上的偶函数，∀x ∈R ，都有f(2−x)=f(2+x)，且当x ∈[0, 2]时，f(x)=2x −2，若函数g(x)=f(x)−log a (x +1)(a >0，a ≠1)在区间(−1, 9]内恰有三个不同零点，则实数a 的取值范围是( )A.(19,1)∪(1, √3) B.(0, 19)∪(√7, +∞) C.(19, 15)∪(√3, √7) D.(17, 13)∪(√5, 3) 二、多选题5G 时代已经到来，5G 的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展，进而对GDP 增长产生直接贡献，并通过产业间的关联效应，间接带动国民经济各行业的发展，创造出更多的经济增加值.如图，某单位结合近年数据，对今后几年的5G 经济产出做出预测．由图提供的的信息可知( )A.信息服务商与运营商的经济产出的差距有逐步拉大的趋势B.设备制造商在各年的总经济产出中一直处于领先地位C.运营商的经济产出逐年增加D.设备制造商的经济产出前期增长较快，后期放缓将函数f (x )=3sin (2x −π3)的图像向左平移π3个单位长度后得到y =g (x )的图像，则下列说法正确的是( ) A.函数g (x )的图像的对称轴为直线x =kπ+π6(k ∈Z ) B.函数g (x )为奇函数C.函数g (x )的单调递增区间为[−5π12+kπ,π12+kπ](k ∈Z ) D.函数g (x )的最小正周期为π已知抛物线C:y 2=2px (p >0)的焦点为F ，直线的斜率为√3且经过点F ，直线l 与抛物线C 交于点A ，B 两点(点A 在第一象限)，与抛物线的准线交于点D ，若|AF|=8，则以下结论正确的是( ) A.|BF|=4B.|BD|=2|BF|C.p =4D.DF →=FA →已知函数f (x )是定义在R 上的奇函数，当x <0时，f (x )=e x (x +1)，则下列说法正确的是( )A.f (x )>0的解集为(−1,0)∪(1,+∞)B.当x >0时，f (x )=e x (1−x )C.∀x 1,x 2∈R ，都有|f (x 1)−f (x 2)|<2D.函数 f (x ) 有2个零点三、填空题已知向量a →=(2,1)，b →=(3,4)，c →=(k,2)，若(3a →−b →) // c →，则实数k =________.已知 f (x )={4x +1, x ≥1,12f (x +1), x <1，则f(log 43)=________.在(1−1x )(1+x )5的展开式中，x 2项的系数为________(用数字作答)．已知三棱锥A −BCD 中，二面角A −BC −D 的大小为120∘，AB =AC =BC =CD =BD =2，且A ，B ，C ，D 四点都在球O 的表面上，则球O 的表面积为________. 四、解答题在①m →=(a +b,c −a )，n →=(a −b,c )，且m →⊥n →，②2a −c =2b cos C ，③sin (B +π6)=cos B +12这三个条件中任选一个补充在下面的问题中，并给出解答．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且________. (1)求角B ；(2)若b =4，求△ABC 周长的最大值．已知正项等比数列{a n }的前n 项和为S n ，a 1=2，2S 2=a 2+a 3． (1)求数列{a n }的通项公式； (2)设b n =2n−1a n，求数列{b n }的前n 项和T n ．目前，新冠病毒引发的肺炎疫情在全球肆虐，为了解新冠肺炎传播途径，采取有效防控措施，某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息，数据经过汇总整理得到如图所示的频率分布直方图（用频率作为概率）．潜伏期不高于平均数的患者，称为“短潜伏者”，潜伏期高于平均数的患者，称为“长潜伏者”．(1)求这500名患者潜伏期的平均数（同组中的数据用该组区间的中点值作代表），并计算出这500名患者中“长潜伏者”的人数；(2)为研究潜伏期与患者年龄的关系，以潜伏期是否高于平均数为标准进行分层抽样，从上述500名患者中抽取300人，得到如表表格， (i)请将表格补充完整：(ii)研究发现，某药物对新冠病毒有一定的抑制作用，现需在样本中60岁以下的140名患者中按分层抽样方法抽取7人做Ⅰ期临床试验，再从选取的7人中随机抽取三人做Ⅰ期临床试验，设三人中所含“短潜伏者”的人数为随机变量X ，求X 的分布列和数学期望．如图，△ABC ，△ACD ，△ABE 均为正三角形，AB =2，AB 中点为O ，将△ABE 沿AB 翻折，使得点E 折到点P 的位置．(1)证明：CD ⊥平面POC ；(2)当PC =√6时，求二面角B −PC −D 的余弦值．已知椭圆C:x2a2+y2b2=1的左、右焦点分别为F1，F2，且|F1F2|=4√3，A(√3, −√132)是椭圆上一点．(1)求椭圆方程；(2)若G为椭圆C上异于顶点的任意一点，M，N分别为椭圆的右顶点和上顶点，直线GM与y轴交于点P，直线GN与x轴交于点Q，求证：|PN|⋅|QM|为定值．已知函数f(x)=x2−2x+a ln x(a∈R)(1)当a=−4时，求函数f(x)的单调区间；(2)当a>0时，若函数f(x)有两个极值点x1,x2(x1<x2)，不等式f(x1)≥mx2恒成立，求实数m的取值范围．参考答案与试题解析2020-2021学年广东清远高三上数学月考试卷一、选择题1.【答案】此题暂无答案【考点】并集较其运脱【解析】此题暂无解析【解答】此题暂无解答2.【答案】此题暂无答案【考点】复根的务复于技数触序的混合运算【解析】此题暂无解析【解答】此题暂无解答3.【答案】此题暂无答案【考点】指数表、对烧式守综合员较【解析】此题暂无解析【解答】此题暂无解答4.【答案】此题暂无答案【考点】等差数来的通锰公式【解析】此题暂无解析【解答】此题暂无解答5.【答案】此题暂无答案【考点】分步乘正且数原理【解析】此题暂无解析【解答】此题暂无解答6.【答案】此题暂无答案【考点】利用导于研究轨函数成点有近的问题利用三数定究曲纵上迹点切线方程【解析】此题暂无解析【解答】此题暂无解答7.【答案】此题暂无答案【考点】双曲根气离心率双曲三定定义【解析】此题暂无解析【解答】此题暂无解答8.【答案】此题暂无答案【考点】函数根助点与驶还根的关系函数于析式偏速站及常用方法函表的透象【解析】此题暂无解析【解答】此题暂无解答二、多选题【答案】此题暂无答案【考点】频率都着直方图【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】正弦函因的周激性函数y射Asi过（ω复非φ）的图象变换正弦函射的单调长正弦函明的政偶性【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】抛物使之性质抛物三刺应用抛物常的铝义【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】利用验我研究务能的单调性函数零都问判定定理函数奇明性研性质【解析】此题暂无解析【解答】此题暂无解答三、填空题【答案】此题暂无答案【考点】平面水因共线（平行）的坐似表阻平面向明的推标运算【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】分段水正的应用函使的以值【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】二项正开形的来定恰与特定系数二项式射理的应题【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】球内较多面绕二面角的使面角及爱法球的表体积决体积【解析】此题暂无解析【解答】此题暂无解答四、解答题【答案】此题暂无答案【考点】两角和与表擦正弦公式两角和与验流余弦公式基本常等式簧最母问赤中的应用余于视理正因归理数量积常断换个平只存量的垂直关系【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】数使的种和等比数使的前n种和等比数表的弹项公式【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】概较害应用众数、中正数、平均测频率都着直方图离散来随机兴苯的期钱与方差离散验他空变量截其分布列【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】用空根冬条求才面间的夹角直线与平正垂直的判然【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】圆锥来线中雨配点缺定值问题直线常椭圆至合业侧值问题椭圆较标准划程【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】利用都数资究不长式化成立问题利来恰切研费函数的极值利用验我研究务能的单调性【解析】此题暂无解析【解答】此题暂无解答。

广东省清远市2021届高三数学上学期期末教学质量检测试题 文（含解析）一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的，1.已知集合{}|6M x x =<，{}1,2,3,4,5,6,,7,8,9N =，则RM N ⋂=( )A. {}6,7,8,9B. {}7,8,9C. {}1,2,3,4,5D. {}1,2,3,4,5,6【答案】A 【解析】 【分析】 先求得RM ，然后再求其与集合N 的交集.【详解】依题意{}R|6M x x =≥，所以R M N ⋂={}6,7,8,9.故选：A【点睛】本小题主要考查集合补集、交集的概念和运算，属于基础题. 2.设复数z =i 11i--，则|z |=( )A. 0D. 1【答案】C 【解析】 【分析】利用复数的除法运算化简z ，再求z .【详解】依题意()()111111222i i z i i i i i ++=-=-=-+-+，所以2z ==.故选：C【点睛】本小题主要考查复数的除法运算，考查复数模的计算，属于基础题.3.清远市教育教学研究院想了解清远市某所中学的学生是否赞成该学校的某个新政策，由于条件限制，教学研究院不能询问每位学生的意见，所以需要选择一个合适的样本.最好的方法是询问( )A. 由该学校推选的学生B. 在课间遇见的学生C. 在图书馆学习的学生D. 从学校名单中随机选取的学生 【答案】D 【解析】 【分析】根据抽样的原则，确定正确选项.【详解】按照随机的原则，即保证总体中每一个对象都有已知的、非零的概率被选入作为研究的对象，保证样本的代表性。

随机抽样法就是调查对象总体中每个部分都有同等被抽中的可能，是一种完全依照机会均等的原则进行的抽样调查，被称为是一种“等概率”。

ABC 三个抽样方法，不能保证等可能，D 选项可以保证等可能，所以最好的方法是D. 故选：D【点睛】本小题主要考查随机抽样的等可能性，属于基础题.4.已知双曲线2222:1(0,0)x y C a b a b-=>>的一条渐近线方程为0y +=，则双曲线C 的离心率为（ ）A. 3 C. D. 9【答案】A 【解析】 【分析】由渐近线方程可知,a b 之间关系，将其转化为,a c 关系，即可得离心率.【详解】因为渐近线方程为0y +=故22222883b cb ac a a a a=⇒=⇒-=⇒=. 故选：A.【点睛】本题考查双曲线的,,a b c 之间的关系，本题涉及由渐近线斜率求解离心率的转换.5.已知0.60.60.5log 0.5,0.5,log 6a b c ===，则,,a b c 的大小关系为（ ）A. a b c <<B. c b a <<C. a c b <<D.b c a <<【答案】B 【解析】 【分析】将每个数据与0或者1进行比较，从而区分大小关系.【详解】函数0.6log y x =单调递减，故0,60.6log 0.5log 0.61a =>=. 又0.60.500.51,log 60b c <=<=<，所以c b a <<. 故选：B.【点睛】本题考查指数和对数比较大小，其方法是选择1或者0为基准进行比较.6.函数f （x ）322x x cosxx=+在[﹣π，π]上的图象大致为( ) A.B.C.D.【答案】A 【解析】 【分析】根据函数的奇偶性和特殊点排除错误选项，由此得出正确选项.【详解】由于()()32cos 2xx xf x f x x-=-=-+， 所以()f x 为奇函数，图象关于原点对称，由此排除BC 选项.由于()3322cos 022f ππππππππ⨯==-<++，故D 选项错误.正确的为A.故选：A【点睛】本小题主要考查函数图象的的识别，属于基础题. 7.sin195°sin465°=( )A.4B.14C.4D. 14-【答案】D 【解析】 【分析】利用诱导公式、二倍角公式化简求得表达式的值. 【详解】原式()()sin 18015sin 360105=+⋅+()sin15sin105sin15sin 9015=-⋅=-⋅+1111sin15cos15sin 302224=-⋅=-=-⨯=-.故选：D【点睛】本小题主要考查利用诱导公式、二倍角公式进行化简求值，属于基础题.8.已知F 为抛物线2:4C x y =的焦点，直线1y =+与抛物线C 交于点,A B ，则||AB =（ ）A. B. 16C. 12D. 【答案】C 【解析】 【分析】联立直线方程与抛物线方程，利用焦点弦计算公式代入求解即可.【详解】由题意得(0,1)F ，所以1y =+过焦点F .设()()1122,,,A x y B x y ， 则12||2AB y y =++.联立24,21, x yy x⎧=⎪⎨=+⎪⎩得24240x x--=，所以1242x x+=.又112221,21y x y x=+=+，所以()1212||22412AB y y x x=++=++=.故选：C.【点睛】本题考查抛物线中的弦长求解，本题涉及抛物线焦点弦的求解，属抛物线基础题.9.已知函数()sin()0,0,0||2f x A x Aπωϕωϕ⎛⎫=+>><<⎪⎝⎭的部分图象如图所示，下述四个结论：①2ω=；②3πϕ=-；③12f xπ⎛⎫+⎪⎝⎭是奇函数；④12f xπ⎛⎫-⎪⎝⎭是偶函数中，所有正确结论的编号是（）A. ①②B. ①③④C. ②④D. ①②④【答案】D【解析】【分析】根据图像的最值，周期，以及五点作图法，求得函数解析式，再对选项进行逐一分析即可. 【详解】由图可知，1A=，又函数周期2Tππω==，求得2ω=根据五点作图法：206πϕ⨯+=，解得3πϕ=-故()sin23f x xπ⎛⎫=-⎪⎝⎭，所以①②正确；sin2sin2sin212123636f x x x xππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=+-=+-=-⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，此时函数不是奇函数，所以③错误；sin 2sin 2sin 2cos212123632f x x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=--=--=-=- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，故12f x π⎛⎫- ⎪⎝⎭为偶函数，所以④正确.综上所述，正确的有①②④. 故选：D.【点睛】本题考查由函数图像求三角函数解析式，以及三角函数的奇偶性；注意本题中求初相的方法.10.已知f （x ）是定义域为R 的奇函数，且f （x ）=﹣f （x +2），当x ∈（0，2）时，f （x ）=2x ﹣x 2，则f （﹣1），f （2π），f （π）的大小关系是( ) A. f （2π）<f （﹣1）<f （π） B. f （2π）<f （π）<f （﹣1） C. f （﹣1）<f （π）<f （2π）D. f （﹣1）<f （2π）<f （π）【答案】C 【解析】 【分析】根据已知条件判断出函数()f x 的周期性、奇偶性，由此化简()()1,,2f f f ππ⎛⎫- ⎪⎝⎭，并比较出三者的大小关系.【详解】由于()f x 是R 上的奇函数，且()()2=-+f x f x ，所以()()()()4222f x f x f x f x +=++=-+=，所以()f x 是周期为4的周期函数.当()0,2x ∈时，()2222f x x x x x =-=-+.()()()111210f f -=-=--+=-<.()224402244f πππππππ--⎛⎫⎛⎫=-+==> ⎪ ⎪⎝⎭⎝⎭.()()()()()244424f f f πππππ⎡⎤=-=--=---+-⎣⎦()()268240.98041ππππ=-+=--≈->-.所以()()12f f f ππ⎛⎫-<< ⎪⎝⎭. 故选：C【点睛】本小题主要考查函数的奇偶性、周期性，考查运算求解能力，属于中档题. 11.我国古代在珠算发明之前多是用算筹为工具来记数、列式和计算的.算筹实际上是一根根相同长度的小木棍，如图，算筹表示数1～9的方法有两种，即“纵式”和“横式”，规定个位数用纵式，十位数用横式，百位数用纵式，千位数用横式，万位数用纵式……依此类推，交替使用纵横两式.例如：27可以表示为“”.如果用算筹表示一个不含“0”的两位数，现有7根小木棍，能表示多少个不同的两位数( )A. 54B. 57C. 65D. 69【答案】B 【解析】 【分析】按十位数为1,2,3,4,5,6,7,8,9进行分类讨论，求得所有符合题意的两位数的数量. 【详解】当十位为1时，个位可以是1,2,3,4,5,6,7,8,9，共9种； 当十位为2时，个位可以是1,2,3,4,5,6,7,8,9，共9种； 当十位为3时，个位可以是1,2,3,4,6,7,8，共7种； 当十位为4时，个位可以是1,2,3,6,7，共5种； 当十位为5时，个位可以是1,2,6，共3种；当十位为6时，个位可以是1,2,3,4,5,6,7,8,9，共9种； 当十位为7时，个位可以是1,2,3,4,6,7,8，共7种； 当十位为8时，个位可以是1,2,3,6,7，共5种；当十位为9时，个位可以是1,2,6，共3种； 所以总的有()99753257++++⨯=种. 故选：B【点睛】本小题主要考查中国古代数学文化，考查列举法与分类加法计数原理，属于基础题. 12.如图，在三棱锥P ﹣ABC 中，PA ⊥平面ABC ，AB ⊥BC .若PA =AB =BC =2，E ，F 分别是PB ，PC 的中点，则三棱锥P ﹣AEF 的外接球的表面积为( )A. 3πB. 5πC. 6π3【答案】B 【解析】 【分析】证得,,EP EA EF 两两垂直，由此将三棱锥P AEF -补形成长方体，利用长方体的对角线求得三棱锥P AEF -外接球的半径，进而求得外接球的表面积.【详解】由于PA ⊥平面ABC ，所以PA BC ⊥，由于,AB BC AB PA A ⊥⋂=，所以BC ⊥平面PAB ，所以,BC PB BC AE ⊥⊥，由于,E F 分别是,PB PC 的中点，所以//EF BC ，所以,EF PB EF AE ⊥⊥.而AB PA =，所以AE PB ⊥，所以,,EP EA EF 两两垂直.故可将三棱锥P AEF -补形成长方体，且111,222EF BC AE PE PB =====，所以长方体的对角线长为()()2221225++=，设三棱锥P AEF -外接球的半径为R ，则25R =245R ππ=.故选：B【点睛】本小题主要考查几何体外接球表面积有关计算，考查空间想象，考查化归与转化的数学思想方法，属于中档题.二、填空题：本题共4小题，每小题5分，共20分. 13.已知向量a =（m ，3），b =（m 43-，m ﹣1）.若a //b .则m =_____. 【答案】2 【解析】 【分析】根据两个向量共线的坐标表示列方程，解方程求得m 的值. 【详解】由于a //b ，所以()4133m m m ⎛⎫⨯-=⨯-⎪⎝⎭，即2440m m -+=，()220,2m m -==.故答案为：2【点睛】本小题主要考查向量共线的坐标表示，属于基础题.14.已知实数x ，y 满足141x y x y y -≥-⎧⎪+≤⎨⎪≥-⎩，则z =x +2y 的最大值是_____.【答案】132【解析】 【分析】画出可行域，向上平移基准直线20x y +=到可行域边界位置，由此求得2z x y =+的最大值. 【详解】画出可行域如下图所示，向上平移基准直线20x y +=到可行域边界位置点35,22A ⎛⎫⎪⎝⎭，由此求得2z x y =+的最大值为35132222+⨯=.故答案为：132【点睛】本小题主要考查利用线性规划求线性目标函数的最值，考查数形结合的数学思想方法，属于基础题.15.已知S n 为数列{a n }的前n 项和，若a 1=1，a n ⋅a n +1=2n ，则S 15=_____. 【答案】509 【解析】 【分析】根据递推关系式求得23451415,,,,,,a a a a a a ，然后求得15S .【详解】由于111,15n n a a a +=⋅=，12nn na a +=，所以23413142277234514152672222222,2,2,2,,2,2122222a a a a a a ============，所以()()72715212122221212S ⨯-=+⨯+++=+⨯-509=.故答案为：509【点睛】本小题主要考查根据递推关系式求数列的项，考查数列求和的方法，考查合情推理，属于基础题.16.在△ABC中，角A，B，C的对边分别为a，b，c.已知a b2+c2=a2bc，BD=2DC，且∠BAD=90°，则△ABC的面积为_____.【答案】95【解析】【分析】利用余弦定理求得cos A，进而求得A的大小.利用正弦定理求得b=，结合余弦定理求得,b c的值，再由三角形的面积公式求得三角形ABC的面积.【详解】∵b2+c2=a2bc，∴可得cosA2222b c abc+-===∴由A∈（0，π），可得A34π=，∵a＝，BD=2DC，∴CD=BD=，∵边BC上一点D满足BD=2DC，且∠BAD=90°，∴∠CAD4π=，在△ADC中，4DC bsin ADCsinπ=∠2bsin ADC=∠，可得b=2sin∠ADC，…①在△ADB中，sin∠ADB=②由①②可得b2=c.在△ABC中，BC2=AB2+AC2﹣2AB⋅AC⋅cos∠BAC，可得18=c2+b22bc=c21 2 +c222c c+⨯⨯，解得c65=，b310=，∴△ABC的面积为S12=bc sin316531029425525π=⨯⨯⨯=.故答案为：95【点睛】本小题主要考查正弦定理、余弦定理解三角形，考查三角形的面积公式，属于中档题.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23为选考题，考生根据要求作答.（一）必考题：共60分.17.已知S n为等差数列{a n}的前n项和，a1>0，a8﹣a4﹣a3=1，a4是a1和a13的等比中项. （1）求数列{a n}的通项公式；（2）证明：对一切正整数n.有1211134nS S S+++<.【答案】（1）a n=2n+1；（2）证明见解析.【解析】【分析】（1）利用等比中项的性质，结合等差数列通项公式的基本量计算，求得1,a d，由此求得数列{}na的通项公式.（2）先求得n S，然后利用裂项求和法证得不等式成立.【详解】（1）解：设等差数列{a n}的公差为d，由题意，()12111121(3)12d aa d a a da-=⎧⎪+=+⎨⎪>⎩，解得132ad=⎧⎨=⎩，∴数列{a n }的通项公式为a n =3+2（n ﹣1）=2n +1；（2）证明：由（1）知，()()12322n n n S n n n -⨯=+=+. ∴()()()1211111111132435112n S S S n n n n +++=+++++⨯⨯⨯-++ 12=[111111111132435112n n n n -+-+-++-+--++]3111342124n n ⎛⎫=-+< ⎪+⎝⎭. 【点睛】本小题主要考查等差数列通项公式的基本量计算，考查等比中项的性质，考查裂项求和法，考查数列不等式的证明，属于中档题.18.广东省的生产总值已经连续30年位居全国第一位，如表是广东省从2012年至2021年7年的生产总值以人民币（单位：万亿元）计算的数据：（1）从表中数据可认为x 和y 的线性相关性较强，求出以x 为解释变量、y 为预报变量的线性回归方程（系数精确到0.01）；（2）广东省2021年人口约为1.13亿，德国2021年人口约为0.83亿.从人口数量比较看，广东省比德国人口多，但德国2021年的生产总值为4.00万亿美元，以（1）的结论为依据，预测广东省在哪年的生产总值能超过德国在2021年的生产总值？参考数据：71 i =∑y i =52.81，71i =∑ x i y i =230.05，71i =∑ y i 2=411.2153，71i =∑ x i 2=140. 货币兑换：1美元≈7.03元人民币参考公式：回归方程y b =x a +中斜率b 和截距a 的最小二乘估计公式分别为：()()1122211 ()? n n i i iii i n n iii i x x y y x y nx y b x x x nx ====---⋅==--∑∑∑∑，a y b x =-.【答案】（1） 2.83 3.78y x=-；（2）2023年.【解析】【分析】（1）利用回归直线方程计算公式，计算出回归直线方程. （2）求得4万亿美元对应的人民币，然后根据回归直线方程列不等式，由此求得所求的年份. 【详解】（1）123456747x++++++==，7117iy==∑y i=52.81=7.544，12221230.05547.5442.8314074ni iiniix y nx ybx nx==-⋅-⨯⨯==≈-⨯-∑∑，a y b x=-=7.544﹣2.83×4≈﹣3.78.∴线性回归方程为 2.83 3.78y x=-；（2）由题意，德国2021年的生产总值为4.00万亿美元≈4.00×7.03=28.12万亿元.由2.83x﹣3.78>28.12，解得x≈11.27.∴预测广东省在2023年的生产总值能超过德国在2021年的生产总值.【点睛】本小题主要考查回归直线方程的计算，考查利用回归直线方程进行预测，考查运算求解能力，属于中档题.19.如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=45°，PD⊥平面ABCD，AP⊥BD.（1）证明：BC⊥平面PDB，（2）若AB2=PB与平面APD所成角为45°，求点B到平面APC的距离.【答案】（1）证明见解析；（26.【解析】【分析】（1）通过证明BD ⊥平面APD 证得BD AD ⊥，即有BC BD ⊥，结合BC PD ⊥，证得BC ⊥平面PBD .（2）利用等体积法，由P ABC B PAC V V --=列方程，解方程求得点B 到平面APC 的距离.【详解】（1）证明：∵PD ⊥平面ABCD ，BC 在平面ABCD 内，BD 在平面ABCD 内，∴PD ⊥BC ，PD ⊥BD ，又AP ⊥BD ，AP ∩PD =P ，且AP ，PD 均在平面APD 内，∴BD ⊥平面APD ，又AD 在平面APD 内，∴BD ⊥AD ，又底面ABCD 为平行四边形，∴BC ⊥BD ，又PD ∩BD =D ，且都在平面PBD 内，∴BC ⊥平面PDB ；（2）由（1）知，PB 与平面APD 所成角即为∠BPD ，故∠BPD =45°，又AB =DAB =45°，∴1AD BD PD AP PC =======，AC == ∴AP 2+PC 2=AC 2，即AP ⊥CP ，∴122APC S ==，11122ABC S =⨯=， 又V P ﹣ABC =V B ﹣PAC ，∴1133ABC PAC S PD S h ⋅=⋅，即1122⨯=，解得6h =，即点B 到平面APC 【点睛】本小题主要考查线面垂直的证明，考查点到面的距离的求法，考查空间想象能力和逻辑推理能力，属于中档题.20.已知椭圆22221(0)x y a b a b +=>>，点(2,0)N 椭圆的右顶点.（1）求椭圆的方程；（2）过点(0,2)H 的直线l 与椭圆交于,A B 两点，直线NA 与直线NB 的斜率和为13-，求直线l 的方程.【答案】（1）22142x y +=；（2）22y x =+【解析】【分析】（1）根据椭圆离心率以及顶点坐标即可得,,a b c 方程，求解即可；（2）设出直线，联立椭圆方程，根据韦达定理，利用已知条件求解即可.【详解】（1）因为点(2,0)N 是椭圆的右项点，所以2a =.又c a =，所以c =又222b c a +=，所以22b = 所以椭圆的方程为22142x y +=.（2）若直线l 与x轴垂直，则(0,A B，则413NA NB N NB k k k k ==+≠-，所以直线l 的斜率存在.设直线l 的方程为()()11222,,,,y kx A x y B x y =+， 联立222142y kx x y =+⎧⎪⎨+=⎪⎩，消去y ，得()2221840k x kx +++= 则有12122284,2121kx x x x k k -+==++()2221(8)421402k k k =-⨯+⨯>⇒>△直线NA 的斜率为112y x -，直线NB 的斜率为）222y x -，所以()()()()122112121222122223y x y x y y x x x x -+-+==-----. 又11222,2y kx y kx =+=+()()()()()()122112121222222222kx x kx x y y x x x x +-++-+=----()()121212122(22)81243kx x k x x x x x x +-+-==--++， 化简得()1212(61)(46)200k x x k x x ++-+-=. 又12122284,2121k x x x x k k -+==++， 所以2248(61)(46)2002121k k k k k -+⨯+-⨯-=++， 化简得220--=k k ，解得12k =或21k =-，又21k =-时，过点N ，故舍去，所以直线l 的方程为22y x =+.【点睛】本题考查椭圆方程的求解，以及直线与椭圆相交，利用韦达定理及其他条件求直线方程；本题中需要注意分类讨论直线的斜率是否存在.21.设函数()ln a f x x x=+. （1）讨论函数()f x 的单调性； （2）若1a ，证明1()x f x e >恒成立. 【答案】（1）当0a ≤时，()f x 在区间(0,)+∞上单调递增；当0a >时，()f x 在区间(0,)a 上单调递减，在区间(,)a +∞上单调递增；（2）证明见详解.【解析】【分析】（1）求导，对参数进行分类讨论，进而求得函数的单调区间；（2）将恒成立问题，转化两个函数最值之间的问题，进而求解.【详解】（1）由题意得0x >，221()a x a f x x x x'-=-+=. ①当0a ≤时，()0f x '，故函数()f x 在区间(0,)+∞上单调递增；优质资料\word 可编辑②当0a >时，在区间(0,)a 上，()0f x '<，在区间(,)a +∞上，()0f x >，故函数()f x 在区间(0,)a 上单调递减，在区间(,)a +∞上单调递增.（2）证明： 要证1()x f x e >，只需证1ln xa x x e +>. 又0x >，故只需证ln x x a x x e +>即可. 设()ln g x a x x =+，则()1ln g x x '=+， 在区间10,e ⎛⎫ ⎪⎝⎭上，()0g x '<，在区间1,e ⎛⎫+∞ ⎪⎝⎭上，()0g x '>， 故函数()g x 在区间10,e ⎛⎫ ⎪⎝⎭上单调递减，在区间1,e ⎛⎫+∞ ⎪⎝⎭上单调递增， 所以11()g x g a e e ⎛⎫=- ⎪⎝⎭. 设()x x h x e =，则1()xx h x e '-=， 在区间(0,1)上，()0h x '>，在区间(1,)+∞上，()0h x '<，故函数()h x 在区间(0,1)上单调递增，在区间(1,)+∞上单调递减， 所以1()(1)h x h e =. 又1a ≥，所以111a e e --. 又因为2e >，所以21e>， 所以111e e ->， 故在(0,)+∞上，()()g x h x >，综上，1()x f x e>恒成立. 【点睛】本题考查利用导数研究含参函数的单调性，以及证明不等式恒成立的问题，属导数经典题型.（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.选修4-4：坐标系与参数方程22.在直角坐标系xOy 中，曲线1C 的参数方程为2212,22x t t y t t ⎧=++⎪⎪⎨⎪=+⎪⎩（t 为参数），曲线2C 的参数方程为2,x y αα⎧=+⎪⎨=⎪⎩，（α为参数）以O 为极点，x 轴的正半轴为极轴建立极坐标系. （1）求曲线2C 的极坐标方程；（2）直线l 的极坐极方程为4πθ=，直线l 与曲线1C 和2C 分别交于不同于原点的,A B 两点，求||AB 的值.【答案】（1）24cos 20ρρθ-+=；（2）【解析】【分析】（1）将参数方程化简为普通方程，再利用公式转化为极坐标方程即可；（2）根据题意，利用,A B 在极坐标中对应的θ相同，将方程转化为极坐标进而求解. 【详解】（1）由2,,x y αα⎧=+⎪⎨=⎪⎩得2,,x y αα=-=两式平方相加，得22(2)2x y -+=，又222,cos ,sin x y x y ρρθρθ=+==，所以曲线2C 的极坐标方程为24cos 20ρρθ-+=. （2）由2212,22,x t t y t t ⎧=++⎪⎪⎨⎪=+⎪⎩得222221142,2,4y t x t x t t ⎛⎫=++=++ ⎪⎝⎭ 消去t ，得24,4y x x =，曲线1C 的极坐标方程为22(sin )4cos sin 4cos ,42ρθρθρθθρ=⇒=.设12,,,44A B ππρρ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，所以124cos4sin 4πρπ==(2222220ρρ-+==解得2ρ=12||||AB ρρ=-==故AB =【点睛】本题考查将参数方程转换为极坐标方程，以及在极坐标方程中求解两点之间的距离. 选修4-5：不等式选讲23.已知0a b >>，函数24()()f x x a x b a b =-++-. （1）若1,2b a ==，求函数()f x 的最小值；（2）证明：()8f x .【答案】（1）8；（2）证明见详解.【解析】【分析】（1）根据绝对值三角不等式，即可求得；（2）利用绝对值三角不等式，巧妙构造，进行证明.【详解】（1）当1,2b a ==时， ()44f x x x =-++()()448x x ≥--+=当且仅当[]4,4x ∈-时取得故()f x 的最小值为8.（2）证明： ()222444()()()()f x x a x x a x a b a b b a b b a b ⎡⎤=-++--+=+⎢⎥---⎣⎦，优质资料\word 可编辑- 21 - / 21- 21 - 故24()()f x a b a b +-. 又()2(a b a b b a b =+--故2416()b a b a -，22222416168()a a a b a b a a ++⨯=-， 当且仅当2,1a b ==时等号成立，故()8f x .【点睛】本题考查绝对值三角不等式的应用，构造利用的条件，是解决问题的关键.。

广东省清远市高桥中学2021年高三数学文模拟试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 在△ABC中，点D满足，则（）A．B．C．D．参考答案：D2. 设函数，的定义域都为R，且是奇函数，是偶函数，则下列结论正确的是.是偶函数.||是奇函数.||是奇函数.||是奇函数参考答案：C设，则，∵是奇函数，是偶函数，∴，为奇函数，选C.3. 设，是非零向量，且．则“”是“”的（）．A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件参考答案：C充分性：当时，，∴，必要性：当时，，∵，∴．故选．4. 某人向东方向走了x千米，然后向右转，再朝新方向走了3千米，结果他离出发点恰好千米，那么x 的值是．参考答案：4根据题意画出相应的图形，如图所示：在△ABC中，AB=x千米，BC=3千米，AC= 千米，∠ABC=180°-120°=60°，由余弦定理得：，即（x-4）（x+1）=0，解得：x=4或x=-1（舍去），因此x的值为4千米．5. 椭圆的离心率是A．B．C．D．参考答案：B试题分析：e=，选B．【名师点睛】解决椭圆和双曲线的离心率的求值及范围问题，其关键就是确立一个关于a，b，c的方程或不等式，再根据a，b，c的关系消掉b得到a，c的关系式，建立关于a，b，c的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等．6.函数的反函数为（）A. B.C. D.参考答案：答案:C7. 在数列{}中，若且对所有, 满足，则 ( )A． B． C． D．参考答案：B 解．，，，故选B．此题也可求，，，．8. 在平面直角坐标系中，点，对于某个正实数，存在函数，使得(为常数)，这里点的坐标分别为，则的取值范围为A. B. C.D.参考答案：【知识点】平面向量综合问题 F2 F4【答案解析】A 解析：由已知得，点，故选：A【思路点拨】根据已知条件求出向量的坐标，代入中，利用向量相等的条件得到两个方程，化简即可解得的取值范围9. 设集合则“”是“”的（）A.充要条件B.必要不充分条件C.充分不必要条件D.既不充分也不必要条件参考答案：C试题分析：，，∵,选C.考点：1、分式不等式和绝对值不等式的解法；2、充分条件和必要条件.10. 若对任意x∈[1，2]，不等式4x+a?2﹣x+1﹣a2＜0（a∈R）恒成立，则a的取值范围是( )A．a＞或a＜﹣2 B．a＞或a＜﹣4 C．a＞或a＜﹣2 D．a＞或a＜﹣4参考答案：B考点：函数恒成立问题．专题：函数的性质及应用．分析：分别取a=3，x=2或者a=﹣3，x=2排除即可．解答：解：当a=3时，4x+3?2﹣x+1﹣9＜0，若x=2，则42+3?2﹣2+1﹣9＞0，故A，D不符合，当a=﹣3时，4x﹣3?2﹣x+1﹣9＜0，若x=2，则42﹣3?2﹣2+1﹣9＞0，故C不符合，故选：B．点评：考查学生理解掌握不等式恒成立的条件，直接算很难，采取举反例，属于中档题．二、填空题:本大题共7小题,每小题4分,共28分11. 等差数列各项为正,且,则公差.参考答案：略12. 如果向量与共线且方向相反，则参考答案：-213. 设函数的定义域为D，若函数满足下列两个条件，则称在定义域D 上是闭函数．①在D上是单调函数；②存在区间，使在上值域为．如果函数为闭函数，则的取值范围是_______参考答案：14. 设等比数列的公比，前项和为，则．参考答案：1515. 已知，则的最大值为 .参考答案：16. 定义在上的函数满足，当时，，则函数的图像与函数的图像的所有交点的横坐标之和等于▲参考答案：817. 如图，正方形边长是2，直线x+y﹣3=0与正方形交于两点，向正方形内投飞镖，则飞镖落在阴影部分内的概率是．参考答案：【考点】几何概型．【分析】根据几何概率的求法，可以得出镖落在阴影部分的概率就是阴影区域的面积与总面积的比值．【解答】解：观察这个图可知：阴影部分是正方形去掉一个小三角形，设直线与正方形的两个交点为A，B，∴在直线AB的方程为x+y﹣3=0中，令x=2得A（2，1），令y=2得B（1，2）．∴三角形ABC的面积为s==，则飞镖落在阴影部分的概率是：P=1﹣=1﹣=1﹣=．故答案为：．三、解答题：本大题共5小题，共72分。