裂区实验设计的spss分析

使用SPSS软件进行数据分析文档通过自己论证属实。

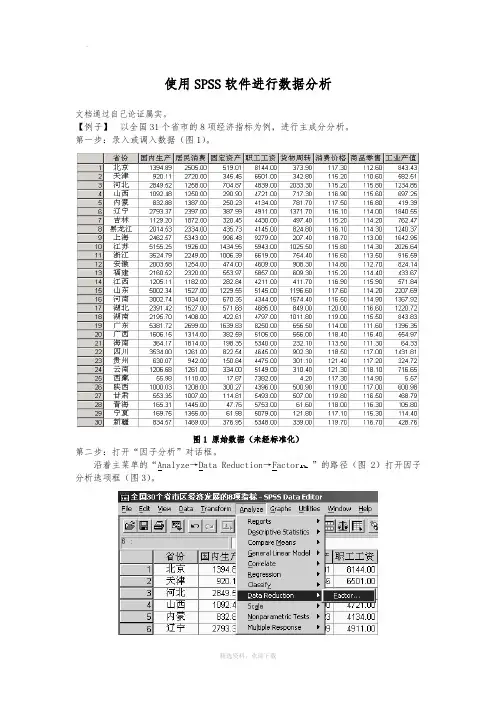
【例子】以全国31个省市的8项经济指标为例，进行主成分分析。

第一步：录入或调入数据（图1）。

图1 原始数据（未经标准化）第二步：打开“因子分析”对话框。

沿着主菜单的“Analyze→Data Reduction→Factor ”的路径（图2）打开因子分析选项框（图3）。

图2 打开因子分析对话框的路径图3 因子分析选项框第三步：选项设置。

首先，在源变量框中选中需要进行分析的变量，点击右边的箭头符号，将需要的变量调入变量（Variables）栏中（图3）。

在本例中，全部8个变量都要用上，故全部调入（图4）。

因无特殊需要，故不必理会“Value ”栏。

下面逐项设置。

图4 将变量移到变量栏以后⒈设置Descriptives选项。

单击Descriptives按钮（图4），弹出Descriptives对话框（图5）。

图5 描述选项框在Statistics 栏中选中Univariate descriptives 复选项，则输出结果中将会给出原始数据的抽样均值、方差和样本数目（这一栏结果可供检验参考）；选中Initial solution 复选项，则会给出主成分载荷的公因子方差（这一栏数据分析时有用）。

在Correlation Matrix 栏中，选中Coefficients 复选项，则会给出原始变量的相关系数矩阵（分析时可参考）；选中Determinant 复选项，则会给出相关系数矩阵的行列式，如果希望在Excel 中对某些计算过程进行了解，可选此项，否则用途不大。

其它复选项一般不用，但在特殊情况下可以用到（本例不选）。

设置完成以后，单击Continue 按钮完成设置（图5）。

⒉ 设置Extraction 选项。

打开Extraction 对话框（图6）。

因子提取方法主要有7种，在Method 栏中可以看到，系统默认的提取方法是主成分（∏ρινχιπαλ χομπονεντσ），因此对此栏不作变动，就是认可了主成分分析方法。

3因素随机裂区试验设计及其统计分析提出一种新的3因素随机裂区试验设计，给出了自由度与平方和分解方案，以及固定模型、随机模型及2种混合模型的均方构成，同时提出了随机模型误差方差计算方法。

作物科学研究领域，常用3因素试验设计，一般3因素试验有完全随机区组试验、品种多年多点试验和再裂区试验，至今很少有其他的3因素试验设计报道，通用统计软件SPSS＼SAS＼STATA等也未提供相应分析方法[1-3]。

完全随机区组试验对于栽培研究很不适用，不同的栽培因素如密度、水分管理、施肥方式等，不适合小区操作，但试验面积又不能过大。

再裂区设计，3个因素误差精度不同，主区试验面积最大、误差较大，裂区试验面积较大、误差中等，再裂区试验面积小、误差小、精度高。

如2个栽培因素均要求较大小区，或重要程度均较高，则可以将这2个因素作完全随机组合排列，较适宜操作且有相同试验误差，将2个因素组合作为主区，另一因素对小区面积要求不高，或重要性高，则将其在主区内裂区排列，则该试验设计称为3因素随机裂区设计。

笔者提出了一种新的3因素随机裂区试验设计，给出了自由度与平方和分解方案，以及固定模型、随机模型及2种混合模型的均方构成，同时提出了随机模型误差方差计算方法，以期为生物统计提供新思路。

1 试验设计方法设A、B、C 3个试验因素，分别有a、b、c 3个水平，每水平重复r次。

A、B共ab个组合，将区组划分为a×b个主区，C为副区因素，在每个AB组合主区内裂区排列。

该设计遵循重复、随机排列及局部控制原则。

先按田间肥力梯度划分为r个区组，每个区组划分为a×b个主区，分别随机安排A、B因素的a×b 个组合，每个AB组合构成一个主区，对每个主区再随机排入C因素的c个水平，保证每个主区内均再随机裂区。

播种期、栽插期或水分管理及N、K肥运筹间的主区间以田埂区隔，密度主区间可以走道间隔，品种、种苗处理、药剂处理、移动性弱的P肥运筹适宜作副区因素，副区间以走道间隔。

使用SPSS进行实验设计与数据分析的步骤在科学研究中，实验设计和数据分析是非常重要的环节。

SPSS（Statistical Package for the Social Sciences）是一种常用的统计分析软件，它提供了丰富的功能和工具，可以帮助研究人员进行实验设计和数据分析。

本文将介绍使用SPSS进行实验设计和数据分析的步骤。

1. 实验设计实验设计是研究中的第一步，它决定了实验的目的、变量和样本选择。

在SPSS中，可以使用实验设计向导来帮助完成实验设计的过程。

首先，打开SPSS软件并选择“Analyze”菜单，然后选择“General Linear Model”选项。

接下来，选择“Univariate”选项，然后点击“Define”按钮。

在弹出的对话框中，输入因变量和自变量，并选择合适的因子水平。

完成后，点击“OK”按钮，SPSS会生成实验设计的语法代码。

2. 数据收集实验设计完成后，需要进行数据收集。

在SPSS中，可以使用数据编辑器来输入和编辑数据。

打开SPSS软件并选择“Data”菜单，然后选择“Data Editor”选项。

在数据编辑器中，可以创建变量并输入相应的数据。

在输入数据时，需要确保数据的准确性和完整性。

完成数据输入后，可以保存数据文件。

3. 数据清洗数据清洗是数据分析的重要步骤，它包括数据筛选、缺失值处理和异常值处理等。

在SPSS中，可以使用数据筛选功能来选择特定的数据子集。

选择“Data”菜单，然后选择“Select Cases”选项。

在弹出的对话框中，可以定义筛选条件并应用到数据中。

对于缺失值处理，SPSS提供了多种方法，如删除缺失值、替换缺失值和插补缺失值等。

可以选择“Transform”菜单，然后选择“Missing Value Analysis”选项，根据需要选择相应的缺失值处理方法。

异常值处理是为了排除数据中的异常值对分析结果的影响。

在SPSS中，可以使用异常值检测功能来识别和处理异常值。

裂区实验方差分析裂区设计（split–plot design）与两因素随机区组设计近似，但是两者不一样的。

不同点之一是后者在每一区组内A、B两因素的ab次处理是完全随机化的。

而裂区设计的每一区组内A因素先分为a个处理，在每一处理内B因素再分为b个处理。

随机化过程只能在A因素的a个处理和B 因素的b个处理之间进行。

由A因素所划分的A个部分称为主区或整区，每一主区再划分的b个部分称为裂区或副区。

不同点之二是方差分析计算时F值时误差项的选择，裂区设计方差分析时有两个误差项，区组和整区是同一个误差，而裂区和交互作用则用另一个误差项，而二因素随机区组设计方差分析时用一个误差项。

进行裂区试验设计时首先要分清主要因子和次要因子，主要因子是想要获得较高精确度的因子，次要因子是精确度可以低些的因子。

裂区设计的原则是：主要因子的各个水平随机安排在裂区，次要因子的各个水平随机安排在整区，只有这样，主要因子的各水平的重复数才会大大的多于次要因子的各个水平的重复数，才能获得较高的精确度。

１．在同一个区组的各个整区中，随机安排次要因子的各个水平，称为整区处理。

２．在每个整区的各个裂区上随机安排主要因子的各个水平，称为裂区处理。

适用范围： １．复因子试验中，两个因子要求的精确度不一时，可用裂区设计。

２．各个因子的各个水平需要的面积大小不一时，亦可用裂区设计。

３．在原有的试验的基础上，临时加入一个研究因子时，可用裂区设计。

优点： １．田间实施比较方便。

２．能利用原有的试验地及试验材料，进行深一步的研究。

３．某个因予可获得较高的精确度。

缺点： １．资料的统计分析比较复杂，不易掌握。

２．次要因子的精确度较低。

下面以两个因素的裂区设计进行方差分析：设有A、B两个试验因素，A因素有a个水平，安排在整区，B因素有b个水平，安排在裂区，整个试验有n个重复区组。

总变异分解为整区部分和裂区部分，整区部分总平方和（SS1）可分解为区组平方和（SSr）、A因素水平间平方和（SS A）和整区误差平方和（SS eA）；裂区部分分解为B因素水平间平方和（SS B）、交互作用AxB 平方和（SS AB）和裂区误差平方和（SS eB）。

实验八、裂区试验设计结果资料的方差分析
一、实验目的：
练习使用电子表格软件（Excel）对裂区设计的试验结果资料进行方差分析。

二、方法和步骤：
（一）、裂区试验设计特点：
(注：上表中A1、A2、A3表示因素A的三个水平，B1、B2、B3、B4表示因素B的四个水平37、15……表示小区的产量。

)
（二）、自由度和平方和的分解：
（三）操作步骤：
例：有一果树试验，主处理为A，分为A1、A2、A3共3个水平，副处理为B，分为B1、B2、B3、B4共4个水平，裂区设计，重复3次（r=3）,其田间排列和产量如下表所示，试对结果作方差分析。

具体操作步骤：
1、对原始数据表进行整理，得到两张新表
表－1 A处理和B处理两向表
表－2 区组和A处理两向表
2、“工具”→“数据分析”→“方差分析：可重复双因素分析”→选取
表－1→设置“输入”和“输出”选项
3、“工具”→“数据分析”→“方差分析：可重复双因素分析”→选取表－2→设置“输入”和“输出”选项
4、整理上面两次的结果得到最终方差分析结果
5、算出主处理的F值（F A）和副处理的F值（F B）进行F测验。

附：
1、设置输入单元格数据的有效性
2、自定义Excel的用户界面（工具栏、工具按钮、菜单）
3、工作簿和工作表的保护。

利用SPSS进行方差分析以及正交试验设计方差分析是一种常见的统计方法，用于比较两个或多个组之间的差异。

正交试验设计是一种实验设计方法，能够同时考虑多个因素对结果的影响。

本文将利用SPSS进行方差分析和正交试验设计的步骤介绍，并讨论如何解读分析结果。

首先，我们将介绍方差分析的步骤。

方差分析的基本思想是比较组间和组内的变异程度。

假设我们有一个因变量和一个自变量，自变量有两个或多个水平。

下面是方差分析的步骤：1.导入数据：将数据导入SPSS软件，并确保每个变量都已正确标记。

2.选择统计分析：点击SPSS菜单栏上的"分析"，然后选择"方差"，再选择"单因素"。

3.设置因变量和自变量：在弹出的对话框中，将需要进行方差分析的因变量拖放到因素列表框中，然后将自变量也拖放到因素列表框中。

4.点击"设定"按钮：点击"设定"按钮，设置方差分析的参数，例如是否需要进行正态性检验、多重比较等。

然后点击"确定"。

5.查看结果：SPSS将输出方差分析的结果，包括各组之间的F值、p值等统计指标。

可以根据p值判断各组之间是否存在显著差异。

接下来，我们将介绍正交试验设计的步骤。

正交试验设计是一种多因素独立变量的实验设计方法，可以在较小的实验次数内获得较高的信息量。

下面是正交试验设计的步骤：1.设计矩阵：根据研究目的和独立变量的水平，构建正交试验的设计矩阵。

2.导入数据：将设计矩阵导入SPSS软件，并将每个变量的水平标注为自变量。

3.选择统计分析：点击SPSS菜单栏上的"分析"，然后选择"一般线性模型"，再选择"多元方差分析"。

4.设置因变量和自变量：在弹出的对话框中，将因变量拖放到因子列表框中，然后将自变量也拖放到因子列表框中。

5.点击"设定"按钮：点击"设定"按钮，设置正交试验设计的参数，例如交互作用是否显著、多重比较等。

裂区试验设计与结果的统计分析裂区试验（split-plot design）是一种常用的设计方法，适用于在同一个实验中比较多个处理的效果，同时考虑到不同处理之间的相关性。

这种设计方法是多个因素的正交组合，通过将实验单位进行分区，以达到同时考虑多个因素的目的。

裂区试验包括两种类型的因素：主区因素（whole plot factor）和副区因素（sub plot factor）。

主区因素是指主要的实验处理，它在试验开始时就确定下来，并且针对每个实验区域进行随机分配。

副区因素是在主区因素设置完成后再确定的次要因素，它在主区因素内的每个实验区域中进行随机分配。

这种设计方法的优势在于可以同时考虑多个因素的影响，并通过分析不同因素之间的交互作用来提高实验效果。

裂区试验的设计步骤如下：1.确定主区因素和副区因素：根据实验目的确定需要考虑的因素，并确定它们的类型（定性或定量）和水平（多个水平或二元水平）。

2.确定实验单位：确定实验单位的大小和数量，这是根据研究对象和实验条件来确定的，在实验区域内进行分区。

3.随机分配主区因素：将主区因素随机分配给每个实验区域，确保每个实验区域都包含不同的主区因素水平组合。

4.随机分配副区因素：在每个实验区域内，将副区因素随机分配给各个实验单位。

5.数据收集：对实验单位进行观测与测量，记录主区因素和副区因素的水平以及观测结果。

6.数据分析：进行统计分析，根据实验设计的要求，使用适当的统计方法（方差分析、回归分析等）来分析主区因素和副区因素的效应，检验主效应和交互作用的显著性。

7.结果解释：根据统计分析的结果，对各个因素的效应进行解释和比较，得出结论。

裂区试验结果的统计分析主要包括方差分析和回归分析两种方法。

方差分析是一种用于比较多个处理效果的统计方法，通过计算各个因素的方差来判断它们的影响程度。

在裂区试验中，可以使用方差分析方法来分析主区因素和副区因素的效应，以及它们之间的交互作用。

SPSS软件在正交试验设计、结果分析中的应用SPSS软件在正交试验设计与结果分析中的应用一、引言正交试验设计是一种经典的统计方法，用于研究多个因素对于实验结果的影响。

该方法将实验因素进行有序的组合，既能减少试验次数，又能避免因素之间的相互影响。

而SPSS软件作为统计分析领域中的瑞士军刀，拥有强大的数据处理和分析功能，为研究者提供了便利的工具。

本文将探讨SPSS软件在正交试验设计与结果分析中的应用。

二、正交试验设计的基本原理正交试验设计遵循一定的规则和原则。

首先，需要明确要研究的因素，这些因素可以是实验操作，也可以是实验条件。

其次，确定各个因素的水平，水平的选择要充分考虑实验的目的和研究对象。

然后，在确定因素和水平的基础上，构建正交试验设计表，以便按照设计表中的规则进行试验。

最后，根据试验结果，进行数据分析和结果解释。

三、SPSS软件在正交试验设计中的应用1. 设计试验方案SPSS软件提供了一系列的数据输入工具和试验设计模块，可以帮助研究者轻松地构建正交试验设计。

通过SPSS软件，可以灵活地选择因素和水平，并生成正交试验设计表。

同时，SPSS软件还提供了随机分组和重复设计等功能，以满足实验设计的要求。

2. 数据输入与整理SPSS软件支持多种数据输入方式，可以通过导入Excel表格、文本文件等格式的数据，或者直接在软件中手动输入数据。

在正交试验设计中，往往涉及大量的数据输入，SPSS软件的数据输入功能可以帮助研究者快速、准确地输入数据。

同时，SPSS软件还提供了数据整理和清理功能，可以对异常值、缺失值等进行处理，使得数据更加可靠。

3. 数据分析与解释SPSS软件的数据分析功能非常强大，可以进行多元方差分析、协方差分析、回归分析、相关分析等多种统计分析方法。

在正交试验设计中，可以使用SPSS软件进行多因素方差分析，以确定各个因素对实验结果的影响。

同时，SPSS软件还提供了图表制作功能，可以直观地展示分析结果。