下载文档原格式
共轭双曲线的性质
性质
（1）共轭双曲线有共同的渐近线；
共轭双曲线
（2）共轭双曲线的四个焦点共圆，即c相等；
（3）共轭双曲线离心率平方的倒数和等于1.
例过双曲线的一个顶点的切线交共轭双曲线于两点，求证：过交点所作共轭双曲线的两切线必通过原双曲线的另一顶点点A′．
方程：x2/a2-y2/b2=1与y2/b2-x2/a2=1互为共轭双曲线。
2特殊的双曲线
有两种特殊的双曲线，它们有一些特殊的性质。
一类是等轴双曲线。
其主要性质有：a=b，离心率为
，两条渐近线互相垂直，等轴双曲线上任意一点到中心的距离是它到两个焦点的距离的比例中项。
另一类是共轭双曲线，其主要性质有：它们有共同的渐近线，它们的四个焦点共圆，它们的离心率的倒数的平方和等于1。
等轴双曲线是一个方程所对应的几何图形。
有两支曲线：而互为共轭双曲线则是两个方程所对应的几何图形，每个方程各对应两支曲线。
等轴双曲线也有它的共轭双曲线。
常用三角恒等变换技巧解答三角函数问题，几乎都要通过恒等变换将复杂问题简单化，将隐性问题明朗化。
三角恒等变换的公式很多，主要有“同角三角函数的基本关系”、“诱导公式”、“和、差、倍、半角公式”、“辅助角公式（化一公式）”等，这些公式间一般都存在三种差异，如角的差异、函数名的差异和运算种类的差异，只有灵活有序地整合使用这些公式，消除差异、化异为同，才能得心应手地解决问题，这是三角问题的特点。
下面从九个方面解读三角恒等变换的常用技巧。
一、“角变换”技巧角变换的基本思想是，观察发现问题中出现的角之间的数量关系，把“未知角”分解成“已知角”的“和、差、倍、半角”，然后运用相应的公式求解。
例1 已知534cos =⎪⎭⎫ ⎝⎛+πx ，4743ππ<<x ，求x x x tan 1sin 22sin 2-+的值。
【分析】考虑到“已知角”是4π+x ，而“未知角”是x 和x 2，注意到44ππ-⎪⎭⎫ ⎝⎛+=x x ，可直接运用相关公式求出x sin 和x cos 。
【简解】因为ππ4743<<x ，所以πππ24<+<x ， 又因为0534cos >=⎪⎭⎫ ⎝⎛+πx ，所以πππ2423<+<x ，544sin -=⎪⎭⎫ ⎝⎛+πx 10274sin 4cos 4cos 4sin 44sin sin -=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛+=ππππππx x x x ， 从而102cos -=x ，7tan =x . 原式=7528tan 1sin 2cos sin 22-=-+x x x x . 【反思】（1）若先计算出102cos -=x ，则在计算x sin 时，要注意符号的选取；（2）本题的另一种自然的思路是，从已知出发，用和角公式展开，结合“平方关系”通过解二元二次方程组求出x sin 和x cos . 但很繁琐，易出现计算错误；（3）本题也可由2422ππ-⎪⎭⎫ ⎝⎛+=x x ，运用诱导公式和倍角公式求出x 2sin 。
等弦对等角定理《等弦对等角定理》是几何学中的重要定理，很多年以来，这一定理在数学中发挥着重要作用。
在其中，等弦对等角定理指明了在同一个平面内，任何一条直线上的两角所成的比值都是相同的。
下文将对等弦对等角定理进行详细的论述，以及所具有的重要意义。
等弦对等角定理的概念可以追溯到古希腊的几何学家亚里士多德所提出的“无穷近似准则”。
这项定理主要指出，在一个平面上的任何一条直线上的两个角之间的比例是相同的。
这个定理被证实为有效，因为对于一条直线上的任意两个角，它们所成的比例是相同，这也就意味着它们之间的内角也是相同的。
这被证实为等弦对等角定理。
等弦对等角定理的重要意义主要在于它不仅有助于解决几何问题，而且也有助于解决许多其他的相关问题。
其中最重要的是，等弦对等角定理有助于我们解决运动物体在固定水平面内的抛物线运动问题。
由于等弦对等角定理给出了一个精准的数学公式，因此可以帮助我们更好地分析抛物线运动的物理原理，从而使我们更好地理解航空，交通，以及其他有关具有抛物线运动的现象。
此外，等弦对等角定理还可以应用到另一个类似的几何计算上，比如几何形状的平面分析。
等弦对等角定理的重要意义不仅仅体现在几何学上，它也可以应用到更广泛的领域，比如建筑，摄影，平面设计等。
比如，等弦对等角定理可以帮助我们更好地控制建筑物的外观，通过控制建筑物的结构和大小，更好地构建出适合的外观来满足每个任务的要求。
此外，等弦对等角定理还可以帮助摄影师更好地创作出更美的作品，比如更炫酷的图片，更完美的平面设计等。
综上所述，在以上几何领域中，等弦对等角定理都发挥着重要作用，它不仅帮助我们解决几何学上的问题，还可以应用到实际的生活中，以及摄影，建筑，平面设计等相关领域中。
它是实用的，也是重要的，有助于我们更好地理解许多有关自然现象的问题。
高中数学的归纳三角函数的性质与像分析技巧三角函数是数学中一类重要的函数，广泛应用于各种学科领域，特别是在物理学和工程学中。
在高中数学中，归纳三角函数的性质以及像分析技巧是一个基础而又关键的内容。
本文将从归纳三角函数的性质和像分析技巧两个方面进行论述。
一、归纳三角函数的性质1. 周期性：三角函数中，正弦函数和余弦函数的周期都是2π。
在单位圆上，将弧长2π分成等分，每个等分对应一个周期。
例如，sin(x)在[0，2π]区间上的图像与在[2π，4π]、[4π，6π]等区间上的图像是完全相同的。
2. 奇偶性：正弦函数是奇函数，即sin(-x)=-sin(x)；余弦函数是偶函数，即cos(-x)=cos(x)。
奇偶性的性质可通过单位圆上的几何解释进行理解。
3. 对称性：正弦函数和余弦函数在关于y轴对称的点上取相同的函数值。
例如，sin(π/6)=sin(π-π/6)，cos(π/6)=cos(π-π/6)。
4. 单调性：在特定的定义域内，正弦函数和余弦函数都具有单调性。
以正弦函数为例，当x1<x2时，sin(x1)<sin(x2)。
由于周期性的存在，单调性只在一个周期的范围内成立。
5. 运算性质：三角函数之间具有一系列的运算性质。
例如，sin(x)和cos(x)满足勾股定理：sin^2(x)+cos^2(x)=1；tan(x)可由sin(x)和cos(x)表示为tan(x)=sin(x)/cos(x)。
二、像分析技巧1. 变量替换：在解决三角函数相关问题时，常常采用变量替换的方法简化计算。
通过选择合适的替代变量，可以将问题转化为更简单的形式。
例如，将sin2(x)替换为1-cos2(x)，可以简化计算和推导的过程。
2. 和差化积：和差化积是将三角函数的和差形式转化为乘积形式的技巧。
通过和差化积，可以将一些复杂的三角函数表达式转化为较简单的形式，方便计算和分析。
3. 积化和差：积化和差是将三角函数的积形式转化为和差形式的技巧。
三角恒等式的特殊证明方法与应用解析与归纳三角恒等式在数学中起着重要的作用，它们让我们可以通过等式推导得出其他三角函数的值。
在本文中，我们将讨论一些特殊的证明方法，并探讨恒等式的应用，以及如何通过解析和归纳方法来理解和证明这些三角恒等式。
一、特殊证明方法1. 双倍角恒等式的证明双倍角恒等式是三角恒等式的重要组成部分，它们表示一个角的两倍角与其他三角函数之间的关系。
我们可以通过以下方法来证明双倍角恒等式：以sin 2θ为例，我们可以利用三角函数的定义sinθ =opposite/hypotenuse以及余弦函数的定义cosθ = adjacent/hypotenuse来推导sin 2θ。
根据正弦和余弦函数定义可得，sin2θ = (opposite/hypotenuse) × (opposite/hypotenuse)= (opposite/hypotenuse) × (adjacent/adjacent)= 2 × (opposite × adjacent)/(hypotenuse × adjacent)= 2 × (opposite × adjacent)/(hypotenuse × hypotenuse)= 2 × sinθ × cosθ这样，我们成功地推导出了sin 2θ的值与sinθ和cosθ之间的关系。
同样的原理也可以用于证明其他双倍角恒等式。
2. 和差角恒等式的证明和差角恒等式描述了两个角的和差与其他三角函数之间的关系。
举个例子，我们来证明sin(α + β) = sinα × cosβ + cosα × sinβ。
根据正弦函数的定义，我们有，sin(α + β) = opposit e/hypotenuse= (opposite/h) × (h/hypotenuse)= (opposite/h) × (adjacent/adjacent) + (opposite/opposite) ×(opposite/h)= sinα × cosβ + cosα × sinβ通过这种方式，我们可以证明和差角恒等式中的其他等式。
最新中考数学共边定理及其应用与推广共边定理及其应用与推广几何一直是初中数学的重难点，初中几何主要研究边角关系，并要求对边，角关系进行严格的证明、推理.学生普遍感觉几何好学但解题难，难在思维的深度，尤其难在辅助线的添加，许多几何题目往往受制于这神来一笔的辅助线.如何攻克这座堡垒呢?本文将介绍共边定理这一用途极广的几何解题工具，以供广大读者参考.一、共边定理共边定理建立在共边三角形的基础上，它是指，共边三角形的面积比等于第三个顶点的连线被公共边所截得的线段比.定理如图1，设直线AB 与CD 交于M ，则有ABC ABD S CM S DM ??= (共有四种情形).这个定理的证明基于一个基本的事实:共高三角形的面积比等于底的比.具体证明如下.证明 ABC ABC ACM ADM ABD ACM ADM ABD S S S S S S S S =g gAB CM AM CM AM DM AB DM ==g g .由于共边定理有四种位置情形却对应同一个比值，所以，如何选择两个合适的三角形，是运用共边定理解决间题的关键，而图形的选择差异使得解法往往不唯一共边定理虽然是对等高等底三角形面积相等这一基本性质的推广，但是它的用途却相当的广泛.它在线段和面积之间建立了天然的桥梁，由此可利用这两种几何量的反复转化，证明一大批几何问题，尤其是在没有特别条件下只涉及直线相交、平行、同一直线上的线段比以及面积比等问题中，运用共边定理会得到易想不到的效果.下面通过几个例题来说明共边定理的应用.二、共边定理的应用1.有关线段的问题例1 凸四边形ABCD 的两边,AD BC 延长后交于点K ；两边,AB CD 延长交于L ，对角线,BD AC 延长后分别与直线KL 交于,F G ，如图2.求证:KF KG LF LG =.该题的叙述比较复杂，但其实不看文字，只看图也是一目了然的，即为几条直线相交后证同一直线的线段比.此题是数学大师华罗庚在《1978年全国中学生数学竞赛题》前言中提到的有趣的几何题.题目的证明较难，难点在于图中没有相似三角形和全等的三角形，只有几条线段相交的条件.但此题倘若利用共边定理来解决会变得很简单，具体证法如下.证明 KBD KBD KBL LBD KBL LBDS S S KF LF S S S ==g =ACD ACK ACL ACD S S CD AK CL AD S S =g g =ACK ACL S KG S LG ??=注该题将共边定理面积比用于证明线段成比例，相反也可以利用线段成比例来证明面积比.2.有关面积的问题例2 在ABC ?的三边,,BC CA AB 上，分别取点,,X Y Z ，使13CX BC =，13AY AC =，13BZ AB =.连,,AX BY CZ 三条线，围成LMN ?，如图3.问LMN ?的面积是ABC ?面积的几分之几解由于LMN ?与ABC ?不是公边三角形，为计算LMN ?，将其转化为与ABC ?公边的三角形MBC ?，NCA ?，LMN ?来计算.先求MBC S ?.ABC ABM BCM ACM MBC MBC S S S S S S ++=712AY AZ CY BZ =++=. 又27NCAABC S S ??=，∴27MBC ABC S S ??=. 同理，27LAB ABC S S ??=，∴17LMN ABC S S ??=. 3.有关平行的问题现在我们反过来思考，共边定理的前提是直线AB 与CD 交于一点M ，但是如果AB 与CD 不相交呢，会有什么情况?首先会不会有AB 与CD 不相交的情况呢?当然会.当ABC ABD S S ??=，且CD 与AB 同侧的时候，它们会平行从而不相交，如图4:通过上述反向的思考得到了一个新的思路，即把共边三角形与平行直线联系到一起了.这个几何事实描述为:若点,C D 在AB 的同侧，//CD AB 的充要条件为ABC ABD S S ??=.有了这一定理就可以不用平行线的性质来证明两直线的平行，张景中教授把这种方法称为“平行线面积判定法”.下面我们通过一个例题来说明其应甩例3 已知线段AB 与一条平行于AB 的直线l ，取不在AB 上也不在l 上的一点P ，作,PA PB 分别与直线l 交于点,M N ，连结,AN BM 交于O ，连PO 交直线AB 于Q ，如图5.求证:AQ BQ =.证明：AOP AOP AOB POB AOB PPOBS S S AQ BQ S S S ==g PMN AMN BMN MNP S S PN AM NB PM S S ==g g 1AMN BMNS S ??==. 注在证明最后一步中运用了//AB l ，推导出了AMN BMN S S ??=.实际上此题还解决了在平面内给定两点,A B 和平行于AB 的一条直线，仅利用没有刻度的直尺如何作出AB 的中点的操作方法.类似的方法还可以证明出PQ 平分l .如此一来，便得到了梯形中常见的一个结论，即延长梯形两腰的交点与梯形对角线的连线平分梯形的上下底. 此外，在这个过程中还有一个结论1PN AM NB PM =g ，实际上得到了平行线分线段成比例定理. 共边定理不仅能推导出以上的定理，它还可以推导出相似形基本定理，平行四边形的性质，三角形重心的性质，“共角定理”等.还有一些用传统方法比较难证的定理如“赛瓦定理”，“帕普斯定理”，“德沙格定理”等等，在这里就不一一赘述了，有兴趣的读者可以尝试证明.三、共边定理的推广下面将共边定理进行空间上的推广，即得到共面定理.共面定理：设直线PQ 与平面ABC 交于一点S ，如图6，则有P ABC Q ABC V PS V QS --=.该定理可用于立体几何的计算与证明.此外，共边定理还可以用于解决应用题.例如在行程问题当中，时间不变就等价于三角形中一的高不变，一般涉及正比例的应用题都可以考虑用共边定理来解决，而不仅限于解决平面几何的问题.那么，相比传统方法，共边定理有哪些优点呢?(1)可接受性共边定理基于一个基本的事实，即共高三角形的面积比等于底的比.这个道理在小学就接触过，学生学起来简单，相比相似三角形和全等三角形，需要判定相似或全等的条件比较多，学生的可接受性较强一(2)通用性平面几何中的基本图形是三角形，从统计学的角度来看，一般几何图形中出现全等三角形或相似三角形的可能性太小了.为了能利用相似三角形和全等三角形性质来解题，就需要添加辅助线，但辅助线的添加往往无章可循，而共边三角形却比比皆是，因而它的性质具有通用性.(3)对等性利用相似三角形和全等三角形性质解决问题，需要三个判定条件证明全等或相似.相比之下，共边定理则是一个条件对应一个结论，正是这种对等性，往往能简化几何证明的过程.在这里需要说明的是，共边定理的应用并不排斥传统几何方法中那些有效的方法，相反，它能为传统方法提供更简捷的证明思路一个定理的用途越广，就越能凸显该定理的重要性从上述的例题可以看出，共边定理的作用不容小觑，掌握好这个定理，对初中几何学习是大有帮助的.。
第17章 投影多边形 等角共轭点定义1 从平面上一点P 向凸多边形各边作垂线，以各垂足为顶点的多边形称为投影多边形． 如三角形三条高线的垂足作为顶点的三角形，就是垂心的投影三角形（常称为垂心的垂足三角形）． 性质1 若点P 关于ABC △的投影三角形是△111A B C ． (1)当P 是ABC △的内心或旁心时，P 是△111A B C 的外心． (2)当P 是ABC △的外心时，P 是△111A B C 的垂心．(3)当P 是ABC △的垂心时，若ABC △是锐角三角形，P 是△111A B C 的内心；若ABC △是钝角三角形，P 是△111A B C 的旁心．证明 只证(3)中ABC △是钝角三角形的情形，如图17-1，BAC ∠是钝角，P 是ABC △的垂心，则P 在ABC △和△111A B C 的外部，在111B AC ∠的内部，易证A 1C 1B 1PACBDE 图17-1111111B A P PBC PCB C A P ===∠∠∠∠1111111B C P B AP A AC AC C DC P ====∠∠∠∠∠故P 是△111A B C 的旁心．性质2 一点P 的投影三角形的面积，与点P 关于外接圆的幂成比例．证明 如图17-2，点P 在△123A A A 的边23A A 、31A A 、12A A 上的投影分别为1P 、2P 、3P ，联结2A P 并延长△123A A A 的外接圆O 于点2B ．则3'A A 图17-223322332=360A PA A PP P PP P PA ︒---∠∠∠∠ 23312312(180)(180)P PP A PP P P A =︒-+︒--∠∠∠ 213312A A A P PP =+∠∠，又22323A B A B A P +∠∠ 23A PA =∠，从而21323P PP B A P =∠∠．于是，12312132131sin 2P P P S PP PP P PP =⋅⋅△∠ 1213231sin 2PP PP B A P =⋅⋅∠ 3322231sin sin sin 2PA A PA A B A P =⋅⋅⋅⋅∠ 22223231sin sin sin 2PA PB A B A A A =⋅⋅⋅⋅∠ 221231sin sin sin 2R OP A A A =-⋅⋅⋅（其中R 为O 半径） 1232224A A A R OP S R -=⋅△．（注意到2322233sin sin B A P PB A B A PA =∠∠）． 注：性质2常称为施坦纳(Steiner)定理．推论 1 投影三角形的面积为一定的点的轨迹，是一个与三角形外接圆同心的圆．在外接圆内的点，外心的投影三角形面积最大．推论2 三角形外接圆上的点的投影三角形面积为零．推论3 一点P 的投影点外接圆的半径122222()A P A P A Pr R OP ⋅⋅=-．事实上，由1232331124P P P P P P P PP S r⋅⋅=△及2311sin P P A P A =⋅等三式即得．推论4 △123A A A 的外心O 的投影三角形面积123014A A A S S =△．事实上，由2=0OP 即得．推论5 △123A A A 的内心I 的投影三角形面积1232I A A A rS S R=△．事实上，由2222OP OI R Rr ==-即得．推论6 △123A A A 的重心G 的投影三角形面积123222236G A A A a b c S S R ++=△．事实上，由2222221()9OP OG R a b c ==-++即得．推论7 △123A A A 的垂心H 的投影三角形面积1232cos cos cos H A A A S A B C S =⋅⋅⋅△． 事实上，由22228cos cos cos OP OH R R A B C ==-⋅⋅即得． 推论8 △123A A A 的九点圆圆心V 的投影三角形面积12322222516V A A A a b c R S S R ++-=⋅△．事实上，由12OV OH =且3OH OG =，得22222291()44OP OV R a b c ==-++即得．将性质2推广，则有如下结论：性质3 自ABC △所在平面内一点P 向三角形三边作同向等角θ的射线，分别交边BC ，CA ，AB 于点1A ，1B ，1C ．设ABC △外接圆O 的半径为R ，OP d =，则11122224sin A B C ABCR d S S R θ-=△△． ①证明 如图17-3，当点P 在ABC △内，111PA B PB C PC A θ===∠∠∠，延长CP 交圆O 于D ，联结AD ，AP ． 由题意知点A ，1C ，P ，1B 共圆，由正弦定理得B 1A 1C 1M NCBAD图17-311sin sin PA AB C θ=． 同理11sin sin PC CA B θ=． 又11BAD BCP A B P ==∠∠∠，111PB C PAC =∠∠，则 1111111A B C A B P PB C =+∠∠∠ 1BAD PAC PAD =+=∠∠∠．在PAD △中，sin sin PA PAD PD D =∠，而D B =∠∠，即sin sin PA PAD PD B =⋅∠．从而 11111111111sin 2A B C S A B B C A B C =⋅△∠ 2sin sin sin 2sin PA PCA C PAD θ⋅=∠2sin sin sin 2sin PA PCA B C θ⋅=．设MN 为过O ，P 的直径，则()()22PC PD PN PM R d R d R d ⋅=⋅=-+=-．又因22sin sin sin ABC S R A B C =△，则11122224sin A B C ABCS R d S R θ-=△△． 当点P 在ABC △的外部时，如图17-4所示，类似可证得1M 图17-411122224sin A B C ABCS R d S R θ-=△△． 故性质3得证． 显然，当90θ=︒时，有1112224A B C ABCR d S S R -=△△，此即为性质2．定义2 凸多边形所在平面内两点分别与各顶点连线，如果同一顶点所连的线与靠近的边所成的角都相等，则称这两点为凸多边形的等角共轭点． 例如，给定一个ABC △和两个点P ，Q ，如果使其满足PAB QAC =∠∠，PBA QBC =∠∠，PCB =∠ QCA ∠，那这样的P ，Q 两点即为ABC △的等角共轭点．性质4 三角形的外心与垂心是三角形的等角共轭点（参见第4章性质2）．性质5 调和四边形两条对角线的中点是调和四边形的等角共轭点(参见第16章性质4)． 对三角形而言，显然内心是重合的等角共轭点（称为自等角共轭点）；三个旁心也都是自等角共轭点． 对于一个三角形而言，我们可推知：(1)三角形外接圆上除3个顶点外，其余所有点均无实在的等角共轭点和它们相配．或者说外接圆上除顶点外，其等角共轭点为无穷远点．(2)每个顶点可有无限多个等角共轭点，即对边所在直线上的所有点． (3)每边及延长线上的所有点同以对顶点为它们的等角共轭点．(4)除以上所说的点外，每一点都有唯一的等角共轭点和它配成点对．性质6 设P ，Q 是ABC △的一对等角共轭点，则P ，Q 在边BC ，CA ，AB （所在直线）上的射影必共圆，其共圆圆心是等角共轭点P ，Q 连线的中点，如图17-5所示．图17-5事实上，这个命题对多边形来说也是成立的．性质7 如果一个多边形有等角共轭点，那这对等角共轭点在各边（所在直线）上的射影必共圆，所共圆圆心是这对等角共轭点连线的中点．证明 如图17-6，设P 、Q 为凸多边形ABC ……H 的等角共轭点．设P 、Q 在各边AB 、BC 、…、HA 上的投影分别为K 、K '、L 、L '，…，N 、N '．联结AP 、AQ 、NK 、N K ''，则知A 、P 、N 、K 四点共圆，有H N N CA图17-690ANK APK PAK ==︒-∠∠∠．又由A 、Q 、N '、K '四点共圆，有90AK N AQN QAN ''''==︒-∠∠∠．由等角共轭点的定义，有PAK QAN '=∠∠．从而，有ANK AK N ''=∠∠，即知N 、N '、K 、K '四点共圆，这圆的圆心应是线段NN '、KK '的中垂线的交点．但这两条中垂线显然交于PQ 的中点O ，即O 为该圆的圆心． 同样的方法，可证K 、K '、L 、L '四点共圆，且圆心也是PQ 的中点O ．同理，得其他的圆，且这些圆既同心，又轮回有公共点，则自必合而为一． 注：此命题的逆命题虽然成立．从而上述条件为充分必要条件． 于是我们可以得到：(1)若两点在一个多边形各边（所在直线）上的射影共圆，则它们必是该多边形的等角共轭点；(2)若一点在一个多边形各边（所在直线）上的射影共圆，则该点的等角共轭点（关于该多边形而言）必定存在．其实我们还可以把性质6加强为如下一个等价形式的命题．性质 6 设给定ABC △及P ，Q 两点，则P ，Q 两点是ABC △的等角共轭点的充要条件是：点P ，Q 在ABC △各边（所在直线）上的射影必共圆．性质8 设给定ABC △及P ，Q 两点，则P ，Q 两点是ABC △的等角共轭点的充要条件是：点P ，Q 到ABC △各边的距离成反比．证明略（由直角三角形相似来证．）性质9 三角形的一对等角共轭点到各顶点的距离乘积之比等于其等角共轭点到各边的距离乘积之比． 证明 如图17-7，由QCY'Y X'X BZT A 图17-7PAB QAC =∠∠，Z P AB ⊥，QY AC '⊥，易知有Rt Rt PAZ QAY '△∽△，所以 PA PZQA QY ='． 同理由Rt Rt PAY QAZ '△∽△，得PA PYQA QZ ='于是 2PA PY PZQA QY QZ ⎛⎫⋅= ⎪''⋅⎝⎭． 同理 2PB PX PZ QB QX QZ ⎛⎫⋅= ⎪''⋅⎝⎭，2PC PX PYQC QX QY ⎛⎫⋅= ⎪''⋅⎝⎭． 所以PA PB PC PX PY PZQA QB QC QX QY QZ ⋅⋅⋅⋅='''⋅⋅⋅⋅． 性质10 三角形的一对等角共轭点对于三角形的投影三角形的面积之比等于其等角共轭点与各顶点连线所分成对应的三个三角形的面积乘积之比． 为了证明此性质，先给出如下引理．引理 设P ，Q 是ABC △的等角共轭点，如图17-8，则有图17-8PQDCBAsin sin AP BOCAQ BPC=∠∠， sin sin BP CQA BQ CPA =∠∠，sin sin CP AQBCQ APB=∠∠． 事实上，如图17-8，延长BP 至D ，使BCD BQA =∠∠，联结AD ，CD ．由PBC QBA =∠∠，有 DBC ABQ △∽△． 则sin sin sin sin DC BC BQC BQCAQ BQ BCQ PCA===∠∠∠∠， ①且 BDC BAQ CAP ==∠∠∠，从而A ，P ，C ，D 四点共圆，即sin sin sin sin AP PCA PCADC DPC BPC==∠∠∠∠． ②由①⨯②知sin sin AP BQCAQ BPC=∠∠． 同理sin sin BP AQC BQ APC =∠∠，sin sin CP AQBCQ APB=∠∠． 下面给出性质10的证明．证明 如图17-9，因X ，X '，Y ，Y '，Z ，Z '分别是等角共轭点P ，Q 在ABC △的边BC ，CA ，AB 所在直线上的投影，由定理1知，X ，X '，Y ，Y '，Z ，Z '六点共圆，所以BCQP Y'YX'XZ'Z A 图17-9XYZ X Y Z S XY YZ ZXS X Y Y Z Z X '''⋅⋅=''''''⋅⋅△△． ③又由PZ AB ⊥，PY AC ⊥知A ，Y ，P ，Z 四点共圆，且AP 为圆AYPZ 的直径，所以sin YZ AP A =． 同理sin Y Z AQ A ''=，sin ZX BP B =，sin Z X BQ B ''=，sin XY CP C =，sin X Y CQ C ''=，于是XY YZ ZX AP BP CPX Y Y Z Z X AQ BQ CQ⋅⋅⋅⋅=''''''⋅⋅⋅⋅． ①利用三角形面积公式，有1sin 2PAB S AP BP APB =⋅△∠， 1sin 2PBC S BP CP BPC =⋅△∠，1sin 2PCA S CP AP CPA =⋅△∠．所以21()(sin sin sin )8PAB PBC PCA S S S AP BP CP APB BPC CPA ⋅⋅=⋅⋅⋅△△△∠∠∠．同理21()(sin sin sin )8QAB QBC QCA S S S AQ BQ CQ AQB BQC CQA ⋅⋅=⋅⋅⋅△△△∠∠∠．再由引理知sin sin AP BQC AQ BPC =∠∠，sin sin BP CQA BQ CPA =∠∠，sin sin CP AQBCQ APB =∠∠， 所以PAB PBC PCAQAB QBC QCAS S S AP BP CP AQ BQ CQ S S S ⋅⋅⋅⋅=⋅⋅⋅⋅△△△△△． ⑤由式③，④，⑤，可得XYZ PAB PBC PCA X Y Z QAB QBC QCAS S S SS S S S '''⋅⋅=⋅⋅△△△△△△△△．由上述性质10的证明过程，不难推证如下推论．推论9 ABC △的等角共轭点P ，Q 对于△ABC 的投影三角形(如图17-9中的△XYZ ，△X Y Z '')的边长由下式给出sin 2aZY AP A AP R ==⋅sin 2a Z Y AQ A AQ R''==⋅…其中a 表示ABC △边BC 的长，R 表示ABC △的外接圆半径．推论10 ABC △的等角共轭点P (或Q )对于ABC △的投影三角形，如图17-9中的△XYZ ，△X Y Z '''的边垂直于所对的ABC △顶点与等角共轭点Q （或P ）的连线如图17-9中的ZY AQ ⊥（或Z Y AP ''⊥）等． 推论11 ABC △的等角共轭点(P ，Q )对于ABC △的投影三角形的边，与ABC △的对应边乘这边相对的顶点到等角共轭点的距离的积成比例．推论12 ABC △的一对等角共轭点(P ，Q )及其在ABC △相应两边上的投影为顶点的两个对应三角形相似如图17-9中的△PYZ ∽△QZ Y ''等．推论13 ABC △的等角共轭点（P 或Q ）到各顶点的距离之积，与其等角共轭点对于ABC △的投影三角形如图17-9中的△XYZ 或△X Y Z '''的三边之积的比是一定值22R S，其中S ，R 分别表示ABC △的面积、外接圆半径．推论14 三角形的等角共轭点对于三角形的投影三角形的面积之比等于其等角共轭点与顶点连线所分成对应的三个三角形外接圆半径的乘积之比． 例1 在四边形ABCD 中，若AC BD ⊥，则两对角线的等角线交于一点O ，且△OAB 、△OBC 、△OCD 、△ODA 的垂心共线．证明 由于AC BD ⊥，注意到：在两对角线互相垂直的四边形中，过对角线交点向每边作垂线得四垂足，又若每垂线与对边相交得四交点，则所得八点共圆；两点是多边形的等角共轭点的充要条件是这两点在各边上的射影共圆．由此知P 点的等角共轭点存在．设为O ．令△OAB 、△OBC 、△OCD 、△ODA 的垂心分别为1H ，2H ，3H ，4H ．则4cot AH OD DAO =⋅∠， 3cot CH OD DCO =⋅∠，又43H AP H CP =∠∠，故△4AH P ∽△3CH P ． 所以43APH CPH =∠∠，即知4H 、P 、3H 三点共线． 同理，2H 、P 、3H 三点共线，1H 、P 、4H 三点共线． 故1H 、2H 、3H 、4H 四点共线．图17-10例2（2008年国家集训队测试题）设P 、Q 、R 分别是锐角三角形ABC 的边BC 、CA 、AB 上的点，使得△PQR 是正三角形，并且它还是这样的内接正三角形中面积最小的．求证：点A 到QR 的垂线、点B 到RP 的垂线和点C 到PQ 的垂线，这三条直线共点．证明 如图17-11，作△CPQ 、△AQR 、△BRP 的外接圆，交得密克尔点M ，则 BMC BMP PMC BRP PQC =+=+∠∠∠∠∠ (π)(π)ARP PQA =-+-∠∠2πARP PQA RPQ RAQ =--=+∠∠∠∠π3A =+． MXPCBQR 图17-11A同理，π3RMA B =+∠． 由上知，M 为定点，所有这样的正三角形PQR （面积不一定最小）都相当于以M 为中心，将其中的一个三角形作刚体旋转而得．因此，这些三角形都有共同的旋转中心M ．要使△PQR 面积最小，即需MP 最小，这要求P 为M 在BC 上的垂足．同理，Q ，R 分别为M 在AC 、AB 上的垂足． 现在任取一点X ，使得XA PQ ⊥，则 ππ22XAQ AQR AMR MAR ==-=∠-∠∠∠． 因此，A 到QR 的垂线在△BAC 中是AM 的等角线．从而，A 到QR 的垂线，B 到RP 的垂线，C 到PQ 的垂线，都是经过点M 的等角共轭点．故这三条直线共点于定点M 的等角共轭点．例3（2008年国家集训队测试题）设P ，Q 是ABC △内两点，满足A B P CAQ =∠∠，ABP CBQ =∠∠，BCP ACQ =∠∠，△PBC 、△PCA 、△PAB 的外心分别为1O 、2O 、3O ，△QBC 、△QCA 、△QAB 的外心分别为1O '、2O '、3O '．设O 是经过1O 、2O 、3O 三点的圆之圆心，O '是经过1O '、2O '、3O '三点的圆之圆心．求证：OO PQ '∥．证明 设3O 、2O 联线和3O '、2O '联线交于点D ．因3O 、3O '分别为△PAB 、△QAB 的外心，则它们同在AB的中垂线上，即33O O AB '⊥． 同理，32O O AP ⊥，22O O AC '⊥，23O O AQ ''⊥． 从而332O O O BAP '=∠∠， ① 223O O O CAQ ''=∠∠．②由①，②及已知条件BAP CAQ =∠∠，知332223Q O O O O O '''=∠∠． 这就表明3O 、3O '、2O 、2O '四点共圆． 由圆幂定理，有3232O D DO O D DO ''⋅=⋅． ③③表明点D 到O 及O '的幂相等，是这两圆根轴上的一点．另一方面，由于D 既在AP 的中垂线上，又在AQ 的中垂线上，因此，DP DQ =．④1图17-12④表明点D 也在线段PQ 的中垂线上．类似地，若设3O 、1O 的联线和3O '、1O '，联线交于点E ．同理可证点E 到O 及O '的幂相等，且点E 也在线段PQ 的中垂线上．从而，PQ 的中垂线就是O 及O '的根轴．故PQ 垂直于两圆的根轴． 从OO '是两圆的连心线，由此知OO PQ '∥．例 4 圆内接四边形ABCD 的对角线AC 与BD 相交于点P ，则△PAB 与△PCD ，△PAD 与△PBC 的垂心，外心分别四点共圆．证明 为了证明该结论，先看如下引理：引理 过圆内接四边形ABCD 两对角线交点P 作任一边的垂线，则垂线必过以其对边为一边，以交点为一顶点的三角形的外心．事实上，如图17-13，过P 作PH AB ⊥于H ，作DP 的中垂线交HP 于Q ，交DP 于E ，过D 作DR EQ ∥，交HP 于R ，则DR DP ⊥，Q 为PR 的中点．R PQHE D CBA 图17-13由9090DRP EQP EPQ HPB PBH ACD DCP ==︒-=︒-===∠∠∠∠∠∠∠知D ，P ，C ，R 四点共圆．又PDR ∠是直角，所以，知Q 为△CDP 的外心． 下面，回到原问题的证明：如图17-14，设1O 、1H 与2O 、2H 分别为△PAD 、△PBC 的外心与垂心．由上述引理知，1O 、P 、2H 、F 及2O 、P 、1H 、E 分别四点共线．图17-14由于三角形的外心与垂心是等角共轭点，有2BPO CPF =∠∠，1APO DPE =∠∠．所以21NPO MPO =∠∠，12H PR H PQ =∠∠． 所以21NPO MPO =∠∠，12H PR H PQ =∠∠．即知12Rt Rt PO M PO M △∽△，12Rt Rt PH R PH Q △∽△． 从而 121212PAPO PM PAPO PN PBPB ===， 12PH PR PAPH PQ PB==（PAR PBQ △∽△） 于是1122PO PH PO PH =，即1221PO PH PO PH ⋅=⋅，故1O ，2O ，2H ，1H 四点共圆． 同理，△PAB 与△PCD 的外心，垂心四点共圆．例5（2011年第37届俄罗斯数学奥林匹克题）已知非等腰ABC △，N 是其外接圆孤BAC 的中点，M 是边BC 的中点，1I 、2I 分别是△ABM 、△ACM 的内心．证明：1I 、2I 、A 、A 四点共圆．证明 如图17-15，设2I '是2I 关于直线MN 的对称点，联结2BI '，1BI 、2MI '、1MI ，则12BAI BMI '+=∠∠ 121()902BMI CMI BMA CMA BMN +=+=︒=∠∠∠∠∠．图17-15故1MI 、2MI '关于BMN ∠的平分线对称． 同理，1BI 、2BI '关于MBN ∠的平分线对称．这表明1I 、2I '，是△BMN 的一对等角共轭点． 因此，12BNM MN MNI '=+∠∠∠，从而1212112I AI BAC BNM MNI MNI MNI '===+=+∠∠∠∠∠∠ 212MNI I NI =∠∠．故1I 、2I 、A 、N 四点共圆．例6 过ABC △内一点O 引三边AB 、BC 、CA 的平行线与其他两边的交点分别为E 、F ，G 、H ，I 、K ．过O 作ABC △外接圆的弦AL ．求证：OE OF OG OH OI OK OA OL ⋅+⋅+⋅=⋅． 证明 如图17-16，设ABC △的三边的长为BC a =，CA b =，AB c =，对应的高为a h 、b h 、c h ，又设△GKO 、△OEH 、△FOI 与ABC △的相似比分别为λ，u ，v ．过O 作AB 、BC 、CA 的垂线，垂足分别为P 、Q 、S ，则由性质2，知O图17-16E K HI GQFCBA222244PQSR d OA OL S R R -⋅==△．（其中R 为三角形钋接圆半径）．注意到2cS h c =△，2S ha a =△，S =△ 1sin 2ca B ⋅， 则由PQS POQ QOS POS S S S S =++△△△△111sin sin sin 222c a c b b c h vh B h vh A uh vh C λλ=⋅⋅+⋅⋅+⋅⋅ 241sin 2ABCS v B ca λ=⋅∑△（其中“∑”表循环和）2212sin sin 2ABC ABC v B S v B S λλ=⋅⋅=⋅⋅∑∑△△有2sin PQS ABCS v B S λ=⋅∑△△再注意到性质2，有2OA OL v b λ⋅=⋅∑．又2OE OF OG OH OI OK v b λ⋅+⋅+⋅=⋅∑．由此即证得结论． 注：其中OE OF AK GB ⋅=⋅，而bAK OSu AB h ==，即AK uc =． 同理，GB vc =，故2OE OF uv c ⋅=⋅． 同理，2OG OH u a λ⋅=⋅，2OI OK v b λ⋅=⋅．练习十七1．P 及P '两点在ABC △的三边BC ，CA ，AB 所在直线上的身影为X ，Y ，Z 及X '，Y '，Z '，求证：P 与P '是ABC △的等角共轭点的必要且充分的条件为PX P X PY P Y PZ P Z ''''''⋅=⋅=⋅2．设P ，Q 是四边形ABCD 的等角共轭点，求证： (1)△PAB ，△QBC ，△PCD ，△QDA 的垂心共线； (2)△QAB ，△PBC ，△QCD ，△PDA 的垂心也共线；(3)以上所得两直线互相平行． 3．在四边形ABCD 中，设AC BD ⊥，求证：两对角线的等角线交于一点O ，且△OAB ，△OBC ，△OCD ，△ODA 的垂心共线．4．设P 与P '是四边形ABCD 的等角共轭点，求证：（1）四圆PAB ，P BC '，PCD ，P DA '交于一点Q ； （2）四圆P AB '，PBC ，P CD '，PDA 交于一点Q '； (3)Q 与Q '也是四边形ABCD 的等角共轭点． 5．设P ，Q 是ABC △内任意两点，则1AP AQ BP BQ CP CQAB AC AB BC AC BC⋅⋅⋅++⋅⋅⋅≥等号当且仅当PAB QAC =∠∠，PBC QBA =∠∠，PCB QCA =∠∠时成立．6．设P ，Q 是ABC △的等角共轭点，则在BC ，CA ，AB 上分别存在点D ，E ，F ，使得PD DQ += PF EQ PF FQ +=+，且AD ，BE ，CF 三线共点．。
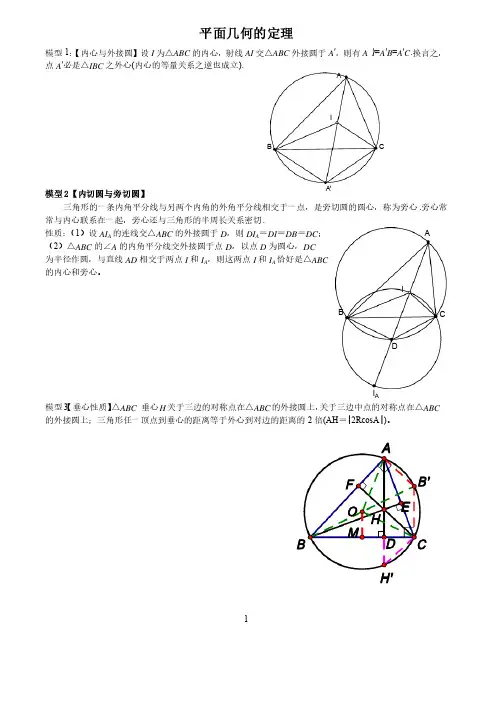
1 平面几何的定理模型1：【内心与外接圆】【内心与外接圆】设设I 为△ABC 的内心，射线AI 交△ABC 外接圆于A ′，则有A ′I =A ′B =A ′C .换言之，点A ′必是△IBC 之外心(内心的等量关系之逆也成立). 模型2【内切圆与旁切圆】三角形的一条内角平分线与另两个内角的外角平分线相交于一点，是旁切圆的圆心，称为旁心.旁心常常与内心联系在一起，旁心还与三角形的半周长关系密切. 性质：（1）设AI A 的连线交△ABC 的外接圆于D ，则DI A ＝DI ＝DB ＝DC ；（2）△ABC 的∠A 的内角平分线交外接圆于点D ，以点D 为圆心，DC 为半径作圆，与直线AD 相交于两点I 和I A ，则这两点I 和I A 恰好是△ABC 的内心和旁心。
模型3【垂心性质】△ABC 垂心H 关于三边的对称点在△ABC 的外接圆上，关于三边中点的对称点在△ABC 的外接圆上；三角形任一顶点到垂心的距离等于外心到对边的距离的2倍(AH ＝|2RcosA |)。
A'IAB CI ADIA BCH'MB'F E D H OCA B模型4【圆幂定理】【圆幂定理】从一定点P 引直线与定圆O 交于两点A 、B ，(A 、B 可能重合为一个点)，（记OP =d ）， 则P A ·PB 等于点P 对于⊙O 的幂:d 2－r 2所以上面的几个定理(相交弦定理、切割线定理、割线定理及切线长定理)也统称圆幂定理．也统称圆幂定理．ïîïíì<=>=在圆内，在圆上，在圆外，的幂P P P P 000模型5【多圆问题】【多圆问题】 相交两圆的性质相交两圆的性质 性质1：相交两圆的连心线垂直平分公共弦。
：相交两圆的连心线垂直平分公共弦。
性质2：相交两圆的公共弦所在直线平分外公切线线段。
：相交两圆的公共弦所在直线平分外公切线线段。
深入理解三角恒等变换的证明三角恒等变换是数学中的重要概念，主要用于证明三角函数之间的等式。
通过利用三角恒等变换，我们可以简化和转换复杂的三角函数表达式，使其更容易处理和理解。
本文将深入探讨三角恒等变换的证明原理和应用。
一、简介三角恒等变换是指在三角函数之间建立等式关系的变换规则。
这些恒等变换可以通过几何、代数或运算等方式得到证明。
三角恒等变换可以帮助我们理解三角函数的性质和相互关系，同时也为解决实际问题提供了数学工具。
二、三角函数的定义在介绍三角恒等变换之前，我们首先需要了解三角函数的基本定义。
常见的三角函数包括正弦函数（sin）、余弦函数（cos）、正切函数（tan）等。
三、基本恒等变换1. 倍角公式倍角公式是最基本的三角恒等变换之一。
它可以将一个角的两倍表示成另外一个角的三角函数表达式。
常见的倍角公式有以下几种形式：- sin(2θ) = 2sinθcosθ- cos(2θ) = cos^2θ - sin^2θ- tan(2θ) = 2tanθ / (1 - tan^2θ)2. 半角公式半角公式是倍角公式的逆运算，可以将一个角的两倍表示成另外一个角的三角函数表达式。
常见的半角公式有以下几种形式：- sin(θ/2) = ±√[(1 - cosθ) / 2]- cos(θ/2) = ±√[(1 + cosθ) / 2]- tan(θ/2) = ±√[(1 - cosθ) / (1 + cosθ)]3. 和差公式和差公式用于将两个角的三角函数表达式转化为一个角的三角函数表达式。
常见的和差公式有以下几种形式：- sin(α ± β) = sinαcosβ ± cosαsinβ- cos(α ± β) = cosαcosβ ∓ sinαsinβ- tan(α ± β) = (tanα ± tanβ) / (1 ∓ tanαtanβ)4. 三角函数的倒数关系三角函数的倒数关系是指正弦函数、余弦函数和正切函数之间的倒数关系。
