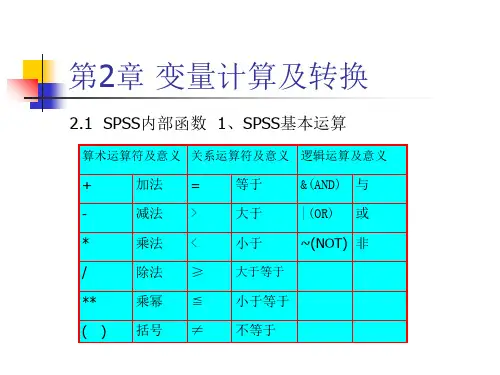
spss变量计算及转换
- 格式:pptx
- 大小:1.83 MB
- 文档页数:42

SPSS基本操作步骤详解本文采用SPSS21.0版本,其它版本操作步骤大体相同一、基本步骤(一)检查数据在进行项目分析或统计分析之前,要检核输入的数据文件有无错误,即检核missing。
例,“XX量表”采用Likert scale五点量表式填答,每个题项的数据只有五个水平:1,2,3,4,5。
1.执行次数分布表的程序Analyze(分析)→Descriptive statistics(描述统计)→将题项变量【例,a1—a10】键入至Variables(变量)框中→Frequencies(频率)→Statistics(统计量)→Minimum (最小值)、Maximum(最大值)→Continue(继续)→OK(确定)2.执行描述统计量的程序Analyze(分析)→(描述统计)→将题项变量【例,a1—a10】键入至Variables(变量)框中→Descriptives(描述)→Options(选项)→Minimum(最小值)、Maximum(最大值)【此处一般为默认状态即可】→Continue(继续)→OK(确定)(二)反项计分若是分析的预试量表中没有反向题,则此操作步骤可以省略;量表或问卷题中如果有反向题,则在进行题项加总之前将反向题反向计分,否则测量分数所表示的意义刚好相反。
例,“XX量表”采用Likert scale五点量表式填答,反向题重向编码计分:1→5,2→4,3→3【可不写】,4→2,5→1。
Transform(转换)→Recode into same Variables(重新编码为相同变量)→将要反向的题目键入至Variables(变量)框中【例,a1,a3,a5】→Old and new values(旧值和新值)→在左边Old value—value中键入1,在右边New value—value中键入5,Add (添加)→……依次进行此步骤……在左边Old value—value中键入5,在右边New value —value中键入1,Add(添加)→Continue(继续)→OK(确定)【注意不同量表计分方式不同,因而反向编码计分也不同,常见的有四点量表、五点量表和六点量表等】(三)题项加总量表题项加总的目的在于便于进行观察值得高低分组。
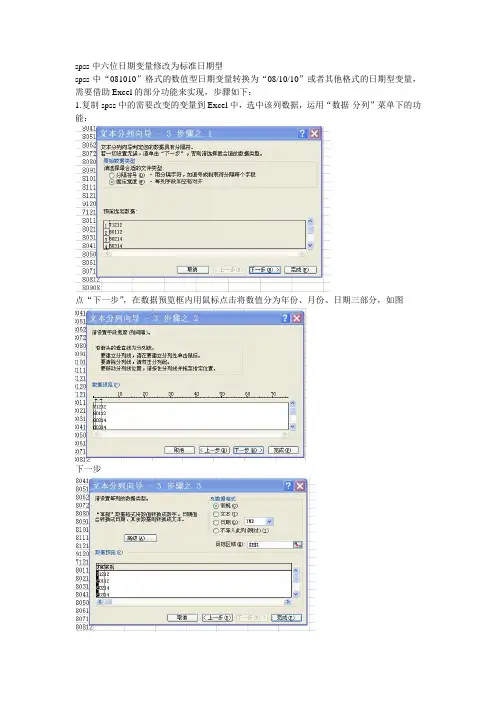
spss中六位日期变量修改为标准日期型
spss中“081010”格式的数值型日期变量转换为“08/10/10”或者其他格式的日期型变量,需要借助Excel的部分功能来实现,步骤如下:
1.复制spss中的需要改变的变量到Excel中,选中该列数据,运用“数据-分列”菜单下的功能:
点“下一步”,在数据预览框内用鼠标点击将数值分为年份、月份、日期三部分,如图
下一步
完成,结果如下
然后将三列结果粘贴回spss中,运用spss中“Transform-Date to the date and wizard”菜单
下一步
分别将年份、月份、日期三个数值放入上图相应位置
命名新生成变量的名称,选择要转换的日期格式,点击完成,结果如下。

SPSS操作指导社会统计学软件包(SPSS)20世纪60年代由美国斯坦福大学的3位研究生研制开发,使国际上最有影响力的统计软件之一,广泛用于社会学、经济学、生物学、教育学、心理学等各个领域。
一、SPSS数据文件管理1、建立一个数据文件菜单“文件”——“新建”——“数据”;(1)单击“变量视图”。
标签:变量名不能超过8个字符,所以需要输入相应变量的文字解释说明。
值:一般适用于定类变量和定序变量。
缺失:定义缺失值没有缺失值,系统默认选项。
离散缺失值,制定3个数值为缺失值。
缺失值的范围。
列:定义列宽测量:尺度指定距和定比数据,用于代表连续数据;有序代表定序数据;名义代表定类数据。
(2)单击“数据视图”进行数据的直接录入。
注意:开放题和简单单选题录入相似。
多选题的录入比较复杂。
多选题又称为多重应答,是社会调查和市场调研中极为常见的一种数据记录类型。
录入时可以采用两类:多重二分法、多重分类法。
多重二分法是指在编码的时候,对应每一个选型都要定义一个变量,有几个选项就有几个变量,这些变量均为二分类,它们各自代表对一个选项的选择结果。
如1代表选择,0代表未选。
多重分类法是利用多个变量来对一个多选题的答案进行定义,这些变量须为数值型变量,利用值标签将答案标出,所有变量采用一套值标签。
适合于选项较多的情况。
2、读取外部数据一般使用EXCEL数据。
菜单“文件”——“打开”——“数据”,调出打开文件对话框,在文件类型下拉列表中选择EXCEL类型。
二、数据整理数据整理的功能主要集中在“数据”和“转换”两个主菜单下。
1、数据“数据”——“个案排序”。
“数据”——“转置”。
“数据”——“选择个案”。
“数据”——“分类汇总”;分组变量一般是离散变量,而汇总变量一般是连续变量。
要同时计算一个变量的两个统计量时需要将该变量移入两次汇总变量。
“数据”——“合并文件”;添加个案是指纵向合并样本量;添加变量是指横向合并变量。
未匹配变量中*变量为工作数据文件中的变量,+为外部数据文件中的变量。


SPSS分析应用的原理一、SPSS简介SPSS(Statistical Package for the Social Sciences),即社会科学统计包,是一种广泛使用的统计分析软件。
它提供了丰富的数据处理方法和统计分析工具,广泛应用于社会科学、市场调研、医学研究等领域。
SPSS应用的原理主要包括数据输入、数据整理、数据分析和结果解释等方面。
二、SPSS数据输入在使用SPSS进行分析之前,首先需要将原始数据导入软件中。
SPSS支持的数据格式包括文本文件、Excel文件和数据库文件等。
用户可以使用SPSS的数据编辑器进行数据输入,也可以通过复制粘贴等方式将数据从其他软件导入SPSS。
数据输入完成后,SPSS会自动识别数据的类型,并生成相应的变量。
三、SPSS数据整理数据整理是数据分析的前提,它包括数据清洗、数据变量定义和数据变量转换等过程。
数据清洗主要是对数据进行筛选、删除缺失值和异常值的处理,确保数据的准确性和完整性。
数据变量定义主要是对数据变量进行命名和定义属性,方便后续的数据分析。
数据变量转换可以根据具体需求对数据进行计算和转换,如计算平均值、合并变量等。
四、SPSS数据分析SPSS提供了丰富的统计分析方法,包括描述性统计分析、推断性统计分析和预测分析等。
常用的统计分析方法包括:频数分析、交叉表分析、t检验、方差分析、回归分析、聚类分析等。
用户可以根据自己的具体需求选择相应的分析方法,并设置相应的参数进行分析。
SPSS会根据用户选择的分析方法进行计算,并生成相应的结果报告。
五、SPSS结果解释在使用SPSS进行数据分析后,需要对分析结果进行解释和理解。
SPSS会生成相应的结果报告,包括表格、图表和统计量等。
用户需要根据具体的分析目的进行结果解释,理解结果的含义和影响。
此外,还可以使用SPSS的可视化功能,将结果以图表的形式展示,更直观地展示数据的特征和趋势。
六、SPSS分析注意事项在使用SPSS进行数据分析时,需要注意以下几点: 1. 数据的准备和整理工作要充分,确保数据的质量和完整性; 2. 在选择分析方法时,需要根据具体的问题和数据类型进行选择,并设置相应的参数; 3. 在分析结果解释时,要注重对结果的合理解读,并结合实际情况进行分析; 4. 在使用SPSS进行高级统计分析时,需要熟悉统计学原理和方法,避免错误的使用和解读。



《统计学软件及应用》上机试验报告试验名称:实验6 变量组数据处理成绩:果存储到-个新变量中去的过程。
例:根据S2性别分组计算S3年龄的秩次。
选择"转换"→"个案排秩"菜单项,打开如图所示的对话框。
(1)"依据"列表框:指的是分组编秩时的分组变量。
(2)"将秩l赋予"单选框组:用于选择将秩次1赋给最小值还是最大值。
(3)"秩的类型"按钮:用于定义秩次类型,默认为最常用的"秩",另有其他几种选择,因为很少用到,这里不再详述。
(4)"结"按钮:用于定义对相同值观测量的处理方式,可以是"均值"、"低"、"高"或"顺序秩到唯一值",默认值为取平均秩次。
这里将变量S3选入"变量"列表框中,分组变量S2选人"排序标准"列表框中,其他设置使用默认值,然后确认即可,此时系统会建立一个新变量Rs3(即原变量名前加R,表示"秩"),其取值为按照S2分组的S3秩次,同时在结果窗口中会给出汇总报表,如图所示。
许多时候参数检验的条件无法满足,需要使用非参数方法,而稍微复杂些的非参数方法就无法直接用对话框来完成了,所以需要先计算秩次再进行分析。
课堂试验内容五、实验步骤(请截图展示详细的操作过程)1、可视分箱-等距分箱S3.年龄(分箱化)频率百分比有效百分比累计百分比有效<=25 277 24.1 24.1 24.1 26-38 437 38.1 38.1 62.239-52 245 21.4 21.4 83.653+ 188 16.4 16.4 100.0总计1147 100.0 100.02、可视分箱-等百分比分组S3.年龄(分箱化)频率百分比有效百分比累计百分比有效<=26 340 29.6 29.6 29.6 27-32 235 20.5 20.5 50.133-46 291 25.4 25.4 75.547+ 281 24.5 24.5 100.0总计1147 100.0 100.03、可视分箱-按标准差分组S3.年龄(分箱化)频率百分比有效百分比累计百分比有效<=23 164 14.3 14.3 14.3 24-36 524 45.7 45.7 60.037-49 220 19.2 19.2 79.250+ 239 20.8 20.8 100.0总计1147 100.0 100.0S0.城市频率百分比有效百分比累计百分比有效100北京378 33.0 33.0 33.0 200上海387 33.7 33.7 66.7300广东382 33.3 33.3 100.0总计1147 100.0 100.0年龄在55岁以上的人计数频率百分比有效百分比累计百分比有效.00 992 86.5 86.5 86.51.00 155 13.5 13.5 100.0总计1147 100.0 100.0年龄是18和19岁秩次依据是:S3年龄年龄是18和19岁的秩次的依据是:S2性别。


实验题1.解:(1)将数据录入SPSS软件中。
(2)点击分析→回归→线性,得回归系数表:由表可知,线性回归方程为:y=0.379x+17.2192.解:(a)将数据录入SPSS软件中, 点击分析→回归→线性,得回归系数表:Y为保单推销数,X为保单推销经历(年数)由图可知,拟合回归方程y=3.364x+51.165( b ) 回归系数为0.410,与0相异,小于0.05(在5%的显著水平),即相应系数显著大于0(c)一个有10年推销经历的保单推销员的销售额为y=3.364×10+51.165=84.8053.解:(a)将数据录入SPSS软件中, 点击分析→回归→线性,得回归系数表:点击分析→相关→双变量,得到:点击图形→旧对话框→散点、点状→确定,即可得到散点图:Y为能力测验分数,X为完成任务时间由表可知,线性回归方程为:Y=-11.959x+125.267(b) 由散点图可看出,这两个变量呈负相关关系。
(c) 由表可知,两个变量的相关系数为—0.930>0.5,又0.865显著异于0,t统计量的显著性概率p为0.000<0.05,说明两个变量在0.05水平上呈显著性差异。
4.解:(1)将数据录入SPSS软件中。
(2)点击分析→回归→线性,得回归系数表:Y 为儿子身高,x 为父亲身高由表可知,经验回归方程y=0.465x+35.977 5.解:(1)将数据录入SPSS 软件中。
(2)点击转换→计算变量→线性→目标变量t=1/x;(3)点击分析→回归→线性→因变量y →自变量t,得回归系数表:Y 为销售额,X 为流通费用率由表可知,选用曲线xba y +=做曲线回归,得回归方程为y=9.707/x -1.2116.解:(1)将数据录入SPSS 软件中, 点击分析→回归→线性,y 为因变量,x 为自变量。
得到回归分析表:y 为上年专利数,x1为上三年R&D 投入,x2为高级工程师数由表可知,“上年专利数”对“上三年R&D 投入”和“高级工程师数”的线性回归方程为: y=0.008x1+0.615x2+7.040由表可得,估计标准误差为3.65724。
【最新整理,下载后即可编辑】数据管理一、实验目的与要求1.掌握计算新变量、变量取值重编码的基本操作。
2.掌握记录排序、拆分、筛选、加权以及数据汇总的操作。
3.了解数据字典的定义和使用、数据文件的重新排列、转置、合并的操作。
二、实验内容提要1.自行练习完成课本中涉及的对CCSS案例数据的数据管理操作2.针对SPSS自带数据Employee data.sav进行以下练习。
(1)根据变量bdate生成一个新变量“年龄”(2)根据jobcat分组计算salary的秩次(3)根据雇员的性别变量对salary的平均值进行汇总(4)生成新变量grade,当salary<20000时取值为d,在20000~50000范围内时取值为c,在50000~100000范围内取值为b,大于等于100000时取值为a三、实验步骤1、针对CCSS案例数据的数据管理操作1.1.计算变量,输入TS3到目标变量,在数字表达式中输入3,把任意年龄段分成三个组20-30设为1组,1-40设为2组41-50设为3组。
图1,图11.2.对已有变量的分组合并,在“名称”文本框中输入新变量名TS3单击“更改”按钮,原来的S3->?就会变为S3->TS3,单击“旧值和新值”按钮,系统打开“重新编码到其他变量:旧值和新值”,如下图2,图2图31.3.可视离散化,选择“转换”->“可视离散化”,打开的对话框要求用户选择希望进行离散化的变量,单击继续,如下图4,图4单击“生成分割点”,设定分割点数量为10,宽度为5,第一个分割点位置为18,单击“应用”,如下图,图5结果显示如下,图62.针对SPSS自带数据Employee data.sav进行以下练习。
2.1.根据变量bdate生成一个新变量“年龄”,选择“转换”->”计算变量”,如下图,图7结果显示如下,图82.2.根据jobcat分组计算salary的秩次,图9结果显示如下,图102.3.根据雇员的性别变量对salary的平均值进行汇总图11结果显示如下,图122.4.生成新变量grade,当salary<20000时取值为d,在20000~50000范围内时取值为c,在50000~100000范围内取值为b,大于等于100000时取值为a图13结果显示如下,图14 四、实验结果与结论。
1、将数据“居民储蓄调查数据.txt”导入SPSS,保存为“我导入的居民储蓄调查数据.sav”文件→打开→数据→(文本)2、根据“居民储蓄调查数据”,找出:城镇户口存款金额最大值、最小值,农村户口存款金额最大值、最小值。
第一种:数据→排序个案→(a13,a5)第二种:城镇户口:数据→选择个案→如果条件满足(a13=1,保存到新数据集),新文件→数据→排序个案→存取款金额3、根据“职工数据”,对职称1至4的职工的基本工资和失业保险分别上浮5%、3%、2%、1%。
转换→计算变量→(sr=sr*1.05)→如果个案满足就包括(职工号=001)4、根据“居民储蓄调查数据,抽样职业为商业服务业的前10个人的存款最大值。
①数据→选择个案→如果条件满足(a14=2,保存到新数据集)②新数据集→数据→选择个案→基于时间或个案全距(范围1-10,)→删除未选定个案③新数集→数据→排序个案5、利用“居民储蓄调查数据”,分析城镇储户和农村储户的一次平均存取款金额的情况。
数据→汇总→分组变量(户口)→变量摘要(存取款金额)→创建只包含汇总变量的新数据6、根据“职工数据”,对员工工资收入按以下标准进行分组,并填写完整以下表格。
按工资分组(元)频数(人)频率(%)850以下851~900901~10001001以上①转换→重新编码为其他变量→输入变量(基本工资)→输出变量(分组)→新值和旧值→旧值:范围,从最低到值(850)→新值:值(1)→添加;旧值:范围(851到900)→新值:值(2)→添加旧值:范围(901到1000)→新值:值(3)→添加旧值:范围,从值到最高(1001)→新值:值(4)→添加→继续→更改→确定②分析→描述统计→频率→变量(分组)→确定7、根据“居民储蓄调查数据”,对存款金额按以下标准进行分组,并填写完整以下表格。
按工资分组(元)频数频率(%)累计百分比有效百分比500以下501~20002001~35003501~50005001以上①转换→重新编码为其他变量→输入变量(存款金额)→输出变量(分组)→新值和旧值→旧值:范围,从最低到值(500)→新值:值(1)→添加;旧值:范围(501到2000)→新值:值(2)→添加旧值:范围(2001到3500)→新值:值(3)→添加旧值:范围(3501到5000)→新值:值(4)→添加旧值:范围,从值到最高(5001)→新值:值(5)→添加→继续→更改→确定②分析→描述统计→频率→变量(分组)→确定8、一家大型门户网站调查了网民的媒体接触习惯,获得“6章__数据1”的数据文件,请分析:网民平常花在哪类媒体上的时间最多?网民哪种最高学历层次的人最多?网民每天看报纸的时间大约平均有多少分钟?①分析→描述统计→频率→变量(你平常花在哪类媒体上的时间最多)→确定②分析→描述统计→频率→变量(最高学历层)→确定③分析→描述统计→描述→变量(你每天的看报纸的时间大约平均有多少分钟?)→确定9、根据“居民储蓄调查数据”,分析被调查者户口和职业的频次分布的情况,得出户口和职业分布的:平均值、中位数、众数、四分位数、方差、标准差、全距/极差、最大值、最小值、偏度、峰度,带分布曲线的直方图、条形图;并回答它们的分布是否满足正态分布?。
spss极差标准化SPSS极差标准化。
在统计学中,极差标准化是一种常用的数据处理方法,它可以帮助我们对不同变量之间的差异进行比较和分析。
在SPSS软件中,极差标准化也是一项常见的操作,下面我们将详细介绍SPSS中如何进行极差标准化的操作步骤。
首先,打开SPSS软件并加载需要进行极差标准化的数据文件。
在数据文件加载完成后,点击菜单栏中的“转换”选项,然后选择“计算变量”。
接着,在弹出的对话框中,我们需要为新的标准化变量命名,并在“数学运算”中选择“极差标准化”。
在“变量”框中选择需要进行极差标准化的原始变量,然后点击“箭头”按钮将其移动到“数学表达式”框中。
在“数学表达式”框中,我们需要输入极差标准化的计算公式。
极差标准化的计算公式为,(X-Min)/(Max-Min),其中X为原始变量的取值,Min为原始变量的最小值,Max为原始变量的最大值。
在SPSS中,我们可以直接使用变量名来表示原始变量的取值、最小值和最大值,无需手动输入具体数值。
完成以上步骤后,点击“确定”按钮,SPSS将会在数据文件中添加新的极差标准化变量,并计算出每个观测值的标准化取值。
通过这种方式,我们可以将原始变量的取值转换为标准化的分数,从而方便进行跨变量的比较和分析。
需要注意的是,极差标准化并不改变数据的分布形态,只是对原始变量进行线性变换,因此在进行极差标准化后,数据的分布形态和变量之间的关系仍然保持不变。
这使得极差标准化成为了一种非常常用的数据处理方法,特别适用于需要进行跨变量比较和分析的情况。
除了极差标准化,SPSS软件还提供了许多其他数据处理和分析的功能,比如标准化、归一化、正态化等。
这些功能可以帮助我们更好地理解和分析数据,从而得出科学、准确的结论。
总之,SPSS中的极差标准化是一项非常实用的数据处理方法,它可以帮助我们对不同变量之间的差异进行比较和分析。
通过本文介绍的操作步骤,相信大家已经掌握了在SPSS中进行极差标准化的方法,希望能对大家的学习和工作有所帮助。