微生物动力学计算例题
- 格式:ppt
- 大小:94.50 KB
- 文档页数:13
例1: 当杀菌温度从120℃升至150 ℃,试计算维生素B1的分解速率常数K B 和嗜热脂肪芽孢杆菌的死亡速率常数K S 。
已知ΔE S =283460 J/mol, As=1.06×1036 (min-1) ;ΔE B =92114 J/mol, A B =1.06×1010 (min-1).解:由(1)式,即㏑K=㏑ A - (ΔE /RT)得 lnKs= ln As - ΔE S /(RT)∴ Ks 在120 ℃时为0.0156 (min -1)150 ℃时为7.54 (min -1)灭菌速率常数提高482倍。
同样地: K B 在120 ℃时为0.00535 (min -1),150 ℃时为0.040 (min -1),同样的温度变化仅提高6.5倍。
例2: 将10000千克的培养基在发酵罐内进行分批灭菌,灭菌温度为120℃,灭菌后要求每1000批中只有一个杂菌,培养基原始污染度为105个/g ,试计算总杀菌效率V 总。
解: N=10-331535001010100001010ln 34.5N N N N--==⨯⨯=即,V 总=34.5例3: 发酵培养基60m 3,杂菌活孢子浓度105/mL ,要求灭菌后残存孢子数 N 为10-3个。
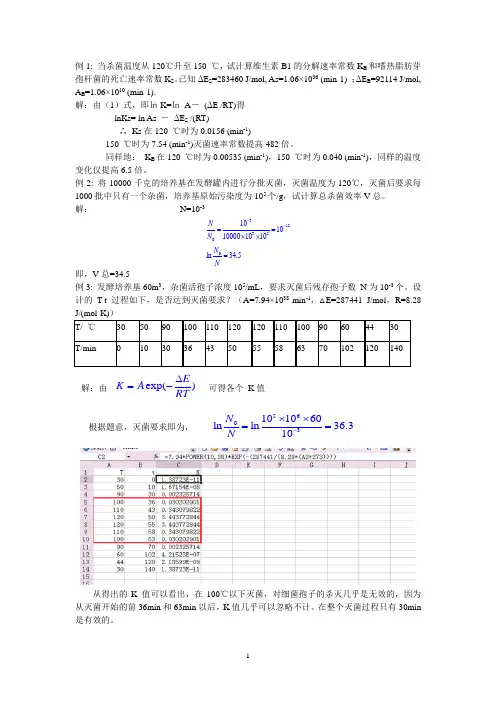
设计的T-t 过程如下,是否达到灭菌要求?(A=7.94×1038 min -1,△E=287441 J/mol ,R=8.28 J/(mol·K)) T/ ℃ 30 50 90 100 110 120 120 110 100 90 60 44 30 T/min103036435055586370102120140exp()EK A RT ∆=-5603101060ln ln 36.310N N -⨯⨯==从得出的K 值可以看出,在100℃以下灭菌,对细菌孢子的杀灭几乎是无效的,因为从灭菌开始的前36min 和63min 以后,K 值几乎可以忽略不计。


微生物电池的化学题1.在微生物电池中,葡萄糖在微生物的作用下将化学能转化为电能。
写出该过程的电极反应式。
答案:负极:C6H12O6+6H2O-24e-=6CO2+24H+;正极:O2+4e-+4H+=2H2O2. 某微生物电池在运行时可同时实现净化有机物污水、净化含Cr2O72-废水(pH约为6)和淡化食盐水。
根据装置中电子的流向,C室为正极区,Cr2O72-离子在此发生得电子的还原反应转化为2Cr(OH)3沉淀。
电极反应式为Cr2O72-+6e-+8H+═2Cr(OH)3↓+H2O。
(1)装置A室是________(填“正极”或“负极”)区,负极上有机物发生________(填“氧化”或“还原”)反应。
(2)根据装置中电子的流向,X为________,Y为________。
(3)淡化食盐水的是________(填“A”或“C”)室。
答案:(1)负极;氧化;(2)有机物污水;含Cr2O72-废水;(3)C3微生物电池可用于有机废水的处理。
某装置运行的微观示意图如下,下列说法中正确的是()A. 该装置中碳棒和多孔石墨之间发生氧化还原反应,构成原电池的两极B. 当电路中转移6个电子时,溶液中c(K^{+})c(H^{+})的值不变C. 碳棒电极上发生反应的电极反应式为:CO(NH_{2})_{2} + 6e^{-} + 8H^{+} = CO_{2} \uparrow + N_{2} \uparrow + 6H_{2}OD. 当有1mol H^{+}通过质子交换膜时,外电路转移的电子的物质的量为1mol答案:C【分析】本题考查了原电池原理的应用,明确原电池反应的实质是解本题关键,结合题给信息来分析解答即可,难度中等。
【解答】A.该装置中碳棒和多孔石墨之间不发生氧化还原反应,不构成原电池的两极,故A错误;B.当电路中转移$6$个电子时,溶液中$c(K^{+})c(H^{+})$的值减小,故B错误;C.根据图示知,碳棒电极上发生反应的电极反应式为:$CO(NH_{2})_{2} + 6e^{-} + 8H^{+} = CO_{2} \uparrow + N_{2} \uparrow + 6H_{2}O$,故C正确;D.当有$1molH^{+}$通过质子交换膜时,外电路转移的电子的物质的量为$0.5mol$,故D错误。

微生物工程习题库(部分示例)第一部分名词解释发酵热临界氧浓度比耗氧速率Monod模型上面酵母比生长速率K L a维持因数稀释度半连续发酵刚性节点上面酵母分离性不稳定原生质体融合得率比生长速率呼吸强度发酵热氧的满足度脱缰质粒分离性不稳定反复补料分批操作:RQPID控制:共固定化技术:前体对数残留定律OUR补料分批操作第二部分填空题1、麦芽干燥过程分_________ 和_________ 两个阶段,其中后者是指水分由10%左右降至5% 左右。
2、啤酒生产中通常用________ 罐作为种子的保藏装置;啤酒发酵液过滤常用_______ 法。
3、在酸酶法制备淀粉水解糖工艺中用到的酶(制剂)是__________ 。
4、谷氨酸发酵普遍采用_______ 级发酵;国内常采用______________法从发酵液中提取谷氨酸。
5、结晶味精无光泽的原因可能是_______________ 、______________________ 。
6、发酵过程生物热的测量可采用___________ 、_________等;发酵液液位测量可采用________法;在线测量发酵液菌体浓度可采用______________法。
7、补料的方式有于预定时间一次补料、____________和________________;中间补料需反馈控制,直接法是以______________________作为反馈控制参数。
8、常用化学消泡剂有__________、_________ 、__________等;消泡的原理是________________________ 、_________________________________________。
9、培养基在管道中不可能呈________ 流,因此在设计连消的维持管时不能简单采用平均停留时间来计算管长,而应采用______________模型来计算。
10、空气贮罐的作用是___________、__________________ 、_______________________。

微生物工程课程练习题微生物工程课程练习题一、名词解释1.发酵动力学2.分批培养3.葡萄糖效应4.代谢互锁5.合作终产物抑制6.巴斯德效应7.同型乳酸发酵8.协同反馈抑制9.初级代谢产物10.补料分批培养11.酵母Ⅰ型发酵12.酵母Ⅱ型发酵13.酵母Ⅲ型发酵14.优先合成途径15.营养缺陷型16.代谢渗漏型17.标准呼吸链18.侧呼吸链19.呼吸强度20.摄氧率21.抗结构类似物突变型22.微生物的热阻23.对数残留定律二、填空题(每空0.5分,共30分)1.当前微生物工业用菌种的总趋势是从发酵菌转向,从野生菌转向,从自然选育转向,从诱发基因突变转向。
2.调节培养基pH值的常用方法有、、。
3.淀粉的糖化过程包括、、等三种化学反应。
4.在酵母Ⅱ发酵液中添加发酵的终产物是。
5.谷氨酸合成中氨的导入方式有、和。
6.微生物发酵中供氧是指氧分子从空气泡里通过、和扩散到中。
7.供氧阻力包括、、和;8.耗氧阻力包括、、和。
9.溶氧系数的测定方法主要有、和。
10.只含有单一液相,且粘度小的典型溶液属于流体;含有固相、气相和液相而且粘度较大的发酵醪属于流体。
11.常用的菌种保藏方法有斜面低温保藏法、、、、和。
12.调节培养基pH值的常用方法有、、。
13.淀粉的糖化过程包括、、等三种化学反应。
14.酵母的Ⅲ型发酵是在条件下进行的,其产物为、、和。
15.微生物发酵中耗氧是指氧分子从液体主流通过、和扩散到。
16.谷氨酸合成中氨的导入方式有、和。
17.Monod方程的表达式为,它描述的是微生物生长和之间的关系。
18.在分批培养中,典型的细菌生长曲线包括、、和四个不同生长阶段。
19.干热灭菌对微生物有、和等作用。
20.干热灭菌主要用于,其特点是、。
21.紫外线灭菌的特点是,只能用于、等空间灭菌。
22.紫外线灭菌以波长nm灭菌效率为最高,一般用功率为的紫外灯照射分钟。
23.紫外线灭菌时,温度高则杀菌效率,湿度大则灯的使用寿命,空气中悬浮杂质多则。

计算题(生物反应工程)20225P1956-1在一定的酶浓度下,液相底物S分解为产物P,该反应器仅有底物S影响其反应速率,其动力学数据如下:cS/(mol/L)122334454.764.985105rS/[mol/(L·min)]1现在CSTR中进行此分解反应,保持相同的酶浓度和其操作条件。
试求:(1)当VR=250L,cS0=10mol/L,某S=0.80时,进料体积流量V0应为多少?(2)当V0=100L/min,,cS0=15mol/L,某S=0.80时,反应器有效体积VR为多少?(3)当VR=3m3,V0=1m3/min,cS0=8mol/L,反应器出口底物浓度和反应器内底物浓度各为多少?(4)当VR=1m3,V0=1m3/min,cS0=15mol/L,其出口底物浓度为多少?解:(1)有cS0cS=某S则cS=2mol/LrS=2mol/(L·min)cS0有VRrS=V0(cS0-cS)250某2=V0(10-2)V0=62.5L/min(2)有cS0cS=某ScS=cS0(1-0.8)=3mol/LrS=3mol/(L·min)cS0VRrS=V0(cS0-cS)VR某3=100某(15-3)VR=400L(3)VRrS=V0(cS0-cS)3某rS=1某(8-cS)当rS=2时,cS=26-2在一5m3CSTR中进行连续发酵,加料中底物浓度为20kg/m3,该反应器的有关参数为:-13ma某=0.45h,KS=0.8kg/m,Y某/S=0.55。
试求:(1)当底物达到90%转化时,所要求的加料速率是多少?(2)如果要求其细胞产率达到最大,加料速率为多少?细胞最大产率是多少?解:(1)cS=cS0(1-90%)=2kg/m3D==ma某0.4520.9cS=2.8KS+cS0.8+2DV03;VV0=1.61m3/hR5m/hVRma某((2)Dopt=1-KS)=0.362h-1KSCS0cS,optKSDoptma某Dopt=3.29kg/m3c某,optY某/S[cS0cS,opt]=0.55某(20-3.29)=9.2kg/m3(P某)ma某Doptc某,opt0.362某9.2=3.33kg/(m3·h)V0=5某0.362=1.8m/h6-10某液相酶反应具有下列动力学数据已知:cS0=10mol/L,V0=100L/min,某S=0.90cS/(mol/L)120.333416180.25100.1rS/[mol/(L·min)]0.1253(1)若采用带循环的CPFR,试求其最佳循环比及相应的反应器有效体积?(2)若要使反应器体积最小,如何设计最佳反应器方案?指出每个反应器的有效体积大小?解:(1)由题意知,出口浓度为1mol/L。


动力学计算题练习与解析动力学是研究物体运动的力学分支,通过计算物体的运动轨迹、速度、加速度等参数,可以深入了解物体的运动规律。
在学习动力学的过程中,解答计算题是非常重要的练习方法。
本文将为大家提供一些动力学计算题的练习与解析,帮助大家更好地理解和掌握动力学知识。
一、匀加速直线运动1. 问题描述:一辆汽车以20 m/s的速度沿直线匀加速行驶,20秒后速度达到40 m/s,求汽车的加速度。
解析:根据匀加速运动的速度-时间关系式v = v0 + at,其中v为终点速度,v0为初点速度,a为加速度,t为时间。
代入已知条件:v =40 m/s,v0 = 20 m/s,t = 20 s,求解a即可。
计算过程:40 = 20 + a × 20解方程可得:a = (40 - 20) / 20 = 1 m/s^2答案:汽车的加速度为1 m/s^2。
2. 问题描述:物体自由落体,从静止开始下落5秒钟后速度达到25 m/s,求物体的加速度。
解析:自由落体是一种匀加速直线运动,其加速度恒定且为重力加速度,记为g。
根据自由落体的速度-时间关系式v = gt,其中v为终点速度,g为加速度,t为时间。
代入已知条件:v = 25 m/s,t = 5 s,求解g即可。
计算过程:25 = g × 5解方程可得:g = 25 / 5 = 5 m/s^2答案:物体的加速度为5 m/s^2。
二、斜抛运动1. 问题描述:小明用力将一个小球水平抛出,抛出角度为30°,速度为10 m/s,求小球的飞行时间和水平位移。
解析:斜抛运动是一个在水平和垂直方向上都有加速度的运动。
首先,根据水平方向上的速度恒定,小球的飞行时间可以通过垂直方向上的运动求解。
根据小球的初速度、抛射角度和重力加速度,可以计算出小球在垂直方向上的运动时间。
然后,水平位移可以通过水平速度与飞行时间的乘积得到。
计算过程:垂直方向上的运动:初速度在垂直方向上的分速度v0y = 10 m/s × sin30° = 5 m/s根据自由落体运动的位移-时间关系式h = v0y × t + 1/2gt^2,其中h为高度,t为时间,g为重力加速度,代入已知条件h = 0,v0y = 5 m/s,g = 9.8 m/s^2,解方程可得t = 1 s水平方向上的运动:水平速度v0x = 10 m/s × cos30° = 10 m/s × √3/2 = 5√3 m/s水平位移d = v0x × t = 5√3 m/s × 1 s = 5√3 m答案:小球的飞行时间为1秒,水平位移为5√3米。

生物反应动力学•一、微生物生长动力学•1、生长速率γx=dX/dt=μX;(1)式中,X为菌体浓度,g·L-1;μ为比生长速率,h-1;【例题】以乙醇为唯一碳源进行产气气杆菌培养,细胞初始浓度X0=0.1kg/m3,培养至3.2h,细胞浓度为8.44kg/m3,如果不考虑延迟期,比生长速率一定,求倍增时间td。
【解】dX/dt=μX (1)当t=0,X=X0,积分(1)得lnX=μt+lnX变形为ln(X/X0)=μt (2)倍增时间是指X/X0=2所需时间,因此ln2=μtd(3)由(2)和(3),可得到t d=............= 0.5(h)•练习•下面为某微生物的生长数据,求此微生物的μ,1小时和2小时时候的生长速率。
•时间/h 0 0.5 1.0 1.5 2.0•细胞干重/(g/L) 0.1 0.15 0.23 0.34 0.512、生长的非结构模型确定论的非结构模型,是一种理想状况,不考虑细胞内部结构,每个细胞之间无差别,细胞群体作为一种溶质;•目前,常使用确定论的非结构模型是Monod方程•μ=μmax[S]/(K s+[S]) (2)•式中,μmax是最大比生长速率,[S]是某限制性营养物的浓度,K s为基质利用常数,相当于μ=μmax /2时的基质浓度.g·I-1,这是菌对基质的亲和力的一种度量。
【例题】乙醇为唯一碳源进行面包酵母培养,获得如下数据:[S]/(g/L) 0.4 0.33 0.18 0.10 0.07 0.049 0.038 0.020 0.014μ/(h-1) 0.161 0.169 0.169 0.149 0.133 0.135 0.112 0.0909 0.0735求μmax 和KS。
•3、基质消耗动力学•以菌体得率为媒介,可确定基质的消耗速率与生长速率的关系。
基质的消耗速率γS可表示为•-γS=d[S]/dt=γX/Y X/S (3)•基质的比消耗速率指基质的消耗速率除以菌体的量,以q S来表示,即qS=γS/X (4)•-q S=μ/Y X/S (5)•【例题】葡萄糖为唯一碳源进行酵母培养,反应式为:• 1.11C6H12O6+2.10O2→C3.92H6.5O1.94+2.75CO2+3.42H2O•μ为0.42h-1,求(1)Y X/S,(2)基质的比消耗速率•练习:•在啤酒酵母的生长试验中,消耗了0.2kg葡萄糖0.0672kgO2,生成0.0746kg酵母细胞和0.12lkg CO2,请计算酵母得率YX/S•μ由Monod 方程表示时,(5)式可变形为:•-q S =(-q S ,max )[S]/(K S +[S]) (6)•当以氮源、无机盐类、维生素等为基质时,由于这些成分只能组成菌体的构成成分,不能成为能源,Y X/S 近似一定,所以式(6)能够成立,但当基质既作为能源又是碳源时,就应考虑维持代谢所消耗的能量。


一、填空题(每空0.5分,数学公式为1分,共21分)1.世界发酵史上曾经历了四个历史发展时期(或阶段),分别是:天然发酵(古老发酵时期) ;纯培养发酵技术(第一代微生物发酵时期) ;深层培养技术(第二代微生物发酵时期;微生物工程(第三代/现代微生物发酵时期)2. 重要工业微生物菌种的获得途径:从已保藏的菌种中获得;从保藏机构购买;从自然环境中采样分离。
3. 原核基因和许多真核基因一般都能够在原核生物中获得表达;但对于需要转录或翻译后加工处理的真核基因,则不能用原核表达系统来表达,这是因为原核细胞缺乏像真核细胞那样的转录和翻译后加工系统,具体说原核表达系统存在以下三方面的缺陷:不能进行蛋白质的糖基化;不能进行氨基酸的修饰(甲基化);不能切除mRNA的内含子。
4基因工程的基本操作步骤为为:目的基因的取得、载体系统的选择、目的基因与载体基因的构建、重组载体导入受体细胞、“工程菌”的表达、筛选及鉴定、工程菌生产性试验及大规模生产;5. 在平衡生长状态下,生长速率、比生长速率及倍增时间之间的数学表达式为:u=0.693/dt(或dx/dt=ux)。
Monod在1942年推导出一个近似的数学表达式来描述比生长速率与底物浓度的关系,该公式数学可表达为:U=Umax[S]/(Ks+[S] 。
6. 研究微生物生长动力学(或发酵动力学)的方法一般有以下几步,即:找出重要理化参数;找出变化规律;建立技术数学模型;验证可行性与适应范围 7.发酵过程的六个基本单元操作是培养基的配制; 培养基及其设备的灭菌;种子发酵;产物发酵;产物的提取和纯化;废液的处理8. 空气除菌中,深层过滤除菌的机制有以下五个方面:纤维介质对颗粒的拦截;颗粒的惯性冲击; 布朗运动(扩散); 颗粒与介质之间的静电引力; 重力。
9. 在20℃下,1大气压空气相平衡时,1升水中的含氧量为0.28mmol (或6.2ml )(注;要写出数值与单位);溶解氧的浓度主要由两个变量通气量和搅拌速度来控制。
第三章微生物反应动力学习题1. 微生物反应的特点,其与化学反应的主要区别有那些?2.简要回答微生物反应与酶促反应的最主要区别?3. 进行微生物反应过程的物量衡算有何意义,请举例说明。
4.Monod 方程建立的几点假设是什么?Monod 方程与米氏方程主要区别是什么?5.举例简要说明何为微生物反应的结构模型?6. 以葡萄糖为单一碳源,进行某种微生物好氧或厌氧培养。
已知此菌的比生长速率μ、葡萄糖的比消耗速率γ、细胞、葡萄糖、二氧化碳和各产物中的碳元素含量α1、α2、α3 和αi,利用这6 个常数给出此菌的与生长相关的物料衡算式。
7. 葡萄糖为碳源的复合培养基进行干酪乳杆菌的厌氧培养,1mol葡萄糖可生成乳酸或乙酸或乙醇或甲酸为0.05mol、1.05mol、0.94mol和1.76mol,试讨论各分解代谢的碳元素的恒算及生成ATP的摩尔数。
8. 荧光假单胞菌(Pseudomonas fluorescens)好氧培养中,已知:Y x/s=180g/mol,Y x/o=30.4g/mol,每消耗1mol葡萄糖可生成2molATP,氧化磷酸化的P:O比为1,求Y ATP?9. 在啤酒酵母的生长试验中,消耗了0.2kg 葡萄糖和0.0672kgO2,生成0.0746kg 酵母菌和 0.121kgCO2,请写出该反应的质量平衡式,计算酵母得率Y X/S 和呼吸商RQ。
10. 微生物物繁殖过程中分裂一次生成两个子细胞,也有4 分裂或8 分裂的,试证明当n 分裂时,有如下式子:,式中: 为倍增时间, 为世代时间。
11.分别采用含有蛋白胨和牛肉膏的复合培养基、含有20 余种氨基酸的合成培养基和基本培养基进行运动发酵单胞菌厌氧培养,碳源为葡萄糖,获得如下表所示结果。
已知菌体的含碳量(以碳源/细胞计)为0.45g/g,求采用不同培养基时的Y KJ。
12. 葡萄糖为碳源进行酿酒酵母培养,呼吸商为1.04,氨为氮源。
消耗100mol 葡萄糖和48mol氨,生成细胞48mol、二氧化碳312mol 和水432mol。
浙江大学工业微生物92-971992 年攻读硕士学位研究生入学考试试题一填空(共15分)1、细菌一般进行a 繁殖,即b 。
酵母的繁殖方式分为有性和无性两类,无性繁殖又可分为c ,d 两种形式,有性繁殖时形成 e ;霉菌在有性繁殖中产生的有性孢子种类有 f ,g ,h ;在无性繁殖中产生的无性孢子种类有i ,j ,k ;放线菌以l 方式繁殖,主要形成m ,也可以通过n 繁殖。
2、一摩尔葡萄糖通过EMP途径和TCA循环彻底氧化,在原核微生物中产生a 摩尔ATP,在真核微生物中产生b 摩尔ATP,这是因为在真核微生物中,c 不能通过线粒体膜,只能借助于d 将EMP途径产生的磷酸二羟丙酮还原成 e ,后者可进入线粒体,将氢转移给f ,形成g ,自身又回复到磷酸二羟丙酮。
这一过程称为“穿梭”,每次穿梭实际损失h 个ATP。
3、微生物基因突变的机制包括a 、b 及c 。
诱发突变的方法分为物理方法和化学方法,物理方法主要是d , e , f 和g ;化学诱变剂包括h ,i 和j 。
二是非题(叙述正确的在括号写T,错误的写F,共10分)1、自养型、专性厌氧型微生物不是真菌()2、在酵母细胞融合时,用溶菌酶破壁()3、从形态上看,毛霉属细菌都有假根()4、营养缺陷型菌株不能在基本培养基上正常生长()5、产黄青霉在工业生产上只用于生产青霉素()6、分子氧对专性厌氧微生物的抑制和制死作用是因为这些微生物内缺乏过氧化氢酶()7、同工酶是指能催化同一个反应,有相同控制特征的一组酶()8、基因位移是借助于酶或定向酶系统实现的主动输送,因此不需要消耗能量()9、培养基中加入一定量NaCl的作用是降低渗透压()10、噬菌体的RNA必须利用寄主的蛋白质合成体系翻译,因此只能在寄主体内繁殖()三. 名词解释(共15分)1、抗代谢物2、温和噬菌体3、阻遏酶4、转化5、活性污泥四在恒化器中培养微生物,在稳态操作时,μ=D,D为稀释率,μ可用Monod公式描述:求:a. 恒化器出口底物浓度S0和微生物浓度X0b. 当稀释率D增加到一定程度后会产生“清洗”现象,求发生清洗现象的最小稀释率Dcritc. 单位体积细胞产率可以用细胞出口浓度X0与稀释率的乘积DX0表示。
第三章 微生物反应动力学习题答案1. 微生物反应的特点,其与化学反应的主要区别有那些? 答:微生物反应与化学反应相比,具有以下特点:1)微生物反应属于生化反应,通常是在常温常压下进行;2)反应原料来源相对丰富;3)易于生产复杂的高分子化合物和光学活性物质;4)通过菌种改良,可大大提高设备的生产能力;5)副产物多,提取有一定难度;6)生产微生物受外界环境影响比较大;7)开发成本较大;8)废水BOD较大2.简要回答微生物反应与酶促反应的最主要区别?答:微生物反应与酶促反应的最主要区别在于,微生物反应是自催化反应,而酶促反应不是。
此外,二者还有以下区别:(1)酶促反应由于其专一性,没有或少有副产物,有利于提取操作,对于微生物反应而言,基质不可能全部转化为目的产物,副产物的产生不可避免,给后期的提取和精制带来困难,这正是造成目前发酵行业下游操作复杂的原因之一。
(2)对于微生物反应,除产生产物外,菌体自身也可是一种产物,如果其富含维生素或蛋白质或酶等有用产物时,可用于提取这些物质。
(3)与微生物反应相比,酶促反应体系较简单,反应过程的最适条件易于控制。
微生物反应是利用活的生物体进行目的产物的生产,因此,产物的获得除受环境因素影响外,也受细胞因素的影响,并且微生物会发生遗传变异,因此,实际控制有一定难度。
(4)酶促反应多限于一步或几步较简单的生化反应过程,与微生物反应相比,在经济上有时并不理想。
4. 答:Monod 方程建立的基本假设:微生物生长中,生长培养基中只有一种物质的浓度(其他组分过量)会影响其生长速率,这种物质被称为限制性基质,并且认为微生物为均衡生长且为简单的单一反应。
Monod 方程与米氏方程的主要区别如下表所示:Monod 方程:SK SS +=max μμ米氏方程:SK Sr r m +=max方程中各项含义: μ:生长比速 μmax :最大生长比速 S: 单一限制性基质浓度 K S : 半饱和常数 方程中各项含义: r:反应速率 r max :最大反应速率 S:底物浓度 K m :米氏常数 微生物生长动力学方程酶促反应动力学方程经验方程 理论推导的机理方程适用于单一限制性基质的情况 适用于单底物、无抑制的情况5、答:由于细胞的组成是复杂的,当微生物细胞内部所含有的蛋白质、脂肪、碳水化合物、核酸、维生素等的含量随环境条件的变化而变化时,建立起的动力学模型称为结构模型。