高斯投影及其计算资料

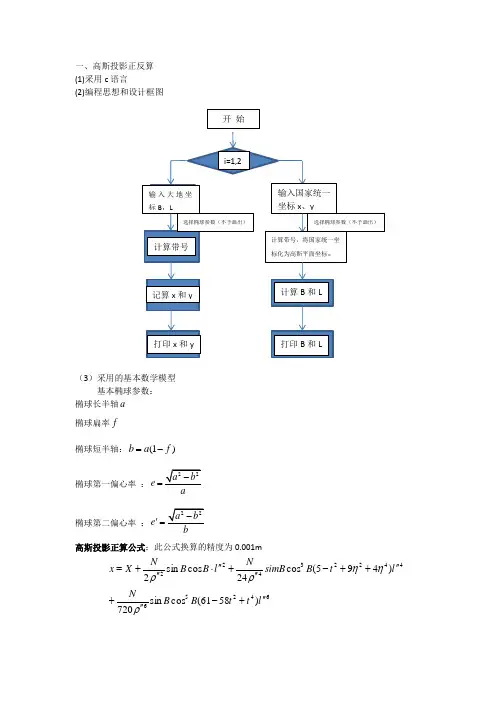
一、高斯投影正反算 (1)采用c 语言(2)编程思想和设计框图（3）采用的基本数学模型 基本椭球参数： 椭球长半轴a 椭球扁率f椭球短半轴：(1)b a f =-椭球第一偏心率：e =椭球第二偏心率：e b'=高斯投影正算公式：此公式换算的精度为0.001m6425644223422)5861(cos sin 720)495(cos 24cos sin 2lt t B B N lt B simB N l B B N X x ''+-''+''++-''+''⋅''+=ρηηρρ5222425532233)5814185(cos 120)1(cos 6cos lt t t B N lt B N l B N y ''-++-''+''+-''+''⋅''=ηηρηρρ其中：角度都为弧度B 为点的纬度，0l L L ''=-，L 为点的经度，0L 为中央子午线经度； N 为子午圈曲率半径，1222(1sin )N a e B -=-； tan t B =；222cos e B η'=1803600ρπ''=*其中X 为子午线弧长：2402464661616sin cos ()(2)sin sin 33X a B B B a a a a a B a B ⎡⎤=--++-+⎢⎥⎣⎦02468,,,,a a a a a 为基本常量，按如下公式计算：200468242684468686883535281612815722321637816323216128m a m m m m m m a m mm a m m m m a m a ⎧=++++⎪⎪⎪=+++⎪⎪⎪=++⎨⎪⎪=+⎪⎪⎪=⎪⎩02468,,,,m m m m m 为基本常量，按如下公式计算：22222020426486379(1);;5;;268m a e m e m m e m m e m m e m =-====；高斯投影反算公式：此公式换算的精度为0.0001’’.()()()()222224324653223524222553922461904572012cos 6cos 5282468120cos f f f ff f f f ff fff f f ff f f f f f f f f f f f f t t B B y tt yM N M Nt y t t yM Ny y l t N B N B y t t t N B L l L ηηηηη=-+++--++=-+++++++=+其中：0L 为中央子午线经度。

高斯投影正反算学院：资源与环境工程工程学院专业：测绘工程 学号：X51414012：超一、高斯投影概述想象有一个椭圆柱面横套在地球椭球体外面，并与某一条子午线相切，椭圆柱的中心轴通过椭球体的中心，然后用一定投影方法，将中央子午线两侧各一定经差围的地区投影到椭圆柱面上，再将此柱面展开即成为投影面。

高斯投影由于是正形投影，故保证了投影的角度不变性，图形的相似性以及在某点各方向上长度比的同一性。

由于采用了同样法则的分带投影，这即限制了长度变形，又保证了在不同投影带中采用相同的简便公式和数表进行变形引起的各项改正的计算，并且带与带间的互相换算也能用相同的公式和方法进行。

高斯投影的这些优点必将使它得到广泛的推广和具有国际意义。

二、高斯投影坐标正算公式1.高斯投影必须满足以下三个条件 1）中央子午线投影后为直线 2）中央子午线投影后长度不变 3）投影具有正形性质，即正形投影条件2.高斯正算公式推导1）由第一个条件可知，由于地球椭球体是一个旋转椭球体，所以高斯投影必然有这样一个性质，即中央子午线东西两侧的投影必然对称于中央子午线。

2）由于高斯投影是换带投影，在每带经差ｌ是不大的，ｌρ是一个微小量，所以可以将X=X （ｌ，q ），Y=Y （l ，q ）展开为经差为l 的幂级数，它可写成如下的形式X=m 0+m 2l 2+m 4l 4+…Y=m 1l+m 3l 2+m 5l 5+…式中m 0,m1,m2,…是待定系数，他们都是纬度B 的函数。

3）由第三个条件：∂y ∂l =∂x ∂q 和∂x ∂l =-∂y∂q ，将上式分别对l 和q 求偏导2340123423401234...........x m m l m l m l m l y n n l n l n l n l =+++++=+++++可得到下式0312123403121234111,,,, 234111,,,,234dm dm dm dm n n n n dq dq dq dq dn dn dn dn m m m m dq dq dq dq ⎧====⎪⎪⎨⎪=-=-=-=-⎪⎩经过计算可以得出232244524632235242225sin cos sin cos (594)224 sin cos (6158)720cos cos (1)6cos (5181458)120N N x X B B l B B t l NB B t t l Ny N B l B t l NB t t t l ηηηηη=+⋅+-+++-+=⋅+-++-++-三、高斯投影坐标反算公式推导1.思路：级数展开，应用高斯投影三个条件，待定系数法求解。

高斯投影正反算原理高斯投影是一种常用于地图制图的投影方式，也被广泛应用于其他领域的空间数据处理。

高斯投影正反算是对于已知的地球坐标系上的位置（经纬度），通过计算得到该点的平面坐标（东、北坐标），或者对于已知的平面坐标（东、北坐标），通过计算得到该点的地球坐标系上的位置（经纬度）的过程。

本文将详细介绍高斯投影正反算的原理。

一、高斯投影简介高斯投影是一种圆锥投影，其投影面在地球表面的某个经线上，也就是说，投影面是以该经线为轴的圆锥面。

经过对圆锥体的调整后，使其切于地球椭球面，在该经线上进行投影，同时保持沿该经线方向的比例尺一致，从而达到地图上各点在包括该经线的垂直面上映射的目的。

这种投影方式在某一特定区域内得到高精度的结果，因此广泛应用于地图制图。

二、高斯投影数学模型对于高斯投影正反算，需要先建立高斯投影坐标系与地球坐标系的转换模型。

1.高斯投影坐标系的建立高斯投影坐标系的建立需要确定圆锥面的基本参数，首先需要确定其所处的中央子午线，再确定该子午线上的经度为零点，并利用该经线上某一点的经度和该点的高度来确定该点所在的圆锥体。

圆锥体的底面包括所有与地球椭球面相切的圆面，通过对这些圆面进行调整，使得圆锥体转动后能够在中央子午线上进行投影。

在此基础上，可建立高斯投影坐标系，其中投影面为圆锥面，且中央子午线与投影面的交点称为该投影坐标系的中心，投影面的上端点和下端点分别对应正北方向和正南方向。

2.地球坐标系的建立地球坐标系是以地球椭球体为基础建立的，其坐标系原点确定为地球椭球体上的一个特定点。

在已知该点经纬度和高度的前提下，可确定以该点为中心的地球椭球体，并可根据它与地球坐标系之间的转换关系得到平面坐标系。

3.高斯投影坐标系与地球坐标系之间的转换关系由于高斯投影坐标系与地球坐标系存在不同的坐标体系和基准面，因此需要通过数学关系式来建立它们之间的转换关系。

（1）高斯投影坐标系转地球坐标系：已知高斯投影坐标系中任意一点的东北坐标（N，E），以及所属的中央子午线经度λ0、椭球参数a和e，则可通过以下公式求出该点的地球坐标系经纬度（φ，λ）和高度H：A0为以地球椭球体中心为原点，高斯投影坐标系中心投影坐标为（0，0）的点到椭球面的距离。