华南理工 网络 大学物理随堂练习

《大学物理C 》随堂测查试题（1）姓名 学号 学院 成绩一、 单项选择题（把正确答案的英文字母填入括号内，每题3分，共15分）1、下列关于定常流动的说法不正确的是（ D ）A. 流速只是空间的函数，与时间无关 C. 流线不随时间变化，且与质元运动轨迹重合B. 流体质元不会任意进出流管 D. 流经空间各点的流速相同2、液体在毛细管中上升（或下降）的高度与下列哪个因素无关（ C ）A. 毛细管的内径B.液体的表面张力系数C. 毛细管的长度D. 液体与毛细管的接触角3、截面不均匀的导水管，假设在A 处的横截面积为S 1，流速为υ1,在B 处的横截面积为S 2, 那么在B 处水的流速为（ B ）A. S 1υ1B. 112S S υ C. υ1 D. 0 4、根据伯努利方程，若流体处于同一高度，下列说法正确的是（ C ）A. 压强大的地方，则流速大 C. 压强大的地方，则流速小B. 不管流速为多少，压强不变 D. 不管压强为多少，流速不变5、对于同一化学种类的理想气体系统，下列说法正确的是（ A ）A. 温度越高，最概然速率越大 C. 温度越高，最概然速率越小B. 最概然速率比平均速率大 D. 最概然速率比方均根速率大二、 计算题（作答篇幅不够，可写在背面）1. （6分）在温度为20摄氏度，大气压为p 0下,一滴水珠的半径为R ,则水珠表面产生的附加压强是多少？ 水珠内部的压强是多少？（20摄氏度时水的表面张力系数为γ） 解：附加压强：s 2P Rγ＝…………………………(3分) 水珠内部压强：0s 02P P +P P +Rγ＝＝………………(3分) 2．（9分）在容积为2升的容器中，有内能E 为500J 的刚性双原子分子理想气体，(1).求气体的压强是多少？(2).若容器中分子总数N 为5×1022个，求分子的平均动能ε和气体的温度T 分别是多少？ 解：(1). 刚性双原子分子理想气体自由度i =5…………………………(1分)根据理想气体内能公式： 2m i E RT M =…………………………(1分) 和气体状态方程：PV m RT M =，得： PV 2i E =，………………(2分) 所以，气体的压强：5-322500P ==110 (Pa)V 5210E i ××××………………(1分) (2). 理想气体内能N E ε=⋅， ………………(1分) 所以分子的平均动能ε：-2022E 500===110 (J)N 510ε××………………(1分) 根据P nkT =，N =Vn 得：………………………………………………(1分) 气体的温度：5-3-2122P PV 102101====410=290 (K)N 510T nk k k k×××⋅×………………(1分) 或根据平均动能=T 2i k ε，得：2121T=410=290 (K)ik k ε−=×⋅ ………(2分)。

姓名 班级 序号机械波1、一平面简谐波表达式为y =5cos （8t+3x +4π），式中各量采用国际单位制。

问： （1）它向什么方向传播？（2）它的频率、波长、波速各是多少？（3）质点的最大振动速度及最大加速度是多少？ （4）x =2m 处，质点的初相位是多少？2．如图，一平面简谐波以波速u 沿x 轴正方向传播，O 为坐标原点．已知P 点的振动方程为cos y A t ω=，则 ［ ］（A ）O 点的振动方程为 []cos (/)y A t l u ω=-； （B ）波的表达式为 {}cos [(/)(/)]y A t l u x u ω=--； （C ）波的表达式为 {}cos [(/)(/)]y A t l u x u ω=+-； （D ）C 点的振动方程为 []cos (3/)y A t l u ω=-。

3．一平面简谐波以速度u 沿x 轴正方向传播，在t t '=时波形曲线如图所示．求坐标原点O 的振动方程和波动方程。

4．平面简谐波沿x 轴正方向传播，振幅为2cm ，频率为50Hz ，波速为 200 m/s ．在0t =时，0x =处的质点正在平衡位置向y 轴正方向运动，求4m x =处媒质质点振动的表达式及该点在2s t =时的振动速度。

5．一平面简谐波沿Ox 轴的负方向传播，波长为λ ，P 处质点的振动规律如图所示．（1）求P 处质点的振动方程； （2）求此波的波动表达式；（3）若图中 λ21=d ，求坐标原点O 处质点的振动方程。

6、一平面简谐波在弹性介质中传播，在介质质元从最大位移运动到平衡位置处的过程中:（ ）。

A.它的动能转换成势能；B.它的势能转换成动能；C.它从相邻一段一段质元获得能量其能量逐渐增大；D.它把自己的能量传给相邻的一段质元，其能量逐渐减少。

7．一平面简谐波，频率为31.010Hz ⨯，波速为31.010m/s ⨯，振幅为m 100.14-⨯，在截面面积为424.010m -⨯的管内介质中传播，若介质的密度为238.010kg m -⨯⋅，则该波的能流密度__________________；该波在60 s 内垂直通过截面的总能量为_________________。

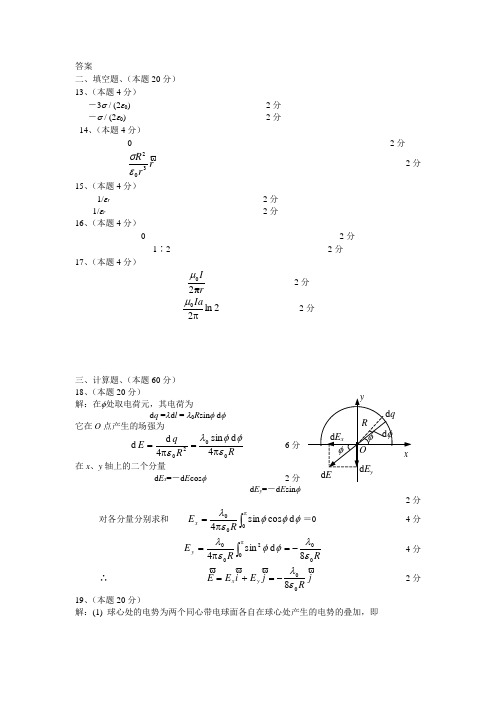
答案二、填空题、（本题20分） 13、（本题4分）－3σ / (2ε0) 2分 －σ / (2ε0) 2分 14、（本题4分）0 2分r r R 302εσ 2分15、（本题4分）1/εr 2分 1/εr 2分 16、（本题4分）0 2分 1∶2 2分17、（本题4分）rIπ20μ 2分2ln 20πIaμ 2分三、计算题、（本题60分） 18、（本题20分）解：在φ处取电荷元，其电荷为d q =λd l = λ0R sin φ d φ它在O 点产生的场强为R RqE 00204d sin 4d d εφφλεπ=π= 6分 在x 、y 轴上的二个分量 d E x =－d E cos φ 2分d E y =－d E sin φ2分对各分量分别求和 ⎰ππ=000d c o s s i n 4φφφελR E x ＝04分RR E y 0002008d sin 4ελφφελ-=π=⎰π 4分 ∴ j Rj E i E E y x008ελ-=+= 2分19、（本题20分）解：(1) 球心处的电势为两个同心带电球面各自在球心处产生的电势的叠加，即⎪⎪⎭⎫ ⎝⎛+π=22110041r q r q U ε⎪⎪⎭⎫ ⎝⎛π-ππ=22212104441r r r r σσε()210r r +=εσ7分2100r r U +=εσ＝8.85×10-9 C / m 2 4分 (2) 设外球面上放电后电荷面密度为σ'，则应有()21001r r U σσε'+='= 0 4分 即σσ21r r -=' 2分 外球面上应变成带负电，共应放掉电荷 ()⎪⎪⎭⎫ ⎝⎛+π='-π='212222144r r r r q σσσ ()20021244r U r r r εσπ=+π=＝6.67×10-9 C 3分20（本题20分） 解：其中3/4圆环在D 处的场 )8/(301a I B μ= 5分 AB 段在D 处的磁感强度 )221()]4/([02⋅π=b I B μ 5分 BC 段在D 处的磁感强度 )221()]4/([03⋅π=b I B μ 5分 1B 、2B 、3B方向相同，可知D 处总的B 为)223(40ba I B +ππ=μ 5分。

大学物理作业答案一、选择题第1题,答案D ，第2题,答案C ， 第3题,答案A C ，第4题,答案C ，第5题,答案B ， 第6题,答案C ，第7题,答案A D ，第8题,答案A ，第9题,答案D ，第10题,答案ADEH 第11题,答案C ，第12题,答案C ，第13题,答案BDF ，第14题,答案C ，第15题,答案A ， 第16题,答案ACE ，第17题,答案AC ，第18题,答案A ，第19题,答案A ，第20题,答案D ， 第21题,答案B ， 二、计第算题100. 质量为M 的木块静止在光滑的水平面上．质量为m 、速率为v 的子弹沿水平方向打入木块并陷在其中，试计算相对于地面木块对子弹所作的功W 1及子弹对木块所作的功W 2． 解：设子弹打入木块后二者共同运动的速率为V ，水平方向动量守恒，有 V M m m )(+=v , )/(M m m V +=v木块对子弹作的功 2212121v m mV W -=22)(2)2(v m M m M Mm ++-=101. 如图所示，质量为m 2的物体与轻弹簧相连，弹簧另一端与一质量可忽略的挡板连接，静止在光滑的桌面上．弹簧劲度系数为k ．今有一质量为m 1速度为0v 的物体向弹簧运动并与挡板正碰，求弹簧最大的被压缩量．km 2m 1v解：弹簧被压缩量最大距离时，m 1、m 2相对速度为零．这时动量守恒 vv )(2101m m m +=机械能守恒 222120121)(2121kx m m m ++=v v 由上二式可解得弹簧的最大被压缩量为)(21210m m k m m x +=v102. 一质量为m 的子弹，水平射入悬挂着的静止砂袋中，如图所示．砂袋质量为M ，悬线长为l ．为使砂袋能在竖直平面内完成整个圆周运动，子弹至少应以多大的速度射入？mMlO解:子弹对木块作的功 2221mV W =222)(2v m M Mm +=解：动量守恒越过最高点条件机械能守恒解上三式，可得103. 如图所示，一内半径为a、外半径为b的金属球壳，带有电荷Q，在球壳空腔内距离球心r 处有一点电荷q．设无限远处为电势零点，试求：(1) 球壳内外表面上的电荷．(2) 球心O点处，由球壳内表面上电荷产生的电势．(3) 球心O点处的总电势．解：(1) 由静电感应，金属球壳的内表面上有感生电荷-q，外表面上带电荷q+Q．(2)(3104. 图示为一半径为a的、带有正电荷Q的导体球．球外有一内半径为b、外半径为c的不带电的同心导体球壳．设无限远处为电势零点，试求内球和球壳的电势.．ROaQbc解：105. 载有电流I的平面闭合回路由半径为R1及R2(R1> R2)的两个同心半圆弧和两个直导线段组成．已知两个直导线段在半圆弧中心O点产生的磁感强度均为零．若闭合回路在O点产生的总的磁感强度B大于半径为R2的半圆弧在O点产生的磁感强度B2，(1) 画出载流回路的形状；(2) 求出O点的总磁感强度B．解：(1) 可知．故闭合回路形状如图所示.qQabOr(2) ，106. 空中电流分布如图，两个半圆共面，且具有公共圆心，试求O 点处的磁感强度．I II OR 2R解：设半径分别为R 和2R 的两个载流半圆环在O 点产生的磁感强度的大小分别 为B1和B2．O 点总磁感强度为 (方向指向纸内)107. 一无限长的直导线载有如图所示的电流，长度为b 的金属杆CD 与导线共面且垂直，相对位置如图．CD 杆以速度v 平行直线电流运动，求CD 杆中的感应电动势，并判断C 、D两端哪端电势较高？a bI CDv解：建立坐标(略)：，方向⊙感应电动势方向为C→D，D 端电势较高108有电流的I 长直导线附近，放一导体半圆环MeN 与长直导线共面，且端点MN 的连线与长直导线垂直．半圆环的半径为b ，环心O 与导线相距a ．设半圆环以速度 v 平行导线平移，求半圆环内感应电动势的大小和方向以及MN 两端的电压U M U N ．b MNeaI Ov解：动生电动势为计算简单，可引入一条辅助线MN ，构成闭合回路MeNM, 闭合回路总电动势负号表示的方向与x 轴相反．方向N→M109已知一平面简谐波的表达式为 )37.0125cos(25.0x t y -= (SI) (1) 分别求x 1 = 10 m ，x 2 = 25 m 两点处质点的振动方程； (2) 求x 1，x 2两点间的振动相位差； (3) 求x 1点在t = 4 s 时的振动位移． 解：(1) x1 = 10 m 的振动方程为(SI)x2 = 25 m 的振动方程为(SI)(2) x2与x1两点间相位差 Df = f2 - f1 = -5.55 rad (3) x1点在t = 4 s 时的振动位移 y = 0.25cos(125×4－3.7) m= 0.249 m 110 一质点按如下规律沿x 轴作简谐振动：)328cos(1.0π+π=t x (SI)．求此振动的周期、振幅、初相、速度最大值和加速度最大值． 解: 周期 s ， 振幅 A = 0.1 m ， 初相 f = 2p/3，vmax = w A = 0.8p m/s ( = 2.5 m/s )， amax = w 2A = 6.4p2 m/s2 ( =63 m/s2 )．111 图示一平面简谐波在t = 0 时刻的波形图，求(1) 该波的波动表达式；x (m) O-0.040.20 u = 0.08 m/sy (m)P0.400.60(2) P 处质点的振动方程. 解：(1) O 处质点，t = 0 时，所以又(0.40/ 0.08) s= 5 s故波动表达式为(SI)(2) P 处质点的振动方程为(SI)112 如图，一平面波在介质中以波速u = 20 m/s 沿x 轴负方向传播，已知A 点的振动方程为 t y π⨯=-4cos 1032 (SI)．(1) 以A 点为坐标原点写出波的表达式； ABxu (2) 以距A 点5 m 处的B 点为坐标原点，写出波的表达式． 解：(1) 坐标为x 点的振动相位为波的表达式为 (SI)(2) 以B 点为坐标原点，则坐标为x 点的振动相位为(SI)波的表达式为(SI) 113 有一平面电磁波其电场强度为 x E t z ˆe 100)102102(i 62⨯π-⨯π-= （SI ）其中x ˆ是x 方向的单位矢量．（以下计算中，答案中要写明单位） (1) 判断电场的振动方向和波传播的方向． (2) 确定该波的圆频率和波长． (3) 确定该波的波速．(4) 若此波的磁场强度为 yH t z ˆe 25)102102(i 62⨯π-⨯π-π= (SI)(1) 电场强度振动的方向与平行，波传播方向为(2) 圆频率w = 2p×106 Hz = 6.28×106 Hz波长l = 2p / k = 2p / 2p×10-2 = 100 m(3) 波速 u = l / T = w l / 2p = 108 m /s(4) 坡印亭矢量，S0 = 79.6 J？m-2？s-1 平均功率79.6 W （A表示面积）。

第二章 运动的守恒量和守恒定律练 习 一一. 选择题1. 关于质心，有以下几种说法，你认为正确的应该是（ C ）(A ) 质心与重心总是重合的； (B ) 任何物体的质心都在该物体内部； (C ) 物体一定有质心，但不一定有重心； (D ) 质心是质量集中之处，质心处一定有质量分布。

2. 任何一个质点系，其质心的运动只决定于（ D ）(A )该质点系所受到的内力和外力； (B) 该质点系所受到的外力；(C) 该质点系所受到的内力及初始条件； (D) 该质点系所受到的外力及初始条件。

3.从一个质量均匀分布的半径为R 的圆盘中挖出一个半径为2R 的小圆盘，两圆盘中心的距离恰好也为2R 。

如以两圆盘中心的连线为x 轴，以大圆盘中心为坐标原点，则该圆盘质心位置的x 坐标应为（ B ） (A )R 4； (B) R 6; (C) R 8； (D R12。

4. 质量为10 kg 的物体，开始的速度为2m/s ，由于受到外力作用，经一段时间后速度变为6 m/s ，而且方向转过90度，则该物体在此段时间内受到的冲量大小为 （ B ） (A )s N ⋅820； (B) s N ⋅1020； (C) s N ⋅620； (D) s N ⋅520。

二、 填空题1. 有一人造地球卫星，质量为m ，在地球表面上空2倍于地球半径R 的高度沿圆轨道运行，用m 、R 、引力常数G 和地球的质量M 表示，则卫星的动量大小为RGMm3。

2．三艘质量相等的小船在水平湖面上鱼贯而行，速度均等于0v ，如果从中间小船上同时以相对于地球的速度v 将两个质量均为m 的物体分别抛到前后两船上，设速度v 和0v 的方向在同一直线上，问中间小船在抛出物体前后的速度大小有什么变化:大小不变。

3. 如图1所示，两块并排的木块A 和B ，质量分别为m 1和m 2，静止地放在光滑的水平面上，一子弹水平地穿过两木块。

设子弹穿过两木块所用的时间分别为∆t 1和∆t 2，木块对子弹的阻力为恒力F ，则子弹穿出后，木块A 的速度大小为 1A BF t m m ⋅∆+，木块B 的速度大小为12F t A BBF t m m m ⋅∆⋅∆++。

华南理工大学网络教育平台大学物理随堂练习.1. 一质点在平面上作一般曲线运动，其瞬时速度为，瞬时速率为v，，某一时间内的平均速度为，平均速率为，它们之间的关系必定有：（A）（B）（C）（D）参考答案：D2. 一质点在平面上运动，已知质点位置矢量的表示式为（其中a、b为常量）, 则该质点作(A) 匀速直线运动．(B) 变速直线运动．(C) 抛物线运动．(D)一般曲线运动．参考答案：B3. 如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率收绳，绳不伸长、湖水静止，则小船的运动是(A) 匀加速运动．(B) 匀减速运动．(C) 变加速运动．(D) 变减速运动．参考答案：C4. 一飞机相对空气的速度大小为200 km/h, 风速为56 km/h，方向从西向东．地面雷达站测得飞机速度大小为192 km/h，方向是(A) 南偏西16.3°．(B) 北偏东16.3°(C) 向正南或向正北．(D) 西偏北16.3°．(E) 东偏南16.3°．参考答案：C5. 对于沿曲线运动的物体，以下几种说法中哪一种是正确的：(A) 切向加速度必不为零．(B) 法向加速度必不为零（拐点处除外）．(C) 由于速度沿切线方向，法向分速度必为零，因此法向加速度必为零．(D) 若物体作匀速率运动，其总加速度必为零．(E) 若物体的加速度为恒矢量，它一定作匀变速率运动．参考答案：B6. 一质点沿直线运动,其运动学方程为x = 6 t－t2 (SI)，则8 m ．(B) 8.25 m ．(C) 5 m ．(D) 10 m 参考答案：A7. 一质点在Oxy平面内运动．运动学方程为2 t和19-（A）（B）（C）（D）参考答案：D2. 一质点在平面上运动，已知质点位置矢量的表示式为（其中a、b为常量）, 则该质点作(A) 匀速直线运动．(B) 变速直线运动．(C) 抛物线运动．(D)一般曲线运动．参考答案：B3. 如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率收绳，绳不伸长、湖水静止，则小船的运动是(A) 匀加速运动．(B) 匀减速运动．(C) 变加速运动．(D) 变减速运动．参考答案：C4. 一飞机相对空气的速度大小为200 km/h, 风速为56 km/h，方向从西向东．地面雷达站测得飞机速度大小为192 km/h，方向是(A) 南偏西16.3°．(B) 北偏东16.3°(C) 向正南或向正北．(D) 西偏北16.3°．(E) 东偏南16.3°．参考答案：C5. 对于沿曲线运动的物体，以下几种说法中哪一种是正确的：(A) 切向加速度必不为零．(B) 法向加速度必不为零（拐点处除外）．(C) 由于速度沿切线方向，法向分速度必为零，因此法向加速度必为零．(D) 若物体作匀速率运动，其总加速度必为零．(E) 若物体的加速度为恒矢量，它一定作匀变速率运动．参考答案：B6. 一质点沿直线运动,其运动学方程为x = 6 t－t2 (SI)，则8 m ．(B) 8.25 m ．(C) 5 m ．(D) 10 m 参考答案：A7. 一质点在Oxy平面内运动．运动学方程为2 t和19：B8. 一物体在某瞬时，以初速度从某点开始运动，在D t时间内，经一长度为S的曲线路径后，又回到出发点，此时速度为，则在这段时间内：物体的平均加速度是_________________．．(A) ．(B) ．(C) ．(D) ．参考答案：B9. 一质点沿半径为R的圆周运动，其路程S随时间t变化的规律为(SI) ，式中b、c为大于零的常量, 且b2Rc.. 则此质点运动的切向加速度at 和法向加速度an为．．(A) - 物体的平均加速度是_________________．．(A) ．(B) ．(C) ．(D) ．参考答案：B9. 一质点沿半径为R的圆周运动，其路程S随时间t变化的规律为(SI) ，式中b、c为大于零的常量, 且b2Rc.. 则此质点运动的切向加速度at 和法向加速度an为．．(A) ：A10. 试说明质点作何种运动时，将出现下述各种情况：(1)；(2)，an=0；at、an分别表示切向加速度和法向加速度．(A) （1）变速率曲线运动（2）变速率直线运动．(B) （1）匀速曲线运动（2）匀速率直线运动．(C) （1）变速率直线运动（2）匀速率直线运动．(D)（1）匀速率直线运动（2）变速率曲线运动．参考答案：A11. 质量为m的小球，放在光滑的木板和光滑的墙壁之间，并保持平衡，如图所示．设木板和墙壁之间的夹角为a，当a逐渐增大时，小球对木板的压力将(A) 增加．(B) 减少．(C) 不变-(1)；(2)，an=0；at、an分别表示切向加速度和法向加速度．(A) （1）变速率曲线运动（2）变速率直线运动．(B) （1）匀速曲线运动（2）匀速率直线运动．(C) （1）变速率直线运动（2）匀速率直线运动．(D)（1）匀速率直线运动（2）变速率曲线运动．参考答案：A11. 质量为m的小球，放在光滑的木板和光滑的墙壁之间，并保持平衡，如图所示．设木板和墙壁之间的夹角为a，当a逐渐增大时，小球对木板的压力将(A) 增加．(B) 减少．(C) 不变：A. B.C. D. E. F. G. H. I. J. K. L. M. N. （已提交）参考答案：D101. 空中电流分布如图，两个半圆共面，且具有公共圆心，试求O点处的磁感强度．答题：A. B. C. D. E. F. G. H. I. J. K. L. M. N. （已提交）参考答案：F102. 一无限长的直导线载有如图所示的电流，长度为b的金属杆CD与导线共面且垂直，相对位置如图．CD杆以速度平行直线电流运动，求CD杆中的感应电动势，并判断C、D两端哪端电势较高？答题：A. B. C. D. E. F. G. H. I. J. K. L. M. N. （已提交）参考答案：E103. 有电流的I长直导线附近，放一导体半圆环MeN与长直导线共面，且端点MN的连线与长直导线垂直．半圆环的半径为b，环心O与导线相距a．设半圆环以速度平行导线平移，求半圆环内感应电动势的大小和方向以及MN两端的电压UM -D101. 空中电流分布如图，两个半圆共面，且具有公共圆心，试求O点处的磁感强度．答题：A. B. C. D. E. F. G. H. I. J. K. L. M. N. （已提交）参考答案：F102. 一无限长的直导线载有如图所示的电流，长度为b的金属杆CD与导线共面且垂直，相对位置如图．CD杆以速度平行直线电流运动，求CD杆中的感应电动势，并判断C、D两端哪端电势较高？答题：A. B. C. D. E. F. G. H. I. J. K. L. M. N. （已提交）参考答案：E103. 有电流的I长直导线附近，放一导体半圆环MeN与长直导线共面，且端点MN的连线与长直导线垂直．半圆环的半径为b，环心O与导线相距a．设半圆环以速度平行导线平移，求半圆环内感应电动势的大小和方向以及MN两端的电压UM ：A. B. C. D. E.F. G. H. I. J. K. L. M. N. （已提交）参考答案：N104. 已知一平面简谐波的表达式为(SI) (1) 分别求x1 = 10 m，x2 = 25 m两点处质点的振动方程；(2) 求x1，x2两点间的振动相位差；(3) 求x1点在t = 4 s时的振动位移．答题：A. B. C. D. E. F. G. H. I. J. K. L. M. N. （已提交）参考答案：H105. 一质点按如下规律沿x轴作简谐振动：(SI)．求此振动的周期、振幅、初相、速度最大值和加速度最大值．答题：A. B. C. D. E. F. G. H. I. J. K. L. M. N. （已提交）参考答案：I106. 图示一平面简谐波在t = 0 时刻的波形图，求(1) 该波的波动表达式；(2) P处质点的振动方程.答题：A. B. C. D. E. F. G. H. I. J. K. L. M. N. （已提交）参考答案：J107. 如图，一平面波在介质中以波速u = 20 m/s沿x轴负方向传播，已知A点的振动方程为(SI)．(1) 以A点为坐标原点写出波的表达式；(2) 以距A点5 m处的B点为坐标原点，写出波的表达式．答题：A. B. C. D. E. F. G. H. I. J. K. L. M. N. （已提交）参考答案：K108. 有一平面电磁波其电场强度为（SI）其中是x方向的单位矢量．（以下计算中，答案中要写明单位）(1) 判断电场的振动方向和波传播的方向．(2) 确定该波的圆频率和波长．(3) 确定该波的波速．(4) 若此波的磁场强度为(SI)其中是y方向的单位矢量，求此平面波通过一个与xy平面平行，面积为2 m2的截面所输送的平均功率．答题：A. B. C. D. E. F. G. H. I. J. K. L. M. N. （已提交）参考答案：Aword教育资料达到当天最大量API KEY 超过次数限制。

姓名 班级 序号气体动理论1.．用分子质量m ，总分子数N ，分子速率v 和速率分布函数()f v 表示下列各量：1）速率大于100m/s 的分子数 ；2）分子平动动能的平均值 ；3）多次观察某一分子速率，发现其速率大于100m/s 的概率 ；2．氢气在不同温度下的速率分布曲线如图所示，则其中曲线1所示温度1T 与曲线2所示温度2T 的高低有1T 2T （填 “大于”、“小于” 或“等于”3．设氢气的温度为300℃。

求速度大小在3000m/s 到3010m/s 之间的分子数N 1与速度大小在p v 到10+p v m/s 之间的分子数N 2之比。

4．导体中自由电子的运动可以看成类似于气体分子的运动，所以常常称导体中的电子为电子气，设导体中共有N 个自由电子，电子气中电子的最大速率为f v （称做费米速率），电子的速率分布函数为：24,0()0,f f Av v v f v v v π⎧≤≤⎪=⎨>⎪⎩ 式中A 为常量，求：（1）用N 和f v 确定常数A ；（2）电子气中一个自由电子的平均动能。

5、 (1)温度为T 的热平衡态下，物质分子的每个自由度都具有的平均动能 。

（2） 温度为T 的热平衡态下，每个分子的平均总能量 。

（3）温度为T 的热平衡态下，νmol(ν为摩尔数)分子的平均总能量 。

（4）温度为T 的热平衡态下，每个分子的平均平动动能 。

6．将1mol温度为T的水蒸气分解为同温度的氢气和氧气，试求氢气和氧气的热力学能（内能）之和比水蒸气的热力学能增加了多少？（所有气体分子均视为刚性分子）。

v m/s 7．质量为50.0g、温度为18.0o C的氦气装在容积为10.0升的封闭容器内，容器以200的速率做匀速直线运动。

若容器突然停止，定向运动的动能全部转化为分子热运动的动能，则平衡后氦气的温度将增加多少？压强将增加多少？。

姓名 班级 序号机械振动1、如图7-5所示，A 球被两个弹簧系住。

弹簧的劲度系数均为k =8N ·m -1，小球的质量m =1kg 。

小球在平衡位置时，两个弹簧为原长。

现自其平衡位置给予小球以初速v 0=12cm ·s -1，方向向右，使小球作微小的振动，试证此振动为简谐振动，求小球的运动方程。

2．一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为A = _______cm ；ω =__________rad/s ；ϕ =________。

3．一质量 = 3.96 kg M 的物体，悬挂在劲度系数 = 400 N/m k 的轻弹簧下端．一质量 = 40g m 的子弹以 = 152 m/s v 的速度从下方竖直朝上射入物体之中 ，然后子弹与物体一起作谐振动 ．若取平衡位置为原点。

x 轴指向下方，如图，求振动方程（因 m M <<，m 射入M 后对原来平衡位置的影响可以忽略）；4．一质点作简谐振动，其振动方程为)4131cos(100.62π-π⨯=-t x (SI) （1）当x 值为多大时，系统的势能为总能量的一半？（2）质点从平衡位置移动到上述位置所需最短时间为多少？k m x M v O x (cm) t (s) 10 5 -10 1 4 7 10 13O·--5、一放在光滑水平面上的弹簧振子，如果小球经平衡位置开始向右运动时的动能为0K E ，振动的周期T =1.0s ，求：再经过31s 时，小球的动能K E 与0K E 之比。

6．两个同方向的简谐振动曲线如图所示。

求合振动的振动方程。

7、有两个同方向的简谐振动，它们的方程为 ⎪⎭⎫ ⎝⎛+=π4310cos 05.01t x ，⎪⎭⎫ ⎝⎛+=π4110cos 06.02t x 式中x 以m 计，t 以s 计。

（1）求它们合成振动的振幅和初相位。

（2）另有一同方向简谐振动的振动方程为()3310cos 07.0ϕ+=t x 。

09华南理工大学网络学院大学物理考试题（A2011）（1）华南理工大学网络教育学院《大学物理》试卷（A 卷）注意事项：1. 本试卷共三大题，满分100分，考试时间120分钟，闭卷；2. 考前请将密封线内各项信息填写清楚；3. 所有答案直接做在试卷上,做在草稿纸上无效；一：选择题（共30分）1．（本题3分）一质点在平面上作一般曲线运动，其瞬时速度为v，瞬时速率为v ，某一时间内的平均速度为v，平均速率为v ，它们之间的关系必定有：（A ）v v v,v == （B ）v v v,v =≠（C ）v v v,v ≠≠ （D ）v v v,v ≠=[ D ]2. （本题3分）质量分别为m A 和m B (m A >m B )、速度分别为A v 和B v(v A > v B )的两质点A 和B ，受到相同的冲量作用，则(A) A 的动量增量的绝对值比B 的小． (B) A 的动量增量的绝对值比B 的大．(C) A 、B 的动量增量相等．(D) A 、B 的速度增量相等．［ C ］3. （本题3分）已知两个物体A 和B 的质量以及它们的速率都不相同，若物体A 的动量在数值上比物体B 的大，则A 的动能E KA 与B 的动能E KB 之间(A) E KB 一定大于E KA ． (B) E KB 一定小于E KA ．(C) E KB ＝E KA ． (D) 不能判定谁大谁小．［ D ］4．（本题3分）一个质点作简谐振动，振幅为A ，在起始时刻质点的位移为A 21，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为［ B ］5．机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则-（密封线内不答题）(A) 其振幅为3 m ． (B) 其周期为s 31．(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播．［ B ］ 6．（本题3分）已知一高斯面所包围的体积内电荷代数和∑q ＝0，则可肯定： (A) 高斯面上各点场强均为零． (B) 穿过高斯面上每一面元的电场强度通量均为零．(C) 穿过整个高斯面的电场强度通量为零．(D) 以上说法都不对．［ C ］7. （本题3分）如图所示，半径为R 的均匀带电球面，总电荷为Q ，设无穷远处的电势为零，则球内距离球心为r 的P 点处的电场强度的大小和电势为：(A) E =0，r QU 04επ=．(B) E =0，RQU 04επ=． (C) 204r QE επ=，r Q U 04επ=． (D) 204r Q E επ=，RQU 04επ=．［ B ］8．（本题3分）如图所示，一根长为ab 的导线用软线悬挂在磁感强度为B的匀强磁场中，电流由a 向b 流．此时悬线张力不为零(即安培力与重力不平衡)．欲使ab 导线与软线连接处张力为零则必须：(A) 改变电流方向，并适当增大电流．(B) 不改变电流方向，而适当增大电流．(C) 改变磁场方向，并适当增大磁感强度B的大小．(D) 不改变磁场方向，适当减小磁感强度B的大小．［ B ］9．（本题3分）将形状完全相同的铜环和木环静止放置，并使通过两环面的磁通量随时间的变化率相等，则不计自感时(A) 铜环中有感应电动势，木环中无感应电动势． (B) 铜环中感应电动势大，木环中感应电动势小．(C) 铜环中感应电动势小，木环中感应电动势大．(D) 两环中感应电动势相等．［ D ］ 10．（本题3分）在真空中波长为λ的单色光，在折射率为n 的透明介质中从A 沿某路径传播到B ，若A 、B 两点相位差为3π，则此路径AB 的光程为(A) 1.5 λ．(B) 1.5 λ/ n ．(C) 1.5 n λ．(D) 3 λ．［Ａ］二、填空题：（共3０分）11．（本题3分）如图所示，一物体放在水平传送带上，物体与传送带间无相对滑动，当传送带作匀速运动时，静摩擦力对物体作功为___零_______；当传送带作加速运动时，静摩擦力对物体作功为____正______；当传送带作减速运动时，静摩擦力对物体作功为____负______．（仅填“正”，“负”或“零”）12. （本题3分）一简谐振子的振动曲线如图所示，则以余弦函数表示的振动方程为．13．（本题3分）如图所示，在点电荷＋q 和－q 产生的电场中，将一点电荷＋q 0沿箭头所示路径由a 点移至b 点，则外力作功A _____-qq 0 / (8πε0 l ) ________．14．（本题3分）如图所示，两同心导体球壳，内球壳带电荷+q ，外球壳带电荷-2q ．静电平衡时，外球壳的电荷分布为：内表面____-q _______ ；外表面___-q ________ ．15．（本题3分）如图，两根导线沿半径方向引到铁环的上A 、A ′两点，并在很远处与电源相连，则环中心的磁感强度为_____ 0 _______．16．（本题3分）如图，一根载流导线被弯成半径为R 的1/4圆弧，放在磁感强度为B 的均匀磁场中，则载流导线ab 所受磁场的作用力的大小为______BIR 2 ______，方向__沿y 轴正向__________． 17．（本题3分）反映电磁场基本性质和规律的积分形式的麦克斯韦方程组为=VSV S D d d ρ，①-=SL S t B l Ed d ，② 0d =??SS B，③ +=SL S t DJ l Hd )(d ．④ 试判断下列结论是包含于或等效于哪一个麦克斯韦方程式的．将你确定的方程式用代号填在相应结论后的空白处．--B(1) 变化的磁场一定伴随有电场；________ ② __________(2) 磁感线是无头无尾的；_______________ ③_________(3)电荷总伴随有电场．_________________①_________ 18．（本题3分）在简谐波的一条射线上，相距0.2 m 两点的振动相位差为π /6．又知振动周期为0.4 s ，则波长为______ 2.4 m ___________，19. （本题3分）如图所示，一段长度为l 的直导线MN ，水平放置在载电流为I 的竖直长导线旁与竖直导线共面，并从静止由图示位置自由下落，则t 秒末导线两端的电势差=-N M U U _________al a t Ig+π-ln 20μ _____________．三、计算题：（共４０分）21. （本题10分）质量为M 的木块静止在光滑的水平面上．质量为m 、速率为v 的子弹沿水平方向打入木块并陷在其中，试计算相对于地面木块对子弹所作的功W 1及子弹对木块所作的功W 2．解：设子弹打入木块后二者共同运动的速率为V ，水平方向动量守恒，有V M m m )(+=v , )/(M m m V +=v木块对子弹作的功 2212121v m mV W -=22)(2)2(v m M m M Mm ++-= 子弹对木块作的功 2221mV W =222)(2v m M Mm +=22.（本题１０分）如图所示，一内半径为a 、外半径为b 的金属球壳，带有电荷Q ，在球壳空腔内距离球心r 处有一点电荷q ．设无限远处为电势零点，试求：(1) 球壳内外表面上的电荷． (2) 球心O 点处，由球壳内表面上电荷产生的电势． (3) 球心O 点处的总电势．解：(1) 由静电感应，金属球壳的内表面上有感生电荷-q ，外表面上带电荷q +Q ．(2) adqU q 04επ=-aq04επ-=(3) q Q q q O U U U U +-++= )111(40b a r q +-π=εbQ04επ+23.（本题10分）已知一平面简谐波的表达式为 )37.0125cos(25.0x t y -= (SI) (1) 分别求x 1 = 10 m ，x 2 = 25 m 两点处质点的振动方程； (2) 求x 1，x 2两点间的振动相位差； (3) 求x 1点在t = 4 s 时的振动位移．解：(1) x 1 = 10 m 的振动方程为 )7.3125cos(25.010-==t y x (SI)x 2 = 25 m 的振动方程为 )25.9125cos(25.025-==t yx (SI)(2) x 2与x 1两点间相位差?φ = φ2 - φ1 = -5.55 rad(3) x 1点在t = 4 s 时的振动位移y = 0.25cos(125×4－3.7) m= 0.249 m24.本题（10分）载有电流I 的平面闭合回路由半径为R 1及R 2 (R 1 > R 2 )的两个同心半圆弧和两个直导线段组成．已知两个直导线段在半圆弧中心O 点产生的磁感强度均为零．若闭合回路在O 点产生的总的磁感强度B 大于半径为R 2的半圆弧在O 点产生的磁感强度B 2， (1) 画出载流回路的形状； (2) 求出O 点的总磁感强度B ．解： (1) 2B B > 可知 21B B B +=．故闭合回路形状如图所示．(2) 1014/R I B μ=，2024/R I B μ= 21B B B +=212104)(R R R R I +=μI I O R 1R 2。

习题一 真空中的静电场院 系： 班 级:_____________ 姓 名:___________ 学 号:____________________一 选择题（共30分）1.如图所示，在坐标(a ，0)处放置一点电荷＋q ，在坐标(－a ，0)处放置另一点电荷－q ．P 点是y 轴上的一点，坐标为(0，y )．当y >>a 时，该点场强的大小为：[ C ] (A)204y q επ． (B)202y q επ． (C)302y qa επ． (D) 304yqa επ．2.半径为R 的均匀带电球面的静电场中各点的电场强度的大小E 与距球心的距离r 之间的关系曲线为：［ B ］3．如图所示，边长为a 的等边三角形的三个顶点上，分别放置着三个正的点电荷q 、2q 、3q ．若将另一正点电荷Q 从无穷远处移到三角形的中心O 处，外力所作的功为： ［ C ］(A) a qQ 023επ ． (B) a qQ 03επ． (C) a qQ 0233επ． (D) aqQ 032επ．4．图中实线为某电场中的电场线，虚线表示等势（位）面，由图可看出：［ D ］ (A) E A ＞E B ＞E C ，U A ＞U B ＞U C ． (B) E A ＜E B ＜E C ，U A ＜U B ＜U C ． (C) E A ＞E B ＞E C ，U A ＜U B ＜U C ． (D) E A ＜E B ＜E C ，U A ＞U B ＞U C ．E Or(D) E ∝1/r 23q2q5．半径为R 的“无限长”均匀带电圆柱面的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为： ［ B ］6．在边长为a 的正方体中心处放置一电荷为Q 的点电荷，则正方体顶角处的电场强度的大小为： (A)2012a Q επ． (B) 206a Q επ． (C) 203a Q επ． (D) 20aQεπ． ［C ］7．图示为一具有球对称性分布的静电场的E ～r 关系曲线．请指出该静电场是由下列哪种带电体产生的． (A) 半径为R 的均匀带电球面． [ B ］(B) 半径为R 的均匀带电球体．(C) 半径为R 的、电荷体密度为＝A r (A 为常数)的非均匀带电球体． (D) 半径为R 的、电荷体密度为＝A/r (A 为常数)的非均匀带电球体．8．选无穷远处为电势零点，半径为R 的导体球带电后，其电势为U 0，则球外离球心距离为r 处的电场强度的大小为(A) 302r U R ． (B) R U 0． (C) 20r RU ． (D) r U 0． ［ C ］9. 设有一“无限大”均匀带正电荷的平面．取x 轴垂直带电平面，坐标原点在带电平面上，则其周围空间各点的电场强度E随距平面的位置坐标x 变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负)：［C ］10. 一个静止的氢离子(H +)在电场中被加速而获得的速率为一静止的氧离子(O +2)在同一电场中且通过相同的路径被加速所获速率的：(A) 2倍． (B) 22倍． (C) 4倍． (D) 42倍． ［ B ］E O rE ∝1/rE Or(D) E ∝1/rR E Or(C) E ∝1/rE Or(A) E ∝1/rO R rE E ∝1/r 2OxE (A)OxE (C)OxE (B)OxE (D)E ∝1/|x|E ∝x11．如图所示，一个电荷为q 的点电荷位于立方体的A 角上，则通过侧面abcd的电场强度通量等于：(A) 06εq ． (B) 012εq ． (C) 024εq ． (D) 048εq． ［ C ］二 填空题1.电荷分别为q 1，q 2，q 3的三个点电荷分别位于同一圆周的三个点上，如图所示．设无穷远处为电势零点，圆半径为R ，则b 点处的电势U ＝___________ ． ()32102281q q q R++πε2.图中所示以O 为心的各圆弧为静电场的等势（位）线图，已知U 1＜U 2＜U 3，在图上画出a 、b 两点的电场强度的方向，并比较它们的大小．E a ＝ E b (填＜、＝、＞)．3.两根相互平行的“无限长”均匀带正电直线1、2，相距为d ，其电荷线密度分别为λ1和λ2如图所示，则场强等于零的点与直线1的距离a 为_____________ ．d 211λλλ+4.如图所示,两同心带电球面，内球面半径为r 1＝5 cm ，带电荷q 1＝3×10-8C ；外球面半径为r 2＝20 cm ， 带电荷q 2＝－6×10­8C ，设无穷远处电势为零，则空间另一电势为零的球面半径r ＝ __________________．10 cm5．已知某静电场的电势函数U ＝a ( x 2+ y )，式中a 为一常量，则电场中任意点的电场强度分量E x ＝－2ax ，E y ＝ －a ，E z ＝ 0．6．如图所示．试验电荷q ，在点电荷+Q 产生的电场中，沿半径为R 的整个圆弧的3/4圆弧轨道由a 点移到d 点的过程中电场力作功为 0 ；从d 点移到无穷远处的过程中，电场力作功为qQ / (4πε0R )．7.一个带电荷q 、半径为R 的金属球壳，壳内是真空，壳外是介电常量为ε 的无限大各向同性均匀电介质，则此球壳的电势U =________________．Rqεπ48．在点电荷q 的电场中，把一个－1.0×10-9C 的电荷，从无限远处(设无限远处电势为零)移到离该点电荷距离 0.1 m 处，克服电场力作功 1.8×10-5 J ，则该点电荷q ＝-2×10-7库伦．(真空介电常量0＝8.85×10-12C 2·N -1·m -2)A b caq2 q 1 q 3OOU 1U 2U 3abλ2a d 12q 1 q 2 r 1r 2+Q R q d∞三 计算题1.厚度为d 的“无限大”均匀带电导体板两表面单位面积上电荷之和为σ．试求图示离左板面距离为a 的一点与离右板面距离为b 的一点之间的电势差．解：选坐标如图．由高斯定理，平板内、外的场强分布为：E = 0 (板内) )2/(0εσ±=x E (板外)1、2两点间电势差⎰=-2121d x E U U x x x d b d d d a d 2d 22/2/02/)2/(0⎰⎰+-+-+-=εσεσ )(20a b -=εσ 2.一环形薄片由细绳悬吊着，环的外半径为R ，内半径为R /2，并有电荷Q 均匀分布在环面上．细绳长3R ，也有电荷Q 均匀分布在绳上，如图所示,试求圆环中心O 处的电场强度(圆环中心在细绳延长线上)．解：先计算细绳上的电荷在O 点产生的场强．选细绳顶端作坐标原点O ，x 轴向下为正．在x 处取一电荷元 d q = d x = Q d x /(3R ) 它在环心处的场强为 ()20144d d x R qE -π=ε ()20412d x R R xQ -π=ε 整个细绳上的电荷在环心处的场强()203020116412RQx R dx R Q E R εεπ=-π=⎰ 圆环上的电荷分布对环心对称，它在环心处的场强E 2=0由此，合场强 i R Qi E E20116επ== 方向竖直向下．3.电荷Q (Q ＞0)均匀分布在长为L 的细棒上，在细棒的延长线上距细棒中心O 距离为a 的P 点处放一电荷为q (q ＞0 )的点电荷，求带电细棒对该点电荷的静电力． 解：沿棒方向取坐标Ox ，原点O 在棒中心处．求P 点场强： ()()20204d 4d d x a xx a q E -π=-π=ελε 3分 ()⎰--π=2/2/204d L L x a xE ελ()2202/2/0414L a Qx a L L -π=-⋅π=-εελ 4分 方向沿x 轴正向. 点电荷受力：==qE F ()2204πL a qQ-ε 方向沿x 轴正方向． 3分1σda1σd abxOO R 3RR /2E 1xR3R x xOPL+Q OaP O L/2L/2d x d q a。

华南理工大学网络教育学院大学物理作业（2020/11/15日前应交）教学中心： 专业层次：学 号： 姓 名： (注: 作业要求先下载，打印，在打印的纸版上用钢笔手写完成,然后拍成照片，把照片放入WORD 文档提交)一：选择题（D ）1．（本题为随堂练习第1题）一质点在平面上作一般曲线运动，其瞬时速度为，瞬时速率为v ，，某一时间内的平均速度为，平均速率为，它们之间的关系必定有：（A ） （B ）（C ） （D ）(D) 2. （本题为随堂练习第5题）质点作半径为R 的变速圆周运动时的加速度大小为(v 表示任一时刻质点的速率)(A) t d d v ． (B) R2v ． (C) R t 2d d v v +． (D) 2/1242d d ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛R t v v ．(A) 3．（本题为随堂练习第8题）设质点运动时，将出现下述两种情况)0(≠v ，试分别指出下述两种情况属于何种运动(1)0,0≠≠n t a a ；(2)0≠ta ，a n =0；a t 、a n 分别表示切向加速度和法向加速度．(A) （1）变速率曲线运动（2）变速率直线运动．(B) （1）匀速曲线运动（2）匀速率直线运动．(C) （1）变速率直线运动（2）匀速率直线运动．(D) （1）匀速率直线运动（2）变速率曲线运动．(C) 4．（本题为随堂练习第14题）在水平冰面上以一定速度向东行驶的炮车，向东南（斜向上）方向发射一炮弹，对于炮车和炮弹这一系统，在此过程中（忽略冰面摩擦力及空气阻力）(A) 总动量守恒．(B) 总动量在炮身前进的方向上的分量守恒，其它方向动量不守恒．(C) 总动量在水平面上任意方向的分量守恒，竖直方向分量不守恒．(D) 总动量在任何方向的分量均不守恒．(A) 5. （本题为随堂练习第18题）如图所示，圆锥摆的小球在水平面内以角速度w匀速转动．下列说法正确的是：(A) 重力和绳子的张力对小球都不做功；(B) 重力和绳子的张力对小球都做功；(C) 重力对小球作功，绳子张力对小球不做功；(D) 重力对小球不作功，绳子张力对小球做功；(C) 6. （本题为随堂练习第25题，3分）如图所示，子弹射入放在水平光滑地面上静止的木块而不穿出．以地面为参考系，下列说法中正确的说法是(A) 子弹的动能转变为木块的动能．(B) 子弹─木块系统的机械能守恒．(C) 子弹动能的减少等于子弹克服木块阻力所作的功．(D) 子弹克服木块阻力所作的功等于这一过程中产生的热(B)7. （本题为随堂练习第30题，3分）图中用旋转矢量法表示了一个简谐振动．旋转矢量的长度为0.04 m ，旋转角速度ω = 4π rad/s ．此简谐振动以余弦函数表示的振动方程为x 为． (A) )t cos(.π+π214040. (B) )214cos(04.0π-πt(C). (D)(C) 8. （本题为随堂练习第31题）一质点作简谐振动，周期为T ．当它由平衡位置向x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为(A) T /12．(B) T /8．(C) T /6．(D) T /4．(B) 9. （本题为随堂练习第34题）机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则(A) 其振幅为3 m． (B) 其周期为．(C) 其波速为10 m/s． (D) 波沿x轴正向传播．(D) 10．（本题为随堂练习第35题）已知一平面简谐波的表达式为（a、b为正值常量），则(A) 波的频率为a． (B) 波的传播速度为 b/a．(C) 波长为π / b． (D) 波的周期为2π / a．(B) 11．（本题为随堂练习第43题）若理想气体的体积为V，压强为p，温度为T，一个分子的质量为m，k为玻尔兹曼常量，R为普适气体常量，则该理想气体的分子数为：(A) pV / m．(B) pV / (kT)．。

1.一质点在平面上作一般曲线运动，其瞬时速度为，瞬时速率为v ，，某一时间内的平均速度为，平均速率为，它们之间的关系必定有：（A）（B）（C）（D）答题： A. B. C. D. （已提交）参考答案： D问题解析：2.一质点在平面上运动，已知质点位置矢量的表示式为（其中a、b 为常量） ,则该质点作(A) 匀速直线运动．(B)变速直线运动．(C)抛物线运动．(D) 一般曲线运动．答题： A. B. C. D. （已提交）参考答案： B问题解析：3.如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率收绳，绳不伸长、湖水静止，则小船的运动是(A)匀加速运动． (B) 匀减速运动． (C) 变加速运动． (D) 变减速运动．答题： A. B. C. D.（已提交）参考答案： C问题解析：4.一飞机相对空气的速度大小为200 km/h,飞机速度大小为192 km/h ，方向是(A)南偏西16.3°．(B)北偏东16.3 ° (C)风速为56 km/h ，方向从西向东．地面雷达站测得向正南或向正北．(D) 西偏北16.3 °．(E)东偏南16.3 °．答题： A. B. C. D.（已提交）参考答案： C问题解析：5.对于沿曲线运动的物体，以下几种说法中哪一种是正确的：(A)切向加速度必不为零．(B)法向加速度必不为零（拐点处除外）．(C)由于速度沿切线方向，法向分速度必为零，因此法向加速度必为零．(D)若物体作匀速率运动，其总加速度必为零．(E)若物体的加速度为恒矢量，它一定作匀变速率运动．答题： A. B. C. D. （已提交）参考答案： B问题解析：6. 一质点沿直线运动,其运动学方程为x = 6 t － t2 (SI) ，则在 t 由 0至 4s的时间间隔内，质点的位移大小为___________， (A)8 m ． (B) 8.25 m ． (C) 5 m． (D) 10 m答题： A. B. C. D. （已提交）参考答案： A问题解析：7.一质点在Oxy 平面内运动．运动学方程为 2 t 和19-2 t2 (SI) ，则在第 2 秒末的瞬时速度大小_______________________．(A) 6.32 m/s． (B) 8.25 m/s． (C) 5 m/s ． (D) 6 m/s ．答题： A. B. C. D. （已提交）参考答案： B问题解析：8.一物体在某瞬时，以初速度从某点开始运动，在 D t 时间内，经一长度为S 的曲线路径后，又回到出发点，此时速度为，则在这段时间内：物体的平均加速度是_________________．．(A)． (B)． (C)． (D)．答题： A. B. C. D. （已提交）参考答案： B问题解析：9.一质点沿半径为R 的圆周运动，其路程S 随时间t 变化的规律为(SI)，式中 b、c 为大于零的常量, 且 b2>Rc..则此质点运动的切向加速度at 和法向加速度an 为．．(A) -c ．和 (b-ct)2/R (B)和(b-ct)2/R．(C) (b-ct)2/R和．(D)和．答题： A. B. C. D. （已提交）参考答案： A问题解析：10.试说明质点作何种运动时，将出现下述各种情况：(1)；(2)， an=0 ；at、 an 分别表示切向加速度和法向加速度．(A)（ 1）变速率曲线运动（ 2）变速率直线运动．(B) （ 1）匀速曲线运动（ 2）匀速率直线运动．(C) （ 1 ）变速率直线运动（2）匀速率直线运动．(D) （ 1 ）匀速率直线运动（2）变速率曲线运动．答题： A. B. C. D.（已提交）参考答案： A问题解析：11.质量为 m 的小球，放在光滑的木板和光滑的墙壁之间，并保持平衡，如图所示．设木板和墙壁之间的夹角为 a ，当 a 逐渐增大时，小球对木板的压力将(A)增加．(B)减少．(C)不变．(D)先是增加，后又减小．压力增减的分界角为a ＝45°．答题： A. B. C. D. （已提交）参考答案： B问题解析：12.两个质量相等的小球由一轻弹簧相连接，再用一细绳悬挂于天花板上，处于静止状态，如图所示．将绳子剪断的瞬间，球 1 和球 2 的加速度分别为(A) a1 ＝ｇ， a2 ＝ｇ．(B) a1 ＝0 ， a2＝ｇ．(C) a1 ＝ｇ， a2 ＝0 ． (D) a1 ＝2ｇ， a2 ＝ 0．答题： A. B. C. D. （已提交）参考答案： D问题解析：13.如图所示，假设物体沿着竖直面上圆弧形轨道下滑，轨道是光滑的，在从 A 至 C 的下滑过程中，下面哪个说法是正确的？(A)它的加速度大小不变，方向永远指向圆心．(B)它的速率均匀增加．(C)它的合外力大小变化，方向永远指向圆心．(D)它的合外力大小不变．(E)轨道支持力的大小不断增加．答题： A. B. C. D. （已提交）参考答案： D问题解析：14.站在电梯中的人，看到用细绳连接的质量不同的两物体，跨过电梯内一个挂在天花板上的无摩擦的定滑轮而处于“平衡静止”状态，由此，他断定电梯在作加速度运动，加速度是：(A) 大小为 g ，方向向上．(B) 大小为 g ，方向向下．(C) 大小为，方向向上．(D)大小为，方向向下．答题： A. B. C. D. （已提交）参考答案： B问题解析：15.在升降机天花板上拴有轻绳，其下端系一重物，当升降机以加速度a1 上升时，绳中的张力正好等于绳子所能承受的最大张力的一半，问升降机以多大加速度上升时，绳子刚好被拉断？(A) 2a1 ． (B) 2(a1+g) ．(C) 2a1 ＋ g．(D) a1 ＋ g．答题： A. B. C. D. （已提交）参考答案： C问题解析：16.一物体质量为M，置于光滑水平地板上．今用一水平力通过一质量为m 的绳拉动物体前进，则物体的加速度a＝ ______________，(A)(B)(C)(D)答题： A. B. C. D. （已提交）参考答案： A问题解析：17. 质量分别为 mA 和 mB (mA>mB)、速度分别为和(vA> vB) 的两质点 A 和 B ，受到相同的冲量作用，则(A) A 的动量增量的绝对值比 B 的小． (B) A 的动量增量的绝对值比 B 的大． (C) A 、B 的动量增量相等．D) A 、 B 的速度增量相等．答题： A. B. C. D. （已提交）参考答案： C问题解析：18. 质量为 m 的质点，以不变速率v 沿图中正三角形ABC 的水平光滑轨道运动．质点越过 A 角时，轨道作用于质点的冲量的大小为(A) mv ．(B)mv ．(C)mv ．(D) 2mv ．答题： A. B. C. D. （已提交）参考答案： C问题解析：19.一质量为 60 kg 的人起初站在一条质量为 300 kg ，且正以 2 m/s 的速率向湖岸驶近的小木船上，湖水是静止的，其阻力不不计．现在人相对于船以一水平速率v 沿船的前进方向向河岸跳去，该人起跳后，船速减为原来的一半，v 应为(A) 2 m/s ．(B) 3 m/s ．(C) 5 m/s ．(D) 6 m/s ．答题： A. B. C. D. （已提交）参考答案： D问题解析：20.在水平冰面上以一定速度向东行驶的炮车，向东南（斜向上）方向发射一炮弹，对于炮车和炮弹这一系统，在此过程中（忽略冰面摩擦力及空气阻力）(A)总动量守恒． (B) 总动量在炮身前进的方向上的分量守恒，其它方向动量不守恒．(C)总动量在水平面上任意方向的分量守恒，竖直方向分量不守恒．(D)总动量在任何方向的分量均不守恒．答题： A. B. C. D. （已提交）参考答案： C问题解析：21.如图所示．一斜面固定在卡车上，一物块置于该斜面上．在卡车沿水平方向加速起动的过程中，物块在斜面上无相对滑动. 此时斜面上摩擦力对物块的冲量的方向(A)是水平向前的． (B) 只可能沿斜面向上． (C) 只可能沿斜面向下． (D) 沿斜面向上或向下均有可能．答题： A. B. C. D. （已提交）参考答案：问题解析：D22. 已知两个物体A 的动能 EKA 与B A 和 B的动能的质量以及它们的速率都不相同，若物体EKB 之间A 的动量在数值上比物体B 的大，则(A) EKB 一定大于EKA ．(B) EKB 一定小于EKA ．(C) EKB ＝ EKA ．(D) 不能判定谁大谁小．答题： A. B. C. D. （已提交）参考答案： D问题解析：23.人造地球卫星，绕地球作椭圆轨道运动，地球在椭圆的一个焦点上，则卫星的(A)动量不守恒，动能守恒．(B)动量守恒，动能不守恒．(C)对地心的角动量守恒，动能不守恒．(D)对地心的角动量不守恒，动能守恒．答题： A. B. C. D. （已提交）参考答案： C问题解析：24.如图所示，一个小球先后两次从P 点由静止开始，分别沿着光滑的固定斜面l1 和圆弧面l2 下滑．则小球滑到两面的底端Q 时的(A) 动量相同，动能也相同． (B) 动量相同，动能不同． (C) 动量不同，动能也不同． (D) 动量不同，动能相同答题： A. B. C. D. （已提交）参考答案： D问题解析：25.如图，在光滑水平地面上放着一辆小车，车上左端放着一只箱子，今用同样的水平恒力拉箱子，使它由小车的左端达到右端，一次小车被固定在水平地面上，另一次小车没有固定．试以水平地面为参照系，判断下列结论中正确的是(A) 在两种情况下，做的功相等．(B) 在两种情况下，摩擦力对箱子做的功相等．(C) 在两种情况下，箱子获得的动能相等．(D)在两种情况下，由于摩擦而产生的热相等．答题： A. B. C. D. （已提交）参考答案： D问题解析：26.速度为 v 的子弹，打穿一块不动的木板后速度变为零，设木板对子弹的阻力是恒定的．那么，当子弹射入木板的深度等于其厚度的一半时，子弹的速度是(A)．(B)．(C)．(D)．答题： A. B. C. D. （已提交）参考答案： D问题解析：27.一质量为M 的弹簧振子，水平放置且静止在平衡位置，如图所示．一质量为m 的子弹以水平速度射入振子中，并随之一起运动．如果水平面光滑，此后弹簧的最大势能为(A)．(B)．(C)．(D)．答题： A. B. C. D. （已提交）参考答案： B问题解析：28.如图所示，子弹射入放在水平光滑地面上静止的木块而不穿出．以地面为参考系，下列说法中正确的说法是(A)子弹的动能转变为木块的动能． (B) 子弹─木块系统的机械能守恒．(C) 子弹动能的减少等于子弹克服木块阻力所作的功．(D)子弹克服木块阻力所作的功等于这一过程中产生的热答题： A. B. C. D. （已提交）参考答案： C问题解析：29. 一颗速率为700 m/s的的子弹，打穿一块木板后,速率降到 500 m/s ．如果让它继续穿过厚度和阻力均与第一块完全相同的第二块木板，则子弹的速率将降到 ______________________________．（空气阻力忽略不计）(A) 6.32 m/s． (B)8.25 m/s．？ (C) 5 m/s ． (D) 100 m/s答题： A. B. C. D. （已提交）参考答案： D问题解析：30. 置于水平光滑桌面上质量分别为m1 和 m2 的物体 A 和 B 之间夹有一轻弹簧．首先用双手挤压 A 和B 使弹簧处于压缩状态，然后撤掉外力，则在 A 和 B 被弹开的过程中(A)系统的动量守恒，机械能不守恒．(B)系统的动量守恒，机械能守恒．(C)系统的动量不守恒，机械能守恒．(D)系统的动量与机械能都不守恒．答题： A. B. C. D. （已提交）参考答案： B问题解析：31.设作用在质量为 1 kg 的物体上的力 F＝ 6t＋ 3（ SI ）．如果物体在这一力的作用下，由静止开始沿直线运动，在0 到 2.0 s 的时间间隔内，这个力作用在物体上的冲量大小Ｉ＝__________________．(A) 20 N·s．(B) 18 N ·s． (C) 34 N·s．(D)68 N ·s．答题： A. B. C. D. （已提交）参考答案： B问题解析：32. 一质量为 m 的小球 A ，在距离地面某一高度处以速度水平抛出，触地后反跳．在抛出t 秒后小球A 跳回原高度，速度仍沿水平方向，速度大小也与抛出时相同，如图．则小球 A 与地面碰撞过程中，地面给它的冲量的方向为________________，冲量的大小为 ____________________ ．(A) 地面给它的冲量的方向为垂直地面向上，冲量的大小为m g t ． (B) 地面给它的冲量的方向为垂直地面向下，冲量的大小为m g t ．(C) 地面给它的冲量的方向为垂直地面向上，冲量的大小为2m g t ． (D) 地面给它的冲量的方向为垂直地面向下，冲量的大小为 m v ．答题： A. B. C. D. （已提交）参考答案： A问题解析：33. 图示一圆锥摆，质量为m 的小球在水平面内以角速度w 匀速转动．在小球转动一周的过程中，(1) 小球动量增量的大小等于__________________．(2)小球所受重力的冲量的大小等于________________ ．(A) （1）小球动量增量的大小等于0，（ 2）小球所受重力的冲量的大小等于2pmg/w ．(B) （1）小球动量增量的大小等于2pmg/w ．（ 2）小球所受重力的冲量的大小等于mg ．．(C) （1）小球所受重力的冲量的大小等于2pmg/w ，（ 2 ）小球所受重力的冲量的大小等于0．(D) （1）小球动量增量的大小等于0，（2 ）小球所受重力的冲量的大小等于mg ，答题： A. B. C. D. （已提交）参考答案： A问题解析：34.如图所示，一物体放在水平传送带上，物体与传送带间无相对滑动，当传送带作匀速运动时，静摩擦力对物体作功为 __________ ；当传送带作加速运动时，静摩擦力对物体作功为 __________ ；（仅填“正”，“负”或“零”）(A)当传送带作匀速运动时，静摩擦力对物体作功为0 ．当传送带作加速运动时，静摩擦力对物体作功为正．(B)：当传送带作匀速运动时，静摩擦力对物体作功为正．当传送带作加速运动时，静摩擦力对物体作功为正．(C)当传送带作匀速运动时，静摩擦力对物体作功为0 ．当传送带作加速运动时，静摩擦力对物体作功为负(D)当传送带作匀速运动时，静摩擦力对物体作功为正．当传送带作加速运动时，静摩擦力对物体作功为正．答题： A. B. C. D. （已提交）参考答案： A问题解析：35.根据高斯定理的数学表达式可知下述各种说法中，正确的是：(A)闭合面内的电荷代数和为零时，闭合面上各点场强一定为零．(B)闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零．(C)闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零．(D)闭合面上各点场强均为零时，闭合面内一定处处无电荷．答题： A. B. C. D. （已提交）参考答案： C问题解析：36.一点电荷，放在球形高斯面的中心处．下列哪一种情况，通过高斯面的电场强度通量发生变(A)将另一点电荷放在高斯面外． (B) 将另一点电荷放进高斯面内．(C)将球心处的点电荷移开，但仍在高斯面内．(D) 将高斯面半径缩小．答题： A. B. C. D. （已提交）参考答案： B问题解析：37.已知一高斯面所包围的体积内电荷代数和∑q＝0，则可肯定：(A)高斯面上各点场强均为零．(B) 穿过高斯面上每一面元的电场强度通量均为零．(C)穿过整个高斯面的电场强度通量为零．(D) 以上说法都不对．答题： A. B. C. D. （已提交）参考答案： C问题解析：38.点电荷Q被曲面S所包围，从无穷远处引入另一点电荷q 至曲面外一点，如图所示，则引入前后：(A)曲面 S 的电场强度通量不变，曲面上各点场强不变．(B)曲面 S 的电场强度通量变化，曲面上各点场强不变．(C)曲面 S 的电场强度通量变化，曲面上各点场强变化．(D)曲面 S 的电场强度通量不变，曲面上各点场强变化．答题： A. B. C. D. （已提交）参考答案： D问题解析：39.半径为r的均匀带电球面1，带有电荷q ，其外有一同心的半径为R 的均匀带电球面2，带有电荷Q，求此两球面之间的电势差U1-U2 ：：(A). (B).(C). (D).答题： A. B. C. D. （已提交）参考答案： A问题解析：40.如图所示，半径为R 的均匀带电球面，总电荷为Q，设无穷远处的电势为零，则球内距离球心为r的 P 点处的电场强度的大小和电势为：(A) E=0 ，．(B) E=0 ，．(C)，．(D)，．答案 :答题： A. B. C. D. （已提交）参考答案： B问题解析：41.如图所示，两个同心球壳．内球壳半径为R1 ，均匀带有电荷 Q；外球壳半径为 R2 ，壳的厚度忽略，r 的 P 点处电场强度的大小与原先不带电，但与地相连接．设地为电势零点，则在两球之间、距离球心为电势分别为：(A)E＝，U＝．(B)E＝，U＝．(C)E＝，U ＝．(D) E ＝0，U＝．答题： A. B. C. D. （已提交）参考答案： B问题解析：42.如图所示，两个“无限长”的、半径分别为 R1 和 R2 的共轴圆柱面均匀带电，沿轴线方向单位长度上所带电荷分别为l1 和 l2 ，则在内圆柱面里面、距离轴线为r 处的 P 点的电场强度大小 E 为_______________________.(A). (B).(C) 0 . (D).答题： A. B. C. D. （已提交）参考答案： C问题解析：43.如图， A 点与 B 点间距离为为 2l，OCD 是以 B 为中心，以 l 为半径的半圆路径 . A 、B 两处各放有一点电荷，电荷分别为＋q 和－ q ．把另一电荷为Q(Q ＜0 ) 的点电荷从 D 点沿路径DCO 移到 O 点，则电场力所做的功为________(A) -Qq / (12pe0) . (B) -Qq / (6pe0) .(C) 0 . (D).答题： A. B. C. D. （已提交）参考答案： B问题解析：44.如图所示，在电荷为q 的点电荷的静电场中，将一电荷为q0 的的试验电荷从 a 点经任意路径移动到b 点，外力所作的功 A ＝______________．(A). (B).(C). (D).答题： A. B. C. D. （已提交）参考答案： C问题解析：45.如图所示，在半径为R 的球壳上均匀带有电荷孔移到球外 b 点．则此过程中电场力作功a＝Q，将一个点电荷q(q<<q)从球内 a 点经球壳上一个小_______________________．(A). (B).(C). (D).</q) 从球内 a 点经球壳上一个小孔移到球外 b 点．则此过程中电场力作功答题： A. B. C. D. （已提交）参考答案： D问题解析：46.如图所示，在点电荷＋q 和－ q 产生的电场中，将一点电荷＋a ＝_______________________q0 沿箭头所示路径由 a 点移．至b 点，则外力作功 A_________________ ．(A) -Qq / (12pe0) . (B) -Qq / (6pe0) . .(C) 0 . (D) -qq0 / (8pe0 l) .答题： A. B. C. D. （已提交）参考答案： D问题解析：47.若匀强电场的场强为，其方向平行于半径为R 的半球面的轴，如图所示．则通过此半球面的电场强度通量Fe为___________________，如果是右图，通量Fe 为___________________。

习题八 波粒二相性院 系： 班 级:_____________ 姓 名:___________ 学 号:_____________________ 一 选择题（共30分）1. 波长λ=500nm 的光沿x 轴正向传播，若光的波长的不确定量Δλ=10-4nm ，则利用不确定关系式h x p x ≥∆∆可得光子的x 坐标的不确定量至少为 ［ ］(A) 25 cm ． (B) 50 cm ． (C) 250 cm ． (D) 500 cm ．2．要使处于基态的氢原子受激发后能发射赖曼系(由激发态跃迁到基态发射的各谱线组成的谱线系)的最长波长的谱线，至少应向基态氢原子提供的能量是 ［ ］(A) 1.5 eV ． (B) 3.4 eV ． (C) 10.2 eV ． (D) 13.6 eV ．3. 在康普顿散射中，如果设反冲电子的速度为光速的60％，则因散射使电子获得的能量是其静止能量的 (A) 2倍． (B) 1.5倍．(C) 0.5倍． (D) 0.25倍． ［ ］4.按玻尔的氢原子理论，电子在以质子为中心、半径为r 的圆形轨道上运动．如果把这样一个原子放在均匀的外磁场中，使电子轨道平面与B垂直，如图所示，则在r 不变的情况下，电子轨道运动的角速度将： ［ ］ (A) 增加． (B) 减小． (C) 不变． (D) 改变方向．5．光电效应和康普顿效应都包含有电子与光子的相互作用过程．对此，在以下几种理解中，正确的是 (A) 两种效应中电子与光子两者组成的系统都服从动量守恒定律和能量守恒定律． (B) 两种效应都相当于电子与光子的弹性碰撞过程．(C) 两种效应都属于电子吸收光子的过程．(D) 光电效应是吸收光子的过程，而康普顿效应则相当于光子和电子的弹性碰撞过程．(E) 康普顿效应是吸收光子的过程，而光电效应则相当于光子和电子的弹性碰撞过程． ［ ］6．求温度为27℃时，对应于方均根速率的氧气分子的德布罗意波长为[ ]。

上册习题一一、选择题1．C ； 2．D ； 3．B ，B ； 4．D ； 5．D 。

二、填空题1．答案：（1）12a gτ=-；（2）2ρ2．答案：（1）48i j - ；（2）2j - ；（3）224x y =-。

3．答案：（1）20()v bt a n b R τ-=- ；（2）224v s n R Rb ππ∆== 4．答案：01012020cos sin cos sin tg v v tg θθθθθθ+=+5．答案：（1）2230.4m/s n a =；（2）24.8m/s a τ=；（3）2.67rad三、计算题1．答案：（1）2002a v a t t τ=+；（2）2300126a x a t t τ=+ 2．答案：11n -。

3．答案：2203x h a v s =-；0x v v s =-4. 答案：（1）2109m s a -=⋅，与法向成12.4角；（2）m 1722=s 。

5．答案：20v x yud =，即运动轨迹为抛物线。

习题二一、选择题 1．A ； 2．B ； 3．B ； ４．D ，C ； 5．B 。

二、填空题1．答案：64.2310J ⨯。

2．答案：()kt m F dt x d -=1022；⎪⎭⎫ ⎝⎛-+=20021kt t m F v v ；⎪⎭⎫ ⎝⎛-+=3200312kt t m F t v x 。

3．答案：202(2)2()()mM m M v f m M l s +=++；202()Mm E v M m ∆=+。

4．答案：54N s I =⋅；27m/s v =。

5．答案：0.2。

三、计算题1．答案：（1）211 1.96m/s 5a g ==；221 1.96m/s 5a g ==；2335.88m/s 5a g ==。

（2）10.16 1.568N T g ==；20.080.784N T g ==。

2．答案：（1）5.09Km/h ；（2） 1.77Km/h -。

2012-2013华南理工大学网络学院大学物理测试题(C1)华南理工大学网络教育学院《大学物理》试卷（C 卷）注意事项：1. 本试卷共 三 大题，满分100分，考试时间120分钟，闭卷；2. 考前请将密封线内各项信息填写清楚；3. 所有答案直接做在试卷上,做在草稿纸上无效；4．考试结束，试卷、草稿纸一并交回。

一：选择题（共30分） 1．（本题3分）下列说法中，哪一个是正确的？(A) 一质点在某时刻的瞬时速度是2 m/s ，说明它在此后1 s 内一定要经过2 m 的路程．（ 密 封线内不答题）学中心： 专业层次： 姓(B) 斜向上抛的物体，在最高点处的速度最小，加速度最大．(C) 物体作曲线运动时，有可能在某时刻的法向加速度为零．(D) 物体加速度越大，则速度越大．］2. （本题3分）在光滑水平桌面上．滑轮与绳的质量以及空气阻力均不计，滑轮与其轴之间的摩擦也不计．系统无初速地释放，则物体A下落的加速度是(A) g.(B) g/3.(C) g/2 .(D) 4g/5 .］3．（本题4分）速度为v的子弹，打穿一块不动的木板后速度变为零，设木板对子弹的阻力是恒定的．那么，当子弹射入木板的深度等于其厚度的一半时，子弹的速度是6. （本题3分） 如图，在一带电量为Q 的导体球外，同心地包有一各向同性均匀电介质球壳，相对介电常数为εr ，壳外是真空．则在壳外P 点处(设r OP =)的场强和电位移的大小分别为(A) E = Q / (4πε0εr r 2)，D = Q /(4πε0r 2)． (B) E = Q / (4πεr r 2)，D = Q / (4πr 2)．(C) E = Q / (4πε0r 2)，D = Q / (4πr 2)．(D) E = Q / (4πε0r 2)，D = Q / (4πε0r 2)．．］ 7．（本题3分）如图，流出纸面的电流为2I ，流进纸面的电流为I ，则下述各式中哪一个是正确的？(A) I l H L 2d 1=⎰⋅． (B)Il H L =⎰⋅2d(C)Il H L -=⎰⋅3d． (D)Il H L -=⎰⋅4d．4］8．（本题3分）在圆柱形空间内有一磁感强度为B 的均匀磁场，如图所示．B 的大小以速率d B/d t变化．在磁场中有A、B两点，其间可放直导线AB和弯曲的导线AB，则(A) AB导线中的电动势小于AB弧(B) 电动势只在弧AB(C) 电动势在AB直导线和AB弧导线中都产生，且两者大小相等．(D) 电动势只在AB直导线中产生．［］9．（本题3分）用劈尖干涉法可检测工件表面缺陷，当波长为λ的单色平行光垂直入射时，若观察到的干涉条纹如图所示，每一条纹弯曲部分的顶点恰好与其左边条纹的直线部分的连线相切，则工件表面与条纹弯曲处对应的部分(A) 凸起，且高度为λ / 4． (B) 凸起，且高度为λ / 2． (C) 凹陷，且深度为λ / 2． （D ）凹陷，且深度为λ / 4．［ ］ 10．（本题3分）在单缝夫琅禾费衍射实验中波长为λ的单色光垂直入射到单缝上．对应于衍射角为30°的方向上，若单缝处波面可分成 3个半波带，则缝宽度a 等于(A) λ． (B) 1.5 λ． (C) 2 λ． (D) 3 λ．]二、填空题：（共3０分） 11．（本题4分）一质量为m 的子弹，水平射入悬挂着的静止砂袋中，如图所示．砂袋质量为M ，悬线长为l ．为使砂袋能在竖直平面内完成整个圆周运动，子弹射入的速度应为___________________。