江苏省句容市第三中学2015届高三数学上学期 解析几何 11椭圆的几何性质(1)教学案(无答案)

椭圆的简单几何性质椭圆是一种具有特定几何性质的曲线。

在本文档中，我们将详细讨论椭圆的简单几何性质，并介绍其定义、焦点、半长轴、半短轴以及离心率等重要概念。

椭圆的定义椭圆可以通过以下方式进行定义：给定平面上的两个焦点F1和F2以及一条固定的长度2a的线段，椭圆是满足以下条件的点的集合：对于任意点P到焦点F1的距离加上点P到焦点F2的距离等于2a。

椭圆的焦点对于给定的椭圆，焦点F1和F2是椭圆上的两个点，且满足任意点P到焦点F1的距离加上点P到焦点F2的距离等于2a。

焦点对于椭圆的性质非常重要，并在许多应用中起着重要的作用。

椭圆的半长轴和半短轴椭圆的半长轴和半短轴是两个关键的几何性质。

半长轴为轴线上从中心点到椭圆上离心率最大的点的距离；半短轴为轴线上从中心点到椭圆上离心率最小的点的距离。

椭圆的半长轴和半短轴的关系可以用离心率来表示。

离心率定义为焦点到椭圆中心的距离除以半长轴的长度。

离心率也可以用半短轴除以半长轴来表示。

椭圆的离心率离心率是一个椭圆的重要几何性质，它描述了椭圆形状的圆度程度。

离心率范围在0和1之间，且离心率为0时表示圆形，离心率为1时表示长椭圆。

离心率越接近于0，椭圆的形状越接近于圆形。

椭圆的参数方程椭圆可以用参数方程来表示，其中x和y的值取决于参数t 的变化。

椭圆的参数方程为：x = a * cos(t)y = b * sin(t)其中，a和b分别是半长轴和半短轴的长度。

椭圆与直线的交点椭圆与直线的交点是椭圆和直线相交的点的集合。

在平面几何中，椭圆和直线的交点有以下几种情况：1.椭圆内部：直线与椭圆相交于两个不同的点。

2.直线刚好接触椭圆：直线与椭圆相切于一个点。

3.椭圆外部：直线与椭圆没有交点。

椭圆的对称性椭圆具有关于x轴和y轴的对称性。

具体来说，椭圆关于x轴对称指的是如果点(x, y)在椭圆上，则点(x, -y)也在椭圆上。

类似地，椭圆关于y轴对称指的是如果点(x, y)在椭圆上，则点(-x, y)也在椭圆上。

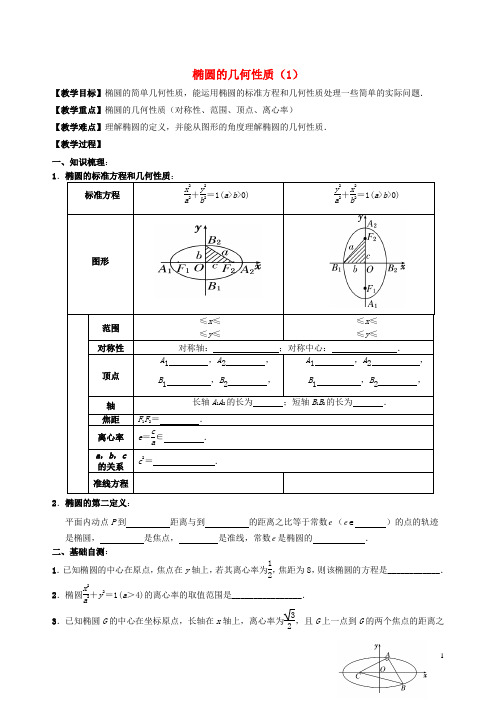
椭圆的几何性质（1）【教学目标】椭圆的简单几何性质，能运用椭圆的标准方程和几何性质处理一些简单的实际问题．【教学重点】椭圆的几何性质（对称性、范围、顶点、离心率） 【教学难点】理解椭圆的定义，并能从图形的角度理解椭圆的几何性质． 【教学过程】 一、知识梳理：12．椭圆的第二定义：平面内动点P 到 距离与到 的距离之比等于常数e （ e ）的点的轨迹 是椭圆， 是焦点， 是准线，常数e 是椭圆的 ．二、基础自测：1．已知椭圆的中心在原点，焦点在y 轴上，若其离心率为12，焦距为8，则该椭圆的方程是____________．2．椭圆x 2a2＋y 2＝1(a ＞4)的离心率的取值范围是________________．3．已知椭圆G 的中心在坐标原点，长轴在x 轴上，离心率为32，且G 上一点到G 的两个焦点的距离之和为12，则椭圆G 的方程为 ． 4．Rt △ABC 中，AB ＝AC ＝1，以点C 为一个焦点作一个椭圆， 使这个椭圆的另一个焦点在AB 边上，且这个椭圆过A 、B 两点，则这个椭圆的焦距长为___________．三、典型例题： 反思：例1．已知F 1、F 2是椭圆C ：x 2a 2＋y 2b2＝1(a ＞b ＞0)的两个焦点，P 为椭圆C 上的一点，且12PF PF ⊥，若△PF 1F 2的面积为9，则b ＝ ．【变式拓展】已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的长轴的一个端点是A (2,0)．直线l 经过椭圆的中心O 且与椭圆相交于B 、C 两点，0=⋅BC AC ，||2||BA BC OB OC -=-，求椭圆的方程．例2．设M 是椭圆1922=+y x 上的一点，21F F 、是焦点． （1）02190=∠MF F ，则21PF F ∆面积为多少？（2）02160=∠MF F ，求21PF F ∆面积为多少？例3．已知F 1、F 2是椭圆的两个焦点，过F 1且与椭圆长轴垂直的直线交椭圆于A 、B 两点，若△ABF 2是正三角形，求这个椭圆的离心率．【变式拓展】（1）设椭圆2222+=1x y a b(>>0)a b 的左、右顶点分别为,A B ，点P 在椭圆上且异于,A B 两点，O 为坐标原点.若直线AP 与BP 的斜率之积为12-，求椭圆的离心率_________.（2）已知椭圆22221(0)x y a b a b+=>>的右焦点为F ，P 点在椭圆上，以P 点为圆心的圆与y 轴相切，且同时与x 轴相切于椭圆的右焦点F ，则椭圆22221y x a b+=的离心率为 ．四、课堂反馈：1．椭圆x 29＋y 24＋k ＝1的离心率为45，则k 的值为________．2．椭圆()222210x y a b a b=>>+的右焦点为1F ,右准线为1l ，若过点1F 且垂直于x 轴的弦的弦长等于点1F到1l 的距离，则椭圆的离心率是_______.3．椭圆Γ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1，F 2，焦距为2c ，若直线y ＝3(x ＋c )与椭圆Γ的一个交点M 满足∠MF 1F 2＝2∠MF 2F 1，则该椭圆的离心率等于________．五、课后作业： 学生姓名：___________1．若椭圆1522=+m y x 的离心率510=e ，则m 的值是_________． 2．若一个椭圆长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是 ． 3．若椭圆短轴一端点到椭圆一焦点的距离是该焦点到同侧长轴一端点距离的3倍， 则椭圆的离心率e = ．4．已知椭圆C 的短轴长为6，离心率为45，则椭圆C 的焦点F 到长轴的一个端点的距离为______ _．5．若椭圆短轴长的两个三等分点与两个焦点构成一个正方形，则椭圆的离心率e =_______．6．已知P 是椭圆x 212＋y 24＝1上的动点，F 1，F 2是椭圆的两个焦点，则1PF ·2PF 的取值范围为________．7．已知正方形ABCD 的四个顶点在椭圆)0(12222>>=+b a by a x 上，AB ∥x 轴，AD 过左焦点F ，则该椭圆的离心率为 ．8．已知椭圆12222=+by a x （a ＞b ＞0），点)0,(2c a A ，英才苑椭圆的上顶点为B ，过它的右焦点F 且垂直于长轴的直线交椭圆于点P （在x 轴上方），直线AB 恰好经过线段FP 的中点D ．（1）求椭圆的离心率； （2）设椭圆的左顶点分别是A 1，且51=B A ，求椭圆的方程．9．设椭圆22221(0)x y a b a b+=>>的左，右两个焦点分别为1F ，2F ，短轴的上端点为B ，短轴上的两个三等分点为P ，Q ，且12F PF Q 为正方形．（1）求椭圆的离心率；（2）若过点B 作此正方形的外接圆的切线在x 轴上的一个截距为324-，求此椭圆的方程．10．如图，在平面直角坐标系xOy 中，A 1，A 2，B 1，B 2为椭圆22221(0)x y a b a b+=>>的四个顶点，F 为其右焦点，直线A 1B 2与直线B 1F 相交于点T ，线段OT 与椭圆的交点M 恰为线段OT 的中点，求该椭圆的离心率．。

（一）椭圆的定义：1、椭圆的定义：平面与两个定点F i 、F 2的距离之和等于定长（大于 IRF 2I ）的点的轨迹叫做椭圆。

这两个定点 F i 、F 2叫做椭圆的 焦点，两焦点的距离 厅汀2|叫做椭圆的 焦距。

对椭圆定义的几点说明：（1） “在平面”是前提，否则得不到平面图形（去掉这个条件，我们将得到一个椭球面）； （2） “两个定点”的设定不同于圆的定义中的“一个定点” ，学习时注意区分；（3） 作为到这两个定点的距离的和的 “常数”，必须满足大于| F i F 2|这个条件。

若不然， 当这个“常数”等于| F i F 2|时，我们得到的是线段 F 1F 2；当这个“常数”小于| F i F 2|时，无 轨迹。

这两种特殊情况，同学们必须注意。

（4） 下面我们对椭圆进行进一步观察，发现它本身具备对称性，有两条对称轴和一个 对称中心，我们把它的两条对称轴与椭圆的交点记为 A i , A 2, B i , B 2，于是我们易得| A i A 2|的值就是那个“常数”，且|B 2F 2|+|B 2F i |、|B i F 2|+|B i F i |也等于那个“常数”。

同学们想一想 其中的道理。

（5）中心在原点、焦点分别在 x 轴上，y 轴上的椭圆标准方程分别为：2 2 2 2i （a b 0）,77i （a b 0）,a ba b2 2 2相同点是：形状相同、大小相同；都有 a > b > 0， a c b 。

不同点是：两种椭圆相对于坐标系的位置不同， 它们的焦点坐标也不同（第一个椭圆的 焦点坐标为（一c , 0）和（c , 0）,第二个椭圆的焦点坐标为（0,— c ）和（0, c ）。

椭圆的 焦点在x 轴上 标准方程中x 2项的分母较大；椭圆的焦点在 y 轴上标准方程中y 2项的分母较大。

（二）椭圆的几何性质：椭圆的几何性质可分为两类：一类是与坐标系有关的性质，如顶点、焦点、中心坐标； 一类是与坐标系无关的本身固有性质，如长、短轴长、焦距、离心率.对于第一类性质，只2 2要X 2 每 i （a b 0）的有关性质中横坐标x 和纵坐标y 互换，就可以得出 a b2 2^2 —2 i （a b 0）的有关性质。

2019-2020学年高三数学上学期 解析几何 11椭圆的几何性质（1）教学案【教学目标】椭圆的简单几何性质，能运用椭圆的标准方程和几何性质处理一些简单的实际问题．【教学重点】椭圆的几何性质（对称性、范围、顶点、离心率） 【教学难点】理解椭圆的定义，并能从图形的角度理解椭圆的几何性质． 【教学过程】 一、知识梳理：12．椭圆的第二定义：平面内动点P 到 距离与到 的距离之比等于常数e （ e ）的点的轨迹 是椭圆， 是焦点， 是准线，常数e 是椭圆的 ．二、基础自测：1．已知椭圆的中心在原点，焦点在y 轴上，若其离心率为12，焦距为8，则该椭圆的方程是____________．2．椭圆x 2a＋y 2＝1(a ＞4)的离心率的取值范围是________________．3．已知椭圆G 的中心在坐标原点，长轴在x 轴上，离心率为32，且G 上一点到G 的两个焦点的距离之和为12，则椭圆G 的方程为 ． 4．Rt △ABC 中，AB ＝AC ＝1，以点C 为一个焦点作一个椭圆， 使这个椭圆的另一个焦点在AB 边上，且这个椭圆过A 、B 两点，则这个椭圆的焦距长为___________．三、典型例题： 反思：例1．已知F 1、F 2是椭圆C ：x 2a 2＋y 2b2＝1(a ＞b ＞0)的两个焦点，P 为椭圆C 上的一点，且12PF PF ⊥，若△PF 1F 2的面积为9，则b ＝ ．【变式拓展】已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的长轴的一个端点是A (2,0)．直线l 经过椭圆的中心O 且与椭圆相交于B 、C 两点，0=⋅BC AC ，||2||BA BC OB OC -=-，求椭圆的方程．例2．设M 是椭圆1922=+y x 上的一点，21F F 、是焦点． （1）02190=∠MF F ，则21PF F ∆面积为多少？（2）02160=∠MF F ，求21PF F ∆面积为多少？例3．已知F 1、F 2是椭圆的两个焦点，过F 1且与椭圆长轴垂直的直线交椭圆于A 、B 两点，若△ABF 2是正三角形，求这个椭圆的离心率．【变式拓展】（1）设椭圆2222+=1x y a b(>>0)a b 的左、右顶点分别为,A B ，点P 在椭圆上且异于,A B 两点，O 为坐标原点.若直线AP 与BP 的斜率之积为12-，求椭圆的离心率_________.（2）已知椭圆22221(0)x y a b a b+=>>的右焦点为F ，P 点在椭圆上，以P 点为圆心的圆与y 轴相切，且同时与x 轴相切于椭圆的右焦点F ，则椭圆22221y x a b+=的离心率为 ．四、课堂反馈：1．椭圆x 29＋y 24＋k ＝1的离心率为45，则k 的值为________．2．椭圆()222210x y a b a b=>>+的右焦点为1F ,右准线为1l ，若过点1F 且垂直于x 轴的弦的弦长等于点1F到1l 的距离，则椭圆的离心率是_______.3．椭圆Γ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1，F 2，焦距为2c ，若直线y ＝3(x ＋c )与椭圆Γ的一个交点M 满足∠MF 1F 2＝2∠MF 2F 1，则该椭圆的离心率等于________．五、课后作业： 学生姓名：___________1．若椭圆1522=+m y x 的离心率510=e ，则m 的值是_________． 2．若一个椭圆长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是 ． 3．若椭圆短轴一端点到椭圆一焦点的距离是该焦点到同侧长轴一端点距离的3倍， 则椭圆的离心率e = ．4．已知椭圆C 的短轴长为6，离心率为45，则椭圆C 的焦点F 到长轴的一个端点的距离为______ _．5．若椭圆短轴长的两个三等分点与两个焦点构成一个正方形，则椭圆的离心率e =_______．6．已知P 是椭圆x 212＋y 24＝1上的动点，F 1，F 2是椭圆的两个焦点，则1PF ·2PF 的取值范围为________．7．已知正方形ABCD 的四个顶点在椭圆)0(12222>>=+b a by a x 上，AB ∥x 轴，AD 过左焦点F ，则该椭圆的离心率为 ．8．已知椭圆12222=+by a x （a ＞b ＞0），点)0,(2c a A ，英才苑椭圆的上顶点为B ，过它的右焦点F 且垂直于长轴的直线交椭圆于点P （在x 轴上方），直线AB 恰好经过线段FP 的中点D ．（1）求椭圆的离心率； （2）设椭圆的左顶点分别是A 1，且51=B A ，求椭圆的方程．9．设椭圆22221(0)x y a b a b+=>>的左，右两个焦点分别为1F ，2F ，短轴的上端点为B ，短轴上的两个三等分点为P ，Q ，且12F PF Q 为正方形．（1）求椭圆的离心率；（2）若过点B 作此正方形的外接圆的切线在x 轴上的一个截距为4-，求此椭圆的方程．10．如图，在平面直角坐标系xOy 中，A 1，A 2，B 1，B 2为椭圆22221(0)x y a b a b+=>>的四个顶点，F 为其右焦点，直线A 1B 2与直线B 1F 相交于点T ，线段OT 与椭圆的交点M 恰为线段OT 的中点，求该椭圆的离心率．。

椭圆几何性质椭圆是数学上的一个重要曲线，具有许多独特的几何性质。

通过了解椭圆的定义和特征，我们可以深入了解椭圆的性质和应用。

本文将介绍椭圆的几何性质，包括焦点、直径、离心率和切线等内容。

1. 椭圆的定义椭圆可以通过以下的数学定义表示：对于给定的两个焦点F1和F2，椭圆是所有到这两个焦点的距离之和等于常数2a的点的轨迹。

椭圆的数学表示可以用标准方程来表示：(x/a)^2 + (y/b)^2 = 1其中，a和b分别是椭圆的半长轴和半短轴的长度，半长轴为椭圆离中心最远的点到椭圆中心的距离。

2. 椭圆的焦点椭圆有两个焦点F1和F2。

根据定义，任意点到这两个焦点的距离之和是一个常数。

对于椭圆，焦距的长度等于2a。

焦点在椭圆的长轴上，且与椭圆中心相距c 的位置，满足关系式c^2 = a^2 - b^2。

因此，我们可以通过椭圆的半长轴和半短轴的长度来计算焦点的位置。

3. 椭圆的直径椭圆的直径是通过椭圆中心的两个相对焦点的连线。

直径的长度等于椭圆的半长轴的两倍，即直径的长度为2a。

4. 椭圆的离心率椭圆的离心率是表示椭圆形状的一个重要参数。

离心率定义为焦距与半长轴之间的比值。

离心率的取值范围为0到1之间，且离心率为0时表示圆形，离心率为1时表示扁平的线段。

椭圆的离心率可以通过以下公式计算得到：e = c / a其中，e是离心率，c是焦距的长度，a是半长轴的长度。

5. 椭圆的切线切线是椭圆的另一个重要性质。

在椭圆上的任意一点P，通过该点的切线与半长轴和半短轴的连线构成的夹角相等。

这个夹角可以用以下公式计算：tan θ = |(b/a) * x|其中，θ为切线与半长轴的夹角，x为点P到椭圆中心的水平距离。

6. 椭圆的对称性椭圆具有两种类型的对称性：轴对称和中心对称。

轴对称是指椭圆关于长轴和短轴分别对称。

这意味着椭圆上的任意一点关于长轴或短轴的投影对称。

中心对称是指椭圆关于椭圆中心对称。

这意味着椭圆上的任意一点关于椭圆中心的对称点也在椭圆上。

椭圆的标准方程及其几何性质1. 椭圆定义：（1）第一定义：平面内与两个定点21F F 、的距离之和为常数|)|2(222F F a a >的动点P 的轨迹叫椭圆,其中两个定点21F F 、叫椭圆的焦点.当21212F F a PF PF >=+时, P 的轨迹为椭圆 ; ; 当21212F F a PF PF <=+时, P 的轨迹不存在;当21212F F a PF PF ==+时, P 的轨迹为 以21F F 、为端点的线段（2）椭圆的第二定义:平面内到定点F 与定直线l (定点F 不在定直线l 上)的距离之比是常数e (10<<e )的点的轨迹为椭圆（利用第二定义,可以实现椭圆上的动点到焦点的距离与到相应准线的距离相互转化）. 2.椭圆的方程与几何性质:3.点),(00y x P 与椭圆)0(12222>>=+b a b y a x 的位置关系:当12222>+b y a x 时,点P 在椭圆外; 当12222>+b y a x 时,点P 在椭圆内; 当12222=+b y a x 时,点P 在椭圆上; 4.直线与椭圆的位置关系直线与椭圆相交0>∆⇔;直线与椭圆相切0=∆⇔;直线与椭圆相离0<∆⇔ 例题分析：题1写出适合下列条件的椭圆的标准方程：⑴两个焦点坐标分别是(-4,0)、（4，0），椭圆上一点P 到两焦点的距离 之和等于10；⑵两个焦点坐标分别是（0，－2）和（0,2）且过（23-,25） (3)两个焦点坐标分别是(-3，0)，(3，0)，椭圆经过点(5，0).(4)两个焦点坐标分别是(0，5)，(0，-5)，椭圆上一点P 到两焦点的距离和为26. (5)焦点在y 轴上，与y 轴的一个交点为P (0，－10)，P 到它较近的一个焦点的距离等于2.解：（1）因为椭圆的焦点在x 轴上，所以设它的标准方程为所以所求椭圆标准方程为92522=+y x ⑵ 因为椭圆的焦点在y 轴上，所以设它的标准方程为由椭圆的定义知，22)225()23(2++-=a ＋22)225()23(-+-10=∴a 又2=c所以所求标准方程为61022=+x y 另法：∵ 42222-=-=a c a b∴可设所求方程142222=-+a x a y ，后将点（23-,25）的坐标代入可求出a ，从而求出椭圆方程(3)∵椭圆的焦点在x 轴上，所以设它的标准方程为： ∵100)35(0)35(222=+-+++=a ，2c =6. ∴3,5==c a∴163522222=-=-=c a b∴所求椭圆的方程为：1162522=+y x . (4)∵椭圆的焦点在y 轴上，所以设它的标准方程为)0(12222>>=+b a bx a y . ∴.144222=-=c a b∴所求椭圆方程为：114416922=+x y （5）∵椭圆的焦点在y 轴上，所以可设它的标准方程为： ∵Ｐ（０，－１０）在椭圆上，∴a ＝１０.又∵P 到它较近的一焦点的距离等于2， ∴－c －（－１０）＝２，故c =8. ∴36222=-=c a b .∴所求椭圆的标准方程是13610022=+x y . 题2。

椭圆知识点梳理总结高中椭圆是一个非常重要的数学概念，它在几何学、物理学、工程学等领域中都有广泛的应用。

椭圆的性质和应用涉及到许多重要的知识点，掌握这些知识点对于提高数学水平和解决实际问题都是非常有益的。

本文将对椭圆的基本概念、性质和应用进行梳理总结，希望能够帮助读者更好地理解和运用椭圆的知识。

一、椭圆的基本概念1.1 椭圆的定义椭圆是平面上到两个定点F1和F2的距离之和为常数2a的点P的轨迹。

称为椭圆，其中a是椭圆的半长轴的长度。

1.2 椭圆的几何特征椭圆的轨迹是一个闭合的曲线，且是对称的。

它的长轴与短轴之间的长度差异是2a，短轴的长度是2b。

1.3 椭圆的标准方程椭圆的标准方程是(x-h)²/a² + (y-k)²/b² = 1，其中(h,k)是椭圆的中心坐标。

1.4 椭圆的离心率椭圆的离心率e定义为e=c/a，其中c是椭圆的焦点距离，a是椭圆的半长轴长度。

1.5 椭圆的参数方程椭圆的参数方程是x=h+a*cosθ，y=k+b*sinθ，其中θ是参数，范围在[0,2π]。

二、椭圆的性质2.1 椭圆的焦点性质椭圆的焦点是F1和F2，椭圆上的任意一点到两个焦点的距离之和是常数2a。

2.2 椭圆的顶点性质椭圆的长轴与短轴的两个端点分别是椭圆的顶点，它们与中心的连线都垂直于长轴。

2.3 椭圆的对称性椭圆关于长轴和短轴都是对称的，具有轴对称和中心对称性质。

2.4 椭圆的直径性质椭圆上的任意一条直径都经过椭圆的中心，并且以中心为对称轴。

2.5 椭圆的焦点方程椭圆的焦点方程是x²/a²+ y²/b²= 1，它表示椭圆上的点到两个焦点的距离之和是常数2a。

三、椭圆的参数方程3.1 参数方程的概念参数方程是用参数表示函数的自变量和因变量的一种方法，它将一个平面曲线的横纵坐标都表示成参数的函数。

3.2 椭圆的参数方程椭圆的参数方程是x=h+a*cosθ，y=k+b*sinθ，其中θ是参数，范围在[0,2π]。