第4章 静定拱
- 格式：ppt
- 大小：217.00 KB
- 文档页数：14
下载文档原格式
合集下载
01-静定拱和悬梁结构知识点小结
K
截面的弯矩、剪力；
K 值为 K 截面法线的倾角（如图 4-1(a)所示的坐标系中），在拱顶铰以左取正，以右
取负。
K 可根据其与拱轴方程 y = f (x) 之间的关系式确定，即：
3、受力特征总结
cosK =
1
1+ ( y)2
, sinK = ycosK
x = xK
（1）支座反力与拱轴线形式无关，只与三个铰的位置有关； （2）两个竖向支座反力与相应简支梁竖向支反力对应相等，这说明竖向支反力与拱高 无关；
以上公式均适用于带拉杆的三铰平拱（承受竖向荷载作用），拉杆拉力即为水平推力 FH ，
其支座反力和内力和的计算公式不变。 5、一般荷载（含水平力）作用下，支座反力和内力不能套用上述公式，而应直接采用截面 法求内力，此时两个支座的水平反力也不相同。
二、三铰斜拱的计算
三铰斜拱在竖向荷载作用下，可根据三个整体平衡条件，以及半拱对拱顶铰 C 的平衡
y = M 0(x) FH
式中， M 0 为相应简支梁的弯矩图表达式， FH 为拱的水平推力。这表明，在竖向荷载 作用下三铰平拱合理轴线的纵坐标 y 与相应简支梁弯矩图的竖标 M 0 成比例。
三铰平拱在满跨竖向均布荷载 q 作用下的合理轴线为二次抛物线（图 4-3），即：
y
=
4f l2
x(l − x)
F 'AV = FA0V ,
F 'BV
=
FB0V ， FA' H
= FB'H
= FH'
=
M
0 C
h
式中，h
为斜拱中拱顶铰
C
至拱趾连线的垂直距离，M
0 C
为相应水平简支梁中相应
第四章-静定拱
§4-1 基本概念 2.常见形式
铰 静 拱 三 拱—— 定 拱两 拱 铰 静 结 无 拱 超 定 构 铰
三铰拱
两铰拱
无铰拱
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-1 基本概念 3. 几何特性：
拱 顶 拱轴线 (拱轴 )拱高 起拱线来自拱趾 、 ) ( 跨度
内力不仅与三铰拱位置有关， 内力不仅与三铰拱位置有关，且与拱轴线形 状有关。
谢
谢 ！
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线
3.方法： 方法： 先作出压力线， ⑴ 先作出压力线，然后以压力线代 替拱轴。 替拱轴。 ° M 利用弯矩方程： ⑵ 利用弯矩方程： = M − Hy ° M∗ 令 M = M − Hy = 0 ⇒ y = H 即为合理拱轴线的纵坐标。 y即为合理拱轴线的纵坐标。
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线（Optimal centre line of arch） 三铰拱的合理拱轴线（ arch）
1.定义： 定义： 在已知荷载作用下， 在已知荷载作用下，能选择三铰拱的 轴线， 轴线，使得拱的所有横截面上的弯矩 为零。该拱的轴线就称为三铰拱的合 为零。该拱的轴线就称为三铰拱的合 理拱轴线。 理拱轴线。 条件： 2.条件： 拱轴线与压力线重合时， 拱轴线与压力线重合时，满足横截面 上的弯矩M Q=0 而仅有轴力N 上的弯矩M＝0、Q=0，而仅有轴力N。
l 9
dy 2 tgϕ = = (6 − x) dx 9
截面1 截面1：x1 = 1.56m
y1 = 1.75m tgϕ1 = 1 ϕ1 = 450
铰 静 拱 三 拱—— 定 拱两 拱 铰 静 结 无 拱 超 定 构 铰
三铰拱
两铰拱
无铰拱
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-1 基本概念 3. 几何特性：
拱 顶 拱轴线 (拱轴 )拱高 起拱线来自拱趾 、 ) ( 跨度
内力不仅与三铰拱位置有关， 内力不仅与三铰拱位置有关，且与拱轴线形 状有关。
谢
谢 ！
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线
3.方法： 方法： 先作出压力线， ⑴ 先作出压力线，然后以压力线代 替拱轴。 替拱轴。 ° M 利用弯矩方程： ⑵ 利用弯矩方程： = M − Hy ° M∗ 令 M = M − Hy = 0 ⇒ y = H 即为合理拱轴线的纵坐标。 y即为合理拱轴线的纵坐标。
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线（Optimal centre line of arch） 三铰拱的合理拱轴线（ arch）
1.定义： 定义： 在已知荷载作用下， 在已知荷载作用下，能选择三铰拱的 轴线， 轴线，使得拱的所有横截面上的弯矩 为零。该拱的轴线就称为三铰拱的合 为零。该拱的轴线就称为三铰拱的合 理拱轴线。 理拱轴线。 条件： 2.条件： 拱轴线与压力线重合时， 拱轴线与压力线重合时，满足横截面 上的弯矩M Q=0 而仅有轴力N 上的弯矩M＝0、Q=0，而仅有轴力N。
l 9
dy 2 tgϕ = = (6 − x) dx 9
截面1 截面1：x1 = 1.56m
y1 = 1.75m tgϕ1 = 1 ϕ1 = 450
结构力学-静定拱
H=M’C/f 2 内力计算：
截面Ｋ的弯矩： M=[Vax－P1(x－a1)]－Hy
即 M=M’－Hy
A
P1
P2
B
ＫC
剪力：
Ｑ=VA cos --P1 cos--H sin V’A
V’B
＝Ｑ’ cos --H sin
轴力：
HA
P1 Ｋ
A
P2
B
HB
N=(VA--P1) sin+
Hcos
第四章 静定拱
§4--1 概述
拱：杆轴线为曲线并且有竖向荷载作用下会产生 水平反力的结构。
拱的常用形式有三种：
1、三铰拱
HA
A
P
HB B
VA
VB
2 两铰拱
3 无铰拱
拱的各部分名称如右图：拱 趾
起拱线
A
拱轴线
拱
拱高f
趾
B
跨度l
§4--2 三铰拱的数解法
1 支座反力计算
如右图： 由MB=0
a1
b1
VA
VB
=Q’sin +Hsin
综上所述，三铰平拱的内力计算公
式可写为：
M=M’--Hy
Q=Q’ cos --H sin
N=Q’ sin --H cos
§4--3 三铰拱的合理拱轴线
当拱上所有截面的弯矩都为零而只有轴力时，这
时的拱轴线为合理拱轴线。其方程为： y=M’/H
q
例４－２
y
a2
b2
P1
P2
MA=0
HA
A
HB B
HA=HB=H
l1
MC=0
VA
l2 VB
VAl1－P1(l1－a1)－Hf=0 l
第四章静定拱
第四章 静定拱
§4–1概述 拱——曲线杆件， 竖向荷载作用下有水平反力。 常用形式： 三铰拱、两铰拱、无铰拱
重要特点：
竖向荷载产生水平推力（与梁相比）
优点：
M减小，FN为主 ——便于使用抗压材料：砖、石、混凝土 缺点：
水平反力要求
——地基、支承结构、（墙、柱、墩等） 更坚固。
——可称拱式结构或推力结构
∑m0 = 0 FNρ-(FN+dFN)ρ=0 dFN=0 FN=常数
∑s = 0（投影方程）
2FNsin(dφ/2)-qρdφ=0
dφ极小，sin(dφ/2)=dφ/2
FN-qρ=0 ρ=FN/q ＝常数 合理拱轴——圆弧线
【例4－3】 q = qc+ γy 解：坐标系如图，
M=M0－FH（f－y）=0
带拉杆的拱 ——消除推力
（消除对支承结构的影响） 拱的各部名称（参数）
基本参数
拱高f 跨度l 高跨比f/l
平拱/斜拱： 拱趾是 / 否 在同一水平线
§4 – 2 三铰拱的计算
1．支座反力计算 （与相应代梁比较）
FVA=F0VA FVB=F0VB
FH
M
0 c
f
M0C—— 代梁
相应截面 C的弯矩
①推力FH∝1/f， 与曲线形式无关， 与铰位置有关，
（a）竖向荷载——计算公式 （b）非竖向荷载——截面法 3、特点(与梁比较） ——水平推力，使M减少 4、代拉杆的三铰拱 5、合理拱轴线：满跨均布荷载
静水压力
f y M0 FH
求导二次： y"
1 FH
d2M 0 dx2
1 FH
(q)
微分方程 解－双曲线函数
y q FH
§4–1概述 拱——曲线杆件， 竖向荷载作用下有水平反力。 常用形式： 三铰拱、两铰拱、无铰拱
重要特点：
竖向荷载产生水平推力（与梁相比）
优点：
M减小，FN为主 ——便于使用抗压材料：砖、石、混凝土 缺点：
水平反力要求
——地基、支承结构、（墙、柱、墩等） 更坚固。
——可称拱式结构或推力结构
∑m0 = 0 FNρ-(FN+dFN)ρ=0 dFN=0 FN=常数
∑s = 0（投影方程）
2FNsin(dφ/2)-qρdφ=0
dφ极小，sin(dφ/2)=dφ/2
FN-qρ=0 ρ=FN/q ＝常数 合理拱轴——圆弧线
【例4－3】 q = qc+ γy 解：坐标系如图，
M=M0－FH（f－y）=0
带拉杆的拱 ——消除推力
（消除对支承结构的影响） 拱的各部名称（参数）
基本参数
拱高f 跨度l 高跨比f/l
平拱/斜拱： 拱趾是 / 否 在同一水平线
§4 – 2 三铰拱的计算
1．支座反力计算 （与相应代梁比较）
FVA=F0VA FVB=F0VB
FH
M
0 c
f
M0C—— 代梁
相应截面 C的弯矩
①推力FH∝1/f， 与曲线形式无关， 与铰位置有关，
（a）竖向荷载——计算公式 （b）非竖向荷载——截面法 3、特点(与梁比较） ——水平推力，使M减少 4、代拉杆的三铰拱 5、合理拱轴线：满跨均布荷载
静水压力
f y M0 FH
求导二次： y"
1 FH
d2M 0 dx2
1 FH
(q)
微分方程 解－双曲线函数
y q FH
结构力学第4章静定拱(f)
FH
FH
由边界条件
x 0, y 0 : x 0, y 0 :
A qc
B0
合理拱轴线的方程为
y qc (cosh x 1)
FH
§4-3 三铰拱的合理拱轴线
例4-3 试求三铰拱在垂直于拱轴线的均布荷载作用下的合理 拱轴线。
解：由图a，荷载为非竖向荷载。
思路：假定拱处于无弯矩状态，根据平衡 条件推求合理拱轴线方程。
Fi ai l
Fx 0 FAH FBH FH
相应简支梁
取左半拱为隔离体
MC 0
FH
FAV l1 F1(l1 a1) f
可 得
FAV FBV
FA0V FB0V
FH
M
0 C
f
三铰拱的反力只与 荷载及三个铰的位置有 关，与拱轴线形状无关；
推力FH 与拱高 f 成反比。
§4-2 三铰拱的计算
§4-2 三铰拱的计算
2、内力的计算
压力为正
任一截面的轴力等于该截面一 侧所有外力在该截面法线方向 上的投影代数和。
FN FAV sin FH cos F1 sin (FAV F1) sin FH cos FS0 sin FH cos
相应简支梁
§4-2 三铰拱的计算
2、内力的计算
区别拱与梁的主要标志：推力的存在与否。
§4-1 概述
拉杆拱： 拱两支座间的拉杆代替支座承受水平推力
拉杆做成折线形可获得较大空间
高跨比：f/l
平拱： 两拱趾在同一水平线上 斜拱： 两拱趾不在同一水平线上
§4-2 三铰拱的计算
1、支座反力的计算
由拱的整体平衡
M B 0 FAV
Fibi l
M A 0 FBV
第四章结构力学静定拱
15kN
A
K左
A
K右
12.5kN
12.5kN
FºSK左＝12.5kN
FºSK右＝－2.5kN
( F H 1 0 k N ,F S 0 K 左 1 2 . 5 k N ,F S 0 K 右 2 . 5 k N )
( s i n 0 .4 4 7 ,c o s 0 .8 9 4 )
FSK左FS0K左cosFHsin12.50.894100.447
r FP1 90。 D D
C
FQD A
FP2 B
FRA
FRB
M D FRD rD
FQD FRD sin D FND FRD cos D
r D ——截面D形心到FRD作用线之距离。
D ——FRD作用线与截面D轴线切线的夹角。
由此看出，确定截面内力的问题归结为确定 截面一边所有外力的合力之大小、方向及作用线 的问题。
tgy'4l2f
(l2x)a b
F
V
0 A
FP1
D
F
0 SD
代梁
a2+b2 a
b
2) FºSD是代梁截面D的剪力，设为正方向。 故FºSD可能大于零、等于零或小于零。
下面用上述公式求FSK、FNK。
xK＝4m y'41 624(1624)1 2 FºSK左＝12.5kN
5
1 2
FºSK右＝－2.5kN
FP2 E FP1
D
FRA A
o
C FP1 FP2
FRA
FRB
FP3
FP3 F
B
FRB
在上图所示力多边形中，射线1－2代表FRA与 FP1合力的大小和方向；射线2－3代表FRA与FP1、 FP2合力的大小和方向。
第四章：静定拱(李廉锟第五版配套)
第4章 静定拱
4.1 概述
4.2 静定拱的计算
4.3 静定拱的合理拱轴线
4.1 概述
静定拱的特点
静定拱的特点
拱的特点： 在竖向荷载作用下有水 平反力或称推力，如图(a)。 推力是拱式结构的主要标志 优点：弯矩小得多，主要承受压力。应力分布均匀。 缺点：地基或者支撑结构要坚固 图(b)为有拉杆的三铰拱， 推力就是拉杆内的拉力。
ql 2
ql 2
先列出简支梁的弯矩方程
q M x x l x 2
拱的推力为：
MC ql 2 H f 8f
注意
*合理轴线对应的是
一组固定荷载； *合理轴线是一组。
所以拱的合理轴线方程为：
q 8f 4f y x x l x 2 2 x l x 2 ql l
f=4m
8 B
பைடு நூலகம்
1 x
y1
A
50.25kN
H 50.25kN
VB 58.5kN
4f y 2 x l x l 制内力图。
计算反力并绘
3m VA 75.5kN
3m 6m 6m
（1）计算支座反力
（2）内力计算
y1
以截面1为例
4f 4 4 x l x 312 1.5 1.75m 2 2 l 12
dy dx
x 3
14 6 9 50 3 75.5kN 12 14 6 3 50 9 VB VB 58.5kN 12 MC 75.5 6 14 6 3 H 50.25kN f 4
VA VA
M1 M1 Hy2 75.5 1.5 141.5 1.5 / 2 50.251.75 9.6kN m
4.1 概述
4.2 静定拱的计算
4.3 静定拱的合理拱轴线
4.1 概述
静定拱的特点
静定拱的特点
拱的特点： 在竖向荷载作用下有水 平反力或称推力，如图(a)。 推力是拱式结构的主要标志 优点：弯矩小得多，主要承受压力。应力分布均匀。 缺点：地基或者支撑结构要坚固 图(b)为有拉杆的三铰拱， 推力就是拉杆内的拉力。
ql 2
ql 2
先列出简支梁的弯矩方程
q M x x l x 2
拱的推力为：
MC ql 2 H f 8f
注意
*合理轴线对应的是
一组固定荷载； *合理轴线是一组。
所以拱的合理轴线方程为：
q 8f 4f y x x l x 2 2 x l x 2 ql l
f=4m
8 B
பைடு நூலகம்
1 x
y1
A
50.25kN
H 50.25kN
VB 58.5kN
4f y 2 x l x l 制内力图。
计算反力并绘
3m VA 75.5kN
3m 6m 6m
（1）计算支座反力
（2）内力计算
y1
以截面1为例
4f 4 4 x l x 312 1.5 1.75m 2 2 l 12
dy dx
x 3
14 6 9 50 3 75.5kN 12 14 6 3 50 9 VB VB 58.5kN 12 MC 75.5 6 14 6 3 H 50.25kN f 4
VA VA
M1 M1 Hy2 75.5 1.5 141.5 1.5 / 2 50.251.75 9.6kN m
结构力学第4章 静定拱结构
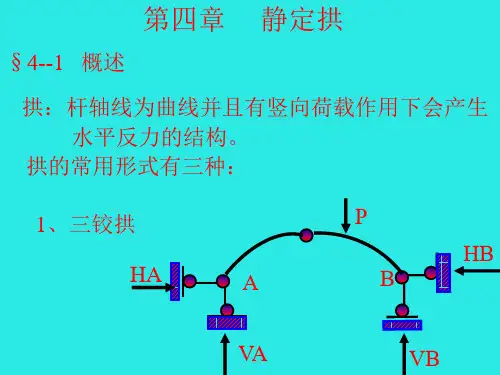
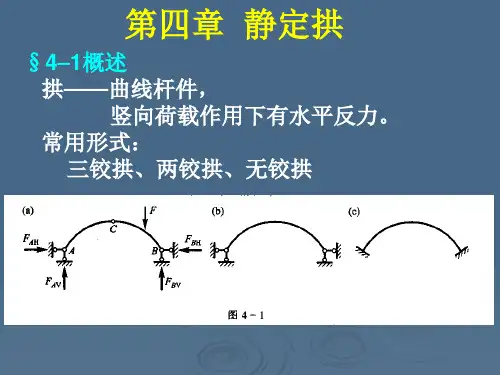
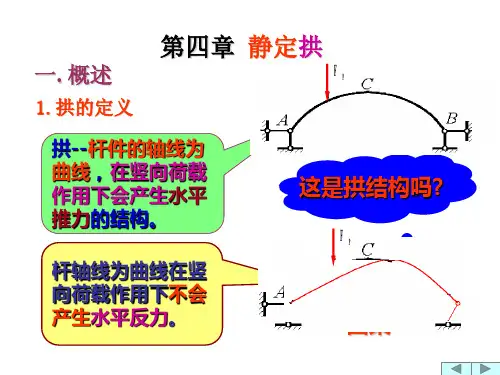
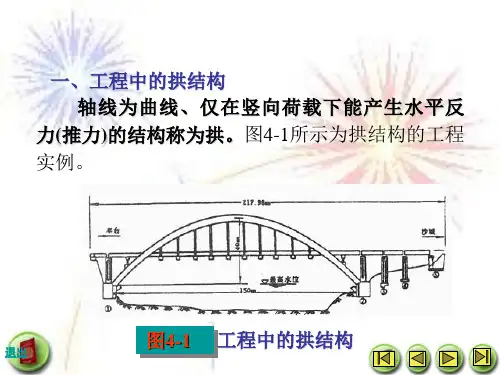
一、工程中的拱结构轴线为曲线、仅在竖向荷载下能产生水平反力(推力)的结构称为拱。
图4-1所示为拱结构的工程实例。
图4-1工程中的拱结构二、拱式结构的特征及其应用1、定义：通常杆轴线为曲线，在竖向荷载作用下，支座产生水平反力的结构。
2、特点：（1）弯矩比相应简支梁小，水平推力存在的原因。
（2）用料省、自重轻、跨度大。
（3）可用抗压性能强的砖石材料。
（4）构造复杂，施工费用高。
3、拱的种类：图4-2拱的种类4、拱各部分的名称：一、支座反力的计算C拱顶铰BA拱肋跨度拱趾铰(a) 等高三铰拱C高差hAB(b) 不等高三铰拱严格的来说，实体三铰拱支座反力的计算与一般三铰刚架结构反力计算相同。
本书介绍的是等代梁解法。
图4-4实体三铰拱第二节实体三铰拱的数解法图4-5等代粱ll 1l 2a 3b 3b 2b 1a 2a 1F P1F P2F P3F P1F P2F P3F A yF B yF A yF B yF B xF A x 00A CBAB C(b)(a )f0CH M F =HB A F F F ==x x 0Ay Ay F F =0ByBy FF =二、拱内截面内力的计算图4-6拱内截面内力1、拱的内力计算原理仍然是截面法。
2、拱通常受压力，所以计算拱时，规定轴力以受压为正。
对于竖向荷载作用三铰拱，其内力计算有简捷公式。
(c)CB A00F B yF A yF P3F P2F P1B F B xAF A x F A yF B y(a )C F P3F P2F P1a 1a 2b 1b 2b 3a 3lϕK F A y F A xF P1KM K F NKF QKx KK ϕy KxyK K(b)yF MM H 0-=ϕϕsin cos H 0Q Q F F F -=ϕϕcos sin H 0Q N F F F --=A0AyFQ F 0M (b) 代梁受力F Ax =F H F Ayx A y k F y FxyϕM(a) 截面k 坐标方向力图4-7拱内截面内力需要指出的是，非竖向荷载作用不等高三铰拱等情形，上述公式是不适用的。
4第四章静定拱
结 构 力 学 （ 08-09
21
12:14
合理拱轴线小结： 1）不同荷载作用下三铰拱的合理拱轴 线不同。 2）实际工程中，尽可能使受力状态接 近无弯矩状态。通常是以主要荷载作用 下的合理拱轴线作为拱的轴线。
学 年 ）
学 年 ）
M y FH
M M FH y 0
0
0
只限于三铰平拱受 竖向荷载作用
在竖向荷载作用下，三 铰拱的合理拱轴线的纵 坐标与相应简支梁弯矩 图的竖标成正比。
§4-3三铰拱的合理拱轴线
12:14
结 试求图示对称三铰拱在均布荷载作用下的合理拱轴线 构 力 q MC0=ql2/8 学 （ C 2/8f y F = ql f H A B 学 x l M0=qlx/2-qx2 /2 年 =qx(l-x)/2 ） q 08-09
0 FP2=50kN FH= MC / f =50.25 KN
8.5 163.5 201
58.5 175.5
FQ(kN)
M(kN.m)
0 MK MK FH y 0 FQK FQK cos FHsin
FNK FQK 0sin FHcos
§4-2三铰拱的计算
17
y=4fx(l-x)/l2
x
抛物线
§4-3三铰拱的合理拱轴线
结 构 力 学 （ 08-09
18
12:14
试求，在填土重量作用下，三铰拱的合理 轴线。土的容重为γ，拱所受的竖向荷载 为q(x)=qc+ γy
学 年 ）
§4-3三铰拱的合理拱轴线
结 构 力 学 （ 08-09
19
12:14
M f y FH
第四章 静定拱
21
12:14
合理拱轴线小结： 1）不同荷载作用下三铰拱的合理拱轴 线不同。 2）实际工程中，尽可能使受力状态接 近无弯矩状态。通常是以主要荷载作用 下的合理拱轴线作为拱的轴线。
学 年 ）
学 年 ）
M y FH
M M FH y 0
0
0
只限于三铰平拱受 竖向荷载作用
在竖向荷载作用下，三 铰拱的合理拱轴线的纵 坐标与相应简支梁弯矩 图的竖标成正比。
§4-3三铰拱的合理拱轴线
12:14
结 试求图示对称三铰拱在均布荷载作用下的合理拱轴线 构 力 q MC0=ql2/8 学 （ C 2/8f y F = ql f H A B 学 x l M0=qlx/2-qx2 /2 年 =qx(l-x)/2 ） q 08-09
0 FP2=50kN FH= MC / f =50.25 KN
8.5 163.5 201
58.5 175.5
FQ(kN)
M(kN.m)
0 MK MK FH y 0 FQK FQK cos FHsin
FNK FQK 0sin FHcos
§4-2三铰拱的计算
17
y=4fx(l-x)/l2
x
抛物线
§4-3三铰拱的合理拱轴线
结 构 力 学 （ 08-09
18
12:14
试求，在填土重量作用下，三铰拱的合理 轴线。土的容重为γ，拱所受的竖向荷载 为q(x)=qc+ γy
学 年 ）
§4-3三铰拱的合理拱轴线
结 构 力 学 （ 08-09
19
12:14
M f y FH
第四章 静定拱
华南理工大结构力学第4章静定拱
拱的特点：
1.支座承受水平推力，需要更坚固的地基和
支承结构。 缺
三铰拱的缺点：
所以工程中 很少采用！
点 1.铰的存在使结构复杂，施工困难，维护费
用高。
2.铰的存在降低了结构抗震能力。
3.拱的挠度曲线在顶铰处有转折，致使拱顶
铰处的桥面下沉，对行车不利。 6
§4-2 三铰拱的计算 1. 支座反力的计算：
13
FS1 =FS10 cos1 FH sin1 =3 kN;FN1 =FS10 sin1 + FH cos1 =74 kN
按上述方法依次求得各截面内力，绘制出内力图
结论
拱轴上内力有以下3个特点：
❖ 不管是在均布荷载下还是在集中荷载 下，拱的三个内力图都是曲线图形。
❖ 在有竖向集中力作用点两侧截面，轴 力图和剪力图都有突变，突变值等于相 应简支梁的剪力分别在拱的轴力和剪力 方向上的投影。
分析：本题为F非N +d竖FN向
荷载，我们可由假定拱
圆
F轴进N 处行于受R无力弯分矩析状，态建入立手平，
衡方程求出合理拱轴线。
M=0 → dM=FQ=0 因此横截面只有轴力FN ,FN+dFN. ∑MO=0 → FNR-(FN +d FN )R=0 → d FN=0 → FN=常数。 沿s-s轴投影方程：2FN sin(d/2)-qRd =0, sin(d/2)=d/2
使拱在给定荷载下只
M
M0
FH
y0
产生轴力的拱轴线，被 称为与该荷载对应的合
拱轴线方程：
理拱轴
M0 y
FH
在竖向荷载作用下，三
铰拱的合理拱轴线的纵
只限于三铰平拱受 坐标与相应简支梁弯矩 竖向荷载作用 图的竖标成正比。
04第四章 静定拱
方程的一般解为
y A cosh
FH
x B sinh
FH
x
qc
由边界条件
x 0, y 0 : x 0, y 0 :
A
qc
B0
合理拱轴线的方程为
y
qc
(cosh
FH
x 1)
在填土重量作用下，三铰拱的合理拱轴线是一悬链线。
§4-3 三铰拱的合理拱轴线
例4-4 试求三铰拱在垂直于拱轴线的均布荷载作用下的合理 拱轴线。
受力特点 （1）在竖向荷载作用下有水平反力 FH ; （2）由拱截面弯矩计算式可见，比相应简支梁小得多 ; （3）拱内有较大的轴向压力FN.
§4-2 三铰拱的计算
q=2kN .m y
1 0 3 4 5
F=8kN
6 7 8
2
2 y2 x
f=4m
B
例1 三铰拱及其所受荷载如 图所示拱的轴线为抛物线方 程 y 4 2f xl x
MC 0
FAV
FB V
d
F1
A
F2
c
f
B
FAV l1 F1 d FH f 0
M MC FH f 0 FH C f
FAV
x
c
F
BV
FH FAV
l1
§4-2 三铰拱的计算
二、内力计算
F1
x-a1 FS
D
FH
FN
y
以截面D为例 截面内弯矩要和竖向力及水平力对D点构成 的力矩相平衡，设使拱内侧受拉为正。 MD 0 M FAV x F1 x a1 FH y
y A cosh
FH
x B sinh
FH
x
qc
由边界条件
x 0, y 0 : x 0, y 0 :
A
qc
B0
合理拱轴线的方程为
y
qc
(cosh
FH
x 1)
在填土重量作用下，三铰拱的合理拱轴线是一悬链线。
§4-3 三铰拱的合理拱轴线
例4-4 试求三铰拱在垂直于拱轴线的均布荷载作用下的合理 拱轴线。
受力特点 （1）在竖向荷载作用下有水平反力 FH ; （2）由拱截面弯矩计算式可见，比相应简支梁小得多 ; （3）拱内有较大的轴向压力FN.
§4-2 三铰拱的计算
q=2kN .m y
1 0 3 4 5
F=8kN
6 7 8
2
2 y2 x
f=4m
B
例1 三铰拱及其所受荷载如 图所示拱的轴线为抛物线方 程 y 4 2f xl x
MC 0
FAV
FB V
d
F1
A
F2
c
f
B
FAV l1 F1 d FH f 0
M MC FH f 0 FH C f
FAV
x
c
F
BV
FH FAV
l1
§4-2 三铰拱的计算
二、内力计算
F1
x-a1 FS
D
FH
FN
y
以截面D为例 截面内弯矩要和竖向力及水平力对D点构成 的力矩相平衡，设使拱内侧受拉为正。 MD 0 M FAV x F1 x a1 FH y
第四章 静定拱
结构力学
第四章 静定拱
海南大学土木工程系
韩建刚
1
三 角 拱 三角拱的内力计算 三角拱的合理拱轴线
2
§4.1 三角拱
拱是在竖向荷载作用下能 产生水平反力的结构，如图。 水平反力 产生负弯矩， 可以抵消一 部分正弯矩
1、拱的特点
C ↓↓↓↓↓
矢高f
A
B
l跨度
与简支梁相比拱的弯矩、剪力较小，轴力较大（压力）, 应力沿截面高度分布较均匀。 节省材料，减轻自重，能跨越大 跨度 , 宜采用耐压不耐拉的材料 ， 如砖石混凝土等。有较大 的可利用空间。 其缺点是：拱对基础或下部结构施加水平推力，增加了下部结构的 拱具有曲线形状，施工不方便. 材料用量；
11
重复上述步骤，可求出各等分截面的内力，作出内力图。 8
0.5 1.5 12 0.71 M° 0.4 2 1.5 M图 (kN.m) 0 20 24 -0.49 24 -1 -6 -1.79 -5.81 -7.6 0.49 1.79 20 2
0.5
Hy -0.40
Q图 (kN) -9.19
其中 ∑MBP 是所 有荷载对B点的矩 VB=YB； H=MC0/f
二、内力计算
M P H VA x P M° YA d Q°Y A
x
P N ϕ H
C
f
↓↓↓↓↓
A
a l/2
B H
l/2
P VB
y
Q VA
c
d
↓↓↓↓↓
l
a
YB
注：1、该组公式仅用于两底铰在
VA ×x 0 MM＝ A×M－P×d ＝VM°－H×y x－P×d－H×y Q＝Q°× cos ϕ－ H×sinϕ Q＝（VA－P）×cosϕ－H×sin ϕ N＝－Q°sin ϕ －Hcos ϕ N＝－（VA－P）sinϕ－Hcosϕ
第四章 静定拱
海南大学土木工程系
韩建刚
1
三 角 拱 三角拱的内力计算 三角拱的合理拱轴线
2
§4.1 三角拱
拱是在竖向荷载作用下能 产生水平反力的结构，如图。 水平反力 产生负弯矩， 可以抵消一 部分正弯矩
1、拱的特点
C ↓↓↓↓↓
矢高f
A
B
l跨度
与简支梁相比拱的弯矩、剪力较小，轴力较大（压力）, 应力沿截面高度分布较均匀。 节省材料，减轻自重，能跨越大 跨度 , 宜采用耐压不耐拉的材料 ， 如砖石混凝土等。有较大 的可利用空间。 其缺点是：拱对基础或下部结构施加水平推力，增加了下部结构的 拱具有曲线形状，施工不方便. 材料用量；
11
重复上述步骤，可求出各等分截面的内力，作出内力图。 8
0.5 1.5 12 0.71 M° 0.4 2 1.5 M图 (kN.m) 0 20 24 -0.49 24 -1 -6 -1.79 -5.81 -7.6 0.49 1.79 20 2
0.5
Hy -0.40
Q图 (kN) -9.19
其中 ∑MBP 是所 有荷载对B点的矩 VB=YB； H=MC0/f
二、内力计算
M P H VA x P M° YA d Q°Y A
x
P N ϕ H
C
f
↓↓↓↓↓
A
a l/2
B H
l/2
P VB
y
Q VA
c
d
↓↓↓↓↓
l
a
YB
注：1、该组公式仅用于两底铰在
VA ×x 0 MM＝ A×M－P×d ＝VM°－H×y x－P×d－H×y Q＝Q°× cos ϕ－ H×sinϕ Q＝（VA－P）×cosϕ－H×sin ϕ N＝－Q°sin ϕ －Hcos ϕ N＝－（VA－P）sinϕ－Hcosϕ
结构力学(拱结构)
14
三铰拱的内力计算
表4-1：三铰拱各截面内力计算表
内力计算时，常通过 公式、列表完成
15
合理拱轴
五、 合理拱轴的概念
1、合理拱轴的概念
定义：在给定荷载作用下，拱各截面只承受轴力， 而弯矩、剪力均为零，这样的拱轴称为合理拱轴。
?
2、合理拱轴的确定
写出任一截面的弯矩表达式，令其等于零即可确 定合理拱轴。
VA0
0 2x、 荷 载 与 跨 度 一 定 M C VAl1 P1 (l 1 a 1 ) V 0 时，水平推力与矢高 MC （4-2） 等代梁计算简图 H 成反比。 f
0 B
作为结构。
7
三铰拱的内力计算
a1
a2 b1 P1 b2 P2 f
2、弯矩计算
M K [VA x K P1 (x K a1 )] H y K
q= 1kN/m
y
4f (l x)x 2 l
P=4kN 3 4 5 C 4m
x
2
6
1
H =6kN A 0
7
B H =6kN
8
VA =7kN
8×2=16m VB =5kN
解： 1、计算支座反力
0 VA VA
1 8 12 4 4 7kN 16 1 8 4 4 12 0 VB VB 5kN 16
拱结构的组成
2、拱结构的组成
3
拱结构的种类
3、拱结构的种类 静定拱
超静定拱
三铰拱
两铰拱 超静定拱
静定拱
无铰拱
高差h
静定拱
带拉杆的三铰拱
斜拱
4
拱结构的特点
4、拱结构的特点
1、弯矩比相应等代梁小；
三铰拱的内力计算
表4-1：三铰拱各截面内力计算表
内力计算时，常通过 公式、列表完成
15
合理拱轴
五、 合理拱轴的概念
1、合理拱轴的概念
定义：在给定荷载作用下，拱各截面只承受轴力， 而弯矩、剪力均为零，这样的拱轴称为合理拱轴。
?
2、合理拱轴的确定
写出任一截面的弯矩表达式，令其等于零即可确 定合理拱轴。
VA0
0 2x、 荷 载 与 跨 度 一 定 M C VAl1 P1 (l 1 a 1 ) V 0 时，水平推力与矢高 MC （4-2） 等代梁计算简图 H 成反比。 f
0 B
作为结构。
7
三铰拱的内力计算
a1
a2 b1 P1 b2 P2 f
2、弯矩计算
M K [VA x K P1 (x K a1 )] H y K
q= 1kN/m
y
4f (l x)x 2 l
P=4kN 3 4 5 C 4m
x
2
6
1
H =6kN A 0
7
B H =6kN
8
VA =7kN
8×2=16m VB =5kN
解： 1、计算支座反力
0 VA VA
1 8 12 4 4 7kN 16 1 8 4 4 12 0 VB VB 5kN 16
拱结构的组成
2、拱结构的组成
3
拱结构的种类
3、拱结构的种类 静定拱
超静定拱
三铰拱
两铰拱 超静定拱
静定拱
无铰拱
高差h
静定拱
带拉杆的三铰拱
斜拱
4
拱结构的特点
4、拱结构的特点
1、弯矩比相应等代梁小；
《结构力学》第四章静定拱
实例演示
通过实例演示内力图的 绘制过程，帮助读者掌
握绘制技巧。
04 静定拱的位移计算
位移计算基本概念
位移的定义
位移是指在外力作用下，结构物 某一点或某一截面位置的变化。
静定拱的位移
静定拱在荷载作用下的位移包括 拱顶竖向位移、拱脚水平位移和
转角位移等。
位移计算的意义
位移计算是结构力学中的重要内 容，对于评估结构的安全性、稳 定性和使用功能具有重要意义。
虚功原理在位移计算中的应用
虚功原理的基本概念
01
虚功原理是结构力学中的一个基本原理，它建立了外
力功与结构内部应变能之间的关系。
虚功原理在静定拱位移计算中的应用
02 通过构建静力可能位移和虚力状态，利用虚功原理可
以求解静定拱在各种荷载作用下的位移。
虚功原理的适用条件
03
虚功原理适用于线弹性结构，即结构在受力过程中满
解题思路
同样需要构建静力可能位移和虚力 状态，利用虚功原理求解位移。
解题步骤
详细列出解题步骤，并解释每一步 的意义和计算方法。
05 静定拱的稳定性分析
稳定性分析基本概念
稳定性
结构在受到外部扰动后，能够恢复原有平衡状态的能力。
临界荷载
使结构失去稳定或发生破坏的最小荷载。
稳定性分析
研究结构在荷载作用下是否会发生失稳或破坏，以及如何提高结 构的稳定性。
通过截取拱的任意截面，利用静 力平衡条件求解截面上的内力。
叠加法
将复杂的拱结构分解为若干简单结 构，分别计算内力后再进行叠加。
力法
通过引入多余未知力，建立力法方 程求解拱的内力。
典型例题解析
圆弧拱内力计算
01
结构力学第4章静定拱
y M0 H
三铰拱合理拱轴线的纵坐标y与相应简支梁弯矩图的竖标成 正比。当荷载已知时，只需求出相应简支梁的弯矩方程式，除 以常数H便得到合理拱轴线方程。
11
例 4－2 求图示对称三铰拱在均布荷载q作用下的合理拱轴线。
解：
相应简支梁的弯矩方程为
y
M 0 qL x qx2 1 qx(L x) 2 22
x
所以
H
M
0 C
qL2
f 8f
y
M0 H
4f L2
x(L x)
x
合理拱轴线为抛物线
12
本章小结
三铰拱是按三刚片规则组成的静定结构； 在竖向荷载作用下，产生竖向反力与水平推力； 拱的主要内力是轴力； 利用合理拱轴可以使拱的弯矩达到最小。
13
y
23
1
50.25kN
→H o
↑VA
75.5kN
4
x
50.25kN
←H ↑ VB
58.5kN
以1截面为例： L=12m、f=4m代入拱轴方程
y
44 122
x(12
x)
x 9
(12
x)
tg dy 2 (6 x) dx 9
9
1截面： x1=1.5m 1=450
y1=1.75m tg1=1 sin 1=0.707 cos 1=0.707
503
755
→H
↑ VA
kN 75.5kN
←H
↑VB
58.5kN
VB VB0 14 6 3 50 9 58 5 kN 12
↑VA0
↑VB0
H
M
0 C
75 5 6 14 6 3
50 25kN
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章 静定拱
§4—1概述 拱——曲线杆件， 竖向荷载作用下有水平反力。 常用形式： 三铰拱、两铰拱、无铰拱
重要特点： 竖向荷载产生水平推力（与梁相比）
优点： M减小，N为主 ——便于使用抗压材料：砖、石、混凝土
缺点： 水平反力要求 ——地基、支承结构、（墙、柱、墩等）
更坚固。 ——可称拱式结构或推力结构
y(x) x1=1.5,y1=1.75 tanφ=y’ sinφ,cosφ
3.M1=M10-FHy1 S1=S10*c-FH*s N1=S10*s+FH*c
4.表4－1，作图。
3．特点： （1）竖向荷载作用下，
有水平推力H （2）推力使拱M减小，
M = M0 － Hy （3）拱截面内轴力较大，
（梁N=0） 4．斜拱与一般荷载作用 ①斜拱
【例4—2】 均布荷载满跨 【解】
M 0 ql x qx2 qx (l x) 2 22
H
M
0 c
1
ql 2
f f8
y M 0 qx (l x) 8 f 4 f x(l x)
H2
ql 2 l 2
具有不同髙跨比的一组抛物线——合理拱轴线
[例4—3]q = qc+ γy 解：坐标系如图，
M=M0－H（f－y）=0
f y M0 H
求导二次：
y"
1 H
d2M 0 dx2
1 H
(q)
y q H
q=qc+γy
y " x y qc HH
微分方程解 边界条件
——二阶常系数线性非齐次方程 ——确定合理拱轴线方程
[例4-4] 静水压力 解：非竖向荷载，设M＝0状态，
用微元平衡求合理拱轴线 微段：N 平衡：
带拉杆的拱 ——消除推力
（消除对支承结构的影响） 拱的各部名称（参数）
基本参数 拱高f 跨度l 高跨比f/l
平拱/斜拱： 拱趾是 / 否 在同一水平线
§4 – 2 三铰拱的计算
1．支座反力计算 （与相应代梁比较）
VA=VA0 VB=VB0
H
M
0 c
f
M0C—— 代梁
相应截面 C的弯矩
①推力H∝1/f， 与曲线形式无关，
（a）竖向荷载——计算公式 （b）非竖向荷载——截面法 3、特点(与梁比较） ——水平推力，使M减少 4、代拉杆的三铰拱 5、合理拱轴线：满跨均布荷载
静水压力
【思考题－3】 试绘制合理拱轴线形状：y＝M0/H
习题
与铰位置有关，
②若f→0， 则H→∞
（瞬变体系）
2．内力计算 M=M0-Hy
c sQ0
N
s
c
H
c－cosφ s－sinφ
φ—为截面轴线切向的锐角。
注意： ①M0，Q0 —— 对应代梁相应截面 的弯矩、剪力 ②M—拱内受拉为正 ③φ—拱左部“+”，
右部“-”
【例4－1】 1.支座反力 2.截面水平8等分：
∑m0 = 0 FNρ-(FN+dFN)ρ=0 dFN=0 FN=常数
∑s = 0（投影方程）
2FNsind(φ/2)-qρdφ=0
dφ极小，sin(dφ/2)=dφ/2
FN-qρ=0 ρ=FN/q ＝常数 合理拱轴——圆弧线
小结： 1、三铰拱——三铰刚架：几何组成、反力计算 2、内力计算——截面法
②一般荷载作用
——与三铰刚架计算相同， 求反力，截面法求内力
合理拱§轴4线—3 三铰拱的合理拱轴线
——在固定荷载作用下， 拱上各截面M＝0（则Q=0），只有N≠0的轴线 ——截面上正应力分布均为，材料得以充分利用 合理轴线方程：M0－Hy = 0
y M0 H
——竖向荷载作用下， 三铰拱合理拱轴线的纵坐标y 与相应代梁弯矩图竖标成正比
§4—1概述 拱——曲线杆件， 竖向荷载作用下有水平反力。 常用形式： 三铰拱、两铰拱、无铰拱
重要特点： 竖向荷载产生水平推力（与梁相比）
优点： M减小，N为主 ——便于使用抗压材料：砖、石、混凝土
缺点： 水平反力要求 ——地基、支承结构、（墙、柱、墩等）
更坚固。 ——可称拱式结构或推力结构
y(x) x1=1.5,y1=1.75 tanφ=y’ sinφ,cosφ
3.M1=M10-FHy1 S1=S10*c-FH*s N1=S10*s+FH*c
4.表4－1，作图。
3．特点： （1）竖向荷载作用下，
有水平推力H （2）推力使拱M减小，
M = M0 － Hy （3）拱截面内轴力较大，
（梁N=0） 4．斜拱与一般荷载作用 ①斜拱
【例4—2】 均布荷载满跨 【解】
M 0 ql x qx2 qx (l x) 2 22
H
M
0 c
1
ql 2
f f8
y M 0 qx (l x) 8 f 4 f x(l x)
H2
ql 2 l 2
具有不同髙跨比的一组抛物线——合理拱轴线
[例4—3]q = qc+ γy 解：坐标系如图，
M=M0－H（f－y）=0
f y M0 H
求导二次：
y"
1 H
d2M 0 dx2
1 H
(q)
y q H
q=qc+γy
y " x y qc HH
微分方程解 边界条件
——二阶常系数线性非齐次方程 ——确定合理拱轴线方程
[例4-4] 静水压力 解：非竖向荷载，设M＝0状态，
用微元平衡求合理拱轴线 微段：N 平衡：
带拉杆的拱 ——消除推力
（消除对支承结构的影响） 拱的各部名称（参数）
基本参数 拱高f 跨度l 高跨比f/l
平拱/斜拱： 拱趾是 / 否 在同一水平线
§4 – 2 三铰拱的计算
1．支座反力计算 （与相应代梁比较）
VA=VA0 VB=VB0
H
M
0 c
f
M0C—— 代梁
相应截面 C的弯矩
①推力H∝1/f， 与曲线形式无关，
（a）竖向荷载——计算公式 （b）非竖向荷载——截面法 3、特点(与梁比较） ——水平推力，使M减少 4、代拉杆的三铰拱 5、合理拱轴线：满跨均布荷载
静水压力
【思考题－3】 试绘制合理拱轴线形状：y＝M0/H
习题
与铰位置有关，
②若f→0， 则H→∞
（瞬变体系）
2．内力计算 M=M0-Hy
c sQ0
N
s
c
H
c－cosφ s－sinφ
φ—为截面轴线切向的锐角。
注意： ①M0，Q0 —— 对应代梁相应截面 的弯矩、剪力 ②M—拱内受拉为正 ③φ—拱左部“+”，
右部“-”
【例4－1】 1.支座反力 2.截面水平8等分：
∑m0 = 0 FNρ-(FN+dFN)ρ=0 dFN=0 FN=常数
∑s = 0（投影方程）
2FNsind(φ/2)-qρdφ=0
dφ极小，sin(dφ/2)=dφ/2
FN-qρ=0 ρ=FN/q ＝常数 合理拱轴——圆弧线
小结： 1、三铰拱——三铰刚架：几何组成、反力计算 2、内力计算——截面法
②一般荷载作用
——与三铰刚架计算相同， 求反力，截面法求内力
合理拱§轴4线—3 三铰拱的合理拱轴线
——在固定荷载作用下， 拱上各截面M＝0（则Q=0），只有N≠0的轴线 ——截面上正应力分布均为，材料得以充分利用 合理轴线方程：M0－Hy = 0
y M0 H
——竖向荷载作用下， 三铰拱合理拱轴线的纵坐标y 与相应代梁弯矩图竖标成正比