2019初中数学因式分解的应用拓展创新题型专项训练八(附答案详解)

七年级下数学因式分解专题训练一．选择题（共13小题）223．一次课堂练习，王莉同学做了如下4道分解因式题，你认为王莉做得不够完整的一题是210．已知a、b、c是△ABC的三边长，且满足a3+ab2+bc2=b3+a2b+ac2，则△ABC的形状是11．任何一个正整数n都可以进行这样的分解：n=s×t（s，t是正整数，且s≤t），如果p×q在n的所有这种分解中两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并规定：F（n）=．例如18可以分解成1×18，2×9，3×6这三种，这时就有F（18）==．给出下列关于F（n）的说法：（1）F（2）=；（2）F（24）=；（3）F（27）=3；（4）若n是一20062005232二．填空题（共12小题）14．若x2+4x+4=（x+2）（x+n），则n=_________．15．多项式ax2﹣4a与多项式x2﹣4x+4的公因式是_________．16．因式分解：ax2y+axy2=_________．17．计算：9xy•（﹣x2y）=_________；分解因式：2x（a﹣2）+3y（2﹣a）=_________．18．若|m﹣4|+（﹣5）2=0，将mx2﹣ny2分解因式为_________．19．因式分解：（2x+1）2﹣x2=_________．20．分解因式：a3﹣ab2=_________．21．分解因式：a3﹣10a2+25a=_________．22．因式分解：9x2﹣y2﹣4y﹣4=_________．23．在实数范围内分解因式：x2+x﹣1=_________．24．已知P=3xy﹣8x+1，Q=x﹣2xy﹣2，当x≠0时，3P﹣2Q=7恒成立，则y的值为_________．25．在日常生活中如取款、上网等都需要密码．有一种用“因式分解”法产生的密码，方便记忆．原理是：如对于多项式x4﹣y4，因式分解的结果是（x﹣y）（x+y）（x2+y2），若取x=9，y=9时，则各个因式的值是：（x﹣y）=0，（x+y）=18，（x2+y2）=162，于是就可以把“018162”作为一个六位数的密码．对于多项式4x3﹣xy2，取x=10，y=10时，用上述方法产生的密码是：_________（写出一个即可）．三．解答题（共5小题）26．化简：（a﹣b）（a+b）2﹣（a+b）（a﹣b）2+2b（a2+b2）27．因式分解：x2（y2﹣1）+2x（y2﹣1）+（y2﹣1）．28．在实数范围内分解因式：．29．计算：1﹣a﹣a（1﹣a）﹣a（1﹣a）2﹣a（1﹣a）3﹣…﹣a（1﹣a）2000﹣[（1﹣a）2001﹣3]30．为进一步落实《中华人民共和国民办教育促进法》，某市教育局拿出了b元资金建立民办教育发展基金会，其中一部分作为奖金发给了n所民办学校．奖金分配方案如下：首先将n所民办学校按去年完成教育、教学工作业绩（假设工作业绩均不相同）从高到低，由1到n排序，第1所民办学校得奖金元，然后再将余额除以n发给第2所民办学校，按此方法将奖金逐一发给了n所民办学校．（1）请用n、b分别表示第2所、第3所民办学校得到的奖金；（2）设第k所民办学校所得到的奖金为a k元（1≤k≤n），试用k、n和b表示a k（不必证明）；（3）比较a k和a k+1的大小（k=1，2，…，n﹣1），并解释此结果关于奖金分配原则的实际意义．七年级下数学因式分解专题训练参考答案与试题解析一．选择题（共13小题）223．一次课堂练习，王莉同学做了如下4道分解因式题，你认为王莉做得不够完整的一题是4．下列各式由左边到右边的变形中，是分解因式的为（）210．已知a、b、c是△ABC的三边长，且满足a3+ab2+bc2=b3+a2b+ac2，则△ABC的形状是11．任何一个正整数n都可以进行这样的分解：n=s×t（s，t是正整数，且s≤t），如果p×q在n的所有这种分解中两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并规定：F（n）=．例如18可以分解成1×18，2×9，3×6这三种，这时就有F（18）==．给出下列关于F（n）的说法：（1）F（2）=；（2）F（24）=；（3）F（27）=3；（4）若n是一是正确的；=，故（，故（=20062005232二．填空题（共12小题）14．若x2+4x+4=（x+2）（x+n），则n=2．15．多项式ax2﹣4a与多项式x2﹣4x+4的公因式是x﹣2．16．因式分解：ax2y+axy2=axy（x+y）．17．计算：9xy•（﹣x2y）=﹣3x3y2；分解因式：2x（a﹣2）+3y（2﹣a）=（a﹣2）（2x﹣3y）．x﹣18．若|m﹣4|+（﹣5）2=0，将mx2﹣ny2分解因式为（2x+5y）（2x﹣5y）．﹣，19．因式分解：（2x+1）2﹣x2=（3x+1）（x+1）．20．分解因式：a3﹣ab2=a（a+b）（a﹣b）．21．分解因式：a3﹣10a2+25a=a（a﹣5）2．22．因式分解：9x2﹣y2﹣4y﹣4=（3x+y+2）（3x﹣y﹣2）．23．在实数范围内分解因式：x2+x﹣1=（x++）（x+）．+x+）﹣）﹣（）﹣]+）24．已知P=3xy﹣8x+1，Q=x﹣2xy﹣2，当x≠0时，3P﹣2Q=7恒成立，则y的值为2．25．在日常生活中如取款、上网等都需要密码．有一种用“因式分解”法产生的密码，方便记忆．原理是：如对于多项式x4﹣y4，因式分解的结果是（x﹣y）（x+y）（x2+y2），若取x=9，y=9时，则各个因式的值是：（x﹣y）=0，（x+y）=18，（x2+y2）=162，于是就可以把“018162”作为一个六位数的密码．对于多项式4x3﹣xy2，取x=10，y=10时，用上述方法产生的密码是：101030或103010或301010（写出一个即可）．三．解答题（共5小题）26．化简：（a﹣b）（a+b）2﹣（a+b）（a﹣b）2+2b（a2+b2）27．因式分解：x2（y2﹣1）+2x（y2﹣1）+（y2﹣1）．28．在实数范围内分解因式：．x+））﹣x+）﹣29．计算：1﹣a﹣a（1﹣a）﹣a（1﹣a）2﹣a（1﹣a）3﹣…﹣a（1﹣a）2000﹣[（1﹣a）2001﹣3]30．为进一步落实《中华人民共和国民办教育促进法》，某市教育局拿出了b元资金建立民办教育发展基金会，其中一部分作为奖金发给了n所民办学校．奖金分配方案如下：首先将n所民办学校按去年完成教育、教学工作业绩（假设工作业绩均不相同）从高到低，由1到n排序，第1所民办学校得奖金元，然后再将余额除以n发给第2所民办学校，按此方法将奖金逐一发给了n所民办学校．（1）请用n、b分别表示第2所、第3所民办学校得到的奖金；（2）设第k所民办学校所得到的奖金为a k元（1≤k≤n），试用k、n和b表示a k（不必证明）；（3）比较a k和a k+1的大小（k=1，2，…，n﹣1），并解释此结果关于奖金分配原则的实际意义．﹣，所以第（）（），，所以﹣。

2019全国中考数学真题知识点05因式分解（解析版）一、选择题8．（2019·株洲）下列各选项中因式分解正确的是（ ）A ．221(1)x x -=-B ．3222(2)a a a a a -+=-C ．2242(2)y y y y -+=-+D ．222(1)m n mn n n m -+=-【答案】D【解析】选项A 是平方差公式应该是（x+1)(x-1)，所以错误；选项B 公因式应该是a ，所以错误；选项C 提取公因式-2y 后，括号内各项都要变号，所以错误；只有选项D 是正确的。

1. （2019·无锡市）分解因式224x y 的结果是 （ ）A.（4x +y ）（4x -y ）B.4（x +y ）（x -y ）C.（2x +y ）（2x -y ）D.2（x +y ）（x -y ）【答案】C【解析】本题考查了公式法分解因式，4x 2-y 2=（2x -y ）（2x +y ），故选C.2. （2019·潍坊）下列因式分解正确的是（ ）A ．22363(2)ax ax ax ax -=-B ．22()()x y x y x y -+=-+-- C ．22224(2)a ab b a b ++=+ D ．222(1)ax ax a a x -+-=--【答案】D【解析】选项A ：2363(2)ax ax ax x -=-；选项B ：22()()x y x y x y -+=-++；选项C 不能分解因式；选项D 正确；故选择D ．二、填空题11．(2019·广元)分解因式:a 3－4a ＝________.【答案】a(a+2)(a －2)【解析】a 3－4a ＝a(a 2－4)＝a(a+2)(a －2).12．（2019·苏州）因式分解：x 2-xy = ．【答案】x (x -y )【解析】本题考查了提公因式法分解因式，x 2-xy = x (x -y )，故答案为x (x -y ).11．（2019·温州）分解因式：m 2+4m+4= ．【答案】(m+2)2【解析】本题考查了运用完全平方公式分解因式，解题的关键是掌握完全平方公式的特征．原式=(m+2)2.11．（2019·绍兴 ）因式分解：=-12x .【答案】（x+1）（x-1）11．（2019·嘉兴）分解因式：x 2﹣5x ＝ ．【答案】(5)x x -11.（2019·杭州）因式分解:1-x 2=_________.【答案】(1-x)(1+x)【解析】直接应用平方差公式进行因式分解，1-x 2=(1-x)(1+x)，故填：(1-x)(1+x).14．（2019·威海）分解因式：2x 2－2x ＋12＝ . 【答案】2122x ⎛⎫- ⎪⎝⎭ 【解析】先提取公因式2，再根据完全平方公式进行二次分解.2x 2－2x ＋12＝2(x 2－x ＋14)＝2122x ⎛⎫- ⎪⎝⎭. 10．（2019·盐城）分解因式：21x -= .【答案】(1)(1)x x -+【解析】直接利用平方差公式分解因式，进而得到答案.7．（2019·江西）因式分解：12-x ＝ .【答案】（x+1）（x-1）【解析】12-x =（x+1）（x-1）14．（2019·长沙，14，3分）分解因式：am 2-9a= ．【答案】a(m+3)(m-3).【解析】先提取公因式a ，再应用平方差公式进行分解因式. am 2-9a=a(m+3)(m-3).13．（2019·衡阳）因式分解：2a 2－8＝ ．【答案】2（a ＋2）（a ＝2）【解析】2a 2－8＝2（a ＋2）（a ＝2），故答案为2（a ＋2）（a ＝2）．11．（2019·黄冈）分解因式3x 2－27y 2＝ .【答案】3（x+3y ）（x-3y ）【解析】先提取公因数3，然后利用平方差公式进行分解，即3x 2－27y 2＝3（x 2－9y 2）＝3（x+3y ）（x-3y ）。

2019初中数学因式分解的应用拓展创新题型专项训练二（附答案详解）1．观察下列一组等式：（a+1）（a2﹣a+1）=a3+1（a+2）（a2﹣2a+4）=a3+8（a+3）（a2﹣3a+9）=a3+27（1）以上这些等式中，你有何发现？利用你的发现填空．①（x﹣3）（x2+3x+9）=_____；②（2x+1）（）=8x3+1；③（）（x2+xy+y2）=x3﹣y3．（2）计算：（a2﹣b2）（a2+ab+b2）（a2﹣ab+b2）．2．阅读材料：若，求、的值.解：∵，∴，∴∴∴，根据你的观察，探究下面的问题：（1）已知求、的值；（2）已知的三边长、、都是正整数，且满足，求的最大边的值.3．材料阅读：若一个整数能表示成a2＋b2(a、b是正整数)的形式，则称这个数为“完美数”．例如：因为13＝32＋22，所以13是“完美数”；再如：因为a2＋2ab＋2b2＝(a＋b)2＋b2(a、b是正整数)，所以a2＋2ab＋2b2也是“完美数”．(1)请你写出一个大于20小于30的“完美数”，并判断53是否为“完美数”；(2)试判断(x2＋9y2)·(4y2＋x2)(x、y是正整数)是否为“完美数”，并说明理由．4．阅读材料：把代数式x2﹣6x﹣7因式分解，可以如下分解：x2﹣6x﹣7=x2﹣6x+9﹣9﹣7=（x﹣3）2﹣16=（x﹣3+4）（x﹣3﹣4）=（x+1）（x﹣7）（1）探究：请你仿照上面的方法，把代数式x2﹣8x+7因式分解；（2）拓展：把代数式x2+2xy﹣3y2因式分解：当________________时，代数式x2+2xy﹣3y2=0．5．阅读下列解答过程：若二次三项式x2-4x+m有一个因式是x+3，求另一个因式及m的值.解：设另一个因式为x+a则x2-4x+m=(x+3)(x+a)=x2+ax+3x+3a=x2+(a+3)x+3a，∴∴∴另一个因式为x-7，m的值为-21.请依照以上方法解答下面问题：（1）已知二次三项式x2+3x-k有一个因式是x-5，求另一个因式及k的值；（2）已知二次三项式2x2+5x+k有一个因式是x+3，求另一个因式及k的值.19．阅读下面题目的解题过程，并回答问题.若,求x2+y2的值.解：设，则原式可化为a2-8a+16=0，即(a-4)2=0，所以a=4.由(x2+y2)2=4，得x2+y2=±2.（1）错误的原因是___________________________________（2）本题正确的结论为_________________________________（3）设“”的方法叫做换元法，它能起到化繁为简的目的.请用“换元法”把(x+y)2-14(x+y)+49因式分解.6．阅读理解并完成下面问题：我们知道，任意一个正整数都可以进行这样的因式分解：（是正整数），在的所有这种分解中，如果两因数之差的绝对值最小，我们就称是的最佳分解．并规定：（其中）．例如：可以分解成，或，因为，所以是的最佳分解，所以．（）如果一个正整数是另外一个正整数的平方，我们称正整数是完全平方数，若是一个完全平方数，求的值；（）如果一个两位正整数，交换其个位数字与十位数字得到的新两位数减去原数所得的差为，那么我们称这个两位正整数为“吉祥数”，求符合条件的所有“吉祥数”；（）在（）中的所有“吉祥数”中，求的最小值．7．当一个多位数的位数为偶数时，在其中间插入一位数k，（0≤k≤9，且k为整数）得到一个新数，我们把这个新数称为原数的关联数．如：435729中间插入数字6可得435729的一个关联数4356729，其中435729=729+435×1000，4356729=729+6×1000+435×10000．请阅读以上材料，解决下列问题．（1）现有一个4位数2316，中间插入数字m（0≤m≤9，且m为3的倍数），得其关联数，求证：所得的2316的关联数与原数10倍的差一定能被3整除；（2）若一个三位关联数是原来两位数的9倍，请找出满足这样的三位关联数．8．把几个图形拼成一个新的图形，再通过图形面积的计算，常常可以得到一些有用的信息，或可以求出一些不规则图形的面积.(1)如图1所示，将一张长方形纸板按图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小长方形，且m>n.观察图形，可以发现代数式2m2＋5mn＋2n2可以因式分解为 .(2)若图1中每块小长方形的面积为12cm2，四个正方形的面积和为50 cm2，试求图中所有裁剪线(虚线部分)长之和.(3)将图2中边长为a和b的正方形拼在一起，B,C,G三点在同一条直线上，连接BD和BF，若这两个正方形的边长满足a+b=10，ab=16，请求出阴影部分的面积.9．探索题：(x﹣1)(x+1)＝x2﹣1，(x﹣1)(x2+x+1)＝x3﹣1，(x﹣1)(x3+x2+x+1)＝x4﹣1，(x﹣1)(x 4+x 3+x 2+x+1)＝x 5﹣1根据前面的规律，回答下列问题：(1)(x ﹣1)(x n +x n ﹣1+x n ﹣2+…+x 3+x 2+x+1)＝_____．(2)当x ＝3时，(3﹣1)(32015+32014+32013+…+33+32+3+1)＝_____． (3)求：22014+22013+22012+…+23+22+2+1的值．(请写出解题过程) (4)求22016+22015+22014+…+23+22+2+1的值的个位数字．(只写出答案)10．对任意一个正整数m ，如果m=n （n+1），其中n 是正整数，则称m 为“优数”，n 为m 的最优拆分点，例如：72=8×（8+1），则72是一个“优数”，8为72的最优拆分点． （1）请写出一个“优数” ，它的最优拆分点是 ； （2）求证：若“优数”m 是5的倍数，则m 一定是10的倍数；（3）把“优数”p 的2倍与“优数”q 的3倍的差记为D （p ，q ），例如：20=4×5，6=2×3，则D （20，6）=2×20﹣3×6=22．若“优数”p 的最优拆分点为t+4，“优数”q 的最优拆分点为t ，当D （p ，q ）=76时，求t 的值并判断它是否为“优数”．11．请阅读下列材料：我们可以通过以下方法求代数式265x x ++的最小值．()22222652333534x x x x x ++=+⋅⋅+-+=+-，∵()23x +≥0，∴当3x =-时， 265x x ++有最小值4-． 请根据上述方法，解答下列问题：（1）()222224122221x x x x x a b +-=+⋅⋅+--=++，则ab 的值是______；（2）求证：无论x 取何值，代数式27x ++的值都是正数；（3）若代数式227x kx ++的最小值为2，求k 的值．12．已知a+b=1，ab=-1.设（1）计算S 2；（2）请阅读下面计算S 3的过程： ()()33332222a b a b b a-b a a b-a b +=+++ =()()()323222a b a b a b b a a b +++-+ =()()()2222a b a a b b ab a b +++-+ =()()()22a b a b ab a b ++-+ ∵a+b=1，ab=-1，∴()()()()33223221111S a b a b a b ab a b S S =+=++-+=⨯--⨯=+=_______. 你读懂了吗？请你先填空完成（2）中S 3的计算结果；再计算S 4；（3）猜想并写出2n S -， 1n S -， n S 三者之间的数量关系（不要求证明，且n 是不小于2的自然数），根据得出的数量关系计算S 3.13．老师在黑板上写出三个算式:52-32=8×2,92-72=8×4,152-32=8×27,王华接着又写了两个具有同样规律的算式:112-52=8×12,152-72=8×22,……(1)请你再写出两个(不同于上面算式)具有上述规律的算式; (2)用文字写出反映上述算式的规律; (3)证明这个规律的正确性. 答案：】1．（1）①x 3﹣27；②4x 2﹣2x+1；③x ﹣y ；（2）a 6﹣b 6．解：（1）①（x﹣3）（x2+3x+9）=x3﹣27；②（2x+1）（4x2﹣2x+1）=8x3+1；③（x﹣y）（x2+xy+y2）=x3﹣y3；故答案为：①x3﹣27；②4x2﹣2x+1；③x﹣y；（2）原式=[（a﹣b）（a2+ab+b2）][（a+b）（a2﹣ab+b2）]=（a3﹣b3）（a3+b3）=a6﹣b6．2．(1) x=−6，y=−3.(2)8，9.解：(1)∵∴∴∴x−2y=0，y+3=0，∴x=−6，y=−3.(2)∵，∴∴∴a−3=0，b−7=0，∴a=3，b=7，∵7−3<c<7+3，∴∴△ABC的最大边c的值可能是8、9.3．解：(1)25=4²+3²，∵53=49+4=7²+2²，∴53是“完美数”；(2)(x²+9y²)⋅(4y²+x²)是“完美数”，(x²+9y²)⋅(4y²+x²)=4x2y²+36++9x²y²=13x²y²+36+=(6y²+x²) ²+x²y²，∴(x²+9y²)⋅(4y²+x²)是“完美数”.4．(1) （x﹣1）（x﹣7）(2)（x+3y）（x﹣y）;﹣3或1解：（1）x2﹣8x+7=x2﹣8x+16﹣16+7=（x﹣4）2﹣32=（x﹣4+3）（x﹣4﹣3）=（x﹣1）（x﹣7）（2）由x2+2xy﹣3y2=0得x2+2xy+y2﹣y2﹣3y2=0，（x+y）2﹣4y2=0，（x+y+2y）（x+y﹣2y）=0，（x+3y）（x﹣y）=0，x+3y=0或x﹣y=0，所以，当=﹣3或1时，x2+2xy﹣3y2的值为0．5．（1）另一个因式为x+8，k的值为40.（2）另一个因式为2x-1，k的值为-3. 解：（1）设另一个因式为（x+a），∴x2+3x-k=（x-5）（x+a），则x2+3x-k=x2+（a-5）x-5a，∴，解得：a=8，k=40，∴另一个因式为x+8，k的值为40；（2）设另一个因式为（2x+a），∴2x2+5x+k =（x+3）（2x+a），则2x2+5x+k=2x2+（6+ a）x+3a，∴，解得：a=-1，k=-3，∴另一个因式为2x-1，k的值为-3.6．（1）x2+y2是非负数（2）x2+y2=2（3）(x+y-7)²解：（1）∵x2≥0，y2≥0，x2+y2≥0，∴由(x2+y2)2=4，得x2+y2=±2，这步发生错误，错误原因为x2+y2必须是非负数；（2）由（1）可得，本题正确的结论为：x2+y2=2；（3）设x＋y=m，∴原式=m2-14m+49=(m-7)2，∴原式=(x+y-7)².7．（1）1；（2）可取，，，，，，；（3）解：（）∵是完全平方数∴且∴（）设正整数，则，则．∵．．．∴可取，，，，，，．（）由（）得．∴，，，，，，．∵．∴的最小值为．8．（1）；（2）135、225、315和405．（1）证明：∵这个4位数的前两位为23，后两位为16，∴2316的关联数是23m16 将关联数与原数10倍相减得：m•102﹣9×16．∵m和9均为3的倍数，∴关联数与原数10倍的差一定能被3整除；（2）（1）解：设原数为ab=10a+b，其关联数为amb=100a+10m+b．∵amb=9ab，∴100a+10m+b=9×（10a+b），∴5a+5m=4b，∴5（a+m）=4b．∵b、m为整数，a为正整数，且a、b、m均为一位数，∴b=5，a+m=4，∴a=1，m=3；a=2，m=2；a=3，m=1；a=4，b=0，∴满足条件的三位关联数为135、225、315和405．9．（1）(1)(m+2n)(2m+n)；（2）42cm;(3)26.解：(1)(m+2n)(2m+n)(2)由题意得：mn=12,2n 2+2m 2=50，∴n 2+m 2=25，∴(m+n)2= n 2+m 2+2mn=49,∵m>n ，∴m+n=7, ∴图中所有裁剪线(虚线部分)长之和=6(m+n)=42(cm) (3) 阴影部分的面积=0.5a 2+b 2-0.5b(a+b)=0.5(a 2+ b 2-ab)=0.5[(a+b)² -3ab]=0.5×(100-48)=26.10．（1）x n+1﹣1；（2）32016﹣1；（3）22015﹣1；（4）1. 解：（1）（x ﹣1）（x n +x n ﹣1+x n ﹣2+…+x 3+x 2+x+1）=x n+1﹣1， 故答案为：x n+1﹣1；（2）当x=3时，（3﹣1）（32015+32014+32013+…+33+32+3+1）=32016﹣1， 故答案为：32016﹣1（3）解：原式=（2﹣1）（22014+22013+22012+…+23+22+2+1）=22015﹣1（4）22016+22015+22014+…+23+22+2+1=（2﹣1）（22016+22015+22014+…+23+22+2+1）=22017﹣1，21的末位数字是2，22的末位数字是4，23的末位数字是8，24的末位数字是6，25的末位数字是2…，所以2n的末位数字是以2、4、8、6四个数字一循环． 2017÷4=504…1， 所以22017的末尾数字是2，22017﹣1的末尾数字是1． 11．（1）56，7；（2）；（3）解：（1）∵56=7×（7+1），∴56是“优数”，它的最优拆分点是7．故答案为：56，7； （2）∵“优数”m 是5的倍数，∴n （n +1）是5的倍数，（n 是正整数），当n 为奇数时，n +1是偶数，∴n （n +1）是能被5整除的偶数，故n （n +1）是10的倍数，当n 为偶数时，∴n （n +1）是能被5整除的偶数，故n （n +1）是10的倍数，即：“优数”m 是5的倍数，则m 一定是10的倍数；（3）由题意知，p =（t +4）（t +5），q =t （t +1）．∵D （p ，q ）=2p ﹣3q =76，∴2（t +4）（t +5）﹣3t （t +1）=76，∴t =3或t =12，∴3不是“优数”，12是“优数”． 12．-10解：（1）()22222412222125x x x x x +-=+⋅⋅+--=+-， 所以a=2，b=-5，所以ab 的值是-10，故答案为：-10；（2）x 2x+7=x 2)2+7=（）2+1，∵（）2≥0，∴x 2x+7最小值为1，∴无论x 取何值，x 2x+7的值都是正数；（3）2x 2+kx+7=）2x×4k+（4k ）2-（4k ）2+7=4）2-18k 2+7，x+4）2≥0，2-18k 2+7的最小值是-18k 2+7， ∴-18k 2+7=2，∴k=±13．（1）S 2=3；（2）4，S 4=7； （3）S n-2+S n-1=S n ， S 8= 47. 解：（1）S 2＝a 2＋b 2＝(a ＋b )2－2ab ＝12－2×(－1)＝3； （2）S 3＝S 2＋1＝3＋1＝4， 故答案为：4；∵S 4＝a 4＋b 4＝( a 2＋b 2)2－2a 2b 2＝( a 2＋b 2)2－2(ab )2， 又∵a 2＋b 2═3，ab ＝－1， ∴S 4＝32－2×1＝7； （3）∵S 1＝1，S 2＝3，S 3＝4，S 4＝7， ∴S 1＋S 2＝S 3，S 2＋S 3＝S 4． 猜想：S n －2＋S n －1＝S n ． ∵S 3＝4，S 4＝7， ∴S 5＝S 3＋S 4＝4＋7＝11， ∴S 6＝S 4＋S 5＝7＋11＝18， ∴S 7＝S 5＋S 6＝11＋18＝29， ∴S 8＝S 6＋S 7＝18＋29＝47．13．（1）72-52=8×3;92-32=8×9；（2）任意两个奇数的平方差是8的倍数；（3）证明解：(1)72-52=8×3;92-32=8×9等.(2)规律:任意两个奇数的平方差是8的倍数.(3)证明设m,n(m≠n)为整数,两个奇数可表示为2m+1和2n+1,则(2m+1)2-(2n+1)2=4(m-n)(m+n+1).∵当m,n同是奇数或偶数时,m-n一定为偶数,∴4(m-n)一定是8的倍数;∵当m,n一偶一奇时,则m+n+1一定为偶数,∴4(m+n+1)一定是8的倍数.∴任意两个奇数的平方差是8的倍数.。

专题09因式分解之八大题型判断是否是因式分解【变式训练】1．（2023下·浙江温州·七年级校考期末）下列变形是因式分解的是（ ）已知因式分解的结果求参数【变式训练】已知二次三项式22x x k +-有一个因式是6x -，求另一个因式以及k 的值．【答案】8x +，48k =【分析】设另一根因式为x n +，可得()()()222666x x k x x n x n x n +-=-+=+--，再建立方程组626n n k-=ìí-=-î，再解方程组即可得到答案．【详解】解：∵二次三项式22x x k +-有一个因式是6x -，∴设另一根因式为x n +，∴()()()222666x x k x x n x n x n +-=-+=+--，∴626n n k -=ìí-=-î，解得：848n k =ìí=î，∴另一根因式为：8x +．【点睛】本题考查的是因式分解的含义，二元一次方程组的解法，熟练的利用待定系数法建立方程组是解本题的关键．公因式例题：（2023上·福建厦门·八年级校考期末）单项式33a b 与239a b 的公因式是（ ）A ．23a bB ．333a bC ．abD ．339a b 【答案】A【分析】根据公因式的概念分别求得系数的最大公因数，相同字母的次数的最低次数即可．【详解】解：单项式33a b 与单项式239a b 的公因式是23a b ．故选：A ．【点睛】此题考查公因式，掌握由几个单项式的各系数最大公约数与各相同字母最小次幂的乘积，组成的式子叫这几个单项式的公因式是解决此题的关键．【变式训练】【变式训练】综合提公因式法和公式法分解因式（2）()()22a x y b y x -+-()()22x y a b =--()()()x y a b a b =-+-．【点睛】本题考查了提公因式法与公式法的综合运用，一定要注意如果多项式的各项含有公因式，必须先提公因式，掌握平方差公式()()22a b a b a b +-=-和完全平方公式()2222a b a ab b ±=±+．【变式训练】1．（2023下·江苏扬州·七年级统考期末）分解因式：(1)228m -；(2)()()244x y x y +-++．【答案】(1)()()222m m +-(2)()22x y +-【分析】（1）先提取公因式2，再用平方差公式进行因式分解即可；（2）将x y +看做一个整体，利用完全平方公式进行因式分解即可．【详解】（1）解：原式()()()224222m m m =-=+-；（2）解：原式()()22222x y x y =+-´++()22x y =+-．【点睛】本题主要考查了因式分解，解题的关键是熟练掌握平方差公式()()22a b a b a b +-=-和完全平方公式()222a b a ab b ±=±+．2．（2023下·江苏盐城·七年级统考期中）分解因式：(1)2273x -+；(2)22344xy x y y --；(3)()()2221619y y ---+.【答案】(1)()()333x x +-(2)()22y x y --(3)()()2222+-y y【分析】（1）利用提公因式法及平方差公式，即可分解因式；（2）利用提公因式法及完全平方公式，即可分解因式；（3）利用完全平方公式及平方差公式，即可分解因式．【详解】（1）解：2273x -+2327x =-()239x =-()()333x x =+-（2）解：22344xy x y y --()2244y x xy y =--+()22y x y =--（3）解：()()2221619y y ---+()()2221619y y =---+()2213y éù=--ëû()224y =-()()222y y =+-éùëû()()2222y y =+-【点睛】本题考查了分解因式的方法，熟练掌握和运用分解因式的方法是解决本题的关键．十字相乘法分解因式例题：（2023下·四川达州·八年级校考期末）将多项式234--x x 分解因式后正确的是（ ）A ．()()223x x x+--B ．()34x x --C ．()()14x x -+D ．()()14x x +-【答案】D【分析】利用十字相乘法进行因式分解即可．【详解】解：()()23414.x x x x --=+-故选：D ．【点睛】本题考查了十字相乘法分解因式，运用十字相乘法分解因式，要注意观察，尝试，并体会它实质是二项式乘法的逆过程．【变式训练】【点睛】本题考查了因式分解，熟练掌握十字相乘法进行因式分解是解题的关键．分组分解法分解因式例题：（2023下·山东青岛·八年级统考期末）【问题提出】：分解因式：（1）23355x xy x y +-- （2）2244a b a b-+-【问题探究】：某数学“探究学习”小组对以上因式分解题目进行了如下探究：探究1：分解因式：（1）23355x xy x y+--分析：甲发现该多项式前两项有公因式3x ，后两项有公因式5-，分别把它们提出来，剩下的是相同因式()x y +，可以继续用提公因式法分解．解：()22335533(55)3()5()()(35)x xy x y x xy x y x x y x y x y x +--=+-+=+-+=+-另：乙发现该多项式的第二项和第四项含有公因式y ，第一项和第三项含有公因式x ，把y ，x 提出来，剩下的是相同因式(35)x -，可以继续用提公因式法分解．解：()22335535(35)(35)(35)(35)()x xy x y x x xy y x x y x x x y +--=-+-=-+-=-+探究2：分解因式：（2）2266a b a b-+-分析：甲发现先将22a b -看作一组应用平方差公式，其余两项看作一组，提出公因式6，则可继续再提出因式，从而达到分解因式的目的．解：()222266(66)()()6()()(6)a b a b a b a b a b a b a b a b a b -+-=-+-=+-+-=-++【方法总结】：对不能直接使用提取公因式法，公式法进行分解因式的多项式，我们可把被分解的多项式分成若干组，分别按“基本方法”即提取公因式法和公式法进行分解，然后，再从总体上按“基本方法”继续进行分解，直到分解出最后结果．这种分解因式的方法叫做分组分解法：【学以致用】：尝试运用分组分解法解答下列问题；（1）分解因式：3244x x x +--；（2）分解因式：22229y yz z x ++-；【拓展提升】：（3）分解因式：2815m m -+．【答案】（1）()()()122x x x ++-；（2）()()33y z x y z x +++-；（3）()()53m m --．【分析】（1）把前面两个和后面两个分别组成两组，提公因式()1x +后再利用平方差公式继续分解；（2）把前面三个和后面一个组成两组，利用公式分解即可；（3）把15分解成161-，再把前面三个和后面一个组成两组，利用公式分解即可．【详解】解：（1）3244x x x +--()()3241x x x =+-+()()2141x x x =+-+()()214x x =+-()()()122x x x =++-；（2）22229y yz z x ++-()22229y yz z x =++-()()223y z x =+-()()33y z x y z x =+++-；（3）2815m m -+()28161m m =-+-()241m =--()()4141m m =-+--()()53m m =--．【点睛】解答本题的关键是注意用分组分解法时，一定要考虑分组后能否提取公因式，运用公式．【变式训练】1．（2023上·河南南阳·八年级统考期末）常用的分解因式的方法有提取公因式法、公式法等，但有的多项式则不能直接用上述两种方法进行分解，比如多项式22424x y x y -++．这样我们就需要结合式子特点，探究新的分解方法．仔细观察这个四项式，会发现：若把它的前两项结合为一组符合平方差公式特点，把它的后两项结合为一组可提取公因式，而且对前后两组分别进行因式分解后会出现新的公因式，提取新的公因式就可以完成对整个式子的因式分解．具体过程如下：例1：22424x y x y-++()()22424x y x y =--- 分成两组()()()2222x y x y x y =+--- 分别分解()()222x y x y =-+- 提取公因式完成分解像这种将一个多项式适当分组后，再分解因式的方法叫做分组分解法．分组分解法一般是针对四项或四项以上的多项式，关键在恰当分组，分组须有“预见性”，预见下一步能继续分解，直到完成分解．(1)关于以上方法中“分组”目的的以下说法中所有正确的序号是______．①分组后组内能出现公因式；②分组后组内能运用公式；③分组后组间能继续分解．(2)若要将以下多项式进行因式分解，怎样分组比较合适？①22x y x y -++=______．②22222a a b ab b +--+=______．(3)利用分组分解法进行因式分解：22441x x y +-+．【答案】(1)①②③(2)①()()22x y x y -++，②()()22222a b a ab b -+-+；(3)()()2121x y x y ++-+【分析】(1)根据阅读材料解答即可；(2)运用分组分解法直接作答即可；(3)运用分组分解法直接作答即可．【详解】（1）解：从材料可知：“分组”的目的是：①分组后组内能出现公因式；②分组后组内能运用公式；③分组后组间能继续分解；故正确的序号是①②③，故答案为：①②③；（2）解：①()()2222x y x y x y x y -++=-++，②()()2222222222a a b ab b a b a ab b +--+=-+-+，故答案为：①()()22x y x y -++，②()()22222a b a ab b -+-+；（3）解：22441x x y +-+()22441x x y =++-()2221x y =+-()()2121x y x y =++-+【点睛】本题考查了因式分解，能够灵活运用分组分解法进行因式分解是解答本题的关键．因式分解的应用例题：（2023下·辽宁丹东·八年级统考期末）已知a ，b ，c 是三角形的三边，且满足()2222333a b c a b c ++=++则ABC V 的形状为（ ）A ．直角三角形B ．等腰三角形C ．等边三角形D ．等腰直角三角形【答案】C【分析】将()2222333a b c a b c ++=++进行变形得2222222220a b c ab ac bc ++---=，根据完全平方公式得222()()()0a b b c a c -+-+-=，即可得a b c ==，即可得．【详解】解：()2222333a b c a b c ++=++，222222222333a b c ab ac bc a b c +++++=++，2222222220a b c ab ac bc ++---=，222()()()0a b b c a c -+-+-=，0a b -=，0b c -=，0a c -=，a b =，b c =，a c =，∴a b c ==，∴三角形ABC 为等边三角形，故选：C ．【点睛】本题考查了因式分解，完全平方公式，等边三角形的判定，解题的关键是掌握因式分解，完全平方公式，等边三角形的判定．【变式训练】(2)14【分析】（1）①仿照例题的方法，根据分组分解法分解因式；②仿照例题的方法，根据拆项法分解因式；（2）仿照例题的方法，根据分组分解法分解因式，根据非负数的性质，求得,,a b c 的值，即可求解．【详解】（1）①()()()222222961961313131x x y x x y x y x y x y +-+=++-=+-=+++-；②()()()()()2226869131313124x x x x x x x x x -+=-+-=--=-+--=--（2）a ，b ，c 为ABC V 的三条边，22254610340a b c ab b c --++-=+，∴2222446910250a b ab b b c c +-+-++-+=，∴()()()2222350a b b c -++-=-，∴20a b -=，30b -=，50c -=，∴6a =，3b =，5c =，∴ABC V 的周长为63514++=．【点睛】本题考查了因式分解以及因式分解的应用，仿照例题的方法因式分解是解题的关键．一、单选题1．（2023下·云南昭通·八年级校联考期末）在多项式323124a b a bc -中，各项的公因式是（ ）A ．34a bcB ．34a bC ．24abD ．224a b 【答案】B【分析】根据多项式的公因式来进行求解即可．【详解】解： ()323312443a b a bc a b b c =--Q ，34a b \是多项式323124a b a bc -中各项的公因式．故选：B ．【点睛】本题主要考查了多项式的公因式，理解多项式的公因式是解答关键．2．（2023下·陕西渭南·八年级统考期末）下列因式分解正确的是（ ）A ．()1ax ay a x y +=++B ．()ma mb m a b -=-C ．()22444x x x ++=+D ．()2211x x -=-【答案】B【分析】根据因式分解的定义和方法逐项判断即可．【详解】A 、()ax ay a x y +=+，因式分解错误，该选项不符合题意；B 、因式分解正确，该选项符合题意；C 、()22442x x x ++=+，因式分解错误，该选项不符合题意；D 、()()2111x x x -=-+，因式分解错误，该选项不符合题意．故选：B ．【点睛】本题主要考查因式分解，牢记因式分解的定义（把一个多项式化成几个整式的积的形式叫做因式分解）和方法（提公因式法和公式法）是解题的关键．3．（2023上·河南许昌·八年级统考期末）如果()()21052x kx x x ++=--，则k 应为（ ）A ．3-B ．3C ．7D ．7-【答案】D 【分析】先利用整式乘法化简等式的左边代数式，再根据对应系数相等求解k 值即可．【详解】解：∵()()22525210710x x x x x x x --=--+=-+，∴2210710x kx x x ++=-+，∴7k =-，故选：D ．【点睛】本题考查因式分解，熟知因式分解和整式乘法是互为逆运算是解答的关键．4．（2023上·福建厦门·八年级统考期末）要使多项式22x M x ++能运用平方差公式进行分解因式，整式M 可以是（ ）A ．1B ．1-C ．24x -+D ．24x --【答案】D【分析】利用平方差公式的结构特征判断即可．【详解】解：A .()22211x x x ++=+是完全平方公式因式分解，不合题意；B .221x x +-不能用平方差公式因式分解，故该选项不正确，不符合题意；C .222424x x x x x -++=+，不能用平方差公式因式分解，故该选项不正确，不符合题意；D . ()()22242422x x x x x x --+=-=+-，能用平方差公式因式分解，故该选项正确，符合题意；故选：D ．【点睛】此题考查了因式分解-运用公式法，熟练掌握平方差公式是解本题的关键．5．（2023下·安徽宿州·八年级校考期末）已知ABC V 的三边长分别为a ，b ，c ，且满足22a ac b bc -=-，则ABC V 一定是（ ）A ．直角三角形B ．等边三角形C ．锐角三角形D ．等腰三角形【答案】D 【分析】依据题意，由22a ac b bc -=-得220a b ac bc --+=，从而()()0a b a b c -+-=，由两边之和大于第三边可得a b c +>，即0a b c +->，进而0a b -=，故可得解．【详解】解：由题意，∵22a ac b bc -=-，∴220a b ac bc --+=．∴()()0a b a b c -+-=．又∵a b c +>，即0a b c +->，∴0a b -=，即a b =．∴ABC V 是等腰三角形．故选：D ．【点睛】本题主要考查了因式分解的应用，解题时需要熟练掌握并能理解．二、填空题【点睛】本题主要考查了因式分解的应用，正确理解题意是解题的关键．三、解答题11．（2023下·四川达州·八年级校考期末）分解因式：(1)32231212a a b ab -+-；(2)229()()m n m n +--．【答案】(1)23(2)a a b --(2)()()422m n m n ++【分析】（1）原式提取公因式，再利用完全平方公式分解即可；（2）原式利用平方差公式分解即可．【详解】（1）原式()22344a a ab b =--+23(2)a a b =--；（2）()2原式()()()()33m n m n m n m n =++-+--éùéùëûëû()()422m n m n =++．【点睛】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．12．（2023下·四川达州·八年级校考期末）因式分解：(1)()()42a x y b y x ---；(2)22168x xy y -+；【答案】(1)()()22x y a b -+(2)2(4)x y -【分析】（1）利用提公因式法进行分解，即可解答；（2）利用完全平方公式进行分解，即可解答．【详解】（1）解：()()42a x y b y x ---【答案】(1)(3)(3)+++-a b a b (2)ABC V 是等腰三角形，理由见解析【分析】（1）运用完全平方公式分解222a ab b ++，再运用平方差公式进行分解即可；（2）运用乘法公式进行分组分解法分解因式即可．【详解】（1）解：2229a ab b ++-2()9a b =+-(3)(3)a b a b =+++-．（2）解：20a ab ac bc -+-=，因式分解为：()2()0a ab ac bc -+-=，()()0a a b c a b -+-=，()()0a b a c -+=，0a b \-=，即a b =，∴ABC V 是等腰三角形．【点睛】本题主要考查因式分解的知识，掌握乘法公式的运用，因式分解的方法是解题的关键．15．（2023下·甘肃陇南·八年级统考期末）阅读与思考请仔细阅读并完成相应任务．生活中我们经常用到密码，例如用支付宝或微信支付时．有一种用“因式分解”法产生的密码，方便记忆，其原理是：将一个多项式分解因式，如多项式：3222x x x +--可以因式分解为()()()112x x x -++，当29x =时，128x -=，130x +=，231x +=，此时可以得到数字密码283031．任务：(1)根据上述方法，当15x =，5y =时，对于多项式32x xy -分解因式后可以形成哪些数字密码？(2)已知一个直角三角形的周长是24，斜边长为11，其中两条直角边分别为x ，y ，求出一个由多项式33x y xy +分解因式后得到的密码（只需一个即可）．【答案】(1)可得数字密码是151020；也可以是152010；101520；102015，201510，201015(2)24121（或12124）【分析】（1）先将32x xy -进行因式分解，再根据题意代入15x =，5y =计算，即可求解；（2）根据勾股定理和三角形周长公式得2213121x y x y +=ìí+=î，解得24xy =，再将多项式33x y xy +分解因式后，代入24xy =，22121x y +=进行计算即可求解．【详解】（1）解：()()32x xy x x y x y -=-+，当15x =，5y =时，10x y -=，20x y +=，可得数字密码是151020；也可以是152010；101520；102015，201510，201015．（2）由题意得：2213121x y x y +=ìí+=î，解得24xy =，而()3322x y xy xy x y +=+，所以可得数字密码为24121（或12124）．【点睛】本题考查因式分解和因式分解的应用，解题的关键是掌握因式分解的方法以及题目中数字密码的计算方法．16．（2023下·辽宁锦州·八年级统考期末）数形结合是解决数学问题的重要思想方法，借助图形可以对很多数学问题进行直观推导和解释.如图1，有足够多的A ，B ，C 三种纸片：A 种是边长为m 的正方形，B 种是边长为n 的正方形，C 种是宽为m ，长为n 的长方形．用A 种纸片1张，B 种纸片1张，C 种纸片2张可以拼出（不重不漏）如图2所示的正方形．根据正方形的面积，可以用来解释整式乘法()()222m n m n m mn n ++=++，反过来也可以解释多项式222m mn n ++，因式分解的结果为2222()m mn n m n ++=+，依据上述积累的数与形对应关系的经验，解答下列问题：(1)若多项式2223m n mn ++表示分别由1，2，3张A ，B ，C 三种纸片拼出如图3所示的大长方形的面积，请根据图形求出这个长方形的长和宽，并对多项式2232m mn n ++进行因式分解；(2)我们可以借助图3再拼出一个更长方形，使该长方形刚好由3张A 种纸片，2张B 种纸片，7张C 种纸片拼成，那么这个长方形的面积可以表示为多项式______，据此可得到该多项式因式分解的结果为______．【答案】(1)长是2m n +，宽是m n +，因式分解结果是()()2m n m n ++(2)22372m mn n ++，()()23m n m n ++【分析】（1）根据A ，B ，C 三种纸片的边长即可求出图2中长方形的长和宽，根据长方形的面积等于长乘宽即可进行因式分解；（2）根据长方形由3张A 种纸片，2张B 种纸片，7张C 种纸片拼成，即可求出这个长方形的面积，然后进行因式分解即可．【详解】（1）解：根据图形可知这个长方形的长是2m n +，宽是m n +，2232(2)()m mn n m n m n \++=++；（2）根据长方形刚好由3张A 种纸片，2张B 种纸片，7张C 种纸片拼成，则这个长方形的面积可以表示为多项式22372m mn n ++，22372(2)(3)m mn n m n m n \++=++，故答案为：22372m mn n ++，(2)(3)m n m n ++．【点睛】本题主要考查了因式分解的应用，多项式乘多项式，利用数形结合思想与长方形的面积解答是解题的关键．。

因式分解专项练习题(含答案)1. 二次多项式的因式分解问题描述给定一个二次多项式ax2+bx+c，请将其进行因式分解。

解答步骤1.首先确定二次多项式的系数a、b和c。

2.接着，我们需要找到两个因子，使得它们的乘积等于ac，并且它们的和等于b。

3.最后，将多项式按照因子的形式进行因式分解。

示例问题：将二次多项式2x2+3x−2进行因式分解。

解答：1.确定系数a=2，b=3和c=−2。

2.找到两个因子，它们的乘积等于ac=−4，并且它们的和等于b=3。

在本例中，-2 和 2 是满足要求的因子。

3.将多项式进行因式分解：2x2+3x−2=(x−2)(2x+1)。

因此，二次多项式2x2+3x−2的因式分解结果为(x−2)(2x+1)。

答案(x−2)(2x+1)2. 完全平方式的因式分解问题描述给定一个完全平方式a2−b2，请将其进行因式分解。

解答步骤1.首先确定完全平方式的两个因子a和b。

2.接着，根据公式(a−b)(a+b)进行因式分解。

示例问题：将完全平方式9x2−4进行因式分解。

解答：1.确定完全平方式的两个因子a=3x和b=2。

2.根据公式进行因式分解：9x2−4=(3x−2)(3x+2)。

因此，完全平方式9x2−4的因式分解结果为(3x−2)(3x+2)。

答案(3x−2)(3x+2)3. 其它特殊情况的因式分解问题描述除了二次多项式和完全平方式外，还有一些特殊情况需要进行因式分解。

下面是几个例子：1.差平方式：形式为a2−b2的差平方式可以利用公式(a−b)(a+b)进行因式分解。

2.特殊二次多项式：形式为ax2+bx+c的二次多项式，如果不能直接进行因式分解，可以尝试使用求根公式进行因式分解。

3.多项式的公因式提取：对于多项式ax2+bx，可以提取公因式得到x(ax+b)进行因式分解。

示例问题：将差平方式16x2−9进行因式分解。

解答：根据公式(a−b)(a+b)进行因式分解：16x2−9=(4x−3)(4x+3)。

中考数学《因式分解》专项练习题及答案一、单选题1．下列多项式中,能用提公因式法因式分解的是()A．x2-y B．x2+2x C．x2+y2 D．x2-xy+y22．下列式子变形是因式分解的是（）A．x2－5x＋6＝x(x－5)＋6B．x2－5x＋6＝(x－2)(x－3)C．(x－2)(x－3)＝x2－5x＋6D．x2－5x＋6＝(x＋2)(x＋3)3．下列因式分解正确的是（）A．x2y2﹣z2＝x2（y+z）（y﹣z）B．﹣x2y﹣4xy+5y＝﹣y（x2+4x+5）C．（x+2）2﹣9＝（x+5）（x﹣1）D．9﹣12a+4a2＝﹣（3﹣2a）24．把多项式ax3﹣2ax2+ax分解因式，结果正确的是（）A．ax（x2﹣2x）B．ax2（x﹣2）C．ax（x+1）（x﹣1）D．ax（x﹣1）25．下面从左到右的变形是因式分解的是（）A．6xy=2x⋅3y B．(x+1)(x−1)=x2−1C．x2−3x+2=x(x−3)+2D．2x2−4x=2x(x−2)6．对于①(x+3)(x−1)=x2+2x−3，②x−3xy=x(1−3y)从左到右的变形，表述正确的是（）A．都是因式分解B．都是整式的乘法C．①是因式分解，②是整式的乘法D．①是整式的乘法，②是因式分解7．若x2+kx+16=(x−4)2，那么（）A．k=－8，从左到右是乘法运算B．k=8，从左到右是乘法运算C．k=－8，从左到右是因式分解D．k=8，从左到右是因式分解8．把代数式mx2-6mx+9m分解因式，下列结果中正确的是（）A．m（x+3）2B．m（x+3）（x-3）C．m（x-4）2D．m（x-3）29．下列等式中，从左到右的变形是因式分解（）A．2x2y+8xy2+6=2xy(x+4y)+6B．(5x−1)(x+3)=5x2−14x−3C．x2−y2=(x+y)(x−y)D．x3+y2+2x+1=(x+1)2+y210．下列等式中，从左到右的变形是因式分解的是（）A ．x(x −2)=x 2−2xB ．(x −1)2=x 2−2x −1C ．x 2−4=(x +2)(x −2)D ．x 2+3x +2=x(x +3)+211．若多项式mx 2-1n 可分解因式为（3x+15）（3x-15），则m 、n 的值为（ ）A ．m=3，n=5B ．m=-3，n=5C ．m=9，n=25D ．m=-9，n=-2512．下列因式分解正确的是（ ）A ．a 4b ﹣6a 3b ＋9a 2b ＝a 2b （a 2﹣6a ＋9）B ．x 2﹣x ＋ 14 ＝（x ﹣ 12 ）2C ．x 2﹣2x ＋4＝（x ﹣2）2D ．x 2﹣4＝（x ＋4）（x ﹣4）二、填空题13．分解因式： 2a 2−2= ． 14．分解因式：2 a 3−8a ＝ . 15．因式分解：a 3﹣2a 2b+ab 2= ． 16．已知x+y=6，xy=3，则x 2y+xy 2的值为 . 17．因式分解： 3a 2−6a +3 ＝ ． 18．分解因式：xy 2﹣9x= ．三、综合题19．综合题（1）已知a+b=1,ab= 14 ,利用因式分解求a(a+b)(a-b)-a(a+b)2的值.（2）若x 2+2x=1,试求1-2x 2-4x 的值.20．我们用xyz ̅̅̅̅̅表示一个三位数，其中x 表示百位上的数，y 表示十位上的数，z 表示个位上的数，即xyz̅̅̅̅̅=100x +10y +z . （1）说明abc ̅̅̅̅̅+bca ̅̅̅̅̅+cab̅̅̅̅̅一定是111的倍数； （2）①写出一组a 、b 、c 的取值，使abc ̅̅̅̅̅+bca ̅̅̅̅̅+cab̅̅̅̅̅能被11整除，这组值可以是a= ，b= ，c= ；②若abc ̅̅̅̅̅+bca ̅̅̅̅̅+cab̅̅̅̅̅能被11整除，则a 、b 、c 三个数必须满足的数量关系是 .21．把代数式通过配凑等手段，得到局部完全平方式，再进行有关运算和解题，这种解题方法叫做配方法.如：①用配方法分解因式：a 2+6a+8 解：原式=a 2+6a+8+1-1=a 2+6a+9-1=(a+3)2－12= [(a +3)+1][(a +3)−1]=(a +4)(a +2)②M=a2-2a－1，利用配方法求M的最小值.解：a2−2a−1=a2−2a+1−2=(a−1)2−2∵(a-b)2≥0，∴当a=1时，M有最小值－2.请根据上述材料解决下列问题：2+2x−3.（1）用配方法．．．因式分解：x（2）若M=2x2−8x，求M的最小值.（3）已知x2+2y2+z2-2xy-2y-4z+5=0，求x+y+z的值.22．由多项式乘法：（x+a）（x+b）=x2+（a+b）x+ab，将该式从右到左使用，即可得到“十字相乘法”进行因式分解的公式：x2+（a+b）x+ab=（x+a）（x+b）示例：分解因式：x2+5x+6=x2+（2+3）x+2×3=（x+2）（x+3）（1）尝试：分解因式：x2+6x+8=（x+）（x+）；（2）应用：请用上述方法解方程：x2﹣3x﹣4=0．23．将下列各式分解因式：（1）2x2y−8xy+8y（2）a2(x−y)−9b2(x−y)24．因式分解：（1）−20a−15ax（2）(a−3)2−(2a−6)参考答案1．【答案】B 2．【答案】B 3．【答案】C 4．【答案】D 5．【答案】D 6．【答案】D 7．【答案】C 8．【答案】D 9．【答案】C 10．【答案】C 11．【答案】C 12．【答案】B13．【答案】2(a+1)(a-1) 14．【答案】2a(a+2)(a-2) 15．【答案】a （a ﹣b ）2 16．【答案】18 17．【答案】3（a -1）2 18．【答案】x （y ﹣3）（y+3）19．【答案】（1）解：原式=a(a+b)(a-b-a-b)=-2ab(a+b).∵a+b=1,ab= 14∴原式=-2× 14 ×1=- 12 .（2）解：∵x 2+2x=1, ∴1-2x 2-4x=1-2(x 2+2x) =1-2×1=-1.20．【答案】（1）解：abc ̅̅̅̅̅+bca ̅̅̅̅̅+cab̅̅̅̅̅ =100a +10b +c +100b +10c +a +100c +10a +b=111a +111b +111c =111(a +b +c)∵a 、b 、c 都是整数 ∴a +b +c 也是整数∴111(a +b +c)是111的倍数∴abc ̅̅̅̅̅+bca ̅̅̅̅̅+cab̅̅̅̅̅一定是111的倍数 （2）2；4；5（答案不唯一）；a +b +c =11或a +b +c =22（1≤a ≤9，1≤b ≤9，1≤c ≤9）21．【答案】（1）解：原式 =x 2+2x −3+4−4=x 2+2x +1−4 =(x +1)2−22 =[(x +1)+2][(x +1)−2]=(x +3)(x −1) ；（2）解： 2x 2−8x =2(x 2−4x)=2(x 2−4x +4−4) =2[(x −2)2−4] =2(x −2)2−8 ∵(x −2)2≥0∴ 当 x =2 时， M 有最小值 −8 ； （3）解： x 2+2y 2+z 2−2xy −2y −4z +5=(x 2−2xy +y 2)+(y 2−2y +1)+(z 2−4z +4)=(x −y)2+(y −1)2+(z −2)2 ∵(x −y)2+(y −1)2+(z −2)2=0∴{x −y =0y −1=0z −2=0解得 {x =1y =1z =2则 x +y +z =1+1+2=4 .22．【答案】（1）2；4（2）解：∵x 2﹣3x ﹣4=0 x 2+（﹣4+1）x+（﹣4）×1=0 ∴（x ﹣4）（x+1）=0 则x+1=0或x ﹣4=0 解得：x=﹣1或x=4．23．【答案】（1）解：原式＝2y （x 2﹣4x+4）＝2y （x ﹣2）2；（2）解：原式＝（x ﹣y ）（a 2﹣9b 2） ＝（x ﹣y ）（a+3b ）（a ﹣3b ）.24．【答案】（1）解： −20a −15ax= −5a×4−5a⋅3x=−5a(4+3x)；（2）解：(a−3)2−(2a−6) = (a−3)2−2(a−3)= (a−3)(a−3−2)=(a−3)(a−5)。

2019初中数学因式分解的应用拓展创新题型专项训练七（附答案详解）1．阅读例题，回答问题：例题：已知二次三项式：x2﹣4x+m有一个因式是x+3，求另一个因式以及m的值．解：设另一个因式为x+n，得x2﹣4x+m＝(x+3)(x+n)，则x2﹣4x+m＝x2+(n+3)x+3n．∴∴∴另一个因式为x﹣7，m＝21．仿照以上方法解答下面的问题：已知二次三项式2x2+3x+k有一个因式是2x﹣5，求另一个因式以及k的值．2．分解因式x2－4y2－2x＋4y，细心观察这个式子就会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式，过程为：x2－4y2－2x＋4y＝(x＋2y)(x－2y)－2(x－2y)＝(x－2y)(x＋2y－2)．这种分解因式的方法叫分组分解法，利用这种方法解决下列问题：(1)分解因式：a2－4a－b2＋4；(2)若△ABC三边a、b、c满足a2－ab－ac＋bc＝0，试判断△ABC的形状．3．任何一个正整数n都可以进行这样的分解：n＝p×q（p、q是正整数，且p≤q）．如果p×q 在n的所有这种分解中两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并且规定F（n）＝．例如18＝1×18＝2×9＝3×6，这时就有F（18）＝．请解答下列问题：(1)计算：F（24）；(2)当n为正整数时，求证：F（n3+2n2+n）＝．4．阅读以下文字并解决问题：对于形如这样的二次三项式，我们可以直接用公式法把它分解成的形式，但对于二次三项式，就不能直接用公式法分解了．此时，我们可以在中间先加上一项，使它与的和构成一个完全平方式，然后再减去，则整个多项式的值不变．即：，像这样，把一个二次三项式变成含有完全平方式的形式的方法，叫做配方法．利用“配方法”因式分解：如果，求的值．5．嘉嘉同学动手剪了如图①所示的正方形与长方形纸片若干张．问题发现(1)他用1张Ⅰ型、1张Ⅱ型和2张Ⅲ型卡片拼出一个新的图形(如图②)．根据图形的面积关系写出一个你所熟悉的乘法公式，这个乘法公式是________________；(2)如果要拼成一个长为a＋2b，宽为a＋b的大长方形，那么需要Ⅱ型卡片________张，Ⅲ型卡片________张．拓展探究(3)若a＋b=5，ab=6，求a2＋b2的值；(4)当他拼成如图③所示的长方形时，根据图形的面积，可把多项式a2＋3ab＋2b2分解因式，其结果是________．解决问题（5）请你依照嘉嘉的方法，利用拼图分解因式：a2＋5ab＋6b2=________．6．阅读理解：例：已知： ，求： 和 的值．解：，，，，，，，解决问题：（1）若 ，求 x 、y 的值；（2）已知 ，， 是的三边长且满足，①直接写出a=__________．b=___________．②若 是中最短边的边长（即c<a ；c<b ），且 为整数，直接写出 的值可能是 ．7．先阅读下面的内容，再解决问题，例题：若2222690m mn n n ++-+=，求m 和n 的值． 解：∵2222690m mn n n ++-+= ∴2222690m mn n n n +++-+=∴()()2230m n n ++-= ∴0,30,m n n +=-= ∴3, 3.m n =-=问题（1）若△ABC的三边长a b c 、、都是正整数，且满足22661830a b a b c +--++-=，请问△ABC 是什么形状?说明理由.（2）若224212120x y xy y +-++=，求y x 的值．（3）已知24,6130a b ab c c -=+-+=，则a b c ++= ．8．设a1=32﹣12，a2=52﹣32，……，a n=（2n+1）2﹣（2n﹣1）2，（n为正整数）（1）试说明a n是8的倍数；（2）若△ABC的三条边长分别为a k、a k+1、a k+2（k为正整数）①求k的取值范围．②是否存在这样的k，使得△ABC的周长为一个完全平方数，若存在，试举出一例，若不存在，说明理由．9．如图1所示，边长为a的正方形中有一个边长为b的小正方形，图2是由图1中阴影部分拼成的一个长方形，设图1中阴影部分面积为S1，图2中阴影部分面积为S2．（1）请直接用含a，b的代数式表示S1＝______，S2＝_____；（2）写出利用图形的面积关系所揭示的公式：_______；（3）利用这个公式说明216﹣1既能被15整除，又能被17整除．10．观察下列分解因式的过程：x2+2ax﹣3a2=x2+2ax+a2﹣a2﹣3a2（先加上a2，再减去a2）=（x+a）2﹣4a2（运用完全平方公式）=（x+a+2a）（x+a﹣2a）（运用平方差公式）=（x+3a）（x﹣a）像上面那样通过加减项配出完全平方式后再把二次三项式分解因式的方法，叫做配方法．请你用配方法分解因式：m2﹣4mn+3n211．已知x≠1，计算：(1－x)(1＋x)＝1－x2，(1－x)(1＋x＋x2)＝1－x3，(1－x)(1＋x＋x2＋x3)＝1－x4.(1)观察以上各式并猜想：(1－x)(1＋x＋x2＋…＋x n)＝________(n为正整数)．(2)根据你的猜想计算：①(1－2)×(1＋2＋22＋23＋24＋25)＝________；②2＋22＋23＋…＋2n＝________(n为正整数)；③(x－1)(x99＋x98＋x97＋…＋x2＋x＋1)＝________．(3)通过以上规律请你进行下面的探索：①(a－b)(a＋b)＝________；②(a－b)(a2＋ab＋b2)＝________；③(a－b)(a3＋a2b＋ab2＋b3)＝________．12．你会对多项式(x2+5x+2)(x2+5x+3)﹣12分解因式吗？对结构较复杂的多项式，若把其中某些部分看成一个整体，用新字母代替(即换元)，能使复杂的问题简单化、明朗化．从换元的个数看，有一元代换、二元代换等．对于(x2+5x+2)(x2+5x+3)﹣12．解法一：设x2+5x＝y，则原式＝(y+2)(y+3)﹣12＝y2+5y﹣6＝(y+6)(y﹣1)＝(x2+5x+6)(x2+5x﹣1)＝(x+2)(x+3)(x2+5x﹣1)．解法二：设x2+5x+2＝y，则原式＝y(y+1)﹣12＝y2+y﹣12＝(y+4)(y﹣3)＝(x2+5x+6)(x2+5x﹣1)＝(x+2)(x+3)(x2+5x﹣1)．解法三：设x2+2＝m，5x＝n，则原式＝(m+n)(m+n+1)﹣12＝(m+n)2+(m+n)﹣12＝(m+n+4)(m+n﹣3)＝(x2+5x+6)(x2+5x﹣1)＝(x+2)(x+3)(x2+5x﹣1)．按照上面介绍的方法对下列多项式分解因式：(1)(x2+x﹣4)(x2+x+3)+10；(2)(x+1)(x+2)(x+3)(x+6)+x2；(3)(x+y﹣2xy)(x+y﹣2)+(xy﹣1)2．答案：1．另一个因式为(x+4)，k的值为20．解：设另一个因式为(x+n)，得2x2+3x﹣k＝(2x﹣5)(x+n)＝2x2+(2n﹣5)x﹣5n，则解得：n＝4，k＝20，故另一个因式为(x+4)，k的值为20．2．(1) (a＋b－2)(a－b－2);(2) △ABC是等腰三角形解:(2)或或∴△ABC是等腰三角形．3．(1) ；(2) .解：(1)∵24＝1×24＝2×12＝3×8＝4×6，其中4与6的差的绝对值最小，∴F(24)＝＝.(2)∵n3＋2n2＋n＝n(n＋1)2，其中n(n＋1)与(n＋1)的差的绝对值最小，且(n＋1)≤n(n＋1)，∴F(n3＋2n2＋n)＝＝.4．；．解：（1）x2+4xy﹣5y2=（x2+4xy+4y2）﹣4y2﹣5y2=（x+2y）2﹣（3y）2=（x+2y+3y）（x+2y﹣3y）=（x+5y）（x﹣y）；（2）∵a2+2b2+c2﹣2ab﹣6b﹣4c+13=0，∴（a2﹣2ab+b2）+（b2﹣6b+9）+（c2﹣4c+4）=0，（a﹣b）2+（b﹣3）2+（c﹣2）2=0，∴a﹣b=0，b﹣3=0，c﹣2=0，解得：a=b=3，c=2，∴a+b+c=8．5．（1）(a＋b)2=a2＋2ab＋b2；（2）2，3；（3）13；（4）(a＋2b)(a＋b)；（5）(a＋2b)(a＋3b) 解：（1）这个乘法公式是（a+b）2=a2+2ab+b2．故答案为：（a+b）2=a2+2ab+b2．（2）由如图③可得要拼成一个长为（a+2b），宽为（a+b）的大长方形，则需要2号卡片2张，3号卡片3张．故答案为：2，3．（3）a2＋b2=（a+b）2－2ab=25－2×6=25－12=13．（4）由图③可知矩形面积为（a+2b）•（a+b），所以a2+3ab+2b2=（a+2b）•（a+b）．故答案为：（a+2b）•（a+b）．（5）a2+5ab+6b2=（a+2b）（a+3b），如图：故答案为：（a+2b）（a+3b）．6．（1），；（2）①，；②、、；解：（1），，即，；解得，，（2）①，，②，，，，，，，，为最短边，且 为整数，为 、、．7．（1）△ABC 是等边三角形；（2）14；（3）3 解：（1）△ABC 是等边三角形由题意得()()223330a b c -+-+-= ∴3a b c ===∴△ABC 是等边三角形． （2）由题意得()()22320x y y -++= ∴2x y ==-． ∴1144y y x x ==． （3）∵a –24,6130a b ab c c -=+-+=b=4，即a=b+4，（b+4)b+c 2 –6c+13=0，∴（b 2+4b+4 ）+（c 2–6c+9）=0，∴b+2=0，c –3=0， ∴b = –2，c =3，a =2， ∴a+b+c=3．8．（1）证明；（2）①k ＞1；②当k=5时，△ABC 的周长为一个完全平方数．解：（1）∵a n =（2n+1）2﹣（2n ﹣1）2=[（2n+1）﹣（2n ﹣1）][（2n+1）+（2n ﹣1）]=2×4n=8n ， ∵8n 能被8整除， ∴a n 是8的倍数；（2）①由（1）可得，a k =8k ，a k+1=8（k+1），a k+2=8（k+2）， ∴8k+8（k+1）＞8（k+2），解得，k ＞1， 即k 的取值范围是：k ＞1；②存在这样的k ，使得△ABC 的周长为一个完全平方数，理由：∵△ABC的周长是：8k+8（k+1）+8（k+2）=24k+24=24（k+1）=4×6×（k+1），∵△ABC的周长为一个完全平方数，则k+1=6m，（m为1，3，5，…奇数），取m=1；∴k=5；即当k=5时，△ABC的周长为一个完全平方数．9．（1）a2﹣b2；（a+b）（a﹣b）；（2）a2﹣b2＝（a+b）（a﹣b）；（3）证明解：（1）图1用大正方形的边长为a，小正方形的边长为b，故阴影部分面积为a2﹣b2，图2用长方形的长为（a+b），宽为（a﹣b），故阴影部分面积为（a+b）（a﹣b）；（2）观察图1和图2中阴影部分面积是相等的，故a2﹣b2=（a+b）（a﹣b）；（3）216﹣1=（28﹣1）（28+1）=（24﹣1）（24+1）（28+1）=15×17×（28+1）因为28+1是整数，故216﹣1既能被15整除，又能被17整除．10．（m﹣n）（m﹣3n）解：原式=m2﹣4mn+4n2﹣n2=（m﹣2n）2﹣n2=（m﹣2n+n）（m﹣2n﹣n）=（m﹣n）（m﹣3n）11．(1)①－63；②2n＋1－2；③x100－1.(2)①a2－b2；②a3－b3；③a4－b4解：（1）由题意知(1−x)(1+x+x2+…+x n)=1−x n+1；所以①(1−2)(1+2+22+23+24+25)=1−26=1−64=−63；②2+22+23+24+…+2n=2(1+2+22+23+24+…+2n−1)=−2(1−2)(1+2+22+23+24+…+2n−1)=−2(1−2n)=2n+1−2；③(x−1)(x99+x98+x97+…+x2+x+1)=−(1−x)(1+x+x2+…+x99)=−(1−x100)=x100−1，(3)①(a−b)(a+b)=a2−b2；②(a−b)(a2+ab+b2)=a3−b3；③(a−b)(a3+a2b+ab2+b3)=a4−b4.故答案为：(1)①－63；②2n＋1－2；③x100－1.(2)①a2－b2；②a3－b3；③a4－b412．（1）(x+2)(x-1) (+1)(2)()2(3) (x+y-xy-1)2解：（1）令m=,原式==m2-m-2=(m-2)(m+1)= (-2)(+1)=(x+2)(x-1) (+1)(2)=()()+, 令n=，原式=（n+2）n+x2=n2+2n+x2=(n+x)2=()2(3) 令a=x+y,b=xy，原式==(a-b)2-2(a-b)+1=(a-b-1)2=(x+y-xy-1)2。

因式分解练习题带答案初二1. 题目：因式分解练习题带答案初二因式分解是初中数学中的重要内容，本文将提供一些初二年级的因式分解练习题，每道题都附带详细答案，帮助学生巩固和提高因式分解的能力。

一、基础练习题1. 将下列代数式进行因式分解：a) 4x^2 - 9y^2b) 2xy + 6x解答：a) 4x^2 - 9y^2 = (2x + 3y)(2x - 3y)b) 2xy + 6x = 2x(y + 3)2. 将下列代数式进行因式分解：a) 2x^3 - 8x^2b) 3x^2 + 12x + 9解答：a) 2x^3 - 8x^2 = 2x^2(x - 4)b) 3x^2 + 12x + 9 = (x + 3)(3x + 3)二、应用练习题1. 将以下代数式进行因式分解，并求解方程：a) x^2 + 6x + 9 = 0b) 2x^2 - 18 = 0解答：a) x^2 + 6x + 9 = (x + 3)(x + 3) = (x + 3)^2解方程：(x + 3)^2 = 0x + 3 = 0x = -3b) 2x^2 - 18 = 2(x^2 - 9) = 2(x + 3)(x - 3)解方程：2(x + 3)(x - 3) = 0x + 3 = 0 或者 x - 3 = 0x = -3 或者 x = 32. 将以下代数式进行因式分解，并求解方程：a) 4x^2 + 12x + 9 = 0b) x^2 + 8x - 20 = 0解答：a) 4x^2 + 12x + 9 = (2x + 3)(2x + 3) = (2x + 3)^2解方程：(2x + 3)^2 = 02x + 3 = 0x = -1.5b) x^2 + 8x - 20 = (x + 10)(x - 2)解方程：(x + 10)(x - 2) = 0x + 10 = 0 或者 x - 2 = 0x = -10 或者 x = 2以上是一些初二年级的因式分解练习题及答案，通过练习这些题目，学生可以更好地理解因式分解的概念和方法，并能够熟练地应用于实际问题的解决中。

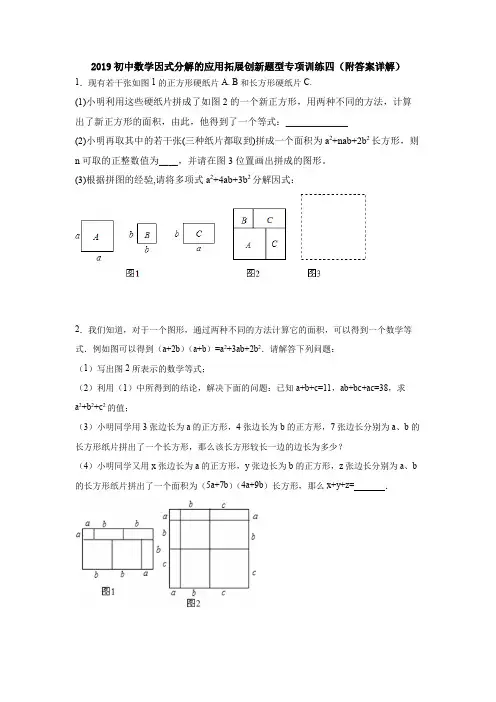
2019初中数学因式分解的应用拓展创新题型专项训练四（附答案详解）1．现有若干张如图1的正方形硬纸片A. B和长方形硬纸片C.(1)小明利用这些硬纸片拼成了如图2的一个新正方形，用两种不同的方法，计算出了新正方形的面积，由此，他得到了一个等式：_____________(2)小明再取其中的若干张(三种纸片都取到)拼成一个面积为a2+nab+2b2长方形，则n可取的正整数值为____，并请在图3位置画出拼成的图形。

(3)根据拼图的经验,请将多项式a2+4ab+3b2分解因式：2．我们知道，对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式．例如图可以得到（a+2b）（a+b）=a2+3ab+2b2．请解答下列问题：（1）写出图2所表示的数学等式；（2）利用（1）中所得到的结论，解决下面的问题：已知a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值；（3）小明同学用3张边长为a的正方形，4张边长为b的正方形，7张边长分别为a、b的长方形纸片拼出了一个长方形，那么该长方形较长一边的边长为多少？（4）小明同学又用x张边长为a的正方形，y张边长为b的正方形，z张边长分别为a、b 的长方形纸片拼出了一个面积为（5a+7b）（4a+9b）长方形，那么x+y+z=．3．阅读与思考：阅读理解问题——代数问题几何化 1.阅读理解以下文字：我们知道，多项式的因式分解就是将一个多项式化成几个整式的积的形式．通过因式分解，我们常常将一个次数比较高的多项式转化成几个次数较低的整式的积，来达到降次化简的目的．这个思想可以引领我们解决很多相对复杂的代数问题．例如：方程2x2+3x=0 就可以这样来解：解：原方程可化为x（2x+3）=0，所以x=0 或者2x+3=0．解方程2x+3=0，得x=-．∴原方程的解为x=0或x=-.根据你的理解，结合所学知识，解决以下问题：（1）解方程：3x2-x=0（2）解方程：（x+3）2-4x2=0；（3）已知△ABC 的三边长为4，x，y，请你判断代数式y2 -8y+16-x2的值的符号．4．一个四位数，记千位上和百位上的数字之和为x，十位上和个位上的数字之和为y，如果x=y，那么称这个四位数为“和平数”.例如:1423，x=1+4，y=2+3，因为x=y，所以1423是“和平数”.(1)请判断:2561 (填“是”或“不是”)“和平数”(2)直接写出:最小的“和平数”是，最大的“和平数”是(3)如果一个“和平数”的十位上的数字是千位上的数字的两倍，且百位上的数字与十位上的数字之和是14的倍数，求满足条件的所有“和平数”.5．下面是某同学对多项式（x2﹣4x﹣3）（x2﹣4x+1）+4进行因式分解的过程．解：设x2﹣4x=y原式=（y﹣3）（y+1）+4（第一步）=y2﹣2y+1 （第二步）=（y﹣1）2（第三步）=（x2﹣4x﹣1）2（第四步）回答下列问题：（1）该同学第二步到第三步运用了因式分解的．A．提取公因式法B．平方差公式法C．完全平方公式法（2）请你模仿以上方法尝试对多项式（x2+2x）（x2+2x+2）+1进行因式分解．6．[数学实验探索活动]实验材料现有若干块如图①所示的正方形和长方形硬纸片．实验目的：用若干块这样的正方形和长方形硬纸片拼成一个新的长方形，通过不同的方法计算面积，得到相应的等式，从而探求出多项式乘法或分解因式的新途径．例如，选取正方形、长方形硬纸片共6 块，拼出一个如图②的长方形，计算它的面积，写出相应的等式有a2+3ab+2b2=(a+2b)(a+b)或(a+2b)(a+b) =a2+3ab+2b2．问题探索：(1) 小明想用拼图的方法解释多项式乘法(2a+b)(a+b) =2a2+3ab+b2 ，那么需要两种正方形纸片张，长方形纸片张；(2)选取正方形、长方形硬纸片共8 块，可以拼出一个如图③的长方形，计算图③的面积，并写出相应的等式；(3)试借助拼图的方法，把二次三项式2a2+5ab+2b2 分解因式，并把所拼的图形画在虚线方框内.7．阅读下列文字与例题，并解答。

2019届初三数学中考复习因式分解专项训练1. 下列各式由左到右的变形中，属于分解因式的是( )A．a(m＋n)＝am＋anB．a2－b2－c2＝(a－b)(a＋b)－c2C．10x2－5x＝5x(2x－1)D．x2－16＋6x＝(x＋4)(x－4)＋6x2. 将下列多项式因式分解，结果中不含有因式a＋1的是( )A．a2－1 B．a2＋a C．a2＋a－2 D．(a＋2)2－2(a＋2)＋13. 把多项式x2＋ax＋b分解因式，得(x＋1)(x－3)，则a，b的值分别是( ) A．a＝2，b＝3 B．a＝－2，b＝－3C．a＝－2，b＝3 D．a＝2，b＝－34. 下列式子从左到右变形是因式分解的是( )A．a2＋4a－21＝a(a＋4)－21 B．a2＋4a－21＝(a－3)(a＋7)C．(a－3)(a＋7)＝a2＋4a－21 D．a2＋4a－21＝(a＋2)2－255. 852－152等于( )A．70 B．700 C．4 900 D．7 0006. 已知a，b，c是△ABC的三边长，且满足a3＋ab2＋bc2＝b3＋a2b＋ac2，则△ABC 的形状是( )A．等腰三角形 B．直角三角形C．等腰三角形或直角三角形 D．等腰直角三角形7. 如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形．根据图形的变化过程写出的一个正确的等式是( )A．(a－b)2＝a2－2ab＋b2 B．a(a－b)＝a2－abC．(a－b)2＝a2－b2 D．a2－b2＝(a＋b)(a－b)8. 分解因式：2a2－4a＋2＝________________9. 已知x＋y＝3，xy＝6，则x2y＋xy2的值为__________10. 分解因式：a2＋a＝_________________．11. 分解因式：2a2－8＝_____________________．12. 将多项式mn2＋2mn＋m因式分解的结果是___________．13. 已知|x－y＋2|＋x＋y－2＝0，则x2－y2的值为_____________14. 分解因式：9x2－115. 分解因式：m3(x－2)＋m(2－x)16. 分解因式：(m＋1)(m－9)＋8m17. 分解因式：a2b－10ab＋25b18. 分解因式：20m3n－15m2n2＋5m2n19. 分解因式：4x2－16y220. 分解因式：m(a－b)＋n(b－a)21. 分解因式：－3x2＋18x－2722. 已知a2＋b2＋6a－10b＋34＝0，求a＋b的值．23. 设y＝kx，是否存在实数k，使得代数式(x2－y2)(4x2－y2)＋3x2(4x2－y2)能化简为x4？若能，请求出所有满足条件的k的值；若不能，请说明理由．参考答案：1---7 CCBBD CD8. 2(a－1)29. 3210. a(a＋1)11. 2(a＋2)(a－2)12. m(n＋1)213. －414. 解：原式＝(3x＋1)(3x－1)．15. 解：原式＝m(m＋1)(m－1)(x－2)．16. 解：原式＝(m＋3)(m－3)．17. 解：原式＝b(a－5)2.18. 解：20m3n－15m2n2＋5m2n＝5m2n(4m－3n＋1)．19. 解：4x2－16y2＝4(x＋2y)(x－2y)．20. 解：m(a－b)＋n(b－a)＝m(a－b)－n(a－b)＝(a－b)(m－n)．21. 解：－3x2＋18x－27＝－3(x2－6x＋9)＝－3(x－3)2.22. 解：∵a2＋b2＋6a－10b＋34＝0，∴a2＋6a＋9＋b2－10b＋25＝0，即(a＋3)2＋(b－5)2＝0，∴a＋3＝0且b－5＝0，∴a＝－3，b＝5，∴a＋b＝－3＋5＝23. 解：(x2－y2)(4x2－y2)＋3x2(4x2－y2)＝(4x2－y2)2，当y＝kx时，原式＝(4x2－k2x2)2＝(4－k2)2x4，令(4－k2)2＝1，解得k＝±3或±5，∴当k＝±3或±5时，原代数式可化简为x4.。