大学物理实验— 光栅衍射实验
- 格式:doc
- 大小:1.48 MB
- 文档页数:3

实验 22 衍射光栅一、实验目的:1.观察光栅的衍射光谱,理解光栅衍射基本规律。
2.进一步熟悉分光计的调节和使用。
3. 测定光栅常数和汞原子光谱部分特征波长。
二、实验仪器:分光计、光栅、汞灯。
三、实验原理及过程简述:1.衍射光栅、光栅常数光栅是由大量相互平行、等宽、等距的狭缝(或刻痕)构成。
其示意图如图 1 所示。
图1图2光栅上若刻痕宽度为 a,刻痕间距为 b,则 d=a 十 b 称为光栅常数,它是光栅基本参数之一。
2.光栅方程、光栅光谱根据夫琅和费光栅衍射理论,当一束平行单色光垂直入射到光栅平面上时,光波将发生衍射,凡衍射角满足光栅方程:, k 0 ,± 1 ,± 2... (1)时,光会加强。
式中λ为单色光波长, k 是明条纹级数。
衍射后的光波经透镜会聚后,在焦平面上将形成分隔得较远的一系列对称分布的明条纹,如图 2 所示。
如果人射光波中包含有几种不同波长的复色光,则经光栅衍射后,不同波长光的同一级( k )明条纹将按一定次序排列,形成彩色谱线,称为该入射光源的衍射光谱。
图 3 是普 0通低压汞灯的第一级衍射光谱。
它每一级光谱中有四条特征谱线:紫色λ14358 A ;绿色λ 0 0 025461 A ;黄色两条λ3=5770 A 和λ45791 A 。
3.光栅常数与汞灯特征谱线波长的测量由方程(1)可知,若光垂直入射到光栅上,而第一级光谱中波长λ1 已知,则测出它相应的衍射角为 1 ,就可算出光栅常数 d;反之,若光栅常数已知,则可由式(1)测出光源发射的各特征谱线的波长 i 。
角的测量可由分光计进行。
4.实验内容与步骤a.分光计调整与汞灯衍射光谱观察(1)调整好分光计。
(2)将光栅按图 4 所示位置放于载物台上。
通过调平螺丝 a 1 或 a 3 使光栅平面与平行光管光轴垂直。
然后放开望远镜制动螺丝,转动望远镜观察汞灯衍射光谱,中央( K 0 )零级为白色,望远镜转至左、右两边时,均可看到分立的四条彩色谱线。


实验五 光栅衍射实验——光栅距的测定与测距实验(一)光栅距的测定实验目的:了解光栅的结构及光栅距的测量方法。
实验原理: 1. 光栅衍射:光栅是利用多缝衍射原理使光发生色散(分解为光谱)的光学元件。
它是一块刻有大量平行等宽、等距狭缝(刻线)的平面玻璃或金属片。
光栅的狭缝数量很大,一般每毫米几十至几千条。
单色平行光通过光栅每个缝的衍射和各缝间的干涉,形成暗条纹很宽、明条纹很细的图样,这些锐细而明亮的条纹称作谱线。
谱线的位置随波长而异,当复色光通过光栅后,不同波长的谱线在不同的位置出现而形成光谱。
光通过光栅形成光谱是单缝衍射和多缝干涉的共同结果。
波在传播时,波阵面上的每个点都可以被认为是一个单独的次波源;这些次波源再发出球面次波,则以后某一时刻的波阵面,就是该时刻这些球面次波的包迹面(惠更斯原理)实验所需部件:光栅、激光器、直尺与投射屏(自备)。
实验条件:记录数据条件:在激光器发射的激光稳定后,在进行测量,记录数据。
实验步骤:1、 激光器放入光栅正对面的激光器支座中,接通激光 电源后调节上下左右位置使光点对准光栅组中点后 用紧定螺丝固定。
2、在光栅后方安放好投射屏,观察到一组有序排列的衍射光斑,与激光器正对的光斑 为中央光斑,依次向两侧为一级、二级、三级…衍射光斑。
如图20-1所示。
观察光斑的大小及光强的变化规律。
3、 根据光栅衍射规律,光栅距D 与激光波长λ、衍射距离L 、中央光斑与一级光斑的间距S 存在下列的关系:(式中单位:L 、S 为mm ,λ为nm, D 为μm) 根据此关系式,已知固体激光器的激光波长为650nm ,用直尺量得衍射距离L 、光斑距S ,即可求得实验所用的光栅的光栅距。
4、 尝试用激光器照射用做莫尔条纹的光栅,测定光栅距,了解光斑间距与光栅距的关系。
SS L D 22+=λ5、 按照光栅衍射公式,已知光栅距、激光波长、光斑间距,就可以求出衍射距离L 。
将激光对准衍射光栅中部,在投射屏上得到一组衍射光斑,根据公式求出L 。

大学物理实验教案实验项目光栅的衍射教学目的1. 观察光的衍射现象,了解光栅分光的原理。
2. 测定光栅常数和光波波长。
实验原理当光射到光栅面上时,在透光狭缝处光线可透过,而在不透光处则不能透过。
若这些透光狭缝的宽为。
相邻狭缝间不透光部分的宽度为,,称为光栅常数。
本实验装置产生的光栅衍射是夫琅和费衍射,因为衍射屏(光栅)与光源及观察屏之间的距离均为无穷远(入射光栅的入射光和出射光栅的衍射光均为平行光)。
根据夫琅和费衍射理论,当波长为λ的平行光束投射到光栅平面上时,光波将在两个透光狭缝处发生衍射,所有狭缝的衍射光又彼此发生干涉,其结果是在透镜的焦平面上得到一排明亮分立的光谱线。
当平行光垂直入射时,相邻两缝对应点出射的光束的光程差为式中d为光栅常数,称为衍射角。
根据衍射光的干涉条件,当衍射角满足下式时则该衍射角方向上的光将会得到加强,叫做主极大,其它方向的光或者完全抵消,或者强度很小在焦平面上形成暗背景。
我们把时所对应的主极大分别称为中央(0级)极大,正负第一级极大,正负第二级极大,……。
如果入射光不是单色光,而是包含几种波长的光,对于同一级次光的波长λ不同,其衍射角也各不相同,于是复色光将被分解,从而在不同的地方形成不同颜色的光谱线。
但是,在中央主极大位置上,即K=0,处,各颜色的光仍重叠在一起,形成中央明条纹。
在中央条纹两侧对称分布着级光谱,各级光谱线都按波长大小的顺序依次排列成一组彩色谱线,对同一级谱线来说,λ越大,衍射角也越大,λ越小,越小,即彩色谱线排列是长波谱线在外侧,短波谱线在内侧。
如果用分光计测出,则当λ已知时d可求,当d已知时λ可求。
衍射角为其中为望远镜对准所要测定的正级谱线时,A,B两游标读数。
为望远镜对准所要测定的负级谱线时,A,B两游标读数。
教学重点与难点重点:1. 分光计的调节(望远镜调焦、望远镜光轴调节、平行光管调节等);2. 光栅放置位置的要求;3. 衍射角测量方法。
难点:1. 分光计调节;2. 游标盘读数。

实验十:光栅衍射一、实验目的1.观察光线通过光栅后的衍射光谱。
2.学会用光栅衍射测定光波波长的方法。
3.学会用光栅衍射原理测定光栅常数。
4.进一步熟悉分光计的调整和使用方法。
二、实验仪器分光计 光栅 钠光灯 平面反射镜三、实验原理光栅是有大量的等间隔、等宽度的狭缝平行放置组成的一种光学元件。
设狭缝宽度(透光部分)为a ,不透光部分为b ,则a b +为光栅常数。
设单色光垂直照射到光栅上,光透过各个狭缝后,向各个方向发生衍射,衍射光经过透镜后会聚后相互干涉,在焦平面上形成一系列的被相当宽的暗区分开的明亮条纹。
衍射光线与光栅平面的夹角称为衍射角。
设衍射角为θ的一束衍射光经透镜会聚到观察屏的点。
在P 点出现明条纹还是暗条纹决定于这束衍射光的光程差。
由于光栅是等宽、等间距,任意两个相邻缝的衍射光的光程差是相等的,两个相邻狭缝的衍射光的光程差为()sin a b θ+,如果光程差为波长的整数倍,在P 点就出现明条纹,即()sin a b k θλ+=±(0,1,2,)k =L 这就是光栅方程。
从上式可知,只要测出某一级的衍射角,就可计算出波长。
四、实验步骤1、调整分光计。
使望远镜、平行光管和载物台都处于水平状态,平行光管发出平行光。
2、安置光栅将光栅放在载物台上,让钠光垂直照射到光栅上。
可以看到一条明亮而且很细的零级光谱,左右转动望远镜观察第一、二级衍射条纹。
S 2S 1S 3()3()2()1()1()2()3G2φ12 φ22φ33.测定光栅衍射的第一、二级衍射条纹的衍射角θ,并记录。
五、数据记录级数 次数 左边衍射条纹 右边衍射条纹第二级'2()θ第一级'1()θ 0级 第一级1()θ 第二级2()θ 第 一 次 右边读数左边 读数衍射角 1θ=2θ=第 二 次 右边 读数左边 读数衍射角 1θ=2θ= 第 三 次右边读书左边 读书衍射角1θ=2θ='111[()θθθ=-(右边读数)+'11()θθ-(右边读数)]/4 '222[()θθθ=-(右边读数)+'22()θθ-(右边读数)]/4六、数据处理将上表中的1θ、2θ分别代入光栅方程()sin a b k θλ+=计算出6个波长,(1300a b mm +=) 1λ= 2λ= 3λ= 4λ= 5λ= 6λ= 计算平均波长:λ=绝对误差:λ∆= (取平均波长与6个波长的差中的最大者)相对误差:100%E λλλ∆=⨯=结果表示:()nm λλλ=±∆= nm 。

大学物理实验教案实验名称:光栅衍射法测定光波长 1 实验目的1)熟练分光计的调节。
2)理解光栅衍射现象;3)学习用光栅衍射法测定光的波长。
2 实验器材分光计、平面透射光栅、汞灯、平面反射镜3 实验原理3.1 实验原理光栅和棱镜一样,是重要的分光光学元件,已广泛应用在光栅光谱仪、光栅单色仪等。
光栅是一组数目极多的等宽、等距和平行排列的狭缝。
它分为透射光栅和反射光栅两种。
应用透射光工作的称为透射光栅,应用反射光工作的称为反射光栅。
现代制造光栅主要有刻划光栅、复制光栅和全息光栅等形式。
本实验用的是平面透射光栅。
描述光栅特征的物理量是光栅常数d ,其大小等于狭缝宽度a 与狭缝间不透光部分的宽度b 之和,即b a d +=,习惯上用单位毫米里的狭缝数目N 来描述光栅特性。
光栅常数d 与N 的关系为N d 1=(1)根据夫琅禾费衍射理论,波长为λ的平行光束垂直入射到光栅平面上时,透射光将形成衍射现象,即在一些方向上由于光的相互加强后光强度特别大,而其他的方向上由于光的相消后光强度很弱就几乎看不到光。
图40-1给出了形成光栅衍射的光路图。
如果入射光源为线光源,经过光栅后衍射图样为一些相距较大的锐利的色彩斑斓的明亮条纹组成。
而这些亮条纹1、光源2、狭缝3、凸透镜4、平面透射光栅5、光栅衍射光谱图40—1 实验原理示意图图40—2 汞灯的部分光栅衍射光谱示意图所在的方位由光栅方程所确定,方程为λφk d =sin ( 2,1,0±±=k ) (2)其中,d 为光栅常数,k 为衍射级别,λ为光波长,φ为衍射角它是光栅法线与衍射方位角之间的夹角。
由(2)式可见,同一级的衍射条纹,如果波长不同其衍射角不同,所以光栅具有分光功能。
图40-2为汞灯的部分光栅衍射光谱示意图。
光栅衍射现象是很容易观察到的,如果手头有一块光栅,可直接透过光栅观察某一光源就可看到衍射现象。
实验室中经常在分光计上利用光栅衍射现象来进行光波长或光栅常数的测量。


大学物理光栅衍射光栅衍射是大学物理中的一项重要内容,它涉及到光的波动性和干涉原理。
本文将从光栅衍射的原理、实验装置、实验方法和结论等方面进行介绍。
一、光栅衍射原理光栅是一种具有周期性结构的衍射器件,它由许多平行且等距的狭缝构成。
当光通过光栅时,会产生一系列明暗相间的衍射条纹,这种现象被称为光栅衍射。
光栅衍射的原理是基于光的波动性和干涉原理。
根据波动理论,光在通过光栅时会产生衍射现象,即光波偏离了直线传播路径。
同时,由于光波的干涉作用,不同狭缝产生的光波相互叠加,形成了明暗相间的衍射条纹。
二、实验装置实验装置主要包括光源、光栅、屏幕和测量工具等。
光源通常采用激光器或汞灯等高亮度光源,以便产生足够的光强度。
光栅是一块具有许多狭缝的透明板,狭缝的数目和间距可以根据实验需要进行选择。
屏幕用于接收衍射条纹,测量工具用于测量衍射条纹的间距和亮度。
三、实验方法实验时,首先将光源、光栅和屏幕按照一定距离放置,确保光束能够照射到光栅上并产生衍射条纹。
然后,通过调整光源的角度和位置,观察衍射条纹的变化。
同时,使用测量工具对衍射条纹的间距和亮度进行测量和记录。
为了获得准确的实验结果,需要进行多次测量并取平均值。
四、结论通过实验,我们可以得出以下1、光栅衍射现象是光的波动性和干涉原理的表现。
2、衍射条纹的间距和亮度受到光源角度和位置的影响。
3、通过测量衍射条纹的间距和亮度,可以推断出光源的角度和位置。
4、光栅衍射现象在光学测量和光学通信等领域具有广泛的应用价值。
大学物理光栅衍射是一个非常重要的实验内容,它不仅有助于我们理解光的波动性和干涉原理,还可以应用于实际生产和科学研究领域。
光,这一神奇的物理现象,是我们日常生活中无处不在的存在。
当我们看到五彩斑斓的世界,欣赏着阳光下波光粼粼的湖面,或是夜空中闪烁的星光,这一切都离不开光的衍射。
在大学物理中,光的衍射是理解波动光学和深入探究光本质的关键。
我们需要理解什么是光的衍射。


光栅衍射实验一、实验目的:1. 了解光栅的结构及光学原理;2. 学会搭建实验模型;3. 测定光波波长及光栅常数等。
二、实验原理:光栅(grating)是大量等宽、等间距的平行狭缝(或发射面)构成的光学元件。
一般常用的光栅是在玻璃片上刻出大量平行的刻痕,刻痕为不透光部分,两刻痕之间的光滑部分可以透光(相当于狭缝)。
这种利用透射光衍射的光栅称为透射光栅。
精制的光栅,在1mm宽度内刻有数百乃至数千条刻痕。
另外一类是利用两刻痕间的反射光衍射的光栅,如在镀有金属层的表面,上刻出许多平行刻痕,两刻痕间的光滑金属面可以反射光。
这种光栅称为反射光栅(常称为闪耀光栅)。
实际应用中,各类光学设备使用的光栅基本上都是反射光栅。
透射光栅和反射光栅的原理如图所示:3.而在我们的日常生活中,具有光栅特性的物品经常用到,例如手机,其显示屏就是正方形网格,每个小方格就是一个显示单元,网格越密,则显示分辨率越高。
这些整齐排列的小方格实际上就形成了反射光栅。
另一种物品就是光盘,它是我们常用的存储介质,从早期的CD、DVD等到现在的蓝光光盘,其存储密度越来越高。
它存储数据的方式是用极细的激光束,沿着近似同心圆环的螺旋形光轨,在光盘表面烧蚀出一个个的小坑,有坑的位置和无坑的位置分别对应0和1。
读取数据时,同样用激光束沿着光轨照射,有坑和无坑的位置反射光强不一样,这样就可以把数据读出来了。
我们可以看到,相邻的这些环状刻痕(光轨)实际上就形成了一个反射光栅(如虚线区域),两条刻痕之间的间距就是光栅常数d。
(实验的示意图)三、实验装置一支绿色激光笔,一个手机(荣耀5X,分辨率为1920×1080),一个CD光盘(高中物理必修一粤教版配套光盘),一条长为1.5m的米尺,一些泡沫塑料、白墙(如图所示)四、实验过程:1.对于手机,激光笔垂直于墙面、手机平行于墙面放置,微调手机平面,使得反射光回到激光笔出光口,然后再让反射光稍稍上移,使得衍射光斑能投射到墙面上,这样就保证光在水。
光栅衍射实验是大学物理实验中的一项基础实验,旨在让学生掌握光栅衍射的原理,熟悉分光计的调整与使用,以及光栅常数和光波波长的测量方法。
通过本实验,学生可以加深对光栅衍射规律的理解,为后续学习和研究光学理论奠定基础。
二、实验目的1. 熟悉分光计的调整与使用;2. 学习利用衍射光栅测定光波波长及光栅常数的原理和方法;3. 加深理解光栅衍射公式及其成立条件;4. 掌握光栅光谱的形成原理及特点;5. 熟悉光栅在光学仪器中的应用。
三、实验原理光栅是由一组数目很多的相互平行、等宽、等间距的狭缝(或刻痕)构成的,是单缝的组合体。
当一束单色光垂直照射在光栅上时,各狭缝的光线因衍射而向各方向传播,经透镜会聚相互产生干涉,并在透镜的焦平面上形成一系列明暗条纹。
光栅常数d是相邻两狭缝上相应两点之间的距离,是光栅基本常数之一。
光栅常数的倒数为光栅密度,即光栅的单位长度上的条纹数。
光栅衍射条纹的间距与光栅常数、光波波长和入射角有关。
根据光栅衍射公式,当光栅常数d、光波波长λ和入射角i确定时,衍射条纹的间距可以表示为:Δθ = λ/d其中,Δθ为衍射条纹的角间距。
四、实验仪器与设备1. 分光计:用于调节入射光的方向和测量衍射条纹的角度;2. 光栅:用于产生衍射条纹;3. 低压汞灯:提供单色光源;4. 平面镜:用于反射光;5. 望远镜:用于观察衍射条纹。
1. 将光栅放置在分光计的载物台上,调整分光计使光栅垂直于入射光;2. 调整低压汞灯,使光束垂直照射在光栅上;3. 调整望远镜,使观察者能够清晰地看到衍射条纹;4. 测量衍射条纹的角间距,计算光栅常数和光波波长;5. 改变入射角,观察光栅衍射条纹的变化。
六、实验结果与分析1. 通过实验,我们成功调整了分光计,使光束垂直照射在光栅上,并观察到清晰的衍射条纹;2. 根据光栅衍射公式,我们计算出光栅常数和光波波长,并与理论值进行了比较,误差在可接受范围内;3. 通过改变入射角,我们观察到光栅衍射条纹的变化,验证了光栅衍射公式的正确性。
大学物理实验报告实验名称光栅实验学号21XXXXX姓名XX辅导教师XXX实验报告开课实验室:3022022年 X 月 X 日一、实验目的1、熟练掌握分光仪的调节和使用2、加深对光栅衍射原理的理解,观察光栅衍射现象3、学会用透射光栅测定光栅常数和光波波长二、实验仪器J JT型分光仪(1台)、双面平面反射镜,透射光栅、低压汞灯及电源三、实验原理1、光栅定义光栅是一种根据多缝衍射原理制成的,将复色光分解成光谱的重要分光元件,由一系列等宽等间距的平行狭缝或刻痕组成,能产生亮度较大,间距较宽的光谱线,常用来精确地测定光波波长及进行光谱分析。
设缝宽为a,间距为b,则d=a+b 为光栅常数,是表征光栅特性的重要参数。
2、光栅方程当单色平行光垂直入射到衍射光栅上,通过每个缝的光都将发生衍射,不同缝的光彼此干涉,当衍射角满足光栅方程时,光波加强,产生主极大。
在光栅后加一会聚透镜,则在焦平面上形成等间隔对称分布的主明纹。
dsinΦ=kλ k=0,±1,±2,d为光栅常数,Φ为第k级衍射角,k是明纹级次,λ为单色光波长。
3、光栅光谱(1)当白光入射时,且满足Φ=0,k=0时,各色光重叠在一起,形成中央明纹,颜色与入射光颜色相同,仍为白光。
(2)在中央明纹两侧对称分布着k=0,±1,±2,级谱线,各级谱线相对于中央明纹从近到远,都按照短波到长波的顺序依次排列,形成一组彩色谱线。
4、测量原理(1)测量光栅常数d(2)测量紫光、黄1、黄2光的波长5、刻度盘读数游标卡尺0刻度的度盘位置是否已半度,如果过了要加上30分四、实验步骤1、调节分光仪(1)调节望远镜能接受平行光(2)调节望远镜光轴与仪器光轴垂直(3)调整平行光管能发出平行光,并垂直于仪器三轴2、光栅的调节(1)将光栅按图示放在载物台上,调节光栅平面与望远镜光轴垂直。
调节载物台的调平螺母a1,或a2,使十字像与分划板上准线重合。
大学物理实验报告
专业班级学号姓名记分
光栅衍射实验(实验名称)
实验目的:1. 了解光栅的结构及光学原理。
2. 学会搭建实验模型,选择合适的参数以便于测量。
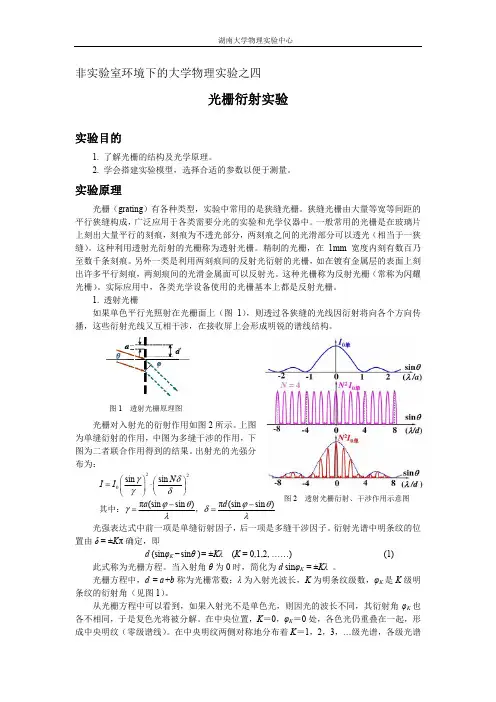
实验原理:d是光栅常数;θ是相对于光栅平面的入射角,φ是衍射角。
入射光投射到光栅平面后,其反射光因单个槽面的衍射和缝间的干涉形成光谱,谱线位置可同样由光栅方程给出:
d (sinφK ± sinθ)= ±Kλ(2)
当入射光与衍射光在法线的不同侧时上式取负号,否则取正号。
对于正入射,上式简化为:d sinφK = ±Kλ。
对于透射光栅和反射光栅,如果知道光栅常数d,通过测量衍射角φ,我们可以计算出光波长λ;反过来,已知光波长,通过测量衍射角,我们可以得到光栅常数d。
(自行调节所需空间)
实验装置与实验过程:
(包括照片)
数据记录:
(1)手机的屏幕分辨率为2310×1080
手机屏幕横向显示区域的宽度b=7cm
屏幕的每个显示单元的尺度为b/1080
屏幕作为光栅的光栅常数d=b/1080
测量水平方向上光斑的间距x=1.5cm
测量手机上的光入射点到衍射光斑中心点的距离L=120cm (2)测出±1级和±2级的衍射光斑之间的间距l2=25cm
光盘和墙面的距离为l1=29cm
数据处理及结果:
计算结果:衍射角φ = tanφ= x/L=0.0125
将测量结果代入公式d sinφ = λ
我们可以计算出激光波长λ=1.41×10-6cm
计算出衍射角:tanφ = l2/(2l1)
使用反三角函数才能得到φ的大小。
从公式d sinφK =λK即可得到光轨宽度d=3.57×10-6cm
(计算过程、结果、误差分析等)
实验体会或感想:
(1)通过实验了解了透射光栅和反射光栅的构成原理和区别
(2)学会了如何用手机估计出激光波长
思考题:
在斜入射的情况下,观察零级光斑时,可能会发现其附近存在较小的光斑,这也是一种干涉条纹。
怎么解释这个现象?
正入射时单缝衍射的零级和缝间干涉的零级重合,斜入射时不重合,单缝衍射中央最大值的位置从没
有色散的零级光谱转移到其他有色散的光谱级上。