2012年数学建模D题

程序问题一程序1A=xlsread('F:\数学建模第二期培训\第三题\新建文件夹 (2)\data',1,'b2:c611'); B=xlsread('F:\数学建模第二期培训\第三题\新建文件夹 (2)\data',2,'b2:c788'); C=xlsread('F:\数学建模第二期培训\第三题\新建文件夹 (2)\data',3,'b2:c271'); D=xlsread('F:\数学建模第二期培训\第三题\新建文件夹 (2)\data',4,'b2:c213'); E=xlsread('F:\数学建模第二期培训\第三题\新建文件夹 (2)\data',5,'b2:c96'); F=xlsread('F:\数学建模第二期培训\第三题\新建文件夹 (2)\data',6,'b2:c35'); G=xlsread('F:\数学建模第二期培训\第三题\新建文件夹 (2)\data',7,'b2:c21'); H=xlsread('F:\数学建模第二期培训\第三题\新建文件夹 (2)\data',8,'b2:c7');I=xlsread('F:\数学建模第二期培训\第三题\新建文件夹 (2)\data',9,'b2:c11'); J=xlsread('F:\数学建模第二期培训\第三题\新建文件夹 (2)\data',10,'b2:c30'); Ax=A(:,1);Ay=A(:,2);Bx=B(:,1);By=B(:,2);Cx=C(:,1);Cy=C(:,2);Dx=D(:,1);Dy=D(:,2);Ex=E(:,1);Ey=E(:,2);Fx=F(:,1);Fy=F(:,2);Gx=G(:,1);Gy=G(:,2);Hx=H(:,1);Hy=H(:,2);Ix=I(:,1);Iy=I(:,2);Jx=J(:,1);Jy=J(:,2);plot(Ax,Ay,'b+',Bx,By,'rh',Cx,Cy,'g*',Dx,Dy,'cd',Ex,Ey,'mo',Fx,Fy,'yp ',Gx,Gy,'kx',Hx,Hy,'b+',Ix,Iy,'b+',Jx,Jy,'rx')legend('A型孔','B型孔','C型孔','D型孔','E型孔','F型孔','G型孔','H型孔','I 型孔','J型孔')title('各种类型孔的分布图')xlabel('x')ylabel('y')grid on %画出分格线plot(Ax,Ay,'b+',Bx,By,'rh',Cx,Cy,'g*',Dx,Dy,'cd',Ex,Ey,'mo',Fx,Fy,'yp ',Gx,Gy,'kx',Hx,Hy,'b+',Ix,Iy,'b+',Jx,Jy,'rx')legend('A型孔','B型孔','C型孔','D型孔','E型孔','F型孔','G型孔','H型孔','I 型孔','J型孔')title('各种类型孔的分布图')xlabel('x')ylabel('y')grid on %画出分格线程序2m=10;Alpha=1;Beta=5;Rho=0.1;NC_max=200;Qx100;%为使程序运行速度更快，取蚂蚁数为10function[R_best,L_best,L_ave,Shortest_Route,Shortest_Length]=yiqunsuanfa(C1,N C_max,m,Alpha,Beta,Rho,QX)%% 主要符号说明%% C1 n个城市的坐标，n×2的矩阵%% NC_max 最大迭代次数%% m 蚂蚁个数%% Alpha 表征信息素重要程度的参数%% Beta 表征启发式因子重要程度的参数%% Rho 信息素蒸发系数%% QX 信息素增加强度系数%% R_best 各代最佳路线%% L_best 各代最佳路线的长度%%第一步：变量初始化n=size(C1,1);%*表示问题的规模（城市个数）D=zeros(n,n);%D表示完全图的赋权邻接矩阵for i=1:nfor j=1:nif i~=jD(i,j)=((C1(i,1)-C1(j,1))^2+(C1(i,2)-C1(j,2))^2)^0.5;elseD(i,j)=eps;endD(j,i)=D(i,j);endendEta=1./D; %Eta为启发因子，这里设为距离的倒数Tau=ones(n,n);%Tau为信息素矩阵Tabu=zeros(m,n);%存储并记录路径的生成NC=1;%迭代计数器R_best=zeros(NC_max,n);%各代最佳路线L_best=inf.*ones(NC_max,1);%各代最佳路线的长度L_ave=zeros(NC_max,1);%各代路线的平均长度while NC<=NC_max%停止条件之一：达到最大迭代次数%%第二步：将m只蚂蚁放到n个城市上Randpos=[];for i=1:(ceil(m/n))Randpos=[Randpos,randperm(n)];endTabu(:,1)=(Randpos(1,1:m))';%%第三步：m只蚂蚁按概率函数选择下一座城市，完成各自的周游for j=2:nfor i=1:mvisited=Tabu(i,1:(j-1));%已访问的城市J=zeros(1,(n-j+1));%待访问的城市P=J;%待访问城市的选择概率分布Jc=1;for k=1:nif length(find(visited==k))==0J(Jc)=k;Jc=Jc+1;endend%下面计算待选城市的概率分布for k=1:length(J)P(k)=(Tau(visited(end),J(k))^Alpha)*(Eta(visited(end),J(k))^Beta);endP=P/(sum(P));%按概率原则选取下一个城市Pcum=cumsum(P);Select=find(Pcum>=rand);to_visit=J(Select(1));Tabu(i,j)=to_visit;endendif NC>=2Tabu(1,:)=R_best(NC-1,:);end%第四步：记录本次迭代最佳路线L=zeros(m,1);for i=1:mR=Tabu(i,:);for j=1:(n-1)L(i)=L(i)+D(R(j),R(j+1));endL(i)=L(i)+D(R(1),R(n));endL_best(NC)=min(L);pos=find(L==L_best(NC));R_best(NC,:)=Tabu(pos(1),:);L_ave(NC)=mean(L);NC=NC+1%第五步：更新信息素Delta_Tau=zeros(n,n);for i=1:mfor j=1:(n-1)Delta_Tau(Tabu(i,j),Tabu(i,j+1))=Delta_Tau(Tabu(i,j),Tabu(i,j+1))+QX/ L(i);endDelta_Tau(Tabu(i,n),Tabu(i,1))=Delta_Tau(Tabu(i,n),Tabu(i,1))+QX/L(i) ;endTau=(1-Rho).*Tau+Delta_Tau;%%第六步：禁忌表清零Tabu=zeros(m,n);end%%第七步：输出结果Pos=find(L_best==min(L_best));Shortest_Route=R_best(Pos(1),:);Shortest_Length=L_best(Pos(1));subplot(1,2,1)DrawRoute(C1,Shortest_Route)subplot(1,2,2)plot(L_best)hold onplot(L_ave)程序3function DrawRoute(C1,R)N=length(R);scatter(C1(:,1),C1(:,2));hold onplot([C1(R(1),1),C1(R(N),1)],[C1(R(1),2),C1(R(N),2)])hold onfor ii=2:Nplot([C1(R(ii-1),1),C1(R(ii),1)],[C1(R(ii-1),2),C1(R(ii),2)])hold onendtitle('旅行商问题优化结果')程序4%求总的路程路线和时间function [Tabu montime]=sj5(M,X,Y,p,Ax,Ay,Bx,By,Cx,Cy,Dx,Dy,Ex,Ey,Fx,Fy,Gx,Gy,Hx,Hy,Ix, Iy,Jx,Jy)n=size(M,1);Tabu=1;tk=3;jk=1;for i=1:n-1tempt=[];for k=1:nif isempty(find(Tabu==k))&&length(find(Tabu==p(2, k)))>0, tempt=[tempt k];endendif length(tempt)==0temptendsum1=inf;for kk=temptif sum1>X(tk,kk)ik=kk;sum1=X(tk,ik);endendTabu=[Tabu ik];tk=ik;endTabu(1)=1;time=0;mon=0;tx=Tabu(1:end-1);ty=Tabu(2:end);for i=1:n-1mon=mon+X(tx(i),ty(i));if p(1,tx(i))~=p(1,ty(i))zty=abs(p(1,tx(i))-p(1,ty(i)));if zty<4st=zty;elsest=8-zty;endif Y(tx(i),ty(i))<18*st;time=time+18*zty;elsetime=time+Y(tx(i),ty(i));endelsetime=time+Y(tx(i),ty(i));endendDrawRoute(M,Tabu,Ax,Ay,Bx,By,Cx,Cy,Dx,Dy,Ex,Ey,Fx,Fy,Gx,Gy,Hx,Hy,Ix,I y,Jx,Jy)。

2012数学建模题目一、题目描述我们要研究如何让快递员在繁忙的城市中快速地交付每个快递。

城市中有许多道路和交通工具，也有许多商铺和住宅小区，城市规划和人口密度不同，道路交通情况也有所不同。

我们的目标是在保证交付时间的前提下，设计最优的配送路线，使得每个快递员在短时间内完成更多的配送任务。

二、问题分析1. 建立模型首先，我们需要建立一个数学模型来描述配送路线和任务量的关系。

我们可以用图论模型来表示城市的路网，用顶点表示城市中的交叉路口，用边表示两个交叉路口之间的道路。

我们还可以用图论中的最短路径算法来计算两个顶点之间的最短路径。

其次，我们需要考虑如何描述每个快递员的配送任务量。

我们可以设计一个算法来计算每个快递员要配送的快递数量和每个配送点的交通状况，然后根据这些信息来给每个快递员安排任务量。

最后，我们需要考虑如何设计一个最优化算法来解决问题。

我们可以利用模拟退火、遗传算法等优化算法，来寻找最优的配送路线和任务量分配方案。

2. 收集数据我们需要收集城市地形、道路交通情况、商铺和住宅小区分布等信息，并对这些信息进行处理和分析，以确定城市的规划和人口密度。

我们还需要收集快递业务的相关数据，包括快递递送和配送任务量、配送时限，以及快递员的工作时间和工作效率等信息。

3. 验证模型我们需要对模型进行验证和测试，以确定模型的可行性和准确性。

我们可以用现有的数据进行模拟实验，对模型的输出结果进行分析和比对。

四、模型求解1. 根据模型和数据，我们可以设计一个软件系统来实现快递配送路线和任务量分配的优化问题。

该系统需要包括以下模块：城市地图模块：用来绘制城市地图、路网和配送点。

路径规划模块：用来计算最短路径和最短时间的算法。

任务分配模块：用来计算每个快递员的配送任务量和时间分配方案。

优化算法模块：用来寻找最优的配送路线和任务量分配方案，包括模拟退火算法、遗传算法等。

2. 对该系统进行模拟实验，验证其可行性和准确性。

2012深圳杯数学建模竞赛D题——打孔机生产效能的提高-参考答案2012深圳杯数学建模竞赛D 题——打孔机生产效能的提高参考答案摘要本文对印刷电路板过孔的生产效益如何提高进行了研究。

打孔机在加工作业时，钻头的行进时间和刀具的转换时间是影响生产效益的两个因素。

在完成一个电路板的过孔加工时，钻头行进时间和刀具转换总时间越短，生产效益越高。

钻头行进总时间由钻头进行路线决定，而刀具转换总时间由线路板上由各孔的位置以及钻头行进方案决定。

钻头行进的路线的确定我们用遗传算法模拟。

令{}0,1ij e ∈，当1ij e =示(,)i j 在得到的最优路径上；当0ij e =表示(,)i j 不在得到的最优路径上。

通过这个变量建立起路线与费用的桥梁关系，进而写出总费用的表达式，建立最优模型，用遗传算法求解。

当打孔机设计成双钻头时，由于作业时各钻头相互独立，且有合作间距的限制，因此在解决双钻头最优作业方案时，我们在单钻头作业的基础上再加上另一个钻头作业所需的各种费用并增加约束条件，保证合作间距在要求范围之内。

关键词:遗传算法; 优化模型; 印刷线路板；生产效益一、问题的重述过孔是印刷线路板（也称为印刷电路板）的重要组成部分之一，过孔的加工费用通常占制板费用的30%到40%，打孔机主要用于在制造印刷线路板流程中的打孔作业。

本问题旨在提高某类打孔机的生产效能。

打孔机的生产效能主要取决于以下几方面：（1）单个过孔的钻孔作业时间，这是由生产工艺决定，为了简化问题，这里假定对于同一孔型钻孔作业时间都是相同的；（2）打孔机在加工作业时，钻头的行进时间；（3）针对不同孔型加工作业时，刀具的转换时间。

目前，实际采用的打孔机普遍是单钻头作业，即一个钻头进行打孔。

现有某种钻头，上面装有8种刀具a，b，c，… , h，依次排列呈圆环状，而且8种刀具的顺序固定，不能调换。

在加工作业时，一种刀具使用完毕后，可以转换使用另一种刀具。

相邻两刀具的转换时间是18 s，例如，由刀具a转换到刀具b所用的时间是18s，其他情况以此类推。

A基因识别问题及其算法实现一、背景介绍DNA 是生物遗传信息的载体，其化学名称为脱氧核糖核酸（Deoxyribonucleic acid ，缩写为DNA ）。

DNA 分子是一种长链聚合物，DNA 序列由腺嘌呤（Adenine, A ），鸟嘌呤（Guanine, G ），胞嘧啶（Cytosine, C ），胸腺嘧啶（Thymine, T ）这四种核苷酸（nucleotide ）符号按一定的顺序连接而成。

其中带有遗传讯息的DNA 片段称为基因（Gene ）（见图1第一行）。

其他的DNA 序列片段，有些直接以自身构造发挥作用，有些则参与调控遗传讯息的表现。

在真核生物的DNA 序列中，基因通常被划分为许多间隔的片段（见图1第二行），其中编码蛋白质的部分，即编码序列（Coding Sequence ）片段，称为外显子（Exon ），不编码的部分称为内含子（Intron ）。

外显子在DNA 序列剪接（Splicing ）后仍然会被保存下来，并可在图1真核生物DNA 序列（基因序列）结构示意图蛋白质合成过程中被转录（transcription ）、复制（replication ）而合成为蛋白质（见图2）。

DNA 序列通过遗传编码来储存信息，指导蛋白质的合成，把遗传信息准确无误地传递到蛋白质（protein ）上去并实现各种生命功能。

图2蛋白质结构示意图对大量、复杂的基因序列的分析，传统生物学解决问题的方式是基于分子实验的方法，其代价高昂。

诺贝尔奖获得者W.吉尔伯特（Walter Gilbert ，1932—；【美】，第一个制备出混合脱氧核糖核酸的科学家）1991年曾经指出：―现在，基于全部基因序列都将知晓，并以电子可操作的方式驻留在数据库中，新的生物学研究模式的出发点应是理论的。

一个科学家将从理论推测出发，然后再回到实验中去，追踪或验证这些理论假设。

‖ 随着世界人类基o DNA 序列外显子(Exon ) 内含子(Intron)DNA 序列蛋白质序列因组工程计划的顺利完成，通过物理或数学的方法从大量的DNA 序列中获取丰富的生物信息，对生物学、医学、药学等诸多方面都具有重要的理论意义和实际价值，也是目前生物信息学领域的一个研究热点。

2012年第五届“认证杯”数学中国数学建模网络挑战赛题目人机游戏中的数学建模关键词最小间距不等式分析人机游戏优化模型摘要：本题是以人机游戏“植物大战僵尸”为背景，问题一中，在第一阶段的基础上重新研究人机输赢的优化问题。

我们把10个方格从左到右依次标为①-⑩，将6朵阳光分为5种情况：（1）产生3株向日葵；（2）产生2株向日葵剩余2朵阳光；（3）6朵阳光产生1朵向日葵剩4朵阳光；（4）产生1株向日葵和1棵豌豆荚；（5）产生1棵豌豆荚剩余2朵阳光。

最终得出第（1）种情况，计算机永远赢；第（2）种情况，得出僵尸间隔为9步时，计算机不会赢；僵尸的间隔为5步，玩家忙碌；僵尸的间隔为3步，玩家更加忙碌，。

第（3）种情况，得出僵尸间的间隔为9步；第5个僵尸以前的僵尸间的间隔为9步,以后僵尸间的间隔为5步；第5个僵尸以前的僵尸间的间隔为9步,第5-13个僵尸间的间隔为5步，第13个僵尸以后僵尸间的间隔为3步。

第（4）种情况中，考虑第三颗种植植物为向日葵，第四颗种植植物为豌豆荚时，得出第1-6只僵尸间的间隔为7步，从第6个僵尸之后的僵尸间隔为5步。

考虑第三颗种植植物为豌豆荚，第四颗种植植物为豌豆荚时，得出第1-6只僵尸间的间隔为7步，从第7-16个僵尸之间的僵尸间隔为5步，从第16个僵尸之后的僵尸间隔为3步。

考虑第三颗种植植物为豌豆荚，第四颗种植植物为向日葵时，得出第1-6只僵尸间的间隔为7步，从第6个僵尸之后的僵尸间隔为5步。

第（5）种情况，得出僵尸之间的间隔不小于9步。

图文并茂，使我们的结果更加一目了然。

通过比较分析，最终得出，第1-6只僵尸间的间隔为7步，从第7-16个僵尸之间的僵尸间隔为5步，从第16个僵尸之后的僵尸间隔为3步。

此时，计算机永远不会赢，并且游戏紧张有趣。

问题二，我们构想了流水车间生产线的一个产品消毒问题。

从第1个格中放置生产设备，第2个格放置消毒设备，其中只有消毒设备的增加，进行分析讨论使得产品的A 产品的消毒效率高的间隔方案，得出分配方案为：第1-6个产品的间隔为6m，第7-18个产品的间隔为4.5m，第18-19个产品的间隔为6m，第19-36个产品的间隔为3m，第36-37个产品的间隔为5.25m，第37-60个产品的间隔为2.25m，第60-61个产品的间隔为2.55m，第61个以后的产品的间隔为1.8m。

2012年数学建模实训D题第一篇：2012年数学建模实训D题2012年数学建模实训D题高校硕士研究生招生指标分配问题高等学校研究生招生指标分配问题，对研究生的培养质量、学科建设和科研成果的取得有直接影响。

特别是2011年研究生招生改革方案中，将硕士研究生招生指标划分为学术型和专业型两类。

这一改革方案的实施，给研究生教育的发展带来发展机遇的同时，也给研究生招生指标分配的优化配置提出了新的思考。

附件的数据是某高校2007-2011年硕士研究生招生实际情况。

研究生招生指标分配主要根据指导教师的数量以及教师岗位进行分配。

其中教师岗位分为七个岗位等级（一级岗位为教师的最高级，七级岗为具备硕士招生资格的最低级）。

另外数据表还列出了各位教师的学科方向，2007-2011年的招生数，科研经费，发表中、英文论文数，专利数，获奖数，获得校、省优秀论文奖数量等信息。

请你参考有关文献、利用附件的数据建立数学模型，并解决下列问题。

1.由于统计数据的缺失，第18、103、110、123、150、168、274、324、335、352位教师的数据不完整，请你用数学模型的方法将这些缺失的数据补充完整。

2.以前的硕士研究生名额分配方案主要参考导师岗位级别进行分配。

请你以岗位级别为指标，分析每个岗位的招生人数、科研经费、发表中英文论文数、申请专利数、获奖数、获得优秀论文数量的统计规律，并给出合理的解释。

3.根据第二问的结论，提出更加合理的研究生名额分配方案，使得新方案既兼顾到岗位又能兼顾到其他因素，例如研究生的招生类型等，并要求用此方案对2012年的名额进行预分配。

4.如果在研究生招生指标分配当中，考虑到学科的特点和学科发展的需要，进行差异分配，请你设计调整方案，并用你的方案给出2012年的调整方案。

5.如果想把分配方案做得更加合理，你认为还需要哪些指标数据，用什么方法可以完成你的方案？请阐述你的思想。

第二篇：数学建模实训报告目录实训项目一线性规划问题及lingo软件求解……………………………1 实训项目二lingo中集合的应用………………………………………….7 实训项目三lingo中派生集合的应用……………………………………9 实训项目四微分方程的数值解法一………………………………………13 实训项目五微分方程的数值解法二……………………………………..15 实训项目六数据点的插值与拟合………………………………………….17 综合实训作品…………………………………………………………….18 每次实训课必须带上此本子，以便教师检查预习情况和记录实验原始数据。

2012年数学建模集训题目第1题A题图像分割技术研究在对图像的研究和应用中，人们往往仅对各幅图像中的某些部分感兴趣。

这些部分常称为目标或前景（其它部分称为背景），它们一般对应图像中特定的、具有独特性质的区域。

为了辨识和分析目标，需要将这些有关区域分离提取出来，在此基础上才有可能对目标进一步利用，如进行特征提取和测量。

图像分割就是指把图像分成各具特性的区域并提取出感兴趣目标的技术和过程。

这里特性可以是灰度、颜色、纹理等，目标可以对应单个区域，也可以对应多个区域。

图像分割是由图像处理进到图像分析的关键步骤，也是一种基本的计算机视觉技术。

这是因为图像的分割、目标的分离、特征的提取和参数的测量将原始图像转化为更抽象更紧凑的形式，使得更高层的分析和理解成为可能。

图像分割多年来一直得到人们的高度重视。

至今已提出了上千种各种类型的算法，而且近年来每年都有上百篇有关研究报道发表。

请研究下列两个问题：（1）建立适当的数学模型分别对图1和图2中的两幅图像进行分割，分离出飞机和帆船。

图1图2（2）对你的图像分割技术进行评价。

B题评价学术论文的重要性随着现代科学技术的发展，每年都有大量的学术论文发表。

如何衡量学术论文的重要性，成为学术界和科技部门普遍关心的一个问题。

有一种确定学术论文重要性的方法是考虑论文被引用的状况，包括被引用的次数以及引用论文的重要性程度。

假如我们用有向图来表示论文引用关系，“A”引用“B”可用下图表示：现有A、B、C、D、E、F六篇学术论文，它们的引用关系如下：请你解决如下两个问题：1）设计依据上述引用关系排出六篇论文重要性顺序的模型与算法，并给出用该算法排得的结果；2）将算法推广到任意N 篇论文的情况，并评价你的排序方法的优缺点。

第2题A 题 在油价波动情况下的生产计划某市某厂按合同规定须于当年每个季度末分别提供A 万,B 万,C 万,D 万台同一规格的机器。

已知该厂各季度的生产能力及生产每台柴油机的成本如表1所示，如果生产出的产品当季不交货，每万台积压一个季度需储存、维护等费用0.15 万元。

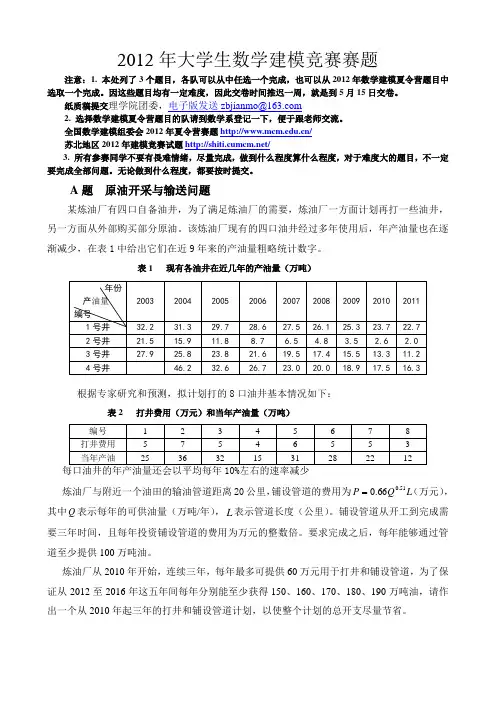
2012年大学生数学建模竞赛赛题注意：1. 本处列了3个题目，各队可以从中任选一个完成，也可以从2012年数学建模夏令营题目中选取一个完成。

因这些题目均有一定难度，因此交卷时间推迟一周，就是到5月15日交卷。

纸质稿提交理学院团委，电子版发送zbjianmo@2. 选择数学建模夏令营题目的队请到数学系登记一下，便于跟老师交流。

全国数学建模组委会2012年夏令营赛题/苏北地区2012年建模竞赛试题/3. 所有参赛同学不要有畏难情绪，尽量完成，做到什么程度算什么程度，对于难度大的题目，不一定要完成全部问题。

无论做到什么程度，都要按时提交。

A题原油开采与输送问题某炼油厂有四口自备油井，为了满足炼油厂的需要，炼油厂一方面计划再打一些油井，另一方面从外部购买部分原油。

该炼油厂现有的四口油井经过多年使用后，年产油量也在逐渐减少，在表1中给出它们在近9年来的产油量粗略统计数字。

表1 现有各油井在近几年的产油量（万吨）根据专家研究和预测，拟计划打的8口油井基本情况如下：表2 打井费用（万元）和当年产油量（万吨）每口油井的年产油量还会以平均每年10%左右的速率减少炼油厂与附近一个油田的输油管道距离20公里，铺设管道的费用为L.0（万元），QP51.066其中Q表示每年的可供油量（万吨/年），L表示管道长度（公里）。

铺设管道从开工到完成需要三年时间，且每年投资铺设管道的费用为万元的整数倍。

要求完成之后，每年能够通过管道至少提供100万吨油。

炼油厂从2010年开始，连续三年，每年最多可提供60万元用于打井和铺设管道，为了保证从2012至2016年这五年间每年分别能至少获得150、160、170、180、190万吨油，请作出一个从2010年起三年的打井和铺设管道计划，以使整个计划的总开支尽量节省。

B稀土资源的开发与储备问题囤积中国廉价稀土。

目前美国90%以上稀土由中国进口，美国政府为保护本土的稀土资源采取了严厉的强制措施，不但完全停止出口，还封存矿山。

机器人避障问题摘要我们了解到我们需要解决的是机器人从O→A、O→B、O→C和O→A→B→C→O的最短路径以及O→A的最短时间问题，但与传统的问题相比因为有了障碍物的制约使得部分区域无法通过，而且物体的运动轨迹也会对其速度造成制约，联系现实生活我们知道对于无法以最短直线路径通过时如果两点间有一根足够长的绳子，在绕开障碍物及其所影响的范围后绳子绷紧状态下所形成的轨迹即为最短路径，在最短的路径和最快的速度间找制约点可获得最短时间，该题时间制约因素为。

受此启发，在分析问题后我们建立了数学模型来合理解决如何使机器人避障的优化问题。

针对问题一；问题一中O→A可简化为两点避开单个障碍物的问题、O→B、O→C为两点避开多个障碍物的问题、对于O→A→B→C→O是一个回路的多点避开多个障碍物的问题，运用几何的求解方式证明。

针对问题二；问题二是时间最优的问题，我假设存在个半径为最优时间半径，然后我们找到个最优圆弧圆心的位置，圆心在两点连线为X轴的最高障碍点作X轴的该条垂线上。

关键词最短路径最优化模型几何求解最短时间一、问题重述1.1、基本情况:在给定的平面场景中，要求机器人绕开障碍物到达指定的目标点（要求目标点与障碍物的距离至少超过10个单位）。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

1.2、相关信息：(1) 机器人直线行走的最大速度为50=v 个单位/秒。

(2) 机器人转弯时，最大转弯速度为21.0100e1)(ρρ-+==v v v ，其中ρ是转弯半径。

如果超过该速度，机器人将发生侧翻，无法完成行走。

1.3、需要解决的问题：(1) 机器人从O(0, 0)出发，O→A 、O→B 、O→C 和O→A→B→C→O 的最短路径。

（请先阅读“全国大学生数学建模竞赛论文格式规范”）A题葡萄酒的评价确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。

每个评酒员在对葡萄酒进行品尝后对其分类指标打分，然后求和得到其总分，从而确定葡萄酒的质量。

酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系，葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。

附件1给出了某一年份一些葡萄酒的评价结果，附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。

请尝试建立数学模型讨论下列问题：1. 分析附件1中两组评酒员的评价结果有无显著性差异，哪一组结果更可信？2. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。

3. 分析酿酒葡萄与葡萄酒的理化指标之间的联系。

4．分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响，并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量？附件1：葡萄酒品尝评分表（含4个表格）附件2：葡萄和葡萄酒的理化指标（含2个表格）附件3：葡萄和葡萄酒的芳香物质（含4个表格）（请先阅读“全国大学生数学建模竞赛论文格式规范”）B题太阳能小屋的设计在设计太阳能小屋时，需在建筑物外表面（屋顶及外墙）铺设光伏电池，光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用，并将剩余电量输入电网。

不同种类的光伏电池每峰瓦的价格差别很大，且每峰瓦的实际发电效率或发电量还受诸多因素的影响，如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式（贴附或架空）等。

因此，在太阳能小屋的设计中，研究光伏电池在小屋外表面的优化铺设是很重要的问题。

附件1-7提供了相关信息。

请参考附件提供的数据，对下列三个问题，分别给出小屋外表面光伏电池的铺设方案，使小屋的全年太阳能光伏发电总量尽可能大，而单位发电量的费用尽可能小，并计算出小屋光伏电池35年寿命期内的发电总量、经济效益（当前民用电价按0.5元/kWh计算）及投资的回收年限。

2012年第五届认证杯数学中国数学建模网络挑战赛A 题：蜘蛛网1 第一阶段问题世界上生存着许多种类的蜘蛛，而其中的大部分种类都会通过结网来进行捕食。

请你建立合理的数学模型，说明蜘蛛网织成怎样的结构才是最合适的。

2012年第五届认证杯数学中国数学建模网络挑战赛B 题：白屋顶计划1 第一阶段问题夏天的城市气温往往格外炎热，这被称为热岛效应。

有专家提出，将城市建筑的屋顶漆成白色，减小对阳光的吸收率，可以使城市的气温降低，进而达到节能和环保的效果。

包括美国能源部长、诺贝尔物理学奖获得者朱棣文在内的一些专家都对这个方案表示支持，但同时也有一些反对意见。

请你建立合理的数学模型，评估“白屋顶计划”对降低城市热岛效应起到的作用。

2012年第五届认证杯数学中国数学建模网络挑战赛C 题：碎片化趋势下的奥运会商业模式从1984 年的美国洛杉矶奥运会开始，奥运会就不在成为一个“非卖品”，它在向观众诠释更高更快更强的体育精神的同时，也在攫取着巨大的商业价值，它与电视结盟，在运动员入场仪式、颁奖仪式、热门赛事、金牌榜发布等受关注的时刻发布赞助商广告，它在每个行业中仅挑选一家奥运全球合作伙伴，这就是“Top 赞助商”的前身。

这个模式经过28 年的发展之后，现在已经是商业社会里最重要的公司的展示舞台。

品牌选择奥运会的理由，是因为这里凝聚了观众的大量时间。

他们希望在观众关注比赛的同时也注意到自己的品牌和产品，而Top 赞助商们，则可以获得在电视奥运频道里排除行业里其他竞争对手广告的特权。

每届奥运会，Top 赞助商的赞助费用都以10% 至20% 的速度在增长。

2008 年，北京奥运会全球合作伙伴最低赞助为6000 万美元，2012 年伦敦奥运会就变成8000 万美元。

这种模式被奥运会主办方发挥到了极致，宣传费用的门槛把绝大多数企业排除在了奥运会之外。

但是越来越多的企业不甘心错过奥运会这个吸引大众眼球的宣传机会，他们在寻找新的新闻传播渠道。

全国研究生数学建模竞赛历届竞赛题目第一届2004 年题目（共4 个题目）2004 年A 题发现黄球并定位2004 年B 题实用下料问题2004 年C 题售后服务数据的运用2004 年D 题研究生录取问题第二届2005 年题目（共4 个题目）2005 年A 题Highway Traveling time Estimate and Optimal Routing2005 年B 题空中加油2005 年C 题城市交通管理中的出租车规划2005 年D 题仓库容量有限条件下的随机存贮管理第三届2006 年题目（共4 个题目）2006 年A 题Ad Hoc 网络中的区域划分和资源分配问题2006 年B 题确定高精度参数问题2006 年C 题维修线性流量阀时的内筒设计问题2006 年D 题学生面试问题第四届2007 年题目（共4 个题目）2007 年A 题建立食品卫生安全保障体系数学模型及改进模型的若干理论问题2007 年B 题械臂运动路径设计问题2007 年C 题探讨提高高速公路路面质量的改进方案2007 年D 题邮政运输网络中的邮路规划和邮车调运第五届2008 年题目（共4 个题目）2008 年A 题汶川地震中唐家山堪塞湖泄洪问题2008 年B 题城市道路交通信号实时控制问题2008 年C 题货运列车的编组调度问题2008 年D 题中央空调系统节能设计问题第六届2009 年题目（共4 个题目）2009 年A 题我国就业人数或城镇登记失业率的数学建模2009 年B 题枪弹头痕迹自动比对方法的研究2009 年C 题多传感器数据融合与航迹预测2009 年D 题110 警车配置及巡逻方案第七届2010 年题目（共4 个题目）2010 年A 题确定肿瘤的重要基因信息2010 年B 题与封堵渍口有关的重物落水后运动过程的数学建模2010 年C 题神经元的形态分类和识别2010 年D 题特殊工件磨削加工的数学建模第八届2011 年题目（共4 个题目）2011 年A 题基于光的波粒二象性一种猜想的数学仿真2011 年B 题吸波材料与微波暗室问题的数学建模2011 年C 题小麦发育后期茎轩抗倒性的数学模型2011 年D 题房地产行业的数学建模第九届2012 年题目（共4 个题目）2012年A 题基因识别问题及其算法实现2012年B 题基于卫星无源探测的空间飞行器主动段轨道估计与误差分析2012年C 题有杆抽油系统的数学建模及诊断2012年D 题基于卫星云图的风矢场（云导风）度量模型与算法探讨第十届2013 年题目（共6 个题目）2013年A题变循环发动机部件法建模及优化2013年B题功率放大器非线性特性及预失真建模2013年C题微蜂窝环境中无线接收信号的特性分析2013年D题空气中PM2.5问题的研究attachment2013年E题中等收入定位与人口度量模型研究2013年F题可持续的中国城乡居民养老保险体系的数学模型研究第十一届2014 年题目（共 5 个题目）2014年A题小鼠视觉感受区电位信号(LFP)与视觉刺激之间的关系研究2014年B题机动目标的跟踪与反跟踪2014年C题无线通信中的快时变信道建模2014年D题人体营养健康角度的中国果蔬发展战略研究2014年E题乘用车物流运输计划问题第十二届2015 年题目（共 6 个题目）2015年A题水面舰艇编队防空和信息化战争评估模型2015年B题数据的多流形结构分析2015年C题移动通信中的无线信道“指纹”特征建模2015年D题面向节能的单/多列车优化决策问题2015年E题数控加工刀具运动的优化控制2015年F题旅游路线规划问题数据来源：/6/list.htm。

福建师范大学第九届大学生数学建模竞赛暨2012年全国大学生数学建模竞赛选拔赛题目注意：1、请在A题和B题中任选一道题作答；2、答卷以论文方式提交，书写格式参照正式发表的论文，包括论文名、作者姓名、中文摘要、内容（问题分析、模型假设、模型建立、模型求解、模型验证等方面）、参考文献（如果是引用互联网上的文章也要注明网址）和附录（例如计算过程中编写的程序）；3、答卷统一使用WORD编排，按照比赛注意事项的要求发送电子版论文，并上交用A4规格的复印纸打印的纸质版论文。

4、请在论文中注明学院、专业、学号、联系电话、电子邮箱。

A题汽车公司的生产计划与决策某汽车公司拟生产一批新款式的轿车，初步确定有以下几种配置方案可供选择（括号内为成本价）：发动机E 2.0L（e1=2.1万元），1.8 L（e2=1.7万元），1.6L（e3=1.5万元）换挡D 手动（d1=1.3万元）自动（d2=2.2万元）天窗W 无天窗（w1=0万元）手动天窗（w2=0.5万元），电动天窗（w3=0.8万元）整车的其他成本是C0=8万元。

（1）各种车型的预计售价和市场需求量如表1，试确定每一种车型的生产成本和预计销售利润。

（2）如果该汽车公司有10条生产线，每条生产线每天工作8小时，试问应该如何安排生产计划可使每月（按30天计算）所获利润最大？（3）公司市场情报部门预测到未来一段时期各种车型的市场需求量会增加一倍，故考虑将生产线由原来的10条增加到15条，此外，考虑到同时生产两种或两种以上配置的轿车的成本较高，公司决定只选择一种配置车型进行生产，同时将生产线由10条增加到15条，此时应该如何安排生产计划可使每月（按30天计算）所获利润最大？（4）由于问题（3）中的市场需求是一个预测值，随着市场行情的变化，实际需求量与该值可能有一定的误差。

因此按预测数据做出的生产计划可能有一定的风险因素。

进一步考虑预期市场的销售量是按一定的概率分布来实现的，具体的概率分布如表2所示。

数学建模网络挑战赛承诺书我们仔细阅读了第五届“认证杯”数学中国数学建模网络挑战赛的竞赛规则。

我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们允许数学中国网站()公布论文，以供网友之间学习交流，数学中国网站以非商业目的的论文交流不需要提前取得我们的同意。

我们的参赛队号为：2153参赛队员(签名) ：队员1：董文静队员2：唐业吉队员3：周亮参赛队教练员(签名)：王文静参赛队伍组别：专科组数学建模网络挑战赛编号专用页参赛队伍的参赛队号：（请各个参赛队提前填写好）：2153竞赛统一编号（由竞赛组委会送至评委团前编号）：竞赛评阅编号（由竞赛评委团评阅前进行编号）：2012年第五届“认证杯”数学中国数学建模网络挑战赛题 目 人机游戏中的数学模型关 键 词 合理假设 死亡距离摘 要：本文首先对僵尸的行进进行合理假设，然后通过对比依据题目条件所产生的多种方案确定出最优化方案。

计算出方案中植物个数和僵尸间隔时间。

问题二：有必要给出对僵尸行走简化假设和定量描述，通过计算僵尸死亡的具体数字合理假设出僵尸走9步即死亡，以n s 来描述第n 个僵尸从出现在格子最右边到其死亡的距离，这个距离()()991+--=d n s n 一定会小于等于8个格子的距离，从而计算出一个豌豆荚第时僵尸之间的最小间隔为9步的时间才能使计算机永远不会获胜。

问题三：当豌豆荚的数量()x 改变时()xd x n s n 991+⎪⎭⎫ ⎝⎛--=这样僵尸的死亡距离与豌豆荚和僵尸之间的间隔成为一定的函数关系。

>> axis([0,800,0,800]);grid onhold ont=deg2rad(0:360);%角度化为弧度。

x=80*cos(t)+550;y=80*sin(t)+450;plot(x,y);hold on;axis equal;%使x，y轴精度相同fill(x,y,'b') %用蓝色填充该圆形。

%图2结束。

hold ont=deg2rad(0:360);%角度化为弧度。

x=10*cos(t)+300;y=10*sin(t)+400;plot(x,y);hold on;axis equal;%使x，y轴精度相同x=10*cos(t)+500;y=10*sin(t)+400;plot(x,y);hold on;axis equal;%使x，y轴精度相同fill(x,y,'g') %用绿色填充该圆形。

x=10*cos(t)+500;y=10*sin(t)+600;plot(x,y);hold on;axis equal;%使x，y轴精度相同fill(x,y,'g') %用绿色填充该圆形。

x=10*cos(t)+300;y=10*sin(t)+600;plot(x,y);hold on;axis equal;%使x，y轴精度相同fill(x,y,'g') %用绿色填充该圆形。

hold on;rectangle('Position',[0,0,5,3],...'LineWidth',2,'LineStyle','-');x=[300 500 500 300];y=[400 400 600 600];fill(x,y,'g')hold onx=[300 500 500 300];y=[400 400 390 390];fill(x,y,'g')hold onx=[500 500 510 510];y=[400 600 600 400];fill(x,y,'g')hold onx=[500 300 300 500];y=[600 600 610 610];fill(x,y,'g')hold onx=[300 300 290 290];y=[400 600 600 400];fill(x,y,'g')hold on%图1结束。