第章 钢梁计算原理
- 格式：doc
- 大小：2.39 MB
- 文档页数：56
下载文档原格式
合集下载
钢结构梁柱章节计算题分解课件
THANKS
感谢观看
详细描述：在钢结构梁柱设计中，稳定性和抗震性能是两个重要的问题 。解决这些问题可以确保梁柱在承受荷载和地震作用时能够保持稳定，
避免发生失稳或破坏。在解决这些问题时，应考虑以下几点
1. 进行详细的结构分析，确定梁柱的应力分布、变形情况以及稳定性指 标。
梁柱的稳定性和抗震性能问题及解决方案
2. 根据结构分析结果，采取有效的稳定性加强措施，如增加支撑、加强连接等。
梁柱的节点设计及优化
2. 确保节点连接的可靠性，采 取有效的连接措施，如焊接、 螺栓连接等。
3. 考虑节点的可施工性，尽量 采用易于加工和安装的节点形 式。
4. 对于大型梁柱节点，应进行 详细的力学分析，确保节点的 承载能力和稳定性满足要求。
梁柱的稳定性和抗震性能问题及解决方案
总结词：解决梁柱的稳定性问题和抗震性能问题，确保结构安全可靠。
梁柱的节点设计及优化
详细描述：梁柱节点的设计及优化是钢结构设计中的 重要环节。节点设计应确保传力路径清晰、连接可靠 ，同时还应考虑施工方便、经济合理等因素。在节点 设计及优化时，应考虑以下几点
总结词：合理设计梁柱节点，确保传力路径清晰、连 接可靠。
1. 根据梁柱的受力特点和连接要求，选择合适的节点 形式和连接方式。
钢柱
分为实腹柱和格构柱，具有承载 力高、自重轻、安装方便等特点 。
梁柱的计算模型及假定
01
02
03
简支梁
采用静力平衡条件，计算 跨中弯矩和支座反力。
连续梁
采用挠曲线方程，计算各 跨内力和支座反力。
悬臂梁
采用静力平衡条件，计算 悬臂端弯矩和固定端反力 。
梁柱的受力分析
弯曲变形
由于荷载作用产生弯矩， 导致梁柱轴线上产生弯曲 变形。
第5章 钢梁计算原理
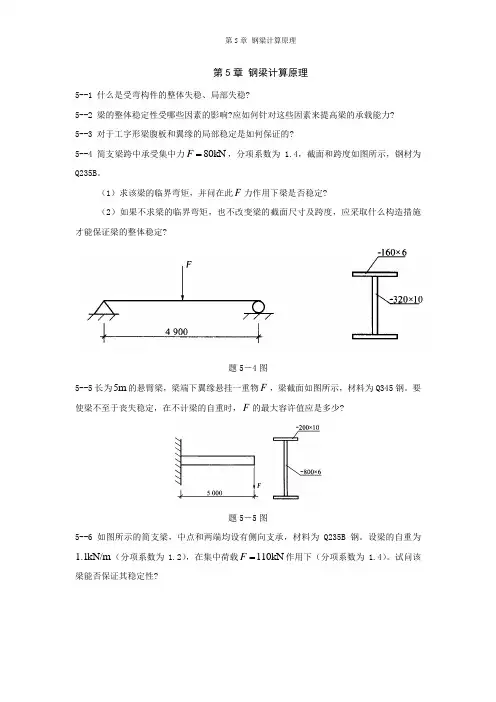
第5章钢梁计算原理5--1 什么是受弯构件的整体失稳、局部失稳?5--2 梁的整体稳定性受哪些因素的影响?应如何针对这些因素来提高梁的承载能力?5--3 对于工字形梁腹板和翼缘的局部稳定是如何保证的?F=，分项系数为 1.4，截面和跨度如图所示，钢材为5--4简支梁跨中承受集中力80kNQ235B。
（1）求该梁的临界弯矩，并问在此F力作用下梁是否稳定?（2）如果不求梁的临界弯矩，也不改变梁的截面尺寸及跨度，应采取什么构造措施才能保证梁的整体稳定?题5－4图5--5长为5m的悬臂梁，梁端下翼缘悬挂一重物F，梁截面如图所示，材料为Q345钢。
要使梁不至于丧失稳定，在不计梁的自重时，F的最大容许值应是多少?题5－5图5--6如图所示的简支梁，中点和两端均设有侧向支承，材料为Q235B钢。
设梁的自重为F=作用下（分项系数为1.4）。
试问该1.1kN/m（分项系数为1.2），在集中荷载110kN梁能否保证其稳定性?题5－6图5--7一跨度为9m 的工作平台简支梁，受均布荷载1q 为35kN/m （分项系数为1.2），2q 为36kN/m （分项系数为1.4），采用Q23B 钢，截面尺寸如图所示。
试验算其强度。
题5－7图5--8某焊接工字形简支梁，荷栽及截面情况如图所示。
其荷载分项系数为1.4，材料为Q235B ，300kN F =，集中力位置处设置侧向支承。
试验算其强度、整体稳定是否满足要求?题5－8图5--9某跨度为3m 的工作平台简支梁，承受均布荷载28kN/m （设计荷载），若采用普通轧制工字钢I18，跨中无侧向支承。
试验算其强度、整体稳定和刚度。
5--10某Q235钢简支梁剖面如图所示，自重为0.9kN/m 1.2⨯，承受悬挂集中荷载110kN 1.4⨯，试验算在下列情况下梁截面能否满足整体稳定要求：（1）梁在跨中无侧向支承，集中荷栽从梁顶作用于上翼缘；（2）同（1）但改用Q345钢；（3）同（1）但采取构造措施使集中荷载悬挂于下翼缘下面；（4）同（1）但跨度中点增设上翼缘侧向支承。
钢梁的长度计算规则
钢梁的长度计算规则钢梁是工业和建筑领域中常用的一种结构材料。
在钢结构设计中，精确计算钢梁长度是至关重要的。
在本文中，我们将介绍如何计算钢梁长度的规则和方法。
1. 钢梁长度的定义在结构设计中，钢梁长度指的是两个支撑节点之间的距离。
这个距离可以通过测量支撑节点之间的距离来确定，或通过计算公式来确定。
2. 计算钢梁长度的公式钢梁长度的计算公式通常是根据菲涅尔动态光学原理得出的。
菲涅尔动态光学原理是指在光线经过钢材时，由于光的折射和反射作用，使得圆锥形光束发生了扭曲。
这种扭曲是由钢材的物理特性和光线的特性共同决定的。
根据这个原理，我们可以得出计算钢梁长度的公式：L = (n+1/2)λ/√σ其中，L表示钢梁的长度，n表示菲涅尔圆纹的数量，λ表示波长，σ表示材料的弹性模量。
这个公式可以帮助工程师精确地计算钢梁的长度，以确保在实际施工中能够达到预期的效果。
3. 钢梁长度计算的注意事项在计算钢梁长度时，需要注意以下几点：（1）弹性模量：弹性模量的值取决于钢材的材质和厚度，不同的钢材和不同的厚度具有不同的弹性模量。
（2）波长：波长指的是钢材中的光线波长，通常使用红光波长。
（3）支撑节点：计算钢梁长度时，需要测量支撑节点之间的距离，确保计算结果准确。
（4）精度：在计算钢梁长度时，需要使用高精度的测量仪器和计算工具，确保结果的准确性。
4. 总结钢梁长度的计算是结构设计中至关重要的一环。
在进行钢结构设计时，需要仔细考虑材料的物理特性、计算公式和测量仪器等因素，以确保计算出的钢梁长度是准确的。
通过本文的介绍，我们相信您已经对钢梁长度计算的规则和方法有了更好的了解。
钢结构梁简易计算
钢结构梁简易计算在建筑和工程领域，钢结构梁的设计和计算是至关重要的环节。
它不仅关系到结构的安全性和稳定性，还直接影响着整个工程的成本和质量。
对于一些不太复杂的钢结构梁，我们可以通过一些简易的计算方法来初步评估其承载能力和性能。
接下来，就让我们一起探讨一下钢结构梁的简易计算方法。
首先，我们需要了解钢结构梁的基本组成和受力情况。
钢结构梁通常由钢材制成，其截面形状有多种，如工字梁、H 型梁、箱型梁等。
在承受荷载时，梁会产生弯曲应力、剪应力和局部承压应力等。
对于弯曲应力的计算，我们可以使用经典的弯曲公式。
假设梁受到一个均布荷载 q，跨度为 L，那么梁的最大弯矩 M 可以表示为 M ＝qL²/8。
然后，根据梁的截面特性，如惯性矩 I 和截面模量 W，弯曲应力σ 可以通过公式σ ＝ M ／ W 计算得出。
接下来是剪应力的计算。
在均布荷载作用下，梁的最大剪力 V 为qL/2。
剪应力τ 可以通过公式τ ＝ V S ／ I b 计算，其中 S 是截面的静矩，b 是截面的宽度。
除了上述的基本应力计算，还需要考虑梁的局部承压应力。
当梁上有集中荷载作用时，在荷载作用处会产生局部承压应力。
这个应力的大小与荷载大小、荷载作用面积以及钢材的强度等因素有关。
在进行钢结构梁的简易计算时，还需要注意一些实际的问题。
例如，钢材的强度取值要根据其材质和规格来确定。
同时，要考虑梁的支撑条件，是简支梁、悬臂梁还是连续梁，不同的支撑条件会影响梁的内力分布。
另外，在计算过程中，还需要考虑安全系数。
安全系数是为了保证结构在使用过程中的安全性和可靠性，通常会根据相关的规范和标准来选取。
让我们通过一个具体的例子来进一步说明钢结构梁的简易计算过程。
假设我们有一个跨度为 6 米的简支工字钢梁，承受均布荷载 5kN/m，钢材采用 Q235，我们来计算其弯曲应力和剪应力是否满足要求。
首先，计算最大弯矩 M ＝ 5×6²/8 ＝ 225 kN·m。
梁钢筋的计算原理
为了防止梁被扭曲，我们需要给梁配置侧面纵筋。有侧面纵筋就一定有固定侧面纵筋的拉筋。
4、当主梁遇到次梁时怎么办?
当主次梁相交时，主梁要承担次梁的荷载，要在主梁上配置吊筋或附加箍筋。
5、梁钢筋种类总结梁的钢筋包括纵筋、箍筋、拉筋、吊筋几种形式，纵筋又包括上下贯通筋、上部支座负筋、侧面纵筋、箍筋包括2肢箍、4肢箍等多种形式
梁钢筋的计算原理
一、梁钢筋的计算原理
1、梁的纵筋怎样配置最合理?
在拉力较小的地方配置钢筋少些,拉力较大的地方配置钢筋多些。
2、怎样固定部贯通筋用以固定梁中间箍筋的上部;如果出现2肢箍以上的多肢箍筋还需要配置架立筋来固定中间箍筋。
3、当梁截面特别高时怎么办?
二、梁钢筋的平法标注KL1(2)300×700集中标注A10@100/200(4) 2B25+(2A12);2B25 G4A16两端支座处6B25 4/2中间支座处6B25 4/2原位标注梁下部6B25 2(-2)/4吊筋标注2B18附加箍筋8A10(4)表示1号框架梁、两跨、截面宽为300，截面高为700表示箍筋为圆10的钢筋，加密区间距为100，非加密区间距为200，4肢箍前面的2B25表示梁的上部贯通筋为两根二级25的钢筋，（2B12）表示两跨的上部无负筋区布置两根圆12的架立筋，后面的2B25表示梁的下部贯通筋为两根二级25的钢筋表示梁的侧面设置4根二级16的构造纵筋，两侧各为2根。表示梁的端支座有6根二级25的钢筋，分两排布置，其中上排为4根，下排为2根，因为上排有两根贯通筋，所有上排只有两根二级25的属于支座负筋。表示梁的中间支座有6根二级25的钢筋，分两排布置，其中上排为4根，下排为2根，因为上排有两根贯通筋，所有上排只有两根二级25的属于支座负筋。，中间支座如果只标注一边另一边不标，说明两边的负筋布筋一致。表示梁的下部有6根二级25的钢筋，分两排布置，其中上排为2根，下排为4根；上排两根不伸入支座，从集中标注可以看出，下部有两根贯通筋，所以下排只有2根二级25的是非贯通筋。表示次梁处布置两根二级18的钢筋做为吊筋。表示梁的次梁处增加8根圆10的4肢箍楼层框架梁钢筋的计算原理（一）、纵筋长度）、纵筋长度1、上下贯通筋、楼层框架梁上下贯通筋长度＝通跨净长L净+伸入左端支座内长度+伸入右端支座内长度+(搭接长度×搭接个数)楼层框架梁上下贯通筋长度计算公式两头均为直锚情况长度计算公式＝max[LaE（La），0.5hc首+5d)]+L净+max[LaE（La），（0.5hc尾+5d)]+LlE×n两头均为弯锚长度计算公式＝(hc首-C+15d)+L净+(hc尾+C+15d)+LlE×n一头直锚，一头弯锚长度计算公式＝max[LaE（La），0.5hc首+5d)]+L净+（hc尾+C+15d）+LlE×n长度计算公式＝(hc首-C+15d)+L净+max[LaE（La），（0.5hc尾+5d)]+LlE×n 2、支座负筋、（1）第一排支座负筋）楼层框架梁第一排支座负筋包括端支座负筋和中间支座负筋端支座中间支座左端支座第一排负筋长度＝伸入左端支座内长度+伸入首跨内长度右端支座第一排负筋长度＝伸入右端支座内长度+伸入尾跨内长度中间支座第一排负筋长度＝伸入中间支座左跨长度+中间支座宽+伸入中间支座右跨长度第一排支座负筋（一）判断直锚或弯锚hc-C>=LaE(或la) hc-C<LaE(或la)（二）计算公式：1.端跨1）直锚：laE+ln首（或尾）/3 2）弯锚：15d+(hc-C)+ln首（或尾）/3 2.中间跨：1）支座两边负筋根数相同时：(max(ln1,ln2)/3)*2+hc中2）支座两边负筋根数相同时：a) max(ln1,ln2)/3+laE b) max(ln1,ln2)/3+(hc-C) + 15d直锚弯锚本节内容1.第二排负筋2.跨中钢筋3.架立筋（2）第二排支座负筋）第二排支座负筋：（一）判断直锚或弯锚hc-C>=LaE(或la) hc-C<LaE(或la)（二）计算公式：1.端跨1）直锚：laE+ln首（或尾）/4 2）弯锚：15d+(hc-C)+ln首（或尾）/4 2.中间跨：1）支座两边负筋根数相同时：(max(ln1,ln2)/4)*2+hc中2）支座两边负筋根数相同时：a) max(ln1,ln2)/4+laE b) max(ln1,ln2)/4+(hc-C) + 15d直锚弯锚3、跨中钢筋(当支座跨度较小时）、跨中钢筋当支座跨度较小时当支座跨度较小时）（1）跨中钢筋在中间跨）一、跨中钢筋在端跨：（一）判断直锚或弯锚hc-C>=LaE(或la) hc-C<LaE(或la)（二）计算公式：1.第一排1）直锚：laE+ln首（或尾）+hc中1+ln中1/3 2 2）弯锚：15d+(hc-C)+ln首（或尾）+hc中+ ln中1 /3 15d+(hc-C)+ln +hc + ln 1 2. 1.第二排1）直锚：laE+ln首（或尾）+hc中+ ln中1 /4 2）弯锚：15d+(hc-C)+ln首（或尾）+hc中+ ln中1 /4二、跨中钢筋在中间跨：1.第一排ln首/3+hc中1+ln中+hc中2+ln尾/3 2.第二排ln首/4+hc中1+ln中+hc中2+ln尾/4直锚弯锚4、架立筋、架立筋1：[ln首-ln首/3-max(ln首，ln中1）/3]+150*2架立筋2：[ln中1-max(ln首，ln中1）/3 - max(ln中1，ln中2）/3]+150*2架立筋3：[ln中2-max(ln中1，ln中2）/3 - max(ln中2，ln尾）/3]+150*2架立筋3：[ln尾-max(ln中2，ln尾）/3 - ln尾/3]+150*2 5、下部非贯通筋、1）、抗震情况）、抗震情况）、下部非贯通钢筋一、在端跨：（一）判断直锚或弯锚hc-C>=LaE(或la) hc-C<LaE(或la)（二）计算公式：1.直锚：max(laE,hc首/2+5d）+ln首（或尾）+max(laE,hc中/2+5d）2.弯锚：15d+(hc首-C)+ln首（或尾）+max(laE,hc中/2+5d）二、在中间跨：直锚：max(laE,hc中1/2+5d）+ln首（或尾）+max(laE,hc中2/2+5d）直锚弯锚2）、非抗震情况）、非抗震情况）、6、下部不伸入支座纵筋、下部不伸入支座钢筋Ln-0.1*ln-0.1*ln=0.8ln 7、侧面纵筋、）、侧面构造纵筋（1）、侧面构造纵筋）、1）、通跨设置）、通跨设置）、2）、每跨设置）、每跨设置）、腹板高hW=梁高hb-板厚h当腹板高Hw>=450mm时,设置侧面构造纵筋（腰筋）侧面纵筋1.通跨设置15d+ln通+15d+n*15*d 2.每跨设置15d+ln+15d）、侧面抗扭纵筋（2）、侧面抗扭纵筋）、1）、通跨设置）、通跨设置）、抗扭钢筋（一）判断直锚或弯锚hc-C>=LaE(或la) hc-C<LaE(或la)（二）长度计算直锚：laE+ln通+laE+n*LlE弯锚: 15d+h-C+ln通+n*LlE +15d+ h-C直锚弯锚2）、每跨设置）、每跨设置）、（二）、箍筋根数）、箍筋根数1、一级抗震、加密区根数：[max(2hb,500)-50）/100+1]*2非加密区根数：[ln-2*max(2hb,500)]/200-1总根数：[max(2hb,500)-50）/100+1]*2+[ln-2*max(2hb,500)]/200-1 2、二至四级抗震、加密区根数：[max(1.5hb,500)-50）/100+1]*2非加密区根数：[ln-2*max(1.5hb,500)]/200-1总根数：[max(1.5hb,500)-50）/100+1]*2+[ln-2*max(1.5hb,500)]/200-1 3、附加箍筋根数的计算、（三）、拉筋计算）、拉筋计算拉筋的间距为梁箍筋非加密区间距的2倍拉筋的间距为梁箍筋非加密区间距的倍拉筋根数计算公式拉筋的排数=侧面纵筋根数/2拉筋根数/排= (Ln－50×2)/(非加密区间距×2)＋1拉筋根数＝[(Ln－50×2)/(非加密区间距×2)＋1]×拉筋的排数（四）、吊筋长度）、吊筋长度1、当梁高hb≤800时、当梁高时当梁高hb≤800时,吊筋斜度为45度。吊筋长度公式推导为：吊筋长度＝b＋50×2＋（hb－2C）/sin45×2＋20d×2（式中b为次梁的宽度,hb为框架梁的高度,C为框架梁的保护层厚度,d为吊筋钢筋直径）2、当梁高＞800时、当梁高hb＞时2、当梁高hb＞800时,吊筋斜度为60度。吊筋长度公式推导为：吊筋长度＝b＋50×2＋（hb－2C）/sin60×2＋20d×2（式中b为次梁的宽度,hb为框架梁的高度,C为框架梁的保护层厚度,d为吊筋钢筋直径）五、屋面层框架梁钢筋的计算原理六、非框架梁钢筋的计算原理
4、当主梁遇到次梁时怎么办?
当主次梁相交时，主梁要承担次梁的荷载，要在主梁上配置吊筋或附加箍筋。
5、梁钢筋种类总结梁的钢筋包括纵筋、箍筋、拉筋、吊筋几种形式，纵筋又包括上下贯通筋、上部支座负筋、侧面纵筋、箍筋包括2肢箍、4肢箍等多种形式
梁钢筋的计算原理
一、梁钢筋的计算原理
1、梁的纵筋怎样配置最合理?
在拉力较小的地方配置钢筋少些,拉力较大的地方配置钢筋多些。
2、怎样固定部贯通筋用以固定梁中间箍筋的上部;如果出现2肢箍以上的多肢箍筋还需要配置架立筋来固定中间箍筋。
3、当梁截面特别高时怎么办?
二、梁钢筋的平法标注KL1(2)300×700集中标注A10@100/200(4) 2B25+(2A12);2B25 G4A16两端支座处6B25 4/2中间支座处6B25 4/2原位标注梁下部6B25 2(-2)/4吊筋标注2B18附加箍筋8A10(4)表示1号框架梁、两跨、截面宽为300，截面高为700表示箍筋为圆10的钢筋，加密区间距为100，非加密区间距为200，4肢箍前面的2B25表示梁的上部贯通筋为两根二级25的钢筋，（2B12）表示两跨的上部无负筋区布置两根圆12的架立筋，后面的2B25表示梁的下部贯通筋为两根二级25的钢筋表示梁的侧面设置4根二级16的构造纵筋，两侧各为2根。表示梁的端支座有6根二级25的钢筋，分两排布置，其中上排为4根，下排为2根，因为上排有两根贯通筋，所有上排只有两根二级25的属于支座负筋。表示梁的中间支座有6根二级25的钢筋，分两排布置，其中上排为4根，下排为2根，因为上排有两根贯通筋，所有上排只有两根二级25的属于支座负筋。，中间支座如果只标注一边另一边不标，说明两边的负筋布筋一致。表示梁的下部有6根二级25的钢筋，分两排布置，其中上排为2根，下排为4根；上排两根不伸入支座，从集中标注可以看出，下部有两根贯通筋，所以下排只有2根二级25的是非贯通筋。表示次梁处布置两根二级18的钢筋做为吊筋。表示梁的次梁处增加8根圆10的4肢箍楼层框架梁钢筋的计算原理（一）、纵筋长度）、纵筋长度1、上下贯通筋、楼层框架梁上下贯通筋长度＝通跨净长L净+伸入左端支座内长度+伸入右端支座内长度+(搭接长度×搭接个数)楼层框架梁上下贯通筋长度计算公式两头均为直锚情况长度计算公式＝max[LaE（La），0.5hc首+5d)]+L净+max[LaE（La），（0.5hc尾+5d)]+LlE×n两头均为弯锚长度计算公式＝(hc首-C+15d)+L净+(hc尾+C+15d)+LlE×n一头直锚，一头弯锚长度计算公式＝max[LaE（La），0.5hc首+5d)]+L净+（hc尾+C+15d）+LlE×n长度计算公式＝(hc首-C+15d)+L净+max[LaE（La），（0.5hc尾+5d)]+LlE×n 2、支座负筋、（1）第一排支座负筋）楼层框架梁第一排支座负筋包括端支座负筋和中间支座负筋端支座中间支座左端支座第一排负筋长度＝伸入左端支座内长度+伸入首跨内长度右端支座第一排负筋长度＝伸入右端支座内长度+伸入尾跨内长度中间支座第一排负筋长度＝伸入中间支座左跨长度+中间支座宽+伸入中间支座右跨长度第一排支座负筋（一）判断直锚或弯锚hc-C>=LaE(或la) hc-C<LaE(或la)（二）计算公式：1.端跨1）直锚：laE+ln首（或尾）/3 2）弯锚：15d+(hc-C)+ln首（或尾）/3 2.中间跨：1）支座两边负筋根数相同时：(max(ln1,ln2)/3)*2+hc中2）支座两边负筋根数相同时：a) max(ln1,ln2)/3+laE b) max(ln1,ln2)/3+(hc-C) + 15d直锚弯锚本节内容1.第二排负筋2.跨中钢筋3.架立筋（2）第二排支座负筋）第二排支座负筋：（一）判断直锚或弯锚hc-C>=LaE(或la) hc-C<LaE(或la)（二）计算公式：1.端跨1）直锚：laE+ln首（或尾）/4 2）弯锚：15d+(hc-C)+ln首（或尾）/4 2.中间跨：1）支座两边负筋根数相同时：(max(ln1,ln2)/4)*2+hc中2）支座两边负筋根数相同时：a) max(ln1,ln2)/4+laE b) max(ln1,ln2)/4+(hc-C) + 15d直锚弯锚3、跨中钢筋(当支座跨度较小时）、跨中钢筋当支座跨度较小时当支座跨度较小时）（1）跨中钢筋在中间跨）一、跨中钢筋在端跨：（一）判断直锚或弯锚hc-C>=LaE(或la) hc-C<LaE(或la)（二）计算公式：1.第一排1）直锚：laE+ln首（或尾）+hc中1+ln中1/3 2 2）弯锚：15d+(hc-C)+ln首（或尾）+hc中+ ln中1 /3 15d+(hc-C)+ln +hc + ln 1 2. 1.第二排1）直锚：laE+ln首（或尾）+hc中+ ln中1 /4 2）弯锚：15d+(hc-C)+ln首（或尾）+hc中+ ln中1 /4二、跨中钢筋在中间跨：1.第一排ln首/3+hc中1+ln中+hc中2+ln尾/3 2.第二排ln首/4+hc中1+ln中+hc中2+ln尾/4直锚弯锚4、架立筋、架立筋1：[ln首-ln首/3-max(ln首，ln中1）/3]+150*2架立筋2：[ln中1-max(ln首，ln中1）/3 - max(ln中1，ln中2）/3]+150*2架立筋3：[ln中2-max(ln中1，ln中2）/3 - max(ln中2，ln尾）/3]+150*2架立筋3：[ln尾-max(ln中2，ln尾）/3 - ln尾/3]+150*2 5、下部非贯通筋、1）、抗震情况）、抗震情况）、下部非贯通钢筋一、在端跨：（一）判断直锚或弯锚hc-C>=LaE(或la) hc-C<LaE(或la)（二）计算公式：1.直锚：max(laE,hc首/2+5d）+ln首（或尾）+max(laE,hc中/2+5d）2.弯锚：15d+(hc首-C)+ln首（或尾）+max(laE,hc中/2+5d）二、在中间跨：直锚：max(laE,hc中1/2+5d）+ln首（或尾）+max(laE,hc中2/2+5d）直锚弯锚2）、非抗震情况）、非抗震情况）、6、下部不伸入支座纵筋、下部不伸入支座钢筋Ln-0.1*ln-0.1*ln=0.8ln 7、侧面纵筋、）、侧面构造纵筋（1）、侧面构造纵筋）、1）、通跨设置）、通跨设置）、2）、每跨设置）、每跨设置）、腹板高hW=梁高hb-板厚h当腹板高Hw>=450mm时,设置侧面构造纵筋（腰筋）侧面纵筋1.通跨设置15d+ln通+15d+n*15*d 2.每跨设置15d+ln+15d）、侧面抗扭纵筋（2）、侧面抗扭纵筋）、1）、通跨设置）、通跨设置）、抗扭钢筋（一）判断直锚或弯锚hc-C>=LaE(或la) hc-C<LaE(或la)（二）长度计算直锚：laE+ln通+laE+n*LlE弯锚: 15d+h-C+ln通+n*LlE +15d+ h-C直锚弯锚2）、每跨设置）、每跨设置）、（二）、箍筋根数）、箍筋根数1、一级抗震、加密区根数：[max(2hb,500)-50）/100+1]*2非加密区根数：[ln-2*max(2hb,500)]/200-1总根数：[max(2hb,500)-50）/100+1]*2+[ln-2*max(2hb,500)]/200-1 2、二至四级抗震、加密区根数：[max(1.5hb,500)-50）/100+1]*2非加密区根数：[ln-2*max(1.5hb,500)]/200-1总根数：[max(1.5hb,500)-50）/100+1]*2+[ln-2*max(1.5hb,500)]/200-1 3、附加箍筋根数的计算、（三）、拉筋计算）、拉筋计算拉筋的间距为梁箍筋非加密区间距的2倍拉筋的间距为梁箍筋非加密区间距的倍拉筋根数计算公式拉筋的排数=侧面纵筋根数/2拉筋根数/排= (Ln－50×2)/(非加密区间距×2)＋1拉筋根数＝[(Ln－50×2)/(非加密区间距×2)＋1]×拉筋的排数（四）、吊筋长度）、吊筋长度1、当梁高hb≤800时、当梁高时当梁高hb≤800时,吊筋斜度为45度。吊筋长度公式推导为：吊筋长度＝b＋50×2＋（hb－2C）/sin45×2＋20d×2（式中b为次梁的宽度,hb为框架梁的高度,C为框架梁的保护层厚度,d为吊筋钢筋直径）2、当梁高＞800时、当梁高hb＞时2、当梁高hb＞800时,吊筋斜度为60度。吊筋长度公式推导为：吊筋长度＝b＋50×2＋（hb－2C）/sin60×2＋20d×2（式中b为次梁的宽度,hb为框架梁的高度,C为框架梁的保护层厚度,d为吊筋钢筋直径）五、屋面层框架梁钢筋的计算原理六、非框架梁钢筋的计算原理
钢结构梁的计算方法
钢结构梁的计算方法钢结构梁是建筑领域中常用的一种结构形式，具有承重能力强、稳定性好等优点。
在设计和施工过程中，正确的计算方法是确保梁结构安全可靠的关键。
本文将介绍钢结构梁的计算方法，帮助读者了解如何准确计算梁的承载能力和稳定性。
钢结构梁的计算主要包括以下几个方面：1.梁的受力分析在进行梁的计算之前，首先需要进行梁的受力分析。
通过对梁所受外部荷载的分析，确定梁的受力情况，包括弯矩、剪力、轴力等。
在计算过程中，需要综合考虑梁的几何形状、材料性质、支座条件等因素，确保得出准确的受力分析结果。
2.受力截面的确定确定梁的受力截面是进行计算的重要一步。
根据梁的受力情况，选取合适的受力截面形状，在截面上建立相应的受力模型。
通常情况下，为了简化计算，可以采用截面法对梁的受力截面进行分析，确定承载力和稳定系数等参数。
3.弯矩和剪力的计算在确定梁的受力截面后，需要计算梁的弯矩和剪力。
弯矩和剪力是梁在受力过程中最常见的两种受力形式，是评估梁承载能力的重要指标。
通过对梁的受力分析，可以得出梁的弯矩和剪力分布规律，进而计算出梁的最大弯矩和最大剪力值。
4.承载能力的计算根据钢结构梁的受力情况和截面参数，可以计算出梁的承载能力。
承载能力是指梁在不发生破坏的情况下能够承受的最大荷载，通常以弯矩或剪力的极限状态来界定。
根据梁的截面形状和材料性质，可以采用相应的公式和计算方法，得出梁的承载能力值。
5.稳定性的分析除了承载能力外，稳定性也是评估钢结构梁安全性的重要指标。
在计算过程中，需要综合考虑梁的侧向稳定性和纵向稳定性，确保梁在受力过程中不会发生严重的屈曲或侧向失稳。
通过对梁的稳定性进行分析，可以确定梁的合理截面形状和尺寸，保证梁结构的整体稳定性。
总之，钢结构梁的计算方法涉及多个方面，包括受力分析、受力截面确定、弯矩和剪力计算、承载能力计算以及稳定性分析等。
设计和施工人员在进行钢结构梁的计算时，应该综合考虑各种因素，按照规范要求进行准确计算，确保梁的结构安全可靠，为工程的顺利进行提供保障。
钢结构梁的计算方法
钢结构梁的计算方法钢结构梁广泛应用于建筑、桥梁和其他工程中，因其承载力强、刚性好等特点备受青睐。
在设计和施工过程中，合理的计算方法对于确保梁的质量和安全至关重要。
本文将介绍钢结构梁的计算方法，包括受力分析、截面计算和抗弯设计等内容。
一、受力分析1. 确定梁的受力形式钢结构梁在使用过程中可能受到集中荷载、均布荷载、温度荷载等多种力的作用。
首先需要明确梁所承受的荷载类型和大小，以及荷载作用的位置。
2. 绘制受力图根据荷载的大小和位置，通过绘制受力图可以清楚地表示出梁所承受的各个力的方向和大小。
受力图能够为后续的计算和设计提供依据。
二、截面计算1. 确定梁的材料性能钢结构梁常用的材料有普通碳素结构钢和高强度合金结构钢等。
需要根据实际情况确定梁的材料性能参数，如弹性模量、屈服强度等。
2. 计算梁的截面特性根据梁所受的荷载和材料性能，可以计算出梁的截面特性，如截面面积、惯性矩、截面模量等参数。
这些参数对于后续的抗弯设计和承载力计算非常重要。
三、抗弯设计1. 确定截面位置根据受力分析结果和截面计算得到的截面特性，确定梁在受力过程中需要做抗弯设计的位置。
通常选择截面惯性矩较大的区域进行抗弯设计。
2. 计算抗弯强度根据材料的弹性模量、截面特性和受力情况，可以计算得到梁的抗弯强度。
在设计过程中，需要确保梁的抗弯强度大于所受荷载产生的弯矩，以保证梁的安全性。
3. 确定梁的尺寸和截面形状根据抗弯设计的要求和计算得到的抗弯强度，确定梁的尺寸和截面形状。
梁的尺寸和形状应满足既定的几何约束和力学性能要求。
四、其他考虑因素1. 考虑梁的整体稳定性在设计过程中，需要考虑梁的整体稳定性，包括侧扭稳定和局部稳定等。
通过增加剪力连接、设置加强件等方式，提高梁的整体稳定性。
2. 考虑梁的疲劳寿命钢结构梁在长期使用过程中，可能会受到循环荷载的影响，导致疲劳破坏。
因此，在设计过程中需要考虑梁的疲劳寿命，采取相应的措施延长梁的使用寿命。
综上所述，钢结构梁的计算方法包括受力分析、截面计算和抗弯设计等步骤。
钢梁计算
Mx My f
xWnx
yWny
式中: Mx，My──绕X轴和Y轴的弯矩
Wnx，Wny──对x轴和y轴的净截面抵抗矩；
γx ,γy──截面塑性发展系数：
f ──钢材的抗弯强度设计值。
梁受压翼 缘宽厚比 不大于
13 235 fy
当需要计 算疲劳的
梁时
x y 1.0
当
235 b
第四节 钢梁的整体稳定
二、梁整体稳定的计算方法 1、梁整体稳定的计算公式
在最大刚度主平面内受弯的构件：
Mx Wx
cr R
cr f y f y R
b f
Mx f
bWx
在两个主平面受弯的工字钢截面构件：
Mx My f
b Wx y Wy
Wx, Wy ──按受压纤维确定的对x轴和对y轴毛截面抵抗矩； b ──绕强轴弯曲所确定的梁整体稳定系数。
第四节 钢梁的整体稳定
3、 整体稳定系数近似公式： （2）Ｔ形截面（弯矩作用在对称轴平面，绕ｘ轴）
弯矩使翼缘受压时： 双角钢Ｔ形截面：
b 1 0.0017y
fy 235
两板组合Ｔ形截面：
b 1 0.0022y
fy 235
弯矩使翼缘受拉且腹板宽厚比不大于
18
235 fy
时：
b 1 0.0005y
a ──集中荷载沿梁跨度方向的支承长度，对钢轨(吊车梁)上的轮压 可取为50mm;
h y ──自吊车梁轨顶或其它梁顶面至腹板计算高度上边缘的距离。 hR ──轨道的高度,对梁顶无轨道的梁, hR 0
梁端 按制作具体情况确定 lz a 2.5hy
c
第章钢梁计算原理
第五章钢梁计算原理5.1 概述在钢结构中，承受横向荷载作用的实腹式构件称为梁类构件，即钢梁。
钢梁在土木工程中应用很广泛，例如厂房建筑中的工作平台梁、吊车梁、屋面檩条和墙架横梁，以及桥梁、水工闸门、起重机、海上采油平台中的梁等。
按制作方法可将钢梁分为型钢梁和组合梁两种。
型钢梁制作简单，成本较低，应用较广。
型钢梁通常采用热轧工字钢、槽钢、H型钢和T型钢（图5－1（a））以及冷弯薄壁型钢（图5－l（c））。
其中H型钢的截面分布最合理，其翼缘内外边缘平行，方便与其他构件连接；槽钢的截面扭转中心在腹板外侧，一般受力情况下容易发生扭转，在使用时应尽量避免。
当荷载较大或跨度较大时，必须采用组合梁（图5－1（b））来提高截面的刚度和承载力，其中箱形截面梁的抗扭强度较高。
组合梁的截面可以根据具体受力情况合理布置，达到节省钢材的目的。
图5－1表示出了两个正交的形心主轴，其中绕x轴的惯性矩、截面抵抗矩最大，称为强轴，另一轴则为弱轴。
对于工形、T形、箱形截面，平行于x轴(弯曲轴)的最外边板称为翼缘，垂直于x轴的板称为腹板。
按支承条件又可将梁分为简支梁、连续梁和悬伸梁等。
其中简支梁应用最广，因其制造、安装、拆换都较方便，而且受温度变化和支座沉陷的影响很小。
梁的设计必须同时满足承载能力极限状态和正常使用极限状态。
钢梁的承载能力极限状态包括强度、整体稳定和局部稳定三个方面。
设计时要求在荷载设计值作用下，梁的抗弯强度、抗剪强度、局部承压强度和折算应力均不超过相应的强度设计值；保证梁不会发生整体失稳；同时保证组成梁的板件不出现局部失稳。
正常使用极限状态主要指梁的刚度，设计时要求在荷载标准值作用下梁具有符合规范要求的足够的抗弯刚度。
图5－1钢梁常用截面类型5.2钢梁的强度和刚度5.2.1 梁的强度梁的强度包括抗弯强度、抗剪强度、局部承压强度和折算应力，设计时要求在荷载设计值作用下，均不超过《钢结构设计规范》规定的相应的强度设计值。
第5章 梁梁计算原理
第5章梁梁计算原理
概述
本章将介绍梁梁计算原理，包括梁的基本概念，计算模型以及
相关的数学原理。
梁是一种常见的结构元素，在工程设计中应用广泛。
梁的定义
梁是一种用于承受和传递荷载的结构元素，通常具有长方形或
梯形的截面形状。
梁可以分为悬臂梁、简支梁和连续梁等不同类型，其截面形状和材料特性都会影响其受力性能。
梁的计算模型
为了对梁进行强度和刚度的计算，可以采用简化的计算模型。
常见的计算模型包括Euler-Bernoulli梁和Timoshenko梁。
这些模型假设梁是线性弹性材料，且在纵向和横向上的应变和应力满足一定
的假设条件。
梁的数学原理
梁的计算涉及到一系列数学原理，包括静力学、力学平衡、弹
性理论以及应力分析等。
为了计算梁的弯曲、剪切和挠度等参数，
需要应用这些数学原理，并结合具体的边界条件和荷载情况进行分析。
结论
梁梁计算原理是工程设计中不可或缺的一部分。
了解梁的基本
概念、计算模型和数学原理，有助于准确分析和计算梁的受力性能，确保结构的安全性和稳定性。
东大工程结构设计原理课件06钢梁承载力计算原理
2.梁的初弯曲、加荷偏心及残余应力等缺陷的影响。
b'
0.282 1.07 1.0
b
轧制普通工字钢简支梁，其 b 值直接查表得到，同样 当 b 值大于0.6时，也需要进行修正。
第32讲：受弯构件－梁（5）
5－45
例题
某简支梁，焊接工字形截面，跨度中点及两端都设有 侧向支承，可变荷载标准值及梁截面尺寸如图6－17
5－48
型钢梁截面设计
首先由荷载计算出梁所承受的最大弯矩，并估算梁截
面的抵抗矩，
1.当梁的整体稳定从构造上可保证时：W nx
M x
x
f
2.当梁的整体稳定从构造上不能保证时：W nx
其中 b 可根据荷载及跨度情况初步估计。
M b
x
f
3. 选择适当型钢截面，验算梁的弯曲正应力，局部压 应力，整体稳定和刚度，一般型钢梁可不验算折算应 力，也可不验算剪应力。
max
1.2V hwtw
fv
(a)
5－25
P
V S
P
(b)
(c)
第30讲：受弯构件－梁（5）
5－26
局部压应力
产生的原因和位置：
集中荷载作用截面；翼缘于腹板结合处（上、下）。
腹板的计算高度边缘
计算公式：
c
F
twlz
f
lZ＝a+2hy
h0 hy
hy
(a)
a
F
45o
45o
tw l = a + hy lz = a + 2hy
σ 、τ 、σ C分别为腹板计算
高度边缘处同一点上同时产
钢结构钢梁计算方法详解
钢结构钢梁计算方法详解范本一：钢结构钢梁计算方法详解一：引言1.1 本章介绍钢结构钢梁计算方法文档的目的和篇章结构。
二：基本原理2.1 钢结构概述2.1.1 钢结构的定义和特点2.1.2 钢结构的分类2.1.3 钢结构的优点和应用范围2.2 钢梁的基本概念2.2.1 钢梁的定义和组成部分2.2.2 钢梁的分类和命名规则2.2.3 钢梁的荷载和受力情况三：计算方法3.1 钢梁计算的基本原理3.1.1 钢梁的强度计算原理3.1.2 钢梁的稳定性计算原理3.2 钢梁的截面计算方法3.2.1 标准截面的计算方法3.2.2 非标准截面的计算方法3.3 钢梁的受力计算方法3.3.1 钢梁在弯曲力作用下的计算方法3.3.2 钢梁在剪力作用下的计算方法3.3.3 钢梁在轴力作用下的计算方法3.4 钢梁的稳定性计算方法3.4.1 钢梁的侧扭稳定性计算方法3.4.2 钢梁的屈曲稳定性计算方法四：计算实例4.1 钢梁截面计算实例4.2 钢梁受力计算实例4.3 钢梁稳定性计算实例附件：1. 钢结构设计规范相关文件2. 钢梁计算所用的公式和计算表格法律名词及注释：1. 钢结构设计规范：指国家有关钢结构设计的法律法规文件，包括《钢结构设计规范》等。
2. 钢梁：指钢结构中用于承担和传递荷载的横向构件。
范本二：钢结构钢梁计算方法详解一：前言1.1 本文档旨在详细介绍钢结构钢梁计算方法，以读者理解和应用该计算方法。
二：基本概念2.1 钢结构基本概念2.1.1 钢结构的定义与分类2.1.2 钢结构的特点与应用范围2.2 钢梁基本概念2.2.1 钢梁的定义与构成2.2.2 钢梁的分类与命名规则2.2.3 钢梁的荷载与受力情况三：计算原理3.1 钢梁计算基本原理3.1.1 钢梁强度计算原理3.1.2 钢梁稳定性计算原理3.2 钢梁截面计算方法3.2.1 标准截面计算方法3.2.2 非标准截面计算方法3.3 钢梁受力计算方法3.3.1 弯曲力作用下的计算方法3.3.2 剪力作用下的计算方法3.3.3 轴力作用下的计算方法3.4 钢梁稳定性计算方法3.4.1 侧扭稳定性计算方法3.4.2 屈曲稳定性计算方法四：计算案例4.1 钢梁截面计算案例4.2 钢梁受力计算案例4.3 钢梁稳定性计算案例附件：1. 相关设计规范文档2. 计算所用公式与表格法律名词及注释：1. 钢结构设计规范：指国家有关钢结构设计的法律法规文件，例如《钢结构设计规范》等。
第5章 钢梁计算原理
第5章 钢梁计算原理
16
、 、 c 分别为腹板计算高度边缘处同一截 面同一点上同时产生的正应力、剪应力和局部压 应力。
My Ix
VS It w
c
ψF
tw lz
1 ——折算应力的强度设计值增大系数（当 和 c 异号时，取 1 1.2 ；当 和 c 同号或 c 0 时，取 1 1.1 ）。
2、约束扭转
t ω
MT M t Mω
式中： t ——因扭转而产生的自由扭转剪应力 ω ——因翼缘弯曲变形而产生的弯曲扭转剪 应力
南航土木工程系 第5章 钢梁计算原理 22
开口薄壁杆件约束扭转微分方程
d d M T GI t EI ω 3 dz dz
南航土木工程系 第5章 钢梁计算原理 30
？问题：求解弯矩 M 为多大的情况下会使梁整 体失稳，即对应 u 和 有非零解，而这个待定 的 M 就是梁失稳时的临界弯矩。
南航土木工程系
第5章 钢梁计算原理
31
将式（3）微分一次，并将（2）式 d u dz 2 代入得：
d 4 d 2 M EI ω 4 GI t 2 0 dz dz EI y (4)
南航土木工程系
第5章 钢梁计算原理
36
2）与荷载的作用位置有关 横向荷载作用在上翼缘，荷载的附加效应加大 了截面的扭转，降低了梁的临界弯矩。反之，可 提高梁的稳定性。
南航土木工程系
第5章 钢梁计算原理
37
3）与梁的侧向抗弯刚度 EI y有关 提高梁的侧向抗弯刚度 EI y可以显著提高梁的 临界弯矩，而增大梁的抗扭刚度 GI t 和抗翘曲刚 度 EI ω 虽然也可以提高 M cr ，但效果不大。增大 受压翼缘的宽度。 4）与受压翼缘的自由长度 l1 有关 减少 l1 可显著提高梁的临界弯矩 M cr ，这可 以通过增设梁的侧向支承来解决。无论跨中有无 侧向支承，在支座处均应采取构造措施以防止梁 端截面的扭转。
第章钢梁计算原理
第章-钢梁计算原理————————————————————————————————作者: ————————————————————————————————日期：第五章ﻩ钢梁计算原理5.1 概述在钢结构中，承受横向荷载作用的实腹式构件称为梁类构件,即钢梁。
钢梁在土木工程中应用很广泛，例如厂房建筑中的工作平台梁、吊车梁、屋面檩条和墙架横梁,以及桥梁、水工闸门、起重机、海上采油平台中的梁等。
按制作方法可将钢梁分为型钢梁和组合梁两种。
型钢梁制作简单，成本较低，应用较广。
型钢梁通常采用热轧工字钢、槽钢、H型钢和T型钢(图5－1（ａ）)以及冷弯薄壁型钢（图５－l(ｃ））。
其中H型钢的截面分布最合理,其翼缘内外边缘平行,方便与其他构件连接;槽钢的截面扭转中心在腹板外侧,一般受力情况下容易发生扭转,在使用时应尽量避免。
当荷载较大或跨度较大时，必须采用组合梁(图５－1（b））来提高截面的刚度和承载力,其中箱形截面梁的抗扭强度较高。
组合梁的截面可以根据具体受力情况合理布置，达到节省钢材的目的。
图５－1表示出了两个正交的形心主轴，其中绕x轴的惯性矩、截面抵抗矩最大，称为强轴，另一轴则为弱轴。
对于工形、T形、箱形截面，平行于x轴（弯曲轴)的最外边板称为翼缘,垂直于x轴的板称为腹板。
按支承条件又可将梁分为简支梁、连续梁和悬伸梁等。
其中简支梁应用最广，因其制造、安装、拆换都较方便，而且受温度变化和支座沉陷的影响很小。
梁的设计必须同时满足承载能力极限状态和正常使用极限状态。
钢梁的承载能力极限状态包括强度、整体稳定和局部稳定三个方面。
设计时要求在荷载设计值作用下,梁的抗弯强度、抗剪强度、局部承压强度和折算应力均不超过相应的强度设计值;保证梁不会发生整体失稳；同时保证组成梁的板件不出现局部失稳。
正常使用极限状态主要指梁的刚度,设计时要求在荷载标准值作用下梁具有符合规范要求的足够的抗弯刚度。
图5-1 钢梁常用截面类型5.2钢梁的强度和刚度5.2.1 梁的强度梁的强度包括抗弯强度、抗剪强度、局部承压强度和折算应力，设计时要求在荷载设计值作用下,均不超过《钢结构设计规范》规定的相应的强度设计值。
梁的计算原理30页PPT
Thank you
•
26、我们像鹰一样，生来就是自由的 ，但是 为了生 存，我 们不得 不为自 己编织 一个笼 子，然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理，即使延续时 间再长 ，也还 是没有 制约力 的。— —爱·科 克
•
28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
•
29、在一切能够接受法律支配的人类 的状态 中，哪 里没有 法律， 那里就 以废除 法律。 ——塞·约翰逊
梁的计算原理
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
•
26、我们像鹰一样，生来就是自由的 ，但是 为了生 存，我 们不得 不为自 己编织 一个笼 子，然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理，即使延续时 间再长 ，也还 是没有 制约力 的。— —爱·科 克
•
28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
•
29、在一切能够接受法律支配的人类 的状态 中，哪 里没有 法律， 那里就 以废除 法律。 ——塞·约翰逊
梁的计算原理
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第五章钢梁计算原理5.1 概述在钢结构中，承受横向荷载作用的实腹式构件称为梁类构件，即钢梁。
钢梁在土木工程中应用很广泛，例如厂房建筑中的工作平台梁、吊车梁、屋面檩条和墙架横梁，以及桥梁、水工闸门、起重机、海上采油平台中的梁等。
按制作方法可将钢梁分为型钢梁和组合梁两种。
型钢梁制作简单，成本较低，应用较广。
型钢梁通常采用热轧工字钢、槽钢、H型钢和T型钢（图5－1（a））以及冷弯薄壁型钢（图5－l（c））。
其中H 型钢的截面分布最合理，其翼缘内外边缘平行，方便与其他构件连接；槽钢的截面扭转中心在腹板外侧，一般受力情况下容易发生扭转，在使用时应尽量避免。
当荷载较大或跨度较大时，必须采用组合梁（图5－1（b））来提高截面的刚度和承载力，其中箱形截面梁的抗扭强度较高。
组合梁的截面可以根据具体受力情况合理布置，达到节省钢材的目的。
图5－1表示出了两个正交的形心主轴，其中绕x轴的惯性矩、截面抵抗矩最大，称为强轴，另一轴则为弱轴。
对于工形、T形、箱形截面，平行于x轴(弯曲轴)的最外边板称为翼缘，垂直于x轴的板称为腹板。
按支承条件又可将梁分为简支梁、连续梁和悬伸梁等。
其中简支梁应用最广，因其制造、安装、拆换都较方便，而且受温度变化和支座沉陷的影响很小。
梁的设计必须同时满足承载能力极限状态和正常使用极限状态。
钢梁的承载能力极限状态包括强度、整体稳定和局部稳定三个方面。
设计时要求在荷载设计值作用下，梁的抗弯强度、抗剪强度、局部承压强度和折算应力均不超过相应的强度设计值；保证梁不会发生整体失稳；同时保证组成梁的板件不出现局部失稳。
正常使用极限状态主要指梁的刚度，设计时要求在荷载标准值作用下梁具有符合规范要求的足够的抗弯刚度。
图5－1 钢梁常用截面类型5.2钢梁的强度和刚度5.2.1 梁的强度梁的强度包括抗弯强度、抗剪强度、局部承压强度和折算应力，设计时要求在荷载设计值作用下，均不超过《钢结构设计规范》规定的相应的强度设计值。
下面分别进行叙述。
一、抗弯强度如图5－2所示，梁在弯矩作用下，截面上正应力的发展过程可分为三个阶段，分述如下。
图5－2 梁的正应力分布（1）弹性工作阶段当弯矩较小时，截面上应力分布呈三角形，中和轴为截面的形心轴，截面上各点的正应力均小于屈服应力y f 。
弯矩继续增加，直至最外边缘纤维应力达到屈服应力y f 时（图5－2（b ）），弹性状态的结束，相应的弹性极限弯矩e M 为 e n y M W f = （5－1） 式中 n W ——梁的净截面弹性抵抗矩。
（2）弹塑性工作阶段弯矩继续增加，在梁截面上、下边缘各出现一个高度为a 的塑性区，其应力σ达到屈服应力y f 。
而截面的中间部分区域仍处于弹性工作状态（图5—2（c ）），此时梁处于弹塑性工作阶段。
（3）塑性工作阶段随着弯矩再继续增加，梁截面的塑性区不断向内发展，直至全部达到屈服应力y f （图5—2（d ）），此时梁的抗弯承载能力达到极限，截面所负担弯矩不再增加，而变形却可继续增大，形成“塑性铰”，相应的塑性极限弯矩p M 为 p 1n 2n y pn y ()M S S f W f =+= （5－2） 式中 1n S ，2n S ——分别为中和轴以上及以下净截面对中和轴的面积矩； pn W ——梁的净截面塑性抵抗矩，pn 1n 2n W S S =+。
塑性抵抗矩与弹性抵抗矩的比值称为截面形状系数γ。
它的大小仅与截面的几何形状有关，而与材料及外荷载无关。
实际上表示出截面在进入弹塑性阶段之后的后续承载力。
γ越大，表示截面的弹塑性后续承载能力越大。
pnpn y p n n y e W W f M W W f M γ=== （5－3）对于矩形截面 1.5γ=，圆截面 1.7γ=，圆管截面 1.27γ=，工字形截面1.17γ≈。
说明在边缘纤维屈服后，矩形截面内部塑性变形发展还能使弯矩承载能力增大50％，而工字形截面的弯矩承载能力增大则较小。
虽然考虑截面塑性发展似乎更经济，但若按截面塑性极限弯矩进行设计，可能使梁产生过大的挠度，受压翼缘过早失去局部稳定。
因此，《钢结构设计规范》只是有限制地利用塑性，取截面塑性发展深度0.125a h ≤，并通过截面塑性发展系数γ来体现，且pn n 1.0W W γ≤<，按附表取值。
因此，梁的抗弯强度计算公式为：单向弯曲时x x nx M f W σγ=≤ （5－4）双向弯曲时y x x nx y ny M M f W W σγγ=+≤ （5－5）式中 x M ，y M ——绕x 轴和y 轴的弯矩；nx W ，ny W ——梁对x 轴和y 轴的净截面抵抗矩；x γ，y γ——截面塑性发展系数，当梁受压翼缘的自由外伸宽度与其厚度之比不大于附表取值，否则x y 1.0γγ==； f ——钢材的抗弯强度设计值，按附表采用。
对于直接承受动力荷载梁及需要计算疲劳的梁，须按弹性工作阶段进行计算，宜取x y 1.0γγ==。
二、抗剪强度一般情况下，梁同时承受弯矩和剪力的共同作用。
对于外加剪力垂直于强轴的实腹梁来说，如工字形和槽形截面梁，翼缘处分担的剪力很小，可忽略不计，截面上的剪力主要由腹板承担。
工字形和槽形截面梁腹板上的剪应力分布分别如图5－3（a）、（b）所示。
截面上的最大剪应力发生在腹板中和轴处。
其承载能力极限状态以截面上的最大剪应力达到钢材的抗剪屈服强度为准，而抗剪强度计算式为v wVSfItτ=≤（5－6）式中V——计算截面处沿腹板平面作用的剪力设计值；S——计算剪应力（此处即为中和轴）以上毛截面对中和轴的面积矩；I——毛截面惯性矩；wt——腹板厚度；vf——钢材的抗剪强度设计值，按附表采用。
图5－3 腹板剪应力由于型钢腹板较厚，一般均能满足上式要求。
三、局部承压强度当梁的翼缘受到沿腹板平面作用的集中荷载（例如此梁传来的集中力、支座反力和吊车轮压等）作用且该处又未设置支承加劲肋时（图5－4（a）、（b）），应验算腹板计算高度边缘的局部承压强度。
图5－4 局部压应力在集中荷载作用下，腹板计算高度边缘的压应力分布如图5－4（c ）的曲线所示。
计算时假定集中荷载从作用点处以45︒角扩散，并均匀分布于腹板的计算高度边缘。
梁的局部承压强度可按下式计算c w z Ff t l ψσ=≤ （5－7）式中 F ——集中荷载（对动力荷载应考虑动力系数）；ψ——集中荷载增大系数（对重级工作制吊车轮压， 1.35ψ=；对其他荷载， 1.0ψ=）；z l ——集中荷载在腹板计算高度边缘的假定分布长度（跨中z y R 52l a h h =++，梁端z y 12.5l a h a =++）；a ——集中荷载沿梁跨度方向的支承长度（对吊车梁可取为50mm ）；y h ——自梁承载的边缘到腹板计算高度边缘的距离；R h ——轨道的高度（无轨道时R 0h =）； 1a ——梁端到支座板外边缘的距离（按实际取值，但不得大于y 2.5h ）。
腹板的计算高度0h 按下列规定采用：①轧制型钢梁，为腹板在与上、下翼缘相接处两内弧起点间的距离；②焊接组合梁，为腹板高度。
当计算不满足式（5－7）时，在固定集中荷载处(包括支座处)应设置支承加劲肋予以加强，并对支承加劲肋进行计算。
对移动集中荷载，则应加大腹板厚度。
四、折算应力当组合梁的腹板计算高度边缘处，同时承受较大的正应力σ、剪应力τ和局部压应力c σ时，或同时承受较大的正应力σ和剪应力τ时，应按下式验算该处的折算应力1f β （5－8） 式中 σ，τ，c σ——腹板计算高度边缘同一点上的弯曲正应力、剪应力和局部压应力，τ按式（5－6）计算，c σ按式（5－7）计算，σ按下式计算nx My I σ= （5－9）nx I ——梁净截面惯性矩；y ——计算点至梁中和轴的距离；σ，c σ——均以拉应力为正值，压应力为负值； 1β——折算应力的强度设计值增大系数（当σ和c σ异号时，取1 1.2β=；当σ和c σ同号或c σ时，取1 1.1β=）。
实际工程中几种应力皆以较大值在同一处出现的概率很小，故将强度设计值乘以1β予以提高。
当σ和c σ异号时，其塑性变形能力比σ和c σ同号时大，因此1β值取更大些。
5.2.2 梁的刚度梁刚度的验算相应于正常使用极限状态。
当梁的刚度不足时，会产生较大的挠度，将影响结构的正常使用。
例如若平台梁的挠度过大，一方面会使人们感到不舒服和不安全，另一方面会影响操作；若吊车梁挠度过大，会使吊车运行困难，甚至不能运行。
因此，应使用下式来保证梁的刚度不至于过小：[]v v ≤ （5－10） 式中 v ——荷载标准值作用下梁的最大挠度；[]v——梁的容许挠度值，《钢结构设计规范》根据实践经验规定的容许挠度值见附表。
挠度计算时，除了要控制受弯构件在全部荷载标准值下的最大挠度外，对承受较大可变荷载的受弯构件，尚应保证其在可变荷载标准值作用下的最大挠度不超过相应的容许挠度值，以保证构件在正常使用时的工作性能。
5.3钢梁的整体稳定5.3.1一般概念如图5－5所示的工字形截面梁，承受弯曲平面内的横向荷载作用，若其截面形式为高而窄，则当荷载增大一定程度时，梁除了仍有弯矩作用平面内的弯曲以外，会突然发生侧向弯曲和扭转，并丧失继续承载的能力，这种现象就称为梁的整体失稳。
此时梁的抗弯承载能力尚未充分发挥。
梁维持其稳定平衡状态所承受的最大弯矩，称为临界弯矩。
图5－5 梁的整体失稳横向荷载的临界值和它沿梁高的作用位置有关。
荷载作用在上翼缘时，如图5－6（a）所示，在梁产生微小侧向位移和扭转的情况下，荷载F将产生绕剪力中心的附加扭矩Fe，它将对梁侧向弯曲和扭转起促进作用，使梁加速丧失整体稳定。
但当荷载F作用在梁的下翼缘时（图5－6（b）），它将产生反方向的附加扭矩Fe，有利于阻止梁的侧向弯曲扭转，延缓梁丧失整体稳定。
因此，后者的临界荷载（或临界弯矩）将高于前者。
图5－6 荷载位置对整体稳定的影响5.3.2 梁的扭转梁整体失稳形态为双向弯曲加扭转，为此有必要简略介绍有关扭转的若干概念。
根据支承条件和荷载形式的不同，扭转分为自由扭转和约束扭转两种形式。
一、自由扭转非圆截面构件扭转时，原来为平面的横截面不再保持为平面，产生翘曲变形，即构件在扭矩作用下，截面上各点沿杆轴方向产生位移。
如果扭转时轴向位移不受任何约束，截面可自由翘曲变形（图5－7），称为自由扭转。
自由扭转时，各截面的翘曲均相同，纵向纤维保持直线且长度保持不变，截面上无正应力，只有剪应力。
沿杆件全长扭矩相等，单位长度扭转角d d z ϕ相等，并在各截面上产生相同的扭转剪应力。
图5－7 杆件的自由扭转剪应力沿板厚方向呈三角形分布，扭矩与截面扭转角ϕ的关系为 t t d d M GI z ϕ= （5－11） 式中 t M ——截面的自由扭转扭矩；G ——材料的剪变模量；ϕ——截面的扭转角； t I ——截面的抗扭惯性矩（扭转常数）。