改进遗传算法

遗传算法的研究与进展一、综述随着科学技术的不断发展和计算能力的持续提高，遗传算法作为一种高效的优化方法，在许多领域中得到了广泛的应用。

本文将对遗传算法的研究进展进行综述，包括基本原理、改进策略、应用领域及最新研究成果等方面的内容。

自1975年Brendo和Wolfe首次提出遗传算法以来，该算法已经发展成为一种广泛应用于求解最优化问题的通用方法。

遗传算法主要基于自然选择的生物进化机制，通过模拟生物基因的自然选择、交叉和变异过程来寻找最优解。

在过去的几十年里，众多研究者和开发者针对遗传算法的性能瓶颈和改进方向进行了深入探讨，提出了许多重要的改进策略。

本文将对这些策略进行综述，并介绍相关的理论依据、实现方法以及在具体问题中的应用。

遗传算法的核心思想是基于种群搜索策略，在一组可行解（称为种群）中通过选择、交叉和变异等遗传操作产生新的候选解，进而根据适应度函数在种群中选择优良的候选解，重复上述过程，最终收敛于最优解。

遗传算法的关键要素包括：染色体表示、适应度函数设计、遗传操作方法等。

为进一步提高遗传算法的性能，研究者们提出了一系列改进策略。

这些策略可以从以下几个方面对遗传算法进行改进：多目标优化策略：针对单点遗传算法在求解多目标优化问题时容易出现陷入局部最优解的问题，可以通过引入多目标遗传算法来求解多目标问题。

精英保留策略：为了避免遗传算法在进化过程中可能出现未成熟个体过早死亡的现象，可以采用精英保留策略来保持种群的优良特性。

基于随机邻域搜索策略：这种策略通过对当前解的随机邻域进行搜索，可以在一定程度上避免陷入局部最优解，并提高算法的全局收敛性。

遗传算法作为一种常用的优化方法，在许多领域都有广泛应用，如组合优化、约束满足问题、机器学习参数优化、路径规划等。

随着技术的发展，遗传算法在深度学习、强化学习和智能交通系统等领域取得了显著成果。

研究者们在遗传算法的设计和应用方面取得了一系列创新成果。

基于神经网络的遗传算法被用于解决非线性优化问题；基于模型的遗传算法通过建立优化问题模型来提高算法的精度和效率；一些研究还关注了遗传算法的鲁棒性和稳定性问题，提出了相应的改进措施。

改进遗传算法解决TSP问题陈林;潘大志【摘要】针对基本遗传算法收敛速度慢，易早熟等问题，提出一种改进的遗传算法。

新算法利用贪婪思想产生初始种群来加快寻优速度，用贪婪思想来引导交叉操作，在交叉操作之前，把当前较差的一半种群替换成随机种群，最后用改进的变异算子和进化逆转操作进行寻优，利用新的遗传算法求解基本的旅行商问题。

仿真结果表明，改进的遗传算法具有全局搜索能力强、收敛速度快的特点，优化质量和寻优效率都较好。

%Aiming at the problem of slow convergence and easy premature convergence, an improved genetic algorithm is proposed. New algorithm uses greedy idea to generate the initial population for speeding up the searching speed and greedy idea to guide the crossover operation, before the crossover operation, selects the random population to replace the half of the poor population, finally with the help of the improved mutation operator and evolutionary reversal operation to realize optimization, constructs a new genetic algorithm for solving the traveling salesman problem. The simulation results show that the improved genetic algorithm has the characteristics of strong global search ability and fast convergence speed.【期刊名称】《智能计算机与应用》【年(卷),期】2016(006)005【总页数】4页(P17-19,23)【关键词】遗传算法;贪婪思想;进化逆转;旅行商问题【作者】陈林;潘大志【作者单位】西华师范大学数学与信息学院，四川南充637009;西华师范大学数学与信息学院，四川南充637009【正文语种】中文【中图分类】TP18遗传算法(GA)是一种进化算法，其基本原理是仿效生物界中的“物竞天择、适者生存”的演化法则。

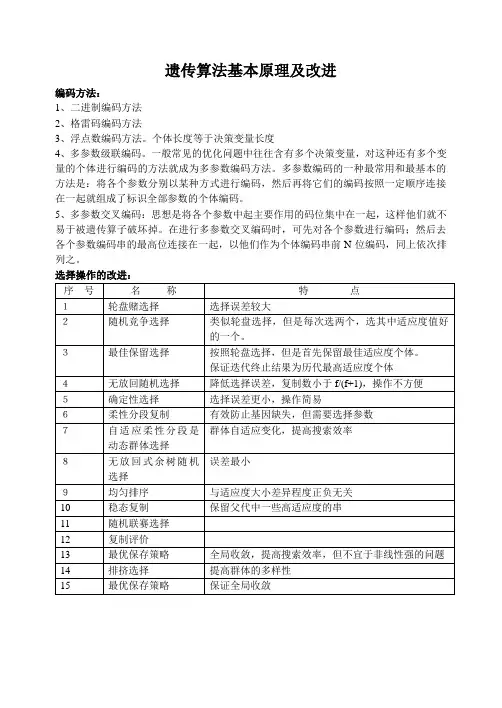
遗传算法基本原理及改进编码方法：1、二进制编码方法2、格雷码编码方法3、浮点数编码方法。

个体长度等于决策变量长度4、多参数级联编码。

一般常见的优化问题中往往含有多个决策变量，对这种还有多个变量的个体进行编码的方法就成为多参数编码方法。

多参数编码的一种最常用和最基本的方法是：将各个参数分别以某种方式进行编码，然后再将它们的编码按照一定顺序连接在一起就组成了标识全部参数的个体编码。

5、多参数交叉编码：思想是将各个参数中起主要作用的码位集中在一起，这样他们就不易于被遗传算子破坏掉。

在进行多参数交叉编码时，可先对各个参数进行编码；然后去各个参数编码串的最高位连接在一起，以他们作为个体编码串前N位编码，同上依次排列之。

改进遗传算法的方法：（1）改进遗传算法的组成成分或实用技术，如选用优化控制参数、适合问题的编码技术等。

（2）采用动态自适应技术，在进化过程中调整算法控制参数和编码精度。

（3）采用混合遗传算法（4）采用并行算法（5）采用非标准的遗传操作算子改进的遗传算法：（1）分层遗传算法（2）CHC算法（3）messy遗传算法；（4）自实用遗传算法（Adaptive Genetic Algorithm）（5）基于小生境技术的遗传算法（Niched Genetic Algorithm，简称NGA）。

（6）并行遗传算法（Parallel Genetic Algorithm）（7）混合遗传算法：遗传算法与最速下降法相结合的混合遗传算法；遗传算法与模拟退火算法相结合的混合遗传算法。

解决标准遗传算法早熟收敛和后期搜索迟钝的方案（1）变异和交叉算子的改进和协调采用将进化过程划分为渐进和突变两个不同阶段采用动态变异运用正交设计或均匀设计方法设计新的交叉和变异算子（2）采用局部搜索算法解决局部搜索能力差的问题（3）采用有条件的替代父代的方法，解决单一的群体更新方式难以兼顾多样性和收敛性的问题（4）收敛速度慢的解决方法；产生好的初始群体利用小生境技术使用移民技术采用自适应算子采用与局部搜索算法相结合的混合遗传算法对算法的参数编码采用动态模糊控制进行未成熟收敛判断。

作者： 金建刚
作者机构： 华北水利水电学院信息工程系,郑州河南,450011
出版物刊名： 科技资讯
页码： 35-36页
主题词： 遗传算法 种群 个体 算子
摘要：遗传算法是一个用来求解高度复杂问题有效方法,由于其初始值的随机性和较大的搜索空间以及其工作机制,保证了该算法能够在全局范围内得到最优解.但是遗传算法在进行编码串交叉时的随机性,却使得计算量增加.针对此提出了人工控制交叉的方法,它保证了交叉是按照最优化方向进行的,从而提高了收敛速度,减少了计算量.并对两种方法进行了仿真实验比较.结果证明这种方法是可行的.。

- 20 -高 新 技 术随着经济快速发展，社会对企业生产质量的要求不断提高。

但是部分企业的生产效能低且其运营管理不精细，严重影响了企业的生产质量，难以实现企业经济效益、社会效益最大化的的目标[1]。

该文从实际角度出发，分析现阶段H 公司生产线的工艺流程、工序以及生产过程中存在的问题，将遗传算法应用到H 公司生产线平衡优化中，可以为同类企业平衡和优化生产线提供科学依据和发展思路。

1 H 公司生产线现状H 公司是一家中小型家用电器生产公司，生产范围十分广泛，产品销售范围遍及全国。

其产品生产线为单一产品生产线，主要生产壁挂式变频空调。

该产品适用于绝大数家庭，通常悬挂于室内墙壁上，无氟环保，能耗比较高，因此有较大的销售市场。

其产品生产线位于18 000 m 2的恒温生产车间内，是一条生产大批量单一品种的生产线，生产线的工艺流程大致分为装配、焊接、检查以及包装4个模块。

整个装配过程分为46个具体的操作单元，可以划分为13个工作站，分别为底板组装、冷凝器的安装、装配系统部件、总装手工焊接、电路系统固定、电机组件安装固定、系统检漏、电控整理、后端装配、贴标签、外壳装配、外观清洁及总检和包装打包。

H 公司的工作内容主要是对产品需要装配部件进行装配，例如底板、系统部件、标签以及外壳材料等，主要采用粘接法、充注法以及螺纹连接法等方法。

因为产品的功能很复杂、部件体积差异大且总量很多，所以装配方式也多种多样。

在产品组装过程中，需要粘接的部件较多，占整产品配件量的30%左右。

对较小的零部件来说，通过采用粘接的方式直接粘贴到产品相关位置即可。

对较大的零部件来说，除部分零件拼装要涂粘接剂外，在部件的粘接面也要涂沫粘接剂，保证连接效果。

2 H 公司产线平衡问题数学描述H 公司是一家传统的制造企业，其产线作业方案制定主要是按照工艺方式和作业顺序。

就现场问题来看，工位安排和产线布局粗糙，同工作站之间作业时间相差较大，不同作业单元的工人劳动强度悬殊，由此导致工人工作人员情绪低落，难以保障工人安全、产品质量。

3 旅行商问题3.1 旅行商问题概述3.1.1 旅行商问题的定义和数学模型① 定义旅行商问题(Traveling Salesman Problem ，简记TSP)是组合数学中一个古老而又困难的问题，它易于描述但至今尚未彻底解决，现己归入所谓的NP 完全问题类，经典提法为：有一货物推销员要去若干个城市推销货物，从城市1出发，经其余各城市一次，然后回到城市1，问选择怎样的行走路线，才能使总行程最短（各城市间距离为己知）。

该问题在图论的意义下就是所谓的最小Hamilton 圈问题，由于在许多领域中都有着广泛的应用，因而寻找其实际而有效的算法就显得颇为重要了。

遗憾的是，计算复杂性理论给予我们的结论却是，这种可能性尚属未知。

若设城市数目为n 时，那么组合路径数则为(n-1)!。

很显然，当城市数目不多时要找到最短距离的路线并不难，但随着城市数目的不断增大，组合路线数将呈指数级数规律急剧增长，以至达到无法计算的地步，这就是所谓的“组合爆炸问题”。

假设现在城市的数目增为20个，组合路径数则为(20-1)! ，如此庞大的组合数目，若计算机以每秒检索1000万条路线的速度计算，也需要花上386年的时间。

尽管现在计算机的计算速度大大提高，而且已有一些指数级的算法可精确地求解旅行商问题，但随着它们在大规模问题上的组合爆炸，人们退而求其次，转向寻找近似算法或启发式算法，经过几十年的努力，取得了一定的进展。

② 数学模型设(,)G V E =为赋权图，{1,2,}V n ="为顶点集，E 为边集，各顶点间距离为ij c ，已知(0,,,)ij ij c c i j V >=+∞∈，并设则旅行商问题的数学模型可写成如下的线性规划形式：ij ij i jMinZ c x ≠=∑1,(,)0,ij i j x ⎧=⎨⎩边在最优路线上其它,1,1,.1,{0,1},ij j i ij i jij i j S ij x i V x j V s t x K K V x i j V ≠≠∈⎧=∈⎪⎪=∈⎪⎨⎪≤−⊂⎪⎪∈∈⎩∑∑∑这里，K 为V 的所有非空子集，K 为集合K 中所含图G 的顶点个数。

遗传算法的优缺点及改进方法
遗传算法是一种基于生物遗传学原理的优化算法，具有自适应性和全局搜索能力。

但是，遗传算法在处理高维问题时存在收敛速度慢、局部最优解等缺点。

针对这些问题，可以通过改进遗传算法的种群初始化、交叉、变异等操作来提升其性能。

同时，也可以结合其他算法如粒子群算法、模拟退火算法等进行协同优化。

此外，选择适当的适应度函数和参数设置也对遗传算法的效果有重要影响。

综上所述，遗传算法在解决实际问题时需要综合考虑其优缺点和改进方法，以达到更好的优化效果。

- 1 -。