101000010010石河子第一中

新疆石河子市兵团八师一四三团第一中学20182018-2019学年高一（上）期末化学试卷考试用时90分钟试卷满分100分可能用到的相对原子质量H-1;C-12;N-14;O-16;Na-23;S-32;Cu-64 第Ⅰ卷一、选择题（每小题只有一个选项符合题意，每小题3分，共48分。

）1.下列为防止产生雾霾的措施中不可行的是 A. 停止冬季供暖，减少有害物质排放 B. 对锅炉和汽车等产生的有害气体和烟尘等进行处理 C. 退耕还林，改善生态环境 D. 寻找新能源，减少化石燃料的使用【答案】A 【解析】试题分析A．停止冬季供暖，虽然减少有害物质排放，但不符合客观实际，A错误；B．对锅炉和汽车等产生的有害气体和烟尘等进行处理可以减少雾霾的产生，B正确；C．退耕还林，改善生态环境有利于节能减排，可以防止雾霾的产生，C正确；D．寻找新能源，减少化石燃料的使用，有利于节约能源，且可以减少雾霾的生成，D正确，答案选A。

考点考查大气污染的有关分析 2.胶体区别与其他分散系的本质特征是 A. 能发生丁达尔现象 B. 胶体粒子能通过滤纸空隙 C. 胶体在一定条件下能稳定存在 D. 胶体分散质粒子直径在1nm～100nm之间【答案】D 【解析】胶体区别于其它分散系的本质特征是胶体粒子直径在1-100nm10-7～10-9m之间，溶液的粒子直径小于1nm，浊液的粒子直径大于100nm，故选D。

3.下列用品的有效成分及用途对应错误的是 A B C D 用品有效成分NaCl Na2CO3 AlOH3 CaClO2 用途做调味品做发酵粉做抗酸药做消毒剂 A. AB. BC. CD. D 【答案】B 【解析】小苏打的有效成分为NaHCO3，Na2CO3称为苏打或纯碱，B项错。

【此处有视频，请去附件查看】4.苹果汁是人们喜爱的饮料，由于此饮料中含有Fe2＋，现榨的苹果汁在空气中会由淡绿色变为黄色Fe3＋。

若榨汁时加入维生素C，可有效防止这种现象发生，这说明维生素C具有 A. 氧化性B. 还原性C. 碱性D. 酸性【答案】B 【解析】试题分析维生素C能把Fe3＋还原为Fe2＋，维生素C具有还原性，故B正确。

石河子143团第一中学三年发展规划（讨论稿）我校地处石河子市西郊15公里处，是一所完全中学，环境优美，学校创建于1954年，目前在校学生1700余人，学校被命名为兵团文明单位，荣获农八师教育教学管理先进单位称号。

学校正努力探索优质中学的建设模式，通过管理创新构建现代学校管理制度，在加强制度建设，队伍建设，教育改革和校园文化改革等方面跨出新的一步，办学质量稳步提升，社会各界和学生家长对学校的满意度不断提高。

一、现状分析1、外在环境学校位于石河子市西郊，具有独特的地域优势，便利的交通和良好的教学质量，吸引了周边团场居民的生源，并对教职员工在此环境中工作具有吸引力。

143团党委把教育摆在优先发展的战略地位，创设了良好的办学环境，尊师重教薇然成风，教师地位明显提高。

师市教育局把我们学校作为重点投入设施建设的地方，对教师业务管理和专业发展培养方面给予了大力扶持，这些都为推进学校教育跨越式发展提供了前所未有的机遇。

2、内在优势（1）学校环境优美，去年投入800万元学校已完成抗震加固工程，今年投入300万元的新建实验楼即将峻工，五月去西安实验仪器订购会落实近50万元的设备。

室内体育馆、300mm塑胶跑道建设已进入起步阶段，校园整洁、现代化教学设施齐全，校园周边环境良好，没有明显的安全隐患，与家长对子女就读学校的要求相接近。

（2）教师素质优良，学校现有教职工166名，其中专任教师136名，学校教师队伍整体素质高，高级教师32名，八师石河子市名师3名，高中学科带头人16名，团教学能手10名，学校骨干教师17名。

3、存在问题（1）教师队伍齐而不尖，年龄结构偏大，编制富余，超编严重，学科比例失调；知识陈旧，教学方法落后，缺乏在教育教学上突出的拔尖教师，学科建设不易，少数教师缺乏积极进取，精益求精的动力，部分教师存在职业倦怠现象，吃苦精神，责任意识有待提高和增强。

（2）德育工作没有形成系统，对学生的教育没有形成合力，德育工作还停留在说教层面上，八大教育重形式，轻内涵，缺实效，学生良好的行为习惯亟待培训、强化；学生综合素质评价工作处在应付阶段，没有发挥其育人功能，学生欠缺主动学习的精神。

2025届新疆石河子第一中学高三最后一模数学试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．当0a >时，函数()()2xf x x ax e =-的图象大致是（ ）A ．B ．C ．D ．2．已知直线y ＝k （x ﹣1）与抛物线C ：y 2＝4x 交于A ，B 两点，直线y ＝2k （x ﹣2）与抛物线D ：y 2＝8x 交于M ，N 两点，设λ＝|AB |﹣2|MN |，则（ ） A ．λ＜﹣16B ．λ＝﹣16C ．﹣12＜λ＜0D ．λ＝﹣123．下列函数中，既是偶函数又在区间0,上单调递增的是（ ）A ．y x =B ．()sin f x x x =C ．()2f x x x =+ D ．1y x =+4．已知函数2sin ()1x f x x =+．下列命题：①函数()f x 的图象关于原点对称；②函数()f x 是周期函数；③当2x π=时，函数()f x 取最大值；④函数()f x 的图象与函数1y x=的图象没有公共点，其中正确命题的序号是（ ） A ．①④B ．②③C ．①③④D ．①②④5．已知定义在R 上的奇函数()f x 满足()()11f x f x +=-，且当[]0,1x ∈时，()2xf x m =-，则()2019f =（ ） A ．1B ．-1C ．2D ．-26．已知集合A={x|y=lg （4﹣x 2）}，B={y|y=3x ，x ＞0}时，A∩B=（ ） A ．{x|x ＞﹣2} B ．{x|1＜x ＜2} C ．{x|1≤x≤2} D ．∅ 7．若点(2，k)到直线5x-12y+6=0的距离是4，则k 的值是( ) A ．1B ．-3C ．1或53D ．-3或1738．已知角a 的终边经过点()()4,30P m m m -≠，则2sin cos a a +的值是( )A ．1或1-B ．25或25- C ．1或25-D ．1-或259．已知函数()(N )k f x k x+=∈，ln 1()1x g x x +=-，若对任意的1c >，存在实数,a b 满足0a b c <<<，使得()()()g a f b g c ==，则k 的最大值是( )A ．3B ．2C ．4D ．510．已知函数f （x ）＝sin 2x +sin 2（x 3π+），则f （x ）的最小值为（ ）A ．12B ．14C ．4D ．211．设22(1)1z i i=+++（i 是虚数单位），则||z =（ ）AB ．1C ．2D12．下列说法正确的是（ ）A ．命题“00x ∃≤，002sin x x ≤”的否定形式是“0x ∀>，2sin x x >”B ．若平面α，β，γ，满足αγ⊥，βγ⊥则//αβC ．随机变量ξ服从正态分布()21,N σ（0σ>），若(01)0.4P ξ<<=，则(0)0.8P ξ>= D ．设x 是实数，“0x <”是“11x<”的充分不必要条件 二、填空题：本题共4小题，每小题5分，共20分。

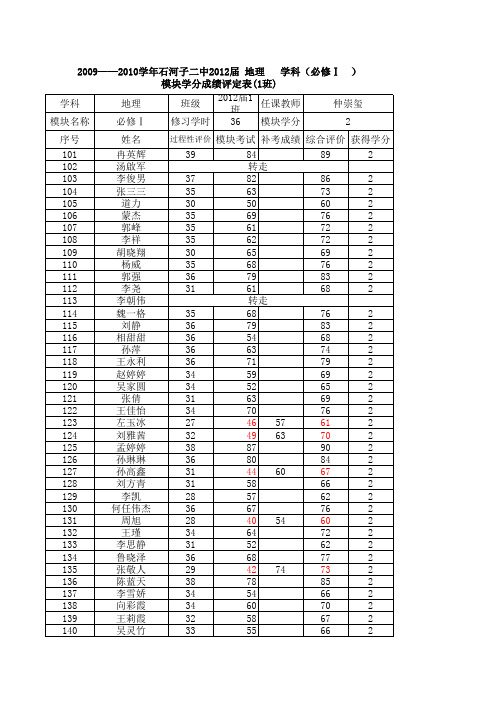
2009——2010学年石河子二中2012届 地理 学科（必修Ⅰ ）
模块学分成绩评定表(1班)
2009——2010学年石河子二中2012届 地理 学科（必修Ⅰ ）
模块学分成绩评定表(3班)
2009——2010学年石河子二中2012届 地理 学科（必修Ⅰ ）
模块学分成绩评定表(4班)
2009——2010学年石河子二中2012届 地理 学科（必修 Ⅰ ）
模块学分成绩评定表(5班)
2009——2010学年石河子二中2012届 地理 学科（必修Ⅰ ）
模块学分成绩评定表(6班)
2009——2010学年石河子二中2012届 地理 学科（必修Ⅰ ）
模块学分成绩评定表(7班)
2009——2010学年石河子二中2012届 地理 学科（必修Ⅰ ）
模块学分成绩评定表(8班)
2009——2010学年石河子二中2012届 地理 学科（必修Ⅰ ）
模块学分成绩评定表(10班)
2009——2010学年石河子二中2012届 地理 学科（必修 ） 模
块学分成绩评定表(12班)
2009——2010学年石河子二中2012届 地理 学科（必修 ）
模块学分成绩评定表(13班)。

2023-2024学年新疆石河子第一中学高一下学期3月月考数学试题一、单选题1．在中，角，，所对的边分别为，，，若，，，则（ ）AB ．C ．2D ．2．已知向量 , 则ABC =A ．30B ．45C ．60D ．1203．已知向量，则与共线且反向的单位向量为 （）A ．B ．C ．或D ．4．在平行四边形中，，设，，则向量（ ）A．B ．C ．D ．5．在中，，，则的面积是（ ）A ．B ．C ．或D ．6．所在平面内一点满足，若，则（ ）AB ．C．D ．7．窗户，在建筑学上是指墙或屋顶上建造的洞口，用以使光线或空气进入室内.如图1，这是一个外框为正八边形，中间是一个正方形的窗户，其中正方形和正八边形的中心重合，正方形的上､下边与正八边形的上､下边平行，边长都是4.如图2，是中间正方形的两个相邻的顶点，是外框正八边形上的一点，则的最大值是（ ）ABC V A B C a b c 1a =6A π=1sin 4B =b =121(2BA =u u v 12BC =u u u v ∠oooo()2,2AB = AB⎛ ⎝⎛ ⎝()2,2ABCD 14AE AC = AB a =BC b = DE =u u u r 1344a b - 3144a b - 2133a b - 1233a b-ABC ∆30B ∠= AB =2AC =ABC ∆P 22sin cos CP CA CB θθ=⋅+⋅ 2PA BP =cos2θ=1313-,A B P AB AP ⋅A ．B ．C ．D ．8．在中，分别为的对边，为的外心，且有，，若，，则A ．B ．CD ．9．已知、、均为非零向量，下列命题错误的是（ ）A ．，B ．可能成立C ．若，则D ．若，则或10．已知向量，，则下列结论正确的是（ ）A．若，则B ．若，则C ．若与的夹角为，则D ．若与方向相反，则在上的投影向量的坐标是11．在中，角A ，B ，C 所对的边分别为a ，b ，c ，下列说法中正确的是（ ）A．若，则B ．若，则C ．若，则为锐角三角形D ．若，则为直角三角形12．“奔驰定理”因其几何表示酷似奔驰的标志得来，是平面向量中一个非常优美的结论．奔驰定理与三角形四心（重心、内心、外心、垂心）有着神秘的关联．它的具体内容是：已知M 是内一点，，16+8816+ABC V ,,a b c ,,A B C O ABC V AB BC AC +=sin (cos cos sin 0C A C A +=AO x AB y AC =+,x y R ∈x y -=2-2a b cR λ∃∈()a b a bλ+=⋅()()a b c a b c ⋅⋅=⋅⋅r r r r r ra b b c ⋅=⋅r r r ra c= 1a b ⋅=1a = 1b = a =(cos ,sin )b αα= //a btan α=a b ⊥tan α=ab π3||3a b -= a b b a 1(,2-ABC V A B >sin sin A B >sin 2sin 2A B =A B=222a b c +>ABC V cos cos sin b C c B a A +=ABC V ABC V BMC △，的面积分别为，，，且．以下命题正确的有（ ）A ．若，则M 为的重心B ．若M 为的内心，则C ．若，，M 为的外心，则D ．若M 为的垂心，，则13．已知，，，则.14．在中，.15．△的内角的对边分别为，已知，，则△的面积为 ．16．如图，在和中，是的中点，，，若，则与的夹角的余弦值等于.17．在中，角的对边分别为．(1)求的值；(2)求边上的高．18．已知，，且与的夹角为，求：AMC V AMB V A S B S C S 0A B C S MA S MB S MC ⋅+⋅+⋅=::1:1:1A B C S S S =AMC V ABC V 0BC MA AC MB AB MC ⋅+⋅+⋅=45BAC ∠=︒60ABC ∠=︒ABC V ::2:1A B C S S S =ABC V 3450MA MB MC ++= cos AMB ∠=()1,2A ()2,3B ()2,5C -AB AC ⋅=ABC V sin :sin :sin 4A B C =A B C +-=ABC A B C ，，a b c ，，sin sin 4sin sin b C c B a B C +=2228b c a +-=ABC ABC V AEF △B EF 2AB EF ==3CA CB ==7AB AE AC AF ⋅+⋅=EF BCABC V ,,A B C 1,,,7,5,cos 7a b c a c B ===b AC 4a = 2b = ab 120(1)；(2)与的夹角；(3)若向量与平行，求实数的值.19．如图，在中，，，，是的中点，点满足，与交于点.（1）设，求实数的值；（2）设是上一点，且，求的值.20．在中，角，，的对边分别为，，．(1)求；(2)若点是上的点，平分，且，求面积的最小值．21．在平面直角坐标系中，为坐标原点，点，，满足.（1）求的值；（2）已知，，，若函数的最大值为3，求实数的值.22．如图，在等腰梯形中，，，，是的中点.(1)记，且，求，值；2a b - aa b +2a b λ- 3a b λ-λABC ∆90BAC ∠=︒2AB =3AC =D BC E 2AE EC =BE AD G AG AD λ=λH BE HA HB HC HA ⋅=⋅ GH BC ⋅ABC V A B C a b c sin cos b A B +=A D BC AD BAC ∠2AD =ABC V O A B C 1233OC OA OB =+ACCB(1,cos )A x (1cos ,cos )B x x +[,0]3x π∈-2()(2)3f x OA OC m AB =⋅-+m ABCD //AD BC 2AD =60ABC ∠= E AD BD m = BA n =228m n -=m n(2)记，是线段上一动点，且，求的取值范围.()12BC AD λλ=<< F CD CD CF λ= 22BE BF λ⋅-答案1．答案：B解：根据正弦定理可得，即，解得，故选：B.2．答案：A解：由题意，得，故选A ．3．答案：B解：因为，所以可设与共线且反向的单位向量，又解得，或（舍去），故.故选：B 4．答案：A解：解：.故选：A.5．答案：C解：解：由，，根据正弦定理得：为三角形的内角，或，或sin sin a bA B=11124b=12b =cos BA BC ABC BA BC⋅∠===30ABC ∠=︒()2,2AB = AB()(),0e m m m =< 1e=1=212m =m =m e ⎛= ⎝ ()()1111344444DE AE AD AC BC AB BC BC a b b a b =-=-=+-=+-=- c AB ==2b AC ==30B ∠=︒sin sin b c B C =sin sin c B C b ==C ∠ 60C ∴∠=︒120︒90A ∴∠=︒30︒在中，由，，或则面积故选C.6．答案：C【解析】根据平面向量基本定理，用作为基底表示出.即可求得，由余弦二倍角公式即可求得.解：所在平面内一点，所以因为所以由余弦二倍角公式可得故选：C 7．答案：A解：记正八边形右下角的两个顶点分别为，连接，由题意易得是等腰直角三角形，，则不妨设，由于题目要求的最大值，故只考虑的情况，过作，垂足为，则，又，c =2b =90A ∠=︒30︒1sin 2S bc A ==,CA CB CP22sin ,cos θθcos 2θP 2PA BP =CP CB BP=+ 13CB BA=+ ()13CB CA CB=+- 2133CB CA +=22sin cos CP CA CBθθ=⋅+⋅ 2212sin ,cos 33θθ==cos2θ=22211cos sin 333θθ-=-=,C D ,BC BD BCD △4CD =BC =,AP AB θ= AB AP ⋅090θ︒≤<︒P PE AB ⊥E cos AP AE θ= 4AB =所以，显然，当点与点重合时，取得最大值，所以的最大值为故选：A.8．答案：A 解：因为， 所以，又因为，所以，所以，所以，即，所以，所以，所以，如图所示：由正弦定理得：，因为，则，所以，cos 4AB AP AB AP AB AE AE θ⋅=== P C AE 4AB BC +=+AB AP ⋅(4416⨯+=+AB BC AC +=c a +=sin (cos cos sin 0C A C A +=sin cos cos sin C A C A C +()sin C A C +=sin B C =b =a c =222222231cos 222a c b c c c B ac c +-+-===-120,30B A C === 12sin cR AO c C===AO x AB y AC =+2x AO AB AB AB A y C ⋅=+⋅ 22221c c x =即，则，所以，即，，.故选：A.9．答案：ACD解：仍是向量，不是向量，A 错；不妨取，，，则，，此时，B 对；若，，，则，但，C 错；若，，则，但，，D 错.故选：ACD.10．答案：ABD解：向量，，对于A ，由，得，因此，A 正确；对于B ，由，因此B 正确；对于C ，与的夹角为，，，因此，C 错误；对于D ，与方向相反，则在上的投影向量为，D 正确.故选：ABD11．答案：AD解：选项A ：因为，所以，由正弦定理，得，即.所以选项A 正确；231x y +=2AO AC xAB AC y AC ⋅=⋅+ 22223323x c c y c =+21x y +=1,1x y =-=2x y -=-()+a b λ a b ⋅()1,1a =r()2,2b = ()3,3c = ()()()43,312,12a b c ⋅⋅== ()()1212,12a b c a ⋅⋅==()()a b c a b c ⋅⋅=⋅⋅r r r r r r ()1,0b = ()3,2a = ()3,3c = 3a b b c ⋅=⋅= a c ≠()2,1a =r ()1,1b =-r 1a b ⋅=1a > 1b > a =(cos ,sin )b αα= //a bsin αα=tan α=a b ⊥cos 0αα+=tan α=ab π3||2,||1a b == 12112a b ⋅=⨯⨯= ||a b -== a b b a211,||22a b a a a ⎛⋅=-=- ⎝A B >a b >2sin 2sin R A R B >sin sin A B >选项B ：在中，因为，所以或，即或，所以选项B 错误；选项C ：因为，所以，所以为锐角，但不一定是锐角三角形，所以选项C 错误；选项D ：因为，所以，即，又因为 ，所以，所以，即，所以为直角三角形，所以选项正确.故选：AD.12．答案：ABD解：对A 选项，因为，所以，取的中点，则，所以，故，，三点共线，且，同理，取中点，中点，可得，，三点共线，，，三点共线，所以为的重心，A 正确；对B 选项，若为的内心，可设内切圆半径为，则，，，所以，即，B 正确；对C 选项，若，，为的外心，则，设的外接圆半径为，故，，，故，，，ABC V sin 2sin 2A B =22A B =22A B π+=A B =2A B π+=222a b c +>222cos 02a b c C ab +-=>C ABC V cos cos sin b C c B a A +=2sin cos sin cos sin B C C B A +=2sin()sin B C A +=A B C π++=sin()sin B C A +=sin 1A =2π=A ABC V D ::1:1:1A B C S S S =0MA MB MC ++=BC D 2MB MC MD += 2MD MA =-A M D 2MA MD =AB E AC F B M F C M E M ABC V M ABC V r 12A S BC r =⋅12B S AC r =⋅12C S AB r =⋅1110222BC r MA AC r MB AB r MC ⋅⋅+⋅⋅+⋅⋅= 0BC MA AC MB AB MC ⋅+⋅+⋅=45BAC ∠=︒60ABC ∠=︒M ABC V 75ACB ∠=︒ABC V R 290BMC BAC ∠=∠=︒2120AMC ABC ∠=∠=︒2150AMB ACB ∠=∠=︒2211sin 9022A S R R =︒=221sin1202B S R =︒=2211sin15024C S R R =︒=所以，C 错误；对D 选项，若为的垂心，，则，如图，，，，相交于点，又，，即，，即，，即，设，，，则，，，因为，，所以，即，D 正确；故选：ABD.13．答案：0解：解：，，::2A B C S S S =M ABC V 3450MA MB MC ++= ::3:4:5A B C S S S =AD BC ⊥CE AB ⊥BF AC ⊥M ABC A B C S S S S =++V 31124AABC S S ==V :3:1AM MD =41123BABCS S ==V :1:2MF BM =512CABC S S =V :5:7ME MC =MD m =MF n =5ME t =3AM m =2BM n =7MC t =CAD CBF ∠=∠sin ,sin 32n m CAD CBF m n∠=∠=32n m m n =m =cos 2m BMD n ∠===()cos cos πAMB BMD ∠=-∠=()1,1AB = ()3,3AC =-.故答案为：0.14．答案：/解：因为由正弦定理得不妨设，由余弦定理得：，因，所以，，故答案为：15解：［方法一］：【最优解】边化角因为，由正弦定理得，因为，所以．又因为，由余弦定理，可得，所以，即为锐角，且，所以的面积为.［方法二］：角化边因为，由正弦定理得，即，又，所以，．又因为，由余弦定理，可得，所以，即为锐角，且，()13130ABAC ⋅=⨯-+⨯= 23π-23π-sin :sin :sin 4A B C =::4:a b c =a 4b =c =222cos 2a b c C ab+-===-()0,πC ∈5π6C =2ππ2=π235π=6A B C C +-=--´-2π3-sin sin 4sin sin b C c B a B C +=sin sin sin sin 4sin sin sin B C C B A B C +=sin sin 0B C ≠1sin 2A =2228b c a +-=2222cos a b c bc A =+-2cos 8bc A =cos 0A >A cos A =bc =ABC V 111sin 222S bc A ===sin sin 4sin sin b C cB a BC +=4sin bc bc ab C +=2sin c a C =sin sin c a C A=1sin 2A =2228b c a +-=2222cos a b c bc A =+-2cos 8bc A =cos 0A >A cos A =bc =所以的面积为.16．答案：解：由图知： ，，∴，又，且，，∴，∴，而，即，又，∴.故答案为：.17．答案：(1)解：（1）在中，由余弦定理，得，因为，所以．（2）由，得，所以的面积为，设边上的高为，则故．18．答案：(1)(2)(3)ABCV 111sin 222S bc A ===13AE AB BE =+ AF AB BF =+ 2()()7AB AE AC AF AB AB BE AB B AC A F BE AB B B A F B AC AC ⋅+⋅=⋅+⋅=+⋅++++=⋅⋅ 2222()29AC AB AC AC AB AB BC -=-⋅+== 3CA =2AB =2AC AB ⋅= 1AB A F C BE B =⋅+⋅ ()AB BE AB BF ⋅=⋅- 1()12BF AC AB EF BC ⋅-=⋅=2EF =3CB =1cos ,3EF BC <>= 138b =ABC V 2222cos b ac ac B =+-214925275647b =+-⨯⨯⨯=0b >8b =()1cos ,0,π7B B =∈sin B ==ABC V 11sin 7522S ac B ==⨯⨯=AC h 142S bh h ===h =π6解：（1），（2），即，所以与的夹角为；（3）若向量与平行，则，，得，所以的值为.19．答案：（1）（2）解：（1）设，，因为，是的中点，所以.①设，，故，整理得，又，即，所以.②2a = ==()cos ,a a b a a b aa b ⋅++==+ ====π,6+=a a b a a b + π62a b λ- 3a b λ- ()23a b k a b λλ-=- 23k k λλ=⎧⎨-=-⎩k λ⎧=⎪⎨⎪=⎩k λ⎧=⎪⎨⎪=⎩λ452-AC a = AB b = AG AD λ= D BC 222AC AB AG a b λλλ+=⋅=+ BG tBE = 01t <<()AG AB t AE AB -=- ()1AG t AE t AB =+- 2AE EC = 23AE AC = ()()221133t AG t AC t AB a t b =⋅+-=+-联立①②，据平面向量其本定理，得解得，，所以实数的值为.（2）因为，所以，即，所以.20．答案：(1)(2)解：（1）由题意知，,,，而，，即又，故；（2）由于点是上的点，平分，且，则，由，得，即，则，当且仅当时取等号，故，当且仅当时取等号，所以即面积的最小值为21．答案：（1）2；（2）.2,231,2t t λλ⎧=⎪⎪⎨⎪=-⎪⎩4=5λ35t =λ45HA HB HC HA ⋅=⋅ ()0HA HB HC ⋅-= 0AH BC ⋅= ()GH BC AH AG BC AH BC AG BC ⋅=-⋅=⋅-⋅ ()()22222555AG BC a b a b a b ⎛⎫=-⋅=-+⋅-=-- ⎪⎝⎭ ()2223225=-⨯-=-2π3A =ABC V sin cos b A B +=sin sin cos C B A A B +=)sin sin cos A B B A A B ++cos cos sin )sin sin cos A B A B B A A B ++=sin sin sin 0A B B A +=(0,π),sin 0B B ∈∴≠sin 0A A +=tan A =(0,π)A ∈2π3A =D BC AD BAC ∠2AD =1π23BAD CAD BAC ∠=∠=∠=ABC ABD ADC S S S =+V V V 12π1π1πsin 2sin 2sin 232323bc c b =⨯⨯⨯+⨯⨯⨯2()bc c b =+2()bc c b =+≥b c =16bc ≥4b c ==1sin 2ABC S bc A =≥V ABC V 12-解：（1）由题意知，，即，所以，即.（2）易知，，，则，，所以，令，则，，其对称轴方程是.当时，的最大值为，解得；当时，的最大值为，解得（舍去）.综上可知，实数的值为.22．答案：(1)，(2)解：（1）依题意，所以，即，即，又，解得，；(2)过点作，如图建立平面直角坐标系，因为，，所以，，，，，32OC OA OB =+ 2()OC OB OA OC -=-2BC CA =2AC CB=(1,cos )OA x =(1cos ,cos )OB x x =+ (cos ,0)AB x = 2(1cos ,cos )3OC x x =+ cos AB x = 2()cos 2cos 1f x x m x =-+cos t x =2()21g t t mt =-+1[,1]2t ∈t m =34m ≤()g t (1)1213g m =-+=12m =-34m >()g t 11(1324g m =-+=74m =-m 12-2n =m =15,2⎡⎫-⎪⎢⎣⎭BD BA AD =+ ()22222BD BA AD BA BA AD AD =+=+⋅+ 2222cos 60BD BA BA AD AD =+⋅︒+ 2224m n n =++228m n -=2n =m =A AO BC ⊥()12BC AD λλ=<< 2AD =()1,0B λ-()1,0C λ+)()1A λ-)()1E λ-)()1D λ-所以，，，因为，所以所以，所以，令，，设且，则，当时，，则，又，所以；当时，，则，又，所以；所以在上单调递减，在上单调递增，又，，，所以，所以，即的取值范围为.)()1BE λλ=- )()11CD λλ=-- ()2,0BC λ= CD CF λ= 1CF CD λ=()21122,0BF BC CF λλλλλλ⎛⎛--+=+=+= ⎝⎝ ()2222312122BE BF λλλλλλ-⋅-=-++- ()2313125λλλλλ-=-+=+-()32f x x x=+()1,2x ∈()12,1,2x x ∈12x x <()()()121212121212233322x x f x f x x x x x x x x x ⎛⎫--=+-+=- ⎪⎝⎭12,x x ⎛∈ ⎝12312x x <<12230x x -<120x x -<()()120f x f x ->12,2x x ⎫∈⎪⎪⎭12342x x <<12230x x ->120x x -<()()120f x f x -<()f x ⎛ ⎝2⎫⎪⎪⎭()15f =()1122f =f =1152<<()112f x ⎡⎫∈⎪⎢⎣⎭31255,2λλ⎡⎫+-∈⎪⎢⎣⎭22BE BF λ⋅- 15,2⎡⎫⎪⎢⎣⎭。

家长和考生都希望能够去一个好的高中读书。

重点学校会有更好的学习环境，让同学们能够更好地冲刺高考。

那么石河子有哪些重点高中？排名靠前的有哪几所？
石河子高中排名
1、石河子第一中学
2、石河子第二中学
3、新疆兵团农八师石河子市第二中学
4、石河子第五中学
5、石河子高级中学
6、石河子第四中学
7、石河子民族中学
8、石河子通联中学
9、石总场一中
10、石河子第八中学
注：学校榜单主要依据了学校的社会知名度，中考录取分数线，高考成绩，升学走向，并通过比较学校师资力量、硬件设施、办学规模面积、建校历史、获得上级荣誉等重点学校指标综合整理而成，供您家小孩报考入学参考使用。

以上高中名单排名不分先后，只提供部份高中名单展示，最终名单学校按地方教育部门提供为准，仅供您参考！
石河子学校简介
石河子第一中学
石河子市第一中学创建于1954年，前身是中国人民解放军第二十二兵团第二子弟校、新疆军区生产建设兵团第二子女校、农八师子女校。

近几年，先后被认定为清华大学、天津大学、兰州大学、北京交通大学、北京化工大学、西南政法大学等优质生源基地学校。

石河子第二中学
石河子第二中学创建于1956年8月10日，是新疆生产建设兵团创建最早的一所中学，原名“中国人民解放军新疆军区生产建设兵团石河子中学”，被誉为“军垦第一校”。

1975年5月，更名为“石河子市第二中学”。

2007年9月，整体搬迁进入国家级石河子经济技术开发区高中学区，更名为“石河子第二中学”。

以上就是石河子重点高中的排名情况，希望对大家有所帮助。