高一拓展训练五：空间立体几何(学生版)

课题：立体几何综合训练个性化教学辅导教案学生姓名年级学科数学上课时间教师姓名课题立体几何综合训练教学过程教师活动1.若三个平面两两相交，有三条交线，则下列命题正确的是（）A．三条交线为异面直线B．三条交线两两平行C．三条交线交于一点D．三条交线两两平行或交于一点2.回顾下直线，平面的平行判断与性质。

3.回顾下直线，平面垂直的性质和判定方法。

4.求线面所成角与二面角的一般步骤是什么？5.若已知条件中，已知三角形中两线段相等，你会想到什么？遇到中点呢？立体几何综合训练例1 如图，直三棱柱111ABC A B C - 中，90BAC ∠=，2AB AC ==，11AA =，点,M N 分别为1A B 和11B C 的中点．(1)证明：MN ∥平面11A ACC ； (2)求三棱锥1A MNC -的体积例2 如图，已知111ABC A B C -是正三棱柱，棱长均为5，E 、F 分别是AC 、11A C 的中点． （1）求证：平面1AB F ∥平面1BEC ； （2）求点A 到平面1BEC 的距离．例3 如图，在直角梯形SABC 中，∠B=∠C=π2，D 为边SC 上的点，且AD ⊥SC ，现将△SAD 沿AD 折起到达PAD 的位置（折起后点S 记为P ），并使得PA ⊥AB ． （1）求证：PD ⊥平面ABCD ；（2）已知PD=AD ，PD +AD +DC=6，G 是AD 的中点，当线段PB 取得最小值时，则在平面PBC 上是否存在点F ，使得FG ⊥平面PBC ？若存在，确定点F 的位置，若不存在，请说明理由．立体几何综合训练教学过程： 突破1： 1.线面平行：①定义：直线与平面无公共点.②判定定理：（线线平行线面平行）③性质定理：（线面平行线线平行）④判定或证明线面平行的依据：（i ）定义法（反证）：（用于判断）；////a b a a b ααα⎫⎪⊄⇒⎬⎪⊂⎭⇒////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭⇒//l l αα=∅⇒（ii ）判定定理：“线线平行面面平行”（用于证明）；（iii ）“面面平行线面平行”（用于证明）； （4）（用于判断）；3.面面平行： ①定义：；②判定定理：如果一个平面内的两条相交直线都平行于另一个平面，那么两个平面互相平行； 符号表述： 【如下图①】图① 图②推论：一个平面内的两条相交直线分别平行于另一个平面的两条直线，那么这两个平面互相平行 符号表述：【如上图②】判定2：垂直于同一条直线的两个平面互相平行. 符号表述：.【如右图】③判定与证明面面平行的依据：（1）定义法；（2）判定定理及推论（常用）（3）判定2 ④面面平行的性质： （1）（面面平行线面平行）； （2）；（面面平行线线平行）（3）夹在两个平行平面间的平行线段相等。

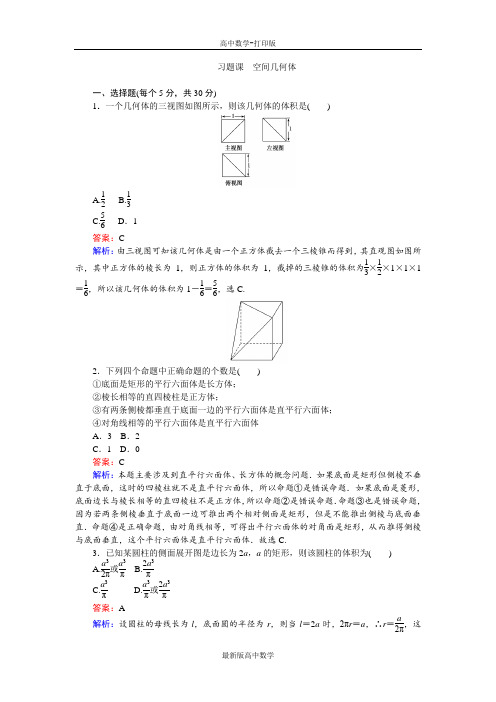
习题课 空间几何体一、选择题(每个5分，共30分)1．一个几何体的三视图如图所示，则该几何体的体积是( )A.12B.13C.56D ．1 答案：C 解析：由三视图可知该几何体是由一个正方体截去一个三棱锥而得到，其直观图如图所示，其中正方体的棱长为1，则正方体的体积为1，截掉的三棱锥的体积为13×12×1×1×1＝16，所以该几何体的体积为1－16＝56，选C.2．下列四个命题中正确命题的个数是( ) ①底面是矩形的平行六面体是长方体； ②棱长相等的直四棱柱是正方体；③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体； ④对角线相等的平行六面体是直平行六面体 A ．3 B ．2 C ．1 D ．0 答案：C解析：本题主要涉及到直平行六面体、长方体的概念问题．如果底面是矩形但侧棱不垂直于底面，这时的四棱柱就不是直平行六面体，所以命题①是错误命题．如果底面是菱形，底面边长与棱长相等的直四棱柱不是正方体，所以命题②是错误命题．命题③也是错误命题，因为若两条侧棱垂直于底面一边可推出两个相对侧面是矩形，但是不能推出侧棱与底面垂直．命题④是正确命题，由对角线相等，可得出平行六面体的对角面是矩形，从而推得侧棱与底面垂直，这个平行六面体是直平行六面体．故选C.3．已知某圆柱的侧面展开图是边长为2a ，a 的矩形，则该圆柱的体积为( ) A.a 32π或a 3π B.2a 3π C.a 3π D.a 3π或2a 3π 答案：A解析：设圆柱的母线长为l ，底面圆的半径为r ，则当l ＝2a 时，2πr ＝a ，∴r ＝a2π，这时V 圆柱＝2a ·π⎝⎛⎭⎫a 2π2＝a 32π；当l ＝a 时，2πr ＝2a ，∴r ＝a π，这时V 圆柱＝a ·π⎝⎛⎭⎫a π2＝a 3π.综上，该圆柱的体积为a 32π或a 3π.4．一个圆锥的底面积为9π，母线长为5，则它的高为( ) A ．4 B ．3C. 5D.7 答案：A解析：易知底面圆的半径r ＝3，由勾股定理h 2＋r 2＝l 2，得h ＝4. 5．有下列命题：①从投影的角度看，三视图画出的直观图是在平行投影下画出来的空间图形； ②平行投影的投影线互相平行，中心投影的投影线相交于一点； ③空间几何体在平行投影与中心投影下有不同的表现形式． 其中正确的命题有( ) A ．1个 B ．2个 C ．3个 D ．0个 答案：D6．甲、乙、丙、丁四人分别面对面地坐在一张四方形桌子旁边，桌上一张纸上写着数字“9”，甲说他看到的是“6”，乙说他看到的是“ 6”丙说他看到的是“ 9”，丁说他看到的是“9”则下列说法中正确的是( )A ．甲在丁的对面，乙在甲的左边，丙在丁的右面B ．丙在乙的对面，丙的左边是甲，右边是乙C ．甲在乙的对面，甲的右边是丙，左边是丁D ．甲在丁的对面，乙在甲的右边，丙在丁的右边 答案：D 解析：桌上一张纸上写着数字9，则看到9的人应坐在桌子的正面，看到6的人应坐在他的对面，如图所示．由此便可判断乙在左侧，而丙应在右侧．所以乙应在甲的右边．所以选D.二、填空题(每个5分，共15分)7．用6根长度相等的火柴搭成边长等于火柴长的正三角形，最多能搭成________个． 答案：4解析：考虑正四面体8．已知半径为5的球的两个平行截面圆的周长分别为6π和8π，则这两个截面间的距离为________．答案：1或7解析：若两个平行截面在球心的同侧，则两个截面间的距离为52－32－52－42＝1；若两个平行截面在球心的异侧，则两个截面间的距离为52－32＋52－42＝7.9．一个几何体的三视图及其尺寸(单位：cm)如图所示，则该几何体的表面积是________，体积是________．答案：24π cm 2 12π cm 3解析：由三视图可知该几何体是底面直径为6 cm ，母线长为5 cm 的圆锥，故S 表＝πrl＋πr 2＝24π(cm 2)，同时求出圆锥的高为4 cm ，故体积为13πr 2h ＝12π(cm 3)．三、解答题10．(15分)把一个圆锥截成圆台，已知圆台的上、下底面半径的比是1：4，母线长是10 cm ，求圆锥的母线长．解：设圆锥的母线长为x cm ， 作圆锥的轴截面，如右图． 在Rt △SOA 中，O ′A ′∥OA ， ∴SA ′：SA ＝O ′A ′：OA . 即(x －10)：x ＝1：4，解得x ＝1313.∴圆锥的母线长为1313cm.11．(20分)如图所示，在多面体FE －ABCD 中，已知ABCD 是边长为1的正方形，且△ADE ，△BCF 均为正三角形，EF ∥AB ，EF ＝2，求该多面体的体积V .解：如图所示，分别过A ，B 作EF 的垂线AG ，BH ，垂足分别为G ，H .连接DG ，CH ，容易求得EG ＝HF ＝12.所以AG ＝GD ＝BH ＝HC ＝32， S △AGD ＝S △BHC ＝12×22×1＝24，V ＝V E －ADG ＋V F －BHC ＋V AGD －BHC＝⎝⎛⎭⎫13×12×24×2＋24×1＝23. 12．(20分)如图，在正三棱锥P －ABC 中，∠APB ＝30°，侧棱长为a ，E ，F 分别是PB ，PC 上的点，求△AEF 周长的最小值．解：将正三棱锥P －ABC 沿棱PA 展开可得如图所示的图形，易知当A ，E ，F ，A ′(A )共线时，△AEF 的周长最小．在展开图中，∠APA ′＝90°，故△APA ′是等腰直角三角形，因此所求的△AEF 周长的最小值即AA ′的长，为2a .。

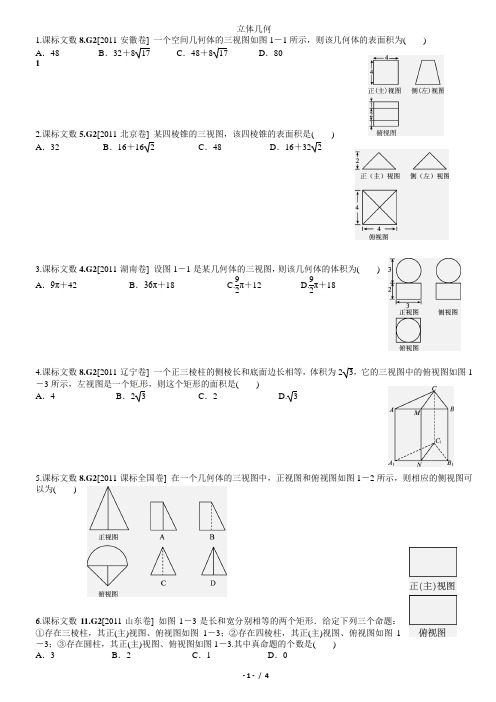
立体几何1.课标文数8.G2[2011·安徽卷] 一个空间几何体的三视图如图1－1所示，则该几何体的表面积为( )A ．48B ．32＋817C ．48＋817D ．8012.课标文数5.G2[2011·北京卷] 某四棱锥的三视图，该四棱锥的表面积是( )A ．32B ．16＋16 2C ．48D ．16＋32 23.课标文数4.G2[2011·湖南卷] 设图1－1是某几何体的三视图，则该几何体的体积为( )A ．9π＋42B ．36π＋18 C.92π＋12 D.92π＋184.课标文数8.G2[2011·辽宁卷] 一个正三棱柱的侧棱长和底面边长相等，体积为23，它的三视图中的俯视图如图1－3所示，左视图是一个矩形，则这个矩形的面积是( )A ．4B ．23C ．2 D. 35.课标文数8.G2[2011·课标全国卷] 在一个几何体的三视图中，正视图和俯视图如图1－2所示，则相应的侧视图可以为( )6.课标文数11.G2[2011·山东卷] 如图1－3是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正(主)视图、俯视图如图1－3；②存在四棱柱，其正(主)视图、俯视图如图1－3；③存在圆柱，其正(主)视图、俯视图如图1－3.其中真命题的个数是( )A ．3B ．2C ．1D ．07.课标文数5.G2[2011·陕西卷] 某几何体的三视图如图1－2所示，则它的体积为( )A ．8－2π3B ．8－π3C ．8－2π D.2π38.课标文数10.G2[2011·天津卷] 一个几何体的三视图如图1－4所示(单位：m)，则该几何体的体积为________ m 3.9.课标文数19.G4，G7[2011·安徽卷] 如图1－4，ABEDFC 为多面体，平面ABED 与平面ACFD 垂直，点O 在线段AD 上，OA ＝1，OD ＝2，△OAB ，△OAC ，△ODE ，△ODF 都是正三角形．(1)证明直线BC ∥EF ； (2)求棱锥F －OBED 的体积．10.课标文数15.G4[2011·福建卷] 如图1－3，正方体ABCD －A 1B 1C 1D 1中，AB ＝2，点E 为AD 的中点，点F 在CD 上，若EF ∥平面AB 1C ，则线段EF 的长度等于________．11.课标数学16.G4，G5[2011·江苏卷] 如图1－2，在四棱锥P－ABCD中，平面PAD⊥平面ABCD，AB＝AD，∠BAD ＝60°，E、F分别是AP、AD的中点．求证：(1)直线EF∥平面PCD；(2)平面BEF⊥平面PAD.12.课标文数4.G4[2011·浙江卷] 若直线l不平行于平面α，且l⊄α，则()A．α内的所有直线与l异面B．α内不存在与l平行的直线C．α内存在唯一的直线与l平行D．α内的直线与l都相交13.课标文数18.G5，G11[2011·课标全国卷] 如图1－8，四棱锥P－ABCD中，底面ABCD为平行四边形，∠DAB ＝60°，AB＝2AD，PD⊥底面ABCD.(1)证明：PA⊥BD；(2)设PD＝AD＝1，求棱锥D－PBC的高．14课标文数16.G5[2011·陕西卷] 如图1－8，在△ABC中，∠ABC＝45°，∠BAC＝90°，AD是BC上的高，沿AD 把△ABD折起，使∠BDC＝90°. (1)证明：平面ADB⊥平面BDC；(2)若BD＝1，求三棱锥D－ABC的表面积．15.课标数学16.G4，G5[2011·江苏卷] 如图1－2，在四棱锥P－ABCD中，平面PAD⊥平面ABCD，AB＝AD，∠BAD＝60°，E、F分别是AP、AD的中点．求证：(1)直线EF∥平面PCD；(2)平面BEF⊥平面PAD.16.大纲文数6.G5[2011·四川卷] l 1，l 2，l 3是空间三条不同的直线，则下列命题正确的是( )A ．l 1⊥l 2，l 2⊥l 3⇒l 1∥l 3B ．l 1⊥l 2，l 2∥l 3⇒l 1⊥l 3C ．l 1∥l 2∥l 3⇒l 1，l 2，l 3共面D ．l 1，l 2，l 3共点⇒l 1，l 2，l 3共面17.课标文数18.G7[2011·辽宁卷] 如图1－8，四边形ABCD 为正方形，QA ⊥平面ABCD ，PD ∥QA ，QA ＝AB ＝12PD. (1)证明：PQ ⊥平面DCQ ； (2)求棱锥Q －ABCD 的体积与棱锥P －DCQ 的体积的比值．18.课标文数20.G12[2011·福建卷] 如图1－5，四棱锥P －ABCD 中，PA ⊥底面ABCD ，AB ⊥AD ，点E 在线段AD 上，且CE ∥AB. (1)求证：CE ⊥平面PAD ；(2)若PA ＝AB ＝1，AD ＝3，CD ＝2，∠CDA ＝45°，求四棱锥P －ABCD 的体积．19.[2011·北京崇文一模] 已知m ，n 是两条不同直线，α，β，γ是三个不同平面，则下列命题中正确的为 ( )A ．若α⊥γ，β⊥γ，则α∥βB ．若m ∥α，m ∥β，则α∥βC ．若m ∥α，n ∥α，则m ∥nD ．若m ⊥α，n ⊥α，则m ∥n。

第二章知识点总结一、平面通常用一个平行四边形来表示.平面常用希腊字母α、β、γ,或拉丁字母M 、N 、P 来表示，也可用表示平行四边形的两个相对顶点字母表示，如平面AC.在立体几何中，大写字母A ，B ，C ，,表示点，小写字母，a,b,c,,l,m,n,,表示直线，且把直线和平面看成点的集合，因而能借用集合论中的符号表示它们之间的关系，例如：a)A ∈l —点A 在直线l 上；A α—点A 不在平面α内；b)l α—直线l 在平面α内；c)aα—直线a 不在平面α内；d)l ∩m=A —直线l 与直线m 相交于A 点；e)α∩l=A —平面α与直线l 交于A 点；f)α∩β=l —平面α与平面β相交于直线l.二、平面的基本性质公理1 如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内. 公理2 如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线.公理3 经过不在同一直线上的三个点，有且只有一个平面.根据上面的公理，可得以下推论.推论1 经过一条直线和这条直线外一点，有且只有一个平面.推论2 经过两条相交直线，有且只有一个平面. 推论3 经过两条平行直线，有且只有一个平面.公理4 平行于同一条直线的两条直线互相平行三、证题方法练习1、已知直线//b c ，且直线a 与,b c 都相交，求证：直线,,a b c 共面（注：《第二教材》25-26页，题型1、题型2）四、空间线面的位置关系共面平行—没有公共点(1)直线与直线相交—有且只有一个公共点异面(既不平行，又不相交)直线在平面内—有无数个公共点(2)直线和平面直线不在平面内平行—没有公共点(直线在平面外) 相交—有且只有一公共点(3)平面与平面相交—有一条公共直线(无数个公共点)平行—没有公共点五、异面直线的判定证明两条直线是异面直线通常采用反证法.有时也可用定理“平面内一点与平面外一点的连线，与平面内不经过该点的直线是异面直线”.证题方法间接证法直接证法反证法同一法ABCD MNS 练习2、求证：两条异面直线不能同时和一个平面垂直练习3、四面体S ABC 中，各个侧面都是边长为a 的正三角形，,E F 分别是SC 和AB 的中点，则异面直线EF与SA 所成的角是多少？六、线面平行与垂直的判定 (1)两直线平行的判定①定义：在同一个平面内，且没有公共点的两条直线平行.②如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行，即若a ∥α,aβ④垂直于同一平面的两直线平行，即若a ⊥α，b ⊥α，则a ∥b （线面垂直的性质定理）⑤两平行平面与同一个平面相交，那么两条交线平行，即若α∥β,α∩γ,β∩γ=b,则a ∥b （面面平行的性质公理）⑥中位线定理、平行四边形、比例线段,,，α∩β=b,则a ∥b.（线面平行的判定定理）③平行于同一直线的两直线平行，即若a ∥b,b ∥c,则a ∥c.（公理4）(2)两直线垂直的判定①定义：若两直线成90°角，则这两直线互相垂直.②一条直线与两条平行直线中的一条垂直，也必与另一条垂直.即若b ∥c,a ⊥b,则a ⊥c③一条直线垂直于一个平面，则垂直于这个平面内的任意一条直线.即若a ⊥α,bα，a ⊥b.④三垂线定理和它的逆定理：在平面内的一条直线，若和这个平面的一条斜线的射影垂直，则它也和这条斜线垂直.⑤如果一条直线与一个平面平行，那么这条直线与这个平面的垂线垂直.即若a ∥α,b ⊥α,则a ⊥b.(3)直线与平面平行的判定①定义：若一条直线和平面没有公共点，则这直线与这个平面平行.②如果平面外一条直线和这个平面内的一条直线平行，则这条直线与这个平面平行.即若aα,bα，a ∥b,则a∥α.（线面平行的判定定理）③两个平面平行，其中一个平面内的直线平行于另一个平面，即若α∥β,lα，则l ∥β.练习4、如图：S 是平行四边形ABCD 平面外一点，,M N 分别是,SA BD 上的点，且SMAM =NDBN ，求证：//MN 平面SBC练习5、两个全等的正方形ABCD 和ABEF 所在平面相交于AB ，M ∈AC ，N ∈FB ，且AM=FN ，求证MN ∥平面BCE（用两种方法来证）(4)直线与平面垂直的判定①定义：若一条直线和一个平面内的任何一条直线垂直，则这条直线和这个平面垂直.②如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面.即若mα，nα，m ∩n=B,l ⊥m,l ⊥n,则l ⊥α.（线面垂直判定定理）③如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于同一平面.即若l ∥a,a ⊥α,则l ⊥α. ④一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面，即若α∥β,l ⊥β，则l ⊥α.⑤如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面，即若α⊥β,a ∩β=α，lβ，l ⊥a,则l ⊥α.(面面垂直的性质定理)练习6、已知E ，F 分别是正方形ABCD 边AD ，AB 的中点，EF 交AC 于M ，GC 垂直于ABCD 所在平面．（1）求证：EF ⊥平面GMC ．（2）若AB ＝4，GC ＝2，求点B 到平面EFG 的距离练习7、如图 2.3.1-2，在正方形ABCD 中，E 、F 分别是BC 、CD 的中点，G 是EF 的中点，现在沿AE 、AF 及EF 把这个正方形折成一个空间图形，使B 、C 、D 三点重合，重合后的点记为H ，那么，在这个空间图形中必有[]A 、AH ⊥△EFH 所在平面B 、AD ⊥△EFH 所在平面C 、HF ⊥△AEF 所在平面D 、HD ⊥△AEF 所在平面练习8 、三棱锥P ABC 的高为PH ，若三个侧面两两垂直，则H 为△ABC 的（）A ．内心B ．外心C ．垂心D ．重心(5)两平面平行的判定①定义：如果两个平面没有公共点，那么这两个平面平行，即无公共点α∥β.②如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行，即若a,bα，a ∩b=P,a ∥β,b∥β,则α∥β.（面面平行判定定理）推论：一个平面内的两条直线分别平行于另一平面内的两条相交直线，则这两个平面平行，即若a,bα,c,dβ,a ∩b=P,a ∥c,b ∥d,则α∥β.(6)两平面垂直的判定①定义：两个平面相交，如果所成的二面角是直二面角，那么这两个平面互相垂直，即二面角α－a －β=90°α⊥β._H _M _N _F _E _D _C _B _A②如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直，即若l ⊥β,l α，则α⊥β.（面面垂直判定定理）练习9、直三棱柱111ABCA B C 中，各侧棱和底面的边长均为a ，点D 是1CC 上任意一点，连接11,,,A B BD A D AD ，则三棱锥1AA BD 的体积为（）A ．361aB．3123aC．363aD．3121a练习10、在三棱锥S ABC 中，△ABC 是边长为4的正三角形，平面SAC平面,23ABC SASC，M 、N 分别为,AB SB 的中点．（Ⅰ）证明：AC ⊥SB ；（Ⅱ）求二面角N -CM -B 的大小；（Ⅲ）求点B 到平面CMN 的距离．练习11、正方体1111ABCDA B C D 中，M 是1AA 的中点．求证：平面MBD平面1BDC 七、空间中的各种角等角定理及其推论定理若一个角的两边和另一个角的两边分别平行，并且方向相同，则这两个角相等.推论若两条相交直线和另两条相交直线分别平行，则这两组直线所成的锐角(或直角)相等.1、异面直线所成的角(1)定义：a 、b 是两条异面直线，经过空间任意一点O ，分别引直线a ′∥a,b ′∥b,则a ′和b ′所成的锐角(或直角)叫做异面直线a 和b 所成的角.(2)取值范围：0°＜θ≤90°.(3)求解方法①根据定义，通过平移，找到异面直线所成的角θ；②解含有θ的三角形，求出角θ的大小.2、直线和平面所成的角——斜线和射影所成的锐角(1)取值范围0°≤θ≤90°(2)求解方法①作出斜线在平面上的射影，找到斜线与平面所成的角θ.②解含θ的三角形，求出其大小.3、二面角及二面角的平面角(1)半平面直线把平面分成两个部分，每一部分都叫做半平面.(2)二面角条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱，这两个平面叫做二面角的面，即二面角由半平面一棱一半平面组成.若两个平面相交，则以两个平面的交线为棱形成四个二面角.二面角的大小用它的平面角来度量，通常认为二面角的平面角θ的取值范围是0°＜θ≤180°(3)二面角的平面角①以二面角棱上任意一点为端点，分别在两个面内作垂直于棱的射线，这两条射线所组成的角叫做二面角的平面角.如图，∠PCD 是二面角α-AB-β的平面角.平面角∠PCD 的大小与顶点C 在棱AB 上的位置无关.②二面角的平面角具有下列性质：(i)二面角的棱垂直于它的平面角所在的平面，即AB ⊥平面PCD.(ii)从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线，垂足必在平面角的另一边(或其反向延长线)上.(iii)二面角的平面角所在的平面与二面角的两个面都垂直，即平面PCD ⊥α，平面PCD ⊥β.③找(或作)二面角的平面角的主要方法.(i)定义法(ii)垂面法(iii)三垂线法(Ⅳ)根据特殊图形的性质(4)求二面角大小的常见方法先找(或作)出二面角的平面角θ，再通过解三角形求得θ的值.练习12、正四棱锥（顶点在底面的射影是底面正方形的中心）的体积为12，底面对角线的长为26，则侧面与底面所成的二面角等于___________________．练习13、在正四面体ABCD 中，E 为AD 的中点，求直线CE 与平面BCD 所成角的正弦值.13.空间的各种距离点到平面的距离(1)定义面外一点引一个平面的垂线，这个点和垂足间的距离叫做这个点到这个平面的距离.(2)求点面距离常用的方法：1)直接利用定义求①找到(或作出)表示距离的线段；②抓住线段(所求距离)所在三角形解之.2)体积法其步骤是：①在平面内选取适当三点，和已知点构成三棱锥；②求出此三棱锥的体积V 和所取三点构成三角形的面积S ；③由V=31S ·h ，求出h 即为所求.这种方法的优点是不必作出垂线即可求点面距离.难点在于如何构造合适的三棱锥以便于计算.直线和平面的距离、平行平面的距离将线面、面面距离转化为点面距离，然后运用解三角形或体积法求解之.ABCDEFH。

2013年G 单元 立体几何G1 空间几何体的结构1．G1，G6[2013·北京卷] 如图1－2，在正方体ABCD －A1B 1C 1D 1中，P 为对角线BD 1的三等分点，P 到各顶点的距离的不同取值有( )A ．3个B ．4个C ．5个D ．6个1．B [解析] 设棱长为1，∵BD 1＝3，∴BP ＝33，D 1P ＝2 33.联结AD 1，B 1D 1，CD 1，得△ABD 1≌△CBD 1≌△B 1BD 1，∴∠ABD 1＝∠CBD 1＝∠B 1BD 1，且cos ∠ABD 1＝33，联结AP ，PC ，PB 1，则有△ABP ≌△CBP ≌△B 1BP ，∴AP ＝CP ＝B 1P ＝63，同理DP ＝A 1P ＝C 1P ＝1，∴P 到各顶点的距离的不同取值有4个．2．G1，G4，G5[2013·广东卷] 如图1－4(1)，在边长为1的等边三角形ABC 中，D ，E 分别是AB ，AC 上的点，F 是BC 的中点，AF 与DE 交于点G ，将△ABF 沿AF 折起，得到如图1－4(2)所示的三棱锥A －BCF ，其中BC ＝22.(1)证明：DE ∥平面BCF ；(2)证明：CF ⊥平面ABF ；(3)当AD ＝23时，求三棱锥F －DEG 的体积． 2．解：G2 空间几何体的三视图和直观图 3．G2，G7[2013·北京卷] 某四棱锥的三视图如图1－3所示，该四棱锥的体积为________．3．3 [解析] 正视图的长为3，侧视图的长为3，因此，该四棱锥底面是边长为3的正方形，且高为1，因此V ＝13×(3×3)×1＝3.4．G2，G4[2013·福建卷] 如图1－3，在四棱锥P －ABCD 中，PD ⊥平面ABCD ，AB ∥DC ，AB ⊥AD ，BC ＝5，DC ＝3，AD ＝4，∠PAD ＝60°.(1)当正视方向与向量AD→的方向相同时，画出四棱锥P －ABCD 的正视图(要求标出尺寸，并写出演算过程)；(2)若M 为PA 的中点，求证：DM ∥平面PBC ；(3)求三棱锥D －PBC 的体积．4．解：(1)在梯形ABCD 中，过点C 作CE ⊥AB ，垂足为E.由已知得，四边形ADCE 为矩形，AE ＝CD ＝3，在Rt △BEC 中，由BC ＝5，CE ＝4，依勾股定理得BE ＝3，从而AB ＝6.又由PD ⊥平面ABCD 得，PD ⊥AD.从而在Rt △PDA 中，由AD ＝4，∠PAD ＝60°，得PD ＝4 3.正视图如图所示．(2)方法一：取PB 中点N ，联结MN ，CN.在△PAB 中，∵M 是PA 中点，∴MN ∥AB ，MN ＝12AB ＝3.又CD ∥AB ，CD ＝3，∴MN ∥CD ，MN ＝CD ，∴四边形MNCD 为平行四边形，∴DM ∥CN.又平面PBC ，平面PBC ，∴DM ∥平面PBC.方法二：取AB 的中点E ，联结ME ，DE.在梯形ABCD 中，BE ∥CD ，且BE ＝CD ，∴四边形BCDE 为平行四边形，∴DE ∥BC.又平面PBC ，平面PBC ，∴DE ∥平面PBC.又在△PAB 中，ME ∥PB ，平面PBC ，平面PBC ，∴ME ∥平面PBC.又DE∩ME ＝E ，∴平面DME ∥平面PBC.又平面DME ，∴DM ∥平面PBC.(3)V D －PBC ＝V P －DBC ＝13S △DBC ·PD ，又S △DBC ＝6，PD ＝4 3，所以V D －PBC ＝8 3. 5．G2[2013·广东卷] 某三棱锥的三视图如图1－2所示，则该三棱锥的体积是( )A.16B.13C.23D ．1 5．B [解析] 由三视图得三棱锥的高是2，底面是一个腰为1的等腰直角三角形，故体积是13×12×1×1×2＝13，选B.6．G2[2013·湖南卷] 已知正方体的棱长为1，其俯视图是一个面积为1的正方形， 侧视图是一个面积为2的矩形，则该正方体的正视图的面积等于( )A.32 B ．1 C.2＋12D. 2 6．D[解析]由题可知其俯视图恰好是正方形，而侧视图和正视图则应该都是正方体的对角面，故面积为2，选D.7．G2[2013·江西卷] 一几何体的三视图如图1－2所示，则该几何体的体积为( )A ．200＋9πB ．200＋18πC ．140＋9πD ．140＋18π7．A [解析] 该几何体上面是半圆柱，下面是长方体，半圆柱体积为12π·32·2＝9π，长方体体积为10×5×4＝200.故选A.8．G2[2013·辽宁卷] 某几何体的三视图如图1－3所示，则该几何体的体积是________．8．16π－16 [解析] 由三视图可知该几何体是一个圆柱里面挖去了一个长方体，所以该几何体的体积为V ＝4π×4－16＝16π－16.9．G2[2013·新课标全国卷Ⅱ] 一个四面体的顶点在空间直角坐标系O －xyz 中的坐标分别是(1，0，1)，(1，1，0)，(0，1，1)，(0，0，0)，画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到的正视图可以为( )9．A [解析] 在空间直角坐标系O －xyz 中画出三棱锥，由已知可知三棱锥O －ABC为题中所描叙的四面体，而其在zOx 平面上的投影为正方形EBDO ，故选A.10．G2[2013·山东卷] 一个四棱锥的侧棱长都相等，底面是正方形，其正(主)视图如图1－1所示，则该四棱锥侧面积和体积分别是( )A ．4 5，8B ．4 5，83C ．4(5＋1)，83D ．8，8 10．B [解析] 由正视图知该几何体的高为2，底面边长为2，斜高为22＋1＝5，∴侧面积＝4×12×2×5＝4 5，体积为13×2×2×2＝83.11．G2[2013·陕西卷] 某几何体的三视图如图1－2所示，则其表．面积为________． 12．3π [解析] 由三视图得该几何体为半径为1的半个球，则表面积为半球面＋底面圆，代入数据计算为S ＝12×4π×12＋π×12＝3π. 13．某几何体的三视图如图1－3所示，则该几何体的体积为( )A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π13．该空间几何体的下半部分是一个底面半径为2，母线长为4的半圆柱，上半部分是一个底面边长为2、高为4的正四棱柱．这个空间几何体的体积是12×π×4×4＋2×2×4＝16＋8π.14．G2[2013·浙江卷] 已知某几何体的三视图(单位： cm)如图1－1所示，则该几何体的体积是( )A ．108 cm 3B ．100 cm 3C ．92 cm 3D ．84 cm 314．B [解析] 此直观图是由一个长方体挖去一个三棱锥而得，如图所示其体积为3×6×6－13×12×3×4×4＝108－8＝100(cm 3)．所以选择B.15．G2和G5[2013·重庆卷] 如图1－4所示，四棱锥P －ABCD 中，PA ⊥底面ABC D ，PA ＝2 3，BC ＝CD ＝2，∠ACB ＝∠ACD ＝π3. (1)求证：BD ⊥平面PAC ；(2)若侧棱PC 上的点F 满足PF ＝7FC ，求三棱锥P －BDF 的体积．15．解：(1)证明：因为BC ＝CD ，即△BCD 为等腰三角形，又∠ACB ＝∠ACD ，故BD ⊥AC.因为PA ⊥底面ABCD ，所以PA ⊥BD ，从而BD 与平面PAC 内两条相交直线PA ，AC 都垂直，所以BD ⊥平面PAC.(2)三棱锥P －BCD 的底面BCD 的面积S △BCD ＝12BC·CD·sin ∠BCD ＝12·2·2·sin 2π3＝ 3.由PA ⊥底面ABCD ，得V P －BCD ＝13·S △BCD ·PA ＝13×3×2 3＝2.由PF ＝7FC ，得三棱锥F －BCD 的高为18PA ，故V F －BCD ＝13·S △BCD ·18PA ＝13×3×18×2 3＝14，所以VP －BDF ＝V P －BCD －V F －BCD ＝2－14＝74. 16．G2和G7[2013·重庆卷] 某几何体的三视图如图1－3所示，则该几何体的表面积为( )A ．180B ．200C ．220D ．24016．D [解析] 该几何体为直四棱柱，其高为10，底面是上底为2，下底为8，高为4，其腰为5的等腰梯形，所以底面面积和为12(2＋8)×4×2＝40.四个侧面的面积和为(2＋8＋5×2)×10＝200，所以该直四棱柱的表面积为S ＝40＋200＝240，故选D.G3 平面的基本性质、空间两条直线G4 空间中的平行关系17．G4，G5，G7[2013·北京卷] 如图1－5，在四棱锥P －ABCD 中，AB ∥CD ，AB ⊥AD ，CD ＝2AB ，平面PAD ⊥底面ABCD ，PA ⊥AD ，E 和F 分别是CD 和PC 的中点．求证：(1)PA ⊥底面ABCD ；(2)BE ∥平面PAD ；(3)平面BEF ⊥平面PCD.图1－517．证明：(1)因为平面PAD ⊥底面ABCD ，且PA 垂直于这两个平面的交线AD ，所以PA ⊥底面ABCD.(2)因为AB ∥CD ，CD ＝2AB ，E 为CD 的中点，所以AB ∥DE ，且AB ＝DE ，所以ABED 为平行四边形，所以BE ∥AD. 又因为平面PAD ，平面PAD ，所以BE ∥平面PAD.(3)因为AB ⊥AD ，而且ABED 为平行四边形，所以BE ⊥CD ，AD ⊥CD.由(1)知PA ⊥底面ABCD ，所以PA ⊥CD. 又因为AD∩PA ＝A ，所以CD ⊥平面PAD ，所以CD ⊥PD.因为E 和F 分别是CD 和PC 的中点，所以PD ∥EF ，所以CD⊥EF，所以CD⊥平面BEF，所以平面BEF⊥平面PCD.18．G4、G5[2013·广东卷] 设l为直线，α，β是两个不同的平面，下列命题中正确的是()A．若l∥α，l∥β，则α∥βB．若l⊥α，l⊥β，则α∥βC．若l⊥α，l∥β，则α∥βD．若α⊥β，l∥α，则l⊥β18．B[解析] 根据空间平行、垂直关系的判定和性质，易知选B.19．G4，G5[2013·江苏卷] 如图1－2，在三棱锥S－ABC中，平面SAB⊥平面SBC，AB⊥BC，AS＝AB.过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．求证：(1)平面EFG∥平面ABC；(2)BC⊥SA.图1－219．证明：(1)因为AS＝AB，AF⊥SB，垂足为F，所以F是SB的中点．又因为E是SA的中点，所以EF∥AB. 因为平面ABC，平面ABC，所以EF∥平面ABC. 同理EG∥平面ABC.又EF∩EG＝E，所以平面EFG∥平面ABC.(2)因为平面SAB⊥平面SBC，且交线为SB，又平面SAB，AF⊥SB，所以AF⊥平面SBC.因为平面SBC，所以AF⊥BC. 又因为AB⊥BC，AF∩AB＝A，AF，平面SAB，所以BC⊥平面SAB. 因为平面SAB，所以BC⊥SA.图1－420．G4，G5[2013·辽宁卷] 如图1－4，AB是圆O的直径，PA垂直圆O所在的平面，C是圆O上的点．(1)求证：BC⊥平面PAC；(2)设Q为PA的中点，G为△AOC的重心，求证：QG∥平面PBC.20．证明：(1)由AB是圆O的直径，得AC⊥BC.由PA⊥平面ABC，平面ABC，得PA⊥BC.又PA∩AC＝A，平面PAC，平面PAC，所以BC⊥平面PAC.(2)联结OG并延长交AC于M，联结QM，QO，由G为△AOC的重心，得M为AC中点，由Q为PA中点，得QM∥PC. 又O为AB中点，得OM∥BC. 因为QM∩MO＝M，平面QMO.平面QMO，BC∩PC＝C，平面PBC，平面PBC，所以平面QMO∥平面PBC.因为平面QMO，所以QG∥平面PBC.21．G4，G7，G11[2013·新课标全国卷Ⅱ] 如图，直三棱柱ABC－A1B1C1中，D，E分别是AB，BB1的中点．(1)证明：BC1∥平面A1CD；(2)设AA1＝AC＝CB＝2，AB＝22，求三棱锥C－A1DE的体积．图1－721．解：(1)证明：联结AC 1交A 1C 于点F ，则F 为AC 1中点．又D 是AB 中点，联结DF ，则BC 1∥DF.因为平面A 1CD ，BC 1平面A 1CD ，所以BC 1∥平面A 1CD.图1－8(2)因为ABC －A 1B 1C 1是直三棱柱，所以AA 1⊥CD.由已知AC ＝CB ，D 为AB 的中点，所以CD ⊥AB.又AA 1∩AB ＝A ，于是CD ⊥平面ABB 1A 1.由AA 1＝AC ＝CB ＝2，AB ＝2 2得∠ACB ＝90°，CD ＝2，A 1D ＝6，DE ＝3，A 1E ＝3，故A 1D 2＋DE 2＝A 1E 2，即DE ⊥A 1D. 所以VC －A 1DE ＝13×12×6×3×2＝1. 22．G4，G5[2013·山东卷] 如图1－5，四棱锥P —ABCD 中，AB ⊥AC ，AB ⊥PA ，AB ∥CD ，AB ＝2CD ，E ，F ，G ，M ，N 分别为PB ，AB ，BC ，PD ，PC 的中点．(1)求证：CE ∥平面PAD ； (2)求证：平面EFG ⊥平面EMN.22．证明：(1)证法一：取PA 的中点H ，联结EH ，DH. 因为E 为PB 的中点， 所以EH ∥AB ，EH ＝12AB. 又AB ∥CD ，CD ＝12AB ， 所以EH ∥CD ，EH ＝CD. 因此四边形DCEH 是平行四边形． 所以CE ∥DH. 又平面PAD ，平面PAD ， 因此CE ∥平面PAD.证法二：联结CF. 因为F 为AB 的中点， 所以AF ＝12AB. 又CD ＝12AB ， 所以AF ＝CD. 又AF ∥CD ， 所以四边形AFCD 为平行四边形． 因此CF ∥AD. 又平面PAD ， 所以CF ∥平面PAD. 因为E ，F 分别为PB ，AB 的中点， 所以EF ∥PA. 又平面PAD ， 所以EF ∥平面PAD. 因为CF∩EF ＝F ， 故平面CEF ∥平面PAD. 又平面CEF ， 所以CE ∥平面PAD.(2)因为E ，F 分别为PB ，AB 的中点， 所以EF ∥PA. 又AB ⊥PA ， 所以AB ⊥EF. 同理可证AB ⊥FG .又EF∩FG ＝F ，平面EFG ，平面EFG ， 因此AB ⊥平面EFG . 又M ，N 分别为PD ，PC 的中点， 所以MN ∥CD. 又AB ∥CD ， 所以MN ∥AB ， 因此MN ⊥平面EFG . 又平面EMN ，所以平面EFG ⊥平面EMN.23．G4，G11[2013·陕西卷] 如图1－5，四棱柱ABCD －A 1B 1C 1D 1的底面ABCD 是正方形，O 是底面中心，A 1O ⊥底面ABCD ，AB ＝AA 1＝ 2.图1－5(1)证明：平面A 1BD ∥平面CD 1B 1；(2)求三棱柱ABD －A 1B 1D 1的体积．23．(1)证明：由题设知，BB 1綊DD 1， ∴四边形BB 1D 1D 是平行四边形， ∴BD ∥B 1D 1.又BD 平面CD 1B 1， ∴BD ∥平面CD 1B 1. ∵A 1D 1綊B 1C 1綊BC ， ∴四边形A 1BCD 1是平行四边形，∴A 1B ∥D 1C. 又A 1B 平面CD 1B 1， ∴A 1B ∥平面CD 1B 1. 又∵BD∩A 1B ＝B ， ∴平面A 1BD ∥平面CD 1B 1.(2)∵A 1O ⊥平面ABCD ， ∴A 1O 是三棱柱ABD －A 1B 1D 1的高． 又∵AO ＝12AC ＝1，AA 1＝2， ∴A 1O ＝AA 21－OA 2＝1， 又∵S △ABD ＝12×2×2＝1， ∴V ABD －A 1B 1D 1＝S △ABD ·A 1O ＝1. 24．G4，G5，G7，G11[2013·四川卷]图1－8[来源:学科网]如图1－8，在三棱柱ABC －A 1B 1C 1中，侧棱AA 1⊥底面ABC ，AB ＝AC ＝2AA 1＝2，∠BAC ＝120°，D ，D 1分别是线段BC ，B 1C 1的中点，P 是线段AD 上异于端点的点．(1)在平面ABC 内，试作出过点P 与平面A 1BC 平行的直线l ，说明理由，并证明直线l ⊥平面ADD 1A 1；(2)设(1)中的直线l 交AC 于点Q ，求三棱锥A 1－QC 1D 的体积．(锥体体积公式：V ＝13Sh ，其中S 为底面面积，h 为高)24．解：(1)如图，在平面ABC 内，过点P 作直线l ∥BC ，因为l 在平面A 1BC 外，BC 在平面A 1BC 内，由直线与平面平行的判定定理可知，l ∥平面A 1BC 由已知，AB ＝AC ，D 是BC 的中点，所以，BC ⊥AD ，则直线l ⊥AD. 因此AA 1⊥平面ABC ，所以AA 1⊥直线l.又因为AD ，AA 1在平面ADD 1A 1内，且AD 与AA 1相交， 所以直线l ⊥平面ADD 1A 1.(2)过D 作DE ⊥AC 于E. 因为AA 1⊥平面ABC ，所以DE ⊥AA 1.又因为AC ，AA 1在平面AA 1C 1C 内，且AC 与AA 1相交， 所以DE ⊥平面AA 1C 1C.由AB ＝AC ＝2，∠BAC ＝120°，有AD ＝1，∠DAC ＝60°， 所以在△ACD 中，DE ＝32AD ＝32. 又S △A 1QC 1＝12A 1C 1·AA 1＝1，所以 V A 1－QC 1D ＝VD －A 1QC 1＝13DE·S △A 1QC 1＝13×32×1＝36. 因此三棱锥A 1－QC 1D 的体积是36. 25．G4，G5[2013·浙江卷] 设m ，n 是两条不同的直线，α，β是两个不同的平面( )A ．若m ∥α，n ∥α，则m ∥nB ．若m ∥α，m ∥β，则α∥βC ．若m ∥n ，m ⊥α，则n ⊥αD ．若m ∥α，α⊥β，则m ⊥β25．C [解析] 对于选项C ，若m ∥n ，m ⊥α，易得n ⊥α.所以选择C.G5 空间中的垂直关系图1－526．G5[2013·安徽卷] 如图1－5，四棱锥P－ABCD的底面ABCD是边长为2的菱形，∠BAD＝60°，已知PB＝PD ＝2，PA＝ 6. (1)证明：PC⊥BD；(2)若E为PA的中点，求三棱锥P－BCE的体积．26．解：(1)证明：联结AC，交BD于O点，联结PO. 因为底面ABCD是菱形，所以AC⊥BD，BO＝DO.由PB＝PD知，PO⊥BD.再由PO∩AC＝O知，BD⊥面APC，又平面APC，因此BD⊥PC.(2)因为E是PA的中点，所以V P－BCE＝V C－PEB＝12V C－PAB＝12V B－APC.由PB＝PD＝AB＝AD＝2知，△ABD≌△PBD.因为∠BAD＝60°，所以PO＝AO＝3，AC＝23，BO＝1.又PA＝6，故PO2＋AO2＝PA2，即PO⊥AC. 故S△APC＝12PO·AC＝3.由(1)知，BO⊥面APC，因此V P－BCE＝12V B－APC＝13·12·S△APC·BO＝12.27．G5、G11[2013·全国卷] 如图1－3所示，四棱锥P—ABCD中，∠ABC＝∠BAD＝90°，BC＝2AD，△PAB和△PAD都是边长为2的等边三角形．图1－3(1)证明：PB⊥CD；(2)求点A到平面PCD的距离．27．解：(1)证明：取BC的中点E，联结DE，则四边形ABED为正方形．过P作PO⊥平面ABCD，垂足为O.联结OA，OB，OD，OE.由△PAB和△PAD都是等边三角形知PA＝PB＝PD，所以OA＝OB＝OD，即点O为正方形ABED对角线的交点．故OE⊥BD，从而PB⊥OE.因为O是BD的中点，E是BC的中点，所以OE∥CD.因此PB⊥CD.(2)取PD的中点F，联结OF，则OF∥PB. 由(1)知，PB⊥CD，故OF⊥CD.又OD＝12BD＝2，OP＝PD2－OD2＝2，故△POD为等腰三角形，因此OF⊥PD.又PD∩CD＝D，所以OF⊥平面PCD. 因为AE∥CD，平面PCD，平面PCD，所以AE∥平面PCD.因此O到平面PCD的距离OF就是A到平面PCD的距离，而OF＝12PB＝1，所以点A到平面PCD的距离为1.28．G5[2013·新课标全国卷Ⅰ] 如图1－5所示，三棱柱ABC－A1B1C1中，CA＝CB，AB＝AA1，∠BAA1＝60°.(1)证明：AB⊥A1C；(2)若AB＝CB＝2，A1C＝6，求三棱柱ABC－A1B1C1的体积．图1－528．解：(1)取AB 的中点O ，联结OC ，OA 1，A 1B ，因为CA ＝CB ，所以OC ⊥AB.由于AB ＝AA 1，∠BAA 1＝60°，故△AA 1B 为等边三角形，所以OA 1⊥AB.因为OC∩OA 1＝O ，所以AB ⊥平面OA 1C.又A 1平面OA 1C ，故AB ⊥A 1C.(2)由题设知△ABC 与△AA 1B 都是边长为2的等边三角形，所以OC ＝OA 1＝ 3. 又A 1C ＝6，则A 1C 2＝OC 2＋OA 21，故OA 1⊥OC.因为OC∩AB ＝O ，所以OA 1⊥平面ABC ，OA 1为三棱柱ABC －A 1B 1C 1的高．又△ABC 的面积S △ABC ＝3，故三棱柱ABC －A 1B 1C 1的体积V ＝S △ABC ·OA 1＝3.G6 三垂线定理G7 棱柱与棱锥G8 多面体与球29．G8[2013·天津卷] 已知一个正方体的所有顶点在一个球面上，若球的体积为9π2，则正方体的棱长为________． 29.3 [解析] 设正方体的棱长为a ，则43π⎝⎛⎭⎫3a 23＝92π，解之得a ＝ 3. 30．G8[2013·新课标全国卷Ⅱ] 已知正四棱锥O －ABCD 的体积为3 22，底面边长为3，则以O 为球心，OA 为半径的球的表面积为________．30．24π [解析] 设O 到底面的距离为h ，则13×3×h ＝3 22＝3 22，OA ＝h 2＋⎝⎛⎭⎫622＝6，故球的表面积为4π×(6)2＝24π.31．G8[2013·新课标全国卷Ⅰ] 已知H 是球O 的直径AB 上一点，AH ∶HB ＝1∶2，AB ⊥平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为________．31.9π2 [解析] 截面为圆，由已知得该圆的半径为1.设球的半径为r ，则AH ＝23r ，所以OH ＝13r ，所以13r 2＋12＝r 2，r 2＝98，所以球的表面积是4πr 2＝9π2. G12 单元综合32．[2013·烟台莱州一中月考] 一个简单几何体的正视图和侧视图如图K29－2所示，则其俯视图不可能为下列图形中的( )①长方形；②直角三角形；③圆；④椭圆．A ．①B ．②C ．③D ．④32．C [解析] 当俯视图为圆时，由三视图可知为圆柱，此时正视图和侧视图应该相同，所以俯视图不可能是圆33．[2013·丹东四校协作体摸底] 设某几何体的三视图如图K30－6所示(尺寸的长度单位为：m)，若该几何体的各个顶点都在同一球面上，则此球的表面积等于2π的式子表示)．33．100π [解析] 由三视图可得该几何体是一个三棱柱，底面外接圆的半径r 满足2r ＝3 3sin 60°＝6，则r ＝3.棱柱的高为8，则球心到底面的距离d ＝4，则球的半径R ＝r 2＋d 2＝5.故此球的表面积S ＝4πR 2＝100π，故答案为100π.。

高中数学1．1 空间几何体1.1．5 三视图优化训练新人教B版必修2 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方,但是任然希望(高中数学 1．1 空间几何体1．1.５三视图优化训练新人教B版必修２）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学 1.1 空间几何体１．１.5 三视图优化训练新人教B版必修２的全部内容。

１.1。

5 三视图5分钟训练(预习类训练,可用于课前)1。

若一个几何体的主视图和左视图都是等腰三角形,俯视图是圆，则这个几何体可能是（）Ａ.圆柱 B.三棱柱 C.圆锥Ｄ．球体答案:C2。

有一辆汽车如图1—1—5-1所示，小红从空中往下看这辆汽车，小红看到的形状是图1—1—5－２中的( ）图1－1—５—１图１—1—５-２解析:小汽车从上面看只能看到驾驶室的顶部和车身的上面,实际上是考查俯视图的画法.答案：B3。

一个几何体的正视图、左视图和俯视图全是一样的，则这个几何体可能是__＿_＿____＿__(要求写出两种）．答案:球、正方体10分钟训练（强化类训练,可用于课中)1。

在几何体：①圆锥;②正方体;③圆柱;④球;⑤正四面体(指四个面都是正三角形的四面体）中,三视图完全一样的几何体是（）Ａ。

①③④B。

④⑤ C。

②④⑤ D。

④解析:只有球的三个视图都是圆。

圆锥的俯视图和左视图不同；正方体放置的位置不同时三视图并不相同；圆柱的俯视图和正视图不同；正四面体的三个视图并不相同．答案:D2．图１-1－５—3表示的是组合在一起的模块,在①②③④四个图形中,是这个模块的俯视图的是( )图１-1—5—３图１-1-５－4Ａ.①B。

③C。

④Ｄ.②解析:两个组合的模块，上面为圆锥，下面为长方体,所以选A。

立体几何题型01 空间几何体的有关计算题型02 点线面位置关系、空间角及距离题型03 内切球、外接球问题题型04 空间向量题型01 空间几何体的有关计算1(2024·山西晋城·统考一模)若一个正n棱台的棱数大于15，且各棱的长度构成的集合为{2,3}，则n 的最小值为，该棱台各棱的长度之和的最小值为．2(2024·浙江·校联考一模)已知圆台的上下底面半径分别是1，4，且侧面积为10π，则该圆台的母线长为．3(2024·安徽合肥·合肥一六八中学校考一模)球O的半径与圆锥M的底面半径相等，且它们的表面积也相等，则圆锥M的侧面展开图的圆心角大小为，球O的体积与圆锥M的体积的比值为．4(2024·湖南长沙·雅礼中学校考一模)已知圆锥的母线长为2，则当圆锥的母线与底面所成的角的余弦值为时，圆锥的体积最大，最大值为．5(2024·广东深圳·校考一模)已知圆锥的侧面展开图是一个半径为4的半圆.若用平行于圆锥的底面，且与底面的距离为3的平面截圆锥，将此圆锥截成一个小圆锥和一个圆台，则小圆锥和圆台的体积之比为.6(2024·辽宁沈阳·统考一模)正方体的8个顶点分别在4个互相平行的平面内，每个平面内至少有一个顶点，且相邻两个平面间的距离为1，则该正方体的棱长为()A.2B.3C.2D.57(2024·云南曲靖·统考一模)为努力推进“绿美校园”建设，营造更加优美的校园环境，某校准备开展校园绿化活动．已知栽种某绿色植物的花盆可近似看成圆台，圆台两底面直径分别为18厘米，9厘米，母线长约为7.5厘米．现有2000个该种花盆，假定每一个花盆装满营养土，请问共需要营养土约为( )(参考数据：π≈3.14)A.1.702立方米B.1.780立方米C.1.730立方米D.1.822立方米8(2024·新疆乌鲁木齐·统考一模)某广场设置了一些石凳供大家休息，这些石凳是由棱长为40cm的正方体截去八个一样的四面体得到的，则()A.该几何体的顶点数为12B.该几何体的棱数为24C.该几何体的表面积为(4800+8003)cm 2D.该几何体外接球的表面积是原正方体内切球、外接球表面积的等差中项9(2024·山西晋城·统考一模)如图，在正四棱柱ABCD -A 1B 1C 1D 1中，AB =2，AA 1=4，C 1 E =3EC，平面ABE 将该正四棱柱分为上、下两部分，记上部分对应的几何体为Ω上，下部分对应的几何体为Ω下，则()A.Ω下的体积为2B.Ω上的体积为12C.Ω下的外接球的表面积为9πD.平面ABE 截该正四棱柱所得截面的面积为25题型02 点线面位置关系、空间角及距离10(2024·河北·校联考一模)已知直线l 、m 、n 与平面α、β，下列命题正确的是()A.若α⎳β，l ⊂α，n ⊂β，则l ⎳nB.若α⊥β，l ⊂α，则l ⊥βC.若l ⊥n ，m ⊥n ，则l ⎳mD.若l ⊥α，l ⎳β，则α⊥β11(2024·浙江·校联考一模)已知直线a ,b 和平面α,a ⊄α,b ∥α，则“a ∥b ”是“a ∥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件12(2024·广东深圳·校考一模)已知α，β是两个不同的平面，m ，n 是两条不同的直线，则下列说法正确的是()A.若m ⊥n ，m ⊥α，n ⊥β，则α⊥βB.若m ⎳n ，m ⎳α，n ⎳β，则α⎳βC.若m ⊥n ，m ⎳α，α⊥β，则n ⊥βD.若m ⎳n ，m ⊥α，α⊥β，则n ⎳β13(2024·吉林白山·统考一模)正八面体可由连接正方体每个面的中心构成，如图所示，在棱长为2的正八面体中，则有()A.直线AE与CF是异面直线B.平面ABF⊥平面ABEC.该几何体的体积为432 D.平面ABE与平面DCF间的距离为26314(2024·河南郑州·郑州市宇华实验学校校考一模)如图，在四棱锥P-ABCD中，PA⊥平面ABCD,PA=AB=2,∠BAD=120°,AC⊥BD，△BCD是等边三角形.(1)证明：平面PAD⊥平面PCD.(2)求二面角B-PC-D的正弦值.15(2024·辽宁沈阳·统考一模)如图，在三棱锥A-BCD中，平面ABC⊥平面BCD，且BC=BD= BA，∠CBA=∠CBD=120°，点P在线段AC上，点Q在线段CD上.(1)求证：AD⊥BC；(2)若AC⊥平面BPQ，求BPBQ的值；(3)在(2)的条件下，求平面ABD与平面PBQ所成角的余弦值.16(2024·重庆·统考一模)如图，四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD中，AB= AP，AB⊥AD,AB+AD=6,CD=2,∠CDA=45°．(1)若E为PB的中点，求证：平面PBC⊥平面ADE；(2)若平面PAB与平面PCD所成的角的余弦值为66．(ⅰ)求线段AB的长；(ⅱ)设G为△PAD内(含边界)的一点，且GB=2GA，求满足条件的所有点G组成的轨迹的长度．17(2024·云南曲靖·统考一模)在图1的直角梯形ABCD中，∠A=∠D=90°,AB=BC=2,DC=3，点E是DC边上靠近于点D的三等分点，以BE为折痕将△BCE折起，使点C到达C1的位置，且AC1= 6，如图2．(1)求证：平面BC1E⊥平面ABED；(2)在棱DC1上是否存在点P，使得二面角P-EB-C1的大小为45°？若存在，求出线段DP的长度，若不存在说明理由．18(2024·云南曲靖·统考一模)如图所示，正方体ABCD -A B C D 的棱长为1，E ,F 分别是棱AA ,CC 的中点，过直线EF 的平面分别与棱BB ,DD 交于点M ,N ，以下四个命题中正确的是()A.四边形EMFN 一定为菱形B.四棱锥A -MENF 体积为13C.平面EMFN ⊥平面DBB DD.四边形EMFN 的周长最小值为419(2024·山东济南·山东省实验中学校考一模)如图，在四棱锥P -ABCD 中，PA ⊥平面ABCD ，PB 与底面ABCD 所成的角为π4，底面ABCD 为直角梯形，∠ABC =∠BAD =π2,AD =2,PA =BC =1，点E 为棱PD 上一点，满足PE =λPD0≤λ≤1 ，下列结论正确的是()A.平面PAC ⊥平面PCD ；B.在棱PD 上不存在点E ，使得CE ⎳平面PABC.当λ=12时，异面直线CE 与AB 所成角的余弦值为255；D.点P 到直线CD 的距离3；20(2024·新疆乌鲁木齐·统考一模)如图，在四棱锥P -ABCD 中，底面ABCD 为正方形，PA ⊥平面ABCD ，PA =AB ，点E ，F 分别是棱PB ，BC 的中点．(1)求直线AF 与平面PBC 所成角的正弦值；(2)在截面AEF 内是否存在点G ，使DG ⊥平面AEF ，并说明理由．21(2024·山西晋城·统考一模)如图，P 是边长为2的正六边形ABCDEF 所在平面外一点，BF 的中点O 为P 在平面ABCDEF 内的射影，PM =2MF．(1)证明：ME ⎳平面PBD ．(2)若PA =2，二面角A -PB -D 的大小为θ，求cos2θ．22(2024·河南郑州·郑州市宇华实验学校校考一模)如图，在正方体ABCD -A 1B 1C 1D 1中，点P 是AD 1的中点，点Q 是直线CD 1上的动点，则下列说法正确的是()A.△PBD 是直角三角形B.异面直线PD 与CD 1所成的角为π3C.当AB 的长度为定值时，三棱锥D -PBQ 的体积为定值D.平面PBD ⊥平面ACD123(2024·浙江·校联考一模)在三棱柱ABC-A1B1C1中，四边形BCC1B1是菱形，△ABC是等边三角形，点M是线段AB的中点，∠ABB1=60°．(1)证明：B1C⊥平面ABC1；(2)若平面ABB1A1⊥平面ABC，求直线B1C与平面A1MC1所成角的正弦值．24(2024·广东深圳·校考一模)如图，在圆锥SO中，AB是圆O的直径，且△SAB是边长为4的等边三角形，C,D为圆弧AB的两个三等分点，E是SB的中点.(1)证明：DE⎳平面SAC；(2)求平面SAC与平面SBD所成锐二面角的余弦值.25(2024·广西南宁·南宁三中校联考一模)在如图所示的五面体ABCDEF中，ABEF共面，△ADF是正三角形，四边形ABCD为菱形，∠ABC=2π3,EF⎳平面ABCD,AB=2EF=2，点M为BC中点．(1)证明：EM∥平面BDF；(2)已知EM=2，求平面BDF与平面BEC所成二面角的正弦值．26(2024·安徽合肥·合肥一六八中学校考一模)如图，菱形ABCD的对角线AC与BD交于点O，AB =5，AC=6，点E，F分别在AD，CD上，AE=CF=54，EF交BD于点H，将△DEF沿EF折到△DEF 位置，OD =10．(1)证明：D H⊥平面ABCD；(2)求平面BAD 与平面ACD 的夹角的余弦值．27(2024·安徽合肥·合肥一六八中学校考一模)设b、c表示两条直线，α、β表示两个平面，则下列命题正确的是()A.若b⎳α，c⊂α，则b⎳cB.若b⊂α，b⎳c，则c⊂αC.若c⎳α，α⊥β，则c⊥βD.若c⎳α，c⊥β，则α⊥β28(2024·吉林延边·统考一模)已知三棱柱ABC-A1B1C1，侧面AA1C1C是边长为2的菱形，∠CAA1 =πA1是矩形，且平面AA1C1C⊥平面ABB1A1，点D是棱A1B1的中点．3，侧面四边形ABB1(1)在棱AC上是否存在一点E，使得AD∥平面B1C1E，并说明理由；(2)当三棱锥B-A1DC1的体积为3时，求平面A1C1D与平面CC1D夹角的余弦值．29(2024·黑龙江齐齐哈尔·统考一模)如图1，在平面四边形PABC中，PA⊥AB,CD⎳AB，CD=2AB=2PD=2AD=4.点E是线段PC上靠近P端的三等分点，将△PDC沿CD折成四棱锥P-ABCD，且AP=22，连接PA,PB,BD，如图2.(1)在图2中，证明：PA⎳平面BDE；(2)求图2中，直线AP与平面PBC所成角的正弦值.30(2024·重庆·统考一模)如图，在边长为1的正方体ABCD-A1B1C1D1中，E是C1D1的中点，M是线段A1E上的一点，则下列说法正确的是()A.当M点与A1点重合时，直线AC1⊂平面ACMB.当点M移动时，点D到平面ACM的距离为定值C.当M点与E点重合时，平面ACM与平面CC1D1D夹角的正弦值为53D.当M点为线段A1E中点时，平面ACM截正方体ABCD-A1B1C1D1所得截面面积为73332 31(2024·福建厦门·统考一模)如图，在四棱锥E-ABCD中，AD⎳BC，2AD=BC=2，AB=2，AB⊥AD，EA⊥平面ABCD，过点B作平面α⊥BD．(1)证明：平面α⎳平面EAC；(2)已知点F为棱EC的中点，若EA=2，求直线AD与平面FBD所成角的正弦值．32(2024·吉林延边·统考一模)如图，在多面体ABCDEF 中，底面ABCD 是边长为2的正方形，DE =BF =1,DE ∥BF ,DE ⊥平面ABCD ，动点P 在线段EF 上，则下列说法正确的是()A.AC ⊥DPB.存在点P ，使得DP ∥平面ACFC.三棱锥A -CDE 的外接球被平面ACF 所截取的截面面积是9π2D.当动点P 与点F 重合时，直线DP 与平面ACF 所成角的余弦值为3101033(2024·福建厦门·统考一模)如图所示，在五面体ABCDEF 中，四边形ABCD 是矩形，△ABF 和△DCE 均是等边三角形，且AB =23，EF =x (x >0)，则()A.EF ⎳平面ABCDB.二面角A -EF -B 随着x 的减小而减小C.当BC =2时，五面体ABCDEF 的体积V (x )最大值为272D.当BC =32时，存在x 使得半径为32的球能内含于五面体ABCDEF 题型03 内切球、外接球问题34(2024·黑龙江齐齐哈尔·统考一模)已知四面体ABCD 的各个面均为全等的等腰三角形，且CA =CB =2AB =4.设E 为空间内任一点，且A ,B ,C ,D ,E 五点在同一个球面上，则()A.AB ⊥CDB.四面体ABCD 的体积为214C.当AE =23时，点E 的轨迹长度为4πD.当三棱锥E -ABC 的体积为146时，点E 的轨迹长度为32π35(2024·吉林白山·统考一模)在四面体A -BCD 中，BC =22，BD =23，且满足BC ⊥BD ，AC ⊥BC ，AD ⊥BD ．若该三棱锥的体积为863，则该锥体的外接球的体积为．36(2024·吉林延边·统考一模)已知一个圆锥的侧面展开图是一个圆心角为25π5，半径为5的扇形.若该圆锥的顶点及底面圆周都在球O 的表面上，则球O 的体积为.37(2024·河南郑州·郑州市宇华实验学校校考一模)已知正三棱柱ABC-A1B1C1的底面边长为2，以A1为球心、3为半径的球面与底面ABC的交线长为3π6，则三棱柱ABC-A1B1C1的表面在球内部分的总面积为．38(2024·江西吉安·吉安一中校考一模)已知球O的直径PQ=4，A，B，C是球O球面上的三点，△ABC是等边三角形，且∠APQ=∠BPQ=∠CPQ=30°，则三棱锥P-ABC的体积为( ).A.334B.934C.332D.273439(2024·湖南长沙·雅礼中学校考一模)如图所示，有一个棱长为4的正四面体P-ABC容器，D是PB的中点，E是CD上的动点，则下列说法正确的是()A.直线AE与PB所成的角为π2B.△ABE的周长最小值为4+34C.如果在这个容器中放入1个小球(全部进入)，则小球半径的最大值为63D.如果在这个容器中放入4个完全相同的小球(全部进入)，则小球半径的最大值为26-25 40(2024·江西吉安·吉安一中校考一模)如图，在正三棱锥P-ABC中，有一半径为1的半球，其底面圆O与正三棱锥的底面贴合，正三棱锥的三个侧面都和半球相切．设点D为BC的中点，∠ADP=α．(1)用α分别表示线段BC和PD长度；(2)当α∈0,π2时，求三棱锥的侧面积S的最小值．41(2024·江西吉安·吉安一中校考一模)地球仪是地理教学中的常用教具.如图1所示，地球仪的赤道面(与转轴垂直)与黄道面(与水平面平行)存在一个夹角，即黄赤交角，大小约为23.5°.为锻炼动手能力，某同学制作了一个半径为4cm 的地球仪(不含支架)，并将其放入竖直放置的正三棱柱ABC -A 1B 1C 1中(姿态保持不变)，使地球仪与该三棱柱的三个侧面相切，如图2所示.此时平面AB 1C 恰与地球仪的赤道面平行，则三棱柱ABC -A 1B 1C 1的外接球体积为.(参考数据：tan23.5°≈0.43)题型04 空间向量42(2024·福建厦门·统考一模)已知平面α的一个法向量为n=(1,0,1)，且点A (1,2,3)在α内，则点B (1,1,1)到α的距离为．43(2024·广西南宁·南宁三中校联考一模)在边长为2的正方体ABCD -A 1B 1C 1D 1中，动点M 满足AM =xAB +yAD +zAA 1 ，(x ,y ,z ∈R 且x ≥0,y ≥0,z ≥0)，下列说法正确的是()A.当x =14,z =0,y ∈0,1 时，B 1M +MD 的最小值为13B.当x =y =1,z =12时，异面直线BM 与CD 1所成角的余弦值为105C.当x +y +z =1，且AM =253时，则M 的轨迹长度为42π3D.当x +y =1,z =0时，AM 与平面AB 1D 1所成角的正弦值的最大值为6344(2024·湖南长沙·雅礼中学校考一模)如图，在平行六面体ABCD -A 1B 1C 1D 1中，AB =AD =AA 1=1，∠DAB =90°，cos <AA 1 ，AB >=22，cos <AA 1 ，AD >=12，点M 为BD 中点.(1)证明：B 1M ⎳平面A 1C 1D ；(2)求二面角B -AA 1-D 的正弦值.。

2012年 G 立体几何 G1 空间几何体的结构1．G1[2012·重庆卷] 设四面体的六条棱的长分别为1,1,1,1，2和a ，且长为a 的棱与长为2的棱异面，则a 的取值范围为( )A ．(0，2)B ．(0，3)C ．(1，2)D ．(1，3)2．G1、G2[2012·陕西卷] 将正方体(如图1－3①所示)截去两个三棱锥，得到图②所示的几何体，则该几何体的左视图为( )3．G1、G12[2012·安徽卷] 若四面体ABCD 的三组对棱分别相等，即AB ＝CD ，AC ＝BD ，AD ＝BC ，则________(写出所有正确结论的编号)．①四面体ABCD 每组对棱相互垂直；②四面体ABCD 每个面的面积相等；③从四面体ABCD 每个顶点出发的三条棱两两夹角之和大于90°而小于180°；④连接四面体ABCD 每组对棱中点的线段相互垂直平分；⑤从四面体ABCD 每个顶点出发的三条棱的长可作为一个三角形的三边长．4．G1[2012·上海卷] 一个高为2的圆柱，底面周长为2π，该圆柱的表面积为________．5．G1、G11[2012·上海卷] 如图1－1，在三棱锥P －ABC 中，PA ⊥底面ABC ，D 是PC 的中点，已知∠BAC ＝π2，AB ＝2，AC ＝23，PA ＝2，求：(1)三棱锥P －ABC 的体积；(2)异面直线BC 与AD 所成的角的大小(结果用反三角函数值表示)．G2 空间几何体的三视图和直观图6．G2[2012·天津卷] 一个几何体的三视图如图1－2所示(单位：m)，则该几何体的体积为________m 3.7．G2[2012·辽宁卷] 一个几何体的三视图如图1－3所示，则该几何体的体积为________．8．G2[2012·课标全国卷] 如图1－2，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为()A．6 B．9 C．12 D．189. G2、G7[2012·浙江卷] 已知某三棱锥的三视图(单位：cm)如图1－1所示，则该三棱锥的体积是() A．1 cm3B．2 cm3 C．3 cm3D．6 cm310.G2[2012·湖北卷] 已知某几何体的三视图如图1－4所示，则该几何体的体积为________．11．G2[2012·广东卷] 某几何体的三视图如图1－1所示，它的体积为()A．72π B．48πC．30π D．24π12．G2[2012·福建卷] 一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是() A．球B．三棱锥C．正方体D．圆柱13．G2、G7[2012·安徽卷] 某几何体的三视图如图1－2所示，则该几何体的体积等于________．14．G2、G7[2012·北京卷] 某三棱锥的三视图如图所示，该三棱锥的表面积是() A．28＋6 5 B．30＋6 5 C．56＋12 5 D．60＋12 515．G2[2012·湖南卷] 某几何体的正视图和侧视图均如图1－1所示，则该几何体的俯视图不可能．．．是( )16．G2[2012·江西卷] 若一个几何体的三视图如图1－2所示，则此几何体的体积为( )A.112 B ．5 C.92D ．4G3 平面的基本性质、空间两条直线G4 空间中的平行关系17．G4、G5[2012·山东卷] 如图1－6，几何体E －ABCD 是四棱锥，△ABD 为正三角形，CB ＝CD ，EC ⊥BD. (1)求证：BE ＝DE ；(2)若∠BCD ＝120°，M 为线段AE 的中点，求证：DM ∥平面BEC.18．G4、G7[2012·辽宁卷] 如图1－5，直三棱柱ABC －A′B′C′，∠BAC ＝90°，AB ＝AC ＝2，AA′＝1，点M ，N 分别为A′B 和B′C′的中点．(1)证明：MN ∥平面A′ACC′；(2)求三棱锥A′－MNC 的体积．(锥体体积公式V ＝13Sh ，其中S 为底面面积，h 为高)19．G4、G5[2012·江苏卷] 如图1－4，在直三棱柱ABC －A 1B 1C 1中，A 1B 1＝A 1C 1，D ，E 分别是棱BC ，CC 1上的点(点D 不同于点C)，且AD ⊥DE ，F 为B 1C 1的中点．求证：(1)平面ADE ⊥平面BCC 1B 1；(2)直线A 1F ∥平面ADE.20．G4、G5[2012·浙江卷] 设l 是直线，α，β是两个不同的平面( ) A ．若l ∥α，l ∥β，则α∥β B ．若l ∥α，l ⊥β，则α⊥β C ．若α⊥β，l ⊥α，则l ⊥β D ．若α⊥β，l ∥α，则l ⊥βG5 空间中的垂直关系21．G5[2012·江西卷] 如图1－7，在梯形ABCD 中，AB ∥CD ，E ，F 是线段AB 上的两点，且DE ⊥AB ，CF ⊥AB ，AB ＝12，AD ＝5，BC ＝42，DE ＝4，现将△ADE ，△CFB 分别沿DE ，CF 折起，使A ，B 两点重合于点G ，得到多面体CDEFG.(1)求证：平面DEG ⊥平面CFG ； (2)求多面体CDEFG 的体积．图1－722．G5、G7[2012·陕西卷] 直三棱柱ABC －A 1B 1C 1中，AB ＝AA 1，∠CAB ＝π2.(1)证明：CB 1⊥BA 1；(2)已知AB ＝2，BC ＝5，求三棱锥C －ABA 的体积．23．G5、G12[2012·广东卷] 如图1－5所示，在四棱锥P －ABCD 中，AB ⊥平面PAD ，AB ∥CD ，PD ＝AD ，E 是PB 的中点，F 是DC 上的点且DF ＝12AB ，PH 为△PAD 中AD 边上的高．(1)证明：PH ⊥平面ABCD ；(2)若PH ＝1，AD ＝2，FC ＝1，求三棱锥E －BCF 的体积； (3)证明：EF ⊥平面PAB.24．G5、G11[2012·安徽卷] 如图1－3，长方体ABCD －A 1B 1C 1D 1中，底面A 1B 1C 1D 1是正方形，O 是BD 的中点，E 是棱AA 1上任意一点．(1)证明：BD ⊥EC 1；(2)如果AB ＝2，AE ＝2，OE ⊥EC 1，求AA 1的长．G6 三垂线定理G7 棱柱与棱锥25．G7[2012·山东卷] 如图1－3所示，正方体ABCD －A 1B 1C 1D 1的棱长为1，E 为线段B 1C 上的一点，则三棱锥A －DED 1的体积为________．226．G7[2012·江苏卷] 如图1－2，在长方体ABCD －A 1B 1C 1D 1中，AB ＝AD ＝3 cm ，AA 1＝2 cm ，则四棱锥A －BB 1D 1D 的体积为________cm 3.G8 多面体与球27．G8[2012·辽宁卷] 已知点P，A，B，C，D是球O表面上的点，PA⊥平面ABCD，四边形ABCD是边长为23的正方形，若PA＝26，则△OAB的面积为________．28．G8[2012·课标全国卷] 平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为2，则此球的体积为()A.6π B．43πC．46π D．63πG12 单元综合29．G12[2012·四川卷] 下列命题正确的是()A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行2012模拟题40．[2012·韶关调研] 三棱柱的直观图和三视图(正视图和俯视图是正方形，侧视图是等腰直角三角形)如图K27－3所示，则这个三棱柱的全面积等于()图A．12＋4 2 B．6＋2 2 C．8＋4 2 D．441．[2012·辽宁两校联考] 已知球的直径SC＝4，A，B是球面上的两点，AB＝2，∠BSC＝∠ASC＝45°，则棱锥S －ABC的体积是()A.33 B.233 C.433 D.53342．[2012·辽宁部分重点中学联考] 棱长为1的正方体和它的外接球被一个平面所截，截面是一个圆及其内接正三角形，那么球心到截面的距离等于________．。

2019-2020年高中数学 空间向量与立体几何 板块七 用空间向量解立方体问题完整讲义（学生版）【例1】 正方体中，与平面所成角的余弦值为（ ） A ．B ．C ．D ．【例2】 在正方体中，如图、分别是，的中点，⑴求证：平面；⑵求异面直线的所成角．【例3】 如图，已知正方体的棱长为，点是正方形的中心，点、分别是棱，的中点．设点，分别是点、在平面内的正投影．⑴证明：直线平面；⑵求异面直线与所成角的正弦值．G F ED 1C 1B 1A 1D CB A【例4】 如图，棱长为的正方体中，、分别为棱、上的动点，且（）．⑴求证：；⑵当的面积取得最大值时，求二面角的大小．FD 1C 1B 1A 1DC A【例5】 在棱长为1的正方体中，分别是的中点，在棱上，且，为的中点，典例分析⑴求证：；⑵求与所成的角的余弦值；⑶求的长．H GF ED 1C 1B 1A 1DC A【例6】 如图，在棱长为的正方体中，分别为的中点，分别为的中点，⑴求证：，；⑵求证：平面；⑶求异面直线与所成角的余弦值；⑷求直线与平面所成角的余弦值；⑸求二面角的余弦值．H GFE D 1C 1B 1A 1DC B A【例7】 如图，在正方体中，、分别是、的中点．⑴证明：；⑵求与所成的角；⑶证明：面面．F ED 1C 1B 1A 1DC B A【例8】 在正方体中，如图、分别是，的中点，⑴求证：平面；⑵求异面直线的所成角．【例9】 如图，在棱长为的正方体中，，截面，截面．⑴证明：平面和平面互相垂直；⑵证明：截面和截面面积之和是定值，并求出这个值；⑶若与平面所成的角为，求与平面所成角的正弦值．图1A'A BE C QC'G HDFP B'D'【例10】 如图，在长方体中，、分别是棱，上的点，，⑴ 求异面直线与所成角的余弦值；⑵ 证明平面【例11】 如图，已知正四棱柱中，底面边长，侧棱的长为，过点作的的垂线交侧棱于点，交于点．⑴求证：平面；⑵求与平面所成的角的正弦值．FED 1C 1B 1A 1DC B A【例12】 正方体的棱长为，是与的交点，是上一点，且．⑴求证：平面；。

8.42021届⾼三数学专题复习练习空间向量与⽴体⼏何（学⽣版）【课前测试】如图，已知正⽅形ABCD和矩形ACEF所在的平⾯互相垂直，AB＝，AF＝1，M是线段EF的中点．（2）求⼆⾯⾓A﹣DF﹣B的⼤⼩；（3）试在线段AC上⼀点P，使得PF与CD所成的⾓是60°．1空间向量与⽴体⼏何【知识梳理】⼀、平⾏、垂直的向量证法设直线l，m的⽅向向量分别为a，b，平⾯α，β的法向量分别为u，ν，则线线平⾏：l∥m?a∥b?a＝k b，k∈R；线⾯平⾏：l∥α?a⊥u?a·u＝0；⾯⾯平⾏：α∥β?u∥ν?u＝kν，k∈R.线线垂直：l⊥m?a⊥b?a·b＝0；线⾯垂直：l⊥α?a∥u?a＝k u，k∈R；⾯⾯垂直：α⊥β?u⊥ν?u·ν＝0.⼆、空间⾓的求法1、异⾯直线所成的⾓设a，b分别是两异⾯直线l1，l2的⽅向向量，则设直线l的⽅向向量为a，平⾯α的法向量为n，直线l与平⾯α所成的⾓为θ，则sin θ＝|cos〈a，n〉|＝|a·n| |a||n|.3、求⼆⾯⾓的⼤⼩23①如图①，AB ，CD 是⼆⾯⾓α-l -β的两个⾯内与棱l 垂直的直线，则⼆⾯⾓的⼤⼩θ＝〈AB →，CD →〉．②如图②③，n 1，n 2分别是⼆⾯⾓α-l -β的两个半平⾯α，β的法向量，则⼆⾯⾓的⼤⼩θ满⾜|cos θ|＝|cos 〈n 1，n 2〉|，⼆⾯⾓的平⾯⾓⼤⼩是向量n 1与n 2的夹⾓(或其补⾓)．4【课堂讲解】考点⼀空间向量法证明平⾏或垂直问题例1、如图，在多⾯体ABC -A 1B 1C 1中，四边形A 1ABB 1是正⽅形，AB ＝AC ，BC ＝2AB ，B 1C 1平⾏且等于12BC ，⼆⾯⾓A 1-AB -C 是直⼆⾯⾓．求证：(1)A 1B 1⊥平⾯AA 1C ； (2)AB 1∥平⾯A 1C 1C .变式训练：1、已知正⽅体ABCD -A 1B 1C 1D 1的棱长为2，E ，F 分别是BB 1，DD 1的中点，求证： (1)FC 1∥平⾯ADE ； (2)平⾯ADE ∥平⾯B 1C 1F .52、如图，在四棱锥E-ABCD中，AB⊥平⾯BCE，CD⊥平⾯BCE，AB＝BC＝CE＝2CD＝2，∠BCE＝120°.求证：平⾯ADE⊥平⾯ABE.3、如右图，在四棱锥P-ABCD中，底⾯ABCD是正⽅形，侧棱PD⊥底⾯ABCD，PD=DC，E是Pc的中点，作EF上PB交PB于F，证明：（1）直线PA∥平⾯EDB；（2）直线PB⊥平⾯EFD．67考点⼆利⽤空间向量求异⾯直线所成⾓例2、如图，在正⽅体ABCD -A 1B 1C 1D 1中，E 为AB 的中点． (1)求直线AD 和直线B 1C 所成⾓的⼤⼩； (2)求证：平⾯EB 1D ⊥平⾯B 1CD .变式训练：1．长⽅体ABCD -A 1B 1C 1D 1中，AB ＝AA 1＝2，AD ＝1，E 为CC 1的中点，则异⾯直线BC 1与AE 所成⾓的余弦值为( ) A.1010B.3010C.21510D.310102.如图，在四棱锥P -ABCD 中，P A ⊥平⾯ABCD ，底⾯ABCD 是菱形，AB ＝2，∠BAD ＝60°. (1)求证：BD ⊥平⾯P AC ；(2)若P A ＝AB ，求PB 与AC 所成⾓的余弦值．8考点三利⽤空间向量求直线与平⾯所成⾓例3、如图，在直棱柱ABCD －A 1B 1C 1D 1中，AD ∥BC ，∠BAD ＝90°，AC ⊥BD ，BC ＝1，AD ＝AA 1＝3.(1)证明：AC ⊥B 1D ；(2)求直线B 1C 1与平⾯ACD 1所成⾓的正弦值．变式训练：1、如图所⽰，在四棱台ABCD -A 1B 1C 1D 1中，AA 1⊥底⾯ABCD ，四边形ABCD 为菱形，∠BAD ＝120°，AB ＝AA 1＝2A 1B 1＝2.(1)若M 为CD 的中点，求证：AM ⊥平⾯AA 1B 1B ； (2)求直线DD 1与平⾯A 1BD 所成⾓的正弦值．2、在三棱柱ABC-A1B1C1中，侧⾯ABB1A1为矩形，AB＝2，AA1＝22，D是AA1的中点，BD与AB1交于点O，且CO⊥平⾯ABB1A1.(1)证明：BC⊥AB1；(2)若OC＝OA，求直线CD与平⾯ABC所成⾓的正弦值．考点四利⽤空间向量求⼆⾯⾓例4、已知正三棱柱ABC－A1B1C1中，AB＝2，AA1＝ 6.点F，E分别是边A1C1和侧棱BB1的中点．(1)证明：FB⊥平⾯AEC；9(2)求⼆⾯⾓F－AE－C的余弦值.1011变式训练：1、如图，在四棱锥S －ABCD 中，底⾯ABCD 是直⾓梯形，侧棱SA ⊥底⾯ABCD ，AB 垂直于AD 和BC ，SA ＝AB ＝BC ＝2，AD ＝1，M 是棱SB 的中点． (1)求证：AM ∥平⾯SCD ；(2)求平⾯SCD 与平⾯SAB 所成的⼆⾯⾓的平⾯⾓的余弦值；2、在四棱锥P －ABCD 中，P A ⊥平⾯ABCD ，E 是PD 的中点，∠ABC ＝∠ACD ＝90°，∠BAC ＝∠CAD ＝60°，AC ＝AP ＝2. (1)求证：PC ⊥AE ；(2)求⼆⾯⾓A －CE －P 的余弦值.3、如图，四边形ABCD 为正⽅形，PD⊥平⾯ABCD ，PD∥QA ，QA = AB =1PD．2（I）证明：平⾯PQC ⊥平⾯DCQ ；考点五解决探索性问题例5、如图，四棱锥P-ABCD的底⾯为直⾓梯形，AD∥BC，AD＝2BC＝2，BC⊥DC，∠BAD ＝60°，平⾯P AD⊥底⾯ABCD，E为AD的中点，△P AD为正三⾓形，M是棱PC上的⼀点(异于端点)．(1)若M为PC的中点，求证：P A∥平⾯BME.(2)是否存在点M，使⼆⾯⾓M-BE-D的⼤⼩为30°？若存在，求出点M的位置；若不存在，说明理由．12变式训练：1、直三棱柱ABC A1B1C1中，AA1＝AB＝AC＝1，E，F分别是CC1，BC的中点，AE⊥A1B1，D为棱A1B1上的点．(1)证明：DF⊥AE；(2)是否存在⼀点D，使得平⾯DEF与平⾯ABC所成锐⼆⾯⾓的平⾯⾓的余弦值为1414？若存在，说明点D的位置，若不存在，说明理由．2、如图，在四棱锥P-ABCD中，P A⊥平⾯ABCD，AD∥BC，AD⊥CD，且AD＝CD＝22，BC＝42，P A＝2.(1)求证：AB⊥PC；(2)在线段PD上，是否存在⼀点M，使得⼆⾯⾓M-AC-D的⼤⼩为45°，如果存在，求BM与平⾯MAC所成⾓的正弦值，如果不存在，请说明理由．1314考点六空间中的距离问题例6、如图，平⾯P AD ⊥平⾯ABCD ，四边形ABCD 为正⽅形，△P AD 是直⾓三⾓形，且P A ＝AD ＝2，E ，F ，G 分别是线段P A ，PD ，CD 的中点． (1)求证：平⾯EFG ⊥平⾯P AB ； (2)求点A 到平⾯EFG 的距离．变式训练：如图，在四棱锥O ABCD -中，底⾯ABCD 四边长为1的菱形，4ABC π∠=OA ABCD ⊥底⾯ 2OA = M 为OA 的中点，N 为BC 的中点(1)证明：直线MN OCD平⾯‖；(2)求异⾯直线AB 与MD 所成⾓的⼤⼩； (3)求点B 到平⾯OCD 的距离。