下载文档原格式
全国2019年4月高等教育自学考试普通逻辑试题课程代码：00024一、单项选择题（本大题共15小题，每小题1分，共15分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.“p∧q→r”与“p∨q←r”这两个逻辑式子中，它们（）A.变项和逻辑常项相同B.变项不同但逻辑常项相同C.逻辑常项不同但变项相同D.变项和逻辑常项都不同2.对于A、B两概念，如果所有a都是b并且有b不是a，那么，A、B两概念具有（）A.全同关系B.真包含于关系C.交叉关系D.全异关系3.□p与□┐p之间关系是（）A.反对关系B.矛盾关系C.差等关系D.下反对关系4.一个相容选言判断p∨q假，那么，一定为（）A.p真q真B.p真q假C.p假q真D.p假q假5.判断间的反对关系，应是（）关系。
A.对称且传递B.对称且非传递C.非对称且反传递D.非对称且传递6.有学生在上课时间去看电影，老师批评时，学生反问：“看革命题材电影不是好事吗？”学生的说法（）A.违反同一律B.违反矛盾律C.违反排中律D.不违反普通逻辑的基本规律7.直接推理“SEP→PA S”，属于（）推理。
A.换质法B.换位法C.换质位法D.换位质法8.“（p→q）∧（r→s）∧(┐q∨┐s)→(┐p∨┐r)”，这一推理式是（）A.二难推理的简单构成法B.二难推理的简单破坏式C.二难推理的复杂构成式D.二难推理的复杂破坏式9.“因为aRb并且bRc，所以，a R c”,这一推理式是（）A.对称关系推理B.反对称关系推理C.传递关系推理D.反传递关系推理10.反证法是先论证与原论题相矛盾的论断为假，然后根据（）确定原论题真的论证方法。
A.同一律B.矛盾律1C.排中律D.充足理由律11.一国丧失过量的表土，需进口更多的粮食，这就增加了其他国家土壤的压力；一国大气污染，导致邻国受到酸雨的危害；二氧化碳过度排放，造成全球变暖，海平面上升，几乎可以危及所有的国家和地区。
高等数学（理专）交卷时间：2015-11-21 12:02:24一、单选题1.(5分)以函数为特解的二阶线性常系数齐次微分方程为（）.• A. ；•；•；•.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案C解析考查要点：试题解答：总结拓展：2.(5分)设函数在点处连续，且，则常数等于（）.• A. ；•；•；• D. 2.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案A解析考查要点：试题解答：总结拓展：3.(5分)定积分等于（）.• A. 100；•；• C. 200；•.得分：0知识点：高等数学(理、专)作业题,高等数学（理专）作业题收起解析答案D解析考查要点：试题解答：总结拓展：4.(5分)定积分等于（）.• A. 1；• B. 2；• C. 3；• D. 4.得分：0知识点：高等数学(理、专)作业题,高等数学（理专）作业题收起解析答案C解析考查要点：试题解答：总结拓展：5.(5分)下列命题正确的是（）.• A. 函数在点处无定义，则极限不存在；• B. 函数在点处有定义，则极限存在；• C. 函数在点处有定义，极限存在，则；• D. 极限存在与否，与函数在点处是否有定义无关.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案D解析考查要点：试题解答：总结拓展：6.(5分)初等函数在其定义区间内必定（）.• A. 可导；• B. 可微；• C. 存在原函数；• D. 不确定.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案C解析考查要点：试题解答：总结拓展：7.(5分)设，在处连续，则（）.• A. 0；•；• C. 1；•.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案A解析考查要点：试题解答：总结拓展：8.(5分)不定积分等于（）.• A. ；•；•；•.得分：0知识点：高等数学(理、专)作业题,高等数学（理专）作业题收起解析答案D解析考查要点：试题解答：总结拓展：9.(5分)设是二阶线性常系数齐次微分方程微分方程的两个特解，则函数（）.• A. 是所给方程的解，但不是通解；• B. 是所给方程的解，但不一定是通解；• C. 是所给方程的通解；• D. 不是所给方程的通解.得分：0知识点：高等数学(理、专)作业题,高等数学（理专）作业题收起解析答案B解析考查要点：试题解答：总结拓展：10.(5分)设函数在点内连续，则常数分别等于（）.• A. 0，0；• B. 1，1；• C. 2，3；• D. 3，2.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案C解析考查要点：试题解答：总结拓展：11.(5分)下列微分方程中是一阶线性非齐次微分方程的是（）.• A. ；•；•；•.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案C解析考查要点：试题解答：总结拓展：12.(5分)极限等于（）.• A. 0；•；•.；•.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案A解析考查要点：试题解答：总结拓展：13.(5分)已知，则常数等于（）.• A. -2；• B. 2；•；•.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案A解析考查要点：试题解答：总结拓展：14.(5分)，则等于（）.• A. ；•；•；•.得分：0知识点：高等数学(理、专)作业题,高等数学（理专）作业题收起解析答案C解析考查要点：试题解答：总结拓展：15.(5分)微分方程的通解中含有的相互独立的任意常数的个数是（）.• A. 1；• B. 2；• C. 3；• D. 4.得分：0知识点：高等数学(理、专)作业题,高等数学（理专）作业题收起解析答案B解析考查要点：试题解答：总结拓展：16.(5分)抛物线，与轴所围成的平面图形的面积等于（）.• A. ；•；• C. 1；•.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析解析考查要点：试题解答：总结拓展：17.(5分)设函数在点处连续，则常数等于（）.• A. 2；• B. 1；• C. -1；• D. -2.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案D解析考查要点：试题解答：总结拓展：18.设函数在点处连续，则等于（）.• A. 0；• B. 1；• C. 2；• D. 3.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案B解析考查要点：试题解答：总结拓展：19.(5分)下列不定积分不正确的是（）.• A. ；•；•；•.得分：0知识点：高等数学(理、专)作业题,高等数学（理专）作业题收起解析答案B解析考查要点：试题解答：总结拓展：20.(5分)下列所给微分方程的解中，是通解的是（）.• A. ；•；•；•.得分：0知识点：高等数学(理、专)作业题,高等数学（理专）作业题收起解析答案D解析考查要点：试题解答：总结拓展：高等数学（理专）交卷时间：2015-11-21 12:11:05一、单选题1.(5分)设函数在点处连续，且，则常数等于（）.• A. ；•；•；• D. 2.得分：0知识点：高等数学（理专）作业题,高等数学(理、专)作业题收起解析答案A解析考查要点：试题解答：。
吉林大学2020年秋季《高等数学（理专）》在线作业二附满分答案试卷总分:100 得分:100一、单选题 (共 15 道试题,共 60 分)1.微分方程ydx+xdy=0的通解是()A.xy=CB.xy=0C.x+y=CD.x-y=0答案:A2.集合A={±2，±3，±4，±5，±6}表示A.A是由绝对值小于等于6的全体整数组成的集合B.A是由绝对值大于等于2，小于等于6的全体整数组成的集合C.A是由全体整数组成的集合D.A是由绝对值大于2，小于6的整数组成的集合答案:B更多加微boge30619,有惊喜！！！3.f(x)={0 (当x=0)} {1(当x≠0)}则（）A.x->0,lim f(x)不存在B.x->0,lim [1/f(x)]不存在C.x->0,lim f(x)=1D.x->0,lim f(x)=0答案:C4.曲线y=f(x)关于直线y=x对称的必要条件是（）A.f(x)=xB.f(x)=1/xC.f(x)=-xD.f[f(x)]=x答案:D5.已知z=f(x，y)由隐函数xy+g(z)=0确定,其中g(z)关于z 可导且导数恒大于0, 则x=0,y=0时的全微分dz=（）A.dxB.dyC.0D.dx-dy答案:C6.x=0是函数f(x)=x arctan(1/x)的（）A.连续点B.可去间断点C.跳跃间断点D.无穷间断点答案:B7.微分方程sinxdx-sinydy=0的通解是()A.cosx+cosy=0B.cosx-cosy=0C.cosx+cosy=CD.cosx-cosy=C答案:D8.已知f(x)的原函数是cosx,则f '(x)的一个原函数是（）A.sinxB.-sinxC.cosxD.-cosx答案:B9.f(x)在（-∞，+∞）上有定义，且0≤f(x)≤M，则下列函数必有界的是（）A.1/f(x)B.ln(f(x))C.e^(1/f(x))D.e^(-1/f(x))答案:D10.函数y=|sinx|在x=0处( )A.无定义B.有定义，但不连续C.连续D.无定义，但连续答案:C11.y=x+arctanx的单调增区间为A.(0,+∞)B.(-∞,+∞)C.(-∞,0)D.(0,1)答案:B12.由曲线y=cosx (0=<x<=3π/2) 与坐标轴所围成的图形面积=（）A.4B.3C.4πD.3π答案:B13.f(x)=m|x+1|+n|x-1|,在（-∞，+∞）上（）A.连续B.仅有两个间断点x=±1，它们都是可去间断点C.仅有两个间断点x=±1，它们都是跳跃间断点D.以上都不对，其连续性与常数m，n有关。
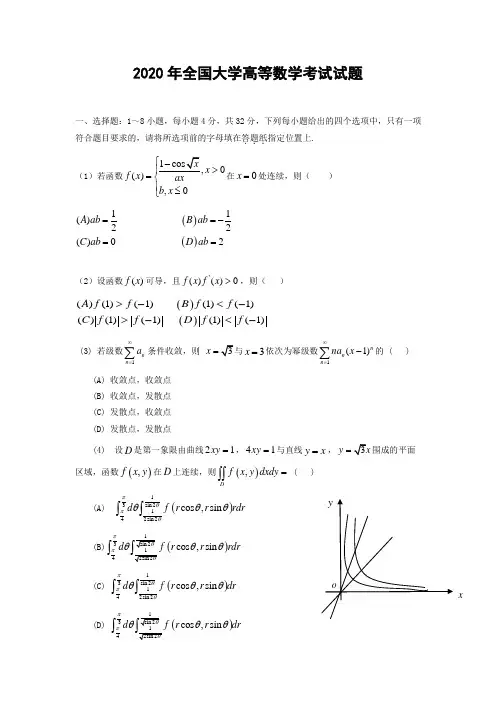
2020年全国大学高等数学考试试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸．．．指定位置上. （1）若函数1,0(),0x f x axb x ⎧->⎪=⎨⎪≤⎩在0x =处连续，则（ ） ()()11()22()02A abB abC abD ab ==-==（2）设函数()f x 可导，且'()()0f x f x >，则（ ）()()()(1)(1)(1)(1)()(1)(1)(1)(1)A f fB f fC f fD f f >-<->-<-(3) 若级数1∞=∑nn a条件收敛，则=x 3=x 依次为幂级数1(1)∞=-∑n n n na x 的 ( )(A) 收敛点，收敛点 (B) 收敛点，发散点 (C) 发散点，收敛点 (D) 发散点，发散点(4) 设D 是第一象限由曲线21xy =，41xy =与直线y x =，y =围成的平面区域，函数(),f x y 在D 上连续，则(),Df x y dxdy =⎰⎰ ( )(A)()13sin 2142sin 2cos ,sin d f r r rdr πθπθθθθ⎰⎰(B)()34cos ,sin d f r r rdr ππθθθ⎰(C)()13sin 2142sin 2cos ,sin d f r r dr πθπθθθθ⎰⎰(D)()34cos ,sin d f r r dr ππθθθ⎰x（5）设α是n 维单位列向量，E 为n 阶单位矩阵，则（ ）()()()()22T T TT A E B E C E D E αααααααα-++-不可逆不可逆不可逆不可逆（6）设矩阵200210100021,020,020*********A B C ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,则（ ） ()()(),,(),,A A C B C B A C B C C A C B C D A C B C 与相似与相似与相似与不相似与不相似与相似与不相似与不相似(7) 若A,B 为任意两个随机事件，则 ( )(A) ()()()≤P AB P A P B (B) ()()()≥P AB P A P B (C) ()()()2≤P A P B P AB (D) ()()()2≥P A P B P AB(8)设随机变量,X Y 不相关，且2,1,3===EX EY DX ，则()2+-=⎡⎤⎣⎦E X X Y ( )(A) 3- (B) 3 (C) 5- (D) 5二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸．．．指定位置上. (1) 已知函数21()1f x x=+，则(3)(0)f =__________ (2) 微分方程'''230y y y ++=的通解为y =_________(3) 若曲线积分221L xdx aydy x y -+-⎰在区域{}22(,)|1D x y x y =+<内与路径无关，则 a =__________(4)设Ω是由平面1++=x y z 与三个坐标平面平面所围成的空间区域，则(23)__________.x y z dxdydz Ω++=⎰⎰⎰(5)设二维随机变量(,)x y 服从正态分布(1,0;1,1,0)N ，则{0}________.P XY Y -<=三、解答题：15—23小题，共94分.请将解答写在答题纸．．．指定位置上.解答应写出文字说明、证明过程或演算步骤. （1）（本题满分10分）设函数(,)f u v 具有2阶连续偏导数，(,cos )xy f e x =，求0x dy dx=，22x d y dx=（2）（本题满分10分）求21lim ln 1nn k kk nn →∞=⎛⎫+ ⎪⎝⎭∑（3）（本题满分10分）已知函数()y x 由方程333320x y x y +-+-=确定，求()y x 的极值(4)(本题满分 10 分)（I ）设函数()()u x ,v x 可导，利用导数定义证明u x v x u x v x u x v x '''=+[()()]()()()()（II ）设函数()()()12n u x ,u x ,,u x 可导，n f x u x u x u x =12()()()()，写出()f x 的求导公式.(5)(本题满分 10 分)已知曲线L的方程为,z z x ⎧=⎪⎨=⎪⎩起点为()A，终点为()0,B ，计算曲线积分()()2222d d ()d LI y z x z x y y x y z =++-+++⎰.(6) (本题满11分)设向量组1,23,ααα内3R 的一个基，113=2+2k βαα，22=2βα，()313=++1k βαα.（I ）证明向量组1β2β3β为3R 的一个基;（II ）当k 为何值时，存在非0向量ξ在基1,23,ααα与基1β2β3β下的坐标相同，并求所有的ξ.（7）（本题满分11分）设二次型222123123121323(,,)2282f x x x x x ax x x x x x x =-++-+在正交变换X QY =下的标准型221122y y λλ+，求a 的值及一个正交矩阵Q（8）（本题满分11分）设随机变量,X Y 相互独立，且X 的概率分布为1(0)(2)2P X P X ====，Y 的概率密度为201()0,y y f y <<⎧=⎨⎩，其他()I 求()P Y EY ≤()∏求Z X Y =+的概率密度。
吉大20秋学期《高等数学（理专）》在线作业一-0001试卷总分:100 得分:100一、单选题 (共 15 道试题,共 60 分)1.微分方程y'+y=x+1的一个特解是（）A.x+y=0B.x-y=0C.x+y=1D.x-y=1答案:B2.x->x0时，a(x)和b(x)都是关于x-x0的n阶无穷小量，而a(x)+b(x)是关于x-x0的m阶无穷小量，则（）A.必有m=nB.必有m≥nC.必有m≤nD.以上几种可能都可能答案:C3.下列函数中（）是奇函数A.xsinxB.x+cosxC.x+sinxD.|x|+cosx答案:C4.以下数列中是无穷大量的为（）A.数列{Xn=n}B.数列{Yn=cos(n)}C.数列{Zn=sin(n)}D.数列{Wn=tan(n)}答案:A5.微分方程dx+2ydy=0的通解是（）A.x+y^2=CB.x-y^2=CC.x+y^2=0D.x-y^2=0答案:A6.集合B是由能被3除尽的全部整数组成的，则B可表示成A.{3，6，…，3n}B.{±3，±6，…，±3n}C.{0，±3，±6，…，±3n…}D.{0，±3，±6，…±3n}答案:C7.已知f(x)的原函数是cosx,则f '(x)的一个原函数是（）A.sinxB.-sinxC.cosxD.-cosx答案:B8.已知z= 3cos(cos(xy)),则x=0,y=0时的全微分dz=（）A.dxB.dyC.0D.dx+dy答案:C9.已知u= xyz, 则x=0,y=0,z=1时的全微分du=（）A.dxB.dyC.dzD.0答案:D10.求极限lim_{n->无穷} n^2/(2n^2+1) = ( )A.0B.1C.1/2D.3答案:C11.∫{lnx/x^2}dx 等于( )A.lnx/x+1/x+CB.-lnx/x+1/x+CC.lnx/x-1/x+CD.-lnx/x-1/x+C答案:D12.设F(x)=∫e^(sint) sint dt,{积分区间是x->x+2π},则F（x）为()A.正常数B.负常数C.正值但不是常数D.负值但不是常数答案:A13.f(x)在（-∞，+∞）上有定义，且0≤f(x)≤M，则下列函数必有界的是（）A.1/f(x)B.ln(f(x))C.e^(1/f(x))D.e^(-1/f(x))答案:D14.微分方程y'=2x+sinx的一个特解是（）A.y=x^2+cosxB.y=x^2-cosxC.y=x+cosxD.y=x-cosx答案:B15.设分段函数f(x)={x+1,当0≤x＜1},{x-1,当1≤x≤2}则，F(x)=∫f(t)dt,{积分区间是a->x}，则x=1是函数F(x)的（）A.跳跃间断点B.可去间断点C.连续但不可导点D.可导点答案:C二、判断题 (共 10 道试题,共 40 分)16.对于任意正项级数，删去级数的前有限项，不影响级数的收敛与发散（）答案:正确17.罗尔定理的几何意义是：一条两个端点的纵坐标相等的连续光滑曲线弧上至少有一点C （ξ，f(ξ)），曲线在C点的切线平行于x轴答案:正确18.对一个函数先求不定积分再求微分，两者的作用抵消后只差一个常数。
吉林大学2020年秋季《高等数学（理专）》在线作业一附满分答案试卷总分:100 得分:100一、单选题 (共 15 道试题,共 60 分)1.曲线y=x^2+x-2在点(1.5,1.75)处的切线方程为( )A.16x-4y-17=0B.16x+4y-31=0C.2x-8y+11=0D.2x+8y-17=0答案:A2.设X0是函数f(x)的可去间断点，则()A.f(x)在x0的某个去心领域有界B.f(x)在x0的任意去心领域有界C.f(x)在x0的某个去心领域无界D.f(x)在x0的任意去心领域无界答案:A更多加微boge30619,有惊喜！！！3.直线y=2x,y=x/2,x+y=2所围成图形的面积为()A.2/3B.3/2C.3/4D.4/3答案:A4.计算y= 3x^2在[0,1]上与x轴所围成平面图形的面积=（）A.0B.1C.2D.3答案:B5.f(x)={0 (当x=0)} {1(当x≠0)}则（）A.x->0,lim f(x)不存在B.x->0,lim [1/f(x)]不存在C.x->0,lim f(x)=1D.x->0,lim f(x)=0答案:C6.x=0是函数f(x)=x arctan(1/x)的（）A.连续点B.可去间断点C.跳跃间断点D.无穷间断点答案:B7.设f(x)是可导函数，则（）A.∫f(x)dx=f'(x)+CB.∫[f'(x)+C]dx=f(x)C.[∫f(x)dx]'=f(x)D.[∫f(x)dx]'=f(x)+C答案:C8.已知y= 4x^3-5x^2+3x-2, 则x=0时的二阶导数y"=（）A.0B.10C.-10D.1答案:C9.集合A={±2，±3，±4，±5，±6}表示A.A是由绝对值小于等于6的全体整数组成的集合B.A是由绝对值大于等于2，小于等于6的全体整数组成的集合C.A是由全体整数组成的集合D.A是由绝对值大于2，小于6的整数组成的集合答案:B10.集合A={±2，±3，±4，±5，±6}表示A.A是由绝对值小于等于6的全体整数组成的集合B.A是由绝对值大于等于2，小于等于6的全体整数组成的集合C.A是由全体整数组成的集合D.A是由绝对值大于2，小于6的整数组成的集合答案:B11.设函数f(x)=x(x-1)(x-3)，则f ＇( 0 ) = ( )A.0B.1C.3D.2答案:C12.已知z= 3sin(sin(xy)),则x=0,y=0时的全微分dz=（）A.dxB.dyC.dx+dyD.0答案:D13.下列结论正确的是（）A.若|f(x)|在x=a点处连续，则f(x)在x=a点也必处连续B.若[f(x)]^2在x=a点处连续，则f(x)在x=a点也必处连续C.若[f(x)]^3在x=a点处连续，则f(x)在x=a点也必处连续D.若f(x)在x=a点处连续，则1/f(x)在x=a点也必处连续答案:C14.设函数f(x-2)=x^2+1，则f(x+1)=( )A.x^2+2x+2B.x^2-2x+2C.x^2+6x+10D.x^2-6x+10答案:C15.设函数f(x)，g(x)在[a,b]上连续，且在[a,b]区间积分∫f(x)dx=∫g(x)dx，则（）A.f(x)在[a,b]上恒等于g(x)B.在[a,b]上至少有一个使f(x)≡g(x)的子区间C.在[a,b]上至少有一点x，使f(x)=g(x)D.在[a,b]上不一定存在x，使f(x)=g(x)答案:C二、判断题 (共 10 道试题,共 40 分)16.无穷小量是一种很小的量。
吉大20春学期《高等数学(理专)》在线作业一答卷吉大18春学期《高等数学（理专）》在线作业一-0002试卷一、单选题(共15道试题,共60分)1.设函数$f(x)=x(x-1)(x-3)$，则$f'(0)=$（）A.0B.1C.3D.2答案：C2.曲线$y=(x-1)^2\times(x-3)^2$的拐点个数为（）A.0B.1C.2D.3答案：C3.已知$f(x)$的一个原函数是$e^{-x}$，则$\int xf'(x)dx$等于（）A.$xe^{-x}+e^{-x}+C$B.$xe^{-x}-e^{-x}+C$C.$-xe^{-x}-e^{-x}+C$D.$-xe^{-x}+e^{-x}+C$答案：C4.$f(x)=m|x+1|+n|x-1|$，在$(-\infty,+\infty)$上（）A.连续B.仅有两个间断点$x=\pm1$，它们都是可去间断点C.仅有两个间断点$x=\pm1$，它们都是跳跃间断点D.以上都不对，其连续性与常数$m$，$n$有关。
答案：A5.若$F'(x)=f(x)$，则$\int dF=$（）A.$f(x)$B.$F(x)$C.$f(x)+C$D.$F(x)+C$答案：D6.已知函数$y=2x\sin3x-5e^{2x}$，则$x=0$时的导数$y'=$（）A.0B.10C.-10D.1答案：C7.由曲线$y=\cos x(0\leq x\leq \frac{3\pi}{2})$与坐标轴所围成的图形面积=（）A.4B.3C.$4\pi$D.$3\pi$答案：B8.设函数$f(x)$连续，则积分区间$(0,x)$，$\frac{d}{dx}\{\int_{0}^{x}f(x^2-t^2)dt\}=$（）A.$2xf(x^2)$B.$-2xf(x^2)$C.$xf(x^2)$D.$-xf(x^2)$答案：C9.一枚硬币前后掷两次所出现可能结果的全部所组成的集合，可表示为$A=\{$正面，反面$\}$，$B=\{$(正面，正面)，(反面，反面)$\}$，$C=\{$(正面，反面)，(反面，正面)$\}$和$D=\{$(正面，正面)，(反面，正面)，(正面，反面)，(反面，反面)$\}$答案：D10.已知函数$y=2\cos3x-5e^{2x}$，则$x=0$时的微分$dy=$（）A.10B.$10dx$C.-10D.-$10dx$答案：D11.设$a(x)=x^m-1$，$b(x)=x^n-1$，$m>n>0$，且当$x\to1$时，有（）A.$a=o(b)$B.$b=o(a)$C.$a\sim b$D.$a(x)$和$b(x)$是同阶无穷小，但不是等价无穷小答案：D12.原函数为xlnx，对其求导得到f(x)=lnx+1，将其带入∫xf(x)dx中得到∫xlnx+xd x，对xlnx使用分部积分法，得到xlnx-x+C，再对x使用分部积分法，得到x^2/2lnx-x^2/4+C，化简得到B选项。
吉大20春学期《高等数学（理专）》在线作业二1 单选题1 直线 y=2x, y=x/2, x+y=2 所围成图形的面积为 ( )A 3/2B 2/3C 3/4D 4/32 已知u= xyz, 则x=0,y=0,z=1时的全微分du=（）A dxB dyC dzD 03 f(a)f(b)<0,是方程f(x)=0在（a,b）有解的（）A 充分条件，非必要条件B 非充分条件，必要条件C 充分必要条件D 无关条件4 已知函数y= 2cos3x-5e2x, 则x=0时的微分dy=（）A 10B 10dxC -10D -10dx5 设函数f(x-2)=x^2+1，则f(x+1)=( )A x^2+2x+2B x^2-2x+2C x^2+6x+10D x^2-6x+106 集合B是由能被3除尽的全部整数组成的，则B可表示成A {3，6，…，3n}B {±3，±6，…，±3n}C {0，±3，±6，…，±3n…}D {0，±3，±6，…±3n}7 集合A={±2，±3，±4，±5，±6}表示A A是由绝对值小于等于6的全体整数组成的集合B A是由绝对值大于等于2，小于等于6的全体整数组成的集合C A是由全体整数组成的集合D A是由绝对值大于2，小于6的整数组成的集合8 已知z= 3cos(cos(xy)),则x=0,y=0时的全微分dz=（）A dxB dyC 0D dx+dy9 曲线ln(x+y)=xy在（1，0）点处的切线（）A 不存在B x=1。
