生活中的立体图形练习题

二．选择题
第1页 共4页
11．将下列几何体分类，柱体有： ，锥体有 （填序号） ；
12．长方体由_______________个面_______________条棱_______________个顶点；
13．半圆面绕直径旋转一周形成__________；
4． 围成几何体的侧面中，至少有一个是曲面的是______________；（举一例）
5． 正方体有_____个顶点，经过每个顶点有_________条棱，这些棱都____________；
6． 圆柱、圆锥、球的共同点是_____________________________；
7．线,说明了______________,时钟秒针旋转时，形成一个圆面，这说明了_______________，三角板绕它的一条直角边旋转一周，形成一个圆锥体，这说明了___________________；
8． 圆可以分割成_____ 个扇形，每个扇形都是由___________________；
9． 从一个七边形的某个顶点出发，分别连结这个点与其余各顶点，可以把七边形分割成__________个三角形；
10．在乒乓球、橄榄球、足球、羽毛球、冰球中，是球体的有 ；
《生活中的立体图形》试卷
第1.1.1课时家庭作业 （生活中的立体图形1） 姓名 学习目标：
1．经历从现实世界中抽象出几何图表的过程，感受图形世界的丰富多彩。
2．在具体情境中认识圆柱、圆锥、正方体、长方体、棱柱、棱台、球，并能用自已的语言描述它们的某些特征。
一．填空题：
1．立体图形的各个面都是__________的面，这样的立体图形称为多面体.；
2．图形是由________，_________，________构成的；

《生活中的立体图形》课后练习一、填空题1.立体图形的各个面都是__________的面,这样的立体图形称为多面体.2.图形是由________,__________,____________构成的.3.物体的形状似于圆柱的有________________;类似于圆锥的有______________;类似于球的有_________________.4.围成几何体的侧面中,至少有一个是曲面的是______________.5.正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都____________.6.圆柱,圆锥,球的共同点是_____________________________.7.假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________.8.圆可以分割成_____个扇形,每个扇形都是由___________.9.从一个七边形的某个顶点出发,分别连结这个点与其余各顶点,可以把七边形分割成__________个三角形.二、选择题10. 从一个十边形的某个点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成( )个三角形A. 10B. 9C. 8D. 711. 图1-1是由( )图形饶虚线旋转一周形成的13.图1-2绕虚线旋转一周形成的图形是( )14.图1-3这个美丽的图案是由我们所熟悉的( )图形组成A.三角形和扇形B圆和四边形C.圆和三角形D圆和扇形15.下面全由圆形组成的图案是( )三、解答题16.请观察丰富多彩的生活世界,有哪些物体的形状与下列几何体类似?(1)六面体(2)圆柱(3)圆锥(4)棱锥17.请写出下列几何体的名称( ) ( ) ( )( ) ( )18.请说出生活中至少4个规则的物体,并说出和它们类似的立体图形?19.动手做一做.将一个长方体切去一部分,看一看剩余的部分是几面体呢?四.开放创新提高题20.如图1-4,一长方体土地,用两条直线把它分成形状相同,大小相等的四块,你能做到吗,能用不同的方法完成这个任务吗?21.一个圆绕着它的直径的直线旋转一周就形成球体,那么现有一个长方形(如图1-5)你有几种方法使它类似于圆柱的几何体?请你画出这些立体圆形。

1.1 生活中的立体图形(1)练习
一、基础过关
1.体会下列立体图形的画法，并在横线上相应位置写出他们的名称.
2.几何图形是由点、线、面组成的，其中点是，线分为
两类，面分为两类；常见的立体图形有柱体、锥体、球三大类，其中柱体分为两类，锥体分为两类.
3.下列说法，不正确的是( )
A.圆锥和圆柱的底面都是圆.
B.棱锥底面边数与侧棱数相等.
C.棱柱的上、下底面是形状、大小相同的多边形.
D.长方体是四棱柱，四棱柱是长方体.
4.判断题：
(1)棱柱侧面的形状可能是一个三角形 ( )
(2)棱柱的每条棱长都相等. ( )
(3)正方体和长方体既是特殊的四棱柱，又是特殊的六面体. ( )
5.如图所示的几何体是由一个正方体截
去后而形成的，那么此几何体是由
个面围成的，其中正方形有
个，长方形有个.
二、能力提升
6.如图所示，把立方体的六个面分别涂上六种不同的颜色(红、黄、紫、蓝、白、绿),现将大小相同,颜色分布完全一样的四个立方体拼成一个水平放置的长方体,则立方体红色面的对面是什么颜色？蓝色面的对面是什么颜色？与同学们交流你的分析方法！
7.已知一圆柱内恰好能容纳一个球体，请画出示意图并尽可能多地写出一些你发现的关系式.
8.雨哗哗地不停地下着，如在雨地里放一个如图那样的长方体的容器(单位：厘米)，雨水将它下满要用1时.有下列(1)～(5)不同的容器，雨水下满各需多长时间？
(注:面是朝上的敞口部分)
⑴⑵⑶⑷⑸
三、聚沙成塔
小明说下面两幅图中“一圈圈”画的都是同心圆，千万不要被自己的眼睛欺骗了！你的看法呢？动手用圆规比对一下好吗？
那么下面的两幅图又有什么“蹊跷之处”呢？拿出勇气与你的同学、老师讨论一下！。

第一章丰富的图形世界一.填空题1.立体图形的各个面都是__________的面,这样的立体图形称为多面体.2.图形是由________,__________,____________构成的.3.物体的形状似于圆柱的有________________;类似于圆锥的有_____________________;类似于球的有__________________.4.围成几何体的侧面中,至少有一个是曲面的是______________.5.正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都____________.6.圆柱,圆锥,球的共同点是_____________________________.7.假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________.8.圆可以分割成_____个扇形,每个扇形都是由___________________.9.从一个七边形的某个顶点出发,分别连结这个点与其余各顶点,可以把七边形分割成__________个三角形.二.选择题10. 从一个十边形的某个点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成( )个三角形A. 10B. 9C. 8D. 711. 图1-1是由( )图形饶虚线旋转一周形成的A B C D 图1-113.图1-2绕虚线旋转一周形成的图形是 ( )图1-2A B C D14.图1-3这个美丽的图案是由我们所熟悉的( )图形组成A.三角形和扇形B圆和四边形 C.圆和三角形D圆和扇形15.下面全由圆形组成的图案是( )A B C D三.解答题16.请观察丰富多彩的生活世界,有哪些物体的形状与下列几何体类似?(1)六面体(2)圆柱(3)圆锥(4)棱锥17.请写出下列几何体的名称( ) ( ) ( )( ) ( ) ( )18.请说出生活中至少4个规则的物体,并说出和它们类似的立体图形?19.动手做一做.将一个长方体切去一部分,看一看剩余的部分是几面体呢?四.开放创新提高题20.如图1-4,一长方体土地,用两条直线把它分成形状相同,大小相等的四块,你能做到吗,能用不同的方法完成这个任务吗?21.一个圆绕着它的直径的直线旋转一周就形成球体,那么现有一个长方形(如图1-5)你有几种方法使它类似于圆柱的几何体?请你画出这些立体圆形。

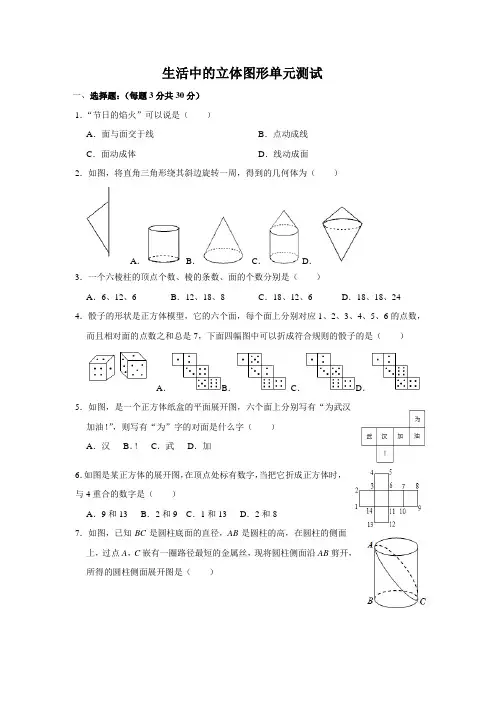
生活中的立体图形单元测试一、选择题：（每题3分共30分）1．“节日的焰火”可以说是（）A．面与面交于线B．点动成线C．面动成体D．线动成面2．如图，将直角三角形绕其斜边旋转一周，得到的几何体为（）A．B．C．D．3．一个六棱柱的顶点个数、棱的条数、面的个数分别是（）A．6、12、6B．12、18、8C．18、12、6D．18、18、24 4．骰子的形状是正方体模型，它的六个面，每个面上分别对应1、2、3、4、5、6的点数，而且相对面的点数之和总是7，下面四幅图中可以折成符合规则的骰子的是（）A．B．C．D．5．如图，是一个正方体纸盒的平面展开图，六个面上分别写有“为武汉加油！”，则写有“为”字的对面是什么字（）A．汉B．！C．武D．加6．如图是某正方体的展开图，在顶点处标有数字，当把它折成正方体时，与4重合的数字是（）A．9和13 B．2和9 C．1和13 D．2和87．如图，已知BC是圆柱底面的直径，AB是圆柱的高，在圆柱的侧面上，过点A，C嵌有一圈路径最短的金属丝，现将圆柱侧面沿AB剪开，所得的圆柱侧面展开图是（）A．B．C．D．8．已知一个不透明的正方体的六个面上分别写着1﹣6六个数字，如图是我们能看到的三种情况，那么数字5的对面的数字是（）A．6B．4C．3D．6或4或3 9．用一个平面去截一个圆柱体，截面图形不可能是（）A．长方形B．梯形C．圆形D．椭圆形10．用一个平面去截一个几何体，截面是三角形，这个几何体不可能是（）A．棱柱B．圆柱C．圆锥D．棱锥二、填空：（每题4分，共32分）11．如图是一个正方体的表面沿着某些棱剪开后展成的一个平面图形，若这个正方体的每两个相对面上的数字的和都相等，则这个正方体的六个面上的数字的总和为．11题图12题图13题图12．如图，将甲、乙、丙、丁四个小正方形中的一个剪掉，使余下的部分不能围成一个正方体，则剪掉的这个小正方形是．13．一个无盖长方体的包装盒展开图如图所示，则该长方体的体积为cm3．14．钻石原石看起来并不起眼，但经过精心设计、切割、打磨，就会成为璀璨夺目的钻石．钻石切割是多面体截面在实际生活中的一个应用．将已经加工成三棱柱形状的钻石原石进行切割，只切一刀，切截面的形状可能是．15．如果用平面截掉一个长方体的一个角（即切去一个三棱锥），则剩下的几何体最多有顶点，最少有条棱．16．如图从边长为10的正方体的一顶点处挖去一个边长为1的小正方体，则剩下图形的表面积为．17．用一个平面去截一个正方体，图中画有阴影的部分是截面，下面有关截面画法正确的序号有．18．有一个盛有水的圆柱体玻璃容器，它的底面半径为10cm，容器内水的高度为12cm，把一根半径为2cm的玻璃棒垂直插入水中直达容器底部，容器里的水升cm．三、解答题：19．用平面截几何体可得到平面图形，在表示几何体的字母后填上它可截出的平面图形的号码．（8分）如A（1、5、6）；则B（）；C（）；D（）；E（）．20．已知一个直棱柱，它有21条棱，其中一条侧棱长为20，底面各边长都为4．（7分）（1）这是几棱柱？（2）它有多少个面？多少个顶点？（3）这个棱柱的所有侧面的面积之和是多少？21．如图所示，两个圆和一个长方形（阴影部分）恰好可以围成一个圆柱，求这个圆柱的体积（π取3.14）．（7分）22．如图所示的长方形是圆柱的侧面展开图，如果这个长方形相邻的两边长分别为6，4π，求圆柱的体积（温馨提示：考虑问题要全面哦！）．（8分）23．如图是一个棱柱形状的食品包装盒的侧面展开图．（8分）（1）请写出这个包装盒的几何体的名称：；（2）若AC＝3，BC＝4，AB＝5，DF＝6，计算这个多面体的侧面积．。

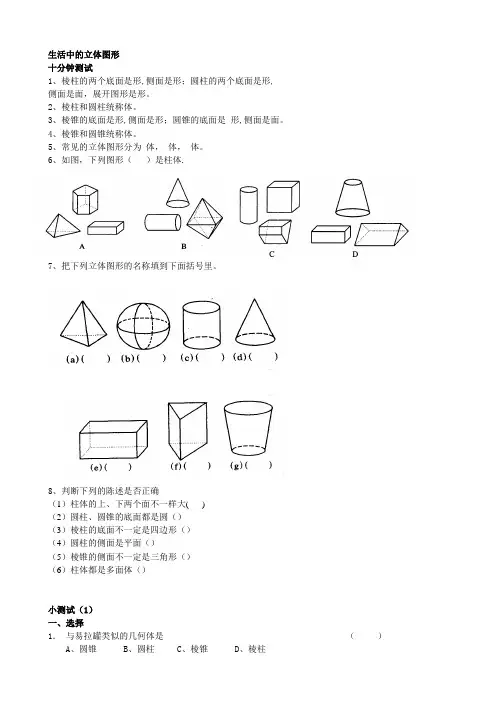
生活中的立体图形十分钟测试1、棱柱的两个底面是形,侧面是形；圆柱的两个底面是形,侧面是面，展开图形是形。

2、棱柱和圆柱统称体。

3、棱锥的底面是形,侧面是形；圆锥的底面是形,侧面是面。

4、棱锥和圆锥统称体。

5、常见的立体图形分为体，体，体。

6、如图，下列图形（）是柱体.7、把下列立体图形的名称填到下面括号里。

8、判断下列的陈述是否正确（1）柱体的上、下两个面不一样大( )（2）圆柱、圆锥的底面都是圆（）（3）棱柱的底面不一定是四边形（）（4）圆柱的侧面是平面（）（5）棱锥的侧面不一定是三角形（）（6）柱体都是多面体（）小测试（1）一、选择1．与易拉罐类似的几何体是（）A、圆锥B、圆柱C、棱锥D、棱柱2.下图中是三棱锥的立体图形是（ ）3．埃及金字塔类似于几何体 （ ）A 、圆锥B 、圆柱C 、棱锥D 、棱柱 4.下列各组图形中都是平面图形的是（ ）A.三角形、圆、球、圆锥B.点、线、面、体C.角、三角形、正方形、圆D.点、相交线、线段、长方体 5．下列说法正确的是 （ ） A ．有六条侧棱的棱柱的底面一定是三角形 B ．棱锥的侧面是三角形 C ．长方体和正方体不是棱柱D ．柱体的上、下两底面可以大小不一样二、填空6．立体图形的各个面都是__________的面,这样的立体图形称为多面体. 7．篮球、排球、足球、乒乓球都是球形的，不是球形的球是。

8．棱柱的长相等，上下底面是的多边形，侧面是。

9．一个棱锥有7个面，这是棱锥，有个侧面。

10．长方体ABCD －A ′B ′C ′D ′有个面，条棱，个顶点。

与棱AB 垂直相交的棱有条，与棱AB 平行的棱有条。

11.如图所示立体图形中，（1）球体有___________；（2）柱体有_________；（3）锥体有____________．12.如图,是一座粮仓，它可以看作是由和几何体组成的.13.如图，用边长为4的正方形，做了一套七巧板，拼成如图所示的一座桥，则桥中阴影部分的面积是______.14、判断（1）柱体上下两个面一样大。

一、基础概念题1. 请列举出三种常见的立体图形。

2. 立体图形的体积和表面积分别是什么？3. 立体图形的三视图分别是什么？4. 简述长方体、正方体、圆柱体、圆锥体的特征。

二、计算题1. 已知长方体的长、宽、高分别为10cm、6cm、4cm，求其体积和表面积。

2. 一个正方体的边长为8cm，求其体积和表面积。

3. 圆柱体的底面半径为5cm，高为10cm，求其体积和表面积。

4. 圆锥体的底面半径为3cm，高为4cm，求其体积和表面积。

三、应用题1. 一个长方体木块，长、宽、高分别为15cm、10cm、6cm，将其切割成最大的正方体，求正方体的边长。

2. 一个圆柱体水池，底面直径为10m，深为2m，求水池的容积。

3. 一个圆锥形帐篷，底面半径为6m，高为10m，求帐篷的占地面积。

4. 一块长方体铁块，长、宽、高分别为20cm、15cm、10cm，将其熔铸成一个球体，求球体的半径。

四、作图题1. 请画出长方体的三视图。

2. 请画出正方体的三视图。

3. 请画出圆柱体的三视图。

4. 请画出圆锥体的三视图。

五、判断题1. 立体图形的体积和表面积都是固定的。

（）2. 长方体和正方体都是特殊的立方体。

（）3. 圆柱体的底面一定是圆形。

（）4. 圆锥体的侧面展开是一个扇形。

（）六、选择题1. 下列哪个立体图形的体积公式是V = πr²h？A. 长方体B. 正方体C. 圆柱体D. 圆锥体2. 下列哪个立体图形的表面积公式是S = 2πrh + 2πr²？A. 长方体B. 正方体C. 圆柱体D. 圆锥体3. 一个正方体的边长为2cm，其体积为多少？A. 4cm³B. 8cm³C. 12cm³D. 16cm³4. 一个圆锥体的底面半径为3cm，高为4cm，其体积为多少？A. 12πcm³B. 36πcm³C. 48πcm³D. 144πcm³七、填空题1. 一个立方体的边长为5cm，其体积是______cm³，表面积是______cm²。

20212021数学北师大版七年级上册1.1《生活中的立体图形》同步训练一、选择题1.下面几何体中，全是由曲面围成的是（）A.圆柱B.圆锥C.球D.正方体2.下列说法错误的是（）A. 长方体、正方体都是棱柱B. 三棱柱的侧面是三角形C. 直六棱柱有六个侧面、侧面为矩形D. 球体的三种视图均为同样大小的图形3.下列立体图形中，有五个面的是（）A. 四棱锥B. 五棱锥C. 四棱柱D. 五棱柱4.将一个直角三角形绕它的最长边（斜边）旋转一周得到的几何体为（）A. B. C. D.5.将四个棱长为1的正方体如图摆放，则这个几何体的表面积是（）A. 3B. 9C. 12D. 18二、填空题6.一个直棱柱有12条棱，则它是________棱柱．7.一个几何体的面数为12，棱数为30，它的顶点数为________．8.如图，在长方体ABCDEFGH中，与平面ADHE垂直的棱共有________条．9.两个完全相同的长方体的长．宽．高分别为5cm．4cm．3cm，把它们叠放在一起组成个新长方体，在这个新长方体中，体积是________cm3，最大表面积是________cm2．10.一只小蚂蚁从如图所示的正方体的顶点A沿着棱爬向有蜜糖的点B，它只能经过三条棱，请你数一数，小蚂蚁有________种爬行路线．三、解答题11.从棱长为2的正方体毛坯的一角挖去一个棱长为1的小正方体，得到一个如图的零件，求：（1）这个零件的表面积（包括底面）；（2）这个零件的体积．12.有3个棱长分别是3cm，4cm，5cm的正方体组合成如图所示的图形．其露在外面的表面积是多少？（整个立体图形摆放在地上）13.现有一个长为5cm，宽为4cm的长方形，绕它的一边旋转一周，得到的几何体的体积是多少？14.已知长方形的长为4cm．宽为3cm，将其绕它的一边所在的直线旋转一周，得到一个几何体，（1）求此几何体的体积；（2）求此几何体的表面积．（结果保留π）15.观察图形，回答下列问题：（1）图 是由几个面组成的，这些面有什么特征？（2）图②是由几个面组成的，这些面有什么特征？（3）图①中共形成了多少条线？这些线都是直的吗？图②呢？（4）图①和图②中各有几个顶点？答案解析部分一、选择题1.【答案】C【考点】几何体的表面积【解析】【解答】解：A、圆柱由上下两个平面和侧面一个曲面组成，不符合题意；B、圆锥由侧面一个曲面和底面一个平面组成，不符合题意；C、球只有一个曲面组成，符合题意；D、正方体是由六个平面组成，不符合题意．故答案为：C．【分析】圆锥两个面围成，一个曲面，一个平面；圆柱三个面围成，一个曲面，两个平面；正方体由6个面围成，六个面都是平面；球球只有一个曲面组成。

7．一个几何体的展开图如图所示，则该几何体的顶点有（）.
A．6B．8C．9D．10
二、填空题
8．一个棱柱有 个面，它的底面边长都是 ，侧棱长 ，这个棱柱的所有侧面的面积之和是__________．
9．如图所示的几何体的名称是____，它由____个面组成，它有____个顶点，经过每个顶点有____条边．
D、将平面图形绕轴旋转一周，得到的是一个圆台，则此项不符题意；
故选：B．
【点睛】
本题考查了平面图形旋转后的几何体，熟练掌握平面图形旋转的特点是解题关键．
4．C
【解析】选项A，用平口铲子铲去墙面上的大片污渍，说明“线动成面”；选项B，用一条拉直的细线切一块豆腐，说明“线动成面”；选项C，流星划过天空留下运动轨迹说明“点动成线”；选项D，用木板的边缘将沙坑里的沙推平，说明“线动成面”.故选C．
14．若一个直n棱柱共有18条棱，则它是________棱柱，有________个面，________个顶点．
15．将图所示的Rt△ABC绕AB旋转一周所得的几何体的主视图是图中的________（只填序号）．
三、解答题
16．画出下面图形的三视图：主视图，左视图，俯视图.
17．将一个正方体的表面全涂上颜色．
10．一根长方体木料长 米，当把它按下图方式截成 个小长方体木料时，表面积比原来增加了 平方厘米，则原来的体积是_______立方厘米．
11．一个棱柱有10个顶点，所有的侧棱长之和为 ，则每条侧棱的长为_____ ．
12．在如图所示的长方体中，与AB垂直且相交的棱有______条．
13．直角三角形的两条边的长分别是 和 ，以直角边所在的直线为轴，将三角形旋转一周，所得几何体的俯视图的面积是__________．

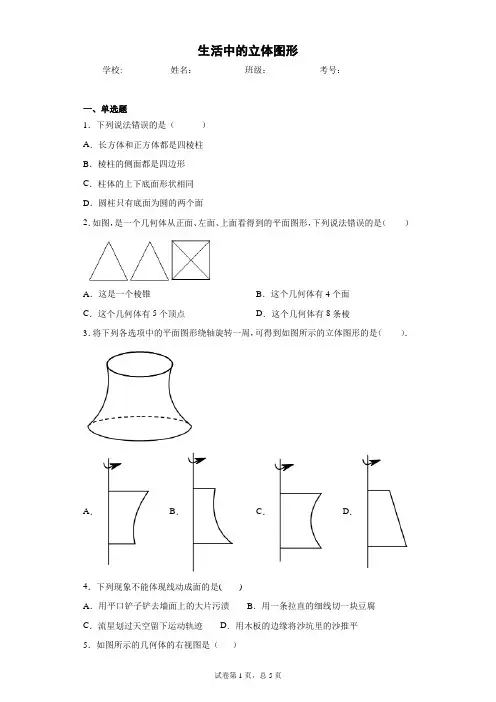
初一数学《生活中的立体图形》测试题（北师大版）初一数学《生活中的立体图形》测试题（北师大版）北师大版七上数学生活中的立体图形例题分析（含解析）1．生活中常见的立体图形(1)常见的立体图形和对应的几何体图(1)是生活中几种常见的实物图形，其对应的几何体如图(2)所示．图(1)图(2)生活中蕴含着大量的几何图形，这些几何图形可以抽象为几何体．常见的几何体有长方体、正方体、圆柱、圆锥、球和棱柱等．注意：棱锥也是一种常见的几何体．如上面的最后一图．(2)几何体的组成几何体是由平面或曲面围成的立体图形．如果围成的面都是平的，叫做多面体．【例1】下列图形中，上面一行是一些具体的实物图形，下面一行是一些几何体，试用线连接几何体和类似的实物图形．分析：对照实物图与几何体，从实物图形中抽象出数学几何体即可．一个是曲面．两个底面与曲侧面相交成两条曲线，两个底面与平侧面相交成两条直线，两个侧面相交成两条直线．答案：43162点技巧线与面的数法对于几何体，面与面相交得到线，线与线相交得到点．在数面时可先数底面，再数侧面；数线时，可先数底面与侧面相交成的线，再数侧面与侧面相交成的线．3．立体图形的识别几何图形的特征：(1)圆柱：两个底面是等圆，侧面是曲面．如八宝粥盒、茶杯等．(2)圆锥：底面是圆，侧面是曲面．像锥子．如烟囱帽、铅锤、漏斗等．(3)长方体：有6个面，底面是长方形，相对的两个面平行且完全相同．如砖、文具盒等．(4)正方体：6个面是大小完全相同的正方形．如魔方等．(5)棱柱：所有侧棱长都相等，底面是多边形，上、下底面的形状相同，侧面的形状都是平行四边形．(6)球：由一个曲面组成，圆圆的．如足球、乒乓球等．(7)棱锥：一个面是多边形，其余各面是一个有公共顶点的三角形．多边形的面称为棱锥的底面，其余各面称为棱锥的侧面．根据底面的边数可将棱锥分为三棱锥、四棱锥……谈重点从哪几个方面认识几何体的特征①有几个面围成，是平面还是曲面；②有无顶点，有几个顶点；③侧面是平面还是曲面；④底面是什么形状，是多边形还是圆，有几个底面等．【例3－1】请在每个几何体下面写出它们的名称．解析：根据立体图形的定义特征就可得出图形的名称．答案：三棱柱圆柱长方体圆锥四棱柱正方体球【例3－2】如图，在下面四个物体中，最接近圆柱的是()．解析：圆柱是“直”的，与弯管B有明显区别；D中的饮料瓶的盖确实可以看成是圆柱，但它在该物中只占很小的一部分，该物体从整体上讲更接近于棱柱；A中烟囱上下粗细不同，不是圆柱，故应排除A，B，D；作为柱体的本质特征之一是“粗细”处处相同，而与高、矮(长、短)无关，C中玩具硬币尽管扁一些，但是最接近圆柱，所以应选C.答案：C4.几何体的分类(1)几何体按柱、锥、球的特征分为：(2)按围成的面分为：分类是数学中的基本方法，在分类时要统一标准，做到不重不漏．___________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ ____【例4－1】在粉笔盒、三棱镜、乒乓球、易拉罐瓶、书本、热水瓶胆等物体中，形状类似于棱柱的有()．A．1个B．2个C．3个D．4个解析：粉笔盒、三棱镜、书本可以看成棱柱，乒乓球是球体，易拉罐瓶是圆柱，热水瓶胆既不是棱柱，也不是圆柱和球体．故答案选C.答案：C【例4－2】将下列几何体分类，并说明理由．分析：分类时，先确定分类标准．分类标准不同，所属类别也不同，同时应注意分类要不重不漏．解：(1)按柱、锥、球划分：①②④⑤为一类，它们都是柱体；③⑦为一类，它们都是锥体；⑥为一类，它是球体．(2)按围成几何体的面是平面或曲面分：①④⑤⑦为一类，它们是多面体；②③⑥为一类，它们是旋转体．(3)按几何体有无顶点分：①③④⑤⑦为一类，它们都有顶点；②⑥为一类，它们都无顶点．5．几何体的形成(1)长方形绕其一边所在直线旋转一周得到圆柱；(2)直角三角形绕其一条直角边所在直线旋转一周得到圆锥；(3)半圆绕其直径所在直线旋转一周得到球体．释疑点旋转体的形成①平面图形旋转会形成几何体；②平面图形绕某一直线旋转一周才可以形成几何体；③由平面图形旋转而得到的几何体有：圆柱、圆锥、球以及它们的组合体．___________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ _______________________________________________________ ____【例5】我们曾学过圆柱的体积计算公式：V＝Sh＝πR2h(R是圆柱底面半径，h为圆柱的高)，现有一个长方形，长为2cm，宽为1cm，以它的一边所在的直线为轴旋转一周，得到的几何体的体积是多少？分析：问题中的几何体可由两种方式旋转得到．一种是绕这个长方形的长所在的直线旋转，另一种是绕这个长方形的宽所在的直线旋转，其结果不同，注意不要漏解．解：(1)当以长方形的宽所在的直线为轴旋转时，如图(1)所示，得到的圆柱的底面半径为2cm，高为1cm.所以，其体积是V1＝π×22×1＝4π(cm3)．(2)当以长方形的长所在的直线为轴旋转时，如图(2)所示，得到的圆柱的底面半径为1cm，高为2cm.所以，其体积是V2＝π×12×2＝2π(cm3)．所以，得到的几何体的体积是4πcm3或2πcm3.。

七年级数学生活中的立体图形练习题第一章丰富的图形世界一. 填空题1. 立体图形的各个面都是__________的面,这样的立体图形称为多面体.2. 图形是由________,__________,____________构成的.3. 物体的形状似于圆柱的有________________;类似于圆锥的有_____________________;类似于球的有__________________.4. 围成几何体的侧面中,至少有一个是曲面的是______________.5. 正方体有_____个顶点,经过每个顶点有_________条棱,这些棱都____________.6. 圆柱,圆锥,球的共同点是_____________________________.7. 假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了______________,时钟秒针旋转时,形成一个圆面,这说明了_______________,三角板绕它的一条直角边旋转一周,形成一个圆锥体,这说明了___________________.8. 圆可以分割成_____个扇形,每个扇形都是由___________________.9. 从一个七边形的某个顶点出发,分别连结这个点与其余各顶点,可以把七边形分割成__________个三角形.二. 选择题10. 从一个十边形的某个点出发,分别连接这个顶点与其余各顶点,可以把这个多边形分割成( )个三角形A. 10B. 9C. 8D. 711. 图1-1是由( )图形饶虚线旋转一周形成的ABCD 图1-113.图1-2绕虚线旋转一周形成的图形是( )图1-2ABCD14.图1-3这个美丽的图案是由我们所熟悉的( )图形组成A.三角形和扇形B圆和四边形 C.圆和三角形D圆和扇形15.下面全由圆形组成的图案是( )CCABCD三. 解答题16.请观察丰富多彩的生活世界,有哪些物体的形状与下列几何体类似?(1)六面体(2)圆柱 (3)圆锥 (4)棱锥17.请写出下列几何体的名称( ) ( ) ( )( ) ( )()18.请说出生活中至少4个规则的物体,并说出和它们类似的立体图形?19.动手做一做.将一个长方体切去一部分,看一看剩余的部分是几面体呢?四.开放创新提高题20.如图1-4,一长方体土地,用两条直线把它分成形状相同,大小相等的四块,你能做到吗,能用不同的方法完成这个任务吗?21.一个圆绕着它的直径的直线旋转一周就形成球体,那么现有一个长方形(如图1-5)你有几种方法使它类似于圆柱的几何体?请你画出这些立体圆形。

生活中的立体图形新题精炼根底稳固 1．如图1—1—17观察以下实物模型，其形状是圆柱体的是〔 〕2．以下图形中不是立体图形的是〔 〕3．如图1—1—18是一个生日蛋糕盒，这个盒子有几条棱〔 〕A ．6条B ．12条C ．18条D ．24条4．以下立体图形中，有五个面的是〔 〕A ．四棱锥B ．五棱锥C ．四棱柱D ．五棱柱5．将下面的直角梯形绕直线l 旋转一周，可以得到如图1—1—19立体图形的是〔 〕6． 汽车的雨刷把玻璃上的雨水刷干净属于的实际应用是〔 〕A ．点动成线B ．线动成面C ．面动成体D ．以上都不对7．假设一个棱柱的底面是一个七边形，那么它的侧面必须有_____个长方形，它一共有_____个面,______个顶点．8．一个棱柱有18条棱，那么它的底面一定是______边形．A ．B ．C ．D ． 1—1—17A ．B ．C ．D ． 1—1—19 1—1—189．六棱柱有_____个顶点，有_______条侧棱．10．如图1—1—20至少找出以下几何体的4个共同点.11．〔1〕如图1—1—21下面这些根本图形和你很熟悉，试一试在括号里写出它们的名称．〔2〕将这些几何体分类，并写出分类的理由．如图1—1—22下面的图形表示四棱柱的是〔 〕能力提升12．多面体是由多个平面围成的几何体，如图1—1—23以下几何体中，属于多面体的有〔 〕A ．2个B ．3个C ．4个D ．5个1—1—20 〔 〕 〔 〕 〔 〕 〔 〕 〔 〕1—1—21 1—1—23 1—1—2213．假设一个直四棱柱的底面是边长为1cm的正方形，侧棱长为2cm，那么这个直棱柱的体积是______________cm3．14．〔1〕探索：如果把一个多面体的顶点数记为V，棱数记为E，面数记为F，填写下表．〔3〕验证：再找出一个多面体，数一数它有几个顶点，几条棱，几个面，看看面数、顶点数、棱数是否满足上述关系．〔4〕应用〔2〕的结论对所有的多面体都成立，伟大的数学家欧拉证明了这个关系式，上述关系式叫做欧拉公式．根据欧拉公式，想一想会不会有一个多面体，它有10个面，30条棱，20个顶点？新题精炼答案根底稳固1．D思路导引:圆柱的上下底面都是圆，所以正确的选项是D．2．C思路导引:圆是平面图形3．C思路导引:观察图形可知上下面的棱数都是6，侧面的棱数是6．那么这个盒子的棱数为：6+6+6=18．4．A思路导引:要明确棱柱和棱锥的组成情况，棱柱有两个底面，棱锥有一个底面．5．B面动成体．由题目中的图示可知：此几何体是直角梯形转成圆台的条件是：绕垂直于底的腰旋转．6．B 思路导引:汽汽车的雨刷实际上是一条线，通过运动把玻璃上的雨水刷干净，所以应是线动成面．7．7,9,14思路导引: n棱柱有个侧面且都是长方形，有〔n+2〕个面，2n个顶点．8．六思路导引: n棱柱有3n条棱，两个底面共有2n条，每个底面n条棱，即故底面有n条边．9．7．12,6思路导引通过观察六棱柱可知，六棱柱有12个顶点、有六条侧棱．点拨：我们知道四棱柱有8个顶点，五棱柱有10个顶点，六棱柱有四个顶点……，以此类推n棱柱有2×n个顶点．10．思路导引:观察图形，可以从图形的组成、侧面等答复．解：答案不惟一，如：都由平面组成，侧面都是长方形，都有上下底面，都有侧棱等．11．〔1〕针对立体图形的特征，直接填写它们的名称即可．〔2〕可以按柱体、锥体和球进行分类，也可以按平面和曲面进行分类，方法不同，答案不同，只要合理即可．解：〔1〕从左向右依次是：球、圆柱、圆锥、长方体、三棱柱．〔2〕观察图形，按柱、锥、球划分，那么有圆柱、长方体、三棱柱为柱体；圆锥为锥体；球为球体．能力提升12．A思路导引:根据多面体意义，没有曲面参与围成，故只有第二、四符合要求．13．2思路导引:根据棱柱体积等于底面积乘以高代入求解即可．1.3 截一个几何体一、判断题1．用一个平面去截一个正方体，截出的面一定是正方形或长方形.〔〕2．用一个平面去截一个圆柱，截出的面一定是圆.〔〕3．用一个平面去截圆锥，截出的面一定是三角形.〔〕4．用一个平面去截一个球，无论如何截，截面都是一个圆.〔〕二、填空题5．用一个平面去截一个球体所得的截面图形是__________．6．如图1，长方体中截面BB1D1D是长方体的对角面，它是__________．7．在正方体中经过从一个顶点出发的三条棱的中点的截面是_________．三、选择题8．用一个平面去截圆锥，得到的平面不可能是〔〕9．用一个平面去截一个圆柱，得到的图形不可能是〔〕10．用一个平面去截一个正方体，截面图形不可能是〔〕A．长方形; B．梯形; C．三角形; D．圆11．用一个平面去截一个几何体，如果截面的形状是圆，那么这个几何体不可能是〔〕A．圆柱; B．圆锥; C．正方体; D．球12．截去四边形的一个角，剩余图形不可能是〔〕A．三角形; B．四边形; C．五边形; D．圆四、解答题13．用平面去截一个正方体，截面的形状可能是平行四边形吗？截一截，想一想．14．用一个平面去截圆锥，可以得到几种不同的图形？动手试一试．15．指出以下几何体的截面形状．______________________ 16．编写一道自己感兴趣并与本节内容相关的题，解答出来．参考答案一、1．×2．×3．×4．√二、5．圆6．矩形7．三角形三、8．C9．D 10．D11．C12．D 四、13．可能14．略15．四、五边形圆形16．略。

~生活中的立体图形练习题一．选择题（共9小题）1．下面的几何体是棱柱的为（）A．B．C． D．2．如图，下列图形全部属于柱体的是（）A．B．C．D．3．如图是一块带有圆形空洞和矩形空洞的小木板，则下列物体中最有可能既可以堵住圆形空洞，又可以堵住矩形空洞的是（））A．正方体B．球C．圆锥 D．圆柱体4．如图所示的平面图形绕直线l旋转一周，可以得到的立体图形是（）A．B． C． D．5．不透明袋子中装有一个几何体模型，两位同学摸该模型并描述它的特征，甲同学：它有4个面是三角形；乙同学，它有6条棱，则该模型对应的立体图形可能是（）A．三棱柱B．四棱柱C．三棱锥D．四棱锥6．如图是正方体的表面展开图，则与“前”字相对的字是（）；A．认B．真C．复D．习7．图1是一个小正方体的表面展开图，小正方体从图2所示的位置依次翻到第1格、第2格、第3格，这时小正方体朝上一面的字是（）A．信B．国C．友D．善8．如图，一个正方体截去一个角后，剩下的几何体面的个数和棱的条数分别为（）A．6，11 B．7，11 C．7，12 D．6，129．某几何体由若干个大小相同的小正方体搭成，其主视图与左视图如图所示，则搭成这个几何体的小正方体最少有（）)A．4个B．5个C．6个D．7个二．填空题（共5小题）10．用一个平面去截下列几何体，截面可能是圆的是（填写序号）．①三棱柱②圆锥③圆柱④长方体⑤球体11．如图，是一个长方体的主视图，左视图与俯视图，根据图中数据计算这个长方体的表面积是．12．一个几何体的主视图和俯视图如图所示，若这个几何体最多有m个小正方体组成，最少有n个小正方体组成，m+n= ．|13．一个几何体有若干大小相同的小立方块搭成，如图分别是从它的正面、左面看到的形状图，则搭成该几何体最多需要个小立方块．14．一个几何体是由一些大小相同的小立方块摆成的，如下图是从正面、左面、上面看这个几何体得到的平面图形，那么组成这个几何体所用的小立方块的个数是．三．解答题（共2小题）15．根据如图视图（单位：mm），求该物体的体积．！16．分别画出图中几何体的主视图、左视图、俯视图．17．如图，该物体是由14块棱长为1厘米的小正方体堆积而成的，求它的表面积．（含底面）。

第一章1.1生活中的立体图形习题精练一、选择题1.下列几何体中，含有曲面的有()A. 1个B. 2个C. 3个D. 4个2.下面几何体中为圆柱的是()A. B. C. D.3.如果一个棱柱有12个顶点，那么它的面的个数是()A. 10B. 9C. 8D. 74.下列图形中，不是立体图形的是()A. 圆锥B. 圆柱C. 圆D. 球5.下列说法中，正确的个数是()①柱体的两个底面一样大；②圆柱、圆锥的底面都是圆；③棱柱的底面是四边形；④长方体一定是柱体；⑤正棱柱的侧面一定是长方形．A. 2个B. 3个C. 4个D. 5个6.如图所示的图形绕虚线旋转一周，所形成的几何体是()A.B.C.D.7.将一个直角三角形绕它的最长边(斜边)旋转一周得到的几何体为()A. B. C. D.8.如图是由()图形绕虚线旋转一周形成的．A.B.C.D.9.一个六棱柱模型如图所示，底面边长都是5 cm，侧棱长为4 cm，这个六棱柱的所有侧面的面积之和是()A. 20cm2B. 60cm2C. 120cm2D. 240cm210.某几何体的三视图及相关数据(单位：cm)如图所示，则该几何体的侧面积是()πcm2A. 652B. 60πcm2C. 65πcm2D. 130πcm211.如图，在平整的地面上，有若干个完全相同的棱长为2cm的小正方体堆成的一个几何体．如果在这个几何体的表面喷上红色的漆(贴紧地面的部分不喷)，这个几何体喷漆的面积是()A. 30cm2B. 32cm2C. 120cm2D. 128cm212.把一个长12cm，宽9cm，厚2cm的长方体铁坯，加工成一个正方体铁锭后，则其表面积的变化是()A. 变大B. 变小C. 不变D. 无法确定二、填空题13.一个五棱柱有______个顶点，______个面，______条棱．14.如图所示的几何体由个面围成，面与面相交成条线，其中直的线有条，曲线有条.15.雨点从高空落下形成的轨迹说明了点动成线，那么一枚硬币在光滑的桌面上快速旋转形成一个球，这说明了．16.如图，一个正方体由27个大小相同的小立方块搭成，现从中取走若干个小立方块，得到一个新的几何体.若新几何体与原正方体的表面积相等，则最多可以取走个小立方块．三、解答题17.观察如图所示的直四棱柱．(1)它有几个面？几个底面？底面与侧面分别是什么图形？(2)侧面的个数与底面多边形的边数有什么关系？(3)若底面的周长为20cm，侧棱长为8cm，则它的侧面积为多少？18.观察图，回答下列问题：(1)图 ①是由几个面组成的?这些面有什么特征?(2)图 ②是由几个面组成的?这些面有什么特征?(3)图 ①中共形成了多少条线?这些线都是直的吗?图 ②呢?(4)图 ①和图 ②中各有几个顶点?19.如图是一个几何体的表面展开图，图中的数字表示相应的棱的长度(单位：cm)(1)写出该几何体的名称；(2)计算该几何体的表面积。

1.生涯中蕴含着大量的几何图形,这些几何图形可以抽象为几何体．罕有的几何体有（）.（）.（）.（）.（）.和（）等.2.几何图形包含立体图形和（）,几何图形是由（）.（）.（）构成.面有平面和（）,面不分厚薄;线有直线和（）,线不分粗细.面与面订交得到（）,线与线订交得到（）,点不分大小.3.从活动的角度看,点动成（）,线动成（）,面动成（）.（例如,把笔尖看做一个点,笔尖在纸上移动就能形成一条线,即点动成线.点动成线的实例还有：流星划过天空.粉笔在黑板上划动.保龄球滚动过的路线等.钟表的分针扭转一周形成一个圆面,即线动成面.线动成面的实例还有：汽车上的雨刷扫过玻璃窗.用刷子涂油漆等.长方形绕它的一边扭转一周就能形成一个圆柱,即面动成体.面动成体的实例还有：以三角形的一边为轴扭转一周形成的几何体等）4.如图所示的立体图形,是由（）个面构成的,个中有（）个平面,有（）个曲面;面与面订交成（）条线,个中曲线有（）条.5.立体图形的辨认.几何图形的特点：(1)圆柱：两个底面是（）,正面是（）.如（）.（）等.(2)圆锥：底面是（）,正面是（）,像锥子.如（）.（）等.(3)长方体：有6个面,底面是（）,相对的两个面平行且（）.如（）.（）等.(4)正方体：6个面是大小完整雷同的（）.如（）.（）等.(5)棱柱：所有（）都相等,底面是（）,上.下底面的（）,正面的外形都是（）.(6)球：由一个（）构成,圆圆的.如足球.乒乓球等.(7)棱锥：一个面是多边形,其余各面是一个有公共极点的（）.多边形的面称为棱锥的（）,其余各面称为棱锥的（）.依据（）可将棱锥分为三棱锥.四棱锥……谈重点从哪几个方面熟悉几何体的特点①有几个面围成,是平面照样曲面;②有无极点,有几个极点;③正面是平面照样曲面;④底面是什么外形,是多边形照样圆,有几个底面等.6.请在每个几何体下面写出它们的名称.7.如图,鄙人面四个物体中,最接近圆柱的是( )．8.几何体的分类(1)几何体按柱.锥.球的特点分为：(2)按围成的面分为：9.在粉笔盒.三棱镜.乒乓球.易拉罐瓶.书本.热水瓶胆等物体中,外形相似于棱柱的有( ).A．1个B．2个C．3个D．4个10.将下列几何体分类,并解释来由．11.几何体的形成(1)长方形绕其一边地点直线扭转一周得到（）;(2)直角三角形绕其一条直角边地点直线扭转一周得到（）;(3)半圆绕其直径地点直线扭转一周得到（）.扭转体的形成①平面图形扭转会形成（）;②平面图形绕某一向线扭转一周才可以形成（）;③由平面图形扭转而得到的几何体有：（）.（）.（）以及（）.12.我们曾学过圆柱的体积盘算公式：V＝Sh＝πR2h(R是圆柱底面半径,h为圆柱的高),现有一个长方形,长为2 cm,宽为1 cm,以它的一边地点的直线为轴扭转一周,得到的几何体的体积是若干？13.典题精讲如图所示的立体图形,是由________个面构成的,面与面订交成________条线.14.变式练习下图是把一圆柱体纵向切开后的图形.问：图中有几个面,有几个面是平的？有几个面曲直的？有几条线？它们是直的照样曲的？线与线订交成若干点？15.写出图1-1-4中所示立体图形的名称.16.绿色通道：分类是数学进修中一种很主要的思惟办法,应留意的是：按统一尺度区分.变式练习下面图形中,属于立体图形的有（）①正方形②圆③球④棱柱⑤圆锥⑥六边形A.①③④B.②④⑤C.③④⑤D.③④⑤⑥答案：1. 长方体.正方体.圆柱.圆锥.球棱柱2. 平面图形点.线.面;曲面曲线线点3.线面体4.4 3 1 6 25.(1)等圆曲面(2)圆曲面 (3)长方形完整雷同(4)正方形(5)侧棱长多边形外形雷同平行四边形(6)曲面(7)三角形底面正面底面的边数6.三棱柱圆柱长方体圆锥四棱柱正方体球7.C解析：圆柱是“直”的,与弯管B有显著差别;D中的饮料瓶的盖确切可以算作是圆柱,但它在该物中只占很小的一部分,该物体从整体上讲更接近于棱柱;A中烟囱高低粗细不合,不是圆柱,故应消除A,B,D;作为柱体的本质特点之一是“粗细”处处雷同,而与高.矮(长.短)无关,C中玩具硬币尽管扁一些,但是最接近圆柱,所以应选C. 8.略9. C解析：粉笔盒.三棱镜.书本可以算作棱柱,乒乓球是球体,易拉罐瓶是圆柱,热水瓶胆既不是棱柱,也不是圆柱和球体．故答案选C.10.剖析：分类时,先肯定分类尺度.分类尺度不合,所属类别也不合,同时应留意分类要不重不漏.解：(1)按柱.锥.球划分：①②④⑤为一类,它们都是柱体;③⑦为一类,它们都是锥体;⑥为一类,它是球体.(2)按围成几何体的面是平面或曲面分：①④⑤⑦为一类,它们是多面体;②③⑥为一类,它们是扭转体.(3)按几何体有无极点分：①③④⑤⑦为一类,它们都有极点;②⑥为一类,它们都无极点.11.圆柱圆锥球体几何体几何体圆柱.圆锥.球以及它们的组合体.12.剖析：问题中的几何体可由两种方法扭转得到．一种是绕这个长方形的长地点的直线扭转,另一种是绕这个长方形的宽地点的直线扭转,其成果不合,留意不要漏解.解：(1)当以长方形的宽地点的直线为轴扭转时,如图(1)所示,得到的圆柱的底面半径为 2 cm,高为 1 cm.,所以,其体积是V1＝π×22×1＝4π(cm3)(2)当以长方形的长地点的直线为轴扭转时,如图(2)所示,得到的圆柱的底面半径为 1 cm,高为 2 cm,所以,其体积是V2＝π×12×2＝2π(cm3)所以,得到的几何体的体积是4π cm3或2π cm313.解析：任何图形都是由点.线.面构成的.点.线.面的变更构成了不合的图形.在数面时可先数底面,再数正面;数线时,可先数底面与正面的订交线.答案:4 614.图中有4个面,3个面是平面,1个正面曲直面;有6条线,4条是直的,2条曲直的;线与线订交成4个点.15.解析：分解各类几何体的特点,卖力地不雅察并给出断定.答案:（1）四棱柱;（2）圆柱;（3）长方体;（4）圆锥;（5）正方体;（6）棱锥.16.答案:C。