质点系动量守恒定律

质点系的动量定理和动量守恒定律
动量定理和动量守恒定律是力学学科中最重要的定律，其定义了显式或隐式的实体响应，有助于我们对物体性质，如形状及运动特性的深入理解。

在物理学中，力学在研究质点系统中被广泛应用，而动量定理与动量守恒定律可以被认为是这一课程的基本元素。

动量定理是从第一定律出发，它引申出了物体的动量保持不变的现象，是物体的运动规律的基本思想。

物体的动量（动量）是指物体的质量和其在空间的运动量的乘积。

具体而言，动量定理指的是物体的外力（外力）与其总变化率的乘积（变化数）之和等于0。

此外，动量守恒定律要求一个物体动量的变化率等于该物体所受的外力之和。

物体运动过程中，动量守恒定律比动量定理更容易证明。

动量定理和动量守恒定律在物理学研究中起着重要作用，并且在研究质点系统中被广泛应用。

它们不仅有助于研究物体的运动特性，而且能够为有关力学问题提供有用的信息，使得我们能够更深入地理解物体的性质。

它们的应用可以追溯到古代物理学家如亚里士多德，而今天也是物理学中研究质点系统不可或缺的重要元素。

质点系动量矩守恒定律一、引言质点系动量矩守恒定律是物理学中一个非常重要的定律，它描述了质点系在运动过程中动量和角动量的守恒规律。

本文将从定义、推导、应用等方面详细介绍这一定律。

二、定义质点系是指由多个质点组成的系统，其中每个质点都有自己的质量和速度。

在运动学中，我们可以用一个坐标系来描述整个质点系的运动状态。

而在动力学中，我们需要考虑到各个质点之间的相互作用力，以及整个系统所受到的外力。

根据牛顿第二定律，一个质点所受到的合力等于其加速度乘以其质量。

同样地，对于一个质点系，在外力作用下，其总动量和总角动量也会发生变化。

当然，在某些情况下，如果系统受到的外力为零，则总动量和总角动量将保持不变。

三、推导1. 总动量守恒我们先来推导总动量守恒定律。

假设一个质点系由n个质点组成，分别为m1, m2, ..., mn，并且每个质点分别具有速度v1, v2, ..., vn。

那么这个质点系的总动量可以表示为：p = m1v1 + m2v2 + ... + mnvn现在假设这个质点系受到一个外力F作用，从而发生了加速度a。

根据牛顿第二定律，每个质点所受到的合力都等于其加速度乘以其质量：F1 = m1a, F2 = m2a, ..., Fn = mna将上述式子代入总动量公式中，可以得到：p' = (m1v1 + F1t) + (m2v2 + F2t) + ... + (mnvn + Fnt)= (m1v1 + m1at) + (m2v2 + m2at) + ... + (mnvn + mnat)= p + at(m1+m2+...+mn)由此可见，在外力作用下，质点系的总动量会发生变化，并且变化的大小与系统的加速度以及系统的总质量有关。

但是，在某些情况下，如果系统受到的外力为零，则系统将不会发生加速度变化。

此时，根据以上公式可知，系统的总动量将保持不变。

因此，我们可以得出结论：当一个质点系受到外力作用时，它的总动量会发生变化，但如果外力为零，则它的总动量将保持不变。

质点系动量矩守恒定律介绍物体的运动是一个复杂的过程，涉及到质点的动量和力矩等概念。

质点系动量矩守恒定律是描述多个质点在相互作用下的动量守恒规律。

本文将深入探讨质点系动量矩守恒定律的原理和应用。

质点系动量矩守恒定律的原理质点系动量矩守恒定律是基于质点的动量和力矩守恒的推导而来的。

在一个封闭系统中，如果没有外力和外力矩的作用，质点系的总动量和总动量矩将保持不变。

质点系动量守恒定律的表达式质点系动量守恒定律可以用以下表达式表示：∑m i⋅v i⃗⃗⃗ =∑m i⋅v i⃗⃗ ′其中，m i表示第i个质点的质量，v i⃗⃗⃗ 表示第i个质点的速度，v i⃗⃗ ′表示第i个质点的速度在相互作用后的值。

质点系动量守恒定律的应用质点系动量守恒定律的应用非常广泛，以下是一些常见的应用场景：1. 弹性碰撞在弹性碰撞中，两个物体之间发生碰撞后会互相作用。

根据质点系动量守恒定律，碰撞前后质点系的总动量保持不变。

这种定律在撞球、弹簧振子等场景中得到了广泛的应用。

2. 力矩平衡在一个力矩平衡的系统中，物体对轴产生的力矩之和为零。

根据质点系动量守恒定律，系统的总动量矩也将保持不变。

这个应用场景常见于杠杆平衡、旋转机械等领域。

3. 爆炸反应在爆炸反应中，物体间发生的爆炸会导致质点系的动量发生变化。

根据质点系动量守恒定律，系统的总动量依然保持不变。

这个原理被应用于爆炸物理学和火箭动力学等领域。

4. 流体力学在流体力学中，质点系动量守恒定律被广泛应用于描述流体的运动。

根据定律，流体中各个质点的总动量保持不变，从而可以推导出流体动力学的一些基本方程。

质点系动量守恒定律的证明质点系动量守恒定律可以通过牛顿定律的推导来证明。

假设在一个封闭系统中，只有内力存在，没有外力作用。

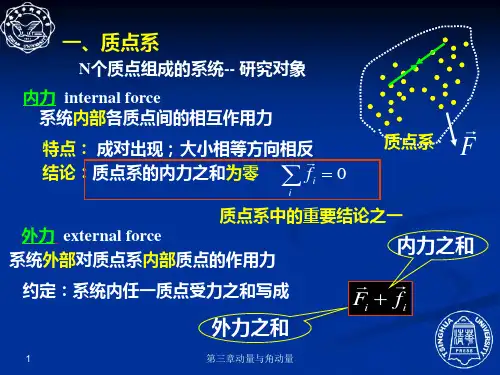
根据牛顿第三定律，内力满足作用力与反作用力相等且方向相反。

因此，内力互相抵消，系统的总动量保持不变。

质点系动量守恒定律的局限性质点系动量守恒定律在某些特殊情况下可能不适用，比如包含外力或外力矩的系统。

动量是物体运动状态的一种量度，它与物体的质量和速度成正比。

质点系的动量定理和动量守恒定律是描述物体运动规律的重要定律，对于理解和研究物体的运动具有重要意义。

本文将从简述质点系的动量定理开始，逐步深入探讨动量守恒定律，希望能够为读者提供一份深入浅出的参考。

1. 质点系的动量定理质点系的动量定理是描述质点系受力情况下动量的变化规律的定理。

根据牛顿第二定律，质点系的动量定理可以表述为：当一个质点系受到合外力时，它的动量随时间的变化率等于合外力的作用，即\[ \frac{d\vec{p}}{dt}=\vec{F} \]其中，\[ \vec{p} \]代表质点系的动量，\[ \vec{F} \]代表合外力的矢量。

这个定理表明了力对物体动量的影响，是经典力学中非常重要的基本定律之一。

2. 动量守恒定律当质点系受到合内力作用时，它的动量不会发生改变，这就是动量守恒定律的基本内容。

对于一个封闭系统来说，合内力为零，因此动量守恒定律可以表述为：在一个封闭系统内，当没有合外力作用时，质点系的动量保持不变，即\[ \vec{p}_1 + \vec{p}_2 + \cdots + \vec{p}_n = \vec{p}_1' +\vec{p}_2' + \cdots + \vec{p}_n' \]其中，\[ \vec{p}_i \]代表质点i的初始动量，\[ \vec{p}_i' \]代表质点i的最终动量。

动量守恒定律是一个非常重要的物理定律，它对于理解和分析自然界中的各种物理现象具有重要作用。

3. 个人观点和理解动量定理和动量守恒定律的提出和应用，使我们能够更深入地理解物体运动规律，并且在工程技术和自然科学研究中得到了广泛的应用。

在实际生活中，通过对动量定理和动量守恒定律的应用，我们可以更好地理解交通事故、火箭发射和碰撞实验等现象。

这些定律的深入理解和应用，有助于我们更加科学地分析和解决相关问题。