数电答案第五章

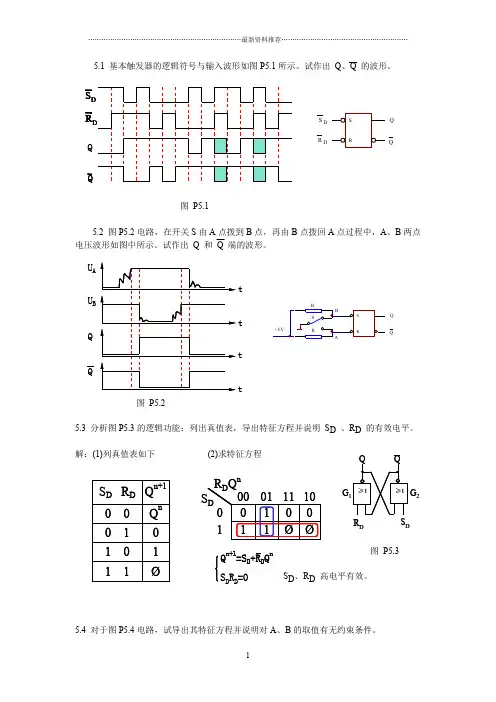
5.4 对于图P5.4电路，试导出其特征方程并说明对A、B的取值有无约束条件。

Q图P5.11P5.125.12 画出图P5.12电路中Q 1、Q 2 的波形。

解：特征方程为： ，Q 端波形如图P5.12所示。

=[D]·CP 1,Q 1n+1Q 2n+1= Q 1n[]·CP 2图P5.14 图P5.155.15 画出图P5.15电路中Q 端的波形。

解：Q 端波形如图P5.15所示。

5.16 试作出图P5.16电路中Q A 、Q B 的波形。

解：特征方程为： ， ，Q 端波形如图P5.16所示。

图P5.16 图P5.17Q A n+1= Q B n[]·A Q B n+1= Q A n []·BA R DB Q A Q BR D CP CP ⊕Q 2Q 1Q 25.17 试作出图P5.17电路中Q 1、Q 2 的波形。

解：特征方程为： ， ，Q 端波形如图P5.17所示。

5.18 试作出图P5.18电路中Q 1和Q 2的波形（设Q 1和Q 2的初态均为“0”），并说明Q 1和 Q 2对于CP 2各为多少分频。

解：特征方程为： ， ，Q 端波形如图P5.18所示。

Q 1和Q 2对于CP 2都是4分频，即图P5.18 图P5.195.19 已知电路如图P5.19，试作出Q 端的波形。

设Q 的初态为“0”。

解：特征方程为： ，Q 端波形如图P5.19所示。

5.20 已知输入u I 、输出u O 波形分别如图P5.20所示，试用两个D 触发器将该输入波形u I 转换成输出波形u O 。

解：输出u O 是对输入u I 的4分频，而采用1个DFF 可实现2分频，故实现电路如图P5.20所示。

图P5.205.21 试分别用公式法和列表图解法将主从SR 触发器转换成JK 触发器。

解1：Q 1n+1= Q 1n []·(CP ⊕Q 2)Q 2n+1= Q 2n []·Q 1?)?,(2221==CP Q CP Q f f f f Q 1n+1= Q 1n []·CP 1Q 2n+1= ·Q 2n []·CP 2Q 1n CP 2CP 1Q 1Q 241,412221==CP Q CP Q f f f f Q n+1= [ A ]·CP CP A Qu Iu OQ n+1=S+RQ n SR =0Q n+1=JQ n +KQn令新老触发器的次态方程相等，则有S=JQ n ，R=K但不满足约束条件SR =0。

自我检查题5.1 时序电路和组合电路的根本区别是什么？同步时序电路与异步时序电路有何不同？解答：从功能上看，时序电路任何时刻的稳态输出不仅和该时刻的输入相关，而且还决定于该时刻电路的状态，从电路结构上讲，时序电路一定含有记忆和表示电路状态的存储器。

而组合电路任何时刻的稳态输出只决定于该时刻各个输入信号的取值，由常用门电路组成则是其电路结构的特点。

在同步时序电路中，各个触发器的时钟信号是相同的，都是输入CP 脉冲，异步时序电路则不同，其中有的触发器的时钟信号是输入cp 脉冲，有的则是其他触发器的输出，前者触发器的状态更新时同步的，后者触发器状态更新有先有后，是异步的。

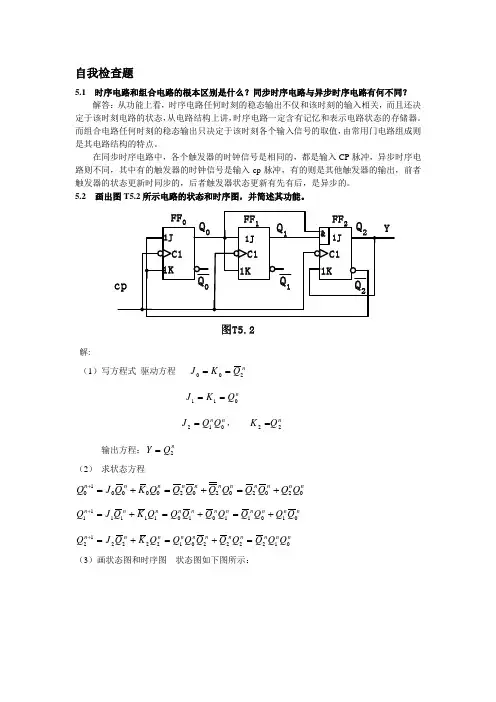
5.2 画出图T5.2所示电路的状态和时序图，并简述其功能。

图T5.2解:（1）写方程式 驱动方程 nQ K J 200==n Q K J 011==n n Q Q J 012=， n Q K 22=输出方程：nQ Y 2= （2） 求状态方程nn n n n n n n n n n Q Q Q Q Q Q Q Q Q K Q J Q 02020202000010+=+=+=+ n n n n n n n n n n n Q Q Q Q Q Q Q Q Q K Q J Q 01011010111111+=+=+=+ n n n n n n n n n n n Q Q Q Q Q Q Q Q Q K Q J Q 01222201222212=+=+=+（3）画状态图和时序图 状态图如下图所示：101时序图如下图所示：CP Q 0Q 1Q 25.3 试用边沿JK 触发器和门电路设计一个按自然态序进行计数的七进制同步加法计数器。

解：（1）状态图如下图：（2）求状态方程、输出方程CQ Q Q n n n /101112+++的卡诺图如下图所示：输出方程为nn Q Q C 12=状态方程：n n n n n Q Q Q Q Q 120112+=+ n n n n n n Q Q Q Q Q Q 0120111+=+ n n n n n Q Q Q Q Q 120110+=+驱动方程：n n n n n n n n n n n n n n n Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q 0122120121220112)(++=++=+n n n n n n Q Q Q Q Q Q 1021011+=+n n n n n Q Q Q Q Q 0012101)(++=+与JK 触发器的特性方程 比较，可以得到驱动方程 n n Q Q J 012= 、 n Q K 12=n Q J 01= 、n n Q Q K 021=n n n n Q Q Q Q J 12120=+= 10=K（4） 无效状态转换情况 111/1000 能自启动（5） 逻辑图如下图所示：5.4 画出用时钟脉冲上升沿触发的边沿D 触发器组成的4位二进制异步加法计数器和减法计数器的逻辑电路图。

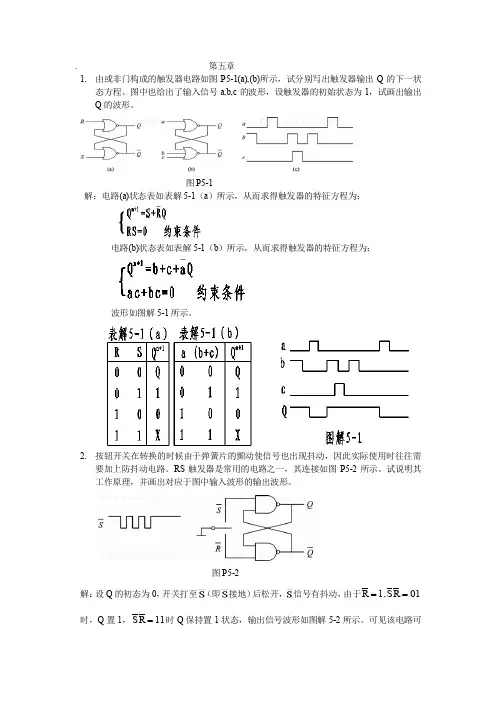
数字集成电路分析与设计第五章答案CHAPTER 5P5.1. For each problem, restate each Boolean equation into a form such that it can be translated into the p and n-complex of a CMOS gate.a. ()()Out ABC BD ABC BD A B C B D =+=+=+++b. ()()()Out AB AC BC AB AC BC A B A C B C =++=++=+++c. ()()Out A B CD A AB C D A A B CD A A B CD A =+++=++=+++=++AbVddVddAb BbAAbVddP5.2.AP5.3. First, convert the equation into its p and n-complex.()()()()()()()()()()()Out A B C BC AB AB C BC AB AB C BC AB AB C BC AB AB C BC AB AB C B C =⊕+=++=++=+=++=+++VddCbP5.4. The truth table is given below in terms of voltages. The function is F A B =The worse case V OH is V DD and the worse case V OL is 0V.P5.5. The first circuit is a NOR gate while the second is a NAND gate. The V OL and V OHcalculated are for the worst-case scenario. To find this, assume only one transistor turns on, this just reduces to a pseudo-NMOS/PMOS inverter, so the other transistors are not important.a. The V OL for the pseudo-NMOS (in 0.18µm) is:()()()2,1N N OXNSAT OX P GSP TPP SATOL W C L N DD TN GSP TP CP PDD TN SAT P N OX v C W V V I V k V V V V E L V V v W L C µ-==--+-=()2DD TP N N OX V V W C µ-()()()()()20.1DD TP CP P DD TN SAT P N DD TPDDN N DD TP CP P DD TN V V E L V V v W L V V V W V V E L V V µ-+--==-+-()()()()()()()()()()()()226440.18100.2100.210 1.80.50.14µm=1.40.11.8270 1.80.5240.2 1.80.5SAT P N DD TPN DD N DD TP CP P DD TN v W L V V W V V V E L V V µλ---=-+--==-+-Since the minimum width is 2λ, we make that the width. The V OH for the pseudo-PMOS (in 0.18µm) is:()()()()()()2221SDPSDP CP PN P V P OX P SGP TP SDP SAT OX N GSN TN V GSN TN CN N N SAT OX I sat I lin C W V V V v C W V V V V E L L v C µ=---= -++()2P OX N DD TN DD TN CN NC W V V V V E L µ-=-+()()()()(01DD OH DD OH CP PV V P DD TPDDOH V V P E L W V V VV L ------+()()()()()()20.1824620.184.8(70) 1.80.50.180.2(10)(810)1.80.51.80.5 1.21P P W L ----=-++4.2P W λ≈The pseudo-PMOS circuit will have bigger devices than the pseudo-NMOS.P5.6. The steps to solving this question are the same as the pseudo-NMOS question in Chapter4.a. For V OH , recognize that GS T V V >= for operation so the output can only be as high asDD T V V -. Since 0SB V ≠, body effect must be taken into account and the full equationis:()()()001.20.40.2OH DD T DDT V V V V Vγγ=-+=-+=-+ Iteration produces V OH =0.73V.b. For V OL , we must first recognize that the worst-case V OL occurs when only one of the pull-down transistors is on. Next we identify the regions of operation of the transistors. In this case, the pull-up transistor is always in saturation and the pull-down is most likely in the linear region since it will have a high input (high V GS ) and a low output (low V DS ). Then, we equate the two currents together and solve for V OL :()()()()2212222221111122460.61(1)(270)1.20.4(0.13)(10)(810)1.20.42(1.20.42)0.61DS DS CN OL OLV N OX GS T DS sat OX GS T V GS T CN E LV OL OL V OL I sat I lin W C V V V W v C V V V V E L L V V V µ-=---=-++--?--=--++ Using a programmable calculator or a spreadsheet program, V OL = 0.205V. The dc current with the output low is: ()()()()222222260.20520.2051(1)(270)(1.610)1.20.4(0.205)146.5DS DS CN V N OX GS T DS DS V ELW C V V V I L Aµµ---=+?--=+=The power with the output low is:(46.5)(1.2)55.8DS DD P I V A V W µµ===P5.7. See Example 5.2 which is based on the NAND gate. This question is the same except thatit addresses the NOR gate.With both inputs tied together, 88N P W W λλ==2χ=== ()()1.80.520.50.77V 112DD TP TNS V V V V χχIn the SPICE solution, the reason why the results vary for input A and B is due to body-effect.P5.8. The solution is shown below. Notice that there is no relevance with the lengths andwidths of the transistors when it comes to V OH , although they the do matter when calculating V OL .01.80.50.3 2.51Vout GG T GG out T V V V V V V γ=-=++=++=P5.9. For t PLH , we need to size the pull-up PMOS appropriately.()()()()15120.70.720.70.73010010845010PLH eqp LOAD p SQ LOAD PLHLt RC R C WL W R C k t λλ--====Ω?=?For V OL :()()()()()()()()()()()()()2246660.120.13 4.210810 1.610 1.20.4 1.08mA1.20.4240.1(270)(1.610)1.20.40.11138.577377232(3OLOL CN P sat OX GS T P GS T CP V N N OX OL TN OLN P V N N NW v C V V I sat V V E LW C V V V W I sat L L W W W stack L µλλλ-----===-+-+--?--==++===?=2)155(2)W stack λ=P5.10.The circuit is shown below:()()()()()()()()31512315120.720.70.7301075106350100.720.70.712.510751026.6275010PLH EQP LOAD P P EQPLOAD PLHPHL EQN LOAD NN EQNLOAD PHLLt RC R C W L W R C t Lt RC R C W L W R C t λλλλλ----====??=?====??=≈?Because the number of transistors in series is more than one, we must multiply the widths by the appropriate number. Here, all the NMOS transistors will have a width of 54λ. The PMOS transistors will have widths of 126λ and 190λ, respectively.P5.11. We estimate the dc power and dynamic switching power for this problem.a. The circuit’s dc power can be computed by computing the dc current when the output is low. This is given by I DS =550uA/um x 0.1um=55uA. Then P DC =66uW when the output is low.b. Its dynamic power can be calculated by simply using the equation 2dyn DD P CV f α=. Therefore, P dyn =(50fF)(V DD -V TN )(V DD )(100MHz)=4.4uW.P5.12. The pseudo-NMOS inverter has static current when the output is low. We can estimate itas:()()()()()()()()224660.110810 1.610 1.20.425.6A 1.20.4240.1P sat OX GS T P GS T CP W v C V V I sat V V E Lµ----===-+-+Then the average static power is P stat =(25.6uA)(1.2)/2 =15.4uW.The dynamic power is dyn DD swing avg P CV V f ==(50fF)(1.2)(1.1)f avg assuming that V OL is 0.1V.For the CMOS inverter, the static power is almost zero: P stat =I sub V DD . It is far less thanthe pseudo-NMOS case. The dynamic power dyn DD swing avg P CV V f ==(50fF)(1.2)2f avg is slightly larger than the pseudo-NMOS case.V VINCMOS InverterV V INPseudo-NMOSP5.13. Model development to compute αsc .P5.14. The energy delivered by the voltage source is:()()200202DDDDV C sourceDD DD L L DDC L DDV CDDcap C LC L C C LdvE i t V dt V C dt C V dv C V dt dv V E i t v dt C v dt C v dv C dt∞∞∞∞========As can be seen, only half the energy is stored in the capacitor. The other half was dissipated as heat through the resistor.P5.15. The average dynamic power does not depend on temperature if the frequency stays thesame. However, the short-circuit current will increase as temperature increases. In addition, the subthreshold current increases as temperature increases. So the overall power dissipation will be higher. P5.16. The circuit is shown below. The delay should incorporate both Q and Qb settling in400ps. All NMOS and PMOS devices are the same size in both NAND gates.()()()()()()()()15331220.70.70.70.720.71001030100.1212.5100.10.72400101µmN P P PHL PLH UP LOAD DOWN LOAD LOAD eqp eqn P N LOAD eqp eqn LOAD eqp eqn PL Lt t t R C R C C R R W W C R L R L WC R L R L W t --??=+=+=+ ?+=++==≈P5.17. The small glitch in J propagates through the flop even though it is small. This is due tothe fact that the JK-flop of Figure 5.20 has the 1’s catching problem. P5.18. The small glitch in J does not propagate through the flop since the edge-triggeredconfiguration does not have a 1’s catching problem.P5.19. The positive-edge triggered FF is as follows:QQDS(a) With CK=D=0 and S=R=1, the outputs are(b) Now CK=0。

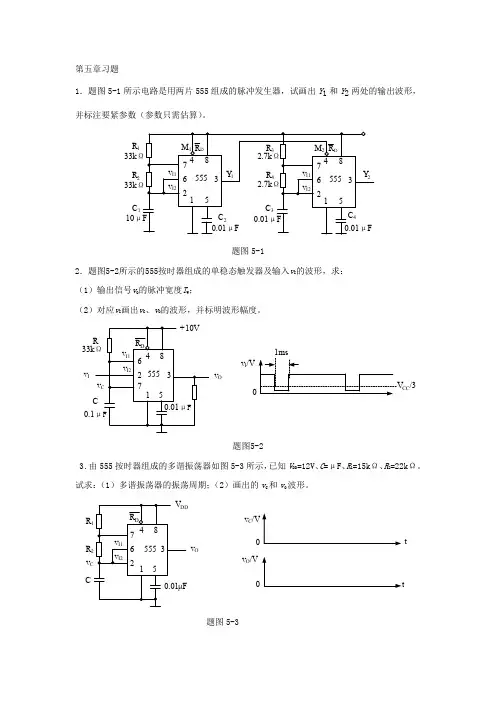
第五章习题1．题图5-1所示电路是用两片555组成的脉冲发生器，试画出Y 1和Y 2两处的输出波形，并标注要紧参数（参数只需估算）。

R 1C 133kR 233k 10题图5-12．题图5-2所示的555按时器组成的单稳态触发器及输入v I 的波形，求： （1）输出信号v O 的脉冲宽度T W ；（2）对应v I 画出v C 、v O 的波形，并标明波形幅度。

v I /V CC /3v Iv O题图5-23．由555按时器组成的多谐振荡器如图5-3所示，已知V DD =12V 、C =μF、R 1=15k Ω、R 2=22k Ω。

试求：（1）多谐振荡器的振荡周期；（2）画出的v C 和v O 波形。

v O /Vv C /V00tR Cv v OR题图5-34．由555按时器、3位二进制加计数器、理想运算放大器A 组成如题图5-4所示电路。

设计数器初始状态为000，且输出低电平V OL =0 V ，输出高电平V OH = V ，R d 为异步清零端，高电平有效。

（1）说明虚框（1）、（2）部份各组成什么功能电路？（2）虚框（3）组成几进制计器？ （3）对应CP 画出v O 波形，并标出电压值。

题图5-45．用集成芯片555组成的施密特触发器电路及输入波形i v 如题图5-5所示，要求： （1）求出该施密特触发器的阈值电压V T ＋、V T －；（2）画出输出v o 的波形。

v I /V tv O /Vv v O题图5-56．用集成按时器555组成的电路及可产生的波形如题图5-6（a ）、（b ）所示，试回答： （1）该电路的名称；（2）指出（b ）图中v C 波形是1～8引脚中，哪个引脚上的电压波形； （3）求出矩形波的宽度t W 。

v Iv O 0.3v v（a ） （b ）题图5-67．题图5-7为简易门铃电路，设电路中元器件参数适合，R >>R 1，S 为门铃按钮，当按钮按一下放开后，门铃可响一段时刻。

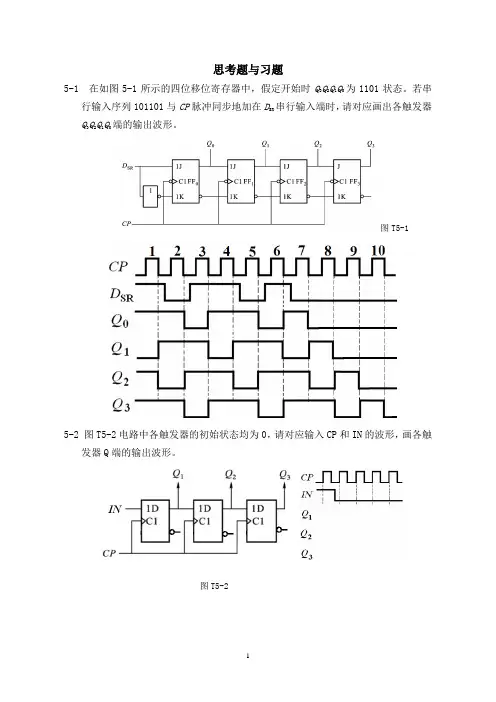
思考题与习题5-1 在如图5-1所示的四位移位寄存器中，假定开始时Q3Q2Q1Q0为1101状态。

若串行输入序列101101与CP脉冲同步地加在D SR串行输入端时，请对应画出各触发器Q 3Q2Q1Q端的输出波形。

图T5-15-2 图T5-2电路中各触发器的初始状态均为0，请对应输入CP和IN的波形，画各触发器Q端的输出波形。

图T5-25-3 试用两片74LS194电路构成一个八位移位寄存器，并画出逻辑电路图。

5-4 请用上升沿触发的D触发器构成一个异步三位二进制加法计数器。

并对应CP画出Q1、Q2、Q3的波形。

图T5-45-5 请用JK 触发器构成一个脉冲反馈式异步六进制加法计数器，并画出对应于CP 脉冲的工作波形。

图T5-5用三位JK 触发器构成八进制计数器，然后在状态110时利用与非门反馈至清零端构成六进制计数器，图略。

5-6请分析如图T5-6所示的阻塞反馈式异步计数器电路的逻辑功能，指出该计数器为几进制，并画出计数状态转换图。

图T5-6解：（1）驱动方程：J I =3Q ,K 1=1; J 2=1,K 2=1;J 3=nQ n Q 21,K 3=1;代入得状态方程: （CP 脉冲下降沿时刻）（Q 1下降沿时刻） （CP 脉冲下降沿时刻）列出状态转换图（略）分析得出该计数器为5进制计数器，状态从000-100，其它的三个状态下一状态均为000，因此该电路是异步五进制计数器，具有自启动功能。

5-7 分析图T5-7同步计数器电路的逻辑功能。

图T5-7nn n n n Q K ,Q J Q K ,Q J Q K ,J 232312323111====== n Q n Q Q n 1311=+n Q Q n 221=+n Q n Q n Q Q n 31231=+nn n nn n nn n n n n n n n n n Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q 23232132123123113111=⋅+⋅=⋅+⋅=+=⋅+=+++n n n Q Q Q 123 111213+++n n n Q Q Q0 0 0 0 0 1 0 0 1 0 0 0 0 1 0 1 0 1 0 1 1 1 1 0 1 0 0 0 1 1 1 0 1 0 1 1 1 1 0 1 0 1 1 1 1 1 1 1因为该计数器设计了清零端，因此可实现从000开始进入循环圈的2进制计数器的功能，但我们也发现，它也可以实现三进制。

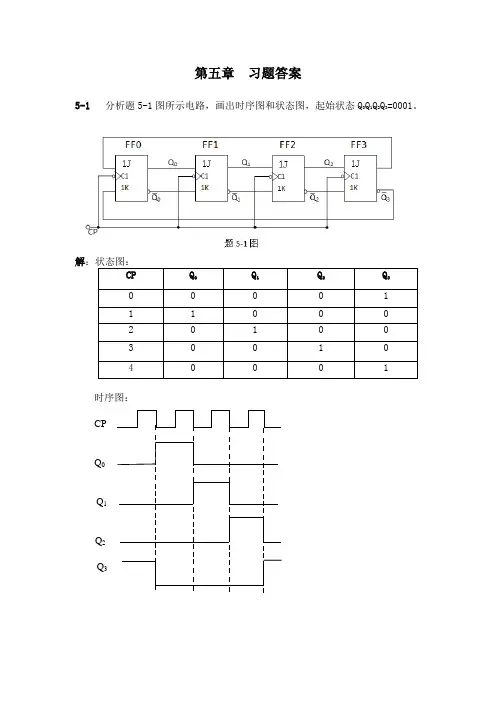
第五章习题答案5-1分析题5-1图所示电路，画出时序图和状态图，起始状态Q0Q1Q2Q3=0001。

解CP Q0 Q1Q2Q30 0 0 0 11 1 0 0 02 0 1 0 03 0 0 1 04 0 0 0 1 时序图：CPQ0Q1Q2Q35-2分析题5-2图所示电路，画出电路的状态图。

解CP Q0 Q1 Q20 0 0 01 1 0 02 0 1 03 0 0 14 0 0 05-3 JK触发器组成5-3图所示电路。

分析该电路为几进制计数器，并画出电路的状态图。

CP Q1 Q2Q30 0 0 01 1 0 02 0 1 03 1 1 04 0 0 15 0 0 0 该电路为五进制计数器5-4JK触发器促成如图5-4图所示的电路。

（1）分析该电路为几进制计数器，画出状态图。

（2）若令K3= 1，电路为几进制计数器，画出其状态图。

解：（1CP Q1 Q2Q30 1 2 3 4 5 6 7 0 0 01 0 00 1 01 1 00 0 11 0 1 0 1 1 0 0 0为7进制计数器CP Q1 Q2Q30 1 2 3 4 5 0 0 01 0 00 1 01 1 00 0 11 0 0为4进制计数器5-5 试画出题5-5图（a）所示电路中B,C端的波形。

输入端A,CP波形如题5-5图(b)所示，触发器的起始状态为零。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19CPAQ0Q1BC5-6分析题5-6图所示电路，画出电路的状态图，说明电路能否自启动。

CP Q1 Q2Q3Z0 1 2 3 4 5 6 7 0 1 0 0 0 01 0 1 0 1 1 1 00 1 1 11 0 0 0 1 1 0 00 1 0 01 0 1 00 0 1 01 0 0 0该电路能够自启动5-7 分析题5-7图所示电路，画出电路的状态图，说明电路能否自启动。

CP Q4 Q3Q2Q11234 567111111111 0 0 0 00 0 0 11 0 0 11 1 0 11 1 1 00 1 1 11 0 1 11 1 0 10 0 1 00 0 0 10 0 1 11 0 0 10 1 0 00 0 1 10 1 0 11 0 1 10 1 1 00 0 1 11 0 0 00 1 0 11 0 1 00 1 0 11 1 0 00 1 1 11 1 1 1 1 1 1 0由状态图可见，电路图能够自启动5-8画出题5-8图所示电路的状态图和时序图，简要说明电路的基本功能。

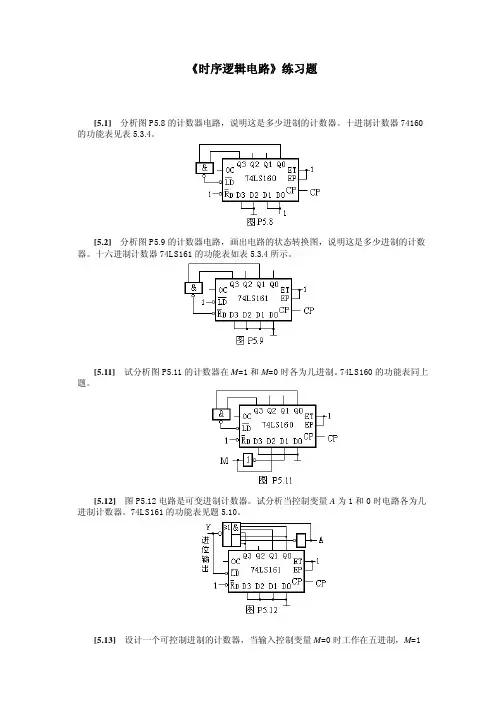
《时序逻辑电路》练习题[5.1] 分析图P5.8的计数器电路，说明这是多少进制的计数器。

十进制计数器74160的功能表见表5.3.4。

[5.2] 分析图P5.9的计数器电路，画出电路的状态转换图，说明这是多少进制的计数器。

十六进制计数器74LS161的功能表如表5.3.4所示。

[5.11]试分析图P5.11的计数器在M=1和M=0时各为几进制。

74LS160的功能表同上题。

[5.12]图P5.12电路是可变进制计数器。

试分析当控制变量A为1和0时电路各为几进制计数器。

74LS161的功能表见题5.10。

[5.13]设计一个可控制进制的计数器，当输入控制变量M=0时工作在五进制，M=1时工作在十五进制。

请标出计数输入端和进位输出端。

[解] 见图A5.13。

[5.15]试分析图P5.15计数器电路的分频比(即Y与CP的频率之比)。

74LS161的功能表见题5.10。

[解] 利用与上题同样的分析方法，可得74LS161(1)和74LS161(2)的状态转换图如图A5.15(a)、(b)所示。

可见，74LS 161(1)为七进制计数器，且每当电路状态由1001~1111时，给74LS 161(2)一个计数脉冲。

74LS 161(2)为九进制计数器，计数状态由0111~1111循环。

整个电路为63进制计数器，分频比为1:63。

[5.16] 图P5.16电路是由两片同步十进制计数器74160组成的计数器，试分析这是多少进制的计数器，两片之间是几进制。

74160的功能表见题5.10。

[解] 第（1）片74160接成十进制计数器，第（2）片74160接成了三进制计数器。

第（1）片到第（2）片之间为十进制，两片中串联组成71~90的二十进制计数器。

[5.17] 分析图P5.17给出的电路，说明这是多少进制的计数器，两片之间多少进制。

74LS161的功能表见题5.10。

[解] 在出现0=LD 信号以前，两片74LS161均按十六进制计数。

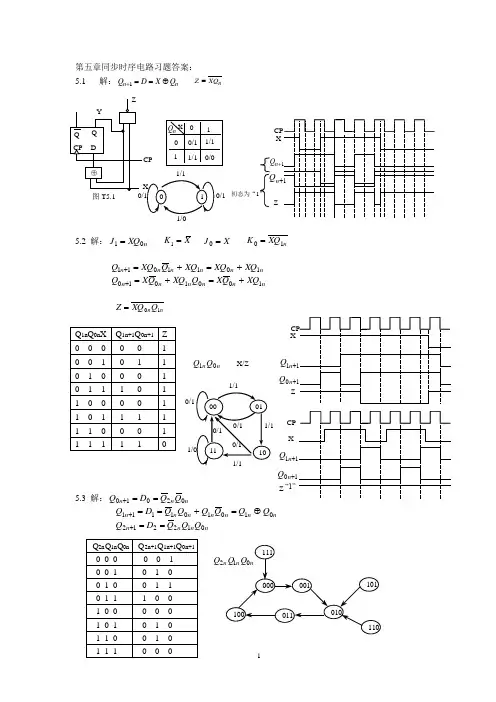
第五章同步时序电路习题答案： 5.1 解：n n Q X D Q ⊕==+1 n XQ Z =5.2 解：n XQ J 01= X K =1 X J =0 n XQ K 10=n n n n n n XQ XQ XQ Q XQQ 1011011+=+=+ n n n n n n XQ Q X Q XQ Q X Q 1001010+=+=+ n n Q XQ Z 10=5.3 解：n n n Q Q D Q 02010==+n n n n n n n Q Q Q Q Q Q D Q 010101111⊕=+==+ n n n n Q Q Q D Q 012212==+1/1 0/1 X 011 0/1 1/1 1/1 0/0n Q+n n Q Z初态为“1”nn Q Q 01X/ZX1+n Q 0+n Q ZX1+n Q 0+n Q Z “1”Q 212+n Q逻辑功能：可自启动的同步五进制加法计数器。

5.45.55.6 解：（1）当X 1X 2=“00”；初始状态为“00”时：112=+n Q 121==n Q J 1111==X J Kn n Q Q 111=+逻辑功能：电路实现2分频。

（2）当X 1X 2=“01”；初始状态为“00”时：n Q J 21= 1111==X J K n n n Q Q Q 1211=+n Q J 12= 1112==X Q K n n n n Q Q Q 1212=+ 逻辑功能： 电路实现3分频。

（3）当X 1X 2=“11”；初始状态为“00”时： n Q J 21= n Q X J K 2111==n n n n n n Q Q Q Q Q Q 2121211=+=+ n Q J 12= n n Q X Q K 1112== n n n n n n Q Q Q Q Q Q 1212112=+=+ 逻辑功能： 电路实现4分频。

Y 3 Y 2 Y 1 Y 0n n n Q Q Q J 1234= n Q K 14= n n Q Q J 143= n n Q Q K 123= n n n Q Q Q J 1342= n Q K 12= 111==K Jn n n n n n n Q Q Q Q Q Q Q 14123414+=+ n n n n n n n Q Q Q Q Q Q Q 31213413)(++=+ n n n n n n n Q Q Q Q Q Q Q 12123412)(++=+ 14+n QCP13+n Q 12+n Q 11+n QZn n Q Q 111=+n n n n Q Q Q Q Z 1234= 时序图：11+n Q12+n Q 11+n Q11+n Q12+n Q5.7 （1）（2）Q D 端输出是12分频，占空比是50%。

5章课后习题解答一同步时序电路如图题所示，设各触发器的起始状态均为0态。

(1) 作出电路的状态转换表； (2) 画出电路的状态图；(3) 画出CP 作用下各Q 的波形图； (4) 说明电路的逻辑功能。

[解] (1) 状态转换表见表解 。

(2) 状态转换图如图解(1)。

(3) 波形图见图解(2)。

(4) 由状态转换图可看出该电路为同步8进制加法计数器。

由JK FF 构成的电路如图题所示。

(1) 若Q 2Q 1Q 0作为码组输出，该电路实现何种功能? (2) 若仅由Q 2输出，它又为何种功能?[解] (1) 由图可见，电路由三个主从JK 触发器构成。

各触发器的J ，K 均固定接1，且为异步连接，故均实现T ＇触发器功能，即二进制计数，故三个触发器一起构成8进制计数。

当Q 2Q 1Q 0作为码组输出时，该电路实现异步8进制计数功能。

(2) 若仅由Q 2端输出，则它实现8分频功能。

图题图题CP Q 0Q 1Q 2(1) (2)图解试分析图题所示电路的逻辑功能。

[解] (1) 驱动程式和时钟方程02n J Q =，01K =；0CP CP =111J K ==；01CP Q =210n nJ Q Q =，21K =；2CP CP = (2) 将驱动方程代入特性方程得状态方程0+1000020 ()n n n n nQ J Q K Q Q Q CP =+=+1111 ()n n Q Q CP =+12210 ()n n n n Q Q Q Q CP =(3) 根据状态方程列出状态转换真值表5进制计数器。

X = 0及X = 1时[解] (1) 写驱动方程和输出方程 0J X =， n 01K X Q = n 10J XQ =， n 10K Q = n 1Y Q = (2) 求状态方程100000010n n n n n n Q J Q K Q X Q X Q Q +=+=+ 1111111010n n n n n n n Q J Q K Q X Q Q Q Q +=+=+图题图解图题(3) 画次态卡诺图求状态转换真值表(4) 作状态转换图如图解(2)所示。

第5章 习题解答5-1 由与非门组成的大体RS 触发器的d d S ,R 之间什么缘故要有约束？当违背约束条件时，输出端Q 、Q 会显现什么情形？试举例说明。

解：由与非门组成的大体RS 触发器的d R 和d S 之间的约束条件是：不许诺d R 和d S 同时为0。

当违背约束条件即当d R =d S =0时，Q 、Q 端将同时为1，作为大体存储单元来讲，这既不是0状态，又不是1状态，没成心义。

5-2 试列出或非门组成的大体RS 触发器的真值表，它的输入端R d 和S d 之间是不是也要有约束？什么缘故？解：真值表如右表所示、Rd 、Sd 之同也要有约束条件，即不许诺Rd=Sd=1， 不然Q 、Q 端会同时显现低电平。

5-3 画出图5-33由与非门组成的大体RS 触发器输出端Q 、Q 的电压波形，输入端D D S R 、的电压波形如图中所示。

图5-33解：见以下图：5-4 画出图5-34由或非门组成的大体RS触发器输出端Q、Q的电压波形，输入端S D、R D的电压波形如图中所示。

图5-34解：见以下图：5-5 图5-35所示为一个防抖动输出的开关电路。

当拨动开关S时，由于开关触点接通R S、的电压波形如图中所示。

试画出Q、Q端对应的电压波形。

刹时发生振颤，D D图5-35解：见以下图：5-6 在图5-36电路中、假设CP、S、R的电压波形如图中所示，试画出Q、Q端与之对应的电压波形。

假定触发器的初始状态为Q＝0。

图5-36解：见以下图：5-7 在图5-37(a)所示的主从RS触发器中，CP、R、S的波形如图5-37(b)所示，试画Q、Q和Q的波形图。

出相应的Q m、m图5-37解：主从RS触发器的工作进程是：在CP＝l期间主触发器接收输入信号，但输出端并非改变状态，只有当CP下降沿到来时从触发器甚才翻转，称为下降沿触发。

依照主从RS 触发器状态转换图可画出波形图如下图所示。

5-8 在图5-38(a)所示的主从JK触发器中，CP、J、K的波形如图5-38(b)所示，试画Q、Q和Q的波形图。

第五章答案5.5ZQ Q XQ Q X Q Q X Q Q X QQ X K Q X J Q Q Q X Q X Q XQ Q Q X Q XQ K Q X J n n =∙++∙=∙+∙=∴∙==∙++∙=+∙∙=∴==++2121212112121221121221112121,,下降沿触发CP X Q1Q25.632113321321121223111131,1,,,1,Q Q Q Q K Q Q J Q Q Q Q K J Q Q Q K Q J n n n ∙=∴==⊕=∴==∙=∴==+++000，100，010，011，111，000 5进制计数器 5.83321132212113111231CP Q Q Q Q CP Q Q CP Q Q Q Q CP CP CP n n n ∙=∙=∙∙===+++000，100，010，011，111，000 5进制 5.92212111100211012100211CP Q Q CP Q Q CP Q Q Q Q Q CP Q Q Q Q CP n n n n ∙=∙=∙==→+=++++能自启动的7进制计数器5.101221120Q CP Q A D Q D AQ D =+===A=0时Q2翻转，Q0不变，Q1不变 A=1时Q2=Q0=1，Q1不变 A 发生变化才会引起变化 5.1174163是同步清零同步置数的思维二进制计数器 只有S0时Z 为0，所以012Q Q Q Z ++=11210121010012X Q Q X Q Q Q X Q Q X Q Q Q LD +++= 0112122X Q X Q Q Q D ++= 11010121X Q X Q Q Q Q D ++= 00100120X Q X Q Q Q Q D ++= 03=D按照表达式就可以画出电路图（略） 5.12两个74161都连成0000，0001，0010，0011，0100，1000，1001，1010，1011，1100循环的10进制计数器，右边只有在左边为1100时才计一个数 100进制计数器 5.137490是异步清0，先连成10进制，当输出为0111清0。

第五章锁存器和触发器1、Q n 1二S RQ n, SR = O2、Q n, 03、324、TCP J I I I I I I I7、4-13题解图8、D= A 二BCP_ I~I I~I I~I I~I I~LI Iz卄I TH 1D i - I i i1 . I | , __ L,I ■ I ______第六章时序逻辑电路1、 输入信号，原来的状态2、 异3、 n 5、反馈清零、反馈置数扌-6、N乂—LJ UU 仑厂 II ~ 7、状态方程和输出方程：㈣ =A®Q'tZ^AQ&激励方程A =Kq = A &/. =e 0=i 状态方程0：戚；忧"无©土死输出方程Z=AQ1Q0根据状态方程组和输出方程可列出状态表，如表题解6 . 2 . 4所示，状态图如图题解2. 4 所示。

Q - M?； + M V ；* Q ； = + “：14、图题解6.2.4Q；・枫"烟00保持，01右移10左移11并行输入当启动信号端输人一低电平时，使S仁1 ,这时有So= Sl= 1 ,移位寄存器74HC194执行并行输人功能，Q3Q2Q1Q0 = D3D2D1D0 = 1110。

启动信号撤消后，由于Q°= 0,经两级与非门后，使S仁0 ,这时有S1S0= 01 ,寄存器开始执行右移操作。

在移位过程中，因为Q3Q2、Q1、Q0中总有一个为0,因而能够维持S1S0=01状态，使右移操作持续进行下去°其移位情况如图题解6, 5, 1所示。

该电路能按固定的时序输出低电平脉冲，是一个四相时序脉冲产生电路。

-JT AAA TL幺I15、状态方程为儿⑷儿個)X(O24、解：74HC194功能由S1S0控制。

本章习题5．1分析图题4.1a 电路的逻辑功能，列出逻辑功能表，画出R、S 输入图b 信号时的输出波形。

题5.1 逻辑功能表解: 见题5.1 逻辑功能表和波形图。

5．2画出图题5.2各触发器在时钟脉冲作用下的输出波形。

（初态为“0”） 解：波形见题5.2图。

5．3 画出图题4.3中各不同触发方式的D 触发器在输入信号作用下的输出波形 (初态为0)。

Q n S R Q n+1 Q —n+1 功能0 1 0 1 0 置位1 1 0 1 0 置位00 1 0 1 复位10 1 0 1 复位00 0 0 1 保持10 0 1 0 保持0 1 1 1 1 非法11111非法解：波形见题5.3图。

5．4 图题5.4a由CMOS或非门和传输门组成的触发器，分析电路工作原理，说明触发器类型。

如果用两个图a的电路构成图b电路，说明图b电路是什么性质的触发器。

解：图a为同步D触发器，CP为使能控制，低电平有效。

当CP=“0”时，TG1通、TG2断，触发器根据D信号改变状态；当CP=“1”时，TG1断、TG2通，触发器状态保持。

逻辑符号如图5.2a。

图b为主从D触发器，时钟CP的上升沿有效，逻辑符号如图5.2b。

5．5 画出图题5.5（a）所示电路在输入图（b）信号时的输出波形。

解：当A=“1”时，CP的下降沿使Q=“1”。

当Q=“1”且 CP =“1”时，Q复位。

波形见题5.5图。

5．6画出图题5.6（a）电路的三个输出Q2、Q1、Q0在图（b）信号输入时的波形变化图（初始状态均为“0”）。

分析三个输出信号和输入信号的关系有何特点。

解：波形见题5.6图。

输出信号按位序递增顺序比输入滞后一个CP周期。

5．7 画出图题5.7所示电路的三个输出Q2、Q1、Q0在时钟脉冲作用下波形变化图（初始状态均为“0”）。

若三个输出组成三位二进制码，Q2为最高位，分析输出码和时钟脉冲输入个数之间的关系。

解：波形见题5.7图，输出码随时钟输入递减：“000”→“111”→“110” →“101” →“100” →“011” →“010” →“011” →“001” →“000”，每8个时钟周期循环一次。