【优质文档】超级画板范例教程-word范文 (25页)

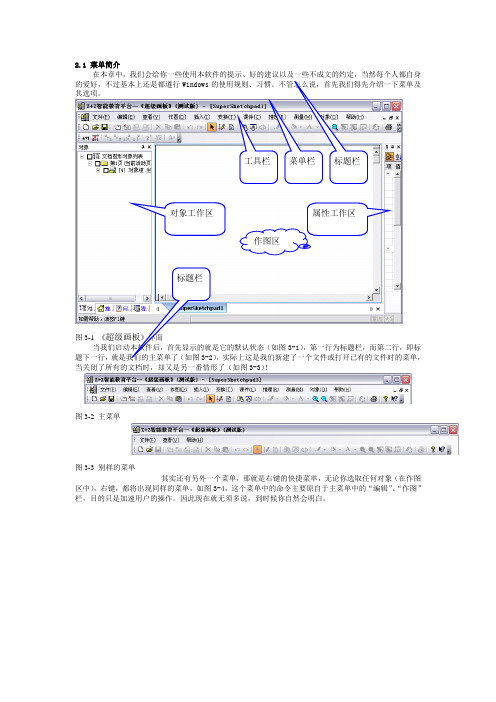
2.1 菜单简介在本章中，我们会给你一些使用本软件的提示、好的建议以及一些不成文的约定，当然每个人都自身的爱好，不过基本上还是都遵行Windows其选项。

3-1），第一行为标题栏，而第二行，即标），实际上这是我们新建了一个文件或打开已有的文件时的菜单，当关闭了所有的文档时，却又是另一番情形了（如图3-3）！其实还有另外一个菜单，那就是右键的快捷菜单，无论你选取任何对象（在作图区中），右键，都将出现同样的菜单，如图3-4，这个菜单中的命令主要原自于主菜单中的“编辑”、“作图”栏，目的只是加速用户的操作。

因此现在就无须多说，到时候你自然会明白。

图3-2 主菜单图3-3 别样的菜单 对象工作区属性工作区作图区当然要重点介绍的是我们的主菜单（图3-1），因为图3-2及图3-3的菜单被包含在图3-1的菜单中，那我们就一一道来吧：文件( F )：建立新的或打开已有的超级画板文件；可以保存，打印及用电子邮件发送当前的版面；可以关闭当前文件或退出立体几何系统。

编辑( E )：撤消或重复上次操作；改变图形、文字的特性；复制、粘贴及剪切等。

查看( V )：更换试图模式及工具栏、状态栏选项，如全屏显示、背景颜色、坐标系模式、OLE 对象，显示或隐藏工具栏等。

作图( D )：作出各种几何图形，这可是“精彩”之一。

插入( I )：插入各式的文字、图片、多媒体、表格等等，做出丰富多彩的课件的任务也许就是它。

变换( T )：平移、旋转、放射变换等等几何意义的变换都在这。

更“精彩”的功能就得靠这些命令。

课件( C )：制作或播放的课件；功能强大的按钮将在这里制作。

解题( S )：附加已知条件，生成题目，或自动解题；在这里“智能的风范”可体现得淋漓尽致。

测量( M )：测量或计算各种对象的数值，如表达式，各种角，两点距离等。

对象( O )：选定对象，查看对象的属性及改变对象性质。

窗口( W )：新建及管理窗口。

帮助( H )：《Z+Z 教育软件智能平台-超级画板》的帮助信息及作者、版权信息。

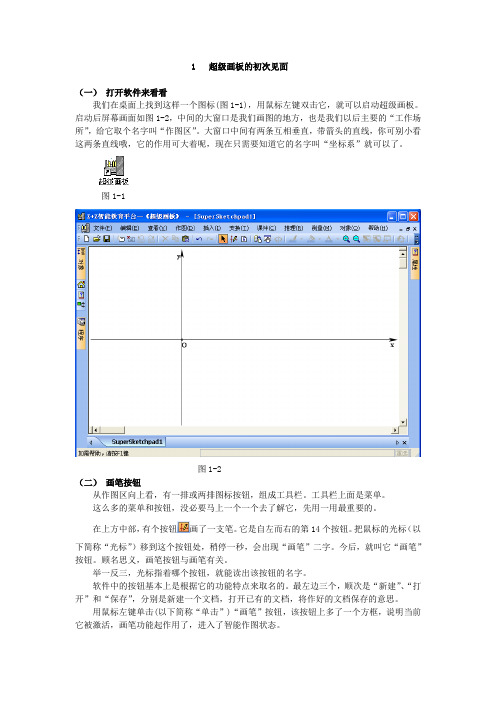
1 超级画板的初次见面（一）打开软件来看看我们在桌面上找到这样一个图标(图1-1)，用鼠标左键双击它，就可以启动超级画板。

启动后屏幕画面如图1-2，中间的大窗口是我们画图的地方，也是我们以后主要的“工作场所”，给它取个名字叫“作图区”。

大窗口中间有两条互相垂直，带箭头的直线，你可别小看这两条直线哦，它的作用可大着呢，现在只需要知道它的名字叫“坐标系”就可以了。

图1-1图1-2（二）画笔按钮从作图区向上看，有一排或两排图标按钮，组成工具栏。

工具栏上面是菜单。

这么多的菜单和按钮，没必要马上一个一个去了解它，先用一用最重要的。

在上方中部，有个按钮画了一支笔。

它是自左而右的第14个按钮。

把鼠标的光标（以下简称“光标”）移到这个按钮处，稍停一秒，会出现“画笔”二字。

今后，就叫它“画笔”按钮。

顾名思义，画笔按钮与画笔有关。

举一反三，光标指着哪个按钮，就能读出该按钮的名字。

软件中的按钮基本上是根据它的功能特点来取名的。

最左边三个，顺次是“新建”、“打开”和“保存”，分别是新建一个文档，打开已有的文档，将作好的文档保存的意思。

用鼠标左键单击(以下简称“单击”)“画笔”按钮，该按钮上多了一个方框，说明当前它被激活，画笔功能起作用了，进入了智能作图状态。

此时将光标移到作图区，光标由一个箭头变成了一只执笔的手，说明已经可以动手作图了，赶紧动手试一试吧。

（三）跟我做（1）你看到屏幕上的点O了么？先用鼠标点击屏幕上方的“画笔”按钮，然后用鼠标左键双击屏幕上的点O，第二击不松开就拖动，画出一个圆。

此时圆上有一点A；（2）将鼠标移到圆上，圆会变色，此时单击则会生成点B；（3）按下鼠标左键拖动，当已经画出（但尚未画完）的线接近垂直于x轴时，x轴即会变色，附近会出现“垂足”字样。

这时松开鼠标左键，就画出了一条垂直x轴的线段BC（图1-3）（4）仿照（3），作出线段BD垂直y轴；（5）将鼠标从点D出发移动到点C，这样就作好了线段CD；（6）当鼠标移动到线段CD 的中点附近时，线段CD变色，附近出现“中点”字样，单击即可作出线段CD的中点E（图1-4）；图1-3 图1-4（7）将鼠标移动到点E，单击鼠标右键，弹出右键菜单后，点击“跟踪”；（8）先用鼠标点击屏幕上方的小图标，再去拖动点B，使之在圆上转圈，你会发现屏幕上多出来了一个小圆圈（图1-5）；图1-5 图1-6（9）单击屏幕空白处，刚才作出来的小圆圈不见了。

超级画板免费版入门教程第一篇走马观花如果你是一位老师（特别是数学或物理老师）或者学生，而且有条件使用计算机，你应当用一用《Z+Z智能教育平台——超级画板》（以下简称《超级画板》）这款国产软件。

它能节省你的劳动，活跃你的思维，给你的工作和学习带来乐趣。

本书所讲的是《超级画板》的免费版本的功能。

一个软件的免费版本有如此丰富多彩的内容，足以使人惊喜，令人入迷。

你可以在下列网站，，下载《超级画板》软件，包括与本书配套的资源以及其他相关资料。

你可以选择安装《超级画板》，也可以即插即用：将相关资料中的“ZjzMath”文件夹复制到计算机即可。

下面就开始吧。

一打开界面看看试试（一）启动安装好《超级画板》之后，桌面上就会多出两个图标。

一个《超级画板》的图标（图1），另一个是《立体几何》图标。

双击《超级画板》图标，就可以启动超级画板了。

启动后屏幕画面上部如图1-2。

图1-1图1-2画有一个坐标系的大窗口是我们写字画图的地方，不妨简称“作图区”。

作图区左方有一个较小的窗口，窗口左上角有“对象”两字。

这个窗口叫做“图形对象工作区”。

（二）图形对象工作区图形对象工作区有什么用？让我们试试。

先不看说明，自己动手试一试，是熟悉软件的好方法。

图形对象工作区里已经有几行字了。

其中有一行是这样的：图1-3这里有“对象组：坐标系”几个字，什么意思？为什么前面有个数字[4]？小方框里的“＋”和“√”又有何作用？单击带“√”的小方框，看看有什么反应。

呵，“√”不见了。

同时，作图区里的坐标系也消失了。

再单击这个小方框，“√”又有了，坐标系又出现了。

原来这个带“√”的小方框是负责作图区里的坐标系的隐藏或显示的。

再单击带＋号的小方框，“＋”立刻变成了“＋”．同时，这一行变成了下面的5行：图1-4每行前面都有带“√”的小方框。

单击第一行的带“√”的小方框，5个勾就都消失了。

当然，如我们所料，作图区的坐标系也隐藏了。

再单击它，隐藏的东西又显示出来。

《超级画板》帮你教数学之12《超级画板》与探究性教学案例（1）彭翕成华中师范大学教育信息技术工程研究中心，武汉 430079江春莲华中师范大学数学与统计学学院，武汉 430079《超级画板》为数学探究性活动提供了有力的工具平台[1-2]，用它作出一些特殊的点、线的轨迹已是一件非常容易之事。

本文将基于《超级画板》从椭圆的作图问题延伸拓展，并从数学的角度解释得到的二次曲线轨迹。

【例1】在人教版普通高中课程标准实验教科书《数学》选修2-1第39页例3是这样的：（如图1）设点A ，B 的坐标分别为(5,0)-，(5,0). 直线AM ，BM 相交于点M ，且它们的斜率之积为4-，求点M 的轨迹方程。

作出两直线及其交点（两直线的斜率可分别用变量t 和49t-），再作出t 的动画并对点M 进行跟踪。

我们不难求出其轨迹方程为221 (5)100259x y x +=≠±. 【椭圆作图的切线法】在众多的椭圆作法中，有个“切线法”。

该法主要步骤是：（1）作圆O 及其直径AB ，（2）分别过A ，B 作O 的切线l ，m ，（3）在O 上任取一点C ，过点C 作O 的切线分别交l ，m 于点G ，H ，连接AH ，BG 交于点M ，则当点C 在O 上运动时，点M 的轨迹为椭圆（图2）。

事实上，若以O 为原点，直径AB 为x 轴建立直角坐标系，则可设O 的方程为222x y r +=，则切线l ，m 的方程分别为x r =-和x r =，若设点C 坐标为(c o s , s i n r r θθ，则切线GH 的方程为cos sin x y r θθ+=，所以点G ，H 的坐标分别为(, cot )2r r θ-，(, tan )2r r θ，所以直线AH ，BG 的方程分别为1tan ()22y x r θ=+和1cot ()22y x r θ=--，两方程联立解得点M 坐标为1(cos , sin )2r r θθ，所以点M 的轨迹方程为2222114x y r r +=。

第九篇经典范例本篇将用更多的例子，展示《超级画板》的高级技巧所能做出的效果。

我们尽量从比较简单的问题开始。

对于每个例子的掌握程度，可以有三个层次。

第一个层次，是能用。

这是最容易的。

只要看看说明，动手做做，就能用了。

第二个层次，是会做。

这要多花点时间和精力，但也不难。

只要对照说明，一步一步地按文件在“对象工作区”中显示的对象性质和顺序来做，有些点的坐标和曲线的方程要复制粘贴一下，就会成功。

第三个层次，是明理。

这比较困难。

特别是有些点的坐标，有些曲线的方程，有些被测量的表达式，这些数学式子是如何设计出来的，不很容易理解。

我们没有对这些数学表达式的由来作进一步的说明。

数学功底较深厚的读者，花些力量能够理解其中的道理。

对多数的读者，只要能用会做就可以了。

如果有读者确实对文件中的某些表达式的设计原理有很大的兴趣而又百思不解，不妨在网上提出来讨论（例如在，或等网站上）。

相信能够得到满意的解答。

一线段和圆弧的动态n等分点1．等分线段的程序和函数作出一条线段的等分点，例如3等分点或8等分点，这很容易。

最基本的做法，是用尺规作图。

《超级画板》可以实现尺规作图，当然能等分线段。

如果想快捷一些，可以使用作定比分点的文本作图命令。

在文本作图对话框的作点类的函数中可以找到这个函数：DivisionPoint(A, B, r );其中参数A、B是要等分的线段的两端的编号，r是分点所分的两端的长度的比。

例如，4个5等分点对应的比值顺次为1/4、2/3、3/2、、4/1。

这样，一行命令只能作1个分点。

如果要一次作出4个5等分点，可以用for循环语句：for (i=1;i<5;i=i+1) {DivisionPoint(A, B, i/(5-i) );}或while 循环语句：i=1;while (i<5) {DivisionPoint(A, B, i/(5-i) );i=i+1;}也可以写成函数便于使用：fd(A,B,n){for (i=1;i<n;i=i+1) {DivisionPoint(A, B, i/(n-i) );}}这些程序运行情形见文件“9-1等分线段.zjz”，如图9-1。

2.1 菜单简介在本章中，我们会给你一些使用本软件的提示、好的建议以及一些不成文的约定，当然每个人都自身的爱好，不过基本上还是都遵行Windows其选项。

3-1），第一行为标题栏，而第二行，即标），实际上这是我们新建了一个文件或打开已有的文件时的菜单，当关闭了所有的文档时，却又是另一番情形了（如图3-3）！其实还有另外一个菜单，那就是右键的快捷菜单，无论你选取任何对象（在作图区中），右键，都将出现同样的菜单，如图3-4，这个菜单中的命令主要原自于主菜单中的“编辑”、“作图”栏，目的只是加速用户的操作。

因此现在就无须多说，到时候你自然会明白。

图3-2 主菜单图3-3 别样的菜单 对象工作区属性工作区作图区当然要重点介绍的是我们的主菜单（图3-1），因为图3-2及图3-3的菜单被包含在图3-1的菜单中，那我们就一一道来吧：文件( F )：建立新的或打开已有的超级画板文件；可以保存，打印及用电子邮件发送当前的版面；可以关闭当前文件或退出立体几何系统。

编辑( E )：撤消或重复上次操作；改变图形、文字的特性；复制、粘贴及剪切等。

查看( V )：更换试图模式及工具栏、状态栏选项，如全屏显示、背景颜色、坐标系模式、OLE 对象，显示或隐藏工具栏等。

作图( D )：作出各种几何图形，这可是“精彩”之一。

插入( I )：插入各式的文字、图片、多媒体、表格等等，做出丰富多彩的课件的任务也许就是它。

变换( T )：平移、旋转、放射变换等等几何意义的变换都在这。

更“精彩”的功能就得靠这些命令。

课件( C )：制作或播放的课件；功能强大的按钮将在这里制作。

解题( S )：附加已知条件，生成题目，或自动解题；在这里“智能的风范”可体现得淋漓尽致。

测量( M )：测量或计算各种对象的数值，如表达式，各种角，两点距离等。

对象( O )：选定对象，查看对象的属性及改变对象性质。

窗口( W )：新建及管理窗口。

帮助( H )：《Z+Z 教育软件智能平台-超级画板》的帮助信息及作者、版权信息。

第二篇平面几何平面几何作为一门系统的学科, 已有两千多年的历史, 其魅力经久不衰。

计算机科技的发展, 推出了动态几何作图软件, 使这门古老的科学焕发青春, 变得更加丰富多彩, 更有吸引力和挑战性。

《超级画板》是由动态几何作图软件发展而来, 平面几何动态作图当然是它的基本功能。

基本功能熟练了, 就有了登堂入室的基础。

这一篇里, 我们将通过一些实例, 学习动态几何作图, 图形的旋转、平移和缩放的操作机制, 图形的测量以及制作控制图形运动和变化的按钮方法。

看了这些例子你会看到, 优秀的作品源于对知识的创造性地运用。

再好的软件也不过是你手中的工具, 不过是圆规直尺铅笔这些古老的工具的发展。

创意永远是最重要的。

首先我们来看看动态几何作图与平时我们在纸上、黑板上作图有什么区别。

（一）共点的三个圆大家一起来试一试, 画出过同一点的三个圆。

合上书本, 自己动手。

完成后, 看看你的制作结果是不是与图中的图形相似？有三个圆, 六个点。

请大家随意拉动几个点试试, 看这三个圆是否还能“过同一点”？拖动结果可能如图2-1所示：图2-1为什么图形会“散架”, 可能作图过程是这样的（图5-2列出了最典型的初学者“画共点的三个圆”的步骤, 受到了传统作图方式如黑板上的绘图或一般绘图软件的影响）。

图2-2在拖动过程中, 动态几何作图能够保持所有给定的几何关系, 因为它就是根据几何关系来设计的！那么, 你思考一下, 上述方法在画圆时, 到底给定了什么样的几何关系？我们知道, 圆是由两个点来决定的, 双击鼠标按下去的点即为圆心, 松开鼠标的点即为圆上的一点。

改变这两个点中的任意一点都可以改变圆。

而在我们刚才的操作中, 我们所给的几何关系是：每个圆都是由两个完全自由的点来决定的（请大家观察一下, 图中共三个圆, 六个自由点）。

根据这样的几何关系, 每个圆都可以随意地改变。

这就表明：在超级画板中, 不能再象在黑板上那样, 随手画出图来, 而每时每刻都得考虑几何关系。

超級畫板(Super Sketchpad)簡易操作手冊一、檔案功能表（一）開啟新檔：建立一個新的超級畫板檔案。

（二）打開：打開超級畫板（系列）軟體製作的課件。

（三）關閉：關閉當前活動的檔案。

如果檔案修改而沒有被保存的情況下，則會彈出保存檔案對話方塊。

（四）存儲檔案：保存當前活動的檔案。

（五）另存新檔：將當前活動的檔案保存為另外一個檔案。

（六）打包：將課件和運行課件的程式一起打包。

這項功能，可使在沒有安裝超級畫板軟體的電腦上運行和使用超級畫板製作的課件。

（七）開啟新頁面：在當前活動的頁面之後，增加一個新的頁面。

（八）編輯文檔的頁面：修改頁面的名稱和調整不同頁面之間的順序。

（九）刪除當前活動頁面：將當前活動的頁面刪除。

（十）打開頁面：打開一個頁面，並增加到當前活動的頁面之後。

（十一）存儲檔案當前活動頁面：將當前活動的頁面，保存為一個獨立的頁面檔案。

頁面檔案的尾碼名為：“.pag”。

（十二）啟動上一頁：將當前活動頁面的上一頁啟動為活動檔案。

（十三）啟動下一頁：將當前活動頁面的下一頁啟動為活動檔案。

（十四）存儲檔案挑選的物件為圖元檔：將選擇的圖形保存為獨立的圖元檔。

（十五）列印：列印當前活動的頁面。

（十六）列印預覽：瀏覽列印的效果。

（十七）列印設置：選擇“橫向”或“縱向”列印以及列印紙的尺度等屬性。

（十八）傳送：將您的當前檔案，通過電子郵件傳送給他人。

（十九）結束：結束超級畫板程式。

二、編輯功能表（一）撤銷和重新執行：執行“撤銷”命令，可以撤銷最近一步的操作；如果又不想撤銷該操作，可執行“重新執行”命令，恢復上一步的操作。

（二）複製和貼上：執行“複製”命令，將選擇的物件複製到剪貼板上；執行“貼上”命令，則將剪貼板上的內容（作為圖片）粘貼到作圖區中。

（三）刪除：將選擇的物件，以及依賴該物件而存在的物件刪除。

（四）全部刪除：將作圖區中的所有物件全部刪除（坐標系除外）。

（五）全部點的名字：控制所有點的名字的顯示或隱藏。

《超级画板》帮你教圆锥曲线(1)彭翕成(华中师范大学教育信息技术工程研究中心,湖北　430079)中图分类号:G642.0 文献标识码:A 文章编号:0488-7395(2007)09-0009-04 笔者曾在大学和中学组织过几何画板的培训,感受最深的就是几何画板处理解析几何问题太麻烦,老师们也反应难以掌握.举例来说,平时作两圆的公切线,椭圆切线等,都只要拿尺往圆上一靠,马上就可以用笔画出来了.但在几何画板中,作两圆的公切线要分内公切线和外公切线两种情况,作椭圆的切线要分点在椭圆上和椭圆外两种情况,而且这些作法相当复杂,除了需要较深的数学功底之外,还要熟练掌握几何画板的各种技巧.但如果使用超级画板,就只要运行简单的函数命令.下面我们就来介绍具体作法.1　探索两圆的位置关系和公切线条数两圆的位置关系有5种情况,通常是通过测量圆心距,计算半径之和与之差来判断.那么我们该如何动态地演示两圆位置的变化过程,以及不同位置关系时,公切线的条数呢?这两个问题可以用一个课件来解决.作法如下:1)作以A为圆心过点B的圆;连线段AB,在线段AB上取点C;2)选定点B,C,点击【变换】|【选定平移向量】,选中点C,点击【变换】|【平移几何对象】,平移复制得点D;3)在平面上任作点E,自E向AB的延长线上引垂足F;4)仿照(2),选定向量DF,将点C平移复制得点G;5)作以G为心过点F的圆;在圆A内, BD的延长线上作点H;在圆A外,AB的延长线上作点I(图1);6)右键单击点C,在右键菜单中单击“属性”打开点C的属性对话框,删去x-拖动参数u000;对点H,I作同样的操作.这样,这几个点就拖不动了(要调整位置时,可修改属性恢复拖动参数);7)打开【对象】|【文本作图】,弹出【文本命令作图对话框】,输入函数命令“Common2 Tangent(7,15,0,);Common Tangent(7,15, 1,);Common Tangent(7,15,2,);Common2 Tangent(7,15,3,);”,点击运行;其中7和15是两个圆的编号;8)依次选择点E和H,在右键菜单中单击动画,作出点E运动到H的动画按钮,将按钮文本改为“无公切线”;同法作出E到D, E到C,E到B和E到I的动画按钮并将文本改为“1条公切线”,“2条公切线”,等;9)单击某个按钮,右边那个圆就会运动,使得公切线条数变成我们所需要的.譬如我们点击按钮“3条公切线”,即可得到图2.这个例子的制作,主要体现用平移安排点的位置的方法,以及用自由点的运动带动收稿日期:2007-02-10垂足和用点带动圆的方法.附带介绍了在属性对话框里去掉拖动参数使对象上的点位置相对固定的小窍门.图　1图　22　探索圆的一般方程中参数对圆的影响圆的一般方程x 2+y 2+Dx +Ey +F =0中有三个参数.我们通过超级画板探索,就能清楚地看出这三个参数对圆的影响.1)在文本作图框输入“ConicOf Equation (x^2+y^2+D 3x +E 3y +F =0,);”,点击运行;此命令是为了作出圆,但此时屏幕上并没出现圆,这与D ,E ,F 当前取值有关.2)在文本作图框输入“Variable (D ,);Variable (E ,);Variable (F ,);”,点击运行;此命令是作出控制圆的3把变量尺;3)打开【测量】|【测量表达式】,弹出【文本命令作图】对话框,计算D 2+E 2-4F ,得到的结果是-1115;4)拖动3把变量尺,改变D ,E ,F 三个参数的值,使得D 2+E 2-4F 的值大于0;在文本作图框输入“ConicCentre (5,);”,点击运行;5)选择点A ,在右键菜单中选择跟踪;选择圆,在右键菜单中选择跟踪;6)在文本作图框输入“MeasureCentre 2OfCircle (5);MeasureNormalOfCircle (5);Measure G eneralOfCircle (5);”,点击运行;此时屏幕如图3所示;7)拖动变量尺D ,可得图4;拖动变量尺E ,可得图5;拖动变量尺F ,可得图6;图　3图　43　探索圆锥曲线的一般方程与圆的一般方程相比,圆锥曲线的一般方程要多几个参数,因此变化也复杂得多,但通过超级画板,也能简单、直观地得到很多我们需要的信息,而且探索方法和圆基本类似,图　5图　6只不过需要多加几个参数.下面就介绍设置控制参数的另一种方法,以及探索过程中需要注意的事项.1)在文本作图框输入“ConicOf Equation (A 3x^2+B 3x 3y +C 3y^2+D 3x +E 3y +F ,);”,点击运行;此时屏幕上没出现任何图象,这说明6个参数的当前取值使得二元二次方程不能表示任何图形.2)在文本作图框输入“Variable (A ,);Variable (B ,);Variable (C ,);Variable (D ,);Variable (E ,);Variable (F ,);”,点击运行;此命令是为了作出控制圆锥曲线的6把变量尺;拖动变量尺,使得屏幕上有图象出现;3)在文本作图框输入“Mea 2sureNormalOfConic (5);”,点击运行;4)拖动变量尺A ,C 使之同号,此时屏幕如图7所示,图象为椭圆;图　75)拖动变量尺A ,C 使之异号,此时屏幕如图8所示,图象为双曲线;图　86)在右键菜单中单击参数A 的动画,参数范围从1到B^2Π(43C ),类型改为一次运动;点击动画按钮,此时屏幕如图9所示,图象为抛物线;图　9如果我们计算出B 2-4AC 的值,可以看出此值的正或负分别对应于双曲线或椭圆;如果我们作出参数B 的动画,使之变为0,曲线的对称轴会变得平行或垂直于x 轴.我们还可以作出更多的尝试.4　圆锥曲线随离心率而变化圆锥曲线有一个统一的定义,就是到一个定点的距离和到一条定直线的距离的比值为定值的点的轨迹.定点叫做该轨迹曲线的焦点,定直线叫做该轨迹曲线的准线,定值叫做该轨迹曲线的离心率.离心率通常用e 表示,e <1时为椭圆,e =1时为抛物线,e >1时为双曲线.这条随离心率变化的曲线是如何画出来的呢?最简单的方法是使用极坐标下圆锥曲线的统一方程:ρ=ep1-e cosθ.需要注意的是,希腊字母ρ和θ分别用rho 和thet 来表示,而离心率不能用e 来表示,因为在超级画板中把e 保留用于自然对数的底,即e =2.71828....不过,虽然内部用b 表示离心率,这并不妨碍我们在显示出来的文本中仍然用e 表示离心率.1)在文本作图框输入“Function (rho =a 3p Π(1-a 3cos (thet ),0,23pi ,500);”,点击运行生成双曲线;2)在文本作图框输入“Variable (a ,);Variable (p ,);”,点击运行作出控制圆锥曲线的2把变量尺;3)拖动变量尺a ,p ,观察两个参数对圆锥曲线的影响,尤其是a 在大于1和小于1时两者之间的不同;4)作出参数a 的动画,参数范围从1到1,类型改为一次运动;点击动画按钮,此时屏幕如图10所示,图象为抛物线;图　105　过五点的圆锥曲线与其切线给了不共线的3个点,可以确定一个圆.类似地,给了5个点,如果其中任意3点都不共线,就可以确定一条圆锥曲线.超级画板有一条文本图命令可以让我们体验这个有趣的事实.1)用智能画笔作5个点,其中任意3点都不共线;2)在文本作图框输入“ConicOf FivePoint (5,6,7,8,9,);MeasureNormalOfConic (10);”,点击运行;此命令作出了过5点的圆锥曲线,以及测量出该圆锥曲线的标准方程;3)用智能画笔作出圆锥曲线上的一点F ,并在文本作图框输入“Tangent (12,10,0,);”,点击运行作出过点F 的切线;其中12是点F 的编号,10是圆锥曲线的编号;4)用智能画笔作出圆锥曲线外的一点G ,并在文本作图框输入“Tangent (14,10,0,);Tangent (14,10,1,);”,点击运行作出过点G 的两条切线(图11);我们可以改变5个点的位置,得到更多的变化;图　11(注:科学出版社2006年出版的《超级画板自由行》(张景中著),该书详细讲述了《超级画板》免费版本的用法和技巧,附赠的光盘中有即插即用并且可以复制的《超级画板》的免费版本和作者制作的200多个范例.书的定价45.00元(邮购另加5.00元邮挂费).需要者可直接汇款到《数学通讯》编辑部购买.)。