哈尔滨工业大学2017硕士研究生单独考试

哈工大单独考试、强军方案考生XX考研复试分数线单独考试、强军方案类考生学校复试根本线有关复试根本线的说明：(1)“少数民族高层次骨干人才方案”、“退役大学生士兵方案”类别考生的复试根本线在全国分数根本要求公布后确定。

(2)工作单位在国务院公布的民族区域自治地方，且定向就业单位为原单位的少数民族在职人员考生，可按规定享受少数民族照顾政策。

(3)参加“大学生志愿效劳西部方案”、“三支一扶方案”、“农村义务教育阶段学校老师特设岗位方案”、“赴外汉语老师志愿者”、“高校学生应征入伍服义务兵役退役”、“选聘高校毕业生到村任职”等工程效劳期满并考核合格的考生，可根据教育部统一规定享受一定加分政策。

(4)符合以上照顾和加分政策的考生，需在复试公布前向校研招办提供相关材料。

学校复试根本线是我校的最低复试分数要求，各学科应在学校复试根本线的根底上，根据生源的实际情况确定本学科的复试资格线。

研究生复试自我介绍分为中文和英文自我介绍两种，中文介绍各个学校的时间不等，但根本在3分钟左右，英文介绍比较简单，1分钟左右就可以。

自我介绍需要依次介绍自己的根本信息，学术学业情况，生活和学习的经历，参加过哪些社会活动，获得过何种表彰，发表过哪些论文，为什么想考研，读研的目的，兴趣爱好等，最后记得加上感谢语。

自我介绍有几个不可或缺的要素：名字，年纪，毕业学校，专业，家乡，特长爱好。

从中要表达考生的科研潜力，要重点突出围绕所报考的专业从“做过什么”，“做成过什么”，“将来想怎么做”几方面展开，突出自己的特长和专长，表达学生的思维逻辑。

1.说明身份：只要介绍好自己的姓名，年龄，原来的院校、专业即可。

注意发音要准，吐字要明晰。

2.概括自己的理论经历和学术学业情况：此部分老师看中的是考生从这些理论经历中获得的收获，对以后学业的帮助，并不仅仅是经历本身。

概括自己的特点此部分用简短的话概括自己的特点，如，性格，爱好等，不要太夸大，也不要太罗嗦，并且表达这些特点对自己身心的提升才能。

14 083203 农产品加工及贮藏工程 100197037095167 孙瑞雪
15 0832Z2
营养与食品安全 100197042086636 谢银侠
16 0832Z1
食品生物技术
100197023213505 陈仁驰
17 083201
食品科学
100197034594103 冯旭东
18 0832Z1
贺秀丽 刘畅 穆硕
班龄尹 冯一洪 燕子馨
徐佳 刘海燕 周晓璐 白家齐
昌萍 赵晓丹 刘宏兰 夏弄玉
魏巍 邹文文 宋艳超 贾倩倩
黄粲 马宛慧
石俊 卢浩成
导师全额资助 战吉宬
导师全额资助 葛克山
导师全额资助 葛克山
导师全额资助 侯彩云
导师全额资助 马长伟
导师全额资助 何计国
导师全额资助 贺晓云
导师全额资助 侯彩云
15 085231
食品工程
100197061157738 王昱儒 导师全额资助
16 085231
食品工程
100197013152546 杨志轩 导师全额资助
17 085231
食品工程
100197037024452 吴梦娇 导师全额资助
18 085231
食品工程
100197037064739 马雪颖 导师全额资助
23 083201
食品科学
100197032113647 齐梦瑶
24 0832Z2
营养与食品安全
100197041336443 李菲
25 0832Z1
食品生物技术
100197032113643 尹剑
26 0832Z1
食品生物技术
100197041336453 王英杰

统考
007
47
周粮
230196728
统考
007
48 张明浩 210399901
统考
007
49 罗蕙佳代 230197267
统考
007
50 张圆圆 140297462
统考
007
51
王涛
420494651
统考
007
52
张帅
230196714
统考
007
53
54
汪凯
421998636
统考
007
75
王维
431594338
统考
007
76 许长寿 230198418
统考
007
77 张希晨 230196177
统考
007
78 谢茂松 345999932
统考
007
79 张国宇 230199946
统考
007
80 潘羿吾 371099427
统考
007
81 柏棣星 230198610
统考
007
82 李永强 371098424
统考
007
39
谭鑫
230198852
统考
007
40 赵大帅 210797516
统考
007
41 李春鹤 230197868
统考
007
42 王美玲 230198657
统考
007
43
李莉
231199226
统考
007
44
马悦
230198044
统考
007
45 王少东 231195197
统考
007

布丁考研网，在读学长提供高参考价值的复习资料 2017年考试内容范围说明考试科目代码：826 考试科目名称：高等代数考试内容范围：一、数域上的一元多项式1. 要求考生理解数域及数域上的一元多项式的基本概念,包括多项式的整除、最大公因 子、互素、多项式的标准分解、重根和重因式及多项式的可约性.2. 要求考生熟悉复数域、实数域和有理数域上多项式的分解及艾森斯坦因定理.二、行列式1. 要求考生理解行列式的基本性质及基本计算,包括n阶行列式的几种计算方法.2. 要求考生理解行列式展开定理、克兰姆法则及它们在理论推理中的应用.三、线性方程组1. 要求考生深刻理解线性方程组的可解性判别定理及解的结构.2. 要求考生深刻理解齐次线性方程组有非零解的判别定理及其基础解系.R中向量组的线性相关性及其判别方法.3. 要求考生深刻理解n四、矩阵1. 要求考生能熟练地进行矩阵的各种常规计算,包括求逆阵.2. 要求考生深刻理解矩阵的秩和等价及等价的几个相关命题.3. 要求考生能熟练地进行有关矩阵的理论推导.五、二次型1. 要求考生理解实对称阵与二次型的对应,理解各类标准形,能判别正定性.2. 要求考生深刻理解矩阵的合同与二次型的惯性定理.六、线性空间1. 要求考生深刻理解线性空间的定义、基及维数、基变换及坐标变换.2. 要求考生深刻理解子空间、子空间的直和、线性空间的同构.七、线性变换1. 要求考生深刻理解线性变换的定义及运算、线性变换的矩阵、线性变换与矩阵的对应.2. 要求考生深刻理解特征多项式及特征值、特征向量与矩阵的对角化及对角化的条件.3. 要求考生深刻理解一个线性变换的值域的维数与核的维数的关系.4. 要求考生深刻理解一个线性变换的不变子空间.5. 要求考生理解矩阵的相似及若当标准形定理.八、欧氏空间1. 要求考生深刻理解欧氏空间的定义、标准基、正交矩阵及正交变换.2. 要求考生深刻理解实对称矩阵的标准形.考试总分：150分 考试时间：3小时 考试方式：笔试考试题型：填空题证明题计算题。

哈尔滨工业大学机电工程学院接收2017级推免生（含直博生）预选拔工作细则哈尔滨工业大学机电工程学院竭诚欢迎全国各高校的优秀应届本科毕业生通过推荐免试方式来我院攻读硕士（博士）学位研究生。

根据学校研院发【2016】48号文件《哈尔滨工业大学接收2017年推免生（含直博生）工作办法》和【2016】46号文件《2017年推免生（含直博生）奖助学金设置和评定办法》等文件和通知要求，结合机电工程学院的具体情况，制定机电工程学院接收推免生预选拔细则如下。

一、推免生本科毕业专业要求超出以上列举范围的，由推免工作组领导审核。

二、推免生条件（1）高等院校获得推荐免试资格的优秀应届本科毕业生（占用申请者所在学校推荐指标）。

（2）学术研究兴趣浓厚，有较强的分析问题、解决问题的能力和较强的创新意识。

（3）大学外语四级考试成绩达到425分及以上。

（4）身心健康，通过国家规定的体育锻炼标准。

（5）诚实守信，学风端正，无任何考试作弊和剽窃他人学术成果记录。

（6）遵纪守法，品行表现优良，无任何违法违纪受处分记录。

三、报名与预选拔1. 预报名系统报名学生预选拔。

1）资格审查。

由学院推免工作小组根据学生报名情况、学生专业排名、所在学校和学科的综合实力等因素，确定参加具有资格参加预选拔考核的学生名单。

2）通过资格审查的学生，将所需材料电子版或扫描件打包压缩后（文件名格式：学校名+姓名，文件中包括本人手机、邮箱、QQ号等联系方式）发送至以下信箱：。

3）哈尔滨市高校学生到我校进行现场预选拔考核，其他省市学生部分参加远程视频预选拔考核，部分参加9月份举行的我院赴各地招生宣传组的现场预选拔考核。

具体时间另行通知。

4）视频考核方式原则上截止到2015年8月31日，9月只进行现场考核。

2. 现场招生宣传及预选拔。

2016年9月1号-20号，学院将赴东北、华北、华东、华南、西南、西北各地进行推免生的招生宣传，并现场进行预选拔，具体时间和地点在机电工程学院网站公布。

一报考条件：根据文件规定，哈尔滨工业大学研究生，本次选拔对象，应符合以下条件：1.在校期间政治思想表现优秀，遵守校纪校规，文明礼貌，未受到任何处分。

2.学历要求：具有本科专业对口，无重考，无重修记录，身心健康。

3.以综合考试成绩为录取依据，首先按各专业实考人数划定分数资格线，再按成绩从高到低择优录取。

4.综合考试成绩将在录取前公示7天，录取过程中，如果有排名在录取名额内的考生自愿放弃，在名额外的学生按顺序递补。

5.我校采取笔试、口试或两者相兼的方式进行，以进一步考察学生的专业基础、综合分析能力、解决实际问题的能力。

具体比例由学校根据学科专业特点安排。

二报考事项：历年真题QQ在线咨询：363.916.816张老师，各相关专业成立考试小组，确定工作中的相关原则政策和办法研究重大事项；负责本学院考试工作的组织宣传事项和实施工作；完成报考成绩统计及综合排名汇总材料并上报填表。

1.各学院要先完成报考专业的成绩综合排名，根据名单确定考生的具体范围。

2.符合上述条件的参加综合考试，按照报考专业并提交书面申请材料审核。

3.工作领导小组审核汇总名单后，将公示7天，期满后不再进行提示。

4.各相关专业按照考试科目的顺序依次进行。

5.考试成绩以书面通知形式发到学生本人。

三考试流程：1.参加初试并获得复试资格的考生，应在复试前填写相关表格，按规定时间提供自身研究潜能的材料，攻读大学阶段的研究计划、科研成果等。

2.报考考生的资格审查由领导小组进行审查，对考生料进行审阅符合报考条件的统计填表。

3.我校采取笔试、口试或两者相兼的方式进行差额复试，以进一步安排加强进行考察学生的专业基础、综合分析能力、解决实际问题的能力和各种应用能力等。

具体比例由学校根据本学科、专业特点及生源状况安排。

四复习方略：1注重课本很多考生会安排各种各样的资料，其实关键要能保证你进行的系统性。

每个要点段落安排以真题为主，时间布局以精读的方式对重点章节相关要点，对课本有一个纲领性的认识。

直录
王萌
统考
393
262.9
655.9
机械电子工程
工学
(全日制)本部培养：工业工程
直录
杜洁瑶
统考
376
252.75
628.75
机械电子工程
工学
(全日制)本部培养：工业工程
直录
苏欣
统考
376
230.13
606.13
机械电子工程
工学
(全日制)本部培养：工业工程
直录齐宝力统考 Nhomakorabea382215.27
597.27
机械电子工程
工学
(全日制)本部培养：工业工程
直录
2017年哈尔滨工业大学硕士研究生拟录取名单
院系： 姓名
卿事成
006机电工程学院 考试方式
统考
初试成绩
404
复试成绩
263.25
总成绩
667.25
录取学科
机械电子工程
学位类别
奖学金 等级
录取校区
(全日制)本部培养：工业工程
备注
直录
工学
李狮伟
统考
414
251.75
665.75
机械电子工程
工学
(全日制)本部培养：工业工程

2017年哈尔滨工业大学硕士研究生招生简章2017年哈工大硕士统一招生考试报考须知一、报考条件1．中华人民共和国公民。

拥护中国共产党的领导，品德良好，遵纪守法。

2．报名参加全国硕士研究生招生考试的人员学历必须符合下列条件之一： （1）国家承认学历的应届本科毕业生（2017年9月1日前须取得国家承认的本科毕业证书。

含普通高校、成人高校、普通高校举办的成人高等学历教育应届本科毕业生，及自学考试和网络教育届时可毕业本科生）；（2）具有国家承认的大学本科毕业学历的人员；（3）可按本科毕业生同等学力身份报考的人员包括：①国家承认学历的本科结业生；②获得国家承认的高职高专毕业学历2年（从毕业后到2017年9月1日）以上，并取得与报考学科相关的高等教育自学考试至少10门课程成绩合格的人员。

以上按同等学力身份报考的人员在报名前必须在核心或核心以上刊物以第一作者发表过至少一篇与报考学科相关的学术论文。

3．已获硕士或博士学位的人员。

4．身体健康状况符合国家和我校规定的体检要求。

5．报考工商管理硕士（MBA）、公共管理硕士（MPA）的考生还须符合以下条件：大学本科毕业后有3年或3年以上工作经验的人员（从毕业到2017年9月1日，下同）；大专毕业后有5年或5年以上工作经验的人员；已获硕士学位或博士学位后有2年或2年以上工作经验的人员。

我校工商管理硕士（MBA）、公共管理硕士（MPA）只招收报考定向就业的研究生。

6．在校研究生报考须在报名前征得所在培养单位同意。

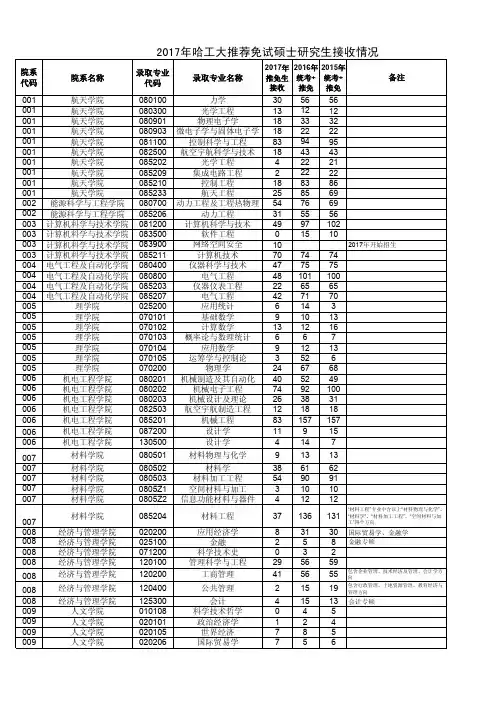
二、招生学科与招生计划具体招生学科详见各院（系）招生学科目录。

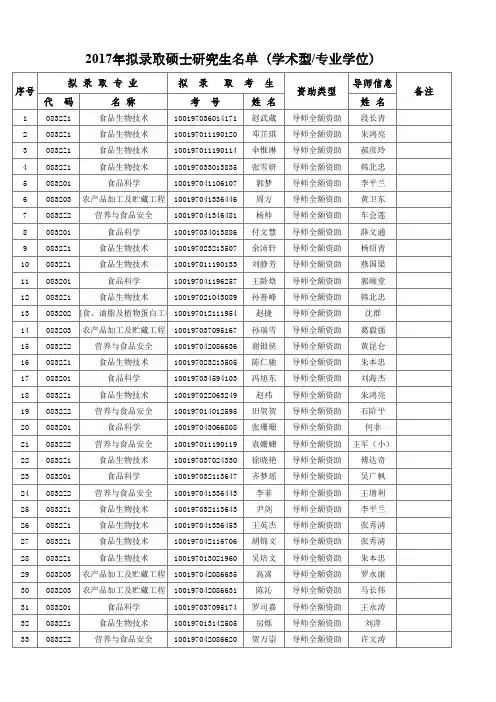
招生学科目录中有括号标记为“专业学位”或“工程硕士”的属于全日制专业学位硕士研究生，未做标记的属于学术型硕士研究生。

目录中所列各院（系）招生计划为参考计划，包含接收校内外推免生的计划，实际招生计划将根据生源情况予以适当减少或增加。

学校预留部分招生计划用于生源质量较好的院（系）和统一接收部分优秀统考调剂生源。

***电工程学院2017年硕士研究生复试工作方案根据《2017年全国硕士学位研究生招生工作管理规定》和研院发【2017】11号文件《哈尔滨工业大学2017年硕士研究生入学考试复试及录取工作办法》，结合2017年机电工程学院的具体实际情况，经院长办公会讨论通过，制定机电工程学院2017年硕士研究生复试工作方案及录取办法如下。

一、学院成立复试工作领导小组指导和协调全院的复试和录取工作，名单如下：组长：刘宏副组长：王振龙组员：杨庆俊、王武义、刘荣强、唐德威、韩振宇、姜力、代勇、叶正茂、吕德生、李孟钰。

二、成立复试督察小组负责对复试工作进行监督、检查，并受理考生的举报和投诉工作，名单如下：组长：赵航组员：李骁宇、李超、王芳督察电话：********，********三、学院招生计划考虑历年各学科的招生情况、导师人均指导学生数量以及学科发展需要，各学科招生计划如下：南方科技大学与哈尔滨工业大学联合培养学生招生共12名，其中包括机械制造及其自动化专业2名，机械电子工程专业2名，机械设计及理论专业2名，机械工程领域6名。

四、推免生的复试2016年秋季已录取为推免生的同学不需要参加此次复试。

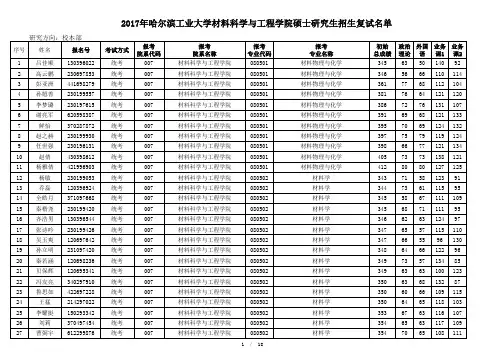
五、复试分数线、参加复试的人员名单及复试考生百分比复试线：机械工程一级学科复试分数线：总分350，政治外语50，业务课85；航空宇航制造工程复试分数线：总分340，政治外语50，业务课85；设计学（0872）：总分350，政治外语50，业务课85。

设计学（1305）：总分350，政治外语55，业务课85。

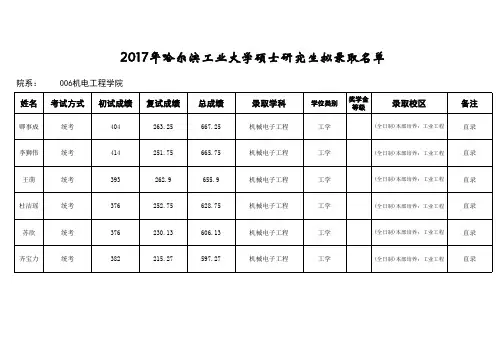
进入复试的考生名单见附件1。

进入复试的考生人数为269人，从中录取221人，参加复试考生人数为录取人数的121.7%。

六、复试报到时间和地点●报到时间：2017年3月10日（上午8:00--11:30 下午13:30--15:30），3月10日下午16:00召开考前相关事宜通报会，具体地点报到时另行通知。

●报到地点：机械楼二楼2011办公室。

3
5
3
010
外国语学院
050201
英语语言文学
1
6
5
010
外国语学院
050202
俄语语言文学
4
8
4
010
外国语学院
050211 外国语言学及应用语言学 2
7
9
010
外国语学院
055100
翻译
13 17 22
011
土木工程学院
080100
力学
0
9
10
含岩土工程、结构工程、防灾减
011
土木工程学院
081400
2017年哈工大推荐免试硕士研究生接收情况
院系 代码
001 001 001 001 001 001 001 001 001 001 002 002 003 003 003 003 004 004 004 004 005 005 005 005 005 005 005 006 006 006 006 006 006 006
深圳研究生院
080903 微电子学与固体电子学 8 14 14
201
深圳研究生院
081000
信息与通信工程
11 48 48
201
深圳研究生院
081100
控制科学与工程
27 39 38
201
深圳研究生院
081200 计算机科学与技术
38 79 79
201
深圳研究生院
081300
建筑学
3 10 10
201
12 18 18
机电工程学院
085201
机械工程
83 157 157
机电工程学院

哈尔滨工程大学2017年推荐免试硕士研究生拟录取人员名单
院系 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院 船舶工程学院
理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院 理学院
文 姜雨薇 李思凡 李霞 李莹 李韫畅 刘洪杉 南金伶 任梓惠 孙晶 孙禹琪 陶冶 张雪 赵舜尧 赵星雯 赵卓安 唐月 赵鹏飞 徐梦书 马赫 徐庆 杨格 段瑞 马占宇 田配轩 王东辉 王月 夏启
余吉波 张毅博 齐芳 王海蓉 王语琦 陈琦 董伟 郭家丰 姜超 靳玉冠 李鑫 刘畅 刘洁 刘圣搏 吕联鑫 吕鑫狄 孙大彬 王金成 王鹏 王新雨 魏征 杨文 姚正大 袁东东 翟佳旺 战春源 张硕 马夺 王靖阳 穆香含 佟浩 王子柔 唐婷姿
080300 080300 030100 030100 030100 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 082700 085226 085226 040303 040303 040303 030500
理学院 理学院 人文社会科学学院 人文社会科学学院 人文社会科学学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 核科学与技术学院 体育部 体育部 体育部 马克思主义学院

9大高校自主招生考试真题汇总(2017年)二、清华大学清华大学2017年自主招生测试主要分为笔试和面试，笔试依然采用机考的模式来进行据悉，2017年清华笔试在全国44个城市设有61考点，相比去年增加25个考点其中，每个城市还设有多个考点。

1、笔试题型理科：数学30题，物理20题，化学18题，一共68题，180分钟合在一起考的。

题。

2、笔试真题文科综合（文史）类笔试试题：考题有明清时的自然经济解、抗日战争、诗词等内容，不是考知识点记忆，主要考查阅读面、逻辑思维深度等，数学与逻辑难度较大。

今年的语文试题对语文基础知识与运用能力提出了更高要求，材料多出自社会热点或经典著作，注重对知识联系实际、学以致用能力的考查注重考查对经典或常识的精准理解，注重对独立思考与批判思维的考查化学试题成为新考查内容今年化学成为新考查内容。

刘震表示，新增化学试题注重对学科基础内容的考查综合多模块内容、加强化学学科的应用性、创新试题的设问模式，充分体现化学学科的学术价值，考查了考生的基础知识、综合能力、科学素养和创新精神，关注环境问题，讨论产生酸雨的原因及危害、食品中的增塑剂与人体健康等社会焦点问题。

物理试题注重基本概念的准确理解和灵活运用。

通过采用单选和多选题随机编排的方式，来考查学生构建正确、合理的物理模型，综合运用物理知识分析、解决实际问题的能力，同时増加了能力考查的区分度。

除了定量的分析和计算外，试题还设置了部分内容来考查学生运用物理学基本原理来定性和半定量分析题的能力3、面试模式复试中，领军人才选拔及自强计划考生需参加综合面试，自主招生考生及部分领军人オ选拔考生需参加学科专业面试。

清华大学2017年自主招生考核的特色有1．综合面试新增材料阋读环节综合面试在清华自主选中已开展多年，今年这一考察方式有了新变化新增了材料阅读环节。

考生在进入考场接受半结构化面试之前，在候场教室里将会得到一份阅读材料，经过半小时备考后进入考场、接受提问。

本人今年已成功考上哈工大机电工程学院，当初借鉴了很多别人的经验，为了帮助下一届考工大的学弟学妹，现将个人经验介绍一下，仅供参考。

关于初试。

首先说初试，哈工大机电院校线就是院线，一直都是。

但要想留本部，考上比较火的专业初试成绩就必须要高一些才有优势。

初试中最重要的就是数学，要想打高分，数学必须要打出足够高的分。

这两年数学都比较难所以复习时要加大难度才可以应付考试，我本人数学不好在此仅介绍一下个人学习经验。

数学是要从最开始准备的，我看书及用书的情况如下，首先看高数课本(同济版)、线性代数(同济第五版)、概率论(浙大第三版)这是打基础阶段，有些人不看教材直接看全书，我认为书是基础，有助于理解复习全书。

其次是复习全书(李永乐、李正元的)，要争取做到全书上每一个例题都要懂，看全书时要先把答案盖上自己做，之后再看答案，对照答案看自己想到了哪歩，哪步卡住了，还有没有更简便的方法，一定要会总结。

第一遍看是要把不会做的标记出来，下一次看时重点看，可以把重要的知识点做笔记以便考前回顾节省时间。

全书现在有很多版本，我认为这一版不错，知识点涵盖的很全，题型也很全面，当然也可以使用其他版本的，只要搞透了，高分不是问题，全书内容很多最好在九月份前看两遍。

之后有精力的可以做一下660题，这本书都是选择填空题，能够查缺补漏，也能够提高一些答题技巧。

从十月份就应该开始做真题，第一遍作时要严格按照考试时间来，我是两天一套题第一天花三个小时作题，第二天再对照答案批改、打分，弄懂每道题，把第一边做错的标记出来，第二遍重点看。

真题应看至少两遍，第二遍可以分题型看。

之后差不多要考试了，可以做一些模拟题(合工大五套题，400题都不错，他们难度好像挺大)保持一下手感，不用作太多，这段时间一定要查缺补漏看自己那里不会，要把重要知识点再看一遍。

数学一定要学会总结!对于英语，单词要一直背诵，直到考试。

单词可应用零散时间背诵，如早上开始学习前，晚上学习结束之前的30~40分钟。

布丁考研网，在读学长提供高参考价值的复习资料 附件7：2017年考试内容范围说明考试科目代码：808 考试科目名称:理论力学考试内容范围:一、静力学1．要求考生掌握刚体和力的概念，掌握静力学基本公理，了解各种约束的性质，熟练掌握物体及物体系统的受力分析过程和受力图的绘制；2．要求考生掌握平面任意力系向作用面内一点简化的方法及结论，了解平面任意力系的平衡条件与平衡方程，熟练求解物体系统的平衡问题，能判定静定和静不定问题；3．要求考生掌握平面和空间力对点的矩的概念，掌握力对轴的矩的概念，掌握平面和空间力偶理论，熟练掌握空间任意力系向一点简化的方法，了解主矢与主矩的概念，了解空间任意力系的简化结果，能应用空间任意力系的平衡方程求解空间任意力系的平衡问题；4.要求考生掌握滑动摩擦、摩擦角的概念，了解自锁现象，了解滚动摩擦的概念，能求解考虑摩擦时物体的平衡问题。

二、运动学1．要求考生掌握计算点的速度和加速度的矢量法、直角坐标法和自然法；2．要求考生掌握刚体的平移、定轴转动和平面运动的基本概念，掌握角速度和角加速度的概念；3．要求考生了解相对运动、牵连运动和绝对运动的概念，掌握点的速度合成定理，熟练掌握牵连运动是平动时点的加速度合成定理，熟练掌握牵连运动是转动时点的加速度合成定理；4．要求考生掌握确定平面图形内各点速度的基点法和瞬心法，掌握用基点法求平面图形各点的加速度的方法，能熟练处理运动学综合问题。

三、动力学1．要求考生了解动力学的基本定律，能熟练处理质点动力学的两类基本问题；2．要求考生了解动量和冲量的概念，掌握质点系的动量定理和动量守恒定律，熟练掌握质心运动定理和质心运动守恒定律；3．要求考生了解动量矩的概念，掌握动量矩定理和动量矩守恒定律，掌握刚体绕定轴转动的微分方程，熟练掌握刚体平面运动微分方程；4．要求考生掌握力的功的概念和计算，掌握质点和质点系动能的计算，掌握势能的计算，熟练掌握动能定理和机械能守恒定律；5．要求考生掌握惯性力的概念，掌握质点系的达朗伯原理，熟练掌握刚体惯性力系的简化，会求解绕定轴转动刚体的轴承动反力。

住房城乡建设部办公厅关于委托哈尔滨工业大学定向招收和培养城市规划专业硕士学位研究生（单独考试）的通知文章属性•【制定机关】住房和城乡建设部•【公布日期】2017.09.05•【文号】建办人函〔2017〕624号•【施行日期】2017.09.05•【效力等级】部门规范性文件•【时效性】现行有效•【主题分类】城乡建设综合规定正文住房城乡建设部办公厅关于委托哈尔滨工业大学定向招收和培养城市规划专业硕士学位研究生（单独考试）的通知建办人函〔2017〕624号各省、自治区住房城乡建设厅，直辖市规划委（局），新疆生产建设兵团建设局，部机关各单位、直属各单位、有关部管社团：为贯彻落实中央城市工作会议精神，加强城市规划建设管理工作，进一步提高城乡规划系统行政管理人员业务素质，经研究，决定2018年继续委托哈尔滨工业大学定向招收和培养城市规划专业硕士学位研究生（单独考试）。

现将有关事项通知如下：一、招生对象招生对象为住房城乡建设系统行政管理人员及相关单位工作人员，所在单位组织人事部门同意，并符合哈尔滨工业大学面向住房城乡建设系统招收硕士研究生招生简章（附件1）报考条件要求。

招生人数30人。

二、入学及学习方式报考学科为城市规划专业硕士，考试时间为2017年12月，地点哈尔滨工业大学。

根据教育部有关规定，对符合报考条件的住房城乡建设系统考生，由哈尔滨工业大学采取“单独考试”方式进行考试及录取。

学习年限为2.5 年至4年。

课程学习在2年内完成，学校分4次集中授课，具体方式及地点由学校根据学员情况安排。

完成学业、成绩合格并通过论文答辩者，可获专业硕士毕业证书和学位证书。

学费每人共3.5万元。

三、报名推荐程序请各省、自治区、直辖市住房城乡建设行政主管部门将本通知转发给相关地区和单位，考生自愿报名，所在单位组织推荐，2017年9月25日前将《2018年哈尔滨工业大学单独考试硕士生报考申请推荐表》（附件2）发送至哈尔滨工业大学建筑学院指定邮箱。

2017年哈尔滨工程大学自主招生笔试时间6月12日为大家提供“2017年哈尔滨工程大学自主招生笔试时间6月12日”供广大考生参考，更多资讯请关注我们网站的更新!高考考试即将结束，研究高考报考的专家提示：在分数正式下发前，应预估分数，并根据自己对未来的规划，提前想好报考志愿。

同时，提前熟悉网上高考志愿填报系统，以免忙中出错。

很多高校招生部门负责人也提醒考生：从2015年开始，所有试点高校自主招生考核统一安排在高考结束后进行，考生不要忘记报名、打印准考证和按时考试。

估分黄金时间是考试当晚哈尔滨市一省重点高中教师吕静告诉记者，估分的黄金时间是考试结束后当晚，“比如不参加9日考试的考生，可以8日晚上找到高考试卷重新答卷，但要等到正确答案公布后进行估分，这比对照答案估分的准确性相对较高。

”我省高考报考专家贾波说，考试结束到报志愿中间的空当时间，考生和家长们应广泛收集各大高校的招生计划，预测自己的可行志愿。

同时，对于目标大学和目标专业的文理、语种、性别等限制条件要有充分了解。

熟悉模拟网报志愿流程我省教育部门相关负责人告诉记者，按照往年惯例，在考生正式网上填报志愿之前，省招生网站会开放志愿填报模拟系统，这是为让考生熟悉网报系统，掌握网报系统的操作程序和方法。

考生最好在模拟系统开放后就登录，进行高考志愿“预报”，练习好操作流程，为正式填报做准备。

自主招生多集中在20日前部分高校招生部门负责人提醒，今年各高校的自主招生时间多集中在20日之前。

哈尔滨工程大学将于15日进行自主招生测试，初审合格的考生须在8日0时至12日14时登录特殊类型招生报名平台进行测试确认并缴纳测试费200元，缴费成功考生可于12日18时后通过报名平台自行打印本人准考证。

哈工程自主招生测试分为学科笔试、学科面试和素质考核，考试时间集中在15日。