deflt-3d

DEFORM-3D基本操作入门QianRF前言有限元法是根据变分原理求解数学物理问题的一种数值计算方法。

由于采用类型广泛的边界条件，对工件的几何形状几乎没有什么限制和求解精度高而得到广泛的应用。

有限元法在40年代提出，通过不断完善，从起源于结构理论、发展到连续体力学场问题，从静力分析到动力问题、稳定问题和波动问题。

随着计算机技术的发展与应用，为解决工程技术问题，提供了极大的方便。

现有的计算方法（解析法、滑移线法、上限法、变形功法等）由于材料的本构关系，工具及工件的形状和摩擦条件等复杂性，难以获得精确的解析解。

所以一般采用假设、简化、近似、平面化等处理，结果与实际情况差距较大，因此应用不普及。

有限元数值模拟的目的与意义是为计算变形力、验算工模具强度和制订合理的工艺方案提供依据。

通过数值模拟可以获得金属变形的规律，速度场、应力和应变场的分布规律，以及载荷-行程曲线。

通过对模拟结果的可视化分析，可以在现有的模具设计上预测金属的流动规律，包括缺陷的产生（如角部充不满、折叠、回流和断裂等）。

利用得到的力边界条件对模具进行结构分析，从而改进模具设计，提高模具设计的合理性和模具的使用寿命，减少模具重新试制的次数。

通过模具虚拟设计，充分检验模具设计的合理性，减少新产品模具的开发研制时间，对用户需求做出快速响应，提高市场竞争能力。

一、刚（粘）塑性有限元法基本原理刚（粘）塑性有限元法忽略了金属变形中的弹性效应，依据材料发生塑性变形时应满足的塑性力学基本方程，以速度场为基本量，形成有限元列式。

这种方法虽然无法考虑弹性变形问题和残余应力问题，但可使计算程序大大简化。

在弹性变形较小甚至可以忽略时，采用这种方法可达到较高的计算效率。

刚塑性有限元法的理论基础是Markov变分原理。

根据对体积不变条件处理方法上的不同（如拉格朗日乘子法、罚函数法和体积可压缩法），又可得出不同的有限元列式其中罚函数法应用比较广泛。

根据Markov变分原理，采用罚函数法处理，并用八节点六面体单元离散化，则在满足边界条件、协调方程和体积不变条件的许可速度场中对应于真实速度场的总泛函为：∏≈∑π（ｍ）＝∏（１，２，…，ｍ）（１）对上式中的泛函求变分，得：∑＝０（２）采用摄动法将式（２）进行线性化：＝＋Δｕｎ（３）将式（３）代入式（２），并考虑外力、摩擦力在局部坐标系中对总体刚度矩阵和载荷列阵，通过迭代的方法，可以求解变形材料的速度场。

Deform-3D（version6.1）使用步骤Deform—3D是对金属体积成形进行模拟分析的优秀软件，最近几年的工业实践证明了其在数值模拟方面的准确性，为实际生产提供了有效的指导。

Deform—3D的高度模块化、友好的操作界面、强大的处理引擎使得它在同类模拟软件中处于领先地位。

以下将分为模拟准备、前处理、求解器、后处理四部分简要介绍Deform—3D的使用步骤。

一、模拟准备模拟准备阶段主要是为模拟时所用的上模、下模、坯料进行实体造型，装配，并生成数据文件。

实体造型可通过UG、Pro-e、Catia、Solidworks等三维作图软件进行设计，并按照成形要求进行装配，最后将装配体保存为STL格式的文件。

该阶段需要注意的是STL格式的文件名不能含有中文字符；另外对于对称坯料，为了节省求解过程的计算时间并在一定程度上提高模拟精度（增加了网格数量），可把装配体剖分为1/4，1/8或更多后再进行保存。

二、前处理前处理是整个数值模拟的重要阶段，整个模拟过程的工艺参数都需要在该阶段设置，各参数设置必须经过合理设置后才能保证模拟过程的高效性和模拟结果的准确性。

首先打开软件，新建（new problem）→选择前处理（Deform-3D preprocessor）→在存放位置（Problem location）选项卡下选择其他（other location）并浏览到想要存放deform 模拟文件的文件夹→下步的problem name可任意填写。

注意：所有路径不能含有中文字符。

simulation controls）→改变单位（units）为SI，接受弹出窗口默认值；选中模式（mode）选项卡下热传导（heat transfer）。

导入坯料、模具并设置参数：导入毛坯：1、general：通常采用刚塑性模型即毛坯定义为塑性（plastic），之后导入的模具定义为刚性（rigid）；温度（temperature）：根据成形要求设定坯料预热温度（温热成形时一定注意）；材料（material）：点击load选择毛坯材料，若材料库中没有对应的材料可选择牌号相近的。

Deform-3d热处理模拟操作热处理工艺在机械制造中占有十分重要的地位。

随着机械制造现代化和热处理质量管理现代化的发展，对热处理工艺提出了更高的要求。

热处理工艺过程由于受到加热方式、冷却方式、加热温度、冷却温度、加热时间、冷却时间等影响，金属内部的组织也会发生不同的变化，因此是个十分复杂的过程，同时工艺参数的差异，也会造成热处理加工对象硬度过高过低、硬度不均匀等现象。

Deform-3d 软件提供一种热处理模拟模块，可以帮助热处理工艺员，通过有限元数值模拟来获得正确的热处理参数，从而来指导热处理生产实际。

减少批量报废的质量事故发生。

热处理模拟，涉及到热应力变形、热扩散和相变等方面，因此计算很复杂，软件采用牛顿迭代法，即牛顿-拉夫逊法进行求解。

它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。

方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。

牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x) = 0的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根等。

但由于目前Deform-3d软件的材料库只带有45钢、15NiCr13和GCr15等三种材料模型，而且受到相变模型的局限，因此只能做淬火和渗碳淬火分析，更多分析需要进行二次开发。

本例以45钢热处理淬火工艺的模拟过程为例，通过应用Deform-3d 热处理模块，让读者基本了解热处理工艺过程有限元模拟的基本方法与步骤。

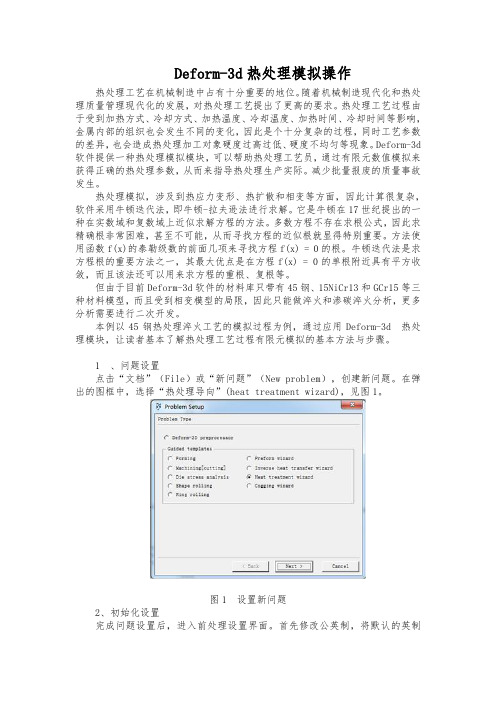
1 、问题设置点击“文档”（File）或“新问题”（New problem），创建新问题。

在弹出的图框中，选择“热处理导向”(heat treatment wizard)，见图1。

图1 设置新问题2、初始化设置完成问题设置后，进入前处理设置界面。

首先修改公英制，将默认的英制（English）修改成公制（SI），同时选中“形变”（Deformation）、“扩散”(Diffusion)和“相变”(Phase transformation)，见图2。

DEFORM-3D基本操作入门QianRF前言有限元法是根据变分原理求解数学物理问题的一种数值计算方法。

由于采用类型广泛的边界条件，对工件的几何形状几乎没有什么限制和求解精度高而得到广泛的应用。

有限元法在40年代提出，通过不断完善，从起源于结构理论、发展到连续体力学场问题，从静力分析到动力问题、稳定问题和波动问题。

随着计算机技术的发展与应用，为解决工程技术问题，提供了极大的方便。

现有的计算方法（解析法、滑移线法、上限法、变形功法等）由于材料的本构关系，工具及工件的形状和摩擦条件等复杂性，难以获得精确的解析解。

所以一般采用假设、简化、近似、平面化等处理，结果与实际情况差距较大，因此应用不普及。

有限元数值模拟的目的与意义是为计算变形力、验算工模具强度和制订合理的工艺方案提供依据。

通过数值模拟可以获得金属变形的规律，速度场、应力和应变场的分布规律，以及载荷-行程曲线。

通过对模拟结果的可视化分析，可以在现有的模具设计上预测金属的流动规律，包括缺陷的产生（如角部充不满、折叠、回流和断裂等）。

利用得到的力边界条件对模具进行结构分析，从而改进模具设计，提高模具设计的合理性和模具的使用寿命，减少模具重新试制的次数。

通过模具虚拟设计，充分检验模具设计的合理性，减少新产品模具的开发研制时间，对用户需求做出快速响应，提高市场竞争能力。

一、刚（粘）塑性有限元法基本原理刚（粘）塑性有限元法忽略了金属变形中的弹性效应，依据材料发生塑性变形时应满足的塑性力学基本方程，以速度场为基本量，形成有限元列式。

这种方法虽然无法考虑弹性变形问题和残余应力问题，但可使计算程序大大简化。

在弹性变形较小甚至可以忽略时，采用这种方法可达到较高的计算效率。

刚塑性有限元法的理论基础是Markov变分原理。

根据对体积不变条件处理方法上的不同（如拉格朗日乘子法、罚函数法和体积可压缩法），又可得出不同的有限元列式其中罚函数法应用比较广泛。

根据Markov变分原理，采用罚函数法处理，并用八节点六面体单元离散化，则在满足边界条件、协调方程和体积不变条件的许可速度场中对应于真实速度场的总泛函为：∏≈∑π（ｍ）＝∏（１，２，…，ｍ）（１）对上式中的泛函求变分，得：∑＝０（２）采用摄动法将式（２）进行线性化：＝＋Δｕｎ（３）将式（３）代入式（２），并考虑外力、摩擦力在局部坐标系中对总体刚度矩阵和载荷列阵，通过迭代的方法，可以求解变形材料的速度场。

Deform-3d热处理模拟操作热处理工艺在机械制造中占有十分重要的地位。

随着机械制造现代化和热处理质量管理现代化的发展，对热处理工艺提出了更高的要求。

热处理工艺过程由于受到加热方式、冷却方式、加热温度、冷却温度、加热时间、冷却时间等影响，金属内部的组织也会发生不同的变化，因此是个十分复杂的过程，同时工艺参数的差异，也会造成热处理加工对象硬度过高过低、硬度不均匀等现象.Deform—3d软件提供一种热处理模拟模块，可以帮助热处理工艺员，通过有限元数值模拟来获得正确的热处理参数，从而来指导热处理生产实际.减少批量报废的质量事故发生.热处理模拟，涉及到热应力变形、热扩散和相变等方面，因此计算很复杂，软件采用牛顿迭代法，即牛顿-拉夫逊法进行求解.它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法.多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。

方法使用函数f（x）的泰勒级数的前面几项来寻找方程f（x） = 0的根.牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x） = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根等.但由于目前Deform-3d软件的材料库只带有45钢、15NiCr13和GCr15等三种材料模型，而且受到相变模型的局限，因此只能做淬火和渗碳淬火分析，更多分析需要进行二次开发.本例以45钢热处理淬火工艺的模拟过程为例，通过应用Deform-3d 热处理模块，让读者基本了解热处理工艺过程有限元模拟的基本方法与步骤.1 、问题设置点击“文档”(File）或“新问题”（New problem），创建新问题。

在弹出的图框中,选择“热处理导向”（heat treatment wizard)，见图1。

图1 设置新问题2、初始化设置完成问题设置后,进入前处理设置界面。

首先修改公英制，将默认的英制（English）修改成公制（SI)，同时选中“形变”（Deformation)、“扩散”（Diffusion）和“相变”(Phase transformation），见图2。

Deform轧制模拟流程1. 建立工作目录2. 前处理（导入模型，调整模型位置，设置物理性质，划分网格，设置边界条件（换热面、对称面）3. 设置辊和推板的速度，设置接触条件，check并生成DB文件）4. 运行计算（多线程计算）5. 后处理（云图、点追踪）建立工作目录在硬盘建立专属文件夹（必须是英文文件夹），在deform软件中打开进入前处理页面添加objects ,分别导入模型（注：下图红色方框所示为主程序，前处理的五个主要功能选项, 即：主菜单、材料库、装配、接触、检查与生成DB 文件。

）i?2D/J0 Ver 10.2:* 云 r«T' -0 aafn^XuReoivi □Ipbwd - S&%D0ORM 计窮hDKD ・L0工3d 亠皐： □ ri- r.in7^-T ：0<3 TT ： n 论亠古调整模型位置（Position object选择top die，在method中选择rotational （旋转），选中x 轴，在角度中输入90,点击apply，将平方的轧辊旋转90度。

如果有必要）在method中选择ofset （平移），选择work piece （轧件）根据道次压下量调整轧件与轧辊之间的相对位置, 推板bottom die同理。

划分网格 选中work piece ，一般默认的是相对网格保证计算速度，而绝对网格的计算精度更 o3o1.2广亠亠I 订工第二『0：企嵌I ；设置边界条件：1.对称面，1/4模型有两个对称面；2•换热面剩余面为换热面高但速度较慢，无论哪种网格划分方式都具有在计算过程中自动重新划分网格的功能 显示单个对象N JE 力打 cf Swi-?:- | ： T■ K :«3ScLrrQGw» ■ M r□ mMo** ■■*=-'； if DCOF'H I-JJ t-r'x l ：2 :J EW lj2d ：F*in<-it*Ml iAKiWi? » * ：」佩-口.7二二_£*1I 「■■ ■■■l ・ | 二■■>1 f -dJ!旧tar :coal ，:yiKt肌 toraatiwiFiwiJiiiilg MPNH .加 Pi •也订driE_U2ifl— □ 壬Pl fsl* SWT HlEMrr u 好M 审帆 J«ih 初MAS!邯油-l*J XJ>JB A Cd||l ■ 00fi ■[ h * 却 UGO 舍仓舍 «■&：<4.■上2陆巴J.…r..-“」Q f^v* W 気- 1JC Vtih j7勺：i 咎si 4母<KAQ6®St卫■ -h / * 4规fsl* Sw'B Vi Wflerr 曲"・《7 Mdn. H M >〕・ A L ” CqiTiMt *Hi■1 --------------------------------------------- G^JzETEfla! 5TKILA-ZDS「皿•常：养帝亡加：3:s>-J@ 0臥範J 超■仙皿就FE- 24M RET •讦Uz ・ xa1□:Ph.j Tup 31*T»B 1 cb^scc: ■'■ 3佥毬■•轟从 0»JM ；IdJlASMfa圭]33」rJ*12Oio2Sirruldtan Cartr^hOtJMK ||>V iM-libhAStJ 町S卜 Feint I 吨詢価 h Ml ； 0£t 心0 titc wr*« 15 ■ 7v*-o«i£tjiHPPi F] If EVIT 冊 EMh D*俱* Mdfil 7x>h Virr ^TlSn?肝:Q!>ja A nd 呂屮少 &也廿门 吕 戶|比却Q 追。

Deflt-3D FLOW模块简明操作手册河海大学第一章引言1.1 特征wL 一Delft HydrauliCS 开发一套功能强大的软件包：Delft3D , 主要应用于自由地表水环境。

该软件具有灵活的框架，能模拟二维（水平面或竖直面）和三维的水流、波浪、水质、生态、泥沙输移及床底地貌，及各个过程之间的相互作用。

Delft3D 的主要特征为：所有程序模块都具有高度的整合性和互操作性；能直接应用最新过程知识，为久誉盛名的水力学研究所的研发成果；采用了市场上最为友好的图形用户界面。

1.2 模块简介Delft3D 具体模拟六种现象的时间、空间变化以及其相互联系。

该软件包原则上广泛适用于多种情况。

运用最为普遍的是海岸、河流以及河口地区。

Delft3D 由一系列经过全面测试和验证的模块组成，是相互联系的有机整体。

有关模块包括：一、水动力模块（Delft3D 一FLOW )该模块主要用于浅水非恒定流模拟。

综合考虑了潮汐、风、气压、密度差（由盐度和温度引起）、波浪、紊流（从简单常量到k-模型）以及潮滩的干湿交替。

本模块集成了热量及物质传输方程求解，并在wL-Delft Hydraulics 有关分层水动力学等前沿理论研究基础上开发而成。

Delft3D 的其它模块均可采用了该模块的输出结果。

二、波浪模块（Delft3D 一WAVE )波浪模块主要计算短波在非平整床底上的非稳定传播，考虑风力、底部摩阻力造成的能量消散、波浪破碎、波浪折射（由于床底地形、水位及流场）、浅水变形及方向分布。

三、水质模块（Delft3D 一WAQ)该模块通过考虑一系列泥沙输移和水质过程来模拟远一中水域的水质及泥沙。

该模块包含了若干对流扩散方程求解工具和一个庞大的标准化过程方程库，其方程组对应用户所选择的物质类型。

四、颗粒跟踪模块（Delft3D 一以RT )颗粒跟踪模块为短期的、邻近水域水质模块，通过即时跟踪个体颗粒轨迹来估算其动态、空间（子网格尺度下）密度分布。

Deform-3d热处理模拟操作热处理工艺在机械制造中占有十分重要的地位。

随着机械制造现代化和热处理质量管理现代化的发展，对热处理工艺提出了更高的要求。

热处理工艺过程由于受到加热方式、冷却方式、加热温度、冷却温度、加热时间、冷却时间等影响，金属内部的组织也会发生不同的变化，因此是个十分复杂的过程，同时工艺参数的差异，也会造成热处理加工对象硬度过高过低、硬度不均匀等现象。

Deform-3d软件提供一种热处理模拟模块，可以帮助热处理工艺员，通过有限元数值模拟来获得正确的热处理参数，从而来指导热处理生产实际。

减少批量报废的质量事故发生。

热处理模拟，涉及到热应力变形、热扩散和相变等方面，因此计算很复杂，软件采用牛顿迭代法，即牛顿-拉夫逊法进行求解。

它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。

方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。

牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x) = 0的单根附近具有平方收敛，而且该法还可以用来求方程的重根、复根等。

但由于目前Deform-3d软件的材料库只带有45钢、15NiCr13和GCr15等三种材料模型，而且受到相变模型的局限，因此只能做淬火和渗碳淬火分析，更多分析需要进行二次开发。

本例以45钢热处理淬火工艺的模拟过程为例，通过应用Deform-3d 热处理模块，让读者基本了解热处理工艺过程有限元模拟的基本方法与步骤。

1 、问题设置点击“文档”（File）或“新问题”（New problem），创建新问题。

在弹出的图框中，选择“热处理导向”(heat treatment wizard)，见图1。

sgniht图1 设置新问题2、初始化设置完成问题设置后，进入前处理设置界面。

首先修改公英制，将默认的英制t h i ng si nt he i rb ei n ga re go od fo rs （English ）修改成公制（SI ），同时选中“形变”（Deformation ）、“扩散”(Diffusion)和“相变”(Phase transformation)，见图2。