三角函数综合问题
- 格式:doc
- 大小:290.50 KB
- 文档页数:4

专题03 三角函数与平面向量综合问题(答题指导)【题型解读】题型特点命题趋势▶▶题型一:三角函数的图象和性质1.注意对基本三角函数y =sin x ,y =cos x 的图象与性质的理解与记忆,有关三角函数的五点作图、图象的平移、由图象求解析式、周期、单调区间、最值和奇偶性等问题的求解,通常先将给出的函数转化为y =A sin(ωx +φ)的形式,然后利用整体代换的方法求解. 2.解决三角函数图象与性质综合问题的步骤 (1)将f (x )化为a sin x +b cos x 的形式. (2)构造f (x )=a 2+b 2⎝⎛⎭⎪⎫a a 2+b 2·sin x +b a 2+b 2·cos x . (3)和角公式逆用,得f (x )=a 2+b 2sin(x +φ)(其中φ为辅助角). (4)利用f (x )=a 2+b 2sin(x +φ)研究三角函数的性质. (5)反思回顾,查看关键点、易错点和答题规范.【例1】 (2017·山东卷)设函数f (x )=sin ⎝ ⎛⎭⎪⎫ωx -π6+sin ⎝ ⎛⎭⎪⎫ωx -π2,其中0<ω<3.已知f ⎝ ⎛⎭⎪⎫π6=0.(1)求ω;(2)将函数y =f (x )的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移π4个单位,得到函数y =g (x )的图象,求g (x )在⎣⎢⎡⎦⎥⎤-π4,3π4上的最小值.【答案】见解析【解析】(1)因为f (x )=sin ⎝ ⎛⎭⎪⎫ωx -π6+sin ⎝⎛⎭⎪⎫ωx -π2,所以f (x )=32sin ωx -12cos ωx -cos ωx =32sinωx -32cos ωx =3⎝ ⎛⎭⎪⎫12sin ωx -32cos ωx =3sin ⎝ ⎛⎭⎪⎫ωx -π3.因为f ⎝ ⎛⎭⎪⎫π6=0,所以ωπ6-π3=k π,k ∈Z .故ω=6k +2,k ∈Z .又0<ω<3,所以ω=2.(2)由(1)得f (x )=3sin ⎝ ⎛⎭⎪⎫2x -π3,所以g (x )=3sin ⎝ ⎛⎭⎪⎫x +π4-π3=3sin ⎝ ⎛⎭⎪⎫x -π12.因为x ∈⎣⎢⎡⎦⎥⎤-π4,3π4,所以x -π12∈⎣⎢⎡⎦⎥⎤-π3,2π3,当x -π12=-π3,即x =-π4时,g (x )取得最小值-32.【素养解读】本题中图象的变换考查了数学直观的核心素养,将复杂的三角函数通过变形整理得到正弦型函数,从而便于对性质的研究,考查数学建模的核心素养.【突破训练1】 设函数f (x )=32-3sin 2ωx -sin ωx cos ωx (ω>0),且y =f (x )的图象的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值;(2)求f (x )在区间⎣⎢⎡⎦⎥⎤π,3π2上的最大值和最小值. 【答案】见解析 【解析】(1)f (x )=32-3·1-cos2ωx 2-12sin2ωx =32cos2ωx -12sin2ωx = -sin ⎝ ⎛⎭⎪⎫2ωx -π3.因为y =f (x )的图象的一个对称中心到最近的对称轴的距离为π4,故该函数的周期T =4×π4=π.又ω>0,所以2π2ω=π,因此ω=1.(2)由(1)知f (x )=-sin ⎝ ⎛⎭⎪⎫2x -π3.当π≤x ≤3π2时,5π3≤2x -π3≤8π3,所以-32=sin 5π3≤sin ⎝ ⎛⎭⎪⎫2x -π3≤sin 5π2=1,所以-1≤f (x )≤32,即f (x )在区间⎣⎢⎡⎦⎥⎤π,3π2上的最大值和最小值分别为32,-1.▶▶题型二 解三角形1.高考对解三角形的考查,以正弦定理、余弦定理的综合运用为主.其命题规律可以从以下两方面看:(1)从内容上看,主要考查正弦定理、余弦定理以及三角函数公式,一般是以三角形或其他平面图形为背景,结合三角形的边角关系考查学生利用三角函数公式处理问题的能力;(2)从命题角度看,主要是在三角恒等变换的基础上融合正弦定理、余弦定理,在知识的交汇处命题. 2.用正、余弦定理求解三角形的步骤第一步:找条件,寻找三角形中已知的边和角,确定转化方向.第二步:定工具,根据已知条件和转化方向,选择使用的定理和公式,实施边角之间的转化. 第三步:求结果,根据前两步分析,代入求值得出结果.第四步:再反思,转化过程中要注意转化的方向,审视结果的合理性.【例2】 在△ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,且cos(C +B)cos(C -B)=cos2A -sin Csin B . (1)求A ;(2)若a =3,求b +2c 的最大值. 【答案】见解析【解析】(1)cos(C +B)cos(C -B)=cos2A -sinCsinB =cos2(C +B)-sinCsinB ,则cos(C +B)[cos(C -B)-cos(C +B)]=-sinCsinB ,则-cosA·2sinCsinB=-sinCsinB ,可得cosA =12,因为0<A <π,所以A=60°.(2)由a sinA =b sinB =csinC =23,得b +2c =23(sinB +2sinC)=23[sinB +2sin(120°-B)]=23(2sinB+3cosB)=221sin(B +φ),其中tanφ=32,φ∈⎝ ⎛⎭⎪⎫0,π2.由B ∈⎝ ⎛⎭⎪⎫0,2π3得B +φ∈⎝⎛⎭⎪⎫0,7π6,所以sin(B +φ)的最大值为1,所以b +2c 的最大值为221.【素养解读】试题把设定的方程与三角形内含的方程(三角形的正弦定理、三角形内角和定理等)建立联系,从而求得三角形的部分度量关系,体现了逻辑推理、数学运算的核心素养.【突破训练2】 (2017·天津卷)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a >b ,a =5,c =6,sin B =35.(1)求b 和sin A 的值; (2)求sin ⎝ ⎛⎭⎪⎫2A +π4的值.【答案】见解析【解析】(1)在△ABC 中,因为a >b ,故由sin B =35,可得cos B =45.由已知和余弦定理,有b 2=a 2+c 2-2ac cos B=13,所以b =13.由正弦定理得sin A =a sin B b =31313. (2)由(1)及a <c ,得cos A =21313,所以sin2A =2sin A cos A =1213,cos2A =1-2sin 2A =-513.故sin ⎝⎛⎭⎪⎫2A +π4=sin2A cos π4+cos 2A ·sin π4=7226.▶▶题型三 三角函数与平面向量的综合1.三角函数、解三角形与平面向量的综合主要体现在以下两个方面:(1)以三角函数式作为向量的坐标,由两个向量共线、垂直、求模或求数量积获得三角函数解析式;(2)根据平面向量加法、减法的几何意义构造三角形,然后利用正、余弦定理解决问题.2.(1)向量是一种解决问题的工具,是一个载体,通常是用向量的数量积运算或性质转化成三角函数问题.(2)三角形中的三角函数要结合正弦定理、余弦定理进行转化,注意角的范围对变形过程的影响. 【例3】 (2019·佛山调考)已知函数f (x )=a ·b ,其中a =(2cos x ,-3sin2x ),b =(cos x,1),x ∈R .(1)求函数y =f (x )的单调递减区间;(2)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,f (A )=-1,a =7,且向量m =(3,sin B )与n =(2,sin C )共线,求边长b 和c 的值. 【答案】见解析【解析】(1)f (x )=a ·b =2cos 2x -3sin2x =1+cos2x -3sin2x =1+2cos ⎝ ⎛⎭⎪⎫2x +π3,由2k π≤2x +π3≤2k π+π(k ∈Z ),解得k π-π6≤x ≤k π+π3(k ∈Z ),所以f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π-π6,k π+π3(k ∈Z ).(2)因为f (A )=1+2cos ⎝ ⎛⎭⎪⎫2A +π3=-1,所以cos ⎝ ⎛⎭⎪⎫2A +π3=-1.因为0<A <π,所以π3<2A +π3<7π3,所以2A +π3=π,即A =π3.因为a =7,由余弦定理得a 2=b 2+c 2-2bc cos A =(b +c )2-3bc =7.①因为向量m =(3,sin B )与n =(2,sin C )共线,所以2sin B =3sinC . 由正弦定理得2b =3c ,② 由①②可得b =3,c =2.【突破训练3】(2019·湖北八校联考) 已知△ABC 的面积为S ,且32AB →·AC →=S ,|AC →-AB →|=3.(1)若f (x )=2cos(ωx +B )(ω>0)的图象与直线y =2相邻两个交点间的最短距离为2,且f ⎝ ⎛⎭⎪⎫16=1,求△ABC 的面积S ;(2)求S +3 3 cos B cos C 的最大值. 【答案】见解析【解析】设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c , 因为32AB →·AC →=S ,所以32bc cos A =12bc sin A , 解得tan A =3,所以A =π3.由|AC →-AB →|=3得|BC →|=a =3.(1)因为f (x )=2cos(ωx +B )(ω>0)的图象与直线y =2相邻两个交点间的最短距离T =2,即2πω=2,解得ω=π,故f (x )=2cos(πx +B ).又f ⎝ ⎛⎭⎪⎫16=2cos ⎝⎛⎭⎪⎫π6+B =1,即cos ⎝ ⎛⎭⎪⎫π6+B =12.因为B 是△ABC 的内角,所以B =π6,从而△ABC 是直角三角形,所以b =3,所以S △ABC =12ab =332.(2)由题意知A =π3,a =3,设△ABC 的外接圆半径为R ,则2R =a sin A = 332=23,解得R =3,所以S+33cos B cos C =12bc sin A +33cos B cos C =34bc +33cos B cos C =33sin B sin C +33cos B cos C =33cos(B -C ),故S +33cos B cos C 的最大值为3 3.。

[A 组 基础练]1.(2021·沈阳监测)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知b 2+c 2=a 2+bc .(1)求角A 的大小;(2)若sin A =2sin B cos C ,试判断△ABC 的形状并给出证明.解析:(1)由b 2+c 2=a 2+bc ,可知b 2+c 2-a 22bc =12, 根据余弦定理可知,cos A =12, 又A 为△ABC 的内角,所以A =π3. (2)法一:△ABC 为等边三角形.证明如下:由三角形内角和定理得,A =π-(B +C ),故sin A =sin(B +C ),根据已知条件,可得sin(B +C )=2sin B cos C ,整理得sin B cos C -cos B sin C =0,所以sin(B -C )=0.又B -C ∈(-π,π),所以B =C ,又由(1)知A =π3,所以△ABC 为等边三角形. 法二:△ABC 为等边三角形.证明如下:由正弦定理和余弦定理及已知条件,得a =2b ×a 2+b 2-c 22ab, 整理得b 2=c 2,即b =C .又由(1)知A =π3,所以△ABC 为等边三角形. 2.(2021·辽宁五校联考)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若sin(A +C )=2sin A cos(A +B ),且sin 2A +sin 2B -sin 2C +2sin A sin B =0.(1)求证:a ,b,2a 成等比数列;(2)若△ABC 的面积是2,求c .解析:(1)证明:∵A +B +C =π,sin(A +C )=2sin A cos(A +B ),∴sin B =-2sin A cos C .在△ABC 中,由正弦定理得,b =-2a cos C ,∵sin 2A +sin 2B -sin 2C +2sin A sin B =0,∴由正弦定理可得a 2+b 2-c 2+2ab =0,∴cos C =a 2+b 2-c 22ab =-22,∴C =3π4, ∴b =2a ,则b 2=2a 2=a ·2a ,∴a ,b,2a 成等比数列.(2)△ABC 的面积S =12ab sin C =24ab =2, 则ab =42,由(1)知,b =2a ,联立两式,解得a =2,b =22,∴c 2=a 2+b 2-2ab cos C =4+8-2×2×22×⎝⎛⎭⎫-22=20, ∴c =2 5.3.(2021·湖北八校联考)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,C .(1)若23cos 2A +cos 2A =0,且△ABC 为锐角三角形,a =7,c =6,求b 的值;(2)若a =3,A =π3,求b +c 的取值范围. 解析:(1)∵23cos 2A +cos 2A =23cos 2A +2cos 2A -1=0, ∴cos 2A =125,又A 为锐角,∴cos A =15. 而a 2=b 2+c 2-2bc cos A ,即b 2-125b -13=0, 解得b =5(负值已舍去),∴b =5.(2)由余弦定理a 2=b 2+c 2-2bc cos A 可得b 2+c 2-3=bc ,即(b +c )2-3=3bc ≤34(b +c )2,当且仅当b =c 时取等号, ∴b +c ≤23,又由两边之和大于第三边可得b +c >3, ∴b +c ∈(3,23].4.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且cos 2B -cos 2C =sin 2A -3sin A sinB .(1)求角C ;(2)若A =π6,△ABC 的面积为43,M 为AB 的中点,求CM 的长. 解析:(1)根据cos 2B +sin 2B =1,cos 2C +sin 2C =1,知cos 2B -cos 2C =sin 2C -sin 2B =sin 2A -3sin A sin B ,根据正弦定理可化为c 2-b 2=a 2-3ab ,即3ab =a 2+b 2-c 2.由余弦定理,得cos C =a 2+b 2-c 22ab =32.因为0<C <π,所以C =π6. (2)因为A =C =π6,所以△ABC 为等腰三角形,且顶角B =2π3, 故S △ABC =12a 2sin B =34a 2=43,所以a =4. 在△MBC 中,由余弦定理得,CM 2=MB 2+BC 2-2·MB ·BC cos B =4+16+2×2×4×12=28,解得CM =27.[B 组 创新练]1.已知在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a ,b ,c 成等比数列,cos B =34. (1)求1tan A +1tan C的值; (2)设BA →·BC →=32,求a +c 的值. 解析:(1)由cos B =34,0<B <π得sin B = 1-⎝⎛⎭⎫342=74,∵a ,b ,c 成等比数列,∴b 2=aC .由正弦定理,可得sin 2B =sin A sin C ,于是1tan A +1tan C =cos A sin A +cos C sin C =sin C cos A +cos C sin A sin A sin C=sin (A +C )sin 2B =sin B sin 2B =1sin B =477. (2)由BA →·BC →=32得ca cos B =32, 而cos B =34,∴b 2=ac =2, 由余弦定理,得b 2=a 2+c 2-2ac cos B ,∴a 2+c 2=5,∴(a +c )2=5+2ac =9,∴a +c =3.2.(2021·黄冈模拟)已知在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,点D 为边BC 的中点,△ABC 的面积为AD 22sin B. (1)求sin ∠BAD ·sin ∠BDA 的值;(2)若BD =2AB ,AD =3,求B .解析:(1)由△ABC 的面积为AD 22sin B 且D 为BC 的中点可得,△ABD 的面积为AD 24sin B ,由三角形的面积公式可知12AB ·AD ·sin ∠BAD =AD 24sin B ,可得sin ∠BAD =AD 2AB ·sin B.在△ABD 中,由正弦定理可得sin ∠BDA =AB ·sin B AD ,所以sin ∠BAD ·sin ∠BDA =12. (2)因为BD =2AB ,所以在△ABD 中,由正弦定理可得BD sin ∠BAD =AB sin ∠BDA ,所以sin ∠BAD =2sin ∠BDA .由(1)可知sin ∠BAD ·sin ∠BDA =12,所以sin ∠BAD =1,sin ∠BDA =12.又因为∠BAD ∈(0,π),所以∠BAD =π2.在Rt △ABD 中,AD =3,sin ∠BDA =12,所以BD =2,AB =c =1,cos B =12.又因为BC =2BD ,所以BC =a =4.在△ABC 中,由余弦定理可得b 2=a 2+c 2-2ac cos B =16+1-2×4×1×12=13,解得b =13. 3.设△ABC 内角A ,B ,C 所对的边分别是a ,b ,c ,且三个内角A ,B ,C 依次成等差数列.(1)若sin 2B =sin A sin C ,求角A ;(2)若△ABC 为钝角三角形,且a >c ,求3sin A 2cos A 2-cos 2C 2+12的取值范围. 解析:(1)∵A ,B ,C 依次成等差数列,∴2B =A +C =π-B ,∴B =π3. ∵sin 2B =sin A sin C ,∴根据正弦定理,得b 2=ac .又由余弦定理,得b 2=a 2+c 2-2ac cos B =a 2+c 2-ac ,∴a 2+c 2-ac =ac ,即(a -c )2=0,∴a =c .∴△ABC 为等边三角形,∴A =π3. (2)由(1)知A +C =2π3,再由二倍角公式得, 3sin A 2cos A 2-cos 2C 2+12=32sin A -1+cos C 2+12 =32sin A -12cos ⎝⎛⎭⎫2π3-A =32sin A +14cos A -34sin A =34sin A +14cos A =12sin ⎝⎛⎭⎫A +π6. ∵a >c 且△ABC 为钝角三角形,∴π2<A <2π3,∴2π3<A+π6<5π6,∴12<sin⎝⎛⎭⎫A+π6<32,∴14<12sin⎝⎛⎭⎫A+π6<34.∴3sin A2cosA2-cos2C2+12的取值范围是⎝⎛⎭⎫14,34.。


[考情分析]以三角形、三角函数为载体,以三角函数的图象与性质、正弦定理、余弦定理为工具,以三角恒等变换为手段来考查三角函数的综合问题是高考的热点题型,主要考查内容有正、余弦定理、三角形面积的计算、三角恒等变换和三角函数的性质.解题时要充分利用三角函数的图象与性质,交替使用正弦定理、余弦定理,利用数形结合、函数与方程思想等进行求解.考点一三角函数图象与性质的综合例1已知函数f (x )=A sin(ωx +φ>0,ω>0,|φ(1)求f (x )=2的解集;(2)求函数g (x )=f 解(1)由图象可知,周期T =5π12+7π12=π,∴ω=2ππ=2,∵,∴A 2×5π12+0,∴0,解得5π6+φ=π+2k π,φ=2k π+π6,k ∈Z ,∵|φ|<π2,∴φ=π6,∵点(0,1)在函数图象上,∴A sin π6=1,A =2,∴函数f (x )的解析式为f (x )=x由f (x )=x 2,得x 1,即2x +π6=π2+2k π,k ∈Z ,解得x =π6+k π,k ∈Z ,∴f (x )=2|x =π6k π,k ∈(2)g (x )=由(1)知f (x )=xg (x )=2sin 2+π6-2sin 2+π6=2sin2x -2sinx =2sin2x -x +32cos2sin2x -3cos2x=x 由-π2+2k π≤2x -π3≤π2+2k π,k ∈Z ,得k π-π12≤x ≤k π+5π12,k ∈Z ,∴函数g (x )=f k π-π12,k π+5π12,k ∈Z .解决三角函数图象与性质综合问题的方法利用图象讨论三角函数的性质,应先把函数化成y =A sin(ωx +φ)(ω>0)或y =A cos(ωx +φ)(ω>0)的形式,然后通过换元法令t =ωx +φ,转化为研究y =A sin t 或y =A cos t 的性质.1.已知函数f (x )=2sin ωx cos φ+2sin φ-4sin 2ωx 2sin φ(ω>0,|φ|<π),其图象的一条对称轴与相邻对称中心的横坐标相差π4,________,从以下两个条件中任选一个补充在空白横线中.①函数f (x )的图象向左平移π6个单位长度后得到的图象关于y 轴对称且f (0)<0;②函数f (x )的图象的一条对称轴为直线x =-π3且f (1).(1)求函数f (x )的解析式;(2)若x ∈π2,3π4,函数h (x )=f (x )-a 存在两个不同零点x 1,x 2,求x 1+x 2的值.解(1)f (x )=2sin ωx cos φ+2sin φ-2(1-cos ωx )sin φ=2sin(ωx +φ),又函数f (x )的最小正周期为T =4×π4=π,所以ω=2πT=2,若选条件①:将函数f (x )的图象向左平移π6个单位长度得到的图象关于y 轴对称,所得函数为y =2sin 2φ=x +π3+由函数y =2sin x +π3+y 轴对称,可得π3+φ=π2+k π(k ∈Z ),解得φ=π6+k π(k ∈Z ),因为|φ|<π,所以φ的可能取值为-5π6,π6,若φ=-5π6,则f (x )=xf (0)=1,符合题意;若φ=π6,则f (x )=x f (0)=2sin π6=1,不符合题意.所以f (x )=x若选条件②:因为函数f (x )图象的一条对称轴为直线x =-π3,所以φ=π2+k π(k ∈Z ),解得φ=7π6+k π(k ∈Z ),因为|φ|<π,所以φ的可能取值为-5π6,π6,若φ=-5π6,则f (x )=x则2<f (1),符合题意;若φ=π6,则f (x )=x则2sin π2=2>f (1),不符合题意.所以f (x )=x(2)令t =2x -5π6∈π6,2π3,此时函数h (x )=f (x )-a 存在两个不同零点x 1,x 2等价于直线y =a 与函数y =2sin t ,t ∈π6,2π3的图象有两个不同交点.当t =π2时,函数取到最大值,所以t 1+t 2=π,即2x 1-5π6+2x 2-5π6=π,所以x 1+x 2=4π3.考点二三角函数与解三角形的综合例2(2023·河北石家庄二中模拟)设函数f (x )=2sin(ωx +φ)(ω>0,0<φ<π),该函数图象上相邻两个最高点间的距离为4π,且f (x )为偶函数.(1)求ω和φ的值;(2)已知角A ,B ,C 为△ABC 的三个内角,若(2sin A -sin C )cos B =sin B cos C ,求[f (A )]2+[f (C )]2的取值范围.解(1)因为f (x )=2sin(ωx +φ)的图象上相邻两个最高点间的距离为4π,所以2πω=4π,解得ω=12,所以f (x )=2sin +又因为f (x )为偶函数,所以φ=k π+π2,k ∈Z .又因为0<φ<π,所以φ=π2.(2)因为(2sin A -sin C )cos B =sin B cos C ,所以2sin A cos B -sin C cos B =sin B cos C ,所以2sin A cos B =sin(B +C ),又因为A +B +C =π,且0<A <π,所以sin(B +C )=sin A ≠0,所以cos B =12,因为0<B <π,所以B =π3,则A +C =2π3,即C =2π3-A ,由(1)知,函数f (x )=2cos 12x ,所以[f (A )]2+[f (C )]2=2cos 212A +2cos 212C =cos A +cos C +2=cos A +2=cos A -12cos A +32sin A +2=32sin A +12cos A +2=2,因为0<A <2π3,所以π6<A +π6<5π6,所以1,则23,即[f (A )]2+[f (C )]23.解三角形与三角函数的综合应用主要体现在以下两个方面:(1)利用三角恒等变换化简三角函数式进行解三角形;(2)解三角形与三角函数图象和性质的综合应用.2.设f (x )=sin x cos x -cos x ∈[0,π].(1)求f (x )的单调递增区间;(2)在锐角三角形ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .若0,a =1,求△ABC面积的最大值.解(1)由题意,得f (x )=12sin2x -12cos x 1=sin2x -12,因为0≤x ≤π,所以0≤2x ≤2π,由正弦函数的单调性可知,当0≤2x ≤π2或3π2≤2x ≤2π,即0≤x ≤π4或3π4≤x ≤π时,函数f (x )=sin2x -12单调递增,所以f (x )的单调递增区间是0,π4和3π4,π.(2)由题意,得sin A -12=0,所以sin A =12,因为△ABC 为锐角三角形,所以A 故A =π6.由余弦定理,得b 2+c 2-2bc cos A =a 2,故b 2+c 2-3bc =1,由基本不等式,得b 2+c 2≥2bc ,故bc ≤2+3,当且仅当b =c 时,等号成立.因此S △ABC =12bc sin A ≤2+34,当且仅当b =c 时,△ABC 的面积取得最大值2+34.考点三三角函数与平面向量的综合例3已知向量a =(sin x ,3sin(π+x )),b =(cos x ,-sin x ),函数f (x )=a ·b -32.(1)求f (x )的最小正周期及f (x )图象的对称轴方程;(2)先将f (x )的图象上每个点的纵坐标不变,横坐标变为原来的2倍,再向左平移π3个单位长度得到函数g (x )的图象,若函数y =g (x )-m 在区间π6,5π6内有两个零点,求m 的取值范围.解(1)因为f (x )=a ·b -32sin x cos x +3sin 2x -32=12sin2x -32cos2x =x 故f (x )的最小正周期为T =2π2=π.由2x -π3=k π+π2,k ∈Z ,得x =k π2+5π12,k ∈Z ,所以f (x )的最小正周期为π,对称轴方程为x =k π2+5π12,k ∈Z .(2)由(1),知f (x )=x由题意,得g (x )=sin x .函数y =g (x )-m 在区间π6,5π6内有两个零点,转化为函数y =sin x ,x ∈π6,5π6的图象与直线y =m 有两个交点.由图象可得,m 的取值范围为12,当题目条件给出的向量坐标中含有三角函数的形式时,首先运用向量数量积的定义、向量共线、向量垂直等,得到三角函数的关系式,然后利用三角函数的图象、性质解决问题.3.已知向量a x b =(cos x ,-1).(1)当a ∥b 时,求2cos 2x -sin2x 的值;(2)求f (x )=(a +b )·b 在-π2,0上的单调递增区间.解(1)由a ∥b ,得(-1)sin x =32cos x ,所以tan x =-32,所以2cos 2x -sin2x =2cos 2x -2sin x cos x cos 2x +sin 2x =2-2tan x 1+tan 2x =2+31+94=2013.(2)f (x )=a ·b +b 2=sin x cos x -32+cos 2x +1=12sin2x +1+cos2x 2-12=22sin x 当x ∈-π2,0时,2x +π4∈-3π4,π4,令-π2≤2x +π4≤π4,得-3π8≤x ≤0.故函数f (x )在-π2,0上的单调递增区间为-3π8,0.考点四解三角形与平面向量的综合例4(2024·四川成都调研)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且m =(2b +c ,a ),n =(cos A ,cos C ),m ⊥n .(1)求角A 的大小;(2)D 是线段BC 上的点,且AD =BD =2,CD =3,求△ABD 的面积.解(1)因为m =(2b +c ,a ),n =(cos A ,cos C ),m ⊥n ,所以m ·n =(2b +c )cos A +a cos C =0,由正弦定理可得2sin B cos A +(sin A cos C +cos A sin C )=0,即2sin B cos A +sin(A +C )=0,又A +C =π-B ,所以2sin B cos A +sin B =0,又B ∈(0,π),则sin B >0,所以cos A =-12,又A ∈(0,π),因此A =2π3.(2)设B =θ,因为A =2π3,则C =π-2π3-θ=π3-θ,因为AD =BD =2,所以∠BAD =B =θ,∠ADC =2θ,∠DAC =2π3-θ,在△ACD 中,由正弦定理可知AD sin C =CD sin ∠DAC,即23即θ-12sin θ+12sin 化简可得5sin θ=3cos θ,即tan θ=35,所以sin2θ=2sin θcos θsin 2θ+cos 2θ=2tan θtan 2θ+1=5314,所以S △ABD =12AD ·BD sin(π-2θ)=12AD ·BD sin2θ=12×22×5314=537.解决解三角形与平面向量综合问题的关键:准确利用向量的坐标运算化简已知条件,将其转化为三角函数的问题解决.4.(2023·广东广州天河区模拟)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且满足b cos B +C 2=a sin B .(1)求A ;(2)若a =19,BA →·AC →=3,AD 是△ABC 的中线,求AD 的长.解(1)因为cos B +C 2=sin A 2,所以b sin A 2=a sin B .由正弦定理,得sin B sin A 2=sin A sin B .因为sin B ≠0,所以sin A 2=sin A .所以sin A 2=2sin A 2cos A 2.因为A ∈(0,π),A 2∈所以sin A 2≠0,所以cos A 2=12.所以A 2=π3.所以A =2π3.(2)因为BA →·AC →=3,所以bc cos(π-A )=3.又A =2π3,所以bc =6.由余弦定理,得b 2+c 2=a 2+2bc cos A =13.又AD →=12(AB →+AC →),所以|AD →|2=14(AB →+AC →)2=14(c 2+b 2+2bc cos A )=74.所以|AD →|=72,即AD 的长为72.课时作业1.(2023·广东佛山模拟)已知函数f (x )=cos 4x +23sin x cos x -sin 4x .(1)求f (x )的最小正周期和单调递减区间;(2)已知△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若f (A )=1,BC 边的中线AD 的长为7,求△ABC 面积的最大值.解(1)∵f (x )=cos 4x +23sin x cos x -sin 4x =(cos 2x -sin 2x )(cos 2x +sin 2x )+3sin2x =cos2x +3sin2x =x 故f (x )的最小正周期T =π,由π2+2k π≤2x +π6≤3π2+2k π,k ∈Z ,得π6+k π≤x ≤2π3+k π,k ∈Z ,∴f (x )的单调递减区间为π6+k π,2π3+k π(k ∈Z ).(2)由(1)得,f (A )=A 1,即A =12,∵0<A <π,∴2A +π6=5π6,∴A =π3,又AD →=12(AB →+AC →),∴AD →2=14(AB →2+AC →2+2AB →·AC →),∴7=14(c 2+b 2+2bc cos A )=14(b 2+c 2+bc ),∵b 2+c 2≥2bc ,∴b 2+c 2+bc ≥3bc ,∴bc ≤283,当且仅当b =c =2213时取等号,∴S △ABC =12bc sin A =34bc ≤34×283=733,∴△ABC 面积的最大值为733.2.(2024·江西南昌模拟)如图为函数f (x )=A sin(ωx +φ>0,ω>0,|φ|<π2,x ∈(1)求函数f (x )的解析式和单调递增区间;(2)若将y =f (x )的图象向右平移π12个单位长度,然后再将横坐标缩短为原来的12得到y =g (x )的图象,求函数g (x )在区间-π4,π12上的最大值和最小值.解(1)由图象知,A =2,T 4=π3-π12=π4,T =π,又ω>0,则ω=2ππ=2,则f (x )=2sin(2x +φ),,2,得π6+φ=2k π+π2,k ∈Z ,解得φ=2k π+π3,k ∈Z ,因为|φ|<π2,所以φ=π3,所以f (x )=x 令-π2+2k π≤2x +π3≤π2+2k π,k ∈Z ,得-5π12+k π≤x ≤π12+k π,k ∈Z ,所以f (x )的单调递增区间为-5π12+k π,π12+k π(k ∈Z ).(2)将f (x )=2sin x 的图象向右平移π12个单位长度,得2sin 2+π3=2sin x ,然后再将横坐标缩短为原来的12,得g (x )=2sin x .因为x ∈-π4,π12,则4x +π6∈-5π6,π2,所以-1≤x 1.故当4x +π6=-π2,即x =-π6时,g (x )取得最小值,为-2;当4x +π6=π2,即x =π12时,g (x )取得最大值,为2.3.设函数f (x )=m ·n ,其中向量m =(2cos x ,1),n =(cos x ,3sin2x )(x ∈R ).(1)求f (x )的最小值;(2)在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,已知f (A )=2,b =1,△ABC 的面积为32,求b sin B的值.解(1)因为m =(2cos x ,1),n =(cos x ,3sin2x ),所以f (x )=2cos 2x +3sin2x =3sin2x +cos2x +1=x 1,所以当x 1,即2x +π6=-π2+2k π,k ∈Z ,即x =-π3+k π,k ∈Z 时,f (x )取得最小值,为-1.(2)由f (A )=2,得A 1=2,则A =12,又A ∈(0,π),所以2A +π6∈故2A +π6=5π6,则A =π3,由S △ABC =12bc sin A =12×1×c ×32=32,可得c =2,在△ABC 中,由余弦定理得a 2=b 2+c 2-2bc cos A =1+4-2×1×2×12=3,所以a =3,所以b sin B =a sin A =332=2.4.(2023·四川成都模拟)已知函数f (x )=2cos 2x +3sin2x .(1)求函数f (x )的单调递增区间;(2)在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,且f (C )=3,c =1,ab =23,求△ABC 的周长.解(1)依题意,f (x )=2cos 2x +3sin2x =1+cos2x +3sin2x =x 1,由-π2+2k π≤2x +π6≤π2+2k π,k ∈Z ,得-π3+k π≤x ≤π6+k π,k ∈Z ,所以函数f (x )的单调递增区间是-π3+k π,π6+k π(k ∈Z ).(2)由(1)知,f (C )=C 1=3,即C 1,而C ∈(0,π),则2C +π6∈于是2C +π6=π2,解得C =π6,由余弦定理c 2=a 2+b 2-2ab cos C ,得1=(a +b )2-(2+3)ab =(a +b )2-23×(2+3),解得a +b =2+3,所以△ABC 的周长为3+ 3.5.(2023·福建福州模拟)已知向量m 23sin x 4,n cos x 4,cos(1)若m ·n =2,求cos (2)记f (x )=m ·n ,在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,且满足(2a -c )cos B =b cos C ,求f (A )的取值范围.解(1)m ·n =23sin x 4cos x 4+2cos 2x 4=3sin x 2+cos x 2+1= 1.因为m ·n =2,所以=12.所以1-2sin =12.(2)因为f (x )=m ·n =1,所以f (A )= 1.因为(2a -c )cos B =b cos C ,由正弦定理,得(2sin A -sin C )cos B =sin B cos C .所以2sin A cos B -sin C cos B =sin B cos C ,所以2sin A cos B =sin(B +C ).因为A +B +C =π,所以sin(B +C )=sin A ,且sin A ≠0.所以cos B =12.因为B ∈(0,π),所以B =π3.所以0<A <2π3.所以π6<A 2+π6<π2,12<sin ,故f (A )的取值范围是(2,3).6.(2024·湖北黄冈调研)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,已知向量m =(b ,a ),n =(sin A ,3cos(A +C )),且m ·n =0.(1)求角B 的大小;(2)若b =3,求3a +c 的最大值.解(1)在△ABC 中,因为m =(b ,a ),n =(sin A ,3cos(A +C )),m ·n =0,所以b sin A -3a cos B =0.由正弦定理,得sin A sin B =3sin A cos B ,又sin A >0,所以sin B =3cos B ,即tan B = 3.又0<B <π,所以B =π3.(2)由(1),知B =π3,b =3,由正弦定理,得a sin A =c sin C =b sin B=2,即a =2sin A ,c =2sin C .又C =2π3-A ,所以3a +c =6sin A +2sin C =6sin A +7sin A +3cos A =213sin(A +θ),其中锐角θ由tan θ=37确定,又0<A <2π3,所以θ<A +θ<2π3+θ.则当且仅当A +θ=π2,即tan A ==733时,sin(A +θ)取最大值1,所以3a +c 的最大值为213.7.已知函数f (x )=cos 4x -2sin x cos x -sin 4x .(1)求f (x )的最小正周期和单调递增区间;(2)求函数f (x )在区间0,π2上的值域;(3)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若0,a =2,求△ABC 面积的最大值.解(1)依题意,f (x )=(cos 2x +sin 2x )(cos 2x -sin 2x )-sin2x =cos2x -sin2x =2sinx 所以f (x )的最小正周期T =2π2=π;由2k π-π2≤2x +3π4≤2k π+π2,k ∈Z ,得k π-5π8≤x ≤k π-π8,k ∈Z ,所以f (x )的单调递增区间为k π-5π8,k π-π8(k ∈Z ).(2)由x ∈0,π2,得2x +3π4∈3π4,7π4,则-1≤x ≤22,即-2≤f (x )≤1,所以函数f (x )在区间0,π2上的值域为[-2,1].(3)由(1)知,=2sin 0,而0<A <π,即有3π4<A +3π4<7π4,则A +3π4=π,解得A =π4,由余弦定理a 2=b 2+c 2-2bc cos A ,得4=b 2+c 2-2bc ≥2bc -2bc ,于是bc ≤4+22,当且仅当b =c 时等号成立,因此S △ABC =12bc sin A =24bc ≤2+1,所以△ABC 面积的最大值为2+1.8.(2024·重庆永川北山中学模拟)已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,cos(A-C )+cos B =32,设m =(b ,c ),n =(a ,b )且m ∥n .(1)求角B 的大小;(2)延长BC 至D ,使BD =5,若△ACD 的面积S =3,求AD 的长.解(1)由cos(A -C )+cos B =32,可知cos(A -C )-cos(A +C )=32,即cos A cos C +sin A sin C -cos A cos C +sin A sin C =32,可得sin A sin C =34.由m ∥n 可得b 2-ac =0,由正弦定理可知sin 2B =sin A sin C =34,因为B ∈(0,π),所以sin B =32,因此B =π3或2π3.分别代入cos(A -C )+cos B =32,可知当B =2π3时,cos(A -C )=2,不成立.因此B =π3.(2)由B =π3可知cos(A -C )=1,即A =C ,因此△ABC 为等边三角形,即a =b =c ,S △ACD =12AC ·CD sin ∠ACD =12b (5-a )sin 2π3=34a (5-a )=3,整理可得a (5-a )=4,即a 2-5a =-4,在△ABD 中,由余弦定理可知,AD 2=AB 2+BD 2-2AB ·BD cos π3=c 2+25-5c =a 2+25-5a =21,因此AD 的长为21.。

圆与相似及三角函数综合问题1典例剖析1(2022·四川·巴中市教育科学研究所中考真题)四边形ABCD内接于⊙O,直径AC与弦BD交于点E,直线PB与⊙O相切于点B.(1)如图1,若∠PBA=30°,且EO=EA,求证:BA平分∠PBD;(2)如图2,连接OB,若∠DBA=2∠PBA,求证:△OAB∽△CDE.【答案】(1)见解析(2)见解析【解析】(1)证明:连接OB,∵直线PB与⊙O相切于点B,∴∠PBO=90°,∴∠PBA+∠ABO=90°,∵∠PBA=30°,∴∠ABO=60°,又∵OA=OB,∴△AOB为等边三角形,又∵OE=AE,∴BE平分∠ABO,∴∠ABE=1∠ABO=30°,2∴BA平分∠PBD;(2)证明:∵直线PB与⊙O相切于点B,∴∠PBO=90°,∴∠PBA+∠ABO=90°,∵AC为直径,∴∠ABC=90°,∴∠OBC+∠ABO=90°,∴∠OBC=∠PBA,∵OB=OC,∴∠PBA=∠OBC=∠OCB,∴∠AOB=2∠OCB=2∠PBA,∵∠ACD=∠ABD=2∠PBA,∴∠AOB=∠ACD,又∵∠BAO=∠BDC,∴△OAB∽△CDE.2(2022·广东深圳·中考真题)一个玻璃球体近似半圆O,AB为直径,半圆O上点C处有个吊灯EF, EF⎳AB, CO⊥AB,EF的中点为D,OA=4.(1)如图①,CM为一条拉线,M在OB上,OM=1.6,DF=0.8,求CD的长度.(2)如图②,一个玻璃镜与圆O相切,H为切点,M为OB上一点,MH为入射光线,NH为反射光线,,求ON的长度.∠OHM=∠OHN=45°,tan∠COH=34(3)如图③,M是线段OB上的动点,MH为入射光线,∠HOM=50°,HN为反射光线交圆O于点N,在M从O运动到B的过程中,求N点的运动路径长.【答案】(1)2(2)ON=207π(3)4+169【解析】(1)∵DF=0.8,OM=1.6,DF∥OB∴DF为△COM的中位线∴D为CO的中点∵CO=AO=4∴CD=2(2)过N 点作ND ⊥OH ,交OH 于点D ,∵∠OHN =45°,∴△NHD 为等腰直角三角形,即ND =DH ,又∵tan ∠COH =34,∴tan ∠NOD =34,∴tan ∠NOD =ND OD=34,∴ND :OD =3:4,设ND =3x =DH ,则OD =4x ,∵OD +DH =OH ,∴3x +4x =4,解得x =47,∴ND =127,OD =167,∴在Rt △NOD 中,ON =ND 2+OD 2=127 2+167 2=207;(3)如图,当点M 与点O 重合时,点N 也与点O 重合.当点M 运动至点A 时,点N 运动至点T ,故点N 路径长为:OB +l BT .∵∠NHO =∠MHO ,∠THO =∠MHO ,∠HOM =50°.∴∠OHA =∠OAH =65°.∴∠THO =65°,∠TOH =50°.∴∠BOT =80°,∴l BT =2π×4×80°360°=169π,∴N 点的运动路径长为:OB +l BT =4+169π,故答案为:4+169π.3(2022·黑龙江哈尔滨·中考真题)已知CH 是⊙O 的直径,点A ,点B 是⊙O 上的两个点,连接OA ,OB ,点D ,点E 分别是半径OA ,OB 的中点,连接CD ,CE ,BH ,且∠AOC =2∠CHB .(1)如图1,求证:∠ODC =∠OEC ;(2)如图2,延长CE 交BH 于点F ,若CD ⊥OA ,求证:FC =FH ;(3)如图3,在(2)的条件下,点G 是BH 上一点,连接AG ,BG ,HG ,OF ,若AG :BG =5:3,HG =2,求OF 的长.【答案】(1)见解析(2)见解析(3)OF =193【解析】(1)如图1.∵点D ,点E 分别是半径OA ,OB 的中点∴OD =12OA ,OE =12OB ∵OA =OB ,∴OD =OE∵∠BOC =2∠CHB ,∠AOC =2∠CHB∴∠AOC =∠BOC∵OC =OC∴△COD ≅△COE ,∴∠CDO =∠CEO ;(2)如图2.∵CD ⊥OA ,∴∠CDO =90°由(1)得∠CEO =∠CDO =90°,∴sin ∠OCE =OE OC=12∴∠OCE =30°,∴∠COE =90°-∠OCE =60°∵∠H =12∠BOC =12×60°=30°∴∠H =∠ECO ,∴FC =FH(3)如图3.∵CO =OH ,FC =FH∴OF ⊥CH∴∠FOH =90°连接AH.∵∠AOC=∠BOC=60°∴∠AOH=∠BOH=120°,∴AH=BH,∠AGH=60°∵AG:BG=5:3设AG=5x,∴BG=3x在AG上取点M,使得AM=BG,连接MH ∵∠HAM=∠HBG,∴△HAM≌△HBG∴MH=GH,∴△MHG为等边三角形∴MG=HG=2∵AG=AM+MG,∴5x=3x+2∴x=1,∴AG=5∴BG=AM=3,过点H作HN⊥MG于点NMN=12GM=12×2=1,HN=HG⋅sin60°=3∴AN=MN+AM=4,∴HB=HA=NA2+HN2=19∵∠FOH=90°,∠OHF=30°,∴∠OFH=60°∵OB=OH,∴∠BHO=∠OBH=30°,∴∠FOB=∠OBF=30°∴OF=BF,在Rt△OFH中,∠OHF=30°,∴HF=2OF∴HB=BF+HF=3OF=19,∴OF=193.【点睛】本题主要考查了圆周角定理,等边三角形的判定和性质,全等三角形的判定与性质,等腰三角形的性质,勾股定理以及解直角三角形等知识,正确作出辅助线构造全等三角形是解答本题的关键.4(2022·黑龙江绥化·中考真题)如图所示,在⊙O的内接△AMN中,∠MAN=90°,AM=2AN,作AB ⊥MN于点P,交⊙O于另一点B,C是AM上的一个动点(不与A,M重合),射线MC交线段BA的延长线于点D,分别连接AC和BC,BC交MN于点E.(1)求证:△CMA∽△CBD.(2)若MN=10,MC=NC,求BC的长.(3)在点C运动过程中,当tan∠MDB=34时,求MENE的值.【答案】【答案】(1)证明见解析(2)310(3)32【解析】(1)解:∵AB⊥MN,∴∠APM=90°,∴∠D+∠DMP=90°,又∵∠DMP+∠NAC=180°,∠MAN=90°,∴∠DMP+∠CAM=90°,∴∠CAM=∠D,∵∠CMA=∠ABC,∴△CMA∽△CBD.(2)连接OC,∵∠MAN=90°,∴MN是直径,∵MN=10,∴OM=ON=OC=5,∵AM=2AN,且AM2+AN2=MN2,∴AN=25,AM=45,∵S△AMN=12AM⋅AN=12MN⋅AP,∴AP=4,∴BP=AP=4,∴NP=AN2-AP2=2,∴OP=5-2=3,∵MC =NC ,∴OC ⊥MN ,∴∠COE =90°,∵AB ⊥MN ,∴∠BPE =90°,∴∠BPE =∠COE ,又∵∠BEP =∠CEO ,∴△COE ∽△BPE∴CO BP =OE PE =CE BE ,即54=OE PE =CE BE由OE +PE =OP =3,∴OE =53,PE =43,∴CE =OC 2+OE 2=52+53 2=5310,BE =BP 2+PE 2=42+43 2=4310,∴BC =5310+4310=310.(3)过C 点作CG ⊥MN ,垂足为G ,连接CN ,则∠CGM =90°,∴∠CMG +∠GCM =90°,∵MN 是直径,∴∠MCN =90°,∴∠CNM +∠DMP =90°,∵∠D +∠DMP =90°,∴∠D =∠CNM =∠GCM ,∵tan ∠MDB =34,∴tan ∠CNM =tan ∠GCM =34,∵tan ∠GCM =GM CG∴设GM =3x ,CG =4x ,∴CM =5x ,∴CN =20x 3,NG =16x 3,∴NM =25x 3,∴OM =ON =25x 6,∵AM =2AN ,且AM 2+AN 2=MN 2,∴AN =553x ,AM =1053x ,∵S△AMN=12AM⋅AN=12MN⋅AP,∴AP=103x=PB,∴NP=53x,∴PG=163x-53x=113x,∵∠CGE=∠BPE=90°,∠CEG=∠BEP,∴△CGE∽△BPE,∴CG BP =GEPE=CEBE,即4x103x=GEPE=CEBE∴GE=2x,PE=53x∴ME=5x,NE=10x3,∴ME:NE=3:2,∴MENE的值为3 2.【点睛】本题考查了圆的相关知识、相似三角形的判定与性质、三角函数、勾股定理等知识,涉及到了动点问题,解题关键是构造相似三角形,正确表示出各线段并找出它们的关系,本题综合性较强,属于压轴题.2满分训练一、解答题【共20题】1(2022·内蒙古内蒙古·中考真题)如图,⊙O是△ABC的外接圆,EF与⊙O相切于点D,EF∥BC 分别交AB,AC的延长线于点E和F,连接AD交BC于点N,∠ABC的平分线BM交AD于点M.(1)求证:AD平分∠BAC;(2)若AB:BE=5:2,AD=14,求线段DM的长.【答案】(1)见解析(2)DM=2【解析】(1)证明:连接OD交BC于点H.∵EF与⊙O相切于点D∴OD⊥EF,∴∠ODF=90°,∵BC∥EF,∴∠OHC=∠ODF=90°,∴OD⊥BC,∴BD=CD,∴∠BAD=∠CAD 即AD平分∠BAC;(2)解:∵BC∥EF,∴BE AE =ND AD,∵AB:BE=5:2,AD=14,∴DN=2147,∵∠BAD=∠CAD,∠CAD=∠CBD,∴∠BAD=∠CBD,∵BM平分∠ABC,∴∠ABM=∠CBM,∴∠BAD+∠ABM=∠CBD+∠CBM,∴∠BMD=∠MBD,∴BD=DM,∵∠NBD=∠BAD,∠BDM=∠ADB,∴△BDN∽△ADB,∴ND BD =DB AD∴BD2=ND⋅AD=2147×14=4,∴BD=2(负值舍去),∴DM=BD=2【点睛】本题主要考查圆的基本性质,切线的性质、相似三角形的判定和性质,平行线分线段成比例定理,等腰三角形的判定和性质;找出相似三角形,列相似比求解是解决本题的关键.2(2022·湖北黄石·中考真题)如图CD是⊙O直径,A是⊙O上异于C,D的一点,点B是DC延长线上一点,连接AB、AC、AD,且∠BAC=∠ADB.(1)求证:直线AB是⊙O的切线;(2)若BC=2OC,求tan∠ADB的值;(3)在(2)的条件下,作∠CAD的平分线AP交⊙O于P,交CD于E,连接PC、PD,若AB=26,求AE ⋅AP的值.【答案】(1)见解析(2)22(3)42【解析】(1)解:如图所示,连接OA ,∵CD 是⊙O 直径,∴∠CAD =90°,∴∠OAC +∠OAD =90°,又∵OA =OD ,∴∠OAD =∠ODA ,∵∠BAC =∠ADB ,∴∠OAD =∠BAC ,∴∠BAC +∠OAC =90°,即∠BAO =90°,∴AB ⊥OA ,又∵OA 为半径,∴直线AB 是⊙O 的切线;(2)解:∵∠BAC =∠ADB ,∠B =∠B ,∴△BCA ∽△BAD ,∴ACAD =BC BA,由BC =2OC 知,令半径OC =OA =r ,则BC =2r ,OB =3r ,在Rt △BAO 中,AB =OB 2-OA 2=22r ,在Rt △CAD 中,tan ∠ADC =AC AD =BC BA =2r 22r=22,即tan ∠ADB =22;(3)解:在(2)的条件下,AB =22r =26,∴r =3,∴CD =23,在Rt △CAD 中,AC AD=22,AC 2+AD 2=CD 2,解得AC =2,AD =22,∵AP 平分∠CAD ,∴∠CAP =∠EAD ,又∵∠APC =∠ADE ,∴△CAP ∽△EAD ,∴AC AE =AP AD,∴AE ⋅AP =AC ⋅AD =2×22=42.【点睛】本题主要考查了圆切线的判定,直径所对的圆周角是直角,相似三角形的性质与判定,解直角三角形,勾股定理,等腰三角形的性质等等,熟知相关知识是解题的关键.3(2022·湖北襄阳·中考真题)如图,AB 是半圆O 的直径,点C 在半圆O 上,点D 为BC 的中点,连接AC ,BC ,AD ,AD 与BC 相交于点G ,过点D 作直线DE ∥BC ,交AC 的延长线于点E .(1)求证:DE 是⊙O 的切线;(2)若AC =BD ,CG =23,求阴影部分的面积.【答案】(1)见解析(2)1532【解析】(1)证明:连接OD ,如图所示,∵点D 为BC 的中点,∴OD ⊥BC∵DE ∥BC ,∴OD ⊥DE .∴DE 是⊙O 的切线.(2)连接BD ,如图所示,∵AC =BD∴BD =AC∵点D 为BC 的中点,∴CD =BD ,∴AC =CD =BD ,∴∠CAD =∠BAD =30°.∵AB 是半圆O 的直径,∴∠ACB =∠ADB =90°,在Rt △ACG 中,tan ∠CAD =CG CA ,sin ∠CAD =CG AG,∴CA =CG tan30°,AG =CG sin30°,∵CG =23,∴CA =23×3=6,AG =43,∴BD =CA =6,∴S △ACG =12CG ⋅AC =63,在Rt △ABD 中,tan ∠BAD =BD AD ,∴AD =BDtan30°=633=6 3.∵DE ∥BC ,∴S △CAG S △EAD =AG AD 2,即63S ΔEAD =49,∴S △EAD =2732.∴S 阴影部分=S △EAD -S △ACG =1532.【点睛】本题主要考查了切线的判定定理、垂径定理、圆周角定理以及相似三角形的性质,解直角三角形,掌握以上知识是解题的关键.4(2022·辽宁鞍山·中考真题)如图,⊙O 是△ABC 的外接圆,AB 为⊙O 的直径,点E 为⊙O 上一点,EF ∥AC 交AB 的延长线于点F ,CE 与AB 交于点D ,连接BE ,若∠BCE =12∠ABC .(1)求证:EF 是⊙O 的切线.(2)若BF =2,sin ∠BEC =35,求⊙O 的半径.【答案】(1)过程见解析(2)3【解析】(1)证明:连接OE .∵∠BCE =12∠ABC ,∠BCE =12∠BOE ,∴∠ABC =∠BOE ,∴OE ∥BC ,∴∠OED =∠BCD .∵EF ∥CA ,∴∠FEC =∠ACE ,∴∠OED +∠FEC =∠BCD +∠ACE ,即∠FEO =∠ACB .∵AB 是直径,∴∠ACB =90°,∴∠FEO =90°,∴FE ⊥EO .∵EO 是⊙O 的半径,∴EF 是⊙O 的切线.(2)∵EF ∥AC ,∵BF =2,sin ∠BEC =35.设⊙O 的半径为r ,∴FO =2+r ,AB =2r ,BC =65r .∵EO BC =FO AB ,∴r 65r =2+r 2r ,解得r =3,∴⊙O 的半径是3.【点睛】本题主要考查了切线的性质和判定,解直角三角形,熟练掌握相关定理是解题的关键.5(2022·辽宁朝阳·中考真题)如图,AC 是⊙O 的直径,弦BD 交AC 于点E ,点F 为BD 延长线上一点,∠DAF =∠B .(1)求证:AF 是⊙O 的切线;(2)若⊙O 的半径为5,AD 是△AEF 的中线,且AD =6,求AE 的长.【答案】(1)见解析(2)365【解析】(1)证明:∵AC 是直径,∴∠ADC =90°,∴∠ACD +∠DAC =90°,∵∠ACD =∠B ,∠B =∠DAF ,∴∠DAF =∠ACD ,∴∠DAF +∠DAC =90°,∴OA ⊥AF ,∵AC 是直径,∴AF 是⊙O 的切线;(2)解:作DH ⊥AC 于点H ,∵⊙O 的半径为5,∴AC =10,∵∠AHD =∠ADC =90°,∠DAH =∠CAD ,∴△ADH ~△ACD ,∴AD AC =AH AD,∴AD 2=AH ⋅AC ,∵AD =6,∴AH =3610=185,∵AD 是△AEF 的中线,∠EAF =90°,∴AD =ED ,AE=2AH=365.【点睛】本题主要考查了圆周角定理,切线的判定定理,相似三角形的判定与性质,等腰三角形的性质等知识,根据相似三角形的判定与性质求出AH的长是解题的关键.6(2022·山东菏泽·中考真题)如图,在△ABC中,以AB为直径作⊙O交AC、BC于点D、E,且D是AC的中点,过点D作DG⊥BC于点G,交BA的延长线于点H.(1)求证:直线HG是⊙O的切线;(2)若HA=3,cos B=25,求CG的长.【答案】(1)见解析(2)65【解析】(1)连接OD,∵DG⊥BC,∴∠BGH=90°,∵D是AC的中点,AB为直径,∴OD∥BC,∴∠BGH=∠ODH=90°,∴直线HG是⊙O的切线;(2)由(1)得OD∥BC,∴∠HBG=∠HOD,∵cos∠HBG=25,∴cos∠HOD=25,设OD=OA=OB=r,∵HA=3,∴OH=3+r,在Rt△HOD中,∠HDO=90°,∴cos∠HOD=ODOH =r3+r=25,解得r=2,∴OD=OA=OB=2,OH=5,BH=7,∵D是AC的中点,AB为直径,∴BC=2OD=4,∵∠BGH=∠ODH=90°,∴△ODH∼△BGH,∴OH BH =ODBG,即57=2BG,∴BG=145,∴CG=BC-BG=4-145=65.【点睛】本题考查了切线的判定,三角形中位线的性质,平行线的判定和性质,相似三角形的判定和性质及解直角三角形,熟练掌握知识点是解题的关键.7(2022·贵州黔西·中考真题)如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交AC于点E,DH⊥AC,垂足为H,连接DE并延长交BA的延长线于点F.(1)求证:DH是⊙O的切线;(2)若E为AH的中点,求EFFD的值.【答案】(1)见解析(2)23【解析】(1)连接OD,则OD=OB.∴∠ODB=∠ABC.∵AB=AC,∴∠ABC=∠C.∴∠ODB=∠C.∴OD∥AC.∴∠DHC=∠HDO.∵DH⊥AC,∴∠DHC=∠HDO=90°.∴DH⊥OD.∴DH是⊙O的切线.(2)连接AD和BE.∵AB是⊙O的直径,∴OA=OB,∠ADB=∠AEB=90°.∵OD∥AC∴OB OA =BD CD=1∴CD=BD.∴OD⎳AC且OD=12AC.∵OD∥AE,∴∠AEF=∠ODF.∵∠F=∠F,∴△FAE∽△FOD.∴FE FD =AE OD.∵∠DHA=∠BEA=90°∴DH∥BE∴CH HE =CD BD=1∴CH=HE.∵E为AH的中点,∴AE=EH=CH.∴AE=13AC∴FE FD =AEOD=13AC12AC=23.【点睛】本题考查了切线的判定和性质,圆周角定律,平行线分线段成比例,三角形相似的判定与性质等知识,熟练掌握以上判定和性质是本题解题的关键.8(2022·贵州安顺·中考真题)如图,AB是⊙O的直径,点E是劣弧BD上一点,∠PAD=∠AED,且DE=2,AE平分∠BAD,AE与BD交于点F.(1)求证:PA是⊙O的切线;(2)若tan∠DAE=22,求EF的长;(3)延长DE,AB交于点C,若OB=BC,求⊙O的半径.【答案】(1)见解析(2)1(3)2【解析】(1)证明:∵AB 是⊙O 的直径,∴∠ADB =90°,∴∠DAB +∠DBA =90°,∵AD =AD ,∴∠AED =∠ABD ,∵∠PAD =∠AED ,∴∠PAD =∠ABD ,∴∠BAD +∠PAD =∠BAD +∠ABD =90°,即∠PAB =90°,∴PA 是⊙O 的切线,(2)如图,连接OE ,EB ,∵AE 平分∠BAD ,∴∠DAE =∠BAE ,∴DE =BE =2∴OE ⊥BD∵OA =OE ,∴∠OEA =∠OAE ,∴∠DAE =∠AEO ,∴AD ∥OE ,∵AB 是⊙O 的直径,∴AD ⊥DB ,AE ⊥EB ,即∠ADF =∠BEF =90°,∵DE ⏜=DE⏜∴∠DAE =∠DBE ,∴tan ∠EBF =tan ∠DAE =22,∴EF EB =22,∴EF =22EB =1;(3)如图,过点B 作BG ∥AD ,由(2)可知AD ∥OE ,∴OE ∥BG ,∵AO =OB =BC ,∴DE =EG =GC ,设⊙O 的半径为x ,则GB =12OE =12x ,∵AD ∥BG ,∴△CGB ∽△CDA ,∴CG CD =GB AD ,∴AD =3GB =32x ,∵OE⊥DB,∴DB⊥GB,∵DE=2,∴DG=2DE=22,在Rt△DBG中,DB2=DG2-GB2=8-12x 2,在Rt△ADB中,AD2+DB2=AB2,即32x2+8-12x2=2x 2,解得:x=2(负值舍去),∴⊙O的半径为2.【点睛】本题考查了切线的判定,圆周角定理的推论,平行线分线段成比例,相似三角形的性质与判定,解直角三角形,综合运用以上知识是解题的关键.9(2022·山东枣庄·中考真题)如图,在半径为10cm的⊙O中,AB是⊙O的直径,CD是过⊙O上一点C的直线,且AD⊥DC于点D,AC平分∠BAD,点E是BC的中点,OE=6cm.(1)求证:CD是⊙O的切线;(2)求AD的长.【答案】(1)见解析(2)AD=365【解析】(1)证明:连接OC,如图:∵AC平分∠BAD,∴∠DAC=∠CAO,∵OA=OC,∴∠CAO=∠OCA,∴∠DAC=∠OCA,∴AD∥OC,∵AD⊥DC,∴CO⊥DC,∵OC是⊙O的半径,∴CD是⊙O的切线;(2)解:∵E是BC的中点,且OA=OB,∴OE是△ABC的中位线,AC=2OE,∵OE=6,∴AC=12,∵AB是⊙O的直径,∴∠ACB=90°=∠ADC,又∠DAC=∠CAB,∴△DAC∽△CAB,∴ADAC =ACAB,即AD12=1220,∴AD=365.【点睛】本题考查圆的切线的判定定理,相似三角形的判定及性质等知识,解题的关键是熟练应用圆的相关性质,转化圆中的角和线段.10(2022·山东济宁·中考真题)如图,在矩形ABCD中,以AB的中点O为圆心,以OA为半径作半圆,连接OD交半圆于点E,在BE上取点F,使AE=EF,连接BF,DF.(1)求证:DF与半圆相切;(2)如果AB=10,BF=6,求矩形ABCD的面积.【答案】(1)见解析(2)2003【解析】(1)证明:连接OF.∵AE=EF,∴∠DOA=∠FOD.∵AO=FO,DO=DO,∴△DAO≅△DFO(SAS)∴∠DAO=∠DFO.∵四边形ABCD是矩形,∴∠DAO=90°∴∠DFO=90°.∴DF与半圆相切.(2)解:连接AF,∵AO=FO,∠DOA=∠DOF,∴DO⊥AF,∵AB为半圆的直径,∴∠AFB=90°,∴BF⊥AF,∴DO∥BF.∴∠AOD=∠ABF.∵∠OAD=∠AFB=90°,∴△AOD∽△FBA∴AO BF =DO AB,∴56 BF =DO10,∴DO=253,在RtΔAOD中,AD=DO2-AO2=2532-52=203.∴矩形ABCD的面积为203×10=2003.【点睛】本题考查了切线的性质,相似三角形的性质与判定,勾股定理,矩形的性质,掌握以上知识是解题的关键.11(2022·青海西宁·中考真题)如图,在Rt△ABC中,∠C=90°,点D在AB上,以BD为直径的⊙O 与AC相切于点E,交BC于点F,连接DF,OE交于点M.(1)求证:四边形EMFC是矩形;(2)若AE=5,⊙O的半径为2,求FM的长.【答案】(1)详见解析(2)253【解析】(1)∵BD是⊙O的直径,∴∠BFD=90°,∴∠CFD=90°,∴⊙O与AC相切于点E,∴OE⊥AC,∴∠OEC=∠AEO=90°,又∴∠C=90°,∴∠C=∠CFD=∠OEC=90°,∴四边形EMFC是矩形.(2)解:在Rt△AOE中∠AEO=90°AE=5OE=OB=2,∴OA2=AE2+OE2,∴OA=AE2+OE2=52+22=3,∴AB=OA+OB=3+2=5,∴∠AEO=∠C=90°,∴OE⎳BC,∴△AEO∼△ACB,∴AE AC =AOAB,即5AC=35,∴AC =553,∴CE =AC -AE =553-5=253,∴四边形EMFC 是矩形,∴FM =CE =253.【点睛】本题考查了矩形的判定,相切,勾股定理,平行线的判定与性质以及相似三角形的判定与性质,解题的关键是:(1)根据各角之间的关系,找出四边形EMFC 的三个角均为直角.(2)利用勾股定理及相似三角形的性质,求出AC 的长度.12(2022·辽宁大连·中考真题)AB 是⊙O 的直径,C 是⊙O 上一点,OD ⊥BC ,垂足为D ,过点A 作⊙O 的切线,与DO 的延长线相交于点E .(1)如图1,求证∠B =∠E ;(2)如图2,连接AD ,若⊙O 的半径为2,OE =3,求AD 的长.【答案】(1)见解析(2)2213【解析】(1)解:∵OD ⊥BC ,∴∠ODB =90°,∵AE 是⊙O 的切线,∴∠OAE =90°,在ΔODB 和ΔOAE 中,∠ODB =∠OAE =90°,∠DOB =∠AOE ,∴∠B =∠E ;(2)解:如图,连接AC .∵⊙O 的半径为2,∴OA =OB =2,AB =4,∵在ΔODB 和ΔOAE 中,∠ODB =∠OAE =90°,∠DOB =∠AOE ,∴ΔODB ∼ΔOAE ,∴OD OA =OB OE ,即OD 2=23,∴OD =43,在RtΔODB中,由勾股定理得:OD2+DB2=OB2,∴DB=OB2-OD2=22-43 2=253.∵OD⊥BC,OD经过⊙O的圆心,∴CD=DB=253,∴BC=2DB=453.∵AB是⊙O的直径,C是⊙O上一点,∴∠ACB=90°,在RtΔACB中,由勾股定理得:AC2+BC2=AB2,2=83.∴AC=AB2-BC2=42-453在RtΔACD中,由勾股定理得:AC2+CD2=AD2,∴AD=AC2+CD2=83 2+253 2=2213.【点睛】本题考查切线的定义、圆周角定理、垂径定理、勾股定理、相似三角形的判定与性质等,综合性较强,熟练掌握上述知识点,通过证明ΔODB∼ΔOAE求出OD的长度是解题的关键.13(2022·青海·中考真题)如图,AB是⊙O的直径,AC是⊙O的弦,AD平分∠CAB交⊙O于点D,过点D作⊙O的切线EF,交AB的延长线于点E,交AC的延长线于点F.(1)求证:AF⊥EF;(2)若CF=1,AC=2,AB=4,求BE的长.【答案】(1)见解析(2)2【解析】(1)证明:连接OD,∵AD平分∠CAB,∴∠CAD=∠OAD,∵OA=OD,∴∠OAD=∠ODA,∴∠CAD=∠ODA,∴OD∥AF,∵EF为⊙O的切线,∴OD⊥EF,∴AF⊥EF.(2)解:由(1)得:OD∥AF,∴△ODE∽△AFE,∵AC=2,CF=1,∴AF=3,∵AB=4,∴OD=2,OB=2,∴OE:AE=OD:AF,设BE为x,∴OE=OB+BE=2+x,∴2+x 4+x =23,解得:x=2,即BE的长为2.【点睛】本题主要考查了切线的性质,相似三角形的判定和性质,熟练掌握切线的性质,相似三角形的判定和性质是解题的关键.14(2022·广西柳州·中考真题)如图,已知AB是⊙O的直径,点E是⊙O上异于A,B的点,点F是EB的中点,连接AE,AF,BF,过点F作FC⊥AE交AE的延长线于点C,交AB的延长线于点D,∠ADC的平分线DG交AF于点G,交FB于点H.(1)求证:CD是⊙O的切线;(2)求sin∠FHG的值;(3)若GH=42,HB=2,求⊙O的直径.【答案】(1)见解析(2)22(3)⊙O的直径为65【解析】(1)证明:连接OF.∵OA=OF,∴∠OAF=∠OFA,∵EF=FB,∴∠CAF=∠FAB,∴∠CAF=∠AFO,∴OF∥AC,∵AC⊥CD,∴OF ⊥CD ,∵OF 是半径,∴CD 是⊙O 的切线.(2)∵AB 是直径,∴∠AFB =90°,∵OF ⊥CD ,∴∠OFD =∠AFB =90°,∴∠AFO =∠DFB ,∵∠OAF =∠OFA ,∴∠DFB =∠OAF ,∵GD 平分∠ADF ,∴∠ADG =∠FDG ,∵∠FGH =∠OAF +∠ADG ,∠FHG =∠DFB +∠FDG ,∴∠FGH =∠FHG =45°,∴sin ∠FHG =sin45°=22(3)解:过点H 作HM ⊥DF 于点M ,HN ⊥AD 于点N .∵HD 平分∠ADF ,∴HM =HN ,S △DHF ∶S △DHB =FH ∶HB =DF ∶DB∵△FGH 是等腰直角三角形,GH =42∴FH =FG =4,∴DFDB=42=2设DB =k ,DF =2k ,∵∠FDB =∠ADF ,∠DFB =∠DAF ,∴△DFB ∽△DAF ,∴DF 2=DB •DA ,∴AD =4k ,∵GD 平分∠ADF∴FG AG =DF AD =12∴AG =8,∵∠AFB =90°,AF =12,FB =6,∴AB =AF 2+BF 2=122+622=65∴⊙O 的直径为65【点睛】本题是一道综合性题目,考查了圆的相关性质、切线的判定、相似三角形的判定和性质、角平分线性、勾股定理等知识,熟练掌握以上知识是解题的关键.15(2022·广西河池·中考真题)如图,AB 是⊙O 的直径,E 为⊙O 上的一点,∠ABE 的平分线交⊙O 于点C ,过点C 的直线交BA 的延长线于点P ,交BE 的延长线于点D .且∠PCA =∠CBD .(1)求证:PC为⊙O的切线;(2)若PC=22BO,PB=12,求⊙O的半径及BE的长.【答案】(1)见解析(2)⊙O的半径为3,BE的长为2【解析】(1)证明:连接OC,∵BC平分∠ABE,∴∠ABC=∠CBD,∵OC=OB,∴∠ABC=∠OCB,∵∠PCA=∠CBD,∴∠PCA=∠OCB,∵AB是直径,∴∠ACB=90°,∴∠ACO+∠OCB=90°,∴∠PCA+∠ACO=90°,∴∠PCO=90°,∴OC⊥PC,∵OC是半径,∴PC是OO的切线;(2)连接AE,设OB=OC=r,∵PC=22OB,∴PC=22r,∴OP=OC2+PC2=r2+(22r)2=3r,∵PB=12,∴4r=12,∴r=3,由(1)可知,∠OCB=∠CBD,∴OC=BD,△PCO∽△PDB∴OC BD =OPPB,∠D=∠PCO=90°,∴3 BD =9 12,∴BD=4,∵AB是直径,∴∠AEB=90°,∴∠AEB=∠D=90°,∴AE⎳PD,∴BE BD =BA BP,∴BE4=6 12,∴BE=2.【点睛】本题考查了切线的判定,勾股定理,等腰三角形的性质、相似三角形的性质与判定,平行线分线段成比例,解题的关键是学会添加常用辅助线,构造平行线解决问题.16(2022·山东聊城·中考真题)如图,点O是△ABC的边AC上一点,以点O为圆心,OA为半径作⊙O,与BC相切于点E,交AB于点D,连接OE,连接OD并延长交CB的延长线于点F,∠AOD=∠EOD.(1)连接AF,求证:AF是⊙O的切线;(2)若FC=10,AC=6,求FD的长.【答案】(1)见解析(2)FD的长为8310-83【解析】(1)根据SAS证△AOF≌△EOF,得出∠OAF=∠OEF=90°,即可得出结论;(2)根据勾股定理求出AF,证△OEC∽△FAC,设圆O的半径为r,根据线段比例关系列方程求出r,利用勾股定理求出OF,最后根据FD=OF-OD求出即可.(1)证明:在△AOF和△EOF中,OA=OE∠AOD=∠EOD OF=OF,∴△AOF≌△EOF(SAS),∴∠OAF=∠OEF,∵BC与⊙O相切,∴OE⊥FC,∴∠OAF=∠OEF=90°,即OA⊥AF,∵OA是⊙O的半径,∴AF是⊙O的切线;(2)解:在Rt△CAF中,∠CAF=90°,FC=10,AC=6,∴AF=FC2-AC2=8,∵BC与⊙O相切,AF是⊙O的切线∴∠OEC=∠FAC=∠90°,∵∠OCE=∠FCA,∴△OEC∽△FAC,∴EO AF =CO CF,设⊙O的半径为r,则r8=6-r10,解得r=8 3,在Rt△FAO中,∠FAO=90°,AF=8,AO=8 3,∴OF=AF2+AO2=8310,∴FD=OF-OD=8310-83,即FD的长为8310-83.【点睛】本题主要考查切线的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质、勾股定理等知识,熟练掌握切线的判定和性质是解题的关键.17(2022·湖南湘西·中考真题)如图,在Rt△ABC中,∠B=90°,AE平分∠BAC交BC于点E,O为AC上一点,经过点A、E的⊙O分别交AB、AC于点D、F,连接OD交AE于点M.(1)求证:BC是⊙O的切线.(2)若CF=2,sin C=35,求AE的长.【答案】(1)见解析(2)1255【解析】(1)连接OE,方法一:∵AE平分∠BAC交BC于点E,∴∠BAC=2∠OAE,∵∠FOE=2∠OAE,∴∠FOE=∠BAC,∴OE∥AB,∵∠B=90°,∴OE ⊥BC ,又∵OE 是⊙O 的半径,∴BC 是⊙O 的切线;方法二:∵AE 平分∠BAC 交BC 于点E ,∴∠OAE =∠BAE ,∵OA =OE ,∴∠OAE =∠OEA ,∴∠BAE =∠OEA ,∴OE ∥AB ,∵∠B =90°,∴OE ⊥BC ,又∵OE 是⊙O 的半径,∴BC 是⊙O 的切线;(2)连接EF ,∵CF =2,sin C =35,∴OE OF +CF=35,∵OE =OF ,∴OE =OF =3,∵OA =OF =3,∴AC =OA +OF +CF =8,∴AB =AC •sin C =8×35=245,∵∠OAE =∠BAE ,∴cos ∠OAE =cos ∠BAE ,即AB AE =AE AF ,∴245AE=AE 3+3,解得AE =1255(舍去负数),∴AE 的长为1255.【点睛】本题主要考查切线的判定和三角函数的应用,熟练掌握切线的判定定理和三角函数是解题的关键.18(2022·甘肃兰州·中考真题)如图,⊙O 是△ABC 的外接圆,AB 是直径,OD ⊥OC ,连接AD ,∠ADO =∠BOC ,AC 与OD 相交于点E .(1)求证:AD 是⊙O 的切线;(2)若tan ∠OAC =12,AD =32,求⊙O 的半径.【答案】(1)见解析(2)2【解析】(1)证明:∵OD⊥OC,∴∠COD=90°,∵∠BOC+∠COD+∠AOD=180°,∴∠BOC+∠AOD=90°,∵∠ADO=∠BOC,∴∠ADO+∠AOD=90°,∵∠ADO+∠AOD+∠OAD=180°,∴∠OAD=90°,∵OA是⊙O的半径,∴AD是⊙O的切线;(2)解:∵AB是⊙O的直径,∴∠ACB=90°,∴∠B+∠BAC=90°,∵∠BAC+∠CAD=∠OAD=90°,∴∠B=∠CAD,∵∠B+∠BOC+∠OCB=∠ADO+∠CAD+∠AED=180°,∠ADO=∠BOC,∴∠AED=∠OCB,∵OB=OC,∴∠B=∠OCB,∴∠AED=∠CAD,∴DE=AD=32,∵OC=OA,∴∠OAC=∠OCA,∵OC⊥OD,∴∠COE=90°,∴tan∠OAC=tan∠OCA=OEOC =12,设OC=OA=R,则OE=12 R,在Rt△OAD中,∠OAD=90°,由勾股定理,得OD2=OA2+AD2,即12R+322=R2+32 2,解得:R=2或R=0(不符合题意,舍去),∴⊙O的半径为2.【点睛】本题考查切线的判定,解直角三角形,勾股定理,等腰三角形的判定,圆周角定理的推论,本题属圆的综合题目,熟练掌握相关性质与判定是解题的关键.19(2022·广东广州·中考真题)如图,AB是⊙O的直径,点C在⊙O上,且AC=8,BC=6.(1)尺规作图:过点O作AC的垂线,交劣弧AC于点D,连接CD(保留作图痕迹,不写作法);(2)在(1)所作的图形中,求点O到AC的距离及sin∠ACD的值.【答案】(1)作图见解析;(2)点O到AC的距离为3,sin∠ACD的值是55【解析】(1)解:①分别以A,C为圆心,适当长(大于AC长度的一半)为半径作弧,记两弧的交点为E;②作直线OE,记OE与AC交点为D;③连结CD,则线段AC的垂线DE、线段CD为所求图形,如下图所示;(2)解:记OD与AC的交点为F,如下图所示:∵OD⊥AC,∴F为AC中点,∴OF是△ABC的中位线,∴OF=12BC=3,∵OF⊥AC,∴OF的长就是点O到AC的距离;Rt△ABC中,∵AC=8,BC=6,∴AB=10,∴OD=OA=12AB=5,∴DF=OD-OF=5-3=2,∵F为AC中点,∴CF=12AC=4,Rt△CDF中,∵DF=2,CF=4,∴CD=25,则sin∠ACD=DFCD=225=55,∴点O到AC的距离为3,sin∠ACD的值是55.【点睛】本题考查了圆的基本性质、垂径定理及其推论、勾股定理、线段垂直平分线的尺规作图、锐角三角函数等,属于综合题,欲求某角的某三角函数值,首先想到的应该是能否在直角三角形中进行,如果没有现成的直角三角形,则需要设法构造(作辅助图形).20(2022·山东淄博·中考真题)已知△ABC是⊙O的内接三角形,∠BAC的平分线与⊙O相交于点D,连接DB.(1)如图1,设∠ABC的平分线与AD相交于点I,求证:BD=DI; 图1(2)如图2,过点D作直线DE∥BC,求证:DE是⊙O的切线; 图2(3)如图3,设弦BD,AC延长后交⊙O外一点F,过F作AD的平行线交BC的延长线于点G,过G作⊙O的切线GH(切点为H),求证:GF=GH. 图3【答案】(1)见解析(2)见解析(3)见解析【解析】(1)证明:∵AD是∠BAC的平分线,BI是∠ABC的平分线,∴∠BAD=∠DAC=∠CBD,∠ABI=∠IBC,∵∠BID=∠ABI+∠BAD,∠DBI=∠IBC+∠CBD,∴∠BID=∠DBI,∴BD=DI;(2)证明:连接OD,∵AD是∠BAC的平分线,∴BD=CD,∴OD⊥BC,∵DE∥BC,∴OD⊥DE,∵OD是⊙O的半径,∴DE是⊙O的切线;(3)证明:过点H作⊙O的直径HI,连接BH,HC,IC,∵HI是⊙O的直径,GH是⊙O的切线,∴∠HCI =∠IHG =90°,∴∠IHC +∠I =90°=∠IHC +∠GHC ,∴∠I =∠GHC ,∵∠HBG =∠I ,∴∠HBG =∠GHC ,∴△HBG ∽△CHG ,∴HG CG =GB HG,∴GH 2=GC ×GB ,∵AD ∥FG ,∴∠DAF =∠GFC ,∵∠DAF =∠DBC ,∴∠GFC =∠DBC ,∴△GFC ∽△GBF ,∴GF GB =GC GF,∴GF 2=GC ×GB ,∴GF 2=GH 2,∴GF =GH .【点睛】本题考查了切线的判定和性质,相似三角形的判定和性质,圆周角定理,垂径定理,解题的关键是正确寻找相似三角形解决问题,学会用转化的思想思考问题.。

三角函数的图象与性质的综合问题1.三角函数的基本性质: 例1.函数)2sin()3sin(ππ++=x x y 的最小正周期是=T _________。
演变1.函数x x y 66cos sin +=的最小正周期为_________ 演变2.函数)1(2cos2cos-=x x y ππ的周期为______;例 2.已知函数)12(cos )(2π+=x x f ,x x g 2sin 211)(+=,则函数)()()(x g x f x h +=的单调增区间为_________。
演变1.函数x x x x y 22cos 2cos sin 3sin ++=,]2,0[π∈x 的单调递减区间为_________例3.函数)3sin()3cos(3)(θθ---=x x x f ,]0,[πθ-∈是奇函数,则=θ_____。
演变1.已知f (x )sin(x )x )θθ=++,[0,]2πθ∈为偶函数,则θ的值为____演变2.若)4sin(3)4sin()(ππ-++=x x a x f 是偶函数,则a = . 2.三角函数图象与性质的综合问题: 例1.已知函数)8cos()8sin(2)8(sin 21)(2πππ++++-=x x x x f ,求:(1)函数)(x f 的最小正周期; (2)函数)(x f 的单调增区间。
演变1.已知函数x x x x x f 22cos 2cos sin 3sin )(++=(R x ∈) (1)求函数)(x f 的最小正周期和单调增区间;(2)函数)(x f 的图象可以由函数x y 2sin =(R x ∈)的图象经过怎样变换得到?演变2.已知函数)(sin )(2ϕω+=x A x f (0>A 、0>ω、20πϕ<<),若函数)(x f 的最大值为2,其图象相邻两对称轴之间的距离为2,并且过点(1,2)。
(1)求ϕ的值以及函数)(x f 的单调递增区间; (2)求(1)(2)(3)(2012)f f f f +++⋅⋅⋅+的值。

三角函数的最值和综合应用作者:吴文尧来源:《数学金刊·高考版》2014年第10期重点:熟悉基本三角函数最值的求法;通过变形、换元等方法把非基本的三角函数化为基本的三角函数或基本的代数函数的最值问题.难点:含参数的三角函数最值问题;三角函数最值的综合应用问题.1. 三角函数的值域或最值的考查,一般有以下两种形式:一种是化为一个角的三角函数的形式,如y=Asin(ωx+φ)+k,要注意角的取值范围的考虑;另一种是转化为以某一三角函数为未知数的常见函数问题,如y=f(sinx),要注意数形结合思想的应用. 具体类型有:(1)y=asinx+b(或y=acosx+b)型:利用三角函数的有界性或单调性求解.(2)y=asinx+bcosx型:引用辅助角化为y=sin(x+φ)的形式再利用三角函数的有界性求解.(3)y=asin2x+bcosx+c(或y=acos2x+bsinx+c)型:先进行换元,化为一个角的同名三角函数形式的一元二次式,利用配方法或图象法求解.(4)y=或y=型:用分离常数法化为只在分母上含有变量的关系,再根据有界性求解.(5)y=或y=型:可借助直线的斜率的关系用数形结合的方法求解.(6)含有sinx±cosx,sinx·cosx型:设t=sinx±cosx,将sinx·cosx转化为t的关系式,化为关于t的函数的最值问题进行处理.(7)y=asinx+型:利用函数的单调性求解.2.对于三角函数最值的应用问题通常可用“目标函数”的方法解决,其解题步骤可总结为:“变量→函数→值域”.变量:选择一个量为目标函数的自变量(通常选择某一个角为变量);函数:求出目标函数的解析式及定义域;最值:求出目标函数的值域,即得所需结论.例1 (2014年高考新课标卷II)设函数f(x)=sin.若存在f(x)的极值点x0满足x+[f (x0)]2A. (-∞,-6)∪(6,+∞)B. (-∞,-4)∪(4,+∞)C. (-∞,-2)∪(2,+∞)D. (-∞,-1)∪(4,+∞)思索要求得m的取值范围,只需要得到m满足的不等式,故把条件“存在f(x)的极值点x0满足x+[f(x0)]2破解由=kπ+解得x0=k+m,此时f(x0)=±. x+[f(x0)]24,即m2. 故选C.例2 在△ABC中,已知内角A=,边BC=2. 设内角B=x,周长为y.(1)求函数y=f(x)的解析式和定义域;(2)求y的最大值.思索三角函数最值的考查更多是综合性的应用,三角函数中的三角形问题与三角公式的恒等变换的结合是近年高考考查的热点.本题第(1)问利用正弦定理表示出三角形另两边关于角B的函数关系;第(2)问利用三角公式进行恒等变换,将函数化为y=Asin(ωx+φ)+k的形式,再求最值.破解(1)△ABC的内角和A+B+C=π,由A=,B>0,C>0得0(2)因为y=4sinx+cosx+sinx+2=4sinx++2例3 (2014年高考浙江卷)如图1,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练. 已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小. 若AB=15 m,AC=25 m,∠BCM=30°,则tanθ的最大值是________.(仰角θ为直线AP和平面ABC所成的角)图1思索(1)注意到在图中没有画出角θ,所以首先要画出直线AP和平面ABC所成的角.图2(2)如图2,要求tanθ的最大值,即求PQ∶QA的最大值,注意到CQ=PQ,所以原问题转化为:在△AQC中,求两边长的比QC∶QA的最大值.已知∠ACQ为定值,因此可选择∠QAC=φ为目标函数的变量,然后把tanθ表示成φ的函数,进而求出tanθ的最大值.破解作PQ⊥BC于Q,则PQ⊥平面ABC,连接AQ,则∠PAQ为直线AP和平面ABC 所成的角θ.由已知,BC=20 m,所以sin∠ACB=,令∠QAC=φ,在△AQC中,由正弦定理可知===AQ,即=sinφ. 又因为CQ=PQ,在Rt△PQA中,tanθ==·sinφ≤,即φ=90°时,tanθ的最大值为.点评这是一个立体几何与三角函数综合的最值问题,解决这类问题通常有以下两种方法:一是利用目标函数法解决;二是利用几何意义法解决. 在用目标函数法求最值时,当可用某一线段长作为目标函数的变量,也可用某一角的大小作为目标函数的变量时,多数情况下选择以角为变量,因为角的几何意义比较明显,且学过的一些三角公式可以发挥作用(如该例题没有选择以BQ或CQ为目标函数的变量,而选择∠QAC为目标函数的变量). 本题还可以利用几何意义法解决,你能想到吗?例4 (2014年高考辽宁卷)对于c>0,当非零实数a,b满足4a2-2ab+4b2-c=0,且使u=2a+b最大时,S=-+的最小值为________.思索本题可以运用三角代换的方法,把它化归为三角函数的最值问题.破解 4a2-2ab+4b2-c=0?圳5(a-b)2+3(a+b)2=2c?圳2+2=1,所以可令a-b=cosθ,a+b=sinθ,解得a=sinθ+cosθ,b=sinθ-cosθ.?摇所以u=2a+b=(3sinθ+cosθ)=(sinθ+cosθ)=sinθ+cosθ=·sin (θ+φ)(其中φ=arcsin). 所以θ+φ=时,umax=,此时,sinθ=cosφ=,cosθ=sinφ=.由此可得a=,b=,所以S=-+=-+= -+=--2.所以=,即c=时,Smin=-2.1.若△ABC的内角满足sinA+sinB=2sinC,则cosC的最小值是________.2. 已知函数f(x)=-sin2x++6sinxcosx-2cos2x+1,x∈R.(1)求f(x)的最小正周期;(2)求f(x)在区间0,上的最大值和最小值.?摇3. 如图3,A是单位圆与x轴正半轴的交点,点B,P在单位圆上,且已知B-,,∠AOB=α,∠AOP=θ(0(1)求cosα+sinα;(2)求·+S的最大值及此时θ的值θ0 .图34. 已知向量a=cosx,sinx,b=cos,-sin,c=(1,-1),其中 -≤x≤, f(x)=(a+c2-3)(b+c2-3),求f(x)的最大值和最小值.5. 如图4,扇形OPQ的半径为R,圆心角∠POQ=α0图4参考答案1.2. (1)函数f(x)的最小正周期为π.(2)函数f(x)的最小值为-2,最大值为2.3. (1)因B-,,∠AOB=α,cosα=-,sinα=,故cosα+sinα=.(2)由已知得,A(1,0),P(cosθ,sinθ),所以=(1+cosθ,sinθ),·=1+cosθ. 又S=sinθ,所以·+S=sinθ+cosθ+1=sinθ++1(04. 最大值为,最小值为-8.5. (1)当内接矩形仅有一个顶点在弧PQ上时(如图5),设∠AOP=θ,在Rt△AOD 中,AD=Rsinθ,OD=Rcosθ.在Rt△BOC中,OC=BCcotα=ADcotα=Rsinθcotα,所以CD=OD-OC=Rcosθ-Rsinθcotα.其面积S=f(θ)=CD·DA=R2(sinθcosθ-cotαsin2θ)?摇=R2(sin2θ+cotα·cos2θ-cotα)=·(sin2θsinα+cosα·cos2θ-cosα)=·[cos(α-2θ)-cosα],所以θ=时,Smax=R2=R2tan.图5 图6(2)当内接矩形有且仅有两个顶点在弧PQ上时(如图6),设弧PQ的中点为T,A,B 在OT上的射影分别为F,E,则矩形ABEF是扇形OTP的内接矩形,且仅有一个顶点在弧TP 上,∠POT=. 由(1)可知,矩形ABEF的面积的最大值为R2tan,所以矩形ABCD的面积的最大值Smax=R2tan.由于tan=>2tan,所以R2tan>R2tan. 由(1)(2)可知,Smax=R2tan.。

高考三角函数问题专题复习一、三角函数基础题1、已知角α的终边通过点P(-3,4),则sinα+cosα+tan α= ( )A.1523-B.1517-C.151-D.15172、π617sin = ( ) A.21 B.23- C.21- D.23-3、x y 2sin 21=的最小正周期是 ( ) A.2π B.π C.2π D. 4π 4、设tan α=2,且sin α<0,则cos α的值等于 ( ) A.55 B.51- C.55- D.51 5、y=cos 2(2x)的最小正周期是 ( )A .2π B. π C.4π D.8π 6、命题甲:sin x=1,命题乙:x=2π,则 ( ) A.甲是乙充分条件但不是必要条件 B.甲是乙的必要条件但不是充分条件C.甲是乙的充分必要条件D.甲不是乙的必要条件也不是乙的充分条件7、命题甲:A=B ,命题乙:sinA=sinB,则 ( )A.甲不是乙的必要条件也不是乙的充分条件B.甲是乙的充分必要条件C.甲是乙的必要条件但不是充分条件D.甲是乙的充分条件但不是必要条件8、函数y=sin x 在区间________上是增函数. ( )A.[0,π]B.[π,2π]C.]25,23[ππ D .]87,85[ππ 9、函数)43tan(π+=x y 的最小正周期为 ( )A.3πB.πC.32π D.3π 10、设角α的终边通过点P (-5,12),则cot α+sin α等于 ( ) A.137 B.-137 C.15679 D.- 1567911、函数y=cos3x -3sin3x 的最小正周期和最大值分别是 ( )A.32π, 1B.32π, 2 C.2π, 2 D.2π, 1 12、若23cos ],2,[-=∈x x ππ ,则x 等于 ( ) A.67πB.34πC.35πD.611π13、已知57cos sin ,51cos sin =-=+αααα,则tan α等于( ) A.34- B.-43C.1D.- 114、 150cos =( ) A.21 B.23 C.﹣21D. ﹣2315、在△ABC 中,AB=3,AC=2,BC=1,则sin A 等于 ( ) A.0 B.1 C.23 D.2116、在]2,0[π上满足sinx≤-0.5的x 的取值范围是区间 ( )A.[0,6π] B.[6π,65π] C.]67,65[ππD .]611,67[ππ17、使等式cosx=a -2有意义的a 的取值范围是区间( ) A .[0,2] B.[1,3] C.[0,1] D.[2,3]18、=-+-)690sin(495tan )585cos( ( ) A .22 B.32C.32- D.219、如果51cos sin =+x x ,且0≤x<π,那么tanx= ( ) A .34- B.43- C.43 D.34。

第20讲 导数与三角函数的综合问题高考预测一:含三角函数的不等式恒成立问题1.设2()cos 12x f x x =+-.(Ⅰ)求证:当0x 时,()0f x ;(Ⅱ)若不等式sin cos 2ax e x x -+对任意的0x 恒成立,求实数a 的取值范围.【解析】(Ⅰ)证明:2()cos 1(0)2x f x x x =+-,则()sin f x x x '=-,设()sin x x x ϕ=-,则()1cos x x ϕ'=-,⋯(2分)当0x 时,()1cos 0x x ϕ'=-,即()sin f x x x '=-为增函数, 所以()(0)0f x f ''=,即()f x 在0x 时为增函数,所以()(0)0f x f =.⋯(4分)(Ⅱ)解法一:由(Ⅰ)知0x 时,sin x x ,2cos 12x x -+,所以21sin cos 22x x x x ++-+,⋯(6分)设2()12xx G x e x =---,则()1x G x e x '=--,设()1x g x e x =--,则()1x g x e '=-,当0x 时()10x g x e '=-,所以()1x g x e x =--为增函数, 所以()(0)0g x g =,所以()G x 为增函数,所以()(0)0G x G =, 所以sin cos 2x e x x -+对任意的0x 恒成立.⋯(8分) 又0x ,1a 时,ax x e e ,所以1a 时sin cos 2ax e x x -+对任意的0x 恒成立.⋯(9分)当1a <时,设()sin cos 2ax h x e x x =-+-,则()cos sin ax h x ae x x '=--,(0)10h a '=-<, 所以存在实数00x >,使得任意0(0,)x x ∈,均有()0h x '<,所以()h x 在0(0,)x 为减函数, 所以在0(0,)x x ∈时()(0)0h x h <=,所以1a <时不符合题意. 综上,实数a 的取值范围为[1,)+∞.⋯(12分)(Ⅱ)解法二:因为sin cos 2ax e x x -+等价于(sin cos 2)ax ln x x -+⋯(6分) 设()(sin cos 2)g x ax ln x x =--+,则sin cos ()sin cos 2x xg x a x x +'=--+可求sin cos [1,1]sin cos 2x xx x +∈--+,⋯(8分)所以当1a 时,()0g x '恒成立,()g x 在[0,)+∞是增函数, 所以()(0)0g x g =,即(sin cos 2)ax ln x x -+,即sin cos 2ax e x x -+ 所以1a 时,sin cos 2ax e x x -+对任意0x 恒成立.⋯(9分) 当1a <时,一定存在00x >,满足在0(0,)x 时,()0g x '<, 所以()g x 在0(0,)x 是减函数,此时一定有()(0)0g x g <=,即(sin cos 2)ax ln x x <-+,即sin cos 2ax e x x <-+,不符合题意,故1a <不能满足题意, 综上所述,1a 时,sin cos 2ax e x x -+对任意0x 恒成立.⋯(12分)2.已知函数()y f x =的定义域为R ,且对任意实数a 、b ,都有()f a b f +=(a )f +(b ),当0x >时,()0f x <恒成立.(1)求证:函数()y f x =是R 上的减函数;(2)若不等式22(1)()f mx x f x mx -+<--对任意实数x 恒成立,求实数m 的取值范围. 【解析】(1)证明:设12x x <,则210x x ->, 当0x >时,()0f x <恒成立,则21()0f x x -<, 12121()()()()f x f x x f x f x ∴+-=<,∴函数()y f x =是R 上的减函数;(2)解:(0)2(0)f f =,则(0)0f =.不等式2222(1)()(1)()(0)f mx x f x mx f mx x f x mx f -+<--⇔-++-<22[(1)(1)1](0)(1)(1)10f m x m x f m x m x ⇔+-++<⇔+-++>. ①当1m =-时,10>,显然成立;②1m ≠-,则1m >-且△2(1)4(1)0m m =+-+<,解得13m -<<. 综上,实数m 的取值范围是[1-,3).3.已知函数()sin x f x e x =,其中x R ∈, 2.71828e ==⋯为自然对数的底数. (Ⅰ)求函数()f x 的单调区间;(Ⅱ)当[0,]2x π∈时,()f x kx ,求实数k 的取值范围.【解析】解:(Ⅰ)()sin cos (sin cos )x x x f x e x e x e x x '=+=+,令sin cos )4y x x x π=+=+,当(24x k ππ∈-,32)4k ππ+,()0f x '>,()f x 单调递增,(2分) 3(24x k ππ∈+,72)4k ππ+,()0f x '<,()f x 单调递减 (4分)(Ⅱ) 令()()sin x g x f x kx e x kx =-=-,即()0g x 恒成立, 而()(sin cos )x g x e x x k '=+-,令()(sin cos )()(sin cos )(cos sin )2cos x x x x h x e x x h x e x x e x x e x =+⇒'=++-=, [0x ∈,]2π,()0()h x h x '⇒在[0,]2π上单调递增,21()h x e π,(6分) 当1k 时,()0g x ',()g x 在[0,]2π上单调递增,()(0)0g x g =,符合题意;当2k e π时,()0()g x g x '⇒在[0,]2π上单调递减,()(0)0g x g =,与题意不合;(8分)当21k e π<<时,()g x '为一个单调递增的函数,而(0)10g k '=-<,2()02g e k ππ'=->,由零点存在性定理,必存在一个零点0x ,使得0()0g x '=, 当[0x ∈,0)x 时,()0g x ',从而()g x 在[0x ∈,0)x 上单调递减, 从而()(0)0g x g =,与题意不合,综上所述:k 的取值范围为(-∞,1](12分) 4.已知函数2()(1)xf x x e-=+,3()12cos 2x g x ax x x =+++,当[0x ∈,1]时,(Ⅰ)若函数()g x 在0x =处的切线与x 轴平行,求实数a 的值; (Ⅱ)求证:11()1x f x x-+; (Ⅲ)若()()f x g x 恒成立,求实数a 的取值范围. 【解析】解:(23)()2(cos sin )2I g x a x x x x '=++-,函数()g x 在0x =处的切线与x 轴平行,则(0)20g a '=+=, 得2a =-.()II 证明:①当[0x ∈,1]时,2(1)1(1)(1)x x x x e x x e x e --+-⇔+-,令()(1)(1)x x h x x e x e -=+--,则()()x x h x x e e -'=-.当[0x ∈,1]时,()0h x ', ()h x ∴在[0,1]上是增函数, ()(0)0h x h ∴=,即()1f x x -.②当[0x ∈,1]时,1()11x f x e x x⇔++,令()1x u x e x =--,则()1xu x e '=-. 当[0x ∈,1]时,()0u x ',()u x ∴在[0,1)单调递增,()(0)0u x u ∴=, 1()1f x x∴+, 综上可知:11()1x f x x-+; (Ⅲ)解:设231()()()(1)(12cos )2x G x f x g x x e ax x x x -=-=+-+++231112cos (12cos )22x x ax x x x x a x -----=-+++.令2()2cos 2x H x x =+,则()2sin H x x x '=-,令()2sin K x x x =-,则()12cos K x x '=-. 当[0x ∈,1]时,()0K x '<, 可得()H x '是[0,1)上的减函数,()(0)0H x H ∴''=,故()H x 在[0,1)单调递减, ()(0)2H x H ∴=.1()3a H x a ∴+++.∴当3a -时,()()f x g x 在[0,1)上恒成立.下面证明当3a >-时,()()f x g x 在[0,1)上不恒成立.23111()()(12cos )(2cos )1212x f x g x ax x x x x a x x x --+++=-+++++.令211()2cos ()121x v x a x a H x x x=+++=++++,则21()()(1)v x H x x -'=+'+. 当[0x ∈,1]时,()0v x ',故()v x 在[0,1]上是减函数, ()(12cos1v x a ∴∈++,3]a +.当3a >-时,30a +>.∴存在0(0,1)x ∈,使得0()0v x >,此时,00()()f x g x <.即()()f x g x 在[0,1)不恒成立. 综上实数a 的取值范围是(-∞,3]-.高考预测二:含三角的不等式证明 5.已知函数()cos sin 1(0)f x x x x x =-+>. (Ⅰ)求()f x 的单调区间;(Ⅱ)记i x 为()f x 的从小到大的第*()i i N ∈个零点,证明:对一切*n N ∈,有2221211123n x x x ++⋯+<. 【解析】解:(Ⅰ)()cos sin 1(0)f x x x x x =-+>,()cos sin cos sin f x x x x x x x ∴'=--=-,由()sin 0f x x x '=-=,解得*()x k k N π=∈,当(2x k π∈,(21))()k k N π+∈,sin 0x >,此时()0f x '<,函数单调递减, 当((21)x k π∈+,(22))()k k N π+∈,sin 0x <,此时()0f x '>,函数单调递增,故()f x 的单调增区间为((21)k π+,(22))k π+,0k ,单调递减区间为(2k π,(21))k π+,*)k N ∈. (Ⅱ)由(Ⅰ)知,()f x 在区间(0,)π上单调递减, 又()02f π=,故12x π=,当*n N ∈,1()((1))[(1)1][(1)(1)1]0n n f n f n n n ππππ++=-+-++<, 且函数()f x 的图象是连续不间断的,()f x ∴在区间(n π,(1))n π+内至少存在一个零点,又()f x 在区间(n π,(1))n π+是单调的, 故1(1)n n x n ππ+<<+, 因此当1n =时,有2211423x π=<成立. 当2n =时,有222121112(41)3x x π+<+<. 当3n 时, ⋯2222222212111111111111111[41][5][51]2(1)12(2)(1)22321n x x x n n n n n πππ++⋯+<+++⋯+<++⋯+<+-+-+⋯+--⨯---- 221162(6)13n ππ<-<<-. 综上证明:对一切*n N ∈,有2221211123n x x x ++⋯+<. 6.已知函数()()f x xln x a =+,a R ∈.()I 若()f x 不存在极值点,求a 的取值范围;(Ⅱ)若0a ,证明:()sin 1x f x e x <+-. 【解析】解:(Ⅰ)()()()xf x ln x a x a x a'=++>-+, 设()()xg x ln x a x a=+++()x a >- 22()()x ag x x a +'=+,()x a >-(1)0a 时:2()0x a x a a x a +=+++>,()0g x '> ()g x 在(,)a -+∞上单增,其值域是(,)-∞+∞,存在0(,)x a ∈-+∞,使00()()0f x g x '==,且()f x '在0x x =处左右两边值异号, 0x x =是()f x 的极值点,得0a 不可取; (2)0a <时:(,2)x a a ∈--时,()0g x '<,()g x 在其上单减 (2,)x a ∈-+∞时,()0g x '>,()g x 在其上单增(2)0g a '-=,()g x 在2x a =-处取极小值也是最小值(2)()2g a ln a -=-+若(2)()20g a ln a -=-+ 即21a e -, ()()0f x g x '=,()f x 在(,)a -+∞上单增,无极值点得21a e-可取, 若(2)()20g a ln a -=-+< 即210a e-<< ()g x 在(2,)a -+∞上的值域是(()2ln a -+,)+∞存在1(2,)x a ∈-+∞,使11()()0f x g x '==,且()f x '在1x x =处左右两边值异号, 1x x =是()f x 的极值点得210a e -<<不可取; 所以a 的取值范围是(-∞,21]e -. (Ⅱ)0a ,x a >-,故0x >,()()f x xln x a xlnx =+, 要证明()sin 1x f x e x <+-,只需证明sin 1x xlnx e x <+-,(1)当01x <时,sin 10x e x +->,0xlnx , 故sin 1x xlnx e x <+-成立;(2)当1x >时,设()sin 1x g x e x xlnx =+--, 则()cos 1x g x e lnx x '=-+-, 设()()h x g x =',则1()sin x h x e x x'=--, 1x >,()110h x e ∴'>-->,故()h x 在[1,)+∞递增,故()h x h >(1)cos110e =+->,即()0g x '>, 故()g x 在[1,)+∞递增,故()g x g >(1)sin110e =+->,即sin 1x xlnx e x <+-, 综上,若0a ,()sin 1x f x e x <+-.7.(1)证明:[0x ∈,1]sin x x (2)若不等式22312(2)cos 342x m x x x x mx +++-++对[0x ∈,1]恒成立,求实数m 的取值范围.【解析】(1)证明:记()sin F x x =,则()cos F x x '=-当(0,)4x π∈时,()0F x '>,()F x 在[0,]4π上是增函数,当(4x π∈,1)时,()0F x '<,()F x 在[4π,1]上是减函数, 又(0)0F =,F (1)0>,∴当[0x ∈,1]时,()0F x ,即2sin 2xx , 记()sin H x x x =-,则当(0,1)x ∈时,()cos 10H x x '=-<,()H x ∴在[0,1]上是减函数. 则()(0)0H x H =,即sin x x .sin x x ; (2)当[0x ∈,1]时,不等式22312(2)cos 342x m x x x x mx +++-++恒成立,即32221(3)42(2)(12)022xx x m m x x sin ++--++-恒成立, 也就是32221(3)24(2)022x x x m m x x x sin ++-+-+恒成立,即322211(3)24(2)028x x m m x x x x ++-+-+恒成立, 则2(32)0m m x -+在[0x ∈,1]上恒成立. 2320m m ∴-+恒成立,解得12m .∴实数m 的取值范围是[1,2].8.(1)证明:当[0x ∈,1]时,22111cos 124x x x --;(2)证明:当2a 时,322(2)cos 402x ax x x x ++++-对[0x ∈,1]恒成立.【解析】证明:(1)21()cos 14f x x x =-+,则1()()sin 2g x f x x x '==-+,1()cos 2g x x '=-+,013x π<,∴1cos 12x <,∴1()cos 02g x x '=-+<,恒成立 ∴1()()sin 2g x f x x x '==-+,在[0,1]上递减, 01x ,∴1()sin (0)02g x x x g =-+=,∴21()cos 14f x x x =-+,在[0,1]上递减, ()(0)0f x f ∴=∴[]210,1,14x cosx x ∈-时;(4分) 记21()cos 12F x x x =-+,则()()sinG x F x x x '==-+,()cos 1G x x '=-+,()cos 10G x x '∴=-+恒成立,()()sin G x F x x x '∴==-+,在[0,1]上递增,01x()sin (0)0G x x x G ∴=-+=,∴21()cos 12F x x x =-+,在[0,1]上递增, ()(0)0F x F ∴=∴[]210,1,12x cosx x ∈-时; ∴[]22110,1,1124x x cosx x ∈--时;(7分) (2)[0x ∈,1]时,332222(2)cos 42(2)(1)4(2)224x x x ax x x x ax x x a x ++++-++++--+,∴当2a 时,322(2)cos 402x ax x x x ++++-对[0x ∈,1]恒成立.(14分) 9.已知函数2()cos 1f x x ax =+-,a R ∈.若对于任意的实数x 恒有()0f x ,求实数a 的取值范围.【解析】解:对于任意的实数x 恒有()0f x ,即有2cos 10x ax +-, 即21cos 0ax x -,显然0a , 0x =时,显然成立;由偶函数的性质,只要考虑0x >的情况.当0x >时,22221cos 2xsin xax x-=,即为2sin22()2x a x , 由0x >,则02xt =>,考虑sin t t -的导数为cos 10t -, 即sin t t -递减,即有sin 0t t -<,即sin t t <,则有sin 1tt<,故2sin2()12xx <,即有21a ,解得12a. 则实数a 的取值范围为1[2,)+∞.10.已知函数1()()f x alnx a R x=+∈.(1)讨论函数()f x 在区间[1,2]上的最小值;(2)当1a =时,求证:对任意(0,)x ∈+∞,恒有cos ()x e xf x x+<成立.【解析】(1)解:函数1()f x alnx x =+的定义域是(0,)+∞,2211()a ax f x x x x-'=-=, ①当0a 时,2110,0ax ax x --<<,则()0f x '<, 则函数()f x 在(0,)+∞上单调递减,即函数()f x 在区间[1,2]上单调递减,故函数()f x 在区间[1,2]上的最小值为1(2)22f aln =+; ②当0a >时,令()0f x '<,得10x a <<;令()0f x '>,得1x a>,故函数()f x 在1(0,)a 上单调递减,在1(,)a+∞上单调递增,()i 当11a,即1a 时,函数()f x 在区间[1,2]上单调递增, 故函数()f x 在区间[1,2]上的最小值为f (1)1=,()ii 当12a,即102a <时,函数()f x 在区间[1,2]上单调递减, 故函数()f x 在区间[1,2]上的最小值为1(2)22f aln =+, ()iii 当112a <<,即112a <<时,函数()f x 在1[1,)a上单调递减,在1(,2]a 上单调递增,此时函数()f x 在区间[1,2]上的最小值为11()f aln a a a=+,综上,当12a时,函数()f x 在区间[1,2]上的最小值为1(2)22f aln =+; 当112a <<时,函数()f x 在区间[1,2]上的最小值为11()f aln a a a=+; 当1a 时,函数()f x 在区间[1,2]上的最小值为f (1)1=.(2)证明:当1a =时,1()f x lnx x=+, 要证cos ()x e x f x x +<,即证1cos x e xlnx x x++<,因为0x >,所以两边同时乘x ,得1cos x xlnx e x +<+, 即证cos 1x xlnx e x <+-,当01x <时,0xlnx ,而cos 11cos11cos10x e x +->+-=>,所以cos 1xxlnx e x <+-成立,即cos ()x e xf x x+<成立,当1x >时,令()cos 1(1)x h x e x xlnx x =+-->,则()sin 1x h x e x lnx '=---,设()sin 1(1)x g x e x lnx x =--->,则因为1()cos x g x e x x'=--,因为1x >,所以1()cos 110x g x e x e x'=-->-->, 所以当1x >时,()g x 单调递增,所以()sin110g x e >-->,即()0h x '>, 所以()h x 在(1,)+∞上单调递增,所以()cos110h x e >+->,即cos ()x e xf x x+<成立,综上,对任意(0,)x ∈+∞,恒有cos ()x e xf x x+<成立.11.已知函数2()cos (0)f x x x x =->.(Ⅰ)求证:()f x 有唯一零点0x ,且0(0,1)x ∈;(Ⅱ)对于(Ⅰ)中的0x ,当0(x x ∈,2)时,()0x e af x -,求实数a 的取值范围.【解析】()I 证明:函数2()cos (0)f x x x x =->,则()2sin f x x x '=+, 又()2cos 0f x x ''=+>,故()f x '在(0,)+∞上单调递增, 所以()(0)0f x f ''>=,故()f x 在(0,)+∞上单调递增, 又(0)10f =-<,f (1)1cos10=->, 所以()f x 在(0,)+∞上存在唯一零点0(0,1)x ∈; ()II 解:由()I 知,0(x x ∈,2)时,0()()0f x f x >=,所以2cos 0x x ->,即问题等价于2cos xe a x x-在0(x x ∈,2)恒成立,令2222(cos 2sin )(),()cos (cos )x x e e x x x x g x g x x x x x ---'==--,令2()2(sin cos )(2))4h x x x x x x x x π=--+=-+,当0(x x ∈,2)时,(2)0x x -<)04x π+>,所以()0h x <,即()0g x '<, 故()g x 在0(x ,2)上单调递减,所以当0(x x ∈,2)时,2()(2)4cos2e g x g >=-,所以24cos2e a -,故实数a 的取值范围是2(,]4cos2e -∞-.12.已知函数()cos f x x =.(1)当0x 时,设2()()12x g x f x =+-,求()(0)y g x x =的最小值;(2)求证:当1a ,0x 时,2()2(1)ax xe xf x x ln x +++.【解析】(1)解:函数()cos f x x =,所以22()()1cos 1(0)22x x g x f x x x =+-=+-,则()sin (0)g x x x x '=-+,故()cos 10g x x ''=-+在[0,)+∞上恒成立, 所以()g x '在[0,)+∞上单调递增,则有()(0)0g x g ''=,所以()g x 在[0,)+∞上单调递增,则有()(0)cos0010g x g =+-=, 故()(0)y g x x =的最小值为0;(2)证明:令2112()x x x m x e ++=,则2()02xx m x e'=-在[0,)+∞上恒成立,所以()m x 在[0,)+∞上单调递减,则有()(0)1m x m =, 所以21121x x x e ++,即2112x e x x ++,由(1)可知,()0g x 对[0,)+∞恒成立,即2cos 102x x +-,即2cos 12x x -,当1a 时,22cos 2(1)cos 2(1)ax x xe x x x ln x xe x x x ln x +--++--+ 22211(1)2(1)(1)2(1)22x x xe x x x ln x x e x x ln x +---+=+---+,因为2112xe x x ++,所以2112x e x x --,所以21122x e x x +--, 故21(1)2(1)22(1)2x x e x x ln x x ln x +---+-+,令()22(1)(0)h x x ln x x =-+,则22()2011x h x x x '=-=++对0x 恒成立,所以()h x 在[0,)+∞上单调递增,则有()(0)h x h ,即22(1)0x ln x -+, 所以21(1)2(1)22(1)02x x e x x ln x x ln x +---+-+,故2()2(1)ax xe xf x x ln x +++. 13.已知函数sin cos 1()xx x f x e+-=. (1)求函数()f x 在(0,)π内的单调递增区间; (2)当[0x ∈,)+∞时,求证:()f x x . 【解析】解:(1)由题意知,12sin ()x xf x e -'=,(0,)x π∈, 所以当()0f x '>时,解得5(0,)(,)66x πππ∈, 即()f x 在(0,)π的单调递增区间是(0,)6π,5(,)6ππ;(2)证明:令()()g x f x x =-,(0)x ,只需证()0g x 即可, 12sin ()1xxg x e -'=-,)14()0xx g x e π--''=<,故()g x '在[0,]6π单调递减,即1()(0)10maxg x g e ''==-<,()()106min g x g π''==-<, 所以()0g x ',从而()g x 在(0,)6π上单调递减,即()(0)0g x g =恒成立,当(,)6x π∈+∞时,()0g x 恒成立,即()f x x ,由(1)知,当(,)6x π∈+∞时,6()62max g x e π=<恒成立, 综上,()f x x 得证. 14.已知函数sin ()2cos xf x x=+,()(1)(x g x a e a =-为常数).(1)求函数()f x 在2x π=处的切线方程;(2)设()()(1)()()n F x f x g x n Z =+-∈.(ⅰ)若n 为偶数,当0a <时,函数()F x 在区间(0,)2π上有极值点,求实数a 的取值范围;(ⅱ)若n 为奇数,不等式()0F x 在[0,)+∞上恒成立,求实数a 的最小值. 【解析】解:(1)函数sin ()2cos xf x x=+,所以22cos (2cos )sin (sin )2cos 1()(2cos )(2cos )x x x x x f x x x +--+'==++,则1()24f π'=,当2x π=时,1()22f π=,故切点为1(,)22π,由点斜式可得函数()f x 在2x π=处的切线方程为11()242y x π-=-,即1448y x π-=+; (2)()i 当n 为偶数时,sin ()()()(1)2cos x xF x f x g x a e x=+=+-+,则22cos 1()(2cos )x x F x a e x +'=+⋅+, 令()()h x F x '=,则32sin (cos 1)()(2cos )x x x h x a e x -'=+⋅+, 因为(0,)2x π∈且0a <,所以()0h x '<在(0,)2x π∈上恒成立,则()h x 在(0,)2π上单调递减,其中1(0)3h a =+,21()24h a e ππ=+⋅,因为()F x 在(0,)2π有极值点,所以(0)0h >且()02h π<,即21134a e π-<<-,当21134a e π-<<-时,存在0(0,)2x π∈,使得0()0h x =,令()0F x '>,即()0h x >,()F x 在0(0,)x 上单调递增;令()0F x '<,即()0h x <,()F x 在0(x ,)2π上单调递减,所以()F x 在(0,)2π有极值点,故实数a 的取值范围为211(,)34e π--.()ii 当n 为奇数时,()()()0F x f x g x =-在[0,)+∞上恒成立,当0x =时,(0)0F =;当0x >时,sin ()(1)02cos x xF x a e x=--+恒成立,又22cos 1()(2cos )x x F x a e x +'=-⋅+,令2cos t x =+,则[1t ∈,3],所以222(2)1231()[1,]3t m t t t t -+==-∈-,因为01x e e >=,①当13a 时,13x a e ⋅>,所以()0F x '<恒成立,所以()F x 在[0,)+∞上单调递减,所以()(0)0F x F =,故13a符合题意; ②当0a 时,则()0F x '>在(0,)2π上恒成立,所以当(0,)2x π∈时,()F x 单调递增,()(0)0F x F >=,与题意不符合;③当103a <<时,1(0)03F a '=->,()10F a e ππ'=--⋅<,则(0)()0F F π''⋅<,所以()F x '在(0,)π上存在零点,设1x 为()F x '在(0,)π上的最小零点,则1(0,)x x ∈时,()0F x '>,因此()F x 在1(0,)x 上单调递增,所以()(0)0F x F >=,不符合题意.综上所述,a 的最小值为13.。

专题17二次函数与三角函数综合问题【例1】(2021•盘锦)如图,抛物线y=﹣x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线y=x﹣2与y轴交于点D,与x轴交于点E,与直线BC交于点F.(1)点F的坐标为;(2)如图1,点P为第一象限抛物线上的一点,PF的延长线交OB于点Q,PM⊥BC于点M,QN⊥BC于点N,若=,求点P的坐标;(3)如图2,点S为第一象限抛物线上的一点,且点S在射线DE上方,动点G从点E出发,沿射线DE方向以每秒4个单位长度的速度运动,当SE=SG,且tan∠SEG=时,求点G的运动时间t.【例2】(2021•十堰)已知抛物线y=ax2+bx﹣5与x轴交于点A(﹣1,0)和B(﹣5,0),与y轴交于点C,顶点为P,点N在抛物线对称轴上且位于x轴下方,连AN交抛物线于M,连AC、CM.(1)求抛物线的解析式;(2)如图1,当tan∠ACM=2时,求M点的横坐标;(3)如图2,过点P作x轴的平行线l,过M作MD⊥l于D,若MD=MN,求N点的坐标.【例3】(2021•荆州)已知:直线y=﹣x+1与x轴、y轴分别交于A,B两点,点C为直线AB上一动点,连接OC,∠AOC为锐角,在OC上方以OC为边作正方形OCDE,连接BE,设BE=t.(1)如图1,当点C在线段AB上时,判断BE与AB的位置关系,并说明理由;(2)直接写出点E的坐标(用含t的式子表示);(3)若tan∠AOC=k,经过点A的抛物线y=ax2+bx+c(a<0)顶点为P,且有6a+3b+2c=0,△POA 的面积为,当t=时,求抛物线的解析式.【例4】(2021•日照)已知:抛物线y=ax2+bx+c经过A(﹣1,0),B(3,0),C(0,3)三点.(1)求抛物线的解析式;(2)如图1,点P为直线BC上方抛物线上任意一点,连PC、PB、PO,PO交直线BC于点E,设=k,求当k取最大值时点P的坐标,并求此时k的值.(3)如图2,点Q为抛物线对称轴与x轴的交点,点C关于x轴的对称点为点D.①求△BDQ的周长及tan∠BDQ的值;②点M是y轴负半轴上的点,且满足tan∠BMQ=(t为大于0的常数),求点M的坐标.1.(2021•镇江二模)已知抛物线y=ax2+bx+10交x轴于点A(﹣10,0)和点B(2,0),其对称轴为直线l,点C在l上,坐标为(m,﹣3),射线AB沿着直线AC翻折,交l于点F,如图(1)所示.(1)a=,b=;(2)如图(2),点P在x轴上方的抛物线上,点E在直线l上,EP=EB且∠BPE=∠BAF,求证:AB •BE=PB•AF.(3)在(2)的条件下,直接写出tan∠BAF的值=;直接写出点P的坐标(,).2.(2021•慈溪市校级四模)如图,边长为4的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含端点),过点P作PM⊥OA于点M,点Q的坐标为(0,3),连接PQ.(1)求出抛物线的解析式;(2)当点P与点A或点C重合时,PQ+PM=,小聪猜想:对于A,C间的任意一点P,PQ与PM之和是一个固定值,你认为正确吗,判断并说明理由;(3)延长MP交BC于点N,当∠NPQ为锐角,cos∠NPQ=时,求点P的坐标.3.(2021•道里区二模)如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx﹣2交y轴于点A,该抛物线的顶点为B(2,﹣4).(1)如图(1),求a,b的值;(2)如图(2),过点B作x轴的垂线,点C为垂足,横坐标为t的点P在抛物线上,点P在第四象限且位于BC右侧,连接PA,PC,△ACP的面积为S,求S与t之间的函数关系式,不要求写出自变量t 的取值范围;(3)如图(3),在(2)的条件下,连接PB,点D与点A关于原点对称,过点D作x轴的平行线与抛物线在第二象限交于点E,点F在第三象限,点G在CB的延长线上,若EF=PC,∠DEF+∠BCP=150°,∠DEG﹣∠PFG=30°,tan∠EGF=,求点P的坐标.4.(2021•金坛区模拟)如图,在平面直角坐标系xOy中,已知二次函数y=﹣(x﹣2)2的图象与y轴交于点B,抛物线的对称轴是直线l,顶点是A,过点B作CD⊥BA交x轴于点C,交抛物线于点D,连接AD.将线段AB沿线段AD平移得到EF(点E与点A对应、点F与点B对应),连接BF.(1)填空:线段OA=;(2)若点F恰好落在直线L上,求AF的长;(3)连接DF并延长交抛物线于点Q,若tan∠ADF=,求点Q的坐标.5.(2021•仙桃校级模拟)如图,已知抛物线C1:y=ax2+bx+c的顶点坐标为(0,﹣2),且经过点A(﹣2,2),动直线l的解析式为:y=﹣4x+e.(1)求抛物线C1的解析式;(2)将抛物线C1向上平移两个单位得到新抛物线C2,过点A的直线交抛物线C2于M、N两点(M位于点N的左边),动直线经过点M,与抛物线C2的另一个交点为点P,求证:直线PN恒过一个定点;(3)图3中,在(1)的条件下,x轴正半轴上有一点B(1,0),M为抛物线C1上在第一象限内的点,若∠MAB为锐角,且tan∠MAB>2,直接写出点M的横坐标x的取值范围.6.(2021•台安县模拟)如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,交抛物线于点M,过点C作CF⊥l于F.(1)求抛物线解析式.(2)如图2,当点F恰好在抛物线上时(与点M重合),①求线段EH的长;②连接DF,求tan∠FDE的值;③试探究在直线l上,是否存在点G,使∠EDG=45°?若存在,请直接写出点G的坐标;若不存在,请说明理由.7.(2021•江阴市模拟)已知二次函数y=ax2﹣2ax+c(a<0)的图象交x轴于点A、B两点(A在B左侧),与y轴交于点C,与其对称轴交于点D,直线BD交y轴于点E,BD=2DE.(1)求点A的坐标;(2)①连接AC,BC,若△ABC外接圆的圆心正好在x轴上,求二次函数表达式;②连接CD,若tan∠CDB=tan∠OBD,求此时二次函数表达式.8.(2021•烟台)如图,抛物线y=ax2+bx+c经过点A(﹣2,0),B(4,0),与y轴正半轴交于点C,且OC=2OA,抛物线的顶点为D,对称轴交x轴于点E.直线y=mx+n经过B,C两点.(1)求抛物线及直线BC的函数表达式;(2)点F是抛物线对称轴上一点,当FA+FC的值最小时,求出点F的坐标及FA+FC的最小值;(3)连接AC,若点P是抛物线上对称轴右侧一点,点Q是直线BC上一点,试探究是否存在以点E 为直角顶点的Rt△PEQ,且满足tan∠EQP=tan∠OCA.若存在,求出点P的坐标;若不存在,请说明理由.9.(2020•海安市一模)已知平面直角坐标系xOy中,抛物线L:y=ax2﹣2ax+a(a>0)与y轴相交于A 点,过点A作x轴的平行线与抛物线L的另一交点为B点.直线y=kx﹣k(k>a)与抛物线L相交于C,D两点(点C在点D的左侧),与y轴交于E点,过点D作DH⊥AB,垂足为H,连接EH交x轴于G 点.(1)若a=1,k=2,求DH的长;(2)当a=13时,求cos∠AHE的值;(3)连接BC,求证:四边形BCGH是平行四边形.10.(2020•惠山区二模)已知:在平面直角坐标系xOy中,二次函数y=mx2+2mx﹣4(m≠0)的图象与x 轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.(1)求这个二次函数的解析式;(2)点D的坐标为(﹣2,1),点P在二次函数的图象上,∠ADP为锐角,且tan∠ADP=2,求出点P的横坐标.11.(2020•肥城市四模)如图所示,在平面直角坐标系中,二次函数y=ax2+bx+6(a≠0)交x轴A(﹣4,0),B(2,0),在y轴上有一点E(0,﹣2),连接AE,D是第二象限内的抛物线上一动点.(1)求二次函数的解析式;(2)求△ADE面积的最大值并写出此时点D的坐标;(3)若tan∠AED=13,求此时点D的坐标.12.(2020•历下区校级模拟)如图所示,在平面直角坐标系中,二次函数y=ax2+bx+6交x轴于A(﹣4,0)、B(2,0),在y轴上有一点E(0,﹣2),连接AE.(1)求二次函数的表达式;(2)点D是第二象限内的抛物线上一动点.若tan∠AED=13,求此时点D坐标;(3)连接AC,点P是线段CA上的动点,连接OP,把线段PO绕着点P顺时针旋转90°至PQ,点Q是点O的对应点.当动点P从点C运动到点A时,判断动点Q的轨迹并求动点Q所经过的路径长.14.(2019•丹东)如图,在平面直角坐标系中,抛物线y=−12x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=−12x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7.(1)求此抛物线的解析式.(2)求点N的坐标.(3)过点A的直线与抛物线交于点F,当tan∠FAC=12时,求点F的坐标.(4)过点D作直线AC的垂线,交AC于点H,交y轴于点K,连接CN,△AHK沿射线AC以每秒1个单位长度的速度移动,移动过程中△AHK与四边形DGNC产生重叠,设重叠面积为S,移动时间为t (0≤t≤5),请直接写出S与t的函数关系式.15.(2020•成都校级模拟)如图,抛物线y=﹣x2+bx+c与直线y=x+4交于C、D两点,其中点C在y轴上,点D的坐标为(6,7).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F,作PM⊥CD于点M.(1)求抛物线的解析式及sin∠PFM的值.(2)设点P的横坐标为m:①若P在CD上方,用含m的代数式表示线段PM的长,并求出线段PM长的最大值;②当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.16.(2020•武汉模拟)如图,抛物线y═−13x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B的坐标为(3,0),点C的坐标为(0,5).有一宽度为1,长度足够长的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.(1)求抛物线的解析式及点A的坐标;(2)当点M和N都在线段AC上时,连接MF,如果sin∠AMF=Q的坐标;(3)在矩形的平移过程中,是否存在以点P,Q,M,N为顶点的四边形是平行四边形,若存在,求出点M的坐标;若不存在,请说明理由.17.(2020•河东区模拟)如图,已知抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为5.设⊙M与y轴交于D,抛物线的顶点为E.(1)求m的值及抛物线的解析式;(2)设∠DBC=α,∠CBE=β,求sin(α﹣β)的值;(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.18.(2019•新都区校级模拟)如图1,在平面直角坐标系xOy中,直线y=﹣x+3与x轴、y轴分别相交于点A和点B,抛物线y=ax2+bx+c经过A,B两点,且其对称轴是直线x=2.(1)求抛物线的函数表达式;(2)设P是抛物线上一动点,若在此抛物线上,有且仅有三个点P,使△ABP的面积等于定值S,请求出该定值S和这三个P点的坐标;(3)如图2,动点C,D分别在x轴上方、下方的抛物线上运动,且满足∠CAO=∠DAO,连接CD交x轴于点E,当点C,D运动时,∠CEO的度数发生变化吗?若不变,求出sin∠CEO的值;若变化,请求出∠CEO的变化范围.。
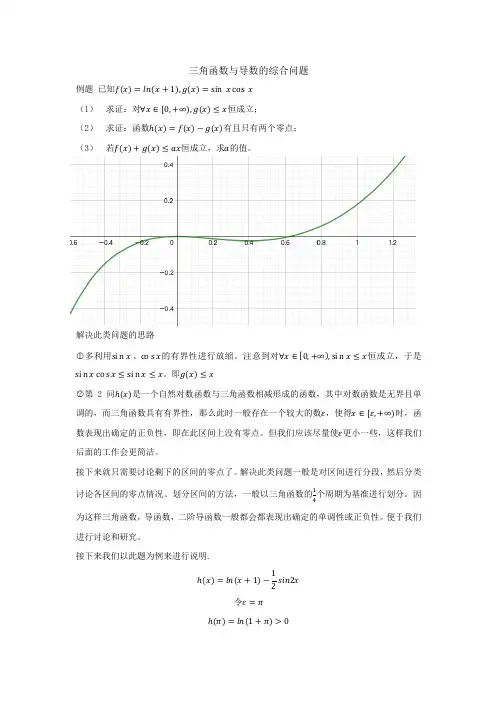
三角函数与导数的综合问题例题 已知f(x)=ln(x+1),g(x)=sin x cos x(1)求证:对∀x∈[0,+∞),g(x)≤x恒成立;(2)求证:函数ℎ(x)=f(x)−g(x)有且只有两个零点;(3)若f(x)+g(x)≤ax恒成立,求a的值。
解决此类问题的思路○1多利用si n x、co s x的有界性进行放缩。
注意到对∀x∈[0,+∞),si n x≤x恒成立,于是si n x co s x≤si n x≤x。
即g(x)≤x○2第2问ℎ(x)是一个自然对数函数与三角函数相减形成的函数,其中对数函数是无界且单调的,而三角函数具有有界性,那么此时一般存在一个较大的数ε,使得x∈[ε,+∞)时,函数表现出确定的正负性,即在此区间上没有零点。
但我们应该尽量使ε更小一些,这样我们后面的工作会更简洁。
接下来就只需要讨论剩下的区间的零点了。
解决此类问题一般是对区间进行分段,然后分类讨论各区间的零点情况。
划分区间的方法,一般以三角函数的!"个周期为基准进行划分。
因为这样三角函数,导函数,二阶导函数一般都会都表现出确定的单调性或正负性。
便于我们进行讨论和研究。
接下来我们以此题为例来进行说明.ℎ(x)=ln(x+1)−12sin2x令ε=πℎ(π)=ln(1+π)>0我们大胆猜测此时函数已经表现出大于零的性质,继续缩小区间令ε=#$ℎ(π2)=ln(1+π2)>0 此时ℎ(x)仍然大于0于是我们可以将定义域分为(−1,#$),(#$,+∞)两个部分进行讨论,先证明x ∈(#$,+∞)时,ℎ(x)≥0.ℎ(x)=ln(x +1)−12sin2x ≥ln(x +1)−12≥ln(1+π2)−12≥0 所以x ∈(#$,+∞)时,ℎ(x)无零点。
接下来先讨论x ∈(−1,0)时的情况ℎ%(x)=11+x−cos2x ℎ&(x)=−1(1+x)$+2sin2x x ∈(−1,0)时, !!'(>1,cos2x ≤1。
题型练3 大题专项(一) 三角函数、解三角形综合问题题型练第62页一、解答题1.已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P(1)求sin(α+π)的值;(2)若角β满足sin(α+β)=,求cos β的值.解:(1)由角α的终边过点P,得sinα=-,所以sin(α+π)=-sinα=(2)由角α的终边过点P,得cosα=-,由sin(α+β)=,得cos(α+β)=±由β=(α+β)-α,得cosβ=cos(α+β)cosα+sin(α+β)sinα,所以cosβ=-或cosβ=2.(2020全国Ⅱ,理17)△ABC中,sin2A-sin2B-sin2C=sin Bsin C.(1)求A;(2)若BC=3,求△ABC周长的最大值.解:(1)由正弦定理和已知条件得BC2-AC2-AB2=AC·AB.①由余弦定理得BC2=AC2+AB2-2AC·ABcosA.②由①②得cosA=-因为0<A<π,所以A=(2)由正弦定理及(1),得=2,从而AC=2sinB,AB=2sin(π-A-B)=3cosB-sinB.故BC+AC+AB=3+sinB+3cosB=3+2sin又0<B<,所以当B=时,△ABC周长取得最大值3+23.△ABC的内角A,B,C的对边分别为a,b,c.已知△ABC的面积为(1)求sin Bsin C;(2)若6cos Bcos C=1,a=3,求△ABC的周长.解:(1)由题设得acsinB=,即csinB=由正弦定理得sinCsinB=故sinBsinC=(2)由题设及(1)得cosBcosC-sinBsinC=-,即cos(B+C)=-所以B+C=,故A=由题设得bcsinA=,即bc=8.题型练3 大题专项(一) 三角函数、解三角形综合问题题型练第62页一、解答题1.已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P(1)求sin(α+π)的值;(2)若角β满足sin(α+β)=,求cos β的值.解:(1)由角α的终边过点P,得sinα=-,所以sin(α+π)=-sinα=(2)由角α的终边过点P,得cosα=-,由sin(α+β)=,得cos(α+β)=±由β=(α+β)-α,得cosβ=cos(α+β)cosα+sin(α+β)sinα,所以cosβ=-或cosβ=2.(2020全国Ⅱ,理17)△ABC中,sin2A-sin2B-sin2C=sin Bsin C.(1)求A;(2)若BC=3,求△ABC周长的最大值.解:(1)由正弦定理和已知条件得BC2-AC2-AB2=AC·AB.①由余弦定理得BC2=AC2+AB2-2AC·ABcosA.②由①②得cosA=-因为0<A<π,所以A=(2)由正弦定理及(1),得=2,从而AC=2sinB,AB=2sin(π-A-B)=3cosB-sinB.故BC+AC+AB=3+sinB+3cosB=3+2sin又0<B<,所以当B=时,△ABC周长取得最大值3+23.△ABC的内角A,B,C的对边分别为a,b,c.已知△ABC的面积为(1)求sin Bsin C;(2)若6cos Bcos C=1,a=3,求△ABC的周长.解:(1)由题设得acsinB=,即csinB=由正弦定理得sinCsinB=故sinBsinC=(2)由题设及(1)得cosBcosC-sinBsinC=-,即cos(B+C)=-所以B+C=,故A=由题设得bcsinA=,即bc=8.。
导数与三角函数的综合的解题技巧
导数与三角函数的综合问题在高中数学中是比较常见的,掌握相关的解题技巧可以提高解题效率。
以下是一些解题技巧:
1. 对于导数问题,首先要掌握导数的定义和求导法则,特别是常见函数的导数。
2. 对于三角函数问题,需要了解各种三角函数的定义、性质和公式,以及它们与圆的关系。
3. 对于综合问题,需要根据题目中的信息建立函数关系式,并利用已知条件求解未知量。
4. 注意变量的定义域和值域,避免出现无解或多解的情况。
5. 利用图像、几何等方法辅助解题,特别是对于三角函数问题,画出对应的三角函数图像可以更好地理解和解决问题。
6. 注意符号的使用,特别是导数的正负号和三角函数的周期性等特点。
综合运用上述技巧,可以较为高效地解决导数与三角函数的综合问题。
但需要注意的是,这些技巧只是解题中的辅助手段,关键还是要理解数学概念和方法,熟练掌握解题技巧才能更好地应对各种高中数学考试题目。
- 1 -。
三角函数计算问题1.sin 15°cos 75°+cos 15°sin 105°等于( )A .0B .12C .32D .1D [原式=sin 15°cos 75°+cos 15°sin 75°=sin 90°=1.] 2.已知α∈(π2,π),sin α=35,则tan(α+π4)等于( )A .17B .7C .-17D .-7A [∵α∈(π2,π),sin α=35,∴cos α=-45,tan α=sin αcos α=-34.∴tan(α+π4)=1+tan α1-tan α=1-341+34=17.]3.化简:sin (60°+θ)+cos 120°sin θcos θ的结果为( )A .1B .32C . 3D .tan θB [原式=sin 60°cos θ+cos 60°sin θ-12sin θcos θ=sin 60°cos θcos θ=sin 60°=32.] 4.若3sin θ=cos θ,则cos 2θ+sin 2θ的值等于( )A .-75B .75C .-35D .35B [∵3sin θ=cos θ,∴tan θ=13.cos 2θ+sin 2θ=cos 2θ-sin 2θ+2sin θcos θ =cos 2θ+2sin θcos θ-sin 2θcos 2θ+sin 2θ=1+2tan θ-tan 2θ1+tan 2θ=1+2×13-191+19=75.] 5.已知3cos(2α+β)+5cos β=0,则tan(α+β)tan α的值为( )A .±4B .4C .-4D .1 C [3cos(2α+β)+5cos β=3cos(α+β)cos α-3sin(α+β)sin α+5cos(α+β)cos α+5sin(α+β)sin α=0, ∴2sin(α+β)sin α=-8cos(α+β)cos α,∴tan(α+β)tan α=-4.]6.若cos θ2=35,sin θ2=-45,则角θ的终边一定落在直线( )上.A .7x +24y =0B .7x -24y =0C .24x +7y =0D .24x -7y =0D [cos θ2=35,sin θ2=-45,tan θ2=-43,∴tan θ=2tanθ21-tan 2θ2=-831-169=247.∴角θ的终边在直线24x -7y =0上.] 7.tan 15°+1tan 15°等于( )A .2B .2+3C .4D .433C8.若3sin α+cos α=0,则1cos 2α+sin 2α的值为( )A .103B .53C .23D .-2A [∵3sin α+cos α=0,∴tan α=-13,∴1cos 2α+sin 2α=sin 2α+cos 2αcos 2α+2sin αcos α=tan 2α+11+2tan α=(-13)2+11+2×(-13)=103.]9.已知θ是第三象限角,若sin 4θ+cos 4θ=59,那么sin 2θ等于( )A .223B .-223C .23D .-23A [∵sin 4θ+cos 4 θ=(sin 2 θ+cos 2 θ)2-2sin 2 θcos 2 θ=1-12sin 2 2θ=59,∴sin 2 2θ=89.∵θ是第三象限角,∴sin θ<0,cos θ<0,∴sin 2θ>0.∴sin 2θ=223.]10.计算sin 89°cos 14°-sin 1°cos 76°= ( ).A.2+64 B.2-64 C.6-24D.24解析 sin 89°cos 14°-sin 1°cos 76° =sin 89°cos 14°-cos 89°sin 14° =sin 75°=sin(45°+30°)=2+64. 答案 A11.若1tan θ=3,则cos 2θ+12sin 2θ的值是( ). A .-65B .-45C.45D.65解析 ∵tan θ=13,∴原式=cos 2θ+sin θcos θsin 2θ+cos 2θ=1+tan θ1+tan 2θ=1+131+19=1210=65. 答案 D12.已知cos(α-β)=35,sin β=-513,且α∈⎝⎛⎭⎫0,π2,β∈⎝⎛⎭⎫-π2,0,则sin α= ( ). A.3365 B.6365 C .-3365D .-6365解析 ∵α∈⎝⎛⎭⎫0,π2,β∈⎝⎛⎭⎫-π2,0,∴α-β∈(0,π), 由cos(α-β)=35得sin(α-β)=45,由sin β=-513得cos β=1213,∴sin α=sin[(α-β)+β]=45×1213+35×⎝⎛⎭⎫-513=3365. 答案 A13.设a =sin 17°cos 45°+cos 17°sin 45°,b =2cos 213°-1,c =32,则有( ). A .c <a <b B .b <c <a C .a <b <cD .b <a <c解析 a =sin(17°+45°)=sin 62°, b =2cos 213°-1=cos 26°=sin 64°, c =32=sin 60°,∴c <a <b .答案 A14.若x ∈⎝⎛⎭⎫-π2,0,cos x =45,则tan 2x 等于 ( ).A.724 B .-724C.247D .-247解析 ∵x ∈⎝⎛⎭⎫-π2,0,cos x =45,∴sin x =-35,∴tan x =-34,∴tan 2x =2tan x 1-tan 2x =-247. 答案 D15.已知sin ⎝⎛⎭⎫π4-x =35,则sin 2x 的值为( ). A.1925 B.1625 C.1425D.725解析 sin 2x =cos ⎝⎛⎭⎫π2-2x =cos 2⎝⎛⎭⎫π4-x =1-2sin 2⎝⎛⎭⎫π4-x =1-2×⎝⎛⎭⎫352=725. 答案 D16.cos 43°cos 77°+sin 43°cos 167°的值是( )A .-32B.12C.32D .-12【解析】 原式=cos 43°sin 13°-sin 43°cos 13°=sin(13°-43°)=sin(-30°)=-12.【答案】 D17.已知tan(π-α)=2,则1sin αcos α等于( )A.52 B.75 C .-52D .-75【解析】 由tan(π-α)=2,得tan α=-2, ∴1sin αcos α=sin 2α+cos 2αsin αcos α=tan 2α+1tan α=-52. 【答案】 C18.tan(α+β)=25,tan(α+π4)=322,那么tan(β-π4)=( )A.15B.1318C.14D.1322【解析】 tan(β-π4)=tan[(α+β)-(α+π4)]=tan (α+β)-tan (α+π4)1+tan (α+β)tan (α+π4)=25-3221+25×322=14.【答案】 C19.若sin α2=33,则cos α=( )A .-23B .-13C.13D.23【解析】 cos α=1-2sin 2α2=1-2×⎝⎛⎭⎫332=1-23=13.【答案】 C20.已知sin(π4-θ)+cos(π4-θ)=15,则cos 2θ的值为( )A .-725B.725 C .-2425D.2425【解析】 将sin(π4-θ)+cos(π4-θ)=15两边平方得,1+2sin(π4-θ)cos(π4-θ)=125,即1+sin(π2-2θ)=125,cos 2θ=-2425.【答案】 C21.若cos α=-45,α是第三象限的角,则1+tanα21-tanα2=( )A .-12B.12 C .2D .-2【解析】 α是第三象限的角且cos α=-45,∴sin α=-35.tan α2=sin α1+cos α=-3515=-3,∴1+tanα21-tanα2=-24=-12.【答案】 A22.cos67°cos7°+sin67°sin7°等于( )A .12B .22C .32D .1[答案] A[解析] cos67°cos7°+sin67°sin7° =cos(67°-7°)=cos60°=12.23.已知α为第二象限角,sin α=35,则sin2α=( )A .-2425B .-1225C .1225D .2425[答案] A[解析] ∵α是第二象限角,sin α=35,∴cos α=-45.∴sin2α=2sin αcos α=2×35×(-45)=-2425.24.下列各式中值为22的是( ) A .sin45°cos15°+cos45°sin15° B .sin45°cos15°-cos45°sin15° C .cos75°cos30°+sin75°sin30° D .tan60°-tan30°1+tan60°tan30°[答案] C[解析] cos75°cos30°+sin75°sin30°=cos(75°-30°)=cos45°=22. 25.已知cos α=23,270°<α<360°,那么cos α2的值为( )A .66B .-66C .306D .-306[答案] D[解析] ∵270°<α<360°,∴135°<α2<180°,∴cos α2=-1+cos α2=-1+232=-306. 26.已知cos(x +π6)=35,x ∈(0,π),则sin x 的值为( )A .-43-310B .43-310C .12D .32[答案] B[解析] ∵x ∈(0,π),∴x +π6∈(π6,7π6),又∵cos(x +π6)=35,∴x +π6∈(π6,π2).∴sin(x +π6)=45.sin x =sin[(x +π6)-π6]=sin(x +π6)cos π6-cos(x +π6)sin π6=32×45-12×35=43-310. 27.已知sin αcos β=1,则sin(α-β)=________. 1解析 ∵sin αcos β=1,∴sin α=cos β=1,或sin α=cos β=-1, ∴cos α=sin β=0.∴sin(α-β)=sin αcos β-cos αsin β=sin αcos β=1.28.若0<α<π2<β<π,且cos β=-13,sin(α+β)=13,则cos α=________.429解析 cos β=-13,sin β=223,sin(α+β)=13,cos(α+β)=-223,故cos α=cos[(α+β)-β] =cos(α+β)cos β+sin(α+β)sin β =(-223)×(-13)+223×13=429.29.设α∈(0,π2),若sin α=35,则2cos(α+π4)等于________.[答案] 15[解析] ∵α∈(0,π2),sin α=35,∴cos α=45,∴2cos(α+π4)=2cos αcos π4-2sin αsin π4=2×45×22-2×35×22=45-35=15. 30.若8sin α+5cos β=6,8cos α+5sin β=10,则sin(α+β)=________. 4780解析 ∵(8sin α+5cos β)2+(8cos α+5sin β)2 =64+25+80(sin αcos β+cos αsin β) =89+80sin(α+β)=62+102=136. ∴80sin(α+β)=47,∴sin(α+β)=4780.31.已知α为第三象限的角,cos 2α=-35,则tan ⎝⎛⎭⎫π4+2α=________. -17解析 由题意,得2k π+π<α<2k π+3π2(k ∈Z ),∴4k π+2π<2α<4k π+3π.∴sin 2α>0.∴sin 2α=1-cos 22α=45.∴tan 2α=sin 2αcos 2α=-43.∴tan ⎝⎛⎭⎫π4+2α=tan π4+tan 2α1-tan π4 tan 2α=1-431+43=-17. 32.设α为第四象限的角,若sin 3αsin α=135,则tan 2α=________.-34解析 由sin 3αsin α=sin (2α+α)sin α=sin 2αcos α+cos 2αsin αsin α=2cos 2α+cos 2α=135.∵2cos 2α+cos 2α=1+2cos 2α=135,∴cos 2α=45.∵α为第四象限角,∴2k π+3π2<α<2k π+2π,(k ∈Z )∴4k π+3π<2α<4k π+4π,(k ∈Z ) 故2α可能在第三、四象限,又∵cos 2α=45,∴sin 2α=-35,tan 2α=-34.33.求值:tan10°+tan50°+3tan10°tan50°=________. [答案]3[解析] tan10°+tan50°+3tan10°tan50° =tan60°(1-tan10°tan50°)+3tan10°tan50° =3-3tan10°tan50°+3tan10°tan50°= 3. 34.化简:1+2sin610°cos430°sin250°+cos790°=________.[答案] -1 [解析] 1+2sin610°cos430°sin250°+cos790°=1+2sin (3×180°+70°)cos (360°+70°)sin (180°+70°)+cos (720°+70°)=1-2sin70°cos70°-sin70°+cos70°=(sin70°-cos70°)2-sin70°+cos70° =sin70°-cos70°-sin70°+cos70°=-1.35.若cos α=45,α∈(0,π2),则cos(α-π3)=________.【解析】 由题意知sin α=35,cos(α-π3)=cos α·cos π3+sin α·sin π3.=45·12+35·32=4+3310.【答案】4+331036.tan(π6-θ)+tan(π6+θ)+3tan(π6-θ)tan(π6+θ)的值是________.【解析】 ∵tan π3=tan(π6-θ+π6+θ)=tan (π6-θ)+tan (π6+θ)1-tan (π6-θ)tan (π6+θ)=3,∴3=tan(π6-θ)+tan(π6+θ)+3tan(π6-θ)tan(π6+θ).【答案】337.已知sin(α+β)=12,sin(α-β)=13,那么log5tan αtan β=________. 【解析】 由题意有sin αcos β+cos αsin β=12,sin αcos β-cos αsin β=13,两式相加得sin αcos β=512,两式相减得cos αsin β=112.则tan αtan β=5,故log 5tan αtan β=2. 【答案】 238.设sin 2α=-sin α,α∈⎝⎛⎭⎫π2,π,则tan 2α的值是________. 【解析】 ∵sin 2α=-sin α,∴2sin αcos α=-sin α. ∵α∈⎝⎛⎭⎫π2,π,sin α≠0, ∴cos α=-12.又∵α∈⎝⎛⎭⎫π2,π,∴α=23π, ∴tan 2α=tan 43π=tan ⎝⎛⎭⎫π+π3=tan π3= 3. 【答案】339.已知sin x -cos x =sin x cos x ,则sin 2x =________. 解析 ∵sin x -cos x =sin x cos x , ∴(sin x -cos x )2=(sin x cos x )2 1-2sin x cos x =(sin x cos x )2, ∴令t =sin x cos x ,则1-2t =t 2.即t 2+2t -1=0,∴t =-2±222=-1±2. 又∵t =sin x cos x =12sin 2x ∈⎣⎡⎦⎤-12,12, ∴t =2-1,∴sin 2x =22-2.答案 22-240.已知sin(α+π2)=-55,α∈(0,π). (1)求sin (α-π2)-cos (3π2+α)sin (π-α)+cos (3π+α)的值; (2)求cos(2α-3π4)的值. 解 (1)sin(α+π2)=-55,α∈(0,π) ⇒cos α=-55,α∈(0,π)⇒sin α=255. sin (α-π2)-cos (3π2+α)sin (π-α)+cos (3π+α)=-cos α-sin αsin α-cos α=-13. (2)∵cos α=-55,sin α=255⇒sin 2α=-45,cos 2α=-35. cos(2α-3π4)=-22cos 2α+22sin 2α=-210. 41.已知|cos θ|=35,且5π2<θ<3π,求sin θ2、cos θ2、tan θ2的值. 解 ∵|cos θ|=35,5π2<θ<3π, ∴cos θ=-35,5π4<θ2<3π2. 由cos θ=1-2sin 2θ2, 有sin θ2=-1-cos θ2=-1+352=-255. 又cos θ=2cos 2θ2-1, 有cos θ2=-1+cos θ2=-55,tan θ2=sinθ2cos θ2=2. 42.已知sin ⎝⎛⎭⎫π4+x sin ⎝⎛⎭⎫π4-x =24,x ∈⎝⎛⎭⎫π2,π,求sin 4x 的值.解 因为⎝⎛⎭⎫π4+x +⎝⎛⎭⎫π4-x =π2,所以sin ⎝⎛⎭⎫π4+x sin ⎝⎛⎭⎫π4-x=sin ⎝⎛⎭⎫π4+x cos ⎝⎛⎭⎫π4+x=12⎣⎡⎦⎤2sin ⎝⎛⎭⎫π4+x cos ⎝⎛⎭⎫π4+x =12sin ⎝⎛⎭⎫π2+2x =12cos 2x =24,所以cos 2x =22. 又x ∈⎝⎛⎭⎫π2,π,所以2x ∈(π,2π),所以sin 2x <0,所以sin 2x =-22. 所以sin 4x =2sin 2x cos 2x =2×⎝⎛⎭⎫-22×22=-1. 43.已知sin α=13,cos β=-23,α、β均在第二象限,求sin(α+β)和sin(α-β)的值. 解 因为sin α=13,cos β=-23,α、β均为第二象限角,所以cos α=-1-sin 2α=-223,sin β=1-cos 2β=53. 故sin(α+β)=sin αcos β+cos αsin β=13×⎝⎛⎭⎫-23+⎝⎛⎭⎫-223×53=-2-2109,sin(α-β)=sin αcos β-cos αsin β=13×⎝⎛⎭⎫-23-⎝⎛⎭⎫-223×53=-2+2109. 44.化简:3tan 12°-3sin 12°(4cos 212°-2). 【解】 原式=3(sin 12°cos 12°-3)sin 12°×2(2cos 212°-1) =3(sin 12°-3cos 12°)2sin 12°cos 12°cos 24° =23(sin 12°cos 60°-cos 12°sin 60°)sin 24°cos 24° =2×23sin (12°-60°)2sin 24°cos 24° =-43sin 48°sin 48°=-4 3. 45.若cos(π4+x )=35,17π12<x <7π4,求:(1)cos x +sin x 的值;(2)sin2x +2sin 2x 1-tan x的值. [解析] (1)由17π12<x <7π4,得5π3<x +π4<2π, 又∵cos(π4+x )=35, ∴sin(π4+x )=-45, ∴cos x +sin x =2sin(x +π4)=-425. (2)cos x =cos[(π4+x )-π4] =cos(π4+x )cos π4+sin(π4+x )sin π4=35×22-45×22=-210. 又由17π12<x <7π4, ∴sin x =-1-cos 2x =-7210, ∴tan x =7,∴原式=2sin x cos x +2sin 2x 1-tan x=-2875. 46.已知sin α=210,cos β=31010,且α、β为锐角,求α+2β的值. [解析] ∵sin α=210,α为锐角, ∴cos α=1-sin 2α=1-⎝⎛⎭⎫2102=7210. ∵cos β=31010,β为锐角, ∴sin β=1-⎝⎛⎭⎫310102=1010. ∴sin2β=2sin βcos β=2×1010×31010=35, cos2β=1-2sin 2β=1-2×⎝⎛⎭⎫10102=45. 又β∈⎝⎛⎭⎫0,π2,∴2β∈(0,π).而cos2β>0,∴2β∈⎝⎛⎭⎫0,π2.∴α+2β∈(0,π). 又cos(α+2β)=cos α·cos2β-sin α·sin2β=7210×45-210×35=22,∴α+2β=π4.。
高考解答题专项二 三角函数中的综合问题1.已知函数f (x )=2sin ωx cos ωx-π6-12(0<ω<2),函数f (x )在[a ,b ]上单调递增,且b-a 的最大值为π2,求f (x )在-π2,π2上的单调递减区间.2.(2021湖南怀化高三二模)在△ABC 中,内角A ,B ,C 所对的边长分别为a ,b ,c ,且满足2tanBtanA+tanB =bc . (1)求角A ;(2)若a=√13,b=3,求△ABC 的面积.3.(2021天津静海一中高三月考)已知锐角三角形ABC的三个角A,B,C所对的边为a,b,c,且b cos C+√3b sin C=a+c.(1)求B;(2)若b=2,△ABC的面积为√3,求a,c.4.平面凸四边形ABCD中,∠BAD=∠BCD=90°,AD=3,AB=4.(1)若∠ABC=45°,求CD;(2)若BC=2√5,求AC.5.(2021江苏徐州高三二模)若f(x)=sin(ωx+φ)ω>0,0<φ<π2的部分图象如图所示,f(0)=12,f5π12=0.(1)求f(x)的解析式;(2)在锐角三角形ABC中,若A>B,f A-B2−π12=35,求cos A-B2,并证明sin A>2√55.6.(2021河南郑州高三三模)在△ABC中,AB=2AC,点D在BC边上,AD平分∠BAC.(1)若sin∠ABC=√5,求cos∠BAC;5(2)若AD=AC,且△ABC的面积为√7,求BC.高考解答题专项二 三角函数中的综合问题1.解f (x )=2sin ωx cos ωx-π6-12=2sin ωx cos ωx cos π6+sin ωx sin π6-12=√3cos ωx sin ωx+sin 2ωx-12=√32sin2ωx-12cos2ωx=sin 2ωx-π6.若f (x )在[a ,b ]上单调递增,且b-a 的最大值为π2, 则T=π=2π2ω,故ω=1,所以f (x )=sin 2x-π6.由π2+2k π≤2x-π6≤3π2+2k π(k ∈Z ),得π3+k π≤x ≤5π6+k π(k ∈Z ),令k=0,得π3≤x ≤5π6;令k=-1,得-2π3≤k ≤-π6.又-π2≤x ≤π2, 所以f (x )在-π2,π2上单调递减区间为-π2,-π6,π3,π2.2.解(1)由2tanBtanA+tanB =bc 及正弦定理可知,2sinBcosB sinA cosA +sinBcosB=sinBsinC ,所以2sinB cosB·cosA ·cosB sin(A+B)=sinB sinC,因此2cos A=1.又A ∈(0,π),所以A=π3.(2)由余弦定理a 2=b 2+c 2-2bc cos A ,得13=9+c 2-3c , 所以c 2-3c-4=0,即(c-4)(c+1)=0,解得c=4. 从而S △ABC =12bc sin A=12×3×4×√32=3√3.3.解(1)由正弦定理得sin B cos C+√3sin B sin C=sin A+sin C=sin(B+C )+sin C=sin B cos C+cos B sin C+sin C. 因为C 为三角形内角,sin C ≠0,所以√3sin B-cos B=1,sin B-π6=12.因为-π6<B-π6<π3,则B-π6=π6,即B=π3. (2)由已知S=12ac sin B=√34ac=√3,得ac=4.又a 2+c 2-b 2=2ac cos B ,即a 2+c 2-4=ac ,解得a=c=2.4.解(1)连接BD ,在Rt △BAD 中,由AB=4,AD=3,∠BAD=90°, 得BD=5,∴sin ∠ABD=35,cos ∠ABD=45.∵∠ABC=45°,∴∠DBC=45°-∠ABD ,∴sin ∠DBC=sin45°·cos ∠ABD-cos45°·sin ∠ABD=√22×45−√22×35=√210. 在Rt △BCD 中,由∠BCD=90°,知CD=BD ·sin ∠DBC=5×√210=√22.(2)连接AC ,由(1)知BD=5,在Rt △ABD 中易知sin ∠ABD=35,cos ∠ABD=45. 在Rt △BCD 中,由BC=2√5,BD=5,得CD=√5. 易知sin ∠CBD=√55,cos ∠CBD=2√55. ∴cos ∠ABC=cos(∠ABD+∠CBD )=cos ∠ABD ·cos ∠CBD-sin ∠ABD ·sin ∠CBD=45×2√55−35×√55=√55. 在△ABC 中,由余弦定理得AC 2=AB 2+BC 2-2AB ·BC cos ∠ABC=42+(2√5)2-2×4×2√5×√55=20, ∴AC=2√5.5.解(1)由f (0)=12,得sin φ=12.又0<φ<π2,故φ=π6. 由f5π12=0,得sin ω·5π12+π6=0,所以ω·5π12+π6=2k π+π(k ∈Z ),即ω=2+24k5(k ∈Z ).由ω>0,结合函数图象可知12·2πω>5π12,所以0<ω<125.又k ∈Z ,所以k=0,从而ω=2,因此f (x )=sin 2x+π6.(2)由fA -B 2−π12=sin(A-B )=35,因为0<B<A<π2,所以0<A-B<π2,故cos(A-B )=45. 因为cos(A-B )=2cos 2A -B2-1,于是cosA -B 2=√1+cos(A -B)2=3√1010. 所以sinA -B 2=√1-cos 2A -B 2=√1010. 又A+B>π2,故A=A+B 2+A -B 2>π4+A -B 2.又y=sin x 在0,π2上单调递增,且A ∈0,π2,π4+A -B 2∈0,π2, 所以sin A>sinπ4+A -B 2=sin π4cosA -B 2+cos π4sinA -B 2=√22×3√1010+√1010=2√55.6.解(1)令△ABC 的边AC ,AB ,BC 为b ,c ,a ,由题意可得c=2b , ∵AB>AC ,∴∠ABC<∠ACB ,∴∠ABC 为锐角,即cos ∠ABC=√1-15=2√55.∵AC sin ∠ABC=AB sin ∠ACB,∴sin ∠ACB=2√55.∵∠ACB ∈(0,π),∴cos ∠ACB=±√55. ∴cos ∠BAC=-cos(∠ABC+∠ACB )=sin ∠ABC sin ∠ACB-cos ∠ABC cos ∠ACB.当cos ∠ACB=√55时,cos ∠BAC=√55×2√55−2√55×√55=0. 当cos ∠ACB=-√55时,cos ∠BAC=√55×2√55+2√55×√55=45.所以cos ∠BAC=0或45.(2)设∠CAD=∠DAB=θ,由于S △ABC =S △ACD +S △ADB , 所以12AC ·AD sin θ+12AB ·AD sin θ=12AB ·AC sin2θ, 由AD=AC ,AB=2AC 可得3sin θ=4sin θcos θ.因为sin θ≠0,则cos θ=34,sin θ=√1-cos 2θ=√74, S △ABC =12AC ·AB sin2θ=b 2sin2θ=2b 2sin θcos θ=√7,解得b 2=83.又cos2θ=2cos 2θ-1=18,∴a=√b 2+4b 2-2b ·2bcos2θ=2√3,即BC=2√3.。
综合算式专项练习题复数与三角函数综合算式专项练习题:复数与三角函数一、复数部分1. 已知复数 z1 = 3 + 4i,z2 = -2 - i ,求下列复数的值:(1)z1 + z2(2)z1 - z2(3)z1 * z2(4)z1 / z22. 已知复数 z = 2 + 3i,求下列复数的值:(1)z的共轭复数(2)|z|^23. 已知复数z = 4(cosα + i sinα),求下列复数的值:(1)z的共轭复数(2)|z|(3)∠z二、三角函数部分1. 已知 a = sinα,b = cosα,请计算:(1)8(a^2 + b^2)(2)sin^2α + cos^2α(3)(a - b)^22. 已知tanα = 2/3,求下列三角函数的值:(1)sinα(2)cosα(3)cotα3. 已知sinα = 1/2,cosβ = -3/5,求下列三角函数的值:(1)sin(α+β)(2)cos(α+β)(3)tan(α+β)三、综合问题1. 已知复数 z = 3 + 4i,将其转化为三角形式,并求出模长和辐角。
2. 已知复数 z1 = 2(cosα + i sinα),z2 = 3(cosβ + i sinβ),求 z1 * z2 的三角形式。
3. 已知复数z = r(cosθ + i sinθ),求复数 z^n 的三角形式,其中 n 为正整数。
四、解答说明1. 在解答复数部分的问题时,可以使用复数的代数运算规则进行计算。
2. 在解答三角函数部分的问题时,可以使用三角函数的定义和性质进行计算。
3. 在解答综合问题时,可以灵活运用复数和三角函数的知识,结合题目要求进行计算。
(以上是文章的一部分内容,总字数约为400字)根据综合算式专项练习题的要求,我们先来解答复数部分的问题。
1.(1)z1 + z2 = (3 + 4i) + (-2 - i) = 1 + 3i(2)z1 - z2 = (3 + 4i) - (-2 - i) = 5 + 5i(3)z1 * z2 = (3 + 4i) * (-2 - i) = -6 - 3i - 8i - 4i^2 = -6 - 11i + 4 = -2 - 11i(4)z1 / z2 = (3 + 4i) / (-2 - i) = (3 + 4i)(-2 + i) / (-2 - i)(-2 + i)= (-6 + 2i - 8i - 4i^2) / (4 + i^2)= (-10 - 6i) / 5= -2 - 1.2i2.(1)z的共轭复数 = 2 - 3i(2)|z|^2 = |2 + 3i|^2 = (2^2 + 3^2) = 133.(1)z的共轭复数= 4(cosα - i sinα)(2)|z| = |4(cosα + i sinα)| = 4(3)∠z = α以下是三角函数部分的解答。
微专题6 与三角函数有关的导数综合问题一、单项选择题曲线y =2sin x +cos x 在点(π,-1)处的切线方程为( )A .x -y -π-1=0B .2x -y -2π-1=0C .2x +y -2π+1=0D .x +y -π+1=0设函数f (x )=x sin x +cos x -x 24,则下列是函数f (x )极小值点的是( ) A .-4π3B .-π3C .π3D .5π3函数f (x )=e x +cos x 在[0,+∞)上的最小值是( )A .0B .1C .2D .3若函数f (x )=cos 2x +a sin x 在区间⎝⎛⎭⎫π6,π2是减函数,则实数a 的取值范围是( ) A .(-∞,2]B .[2,+∞)C .(-∞,4]D .[4,+∞)函数f (x )=x 2-4x sin x -4cos x 在(-π,π)上的零点个数为( )A .1B .2C .3D .4若函数f (x )=12sin 2x -cos x -ax 在(0,π)上有两个极值点,则a 的取值范围是( ) A .(-∞,1]B .(0,1]C .⎝⎛⎭⎫1,98 D .⎣⎡⎭⎫98,+∞ 二、多项选择题关于函数f (x )=x -sin x ,下列说法中正确的有( )A .f (x )是奇函数B .f (x )在(-∞,+∞)上单调递增C .x =0不是f (x )的唯一零点D .f (x )是周期函数下列关于函数f (x )=cos x x+a sin x 的说法,正确的有( ) A .当a ≥0时,f (x )在⎝⎛⎭⎫-π2,π2上不存在零点B .当a ≥0时,f (x )在⎝⎛⎭⎫-π2,π2上存在零点C .当a <0时,f (x )在⎝⎛⎭⎫-π2,π2上不存在零点 D .当a <0时,f (x )在⎝⎛⎭⎫-π2,π2上有两个零点 三、填空题(2018·全国理Ⅰ)已知函数f (x )=2sin x +sin 2x ,则f (x )的最小值是________.若a <sin x x <b 对x ∈⎝⎛⎭⎫0,π2恒成立,则a 的最大值是________;b 的最小值是________.四、解答题已知函数f (x )=x 2+x sin x +cos x .(1)若曲线y =f (x )在点(a ,f (a ))处与直线y =b 相切,求a 与b 的值;(2)若曲线y =f (x )与直线y =b 有两个不同的交点,求b 的取值范围.已知函数f (x )=ln x +a x,其中a ∈R. (1)试讨论函数f (x )的单调性;(2)若a =1,试证明:f (x )<e x +cos x x.。
第32课 三角函数综合问题
一、考纲要求
1.能灵活运用三角公式进行化简、求值、求范围;
2.能综合应用代数中的函数、方程、不等式等知识与方法解决与三角相关的问题。
二、知识梳理
1.在ABC ∆中,= ,=,且2||=,3||=,3-=⋅,则C cos = ,
AB = .
【教学建议】本题是课本习题的改编,考查三角函数与向量简单的综合应用。
教学时先让学生回忆向量的数量积公式,强调向量夹角必须共起点,求出C cos 后,利用余弦定理求出AB 长。
2.函数)12
(cos )(2
π
+
=x x f ,x x g 2sin 2
1
1)(+
=.若0x x =是函数)(x f y =图像的一条对称轴,则)(0x g 的值为 .
【教学建议】本题主要考查三角函数的图像与性质,及三角恒等变形。
教学时,先让学生求出)(x f 的对称轴,带入)(x g 表达式,转化为三角求值题,此题要注意分类讨论,不能漏解。
三、诊断练习
1、教学处理:课前由学生自主完成4道小题,并要求将解题过程扼要地写在学习笔记栏。
上课前抽查批阅部分同学的解答,了解学生的思路及主要错误。
2、结合课件点评。
必要时可借助实物投影,有针对性地投影几位学生的解答过程。
题1:函数2
()(sin cos )f x x x =-的最大值为___________.
【点评】解析式有何特点?平方展开后出现一个定值,另一个表达式怎么处理?,有没有定义域的范围限制?
题2: 若1tan 4tan θθ+
=,则sin 2θ= .答案为:1
2
. 【点评】本题主要考察基本关系式、切化弦的基本思路。
注意学生盲目去解tan θ,或者计算中不及时发现可用公式。
如221sin cos tan 44sin cos 4sin cos tan cos sin θθ
θθθθθθθθ
+=⇒+=⇒+=,左边,右边都直接用公式。
题3:已知角,,αβγ构成公差为3
π
的等差数列,若2cos 3β=-,则cos cos αγ+= .
答案为:2
3
-
. 问题:探求cos cos αγ+的基本思路是什么?
题4:在锐角三角形ABC ∆中,若tan 1,tan 1A t B t =+=-,则实数t 的取值范围
是 .答案为:
)
+∞.
【点评】指导学生认真读题。
引导学生探究锐角三角形角的正切值的范围。
问题1:是否需要向“弦”上转化?
问题2:tan ,tan A B 都大于零,能够保证三角形是锐角三角形吗?如果不能,要研究什么? 3、诊断题归纳
1.研究三角函数的性质,通常将函数解析式化成k x A y ++=)sin(ϕω的形式,如题3和题4
2.会应用代数中的函数、不等式等知识与方法解决与三角相关的问题,同时要注意角的范围对问题的限制。
四、范例导析
例1、例1在ABC ∆中,若13tan ,tan 45
A B ==. (1)求角C ;
(2)若ABC ∆,求最小边的长.
【教学处理】第(1)问,学生自主完成。
第(2)要求学生自己分析,或板演或提问学生口答,教师板书,也可以展示学生解答过程. 第(1)问注意检查学生是否交代30,4
C C π
π∴<<∴=。
【启发谈话与精讲建议】
问题1:如何确定三角形的最小边?
【交流】34C π∴=
,∴最大边为AB =13tan tan ,,0,,452A B A B A B C π⎛⎫
=<=∈∴<< ⎪⎝⎭
,
∴角A 最小,即边BC 最小。
这里要注意学生对三角形基本性质的运用情况,同时运用正切函数的单调性。
问题2:要运用正弦定理,先要求什么?
【交流】由221tan ,sin cos 1,0,42A A A A π⎛⎫
=
+=∈ ⎪⎝⎭
,得sin A =
由
sin sin AB BC C A =,得sin sin AB
BC A C
=⋅=
.
【评注】本题考查三角函数基本关系,正弦定理及两角和正切公式的简单综合运用,注意三角形中基本知识的运用.
例2、已知函数()sin sin()(0)6
4f x x x π
ωωω=+-
>,且其图象的相邻对称轴间的距离为4
π. (1)求()f x 在区间119[
,]128
ππ
上的值域; (2)在锐角ABC ∆中,若1
()82
f A π-=, ,2,1=+=c b a 求ABC ∆的面积.
【教学处理】要求学生自己分析,或板演或提问学生口答教师板书 【启发谈话与精讲建议】
问题1:这是两个正弦相乘的形式,如何化简它?
问题2:把这个三角函数展开后如何合并它?用的是辅助角公式。
问题3:对称轴之间的距离和周期是什么关系?
问题4:周期公式中的分母在本题中是什么?这个地方易错,要特别小心!
问题5:在给定区间上求三角函数的值域,一定要借助图像去解,这样可以有效地避免错误的发生。
问题6:锐角三角形的作用是什么?
问题7:三角形的面积公式是什么?角的问题解决了,如何解决边的问题?
例2变式、设ABC ∆的面积为S
,且20S AB AC +⋅=. (1)求角A 的大小;
(2)若||3BC =,且角B 不是最小角,求S 的取值范围.
解:(1)设ABC ∆中角
,,A B C 所对的边分别为,,a b c ,由2
0S AB AC +⋅=,
得1
2sin
cos 02
bc A A ⨯+=,即
sin 0A A =,
所以tan A =, 又(0,)A π
∈,所以23A π
=.
(2
)因为a =, sin sin 3
b c
B C ==
,所以2sin ,
2sin b B c
C ==, 从而1sin sin sin()23
S
bc A B C B B
π
===-
11cos2sin )2))246B B B B B B π---=+-
又5(,),2(,)63626
B B πππππ∈+∈,所以S ∈.
例3 在ABC ∆中,内角A ,B ,C 的对边分别为a ,b ,c ,已知a ,b ,c 成等比数列,且4
3cos =B . (1)若23=
⋅BC BA ,求c a +的值;(2)求C
C
A A sin cos sin cos +的值.
【教学处理】指导学生认真读题,并将题中条件作初步的转化,能发现条件之间有什么联系?看看能求出
什么?
【启发谈话与精讲建议】 第(1)问:在用3
2
BA BC ⋅=
这一条件时,要注意向量的方向,其夹角是∠B 2
b a
c = 2223cos 42a c b B ac +-== 3
c o s 2
a c B ⋅⋅=;
观察这三个条件,能求出ac ?进而可以求出哪些? 第(2)问:结论式可以转化为sin()sin sin sin sin sin C A B
A C A C
+=
⋅⋅ 对2
,b ac = 3
cos 4
B =
条件式,究竟是从边入手还是角入手呢? 方案一:从角入手,2
b a
c =转化能得到什么?2
sin sin sin B A C =⋅
方案二:从边入手?2223cos 42a c b B ac +-==再结合2
b a
c =能得到什么?2a c =或12
a c = 不妨
2a c =,此时b =
这时的△ABC 的形状是确定的(全是相似的),因而cos ,cos ,cos A B C 都是可求的。
这种方法更为本质。
【变式】若将第2问改为 “求2
2
sin sin A C +的值”?如何求解? 这时方案二的这一本质核心的方法就显示出作用了。
五、解题反思
每一道例题讨论后,都应留出一点时间让学生进行回顾和体悟。
可引导学生对这三道例题作如下反思: 1、 求解与三角有关的函数最值,通常将函数解析式化成k x A y ++=)sin(ϕω的形式,如诊断题3、4,
例2的第(1)问.
2、 注意求解路线的设计和运算的优化。
例3中,边角转化的方向和方法。
要体会什么情境下用余弦定理
或正弦定理转化.
3、体会函数思想在三角中的应用.。