kan试卷二十四试题与答kan案

2025届江苏省东海高级中学高三下学期联合考试数学试题考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知()()()[)3log 1,1,84,8,6x x f x x x ⎧+∈-⎪=⎨∈+∞⎪-⎩ 若()()120f m f x ⎡⎤--≤⎣⎦在定义域上恒成立，则m 的取值范围是（ ）A ．()0,∞+B ．[)1,2C ．[)1,+∞D ．()0,12．已知命题300:2,80p x x ∃>->，那么p ⌝为（ ） A ．3002,80x x ∃>-≤ B ．32,80x x ∀>-≤ C ．3002,80x x ∃≤-≤D ．32,80x x ∀≤-≤3．不等式42,3x y x y -⎧⎨+⎩的解集记为D ，有下面四个命题：1:(,),25p x y D y x ∀∈-；2:(,),22p x y D y x ∃∈-；3:(,),22p x y D y x ∀∈-；4:(,),24p x y D y x ∃∈-.其中的真命题是（ ）A ．12,p pB ．23,p pC ．13,p pD ．24,p p4．已知ABC 是边长为3的正三角形，若13BD BC =，则AD BC ⋅=A ．32- B ．152 C ．32D ．152-5．设i 为虚数单位，复数()()1z a i i R =+-∈，则实数a 的值是（ ） A ．1B ．-1C ．0D ．26．已知三棱锥P ABC -中，O 为AB 的中点，PO ⊥平面ABC ，90APB ∠=︒，2PA PB ==，则有下列四个结论：①若O 为ABC 的外心，则2PC =；②ABC 若为等边三角形，则⊥AP BC ；③当90ACB ∠=︒时，PC 与平面PAB 所成的角的范围为0,4π⎛⎤ ⎥⎝⎦；④当4PC =时，M 为平面PBC 内一动点，若OM ∥平面PAC ，则M 在PBC 内轨迹的长度为1．其中正确的个数是（ ）． A ．1B ．1C ．3D ．47．已知函数在上的值域为，则实数的取值范围为（ ） A ．B ．C ．D ．8．圆柱被一平面截去一部分所得几何体的三视图如图所示，则该几何体的体积为（ ）A ．12πB ．32π C ．2π D ．3π9．已知单位向量a ，b 的夹角为34π，若向量2m a =，4n a b λ=-，且m n ⊥，则n =（ ） A ．2B ．2C ．4D ．610．已知抛物线C ：24x y =的焦点为F ，过点F 的直线l 交抛物线C 于A ，B 两点，其中点A 在第一象限，若弦AB的长为254，则AF BF =（ ） A ．2或12B ．3或13C ．4或14D ．5或1511．已知椭圆22y a +22x b =1(a >b >0)与直线1y a x b -=交于A ，B 两点，焦点F (0，-c )，其中c 为半焦距，若△ABF 是直角三角形，则该椭圆的离心率为（ ） A ．5-12B ．3-12C ．314+ D ．514+ 12．如图，正四面体P ABC -的体积为V ，底面积为S ，O 是高PH 的中点，过O 的平面α与棱PA 、PB 、PC 分别交于D 、E 、F ，设三棱锥P DEF -的体积为0V ，截面三角形DEF 的面积为0S ，则（ ）A ．08V V ≤，04S S ≤B ．08V V ≤，04S S ≥C ．08V V ≥，04S S ≤D ．08V V ≥，04S S ≥二、填空题：本题共4小题，每小题5分，共20分。

2024年西藏高考数学试题及答案本试卷共10页，19小题，满分150分.注意事项：1.答题前，先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.3.填空题和解答题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后，请将本试卷和答题卡一并上交.一、单项选择题：本大题共 8 小题，每小题 5 分，共 40 分. 在每小题给出的四个选项中，只有一个选项是正确的．请把正确的选项填涂在答题卡相应的位置上.1．已知1i z =--，则z =（ ）A ．0B ．1C D ．22．已知命题p ：x ∀∈R ，|1|1x +>；命题q ：0x ∃>，3x x =，则（ ）A ．p 和q 都是真命题B ．p ⌝和q 都是真命题C ．p 和q ⌝都是真命题D ．p ⌝和q ⌝都是真命题3．已知向量,a b满足1,22a a b =+= ，且()2b a b -⊥ ，则b = （ ）A ．12B C D ．14．某农业研究部门在面积相等的100块稻田上种植一种新型水稻，得到各块稻田的亩产量（单位：kg ）并部分整理下表亩产量[900，950）[950，1000）[1000，1050）[1100，1150）[1150，1200）频数612182410据表中数据，结论中正确的是（ ）A ．100块稻田亩产量的中位数小于1050kgB ．100块稻田中亩产量低于1100kg 的稻田所占比例超过80%C ．100块稻田亩产量的极差介于200kg 至300kg 之间D ．100块稻田亩产量的平均值介于900kg 至1000kg 之间5．已知曲线C ：2216x y +=（0y >），从C 上任意一点P 向x 轴作垂线段PP '，P '为垂足，则线段PP '的中点M 的轨迹方程为（ ）A ．221164x y +=（0y >）B ．221168x y +=（0y >）C ．221164y x +=（0y >）D ．221168y x +=（0y >）6．设函数2()(1)1f x a x =+-，()cos 2g x x ax =+，当(1,1)x ∈-时，曲线()y f x =与()y g x =恰有一个交点，则=a （ ）A ．1-B ．12C ．1D ．27．已知正三棱台111ABC A B C -的体积为523，6AB =，112A B =，则1A A 与平面ABC 所成角的正切值为（ ）A ．12B ．1C ．2D ．38．设函数()()ln()f x x a x b =++，若()0f x ≥，则22a b +的最小值为（ ）A ．18B ．14C ．12D ．1二、多项选择题：本大题共 3 小题，每小题 6 分，共 18 分. 在每小题给出的四个选项中，有多项符合题目要求. 全部选对得 6 分，选对但不全的得部分分，有选错的得0分.9．对于函数()sin 2f x x =和π()sin(2)4g x x =-，下列正确的有（ ）A ．()f x 与()g x 有相同零点B ．()f x 与()g x 有相同最大值C ．()f x 与()g x 有相同的最小正周期D ．()f x 与()g x 的图像有相同的对称轴10．抛物线C ：24y x =的准线为l ，P 为C 上的动点，过P 作22:(4)1A x y +-=⊙的一条切线，Q 为切点，过P 作l 的垂线，垂足为B ，则（ ）A ．l 与A 相切B ．当P ，A ，B 三点共线时，||PQ =C ．当||2PB =时，PA AB⊥D ．满足||||PA PB =的点P 有且仅有2个11．设函数32()231f x x ax =-+，则（ ）A ．当1a >时，()f x 有三个零点B ．当0a <时，0x =是()f x 的极大值点C ．存在a ，b ，使得x b =为曲线()y f x =的对称轴D ．存在a ，使得点()()1,1f 为曲线()y f x =的对称中心三、填空题：本大题共 3 小题，每小题 5 分，共 15 分.12．记n S 为等差数列{}n a 的前n 项和，若347a a +=，2535a a +=，则10S = .13．已知α为第一象限角，β为第三象限角，tan tan 4αβ+=，tan tan 1αβ=，则sin()αβ+= .14．在如图的4×4方格表中选4个方格，要求每行和每列均恰有一个方格被选中，则共有 种选法，在所有符合上述要求的选法中，选中方格中的4个数之和的最大值是 ．四、解答题：本题共 5 小题，共 77 分. 解答应写出文字说明、证明过程或演算步骤.15．记ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知sin 2A A =．(1)求A ．(2)若2a =sin sin 2C c B =，求ABC 的周长．16．已知函数3()e x f x ax a =--．(1)当1a =时，求曲线()y f x =在点()1,(1)f 处的切线方程；(2)若()f x 有极小值，且极小值小于0，求a 的取值范围．17．如图，平面四边形ABCD 中，8AB =，3CD =，AD =90ADC ︒∠=，30BAD ︒∠=，点E ，F 满足25AE AD = ，12AF AB =，将AEF △沿EF 对折至PEF !，使得PC =(1)证明：EF PD ⊥；(2)求面PCD 与面PBF 所成的二面角的正弦值．18．某投篮比赛分为两个阶段，每个参赛队由两名队员组成，比赛具体规则如下：第一阶段由参赛队中一名队员投篮3次，若3次都未投中，则该队被淘汰，比赛成员为0分；若至少投中一次，则该队进入第二阶段，由该队的另一名队员投篮3次，每次投中得5分，未投中得0分.该队的比赛成绩为第二阶段的得分总和．某参赛队由甲、乙两名队员组成，设甲每次投中的概率为p ，乙每次投中的概率为q ，各次投中与否相互独立．(1)若0.4p =，0.5q =，甲参加第一阶段比赛，求甲、乙所在队的比赛成绩不少于5分的概率．(2)假设0p q <<，（i ）为使得甲、乙所在队的比赛成绩为15分的概率最大，应该由谁参加第一阶段比赛？（ii ）为使得甲、乙，所在队的比赛成绩的数学期望最大，应该由谁参加第一阶段比赛？19．已知双曲线()22:0C x y m m -=>，点()15,4P 在C 上，k 为常数，01k <<．按照如下方式依次构造点()2,3,...n P n =，过1n P -作斜率为k 的直线与C 的左支交于点1n Q -，令n P 为1n Q -关于y 轴的对称点，记n P 的坐标为(),n n x y .(1)若12k =，求22,x y ；(2)证明：数列{}n n x y -是公比为11kk+-的等比数列；(3)设n S 为12n n n P P P ++ 的面积，证明：对任意的正整数n ，1n n S S +=.1．C【分析】由复数模的计算公式直接计算即可.【详解】若1i z =--=故选：C.2．B【分析】对于两个命题而言，可分别取=1x -、1x =，再结合命题及其否定的真假性相反即可得解.【详解】对于p 而言，取=1x -，则有101x +=<，故p 是假命题，p ⌝是真命题，对于q 而言，取1x =，则有3311x x ===，故q 是真命题，q ⌝是假命题，综上，p ⌝和q 都是真命题.故选：B.3．B【分析】由()2b a b -⊥ 得22b a b =⋅，结合1,22a a b =+= ，得22144164a b b b +⋅+=+= ，由此即可得解.【详解】因为()2b a b -⊥ ，所以()20b a b -⋅= ，即22b a b =⋅，又因为1,22a a b =+=，所以22144164a b b b +⋅+=+= ，故选：B.4．C【分析】计算出前三段频数即可判断A ；计算出低于1100kg 的频数，再计算比例即可判断B ；根据极差计算方法即可判断C ；根据平均值计算公式即可判断D.【详解】对于 A, 根据频数分布表可知, 612183650++=<,所以亩产量的中位数不小于 1050kg , 故 A 错误；对于B ，亩产量不低于1100kg 的频数为341024=+，所以低于1100kg 的稻田占比为1003466%100-=，故B 错误；对于C ，稻田亩产量的极差最大为1200900300-=，最小为1150950200-=，故C 正确；对于D ，由频数分布表可得，亩产量在[1050,1100)的频数为100(612182410)30-++++=，所以平均值为1(692512975181025301075241125101175)1067100⨯⨯+⨯+⨯+⨯+⨯+⨯=，故D 错误.故选；C.5．A【分析】设点(,)M x y ，由题意，根据中点的坐标表示可得(,2)P x y ，代入圆的方程即可求解.【详解】设点(,)M x y ，则0(,),(,0)P x y P x '，因为M 为PP '的中点，所以02y y =，即(,2)P x y ，又P 在圆2216(0)x y y +=>上，所以22416(0)x y y +=>，即221(0)164x y y +=>，即点M 的轨迹方程为221(0)164x y y +=>.故选：A 6．D【分析】解法一：令()()21,cos a x F x ax G x =-=+，分析可知曲线()y F x =与()y G x =恰有一个交点，结合偶函数的对称性可知该交点只能在y 轴上，即可得2a =，并代入检验即可；解法二：令()()()(),1,1h x f x g x x =-∈-，可知()h x 为偶函数，根据偶函数的对称性可知()h x 的零点只能为0，即可得2a =，并代入检验即可.【详解】解法一：令()()f x g x =，即2(1)1cos 2a x x ax +-=+，可得21cos a x ax -=+，令()()21,cos a x F x ax G x =-=+，原题意等价于当(1,1)x ∈-时，曲线()y F x =与()y G x =恰有一个交点，注意到()(),F x G x 均为偶函数，可知该交点只能在y 轴上，可得()()00F G =，即11a -=，解得2a =，若2a =，令()()F x G x =，可得221cos 0x x +-=因为()1,1x ∈-，则220,1cos 0x x ≥-≥，当且仅当0x =时，等号成立，可得221cos 0x x +-≥，当且仅当0x =时，等号成立，则方程221cos 0x x +-=有且仅有一个实根0，即曲线()y F x =与()y G x =恰有一个交点，所以2a =符合题意；综上所述：2a =.解法二：令()()()2()1cos ,1,1h x f x g x ax a x x =-=+--∈-，原题意等价于()h x 有且仅有一个零点，因为()()()()221cos 1cos h x a x a x ax a x h x -=-+---=+--=，则()h x 为偶函数，根据偶函数的对称性可知()h x 的零点只能为0，即()020h a =-=，解得2a =，若2a =，则()()221cos ,1,1h x x x x =+-∈-，又因为220,1cos 0x x ≥-≥当且仅当0x =时，等号成立，可得()0h x ≥，当且仅当0x =时，等号成立，即()h x 有且仅有一个零点0，所以2a =符合题意；故选：D.7．B【分析】解法一：根据台体的体积公式可得三棱台的高h =的结构特征求得AM =111ABC A B C -补成正三棱锥-P ABC ，1A A 与平面ABC 所成角即为PA 与平面ABC 所成角，根据比例关系可得18P ABC V -=，进而可求正三棱锥-P ABC 的高，即可得结果.【详解】解法一：分别取11,BC B C 的中点1,D D ，则11AD A D =可知1111166222ABC A B C S S =⨯⨯==⨯= 设正三棱台111ABC A B C -的为h ，则(11115233ABC A B C V h -==，解得h =如图，分别过11,A D 作底面垂线，垂足为,M N ，设AM x =，则1AADN AD AM MN x=--=，可得1DD==结合等腰梯形11BCC B可得22211622BB DD-⎛⎫=+⎪⎝⎭,即()221616433x x+=-++，解得x=所以1A A与平面ABC所成角的正切值为11tan1A MA ADAMÐ==；解法二：将正三棱台111ABC A B C-补成正三棱锥-P ABC，则1A A与平面ABC所成角即为PA与平面ABC所成角，因为11113PA A BPA AB==，则111127P A B CP ABCVV--=，可知1112652273ABC A B C P ABCV V--==，则18P ABCV-=，设正三棱锥-P ABC的高为d，则11661832P ABCV d-=⨯⨯⨯=，解得d=，取底面ABC的中心为O，则PO⊥底面ABC，且AO=所以PA与平面ABC所成角的正切值tan1POPAOAO∠==.故选：B.8．C【分析】解法一：由题意可知：()f x的定义域为(),b-+∞，分类讨论a-与,1b b--的大小关系，结合符号分析判断，即可得1b a =+，代入可得最值；解法二：根据对数函数的性质分析ln()x b +的符号，进而可得x a +的符号，即可得1b a =+，代入可得最值.【详解】解法一：由题意可知：()f x 的定义域为(),b -+∞，令0x a +=解得x a =-；令ln()0x b +=解得1x b =-；若-≤-a b ，当(),1x b b ∈--时，可知()0,ln 0x a x b +>+<，此时()0f x <，不合题意；若1b a b -<-<-，当(),1x a b ∈--时，可知()0,ln 0x a x b +>+<，此时()0f x <，不合题意；若1a b -=-，当(),1x b b ∈--时，可知()0,ln 0x a x b +<+<，此时()0f x >；当[)1,x b ∈-+∞时，可知()0,ln 0x a x b +≥+≥，此时()0f x ≥；可知若1a b -=-，符合题意；若1a b ->-，当()1,x b a ∈--时，可知()0,ln 0x a x b +<+>，此时()0f x <，不合题意；综上所述：1a b -=-，即1b a =+，则()2222211112222a b a a a ⎛⎫=++=++≥ ⎪⎝⎭+，当且仅当11,22a b =-=时，等号成立，所以22a b +的最小值为12；解法二：由题意可知：()f x 的定义域为(),b -+∞，令0x a +=解得x a =-；令ln()0x b +=解得1x b =-；则当(),1x b b ∈--时，()ln 0x b +<，故0x a +≤，所以10b a -+≤；()1,x b ∈-+∞时，()ln 0x b +>，故0x a +≥，所以10b a -+≥；故10b a -+=， 则()2222211112222a b a a a ⎛⎫=++=++≥ ⎪⎝⎭+，当且仅当11,22a b =-=时，等号成立，所以22a b +的最小值为12.故选：C.【点睛】关键点点睛：分别求0x a +=、ln()0x b +=的根，以根和函数定义域为临界，比较大小分类讨论，结合符号性分析判断.9．BC【分析】根据正弦函数的零点，最值，周期公式，对称轴方程逐一分析每个选项即可.【详解】A 选项，令()sin 20f x x ==，解得π,2k x k =∈Z ，即为()f x 零点，令π()sin(2)04g x x =-=，解得ππ,28k x k =+∈Z ，即为()g x 零点，显然(),()f x g x 零点不同，A 选项错误；B 选项，显然max max ()()1f x g x ==，B 选项正确；C 选项，根据周期公式，(),()f x g x 的周期均为2ππ2=，C 选项正确；D 选项，根据正弦函数的性质()f x 的对称轴满足πππ2π,224k x k x k =+⇔=+∈Z ，()g x 的对称轴满足πππ3π2π,4228k x k x k -=+⇔=+∈Z ，显然(),()f x g x 图像的对称轴不同，D 选项错误.故选：BC 10．ABD【分析】A 选项，抛物线准线为=1x -，根据圆心到准线的距离来判断；B 选项，,,P A B 三点共线时，先求出P 的坐标，进而得出切线长；C 选项，根据2PB =先算出P 的坐标，然后验证1PA AB k k =-是否成立；D 选项，根据抛物线的定义，PB PF =，于是问题转化成PA PF =的P 点的存在性问题，此时考察AF 的中垂线和抛物线的交点个数即可，亦可直接设P 点坐标进行求解.【详解】A 选项，抛物线24y x =的准线为=1x -，A 的圆心(0,4)到直线=1x -的距离显然是1，等于圆的半径，故准线l 和A 相切，A 选项正确；B 选项，,,P A B 三点共线时，即PA l ⊥，则P 的纵坐标4P y =，由24P P y x =，得到4P x =，故(4,4)P ，此时切线长PQ ===，B 选项正确；C 选项，当2PB =时，1P x =，此时244P P y x ==，故(1,2)P 或(1,2)P -，当(1,2)P 时，(0,4),(1,2)A B -，42201PA k -==--，4220(1)AB k -==--，不满足1PA AB k k =-；当(1,2)P -时，(0,4),(1,2)A B -，4(2)601PA k --==--，4(2)60(1)AB k --==--，不满足1PA AB k k =-；于是PA AB ⊥不成立，C 选项错误；D 选项，方法一：利用抛物线定义转化根据抛物线的定义，PB PF =，这里(1,0)F ，于是PA PB =时P 点的存在性问题转化成PA PF =时P 点的存在性问题，(0,4),(1,0)A F ，AF 中点1,22⎛⎫ ⎪⎝⎭，AF 中垂线的斜率为114AF k -=，于是AF 的中垂线方程为：2158x y +=，与抛物线24y x =联立可得216300y y -+=，2164301360∆=-⨯=>，即AF 的中垂线和抛物线有两个交点，即存在两个P 点，使得PA PF =，D 选项正确.方法二：（设点直接求解）设2,4t P t ⎛⎫⎪⎝⎭，由PB l ⊥可得()1,B t -，又(0,4)A ，又PA PB =，214t =+，整理得216300t t -+=，2164301360∆=-⨯=>，则关于t 的方程有两个解，即存在两个这样的P 点，D 选项正确.故选：ABD11．AD【分析】A 选项，先分析出函数的极值点为0,x x a ==，根据零点存在定理和极值的符号判断出()f x 在(1,0),(0,),(,2)a a a -上各有一个零点；B 选项，根据极值和导函数符号的关系进行分析；C 选项，假设存在这样的,a b ，使得x b =为()f x 的对称轴，则()(2)f x f b x =-为恒等式，据此计算判断；D 选项，若存在这样的a ，使得(1,33)a -为()f x 的对称中心，则()(2)66f x f x a +-=-，据此进行计算判断，亦可利用拐点结论直接求解.【详解】A 选项，2()666()f x x ax x x a '=-=-，由于1a >，故()(),0,x a ∞∞∈-⋃+时()0f x '>，故()f x 在()(),0,,a ∞∞-+上单调递增，(0,)x a ∈时，()0f x '<，()f x 单调递减，则()f x 在0x =处取到极大值，在x a =处取到极小值，由(0)10=>f ，3()10f a a =-<，则(0)()0f f a <，根据零点存在定理()f x 在(0,)a 上有一个零点，又(1)130f a -=--<，3(2)410f a a =+>，则(1)(0)0,()(2)0f f f a f a -<<，则()f x 在(1,0),(,2)a a -上各有一个零点，于是1a >时，()f x 有三个零点，A 选项正确；B 选项，()6()f x x x a '=-，a<0时，(,0),()0x a f x '∈<，()f x 单调递减，,()0x ∈+∞时()0f x '>，()f x 单调递增，此时()f x 在0x =处取到极小值，B 选项错误；C 选项，假设存在这样的,a b ，使得x b =为()f x 的对称轴，即存在这样的,a b 使得()(2)f x f b x =-，即32322312(2)3(2)1x ax b x a b x -+=---+，根据二项式定理，等式右边3(2)b x -展开式含有3x 的项为303332C (2)()2b x x -=-，于是等式左右两边3x 的系数都不相等，原等式不可能恒成立，于是不存在这样的,a b ，使得x b =为()f x 的对称轴，C 选项错误；D 选项，方法一：利用对称中心的表达式化简(1)33f a =-，若存在这样的a ，使得(1,33)a -为()f x 的对称中心，则()(2)66f x f x a +-=-，事实上，32322()(2)2312(2)3(2)1(126)(1224)1812f x f x x ax x a x a x a x a +-=-++---+=-+-+-，于是266(126)(1224)1812a a x a x a-=-+-+-即126012240181266a a a a -=⎧⎪-=⎨⎪-=-⎩，解得2a =，即存在2a =使得(1,(1))f 是()f x 的对称中心，D 选项正确.方法二：直接利用拐点结论任何三次函数都有对称中心，对称中心的横坐标是二阶导数的零点，32()231f x x ax =-+，2()66f x x ax '=-，()126f x x a ''=-，由()02af x x ''=⇔=，于是该三次函数的对称中心为,22a a f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，由题意(1,(1))f 也是对称中心，故122aa =⇔=，即存在2a =使得(1,(1))f 是()f x 的对称中心，D 选项正确.故选：AD【点睛】结论点睛：（1）()f x 的对称轴为()(2)x b f x f b x =⇔=-；（2）()f x 关于(,)a b 对称()(2)2f x f a x b ⇔+-=；（3）任何三次函数32()f x ax bx cx d =+++都有对称中心，对称中心是三次函数的拐点，对称中心的横坐标是()0f x ''=的解，即,33b b f a a ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭是三次函数的对称中心12．95【分析】利用等差数列通项公式得到方程组，解出1,a d ，再利用等差数列的求和公式节即可得到答案.【详解】因为数列n a 为等差数列，则由题意得()1111237345a d a d a d a d +++=⎧⎨+++=⎩，解得143a d =-⎧⎨=⎩，则()10110910104453952S a d ⨯=+=⨯-+⨯=.故答案为：95.13．【分析】法一：根据两角和与差的正切公式得()tan αβ+=-αβ+的范围，最后结合同角的平方和关系即可得到答案；法二：利用弦化切的方法即可得到答案.【详解】法一：由题意得()tan tan tan 1tan tan αβαβαβ++===--因为π3π2π,2π,2ππ,2π22k k m m αβ⎛⎫⎛⎫∈+∈++ ⎪ ⎪⎝⎭⎝⎭，,Z k m ∈，则()()()22ππ,22π2πm k m k αβ+∈++++，,Z k m ∈，又因为()tan 0αβ+=-<，则()()3π22π,22π2π2m k m k αβ⎛⎫+∈++++ ⎪⎝⎭，,Z k m ∈，则()sin 0αβ+<，则()()sin cos αβαβ+=-+ ()()22sin cos 1αβαβ+++=，解得()sin αβ+=法二： 因为α为第一象限角，β为第三象限角，则cos 0,cos 0αβ><,cos α==，cos β=则sin()sin cos cos sin cos cos (tan tan )αβαβαβαβαβ+=+=+4cos cos αβ=====故答案为：14． 24 112【分析】由题意可知第一、二、三、四列分别有4、3、2、1个方格可选；利用列举法写出所有的可能结果，即可求解.【详解】由题意知，选4个方格，每行和每列均恰有一个方格被选中，则第一列有4个方格可选，第二列有3个方格可选，第三列有2个方格可选，第四列有1个方格可选，所以共有432124⨯⨯⨯=种选法；每种选法可标记为(,,,)a b c d ，a b c d ,,,分别表示第一、二、三、四列的数字，则所有的可能结果为：(11,22,33,44),(11,22,34,43),(11,22,33,44),(11,22,34,42),(11,24,33,43),(11,24,33,42)，(12,21,33,44),(12,21,34,43),(12,22,31,44),(12,22,34,40),(12,24,31,43),(12,24,33,40)，(13,21,33,44),(13,21,34,42),(13,22,31,44),(13,22,34,40),(13,24,31,42),(13,24,33,40)，(15,21,33,43),(15,21,33,42),(15,22,31,43),(15,22,33,40),(15,22,31,42),(15,22,33,40)，所以选中的方格中，(15,21,33,43)的4个数之和最大，为152********+++=.故答案为：24；112【点睛】关键点点睛：解决本题的关键是确定第一、二、三、四列分别有4、3、2、1个方格可选，利用列举法写出所有的可能结果.15．(1)π6A =(2)2+【分析】（1）根据辅助角公式对条件sin 2A A =进行化简处理即可求解，常规方法还可利用同角三角函数的关系解方程组，亦可利用导数，向量数量积公式，万能公式解决；（2）先根据正弦定理边角互化算出B ，然后根据正弦定理算出,b c 即可得出周长.【详解】（1）方法一：常规方法（辅助角公式）由sin 2A A =可得1sin 12A A =，即sin()1π3A +=，由于ππ4π(0,π)(,)333A A ∈⇒+∈，故ππ32A +=，解得π6A =方法二：常规方法（同角三角函数的基本关系）由sin 2A A =，又22sin cos 1A A +=，消去sin A 得到：224cos 30(2cos 0A A A -+=⇔=，解得cos A =又(0,π)A ∈，故π6A =方法三：利用极值点求解设()sin (0π)f x x x x =<<，则π()2sin (0π)3f x x x ⎛⎫=+<< ⎪⎝⎭，显然π6x =时，max ()2f x =，注意到π()sin 22sin(3f A A A A =+==+，max ()()f x f A =，在开区间(0,π)上取到最大值，于是x A =必定是极值点，即()0cos f A A A '==，即tan A =又(0,π)A ∈，故π6A =方法四：利用向量数量积公式（柯西不等式）设(sin ,cos )a b A A ==，由题意，sin 2a b A A ⋅==，根据向量的数量积公式，cos ,2cos ,a b a b a b a b ⋅== ，则2cos ,2cos ,1a b a b =⇔= ，此时,0a b =，即,a b 同向共线，根据向量共线条件，1cos sin tan A A A ⋅=⇔又(0,π)A ∈，故π6A =方法五：利用万能公式求解设tan 2A t =，根据万能公式，22sin 21t A A t ==+整理可得，2222(2(20((2t t t -+==-，解得tan22A t ==22tan 1t A t ==-，又(0,π)A ∈，故π6A =（2）由题设条件和正弦定理sin sin 2sin 2sin sin cos C c B B C C B B =⇔=，又,(0,π)B C ∈，则sin sin 0B C ≠，进而cos B =π4B =，于是7ππ12C A B =--=，sin sin(π)sin()sin cos sin cos C A B A B A B B A =--=+=+=由正弦定理可得，sin sin sin a b cA B C==，即2ππ7πsin sin sin 6412b c==，解得b c ==故ABC 的周长为216．(1)()e 110x y ---=(2)()1,+∞【分析】（1）求导，结合导数的几何意义求切线方程；（2）解法一：求导，分析0a ≤和0a >两种情况，利用导数判断单调性和极值，分析可得2ln 10a a +->，构建函数解不等式即可；解法二：求导，可知()e '=-xf x a 有零点，可得0a >，进而利用导数求()f x 的单调性和极值，分析可得2ln 10a a +->，构建函数解不等式即可.【详解】（1）当1a =时，则()e 1x f x x =--，()e 1x f x '=-，可得(1)e 2f =-，(1)e 1f '=-，即切点坐标为()1,e 2-，切线斜率e 1k =-，所以切线方程为()()()e 2e 11y x --=--，即()e 110x y ---=.（2）解法一：因为()f x 的定义域为R ，且()e '=-x f x a ，若0a ≤，则()0f x '≥对任意x ∈R 恒成立，可知()f x 在R 上单调递增，无极值，不合题意；若0a >，令()0f x '>，解得ln x a >；令()0f x '<，解得ln x a <；可知()f x 在(),ln a -∞内单调递减，在()ln ,a +∞内单调递增，则()f x 有极小值()3ln ln f a a a a a =--，无极大值，由题意可得：()3ln ln 0f a a a a a =--<，即2ln 10a a +->，构建()2ln 1,0g a a a a =+->，则()120g a a a'=+>，可知()g a 在()0,∞+内单调递增，且()10g =，不等式2ln 10a a +->等价于()()1g a g >，解得1a >，所以a 的取值范围为()1,+∞；解法二：因为()f x 的定义域为R ，且()e '=-x f x a ，若()f x 有极小值，则()e '=-x f x a 有零点，令()e 0x f x a '=-=，可得e x a =，可知e x y =与y a =有交点，则0a >，若0a >，令()0f x '>，解得ln x a >；令()0f x '<，解得ln x a <；可知()f x 在(),ln a -∞内单调递减，在()ln ,a +∞内单调递增，则()f x 有极小值()3ln ln f a a a a a =--，无极大值，符合题意，由题意可得：()3ln ln 0f a a a a a =--<，即2ln 10a a +->，构建()2ln 1,0g a a a a =+->，因为则2,ln 1y a y a ==-在()0,∞+内单调递增，可知()g a 在()0,∞+内单调递增，且()10g =，不等式2ln 10a a +->等价于()()1g a g >，解得1a >，所以a 的取值范围为()1,+∞.17．(1)证明见解析【分析】（1）由题意，根据余弦定理求得2EF =，利用勾股定理的逆定理可证得EF AD ⊥，则,EF PE EF DE ⊥⊥，结合线面垂直的判定定理与性质即可证明；（2）由（1），根据线面垂直的判定定理与性质可证明PE ED ⊥，建立如图空间直角坐标系E xyz -，利用空间向量法求解面面角即可.【详解】（1）由218,,52AB AD AE AD AF AB ====，得4AE AF ==，又30BAD ︒∠=，在AEF △中，由余弦定理得2EF ,所以222AE EF AF +=，则AE EF ⊥，即EF AD ⊥，所以,EF PE EF DE ⊥⊥，又,PE DE E PE DE =⊂ 、平面PDE ，所以EF ⊥平面PDE ，又PD ⊂平面PDE ，故EF ⊥PD ；（2）连接CE，由90,3ADC ED CD ︒∠===，则22236CE ED CD =+=，在PEC中，6PC PE EC ===，得222EC PE PC +=，所以PE EC ⊥，由（1）知PE EF ⊥，又,EC EF E EC EF =⊂ 、平面ABCD ，所以PE ⊥平面ABCD ，又ED ⊂平面ABCD ，所以PE ED ⊥，则,,PE EF ED 两两垂直，建立如图空间直角坐标系E xyz -，则(0,0,0),(0,0,(2,0,0),(0,E P D C F A -，由F 是AB的中点，得(4,B ，所以(4,(2,0,PC PD PB PF =-=-=-=-，设平面PCD 和平面PBF 的一个法向量分别为111222(,,),(,,)n x y z m x y z == ，则11111300n PC x n PD ⎧⋅=+-=⎪⎨⋅=-=⎪⎩，222224020m PB x m PF x ⎧⋅=+-=⎪⎨⋅=-=⎪⎩ ，令122,y x ==，得11220,3,1,1x z y z ===-=，所以(0,2,3),1,1)n m ==-，所以cos ,m nm n m n ⋅===设平面PCD 和平面PBF 所成角为θ，则sin θ==，即平面PCD 和平面PBF.18．(1)0.686(2)（i ）由甲参加第一阶段比赛；（i ）由甲参加第一阶段比赛；【分析】（1）根据对立事件的求法和独立事件的乘法公式即可得到答案；（2）（i ）首先各自计算出331(1)P p q ⎡⎤=--⎣⎦甲，331(1)Pq p ⎡⎤=--⋅⎣⎦乙，再作差因式分解即可判断；(ii)首先得到X 和Y 的所有可能取值，再按步骤列出分布列，计算出各自期望，再次作差比较大小即可.【详解】（1）甲、乙所在队的比赛成绩不少于5分，则甲第一阶段至少投中1次，乙第二阶段也至少投中1次，∴比赛成绩不少于5分的概率()()3310.610.50.686P =--=.（2）（i ）若甲先参加第一阶段比赛，则甲、乙所在队的比赛成绩为15分的概率为331(1)P p q ⎡⎤=--⎣⎦甲，若乙先参加第一阶段比赛，则甲、乙所在队的比赛成绩为15分的概率为331(1)P q p ⎡⎤=--⋅⎣⎦乙，0p q << ，3333()()P P q q pq p p pq ∴-=---+-甲乙()2222()()()()()()q p q pq p p q p pq q pq p pq q pq ⎡⎤=-+++-⋅-+-+--⎣⎦()2222()333p q p q p q pq =---3()()3()[(1)(1)1]0pq p q pq p q pq p q p q =---=---->，P P ∴>甲乙，应该由甲参加第一阶段比赛.(ii)若甲先参加第一阶段比赛，数学成绩X 的所有可能取值为0，5，10，15，333(0)(1)1(1)(1)P X p p q ⎡⎤==-+--⋅-⎣⎦，32123(5)1(1)C (1)P X p q q ⎡⎤==--⋅-⎣⎦，3223(10)1(1)C (1)P X p q q ⎡⎤==--⋅-⎣⎦，33(15)1(1)P X p q ⎡⎤==--⋅⎣⎦，()332()151(1)1533E X p q p p p q⎡⎤∴=--=-+⋅⎣⎦记乙先参加第一阶段比赛，数学成绩Y 的所有可能取值为0，5，10，15，同理()32()1533E Y q q q p=-+⋅()()15[()()3()]E X E Y pq p q p q pq p q ∴-=+---15()(3)p q pq p q =-+-，因为0p q <<，则0p q -<，31130p q +-<+-<，则()(3)0p q pq p q -+->，∴应该由甲参加第一阶段比赛.【点睛】关键点点睛：本题第二问的关键是计算出相关概率和期望，采用作差法并因式分解从而比较出大小关系，最后得到结论.19．(1)23x =，20y =(2)证明见解析(3)证明见解析【分析】（1）直接根据题目中的构造方式计算出2P 的坐标即可；（2）根据等比数列的定义即可验证结论；（3）思路一：使用平面向量数量积和等比数列工具，证明n S 的取值为与n 无关的定值即可.思路二：使用等差数列工具，证明n S 的取值为与n 无关的定值即可.【详解】（1）由已知有22549m =-=，故C 的方程为229x y -=.当12k =时，过()15,4P 且斜率为12的直线为32x y +=，与229x y -=联立得到22392x x +⎛⎫-= ⎪⎝⎭.解得3x =-或5x =，所以该直线与C 的不同于1P 的交点为()13,0Q -，该点显然在C 的左支上.故()23,0P ，从而23x =，20y =.（2）由于过(),n n n P x y 且斜率为k 的直线为()n n y k x x y =-+，与229x y -=联立，得到方程()()229n n x k x x y --+=.展开即得()()()2221290n n n n k x k y kx x y kx ------=，由于(),n n n P x y 已经是直线()n n y k x x y =-+和229x y -=的公共点，故方程必有一根n x x =.从而根据韦达定理，另一根()2222211n n n n nn k y kx ky x k x x x k k ---=-=--，相应的()2221n n nn n y k y kx y k x x y k +-=-+=-.所以该直线与C 的不同于n P 的交点为222222,11n n n n n nn ky x k x y k y kx Q k k ⎛⎫--+- ⎪--⎝⎭，而注意到n Q 的横坐标亦可通过韦达定理表示为()()2291n n ny kx k x----，故n Q 一定在C 的左支上.所以2212222,11n n n n n nn x k x ky y k y kx P k k +⎛⎫+-+- ⎪--⎝⎭.这就得到21221n n n n x k x ky x k ++-=-，21221n n nn y k y kx y k ++-=-.所以2211222211n n n n n nn n x k x ky y k y kx x y k k +++-+--=---()()222222*********n n n n n n n nn n x k x kx y k y ky k k kx y x y k k k k+++++++=-=-=-----.再由22119x y -=，就知道110x y -≠，所以数列{}n n x y -是公比为11k k +-的等比数列.（3）方法一：先证明一个结论：对平面上三个点,,U V W ，若(),UV a b = ，(),UW c d =，则12UVW S ad bc =- .（若,,U V W 在同一条直线上，约定0UVW S = ）证明：1sin ,2UVW S UV UW UV UW =⋅=12UV UW =⋅===12ad bc ===-.证毕，回到原题.加油！有志者事竟成答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

一、复数选择题1．已知复数()2m m m iz i--=为纯虚数，则实数m =（ ）A ．-1B ．0C ．1D ．0或1 2．若复数1z i i ⋅=-+，则复数z 的虚部为（ ） A ．－1 B ．1C ．－iD ．i 3．在复平面内复数Z=i （1﹣2i ）对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．已知复数31iz i -=，则z 的虚部为（ ） A ．1 B ．1-C ．iD ．i -5．复数312iz i=-的虚部是（ ） A ．65i -B ．35iC ．35D ．65-6．如图所示，在复平面内，网格中的每个小正方形的边长都为1，点A ，B 对应的复数分别是1z ，2z ，则12z z -=（ ）A 2B ．2C ．2D ．87．若复数z 满足421iz i+=+，则z =（ ） A ．13i + B ．13i - C ．3i + D ．3i - 8．满足313i z i ⋅=-的复数z 的共扼复数是（ ） A ．3i - B ．3i --C ．3i +D ．3i -+9．若(1)2z i i -=，则在复平面内z 对应的点位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限10．设复数2i1iz =+，则复数z 的共轭复数z 在复平面内对应的点位于（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限11．设复数z 满足方程4z z z z ⋅+⋅=，其中z 为复数z 的共轭复数，若z 的实部为，则z 为（ ）A ．1 BC ．2D ．412．若1i iz ，则2z z i ⋅-=（ ）A ．B ．4C ．D ．813．在复平面内，复数z 对应的点为(,)x y ，若22(2)4x y ++=，则（ ） A ．22z +=B ．22z i +=C ．24z +=D ．24z i +=14．已知(),a bi a b R +∈是()()112i i +-的共轭复数，则a b +=（ ） A ．4B ．2C ．0D ．1-15．已知i 是虚数单位，设复数22ia bi i-+=+，其中,a b ∈R ，则+a b 的值为（ ） A ．75B ．75-C ．15D ．15-二、多选题16．i 是虚数单位，下列说法中正确的有（ ） A ．若复数z 满足0z z ⋅=，则0z =B ．若复数1z ，2z 满足1212z z z z +=-，则120z z =C ．若复数()z a ai a R =+∈，则z 可能是纯虚数D ．若复数z 满足234z i =+，则z 对应的点在第一象限或第三象限17．已知复数cos sin 22z i ππθθθ⎛⎫=+-<< ⎪⎝⎭（其中i 为虚数单位）下列说法正确的是（ ）A ．复数z 在复平面上对应的点可能落在第二象限B ．z 可能为实数C ．1z =D ．1z的虚部为sin θ 18．下列四个命题中，真命题为（ ） A ．若复数z 满足z R ∈，则z R ∈ B ．若复数z 满足1R z∈，则z R ∈ C ．若复数z 满足2z ∈R ，则z R ∈D ．若复数1z ，2z 满足12z z R ⋅∈，则12z z =19．已知复数(),z x yi x y R =+∈，则（ ） A ．20zB ．z 的虚部是yiC ．若12z i =+，则1x =，2y =D ．z =20．已知复数z 满足2724z i =--，在复平面内，复数z 对应的点可能在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限21．若复数z 满足()1z i i +=，则（ ）A ．1z i =-+B ．z 的实部为1C ．1z i =+D ．22z i =22．已知复数1z =-+(i 为虚数单位)，z 为z 的共轭复数，若复数zw z=，则下列结论正确的有（ ）A ．w 在复平面内对应的点位于第二象限B ．1w =C ．w 的实部为12-D ．w 23．若复数z 满足(1i)3i z +=+（其中i 是虚数单位），复数z 的共轭复数为z ，则（ ）A ．|z |=B ．z 的实部是2C ．z 的虚部是1D ．复数z 在复平面内对应的点在第一象限24．已知1z ，2z 为复数，下列命题不正确的是（ ） A ．若12z z =，则12=z z B ．若12=z z ，则12z z =C ．若12z z >则12z z >D ．若12z z >，则12z z >25．下列命题中，正确的是（ ） A ．复数的模总是非负数B ．复数集与复平面内以原点为起点的所有向量组成的集合一一对应C ．如果复数z 对应的点在第一象限，则与该复数对应的向量的终点也一定在第一象限D ．相等的向量对应着相等的复数26．已知复数12ω=-，其中i 是虚数单位，则下列结论正确的是（ ）A ．1ω=B ．2ω的虚部为C ．31ω=-D ．1ω在复平面内对应的点在第四象限27．已知复数z 的共轭复数为z ，且1zi i =+，则下列结论正确的是（ ）A ．1z +=B ．z 虚部为i -C ．202010102z =-D ．2z z z +=28．对于复数(,)z a bi a b R =+∈，下列结论错误．．的是（ ）. A ．若0a =，则a bi +为纯虚数 B ．若32a bi i -=+，则3,2a b == C ．若0b =，则a bi +为实数 D ．纯虚数z 的共轭复数是z -29．已知复数z 满足23z z iz ai ⋅+=+，a R ∈，则实数a 的值可能是（ ）A ．1B ．4-C ．0D ．530．设()()2225322z t t t t i =+-+++，t ∈R ，i 为虚数单位，则以下结论正确的是（ ）A ．z 对应的点在第一象限B ．z 一定不为纯虚数C ．z 一定不为实数D ．z 对应的点在实轴的下方【参考答案】***试卷处理标记，请不要删除一、复数选择题 1．C 【分析】结合复数除法运算化简复数，再由纯虚数定义求解即可 【详解】解析：因为为纯虚数，所以，解得， 故选：C. 解析：C 【分析】结合复数除法运算化简复数z ，再由纯虚数定义求解即可 【详解】 解析：因为()()22m m m iz m m mi i--==--为纯虚数，所以200m m m ⎧-=⎨≠⎩，解得1m =，故选：C.2．B【分析】，然后算出即可. 【详解】由题意，则复数的虚部为1 故选：B解析：B 【分析】1iz i -+=，然后算出即可. 【详解】 由题意()11111i i i i z i i i i -+-+--====+⋅-，则复数z 的虚部为1故选：B3．A 【解析】试题分析：根据复数乘法的运算法则，我们可以将复数Z 化为a=bi （a ，b ∈R ）的形式，分析实部和虚部的符号，即可得到答案． 解：∵复数Z=i （1﹣2i ）=2+i ∵复数Z 的实部2＞0，虚解析：A 【解析】试题分析：根据复数乘法的运算法则，我们可以将复数Z 化为a=bi （a ，b ∈R ）的形式，分析实部和虚部的符号，即可得到答案． 解：∵复数Z=i （1﹣2i ）=2+i ∵复数Z 的实部2＞0，虚部1＞0 ∴复数Z 在复平面内对应的点位于第一象限 故选A点评：本题考查的知识是复数的代数表示法及其几何意义，其中根据复数乘法的运算法则，将复数Z 化为a=bi （a ，b ∈R ）的形式，是解答本题的关键．4．B 【分析】化简复数，可得，结合选项得出答案． 【详解】则，的虚部为 故选：B解析：B 【分析】化简复数z ，可得z ，结合选项得出答案． 【详解】()311==11i iz i i i i i--=-=+- 则1z i =-，z 的虚部为1- 故选：B5．C 【分析】由复数除法法则计算出后可得其虚部． 【详解】 因为，所以复数z 的虚部是． 故选：C ．解析：C 【分析】由复数除法法则计算出z 后可得其虚部． 【详解】 因为33(12)366312(12)(12)555i i i i i i i i +-===-+--+， 所以复数z 的虚部是35． 故选：C ．6．B 【分析】根据复数的几何意义，求两个复数，再计算复数的模. 【详解】由图象可知，，则， 故. 故选:B.解析：B 【分析】根据复数的几何意义，求两个复数，再计算复数的模. 【详解】由图象可知1z i =，22z i =-，则1222z z i -=-+，故12|22|z z i -=-+== 故选:B .7．C 【分析】首先根据复数的四则运算求出，然后根据共轭复数的概念求出. 【详解】 ，故. 故选：C.解析：C 【分析】首先根据复数的四则运算求出z ，然后根据共轭复数的概念求出z . 【详解】()()()()421426231112i i i iz i i i i +-+-====-++-，故3z i =+. 故选：C.8．A 【分析】根据，利用复数的除法运算化简复数，再利用共扼复数的概念求解. 【详解】 因为， 所以，复数的共扼复数是， 故选：A解析：A 【分析】根据313i z i ⋅=-，利用复数的除法运算化简复数，再利用共扼复数的概念求解. 【详解】因为313i z i ⋅=-， 所以()13133iz i i i i-==-=+-， 复数z 的共扼复数是3z i =-， 故选：A9．B 【分析】先求解出复数，然后根据复数的几何意义判断. 【详解】 因为，所以，故对应的点位于复平面内第二象限. 故选：B. 【点睛】本题考查复数的除法运算及复数的几何意义，属于基础题. 化简计解析：B 【分析】先求解出复数z ，然后根据复数的几何意义判断. 【详解】因为(1)2z i i -=，所以()212112i i i z i i +===-+-， 故z 对应的点位于复平面内第二象限. 故选：B.本题考查复数的除法运算及复数的几何意义，属于基础题. 化简计算复数的除法时，注意分子分母同乘以分母的共轭复数.10．D 【分析】先求出，再求出，直接得复数在复平面内对应的点 【详解】因为，所以，在复平面内对应点，位于第四象限. 故选：D解析：D 【分析】先求出z ，再求出z ，直接得复数z 在复平面内对应的点 【详解】 因为211i z i i==++，所以1z i -=-，z 在复平面内对应点()1,1-，位于第四象限.故选：D11．B 【分析】由题意，设复数，根据共轭复数的概念，以及题中条件，即可得出结果. 【详解】因为的实部为，所以可设复数， 则其共轭复数为，又， 所以由，可得，即，因此. 故选：B.解析：B 【分析】由题意，设复数(),z yi x R y R =∈∈，根据共轭复数的概念，以及题中条件，即可得出结果. 【详解】因为z ，所以可设复数(),z yi x R y R =∈∈，则其共轭复数为z yi =，又z z =，所以由4z z z z ⋅+⋅=，可得()4z z z ⋅+=，即4z ⋅=，因此z =故选：B.12．A 【分析】化简复数，求共轭复数，利用复数的模的定义得．因为，所以， 所以 故选：A解析：A 【分析】化简复数z ，求共轭复数z ，利用复数的模的定义得2i z z --． 【详解】 因为1111i z i i i+==+=-，所以1z i =+，所以()()211222z z i i i i i ⋅-=-+-=-= 故选：A13．B 【分析】利用复数模的计算公式即可判断出结论． 【详解】因为复数对应的点为，所以 ，满足则 故选：B解析：B 【分析】利用复数模的计算公式即可判断出结论． 【详解】因为复数z 对应的点为(,)x y ，所以z x yi =+x ，y 满足22(2)4x y ++=则22z i +=故选：B14．A 【分析】先利用复数的乘法运算法则化简，再利用共轭复数的定义求出a+bi ，从而确定a ，b 的值，求出a+b ． 【详解】 ， 故选：A解析：A先利用复数的乘法运算法则化简()()112i i +-，再利用共轭复数的定义求出a +bi ，从而确定a ，b 的值，求出a +b ． 【详解】()()112i i +-1223i i i =-++=-3a bi i ∴+=+ 3,1a b ==，4a b +=故选：A15．D 【分析】先化简，求出的值即得解. 【详解】 ， 所以. 故选：D解析：D 【分析】 先化简345ia bi -+=，求出,ab 的值即得解. 【详解】22(2)342(2)(2)5i i ia bi i i i ---+===++-，所以341,,555a b a b ==-∴+=-. 故选：D二、多选题 16．AD 【分析】A 选项，设出复数，根据共轭复数的相关计算，即可求出结果；B 选项，举出反例，根据复数模的计算公式，即可判断出结果；C 选项，根据纯虚数的定义，可判断出结果；D 选项，设出复数，根据题解析：AD 【分析】A 选项，设出复数，根据共轭复数的相关计算，即可求出结果；B 选项，举出反例，根据复数模的计算公式，即可判断出结果；C 选项，根据纯虚数的定义，可判断出结果；D 选项，设出复数，根据题中条件，求出复数，由几何意义，即可判断出结果.【详解】A 选项，设(),z a bi a b R =+∈，则其共轭复数为(),z a bi a b R =-∈， 则220z z a b ⋅=+=，所以0a b ，即0z =；A 正确；B 选项，若11z =，2z i =，满足1212z z z z +=-，但12z z i =不为0；B 错；C 选项，若复数()z a ai a R =+∈表示纯虚数，需要实部为0，即0a =，但此时复数0z =表示实数，故C 错；D 选项，设(),z a bi a b R =+∈，则()2222234z a bi a abi b i =+=+-=+， 所以22324a b ab ⎧-=⎨=⎩，解得21a b =⎧⎨=⎩或21a b =-⎧⎨=-⎩，则2z i =+或2z i =--， 所以其对应的点分别为()2,1或()2,1--，所以对应点的在第一象限或第三象限；D 正确. 故选：AD.17．BC【分析】分、、三种情况讨论，可判断AB 选项的正误；利用复数的模长公式可判断C 选项的正误；化简复数，利用复数的概念可判断D 选项的正误.【详解】对于AB 选项，当时，，，此时复数在复平面内的点解析：BC【分析】 分02θπ-<<、0θ=、02πθ<<三种情况讨论，可判断AB 选项的正误；利用复数的模长公式可判断C 选项的正误；化简复数1z ，利用复数的概念可判断D 选项的正误. 【详解】对于AB 选项，当02θπ-<<时，cos 0θ>，sin 0θ<，此时复数z 在复平面内的点在第四象限；当0θ=时，1z R =-∈； 当02πθ<<时，cos 0θ>，sin 0θ>，此时复数z 在复平面内的点在第一象限.A 选项错误，B 选项正确；对于C 选项，1z ==，C 选项正确；对于D 选项，()()11cos sin cos sin cos sin cos sin cos sin i i z i i i θθθθθθθθθθ-===-++⋅-，所以，复数1z的虚部为sin θ-，D 选项错误. 故选：BC. 18．AB【分析】利用特值法依次判断选项即可得到答案.【详解】对选项A ，若复数满足，设，其中，则，则选项A 正确；对选项B ，若复数满足，设，其中，且，则，则选项B 正确；对选项C ，若复数满足，设解析：AB【分析】利用特值法依次判断选项即可得到答案.【详解】对选项A ，若复数z 满足z R ∈，设z a =，其中a R ∈，则z R ∈，则选项A 正确； 对选项B ，若复数z 满足1R z ∈，设1a z =，其中a R ∈，且0a ≠， 则1z R a=∈，则选项B 正确； 对选项C ，若复数z 满足2z ∈R ，设z i ，则21z R =-∈，但z i R =∉，则选项C 错误；对选项D ，若复数1z ，2z 满足12z z R ⋅∈，设1z i =，2z i =，则121z z ⋅=-∈R ， 而21z i z =-≠，则选项D 错误；故答案选：AB【点睛】本题主要考查复数的运算，同时考查复数的定义和共轭复数，特值法为解决本题的关键，属于简单题.19．CD【分析】取特殊值可判断A 选项的正误；由复数的概念可判断B 、C 选项的正误；由复数模的概念可判断D 选项的正误.【详解】对于A 选项，取，则，A 选项错误；对于B 选项，复数的虚部为，B 选项错误；解析：CD【分析】取特殊值可判断A 选项的正误；由复数的概念可判断B 、C 选项的正误；由复数模的概念可判断D 选项的正误.【详解】对于A 选项，取z i ，则210z =-<，A 选项错误；对于B 选项，复数z 的虚部为y ，B 选项错误；对于C 选项，若12z i =+，则1x =，2y =，C 选项正确；对于D 选项，z =D 选项正确.故选：CD.【点睛】本题考查复数相关命题真假的判断，涉及复数的计算、复数的概念以及复数的模，属于基础题. 20．BD【分析】先设复数，根据题中条件，由复数的乘法运算，以及复数相等的充要条件求出，即可确定对应的点所在的象限.【详解】设复数，则，所以，则，解得或，因此或，所以对应的点为或，因此复解析：BD【分析】先设复数(),z a bi a b R =+∈，根据题中条件，由复数的乘法运算，以及复数相等的充要条件求出z ，即可确定对应的点所在的象限.【详解】设复数(),z a bi a b R =+∈，则2222724z a abi b i =+-=--，所以2222724z a abi b i =+-=--，则227224a b ab ⎧-=-⎨=-⎩，解得34a b =⎧⎨=-⎩或34a b =-⎧⎨=⎩， 因此34z i =-或34z i =-+，所以对应的点为()3,4-或()3,4-，因此复数z 对应的点可能在第二或第四象限.故选：BD.【点睛】本题主要考查判定复数对应的点所在的象限，熟记复数的运算法则，以及复数相等的条件即可，属于基础题型.21．BC【分析】先利用复数的运算求出复数z ，然后逐个分析判断即可【详解】解：由，得，所以z 的实部为1，，，故选：BC【点睛】此题考查复数的运算，考查复数的模，考查复数的有关概念，考查共轭 解析：BC【分析】先利用复数的运算求出复数z ，然后逐个分析判断即可【详解】解：由()1z i i +=，得2(1)2(1)11(1)(1)2i i z i i i i --====-++-， 所以z 的实部为1，1z i =+，22z i =-，故选：BC【点睛】此题考查复数的运算，考查复数的模，考查复数的有关概念，考查共轭复数，属于基础题22．ABC【分析】对选项求出，再判断得解；对选项，求出再判断得解；对选项复数的实部为，判断得解；对选项,的虚部为,判断得解.【详解】对选项由题得.所以复数对应的点为，在第二象限，所以选项正确解析：ABC【分析】对选项,A 求出1=2w -+，再判断得解；对选项B ，求出1w =再判断得解；对选项,C 复数w 的实部为12-，判断得解；对选项D ,w 判断得解. 【详解】对选项,A 由题得1,z =-1=2w ∴===-.所以复数w 对应的点为1(,22-，在第二象限，所以选项A 正确；对选项B ，因为1w ==，所以选项B 正确； 对选项,C 复数w 的实部为12-，所以选项C 正确；对选项D ,w 所以选项D 错误. 故选：ABC【点睛】 本题主要考查复数的运算和共轭复数，考查复数的模的计算，考查复数的几何意义，考查复数的实部和虚部的概念，意在考查学生对这些知识的理解掌握水平.23．ABD【分析】把已知等式变形，然后利用复数代数形式的乘除运算化简，求出复数，根据共轭复数概念得到，即可判断.【详解】，，，故选项正确，的实部是，故选项正确，的虚部是，故选项错误，复解析：ABD【分析】把已知等式变形，然后利用复数代数形式的乘除运算化简，求出复数z ，根据共轭复数概念得到z ，即可判断.【详解】(1i)3i z +=+，()()()()3134221112i i i i z i i i i +-+-∴====-++-，z ∴==，故选项A 正确，z 的实部是2，故选项B 正确，z 的虚部是1-，故选项C 错误， 复数2z i =+在复平面内对应的点为()2,1，在第一象限，故选项D 正确.故选：ABD .【点睛】本题主要考查的是复数代数形式的乘除运算，考查了复数的代数表示及几何意义，是基础题.24．BCD【分析】根据两个复数之间不能比较大小，得到C 、D 两项是错误的，根据复数的定义和复数模的概念，可以断定A 项正确，B 项错误，从而得到答案.【详解】因为两个复数之间只有等与不等，不能比较大小解析：BCD【分析】根据两个复数之间不能比较大小，得到C 、D 两项是错误的，根据复数的定义和复数模的概念，可以断定A 项正确，B 项错误，从而得到答案.【详解】因为两个复数之间只有等与不等，不能比较大小，所以C 、D 两项都不正确； 当两个复数的模相等时，复数不一定相等， 比如11i i -=+，但是11i i -≠+，所以B 项是错误的；因为当两个复数相等时，模一定相等，所以A 项正确；故选：BCD.【点睛】该题考查的是有关复数的问题，涉及到的知识点有两个复数之间的关系，复数模的概念，属于基础题目.25．ABD【分析】根据复数的几何意义逐项判断后可得正确的选项．【详解】设复数，对于A ，，故A 正确．对于B ，复数对应的向量为，且对于平面内以原点为起点的任一向量，其对应的复数为，故复数集与解析：ABD【分析】根据复数的几何意义逐项判断后可得正确的选项．【详解】设复数(),z a bi a b R =+∈，对于A ，0z =≥，故A 正确．对于B ，复数z 对应的向量为(),OZ a b =，且对于平面内以原点为起点的任一向量(),m n α=，其对应的复数为m ni +， 故复数集与复平面内以原点为起点的所有向量组成的集合一一对应，故B 正确． 对于B ，复数z 对应的向量为(),OZ a b =，且对于平面内的任一向量(),m n α=，其对应的复数为m ni +，故复数集中的元素与复平面内以原点为起点的所有向量组成的集合中的元素是一一对应，故B 正确．对于C ，如果复数z 对应的点在第一象限，则与该复数对应的向量的终点不一定在第一象限，故C 错．对于D ，相等的向量的坐标一定是相同的，故它们对应的复数也相等，故D 正确． 故选：ABD ．【点睛】本题考查复数的几何意义，注意复数(),z a bi a b R =+∈对应的向量的坐标为(),a b ，它与终点与起点的坐标的差有关，本题属于基础题．26．AB【分析】求得、的虚部、、对应点所在的象限，由此判断正确选项.【详解】依题意，所以A 选项正确；，虚部为，所以B 选项正确；，所以C 选项错误；，对应点为，在第三象限，故D 选项错误.故选解析：AB【分析】 求得ω、2ω的虚部、3ω、1ω对应点所在的象限，由此判断正确选项. 【详解】依题意1ω==，所以A 选项正确；2211312442ω⎛⎫=-+=-=- ⎪ ⎪⎝⎭，虚部为，所以B 选项正确；22321111222ωωω⎛⎫⎛⎫⎛⎫=⋅=--⋅-+=-+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，所以C 选项错误；221111222122ω---====-⎛⎛⎫-+ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，对应点为1,22⎛⎫-- ⎪ ⎪⎝⎭，在第三象限，故D 选项错误. 故选：AB【点睛】本小题主要考查复数的概念和运算，考查复数对应点所在象限，属于基础题.27．ACD【分析】先利用题目条件可求得，再根据复数的模的计算公式，以及复数的有关概念和复数的四则运算法则即可判断各选项的真假．【详解】由可得，，所以，虚部为；因为，所以，．故选：ACD ．【解析：ACD【分析】先利用题目条件可求得z ，再根据复数的模的计算公式，以及复数的有关概念和复数的四则运算法则即可判断各选项的真假．【详解】由1zi i =+可得，11i z i i+==-，所以12z i +=-==，z 虚部为1-；因为2422,2z i z =-=-，所以()5052020410102z z ==-，2211z z i i i z +=-++=-=．故选：ACD ．【点睛】本题主要考查复数的有关概念的理解和运用，复数的模的计算公式的应用，复数的四则运算法则的应用，考查学生的数学运算能力，属于基础题． 28．AB由复数的代数形式的运算，逐个选项验证可得．【详解】解：因为当且时复数为纯虚数，此时，故A 错误，D 正确；当时，复数为实数，故C 正确；对于B ：，则即，故B 错误；故错误的有AB解析：AB【分析】由复数的代数形式的运算，逐个选项验证可得．【详解】解：因为(,)z a bi a b R =+∈当0a =且0b ≠时复数为纯虚数，此时z bi z =-=-，故A 错误，D 正确； 当0b =时，复数为实数，故C 正确；对于B ：32a bi i -=+，则32a b =⎧⎨-=⎩即32a b =⎧⎨=-⎩，故B 错误； 故错误的有AB ；故选：AB【点睛】本题考查复数的代数形式及几何意义，属于基础题． 29．ABC【分析】设，从而有，利用消元法得到关于的一元二次方程，利用判别式大于等于0，从而求得a 的范围，即可得答案.【详解】设，∴，∴，∴，解得：，∴实数的值可能是.故选：ABC.【点解析：ABC【分析】设z x yi =+，从而有222()3x y i x yi ai ++-=+，利用消元法得到关于y 的一元二次方程，利用判别式大于等于0，从而求得a 的范围，即可得答案.设z x yi =+，∴222()3x y i x yi ai ++-=+， ∴222223,23042,x y y a y y x a ⎧++=⇒++-=⎨=⎩， ∴244(3)04a ∆=--≥，解得：44a -≤≤， ∴实数a 的值可能是1,4,0-.故选：ABC.【点睛】本题考查复数的四则运算、模的运算，考查函数与方程思想，考查逻辑推理能力和运算求解能力.30．CD【分析】利用配方法得出复数的实部和虚部的取值范围，结合复数的概念和几何意义可判断出各选项的正误，由此可得出结论.【详解】，，所以，复数对应的点可能在第一象限，也可能在第二象限，故A 错误 解析：CD【分析】利用配方法得出复数z 的实部和虚部的取值范围，结合复数的概念和几何意义可判断出各选项的正误，由此可得出结论.【详解】22549492532488t t t ⎛+⎫= ⎪⎝⎭+-->-，()2222110t t t ++=++>， 所以，复数z 对应的点可能在第一象限，也可能在第二象限，故A 错误；当222530220t t t t ⎧+-=⎨++≠⎩，即3t =-或12t =时，z 为纯虚数，故B 错误； 因为2220t t ++>恒成立，所以z 一定不为实数，故C 正确；由选项A 的分析知，z 对应的点在实轴的上方，所以z 对应的点在实轴的下方，故D 正确. 故选：CD.【点睛】本题考查复数的几何意义与复数的概念相关命题真假的判断，解题的关键就是求出复数虚部和实部的取值范围，考查计算能力与推理能力，属于中等题.。

24年国考行测试题在2019年的国家公务员考试中，有一道题引起了广泛的关注和讨论。

这道题被称为“24年国考行测试题”，因为它涉及到了一位考生24年前的行为，引发了许多人对道德和行为规范的思考和讨论。

这道题的内容是这样的：在1995年的一次国家公务员考试中，一名考生在答题卡上写下了他的名字和考试号码，但没有回答任何题目。

24年后的2019年，这名考生参加了同一科目的国家公务员考试，并且在这次考试中取得了优异的成绩。

根据国家公务员考试的规定，考试成绩将会被保留10年，考生在10年内可以利用这个成绩申请各级公务员职位。

考生的这个行为引发了广泛的争议和讨论，其中涉及到了道德、公平和公正的问题。

对于这个题目，一些人认为这名考生的行为是不道德的，因为他在1995年的考试中没有回答任何题目，这不符合公务员考试的规定和要求。

这些人认为，这位考生的考试成绩应该被取消，并且他在2019年的考试中的成绩也应该无效。

另一些人则持不同的观点。

他们认为，这位考生在24年前的行为和他在2019年的考试成绩是两个完全不同的事情，不应该混为一谈。

他们认为，这名考生在2019年的考试中表现出了自己的才能和能力，应该被认可和鼓励。

从道德的角度来看，这个问题确实存在一些争议。

一方面，我们应该遵守规则和规定，不应该为自己的私利而违背道德准则。

另一方面，我们也应该给予人们改过自新的机会，让他们能够发展自己的才能和能力。

从公平和公正的角度来看，取消这位考生在2019年的考试成绩可能是一种公正的做法，因为他在24年前的考试中没有遵守规定。

然而，我们也应该考虑到这位考生的努力和能力，在2019年的考试中取得了优异的成绩，这也应该得到一定的认可和鼓励。

在讨论这个问题的时候，我们也应该考虑到一些特殊情况和因素。

比如，这名考生在24年前是否因为特殊原因没有回答题目？他在24年的时间里是否一直在努力提升自己的能力？这些因素可能对我们的判断和决策有一定的影响。

2023年中国汉字听写大赛全部试题库及答案复赛第一场1汗水涔涔hanshuTcencen2泡蹶子IiaojllmZi3万目睚眦wanmuyazi4嬷嬷r∩6mo5神龛shenkan6哪县豆瓣P∣Xiand∂uban7兄弟阅墙xiδngdixiqiang8荤荤大端（注）IudIuddaduan9雾淞wusong10颠茄dianqie11熨帖yutie12物狗∖husun13图们江TuMenJiang15腭裂elie16秃鹫tujiu17癞蛤蟆Iaihama18惴惴不安zhuizhuιbuan 19骨宽关节kuanguanjie 20繁文婚节fanwenrujie 21咋舌zeshe22裘皮qiUpi23沟壑gδuhe24日臻完善rιzhenwanshan 25悻代英YunDaiYTng26矫揉造作jiW。

rouzaozu∂27名虽水qiangshuT28炉算子Iubιzi29分道扬镶fendaoyangbiao30黑曜石heiyaoshι31攥拳头zuanquantou32黏稠nianchou33三聚氟胺sanjuqingan34暴殄天物baotiantianwu35拾掇shιduo36束河ShuHe37瓮中捉鳖wengzhδngzhuδbie38弩马numa39曾国藩ZengGuoFan40枭首示众xiaoshδushizh∂ng41谥号shihao42襁褓qiangbao43核甘酸hegansuan44凌然长逝keranchangshi 45摩羯座mojiezu∂46陀螺tuoIuo47桀纣Ji4Zhdu48馥郁fuyu 49斧钺fuyue50»pixiu第2期复赛第二场1娱蚣wugong2破绽p∂zhan3驿站yizhan4矫健jiaojian5焦炭jiaotan6涉密shemi7耳熟能详ershunengxiang8隔膜gemo9造次zaoci10青涩qTngse11方兴未艾fang×Tngweiai 12诧异chayi13反刍fanchu14沉湎chenmian15烙饼Iaobιng16华尔兹huaerzT17捉襟见肘ZhuojTnjianzhδ∪18萧瑟xiaose19T区气∂uqi20椭圆tuoyuan21通牒tongdie22辍学chu∂xue23墩布dunbu24揉搓roucuo25蜥蜴Xiyi26端倪duanni27尔虞我诈eryuwδzha28禁锢jingu29炮仗paozhang30殒命yunming32凋敝diaobi33扑尔敏puermin 34毕肖bixiao35造诣zaoyi36天赋异禀tianfuyιbιng37跋扈bahu38桔梗j语geng39皴裂cunlie40颐指气使yιzhιqishι41苔辞taixian42蚩尤ChiY6u43火铳huδch∂ng44囿于成见y∂uyuchengjian 45嵇康JTKang46草菅人命caojianrenming 47槽子糕caoZigao48蘸水钢笔zhanshuTgangbι49壅塞yδngse50日冕rimian51岱宗DaiZong52攫取ju6q153瓜瓢guarang54插科打浑（注）chakedahun复赛第三场1滂沱pangtuo2妖孽yaOnie3嘉陵江JiaLingJiang4疮痂Chuangjia5暮霭muai6杯盘狼藉beipanIangji7湿疹shTzhen8饶恕raoshu9惆怅chouchang10盘桓panhuan11层峦叠嶂cengIuandiezhang 12范畴fanchou13杂”会za hui14蝉蜕chantuι15淤积yd"16扎筏子zafazi17装裱zhuangbiao18中流砥柱zhδngIiudιzhu 19翘楚qiaochu20余烬yUjin21疑窦丛生yid∂ucongsheng 22摒除bingchu23杀手铜shashδ∪jian24噩鼠yanshu25喇嘛Iama26蹶鱼guiyu27赭石zheshι28淄博ZiBo29腌度aza30奉为圭臬fengweiguinie 31矽肺病xTfeibing32自惭形秽zicanxιnghui33虫笏chongzhι34乌相wujiu35轮毂Iungu36每况愈下meikuangyuxia 37瞿塘峡QuTangXia38仇徐qiuyu39踽踽独行juj□dUxing40宁馨儿nιngxlner41Mjianghu42翅越lieqie43温庭筠WenTingYun44穷兵疑武qiongbingduwu 45伽马刀gamadao46喷嚏penti47蕾香hudxiang48遒劲qiujing49居心叵测jCixTnpδce50副蹭guaceng51黑薮薮heiququ52商榷shangque53纵横牌阖z∂nghengbaihe 54白垩纪baieji55缥丝saosT56滁州ChuZhou57烤款kaofu58梦魇mengyan59苜蓿muxu60弄璋之喜nδngzhangzhTxι61顶礼膜拜dingITmobai62阴霾yinmai63虢国夫人GuoGuoFuRen 64厉兵秣马IibTngm∂ma65岳麓书院YueLuShuYuan 66伽邮琴jiayeqιn67隋炀帝SuiYangDi68蹴鞠CCljCi69熠熠生辉yiyishenghuT 70嘴j百ngzuι71成脚waijiao72户枢不蠹（注）huShubudu 复赛第四场1扭捏niunie2蒲扇pushan3乾坤qiankun4按图索骥加tUsuδji5煽情shanqιng6推卸t∪Txie7眼花缭乱yanhuaIiaoIuan 8电饭煲dianfanbao9瓜葛guage10昙花一现tanhuayTxian 11次生林cishengIin12干涸ganhe13稚嫩zhinen14紫檀Zitan15怨天尤人yuantianyouren 16搭档dadang17手榴弹shouIiudan18漕运caoyun19亶页亶页巍巍chanchanweiwei20珞牙geya21日珥rier22擀面杖ganmianzhang23樗挑子Iiaotiaozi24莺尾花yuanweihua25硒鼓xTgu26灯芯绒deng×Tnrong27虹吸hongxT28磨刀霍霍modaohudhud29尊麻疹xunmazhen30卿猴mihou31万马齐喑wanmaqιyin32虱子shizi33矢量shιIiang34辎重zTzh∂ng35美轮美奂meiIunmeihuan36梭镖suδbiao37器宇轩昂/气宇轩昂qiyuxuanang 38嘎D崩脆gabengcui40掣月寸chezhδu41烯赫xuanhe 42捋虎须IUGhuxu43黄疸huangdan44璞玉puyu45豢养huanyang46炭疽杆菌tanjuganjun47鬃毛z6ngmao48紧箍咒jinguzh∂u49银币niebi50t甘堪ganguδ51犁锌Iihua525齿quchi53整饬zhengchi54绥靖s5jing55朝觐Ch旨Ojin57茱萸zhuyu58尺蟾chihud59陶城taoxun60赳赳武夫jiCιjiCιwufu 61丙烷bιngwan62襄樊XiangFan63模事qiushi64妆奁zhuangIian65箭锻jianzu66眄视mianshι67觊觎jiyu68僭越ji3nyue69呦呦鹿鸣youyouIumιng70醍醐灌顶号huguanding71蛭子chengzi72束脩shuxiu73郛城YunCheng 74竣乌（注）Ciinwu复赛第五场1凭证pingzheng2吝啬Iinse3坍塌tanta4拨浪鼓bδIanggu5闰年runnian6胖墩墩pangdundun7荆轲JTngKe8芹菜jicai9诅咒zuzh∂u10感激涕零gWnjitiIing11钝器dunqι12缅甸MianDian13拼凑pinc∂u14牙龈yayin15清冽qTnglie16晕厥yunjue17抑郁yiyu18亦步亦趋yibuyiqu19橄榄g*n后n20水泵shuTbeng21嗅觉xiujue22众口银金zh∂ngkδushu∂jTn 23日薄西山ribo×Tshan24冰激凌bTngjTIing25斑鸠banjiu26炙手可热zhishδukere27轻彳兆qingtiao28纽扣niuk∂u29寅吃卯粮yinchTmaoIiang30愁肠百结chouchangbaijie31挟持/胁持xiechi32钙化gaihua 33秤曲chengtuo34扫帚saozhou35琵琶pipa36窃据要津qiejuyaojTn37宁缺毋滥ningquewuIan38纨绮子弟wankuzιdi39涣散huansan40黄茜huangqi41腱鞘炎ji5nqiaoyan42凌霄花lingxiaohua43改锥gaizhui44品脱pintuδ45浑浑噩噩hunhunee46崔嵬cuTwei47油渍youzi48拜子jiQzi49揣度chuaiduo 50D爹声哮气diashengdiaqi 51荏苒renran52自勿J]ziwen53览菜xiancai54吞噬tunshi55虔诚qiancheng56瑕不掩瑜xiabuyanyu57阻尼zuni58上颗/上腭shange59岑寂cenji60像像族LiSuZu61盥洗室guanxιshi62马褂magua63自怨自艾ziyuanziyi 64蟠桃pantao65镌刻ju2nke66诳语kuangyu67搪瓷tangci68蕨类植物ju6Ieizhiwu 69烤馔kaonang70社稷sh4ji71淳沱河（注）HuTuoHe复赛第六场1意蕴yiyun2扼腕ewan3瑰宝guTbao4浑天仪huntianyι5蚯蚓qiuyin6密密匝匝mimizaza7金銮殿jinIuandian8兆赫zhaohe9门槛/门坎menkan10阡陌qianm∂11楔形文字×iexιngwenzi12诙谐huTxie13洗漱Xishu14斑驳陆离banboIuIi15臼齿jiθchi16肱骨gongg∪17番石榴fanshiIiu18座头鲸zu∂toujTng19阑尾炎Ianweiyan20梭耙ciba21触类旁通chuIeipangtong 22告罄gaoqιng23蓦然回首m∂ranhuishδu 24跷跷板qiaoqiaoban25羌笛qiangdι26考妣kaobι27蒸储水zhengIiushuι28煞有介事shayoujieshi 29怪癖guaipi30岐黄qιhuang31耳蜗erwδ32遴选Iinxuan33消弭xiaomi34怂恿songyδng35犹豫不决youyubujue36睛纶jingIun37卿卿我我qingqingwowδ38滑燔huaIiu39阑珊Ianshan40舍利子sheIizi41蹙额cue42螟蛉mιngIing43钱羽而归shayuerguT44瘠症yizheng45木铎muduo46嘎达梅林GaDaMeiLin47痍毙yubi48胱氨酸guangansuan 49箪食瓢饮dansipiaoyin 50沉痛chenke51裙裾qθnju52廉颇LianPo53蔺相如LinXiangRu54遒遢Iata55革达物DaDa56鳏寡孤独guanguagudu 57兖州YanZhou58翁同解WengTongHe 59醺粉（注）ji传n复赛第七场1集腋成裘j∣yechengqiu 2危如累卵weiruIeiIuan3蹿红cuanhong4拓扑学tu∂puxue5菽粟shusu6舌U族guasha7鳄鱼xueyu8芦笙Iusheng9羸弱Ieiru∂10Slsjiangd∂u11季弃biqi125良铛入狱Iangdangruyu 13莞尔一笑waneryTxiao 14金兀术JTnWuZhu15甘霖ganIin16怙恶不浚huebuquan17蟒虫naochong18苏洵SuXun19髭须zTxu20耄耋之年maodiezhTnian21鳄梨eIi22俄面馒头qiangmianmantou23戎马倒忽rongmakδngzδng24谄谀chanyu25痈疽yδngju26扶乩fujT27东施效颦dongshTxiaopin28缱绻qianquan29月亶月星shan×Tng30蓬单生辉pengbishengh∪T31旖旎yιnι32忝列门墙tianliemenqiang33鹏鹊ermiao34卖官鬻爵maiguanyujue35芒丽山MangDangShan36荫翳/阴翳yTnyι37硬石Ieishι38皋陶GaoYao39袍笏登场paohudengchang 40干啰ganyue41祭酹ji042龙骥虎峙longxianghuzhi 43谢道局XieDaoYun44■fucha45耆寿寺老qιsh∂ugδuIao46瓮牖绳枢wengyδushengshu 47耒特Ieisi48俟河之清sihezhTqing49斫轮老手zh∪6IunIaoshou50水螭shuTXi51越俎代庖yuezudaipao52栉风沐雨zhιfengmuyu53亵渎xiedu54饿殍/饿亭epiao55稗官野史baiguanyeshT56卷帙浩繁ju肩nzhihaofan57九省通衢ji□shengtongqu58馆仃d∂uding59裂璧（注）I沧wen复赛第八场1奚落xTIud2结缔组织ji6dιzuZhT3逻辑Iu6ji4搭讪dashan5肄业yiye6始作俑者shTzu6yδngzhe 7岳B日楼YueYangLou8豆蔻d∂uk∂u9肇事zhaoshι10信手拈来xιnsho∪nianIai 11普惠制puhuiZhi12痉挛jingIuan13秦桧QinHui14纷至沓来fenzhitaIai15泯灭minmie16S≠jianzi17玉玺yuXi18柴扉chaifei19针灸zhenjiu20梅子ju6zi21忖度cunduo22众目睽睽zh∂ngmukuikui 23椅角jijiao24傀儡k∪TIei25振聋发耳贵zhenlongfakui 26卜筮bushi27乖戾guaiIi 28轴稻xiandao29瓦麻bima 30；来源LaiYuan31达斡尔族DaWdErZu32幅岩chanyan33渊薮yuansou34玳瑁daimao35剜肉补疮wanr∂ubuchuang36嵯峨c∪6e37锚铢必较zTzhubijiao38狷介juanjie39信佬族GeLaoZu40醪糟Iaozao41双髻鲨shuangjisha42尘寰chenhuan43佞臣ningchen44燧石Suishι45婺源WuYuan46速船dunch∪an 47篦子bizi48骰子touzi49煮豆燃箕zhud∂uranqι50螯鼓pigu51禳解rangjie52傩戏nuoxi53拓跋氏（注）复赛第九场1昨身孟zemeng2曳光弹yeguangdan3颉九页xiehang4探囊取物tannangquwu 5慧直zhuangzhι6戳脊梁骨ChuojTIianggu 7饥肠辘辘jTchangIuIu8徽号h∪Thao9虹色尊鱼hongzunyu10廛战aozhan11料峭Iiaoqiao12饴倍heIe13合普hejιn14蠡贼maozei15能骨dιgu16罅隙xiaXi17碌晴Iiuzhou18芝聚山ZhTFuShan19旱魅hanba20款血为盟shaxueweimeng21保墙baoshang22嫖祖LeiZu23出案chutiao24倒同kδngtong 25铁蓑藜堆jiIi26楞严经L6ngYanJTng27悭吝qianIin28酬酢chouzu∂29誉录tengIu30痕疡IuoIi31鲤鱼shiyu32得鱼忘筌deyuwangquan 33蝶嫄rongyuan34以儆效尤yιjιngxiaoyou 35五蕴皆空WUyunjiekδng 36乜斜miexie37窖井yinjιng38寤寐求之wumeiqiuzhT 39飨宴xiangyan40握鼻涕xι∩gbiti41程柳chengIiu42牛既niubang43年高德劭niangaodeshao 44斑螯banmao45桁架hengjia46嬉草haocao47格褶gebei48转摭点zhuanliedian49精肥zanba50符箓fuIu51困肥dangfei52玉墀yuchi53督儒maoru54款乃ainai55清灌qingqu56匏瓜paogua57纤尊降贵yuZunjianggui58鞅制rouzhi59喟然长叹kuiranchangtan60怨怒yuandui61芫荽yansuT62砥砺dιIi63®Myinyun64撷英xieyTng65伏羲FuXT66胶柱鼓瑟（注）jiaozhuguse 67里发wanfa复赛第十场1延宕yandang2包!J花板baohuaban3下巴亥页JLxiabaker4J]三dajiao5储馒头Iiumantou6稼木啬jiase7蟾宫折桂changongzhegui 8铳床xTchuang9酚猷fentai10罪愆zuiqian11仓康cangITn12胡子拉硝huziIacha13⅛g⅛gjuyu14—^yTIiu15骈体文piantιwen16鬼喊伎俩guιyujiIiang17嚓碇miding18撅断ju@duan19朗姆酒后ngmujiu20汜水关SiShuTGuan21海暑rushu22刀俎痴zu23臧否zangpi24狰痢SheIi25螺钿Iuodian26草履虫caoIuchong27酉旨化反应zhιhuafanying 28鳗鳏manIi29扬锣tangIuo30竟丝子tusTzT31毛苴maogen32会稽山KuaiJTShan33贻害无穷yιhaiwuqiong34月并手月氐足pianshδuzhTzu 35据客qianke36鸣铺mingdι37鹭鹭IuST38跋拉taIa39山人shanxiao40管管pδIuo41一杯黄土yTpouhuangtu 42笛醇Zaichun43蕴藉yunjie44玉簪yuzan45玉箧yuqie46宽宥kuanyou47髯口rankou48老媪Iaoao49蓬头跣足pengtouxianzu 50如笔ruchuanzhTbι51云岫yunxiu52云瑞波诡yunjuebδguι53关心民瘦guanxTnminm∂54贲门benmen55玉樽yuzun56暴戾恣睢baoIizis∪T57流睇Iiudi58缰素gaosu59咂啖zadan60籀文zhδuwen61悒悒不欢yiyibuhuan62郡如成/丰者B城FengDuCheng 63消液堆YanYuDui64鞋襟xiepan65薨殁hongm∂66颛顼（注）ZhuanXu。

数学高考试卷(附答案)一、选择题1．123{3x x >>是12126{9x x x x +>>成立的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．即不充分也不必要条件2．已知变量x 与y 正相关，且由观测数据算得样本平均数3x =， 3.5y =，则由该观测的数据算得的线性回归方程可能是( ) A ．0.4 2.3y x =+ B ．2 2.4y x =- C ．29.5y x =-+ D ．0.3 4.4y x =-+3．()()31i 2i i --+=（ ）A ．3i +B ．3i --C ．3i -+D ．3i - 4．已知复数z 满足()12i z +=，则复数z 的虚部为（ ）A ．1B ．1-C ．iD ．i -5．函数2||()x x f x e -=的图象是（ ）A ．B ．C ．D ．6．在正方体1111ABCD A B C D -中，E 为棱1CC 的中点，则异面直线AE 与CD 所成角的正切值为 A 2 B 3C 5 D 7 7．已知向量()3,1a =，b 是不平行于x 轴的单位向量，且3a b ⋅=，则b =（ ）A ．312⎫⎪⎪⎝⎭B ．132⎛⎝⎭ C ．1334⎛⎝⎭D ．()1,08．函数()f x 的图象如图所示，()f x '为函数()f x 的导函数，下列数值排序正确是（ ）A ．()()()()02332f f f f ''<<<-B ．()()()()03322f f f f ''<<-<C ．()()()()03232f f f f ''<<<-D ．()()()()03223f f f f ''<-<<9．如图所示，网格纸上小正方形的边长为1，粗线画出的是由一个棱柱挖去一个棱锥后的几何体的三视图，则该几何体的体积为A ．72B ．64C ．48D ．3210．已知全集{}1,0,1,2,3U =-，集合{}0,1,2A =，{}1,0,1B =-，则UA B =（ ）A ．{}1-B ．{}0,1C ．{}1,2,3-D ．{}1,0,1,3-11．已知锐角三角形的边长分别为2，3，x ，则x 的取值范围是（ ） A 513x << B 135x < C ．25x <<D 55x <<12．在ABC ∆中，A 为锐角，1lg lg()lgsin 2b A c+==-，则ABC ∆为（ ） A ．等腰三角形 B ．等边三角形 C ．直角三角形D ．等腰直角三角形二、填空题13．曲线21y x x=+在点（1，2）处的切线方程为______________． 14．有三张卡片，分别写有1和2,1和3,2和3.甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是________．15．已知椭圆22195x y +=的左焦点为F ，点P 在椭圆上且在x 轴的上方，若线段PF 的中点在以原点O 为圆心，OF 为半径的圆上，则直线PF 的斜率是_______. 16．函数log (1)1(01)a y x a a =-+>≠且的图象恒过定点A ，若点A 在一次函数y mx n =+的图象上，其中,0,m n >则12m n+的最小值为 17．已知正三棱锥P ABC -的底面边长为3，外接球的表面积为16π，则正三棱锥P ABC -的体积为________.18．设等比数列{}n a 满足a 1+a 3=10，a 2+a 4=5，则a 1a 2…a n 的最大值为 ．19．已知双曲线1C ：22221(0,0)x y a b a b-=>>的左、右焦点分别为1F 、2F ，第一象限内的点00(,)M x y 在双曲线1C 的渐近线上，且12MF MF ⊥，若以2F 为焦点的抛物线2C ：22(0)y px p =>经过点M ，则双曲线1C 的离心率为_______．20．函数()lg 12sin y x =-的定义域是________．三、解答题21．在ABC ∆中，内角A ，B ，C 的对边a ，b ，c ，且a c >，已知2BA BC ⋅=，1cos 3B =，3b =，求：（1）a 和c 的值； （2）cos()B C -的值.22．在直角坐标系xOy 中，曲线C 的参数方程为2221141t x t t y t ⎧-=⎪⎪+⎨⎪=⎪+⎩，（t 为参数），以坐标原点O为极点，x 轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为2cos sin 110ρθθ++=．（1）求C 和l 的直角坐标方程； （2）求C 上的点到l 距离的最小值．23．（辽宁省葫芦岛市2018年二模）直角坐标系xOy 中，直线l 的参数方程为21x tcos y tsin αα=+⎧⎨=+⎩ (t 为参数)，在极坐标系（与直角坐标系xOy 取相同的长度单位，且以原点为极点，以x 轴正半轴为极轴）中，圆C 的方程为6cos ρθ=.（1）求圆C 的直角坐标方程；（2）设圆C 与直线l 交于点,A B ，若点P 的坐标为()2,1，求PA PB +的最小值. 24．已知函数()32f x x ax bx c =+++，过曲线()y f x =上的点()()1,1P f 处的切线方程为31y x =+．（1）若函数()f x 在2x =-处有极值，求()f x 的解析式； （2）在（1）的条件下，求函数()y f x =在区间[]3,1-上的最大值．25．随着“互联网+交通”模式的迅猛发展，“共享自行车”在很多城市相继出现。

2024年教师资格考试高级中学数学学科知识与教学能力复习试卷(答案在后面)一、单项选择题（本大题有8小题，每小题5分，共40分）1、三种基本数学思想是：公理化思想、演绎思想和_____ 思想。

A. 数形结合B. 转化C. 推理证明D. 模似2、“七种方法”指的数学研究方法有：观察法， _____ ，类比法，的技能；建模法，科学推理，应用软件法。

A. 转化法B. 比较法C. 分析法D. 实验法3、如果有一个函数f(x)，满足f(x)的图像在x轴上方有凹性，那么f(x)的相关导数具有以下哪个性质：A、f’(x)单调递增B、f’(x)单调递减C、f’’(x)>0D、f’’(x)<04、在高中数学教学中，为了教授梯度这一概念，老师应该如何设计教学活动？A、直接给出梯度的定义并让学生记忆B、使用生活中的实例来类比梯度的概念C、通过计算斜率的方式来解释梯度的概念D、只通过数学的理论推导来教授梯度5、下列哪个集合包含所有整数？A．{x|x是偶数} B．{x|x是奇数} C．N D．Z6、某班学生参加了一次运动会，测定每个学生跑步速度（单位：每分钟跑多少米）。

所有学生的跑步速度的平均值为 200 米/分钟，标准差为 10 米/分钟。

如果该班共有40 个学生，则低于 190 米/分钟速度的学生人数有多少？A．5 B．15 C．25 D．357.下列哪一项性质不属于圆的基本性质？A. 圆内接四边形的对角互补B. 圆的所有半径相等C. 圆内角的度数等于它所对的圆心角度数D. 垂径定理，即垂直于弦的直径把圆分成两个相等的部分8.下列等式中，表示得数等于3的平方的是？A. 3 × 3B. (-3) × (-3)C. (0.3) × (0.3)D. -3 × -37.正确答案应该是A。

圆内接四边形的对角互补是正方形的一个性质，不是所有圆的基本性质。

B项表明了圆的定义，即圆上任意两点的距离计算结果相同，均为半径的长度。

图1图2惠州市2024届高三第一次调研考试试题数学全卷满分150分，时间120分钟．注意事项：1．答题前，考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写在答题卡上。

2．作答单项及多项选择题时，选出每个小题答案后，用2B 铅笔把答题卡上对应题目的答案信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案，写在本试卷上无效。

3．非选择题必须用黑色字迹签字笔作答，答案必须写在答题卡各题指定的位置上，写在本试卷上无效。

一、单项选择题：本题共8小题，每小题满分5分，共40分。

在每小题给出的四个选项中，只有一项符合题目要求，选对得5分，选错得0分。

1.已知集合{}*|,6U x x x =∈≤N ，{}1,2,3A =，{}3,5B =，求()U A B = ð（）团用数学软件制作“蚊香”模型，画法如下：在水平直线上取长度为1的线段AB ，作一个等边三角形ABC ，然后以点B 为圆心，AB 为半径逆时针画圆弧交线段CB 的延长线于点D ，由此得到第1段圆弧 AD ，再以点C 为圆心，CD 为半径逆时针画圆弧交线段AC 的延长线于点E ，再以点A 为圆心，AE 为半径逆时针画圆弧……以此类推，当得到如图2所示的“蚊香”恰好有11段圆弧时，则该“蚊香”的长度为（）A ．14πB ．18πC ．30πD ．44π多项符合题目要求。

全部选对得5分，部分选对得2分，有选错的得0分。

三、填空题：本题共4小题，每题5分，共20分。

四、解答题：本题共6小题，共70分。

解答应写出文字说明、证明过程或演算步骤。

18.（本小题满分12分）设等差数列{}n a 的公差为d ，且12d a =，59a =．（1）求数列{}n a 的通项公式；（2）设数列{}n b 满足11222332n n nn a b a b a b ++++=-，求{}n b 的前n 项和n S ．19．（本小题满分12分）如图，在五面体ABCDE 中，AD ⊥平面ABC ，//AD BE ，2AD BE =，AB BC =.（1）问：在线段CD 上是否存在点P ，使得PE ⊥平面ACD ？若存在，请指出点P 的位置，并证明；若不存在，请说明理由．（2）若AB =，2AC =，2AD =，求平面ECD 与平面ABC 夹角的余弦值．21．（本小题满分12分）已知椭圆2222:1(0)x y C a b a b+=>>的左顶点为A ，上顶点为B ，右焦点为()0,1F ，O 为坐标原点，线段OA 的中点为D ，且BD DF =．（1）求C 的方程；（2）已知点M N 、均在直线2=x 上，以MN 为直径的圆经过O 点，圆心为点T ，直线AM AN 、分别交椭圆C 于另一点P Q 、，证明直线PQ 与直线OT 垂直．22．（本小题满分12分）惠州市2024届高三第一次调研考试数学试题参考答案与评分细则一、单项选择题：本题共8小题，每小题满分5分，共40分题号12345678答案BCACDBDA1.【解析】由已知可得{}1,2,3,5A B ⋃=，{}1,2,3,4,5,6U =，所以(){}6,4=B A C U ，故选：B ．5.【解析】由弧长公式r l ⋅=α得：r l ⋅=31，r l 232⋅=，r l 333⋅=，...，r l 11311⋅=，其中1==AB r ，()ππ44113213211321=+⋅⋅⋅+++=+⋅⋅⋅+++=∴l l l l L 蚊香的长度故选：D.二、多项选择题：本题共4小题，每小题满分5分，共20分。

2021年宁夏银川二十四中高考数学二模试卷（文科）一、单选题（本大题共12小题，共60.0分）1.已知集合A={x∈Z||x2−1|<2}，B={0,1，2，3}，则A∩B=()A. {0,1，2}B. {0,1}C. {0}D. {1}2.复数z=−1+i2+i的虚部为()A. −35i B. −35C. 35i D. 353.已知a，b为非零实数，且a>b，则下列不等式成立的是()A. a2>b2B. 1a <1bC. |a|>|b|D. 2a>2b4.不透明的箱子中有形状、大小都相同的5个球，其中2个白球，3个黄球．现从该箱子中随机摸出2个球，则这2个球颜色不同的概率为()A. 310B. 25C. 35D. 7105.已知向量|a⃗|=1，|b⃗ |=√6+√22，|c⃗|=√3+1，且a⃗+b⃗ +c⃗=0⃗，则向量a⃗与c⃗的夹角为()A. 5π6B. 2π3C. π3D. π26.已知等比数列{a n}中，a2a5a8=−8，S3=a2+3a1，则a1=()A. 12B. −12C. −29D. −197.执行如图所示的程序框图，若输出的S=30，则判断框中可填()A. i≥5？B. i≥6？C. i>6？D. i≥7？8.已知直线l过点A(a,0)且斜率为1，若圆x2+y2=4上恰有3个点到l的距离为1，则a的值为()A. 3√2B. ±3√2C. ±2D. ±√29.设双曲线x2a2−y2b2=1(a>b>0)的两条渐近线与圆x2+y2=10相交于A，B，C，D四点，若四边形ABCD的面积为12，则双曲线的离心率是()A. √103B. √10 C. √10或√103D. 2√1010.设f(x)是R上的任意函数，则下列叙述正确的是()A. f(x)f(−x)是奇函数B. f(x)|f(−x)|是奇函数C. f(x)−f(−x)是偶函数D. f(x)+f(−x)是偶函数11.在△ABC中，∠C=90°，∠B=30°，AC=1，M为AB中点，将△ACM沿CM折起，使A、B间的距离为√2，则点M到面ABC的距离为()A. 12B. √32C. 1D. 3212.设函数f(x)=e x−1+4x−4，g(x)=lnx−1x.若f(x1)=g(x2)=0，则()A. 0<g(x1)<f(x2)B. g(x1)<0<f(x2)C. f(x2)<0<g(x1)D. f(x2)<g(x1)<0二、单空题（本大题共4小题，共20.0分）13.若sin(α+π4)=√2(sinα+2cosα)，则sin2α=______．14.设S n是数列{a n}的前n项和，a1=−1，a n+1=S n S n+1，则S n=______．15.设实数x，y满足约束条件{x+y−1≥0x−2y+3≥0x−y−1≤0，则z=y−2x的最小值为______ ．16.已知两条不同的直线m，n，两个不重合的平面α，β，给出下面五个命题：①m//n，m⊥α⇒n⊥α；②α//β，m⊂α，n⊂β⇒m//n；③m//n，m//α⇒n//α；④m⊥α，m//β⇒α⊥β；⑤α//β，m//n，m⊥α⇒n⊥β．其中正确命题的序号为______．三、解答题（本大题共7小题，共82.0分）17.设△ABC的内角A，B，C所对的边分别是a，b，c，且c⋅cosC是a⋅cosB与b⋅cosA的等差中项．(Ⅰ)求角C；(Ⅱ)设c=2，求△ABC周长的最大值．18.一研学实践活动小组利用课余时间，对某公司1至5月份销售某种产品的销售量及销售单价进行了调查，月销售单价x(单位：元)和月销售量y(单位：百件)之间的一组数据如表所示：(1)根据1至5月份的数据，求出y关于x的回归直线方程；(2)预计在今后的销售中，月销售量与月销售单价仍然服从(1)中的关系，若该种产品的成本是1元/件，那么该产品的月销售单价应定为多少元，才能获得最大月利润？(注：利润=销售收入−成本)附：回归直线方程y ̂=b ̂x +a ̂，其中b ̂=∑x i n i=1y i −nx −⋅y−∑x i 2n i=1−nx−2，a ̂=y −−b ̂x −．参考数据：∑x i 5i=1y i =67.2，∑x i 25i=1=20.4．19. 已知椭圆E ：x 2a 2+y 2b 2=1(a >b >0)的右焦点为(2,0)，且经过点(0,2)．(Ⅰ)求椭圆E 的方程以及离心率；(Ⅱ)若直线y =kx +m 与椭圆E 相切于点P ，与直线x =−4相交于点Q.在x 轴是否存在定点M ，使MP ⊥MQ ？若存在，求出点M 的坐标；若不存在，说明理由．20. 如图，三棱柱ABC −A 1B 1C 1中，CA =CB ，AB =AA 1，∠BAA 1=60°(Ⅰ)证明：AB ⊥A 1C ；(Ⅱ)若AB =CB =2，A 1C =√6，求三棱柱ABC −A 1B 1C 1的体积．21. 已知函数f(x)=lnx +a2x 2−(a +1)x ．(Ⅰ)当a >0时，求f(x)在区间(0,1]的最大值；(Ⅱ)若函数g(x)=f(x)+x 有两个极值点x 1、x 2(x 1<x 2)，求证：g(x 1)−g(x 2)<a 2−lna ．22. 在平面直角坐标系xOy 中，曲线C 1的参数方程为{x =2+ty =2|t|−4(t 为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程为ρ2−2ρcosθ+a =0．(1)求曲线C 1的普通方程和曲线C 2的直角坐标方程；(2)若曲线C 1与曲线C 2有且仅有三个不同的交点，求实数a 的值．23. 已知函数f(x)=|x −1|−|x +3|．(1)若不等式f(x)≥2a +3恒成立，求实数a 的取值范围；(2)若函数f(x)的最大值为c ，实数a ，b 满足a >0，b >0，a 2+b 2=c2，求证：(1 a +1b)(a5+b5)≥4．答案和解析1.【答案】B【解析】解：∵A={x∈Z|−2<x2−1<2}={x∈Z|−√3<x<√3}={−1,0,1}，B={0,1，2，3}，∴A∩B={0,1}．故选：B．可求出集合A，然后进行交集的运算即可．本题考查了集合的描述法和列举法的定义，绝对值不等式的解法，交集及其运算，考查了计算能力，属于基础题．2.【答案】D【解析】解：∵z=−1+i2+i =(−1+i)(2−i)(2+i)(2−i)=−15+35i，∴复数z=−1+i2+i 的虚部为35．故选：D．直接利用复数代数形式的乘除运算化简得答案．本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．3.【答案】D【解析】解：A选项不正确，当a=1，b=−2时，不等式就不成立；B选项不正确，因为a=1，b=−2时，不等式就不成立；C选项不正确，因为a=1，b=−2时，不等式就不成立；D选项正确，因为y=2x是一个增函数，故当a>b时一定有2a>2b，故选D．由不等式的相关性质，对四个选项逐一判断，由于a，b为非零实数，故可利用特例进行讨论得出正确选项本题考查不等关系与不等式，解题的关键是熟练掌握不等式的有关性质，且能根据这些性质灵活选用方法进行判断，如本题采用特值法排除三个选项，用单调性判断正确选项．4.【答案】C【解析】【分析】本题考查概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，是基础题．先求出基本事件总数n=C52=10，这2个球颜色不同包含的基本事件个数m=C21C31= 6，由此能求出这2个球颜色不同的概率．【解答】解：不透明的箱子中有形状、大小都相同的5个球，其中2个白球，3个黄球．现从该箱子中随机摸出2个球，基本事件总数n=C52=10，这2个球颜色不同包含的基本事件个数m=C21C31=6，∴这2个球颜色不同的概率为p=610=35610=35．故选：C．5.【答案】A【解析】【分析】根据平面向量的数量积运算和夹角公式，即可求出向量a⃗与c⃗夹角的大小．本题考查了平面向量的数量积与夹角的计算问题，是中档题．【解答】解：设向量a⃗与c⃗的夹角为θ，|a⃗|=1，|b⃗ |=√6+√22，|c⃗|=√3+1，由a⃗+b⃗ +c⃗=0⃗，得−b⃗ =a⃗+c⃗，则b⃗ 2=a⃗2+2a⃗⋅c⃗+c⃗2，即(√6+√22)2=1+2×1×(√3+1)×cosθ+(√3+1)2，所以cosθ=−√32；又θ∈[0,π]，所以向量a⃗与c⃗的夹角为θ=5π．6故选：A．6.【答案】B【解析】【分析】本题考查了等比数列的通项公式及其性质，考查了推理能力与计算能力，属于基础题．设等比数列{a n}的公比为q，a2a5a8=−8，S3=a2+3a1，可得：a53=−8，a3+a2+a1= a2+3a1，解得a5=−2=a1q4，a3=2a1，进而得出．【解答】解：设等比数列{a n}的公比为q，∵a2a5a8=−8，S3=a2+3a1，∴a53=−8，a3+a2+a1=a2+3a1，解得a5=−2=a1q4，a3=2a1，．解得q2=2，a1=−12故选B．7.【答案】B【解析】解：模拟程序的运行，可得S=0，i=1不满足判断框内的条件，执行循环体，S=2，i=2不满足判断框内的条件，执行循环体，S=6，i=3不满足判断框内的条件，执行循环体，S=12，i=4不满足判断框内的条件，执行循环体，S=20，i=5不满足判断框内的条件，执行循环体，S=30，i=6此时，应该满足判断框内的条件，退出循环，输出S的值为30，故判断框中可填i≥6？故选：B．由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．8.【答案】D【解析】解：∵直线l过点A(a,0)斜率为1，∴设l：x−y−a=0，∵圆x2+y2=4上恰有3个点到l的距离为1，∴圆心到直线的距离等于半径减去1，∴圆心(0,0)到直线l：y=x+a的距离为：√2=2−1，解得a=±√2．故选：D．设l：x−y−a=0，由点到直线的距离公式列出方程，由此能求出结果．本题考查满足条件的实数值的求法，解题时要注意直线与圆的位置关系的合理运用，是中档题．9.【答案】A【解析】【分析】本题考查双曲线的几何性质，主要是渐近线方程和离心率，还涉及圆的性质，考查学生的分析能力和运算能力，属于基础题．不妨设点A为一条渐近线y=bax与圆的交点，其坐标为(m,bam)，m>0，由双曲线和圆的对称性可知，四边形ABCD为矩形，于是可用含a、b、m的代数式表示出四边形ABCD的面积，再结合|OA|=√10又可构造a、b、m的关系式，综合两者消去m即可得到ba +ab=103，解之可得ba=13或3(舍3)，最后根据离心率e=ca =√a2+b2a=√103得解．【解答】解：双曲线的两条渐近线方程为y=±ba x，不妨设点A为y=bax与圆的交点，其坐标为(m,bam)，m>0，由双曲线和圆的对称性可知，四边形ABCD为矩形，且4×m⋅ba m=12，即m2=3ab①，圆x 2+y 2=10的半径为√10，∴|OA|=√m 2+(bam)2=√10②，由①②得，b a +a b =103，解得b a =13或3， ∵a >b >0，∴ba =13， ∴双曲线的离心率e =c a=√a 2+b 2a=√103， 故选：A ．10.【答案】D【解析】解：A 中令F(x)=f(x)f(−x)，则F(−x)=f(−x)f(x)=F(x)， 即函数F(x)=f(x)f(−x)为偶函数，B 中F(x)=f(x)|f(−x)|，F(−x)=f(−x)|f(x)|，因f(x)为任意函数，故此时F(x)与F(−x)的关系不能确定，即函数F(x)=f(x)|f(−x)|的奇偶性不确定，C 中令F(x)=f(x)−f(−x)，令F(−x)=f(−x)−f(x)=−F(x)，即函数F(x)=f(x)−f(−x)为奇函数，D 中F(x)=f(x)+f(−x)，F(−x)=f(−x)+f(x)=F(x)，即函数F(x)=f(x)+f(−x)为偶函数， 故选：D ．令题中选项分别为F(x)，然后根据奇偶函数的定义即可得到答案． 本题考查了函数的定义和函数的奇偶性的判断，同时考查了函数的运算．11.【答案】A【解析】解：由已知得AB =2，AM =MB =MC =1，BC =√3，由△AMC 为等边三角形，取CM 中点D ，则AD ⊥CM ，AD 交BC 于E ，则AD =√32，DE =√36，CE =√33． 折起后，由BC 2=AC 2+AB 2，知∠BAC =90°，又cos∠ECA =√33，∴AE 2=CA 2+CE 2−2CA ⋅CEcos∠ECA =23，于是AC 2=AE 2+CE 2． ∴∠AEC =90°．∵AD 2=AE 2+ED 2，∴AE ⊥平面BCM ，即AE 是三棱锥A −BCM 的高，AE =√63 设点M 到面ABC 的距离为h ，则∵S△BCM=√34∴由V A−BCM=V M−ABC，可得13×√34×√63=13×12×√2×1×ℎ，∴ℎ=12故选A．由△AMC为等边三角形，取CM中点D，则AD⊥CM，AD交BC于E，证明AE⊥平面BCM，利用等体积法，即可求得结论．本题考查由平面图形折成空间图形求其体积，考查点到平面距离的计算，求此三棱锥的高是解决问题的关键．12.【答案】B【解析】【分析】本题主要考查零点存在定理以及导数的应用，属于中档题．求导，判断两个函数的单调性，根据函数零点存在定理，求出f(x)和g(x)的零点存在区间，利用函数的单调性即可得到结论．【解答】解：f(x)=e x−1+4x−4，则f′(x)=e x−1+4>0，f(x)在R上单调递增，又f(1)=1>0，f(0)=1e−4<0，f(x1)=0，∴0<x1<1，g(x)=lnx−1x，x>0，g′(x)=1x +1x2>0，则g(x)=lnx−1x在(0,+∞)上单调递增．又g(1)=−1<0，g(2)=ln2−12>0，g(x2)=0，∴1<x2<2，∴g(x1)<g(x2)=0=f(x1)<f(x2)，故选：B．13.【答案】−35【解析】解：∵sin(α+π4)=√2(sinα+2cosα)，∴√22(sinα+cosα)=√2(sinα+2cosα)，∴可得sinα=−3cosα，又∵sin2α+cos2α=1，∴{sinα=3√1010cosα=−√1010，或{sinα=−3√1010cosα=√1010，∴sin2α=2sinαcosα=−35．故答案为：−35．由已知利用两角和的正弦函数公式可求sinα=−3cosα，根据同角三角函数基本关系式可求sinα，cosα的值，进而根据二倍角的正弦函数公式即可求解．本题主要考查了两角和的正弦函数公式，同角三角函数基本关系式，二倍角的正弦函数公式在三角函数化简求值中的应用，考查了计算能力和转化思想，属于基础题．14.【答案】−1n【解析】【分析】根据a n+1=S n S n+1，可得S n+1−S n=S n S n+1，1Sn+1−1S n=−1，再利用等差数列的通项公式即可得出答案．本题考查数列递推关系、等差数列的定义与通项公式，考查了推理能力与计算能力，属于基础题．【解答】解：∵a n+1=S n S n+1，∴S n+1−S n=S n S n+1，∴1S n+1−1S n=−1，又1S1=1a1=−1，∴数列{1S n}是等差数列，首项为−1，公差为−1．∴1S n=−1−(n−1)=−n，解得S n=−1n．故答案为：−1n．15.【答案】−6【解析】解：由约束条件作出可行域如图，联立{x −2y +3=0x −y −1=0，解得A(5,4)，由z =y −2x ，得y =2x +z ，由图可知，当直线y =2x +z 过A 时，直线在y 轴上的截距最小， z 有最小值为−6． 故答案为：−6．由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．本题考查简单的线性规划，考查数形结合思想，是中档题．16.【答案】①④⑤【解析】解：两条不同的直线m ，n ，两个不重合的平面α，β，对于①，由线面垂直的判定定理得：m//n ，m ⊥α⇒n ⊥α，故①正确； 对于②，α//β，m ⊂α，n ⊂β⇒m 与n 相交、平行或异面，故②错误； 对于③，m//n ，m//α⇒n//α或m ⊂α，故③错误；对于④，由面面垂直的判定定理得：m ⊥α，m//β⇒α⊥β，故④正确； 对于⑤，由线面垂直的判定定理得：α//β，m//n ，m ⊥α⇒n ⊥β，故⑤正确． 故答案为：①④⑤．对于①，由线面垂直的判定定理判断；对于②，m 与n 相交、平行或异面；对于③，n//α或m ⊂α；对于④，由面面垂直的判定定理判断；对于⑤，由线面垂直的判定定理判断．本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力，是中档题．17.【答案】解：(1)由题，c ⋅cosC 是a ⋅cosB 与b ⋅cosA 的等差中项，则acosB +bcosA =2ccosC ，即sinAcosB +sinBcosA =2sinCcosC ， 即sin(A +B)=2sinCcosC ，即sinC =2sinCcosC ，解得cosC =12，所以C =π3． (2)由余弦定理及基本不等式，c 2=a 2+b 2−2abcos π3=a 2+b 2−ab =(a +b)2−3ab ≥(a +b)2−3(a+b 2)2=(a+b)24，得a +b ≤4，当且仅当a =b =2时等号成立， 故△ABC 周长a +b +c 的最大值为6．【解析】(Ⅰ)根据等差中项以及正弦定理结合两角和差的正弦公式进行求解即可 (Ⅱ)利用余弦定理以及基本不等式进行求解即可．本题主要考查级正弦定理以及余弦定理的应用，结合基本不等式的性质是解决本题的关键．18.【答案】解：(1)∵x −=1.6+1.8+2+2.2+2.45=2，y −=10+8+7+6+45=7．∴b ̂=∑x i n i=1y i −nx −y−∑x i 2n i=1−nx−2=67.2−5×2×720.4−5×4=−7，a ̂=y −−b ̂x −=7+7×2=21．∴回归直线方程为y ̂=−7x +21．(2)设该产品的月销售单价为x 元，月利润为z 百元，则∵z =(x −1)⋅y ，∴z =(x −1)(−7x +21)=−7x 2+28x −21=−7(x −2)2+7． ∴当x =2时，z max =7(百元)．∴该产品的月销售单价应定为2元才能获得最大月利润为7百元．【解析】(1)求出样本中心，回归直线方程的系数，然后求解回归直线方程． (2)设该产品的月销售单价为x 元，月利润为z 百元，推出利润表达式，利用而城市的性质求解最值即可．本题考查回归直线方程的求法与应用，是中档题．19.【答案】(本小题14分)(Ⅰ)由已知得，c =2，b =2，a 2=b 2+c 2=8， 椭圆E 的方程为x 28+y 24=1，离心率为e =ca =√22；(Ⅱ)在x 轴存在定点M ，M 为(−2,0)使MP ⊥MQ ， 证明：设直线方程为y =kx +m ， 代入x 28+y 24=1得x 2+2(kx +m)2=8，化简得(2k 2+1)x 2+4kmx +2m 2−8=0，由△=(4km)2−4(2k 2+1)(2m 2−8)=0，得8k 2+4−m 2=0，m 2=8k 2+4，x =−2km 2k 2+1=−8k m，设P(x 0,y 0)，则x 0=−8k m，y 0=kx 0+m =k ⋅−8k m+m =m 2−8k 2m=4m，则P(−8k m,4m)，设Q(−4,y 1)，则y 1=−4k +m ，则Q(−4,−4k +m)，MP ⃗⃗⃗⃗⃗⃗ ⋅MQ ⃗⃗⃗⃗⃗⃗⃗ =(x 0+2,y 0)⋅(−2,y 1)=−2(x 0+2)+y 0y 1=−2(−8k m +2)+4m (−4k +m)=16k m−4+4m(−4k +m)=0，所以在x 轴存在定点M(−2,0)使MP ⊥MQ ．解法二：由椭圆的对称性不妨设P(x 0,y 0)(y 0>0)与M(x,0)．x 28+y 24=1得y =2√1−x 28得k =−x2y 0．切线方程为y −y 0=−x 02y 0(x −x 0)，令x =−4得y 1=x2y 0(−4−x 0)+y 0=−4x 0−x 02+2y 022y 0=2x 0+4y 0，Q(−4,2(x 0+2)y 0)．所以，MP ⃗⃗⃗⃗⃗⃗ ⋅MQ ⃗⃗⃗⃗⃗⃗⃗ =(x 0+2,y 0)⋅(−2,y 1)=−2(x 0+2)+y 02(x 0+2)y=0． 所以在x 轴存在定点M(−2,0)使MP ⊥MQ ．【解析】(Ⅰ)直接由题意得，c ，b 的值，再由a ，b ，c 之间的关系求出椭圆的方程及离心率；(Ⅱ)由直线与椭圆相切求出，k ，m 的关系，且求出Q 的坐标，设存在定点M ，由PM ⊥QM 可得MP ⃗⃗⃗⃗⃗⃗ ⋅MQ⃗⃗⃗⃗⃗⃗⃗ =0，求出M 的坐标．考查直线与椭圆的综合应用，属于中档题．20.【答案】(Ⅰ)证明：如图，取AB的中点O，连接OC，OA1，A1B.因为CA=CB，所以OC⊥AB．由于AB=AA1，∠BAA1=60°，故△AA1B为等边三角形，所以OA1⊥AB．因为OC∩OA1=O，OC⊂平面OA1C，OA1⊂平面OA1C，所以AB⊥平面OA1C.又A1C⊂平面OA1C，故AB⊥A1C；(Ⅱ)解：由题设知△ABC与△AA1B都是边长为2的等边三角形，所以OC=OA1=√3．又A1C=√6，则A1C2=OC2+OA12，故OA1⊥OC．因为OC∩AB=O，OC⊂平面ABC，AB⊂平面ABC，所以OA1⊥平面ABC，OA1为三棱柱ABC−A1B1C1的高．又△ABC的面积S△ABC=√3，故三棱柱ABC−A1B1C1的体积V=S△ABC×OA1=√3×√3=3．【解析】本题主要考查了直线与平面垂直的性质，考查了棱柱的体积，考查空间想象能力、运算能力和推理论证能力，属于中档题．(Ⅰ)由题目给出的边的关系，取AB中点O，可通过证明AB⊥平面OA1C得要证的结论；(Ⅱ)在三角形OCA1中，由勾股定理得到OA1⊥OC，再根据OA1⊥AB，得到OA1为三棱柱ABC−A1B1C1的高，利用已知给出的边的长度，直接利用棱柱体积公式求体积．21.【答案】解：(Ⅰ)f(x)=lnx+a2x2−(a+1)x，(x>0)，f′(x)=1x +ax−(a+1)=(ax−1)(x−1)x，x∈(0,1]，x−1<0，1a∈(0,1)即a >1时，f(x)在(0,1a )递增，在(1a ,1]递减， 故f(x)的最大值是f(1a )=−lna +12a −a+1a；0<a ≤1时，f′(x)≥0，f(x)在(0,1]递增， f(x)max =f(1)=−a2−1．(Ⅱ)证明：g(x)=f(x)+x =lnx +a2x 2−ax ，则g(x)的定义域为(0,+∞)， g′(x)=1x +ax −a =ax 2−ax+1x，若g(x)有两个极值点x 1，x 2(0<x 1<x 2)，则方程ax 2−ax +1=0的判别式△=a 2−4a >0，且x 1+x 2=1，x 1x 2=1a >0，得a >4，又0<x 1<x 2，∴x 12<x 1x 2=1a ，即0<x 1<√a …(7分) 所以g(x 1)−g(x 2)=lnx 1+ln(ax 1)+a2−ax 1，设ℎ(t)=lnt +ln(at)+a2−at ，其中t =x 1∈√a )，由ℎ′(t)=2t −a =0得t =2a ……(9分) 又2a√a=2−√a a<0，所以ℎ(t)在区间(0,2a )内单调递增，在区间(2a √a )内单调递减， 即ℎ(t)的最大值为ℎ(2a )=2ln2−lna +a2−2<a2−lna ， 从而g(x 1)−g(x 2)<a 2−lna 恒成立……(12分)【解析】(Ⅰ)求出函数的导数，根据函数的单调性求出f(x)的最大值即可；(Ⅱ)设x 1，x 2(0<x 1<x 2)是函数g(x)=f(x)+x 的两个极值点，证明：g(x 1)−g(x 2)<a 2−lna ．本题考查了函数的单调性、最值问题，考查导数的应用以及分类讨论思想，转化思想，是一道中档题．22.【答案】解：(1)曲线C 1的参数方程为{x =2+ty =2|t|−4(t 为参数)，转换为普通方程为y =2|x −2|−4．曲线C 2的极坐标方程为ρ2−2ρcosθ+a =0，根据{x =ρcosθy =ρcosθx 2+y 2=ρ2转换为直角坐标方程为(x −1)2+y 2=1−a ；(2)曲线C1的方程为：y=2|x−2|−4，即两条射线y=2x−8(x≥2)和射线−2x(x≤2)，图象有两种情况：当圆与射线y=2x−8(x≥2)相切和射线−2x(x≤2)相交时，只需满足6√5=√1−a，解得a=−315．当圆与射线y=2x−8(x≥2)相交和射线−2x(x≤2)相交时，即：(2,−4)在圆上时，解得a=−16．故a的值为−315或−16．【解析】(1)直接利用转换关系，在参数方程极坐标方程和直角坐标方程之间进行转换；(2)利用直线与圆的位置关系的应用求出a的值．本题考查的知识要点：参数方程极坐标方程和直角坐标方程之间的转换，直线与圆的位置关系的应用，主要考查学生的运算能力和数学思维能力，属于中档题．23.【答案】解：(1)∵f(x)=|x−1|−|x+3|，∴f(x)={−4,x>1−2x−2,−3≤x≤14,x<−3，故f(x)min=4，∵不等式f(x)≥2a+3恒成立，∴−4≥2a+3，解得a≤−72，故实数a的取值范围为(−∞,−72].(2)证明：由(1)知，c=4，即a2+b2=2，(1 a +1b)(a5+b5)=a4+b4+a5b+b5a=(a2+b2)2−2a2b2+a5b+b5a≥4−2a2b2+2√a5b ⋅b5a=4−2a2b2+2a2b2=4，当且仅当a=b=1时，等号成立，∴(1a +1b)(a5+b5)≥4，即得证．【解析】(1)求出f(x)的最小值，即f(x)min≥2a+3，解出a的取值范围，即可求解．(2))由(1)知，c=4，即a2+b2=2，再结合基本不等式，即可求解．本题考查了绝对值不等式的求解，以及基本不等式的应用，属于中档题．。

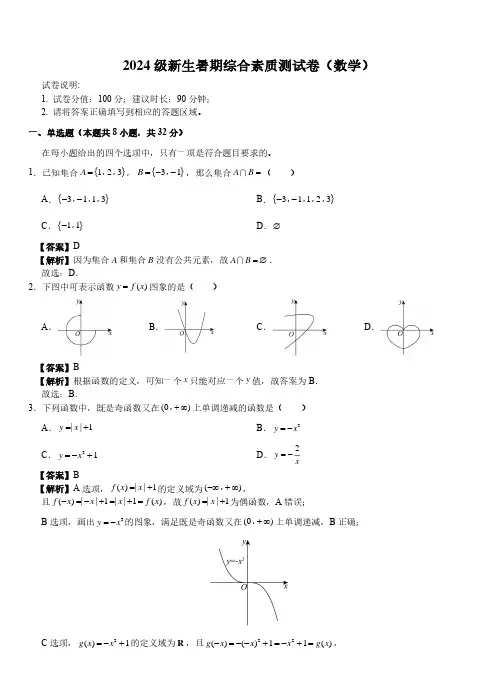
2024级新生暑期综合素质测试卷（数学）试卷说明:1. 试卷分值：100分；建议时长：90分钟；2. 请将答案正确填写到相应的答题区域。

一、单选题（本题共8小题，共32分）在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合{}123A =，，，{}31B =−−，，那么集合A B =（ ）A ．{}3113−−，，， B ．{}31123−−，，，， C ．{}11−，D ．∅【答案】D【解析】因为集合A 和集合B 没有公共元素，故A B =∅．故选：D ．2．下图中可表示函数()y f x =图象的是（ ）A ．B ．C ．D ．【答案】B【解析】根据函数的定义，可知一个x 只能对应一个y 值，故答案为B ． 故选：B ．3．下列函数中，既是奇函数又在(0)+∞，上单调递减的函数是（ ） A ．||1y x =+ B ．3y x =−C ．21y x =−+D 【答案】B【解析】A 选项，()||1f x x =+的定义域为()−∞+∞，， 且()||1||1()f x x x f x −=−+=+=，故()||1f x x =+为偶函数，A 错误；B 选项，画出3y x =−的图象，满足既是奇函数又在(0)+∞，上单调递减，B 正确；C 选项，2()1g x x =−+的定义域为R ，且22()()11()g x x x g x −=−−+=−+=，故2()1g x x =−+为偶函数，C 错误；D 在(0)+∞，上单调递增，D 错误． 故选：B ．4．“黄沙百战穿金甲，不破楼兰终不还”是我国唐代著名诗人王昌龄的《从军行》中的两句诗，描写了当时战事的艰苦以及戍边将士的豪情壮志，从逻辑学的角度看，最后一句中，“破楼兰”是“终还”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 【答案】B【解析】“破楼兰”不一定“终还”，但“终还”一定是“破楼兰”，由充分条件和必要条件的定义判断可得“攻破楼兰”是“返回家乡”必要不充分条件， 故选：B ．5．已知不等式20ax bx c ++>的解集为{}|21x x −<<，则不等式20cx bx a −+<的解集为（ ）A BC D ．(21)−，【答案】A【解析】∵关于x 的不等式20ax bx c ++>的解集为{}|21x x −<<， ∴0a <，且2−和1是方程20ax bx c ++=的两个根， 则420a b c a b c −+=⎧⎨++=⎩，∴b a =，2c a =−， 则关于x 的不等式，即220ax ax a −−+<，∴2210x x +−<，解得故选：A ．6．关于x 的一元二次方程2220x mx m m ++−=的两实数根1x ，2x ，满足122x x =，则2212(2)(2)x x ++的值是（ ） A ．8B ．32C ．20或68D ．16或40【答案】B【解析】由题意可知22Δ44()40m m m m =−−=>，可得0m >， 由韦达定理可得2122x x m m =−=，因为0m >，则2m =， 故原方程为2420x x ++=，所以124x x +=−，故222121212()2162212x x x x x x +=+−=−⨯=， 因此，22222121212(2)(2)()2()44212432x x x x x x ++=+++=+⨯+=． 故选：B ．7．如图，在边长为2的正方形ABCD 中，对角线AC 与BD 相交于点O ，点P 是BD 上的一个动点，过点P 作EF//AC ，分别交正方形的两条边于点E ，F ，连接OE ，OF ，设BP x =，OEF △的面积为y ，则能大致反映y 与x 之间的函数关系的图象为（ ）A ．B ．C ．D ．【答案】B【解析】当点P 在OB 上时，∵四边形ABCD 是正方形，边长为2，∴2AB BC ==，AC BD ⊥，45ACB CAB ∠=∠=︒，∵EF//AC ，∴45BAC BEF ∠=∠=︒，45BFE BCA ∠=∠=︒，90AOB EPB ∠=∠=︒， ∴BEF BFE ∠=∠，∴BE BF =， ∵90BPE ∠=︒，∴BP EP FP x ===，，当点P 在DO 上时，同理可得， 故选：B ．8．若对任意实数0x >，0y >，不等式a 的最小值为（ ）ABCD【答案】D【解析】对于任意实数0x >，0y >恒成立，则只需求（0t >），再设1t m +=（1m >），则a故选：D ．二、多选题（本题共4小题，共16分）在每小题给出的四个选项中，有多项符合题目要求。