数字逻辑名词解释

数字逻辑
在现代科技高度发展的时代，数字逻辑作为一种重要的逻辑思维方式，渗透在
我们生活的方方面面。

数字逻辑的背后是一种思维方式和原理，它在计算机、通信、电子等行业中发挥着重要的作用。

数字逻辑的基础概念
数字逻辑是通过数字信号来描述和处理信息的一种逻辑体系。

在数字逻辑中，
信号只有两种状态：0和1，分别对应逻辑“假”和“真”。

通过不同的逻辑门电路，
可以实现各种复杂逻辑运算，如与、或、非、异或等。

数字逻辑的应用领域
数字逻辑广泛应用于计算机硬件设计、数字电路设计、通信系统等各个领域。

在计算机科学中，数字逻辑是计算机内部运作的基础，所有的计算和数据处理都是通过数字逻辑电路实现的。

在通信系统中，数字逻辑可以对信号进行编码、解码和处理，保证信息的传输质量和可靠性。

数字逻辑的发展趋势
随着科技的不断进步，数字逻辑技术也在不断发展和完善。

现代数字逻辑的设
计越来越复杂和精密，可以实现更快速、更高效的数据处理和传输。

未来，数字逻辑技术将继续向着更高性能、更低功耗、更高可靠性的方向发展。

结语
数字逻辑作为一种重要的逻辑思维方式，已经深入到我们生活的方方面面。

它
不仅是现代科技发展的基础，也是人类智慧的结晶。

我们应该深入学习和理解数字逻辑，不断探索其在各个领域的应用，推动数字逻辑技术的发展和创新。

数字逻辑知识点报告总结1. 数字逻辑的定义数字逻辑是一种以数字为基础的逻辑学科，它研究数字之间的关系和数字系统的运算规律。

在数字逻辑中，数字通常表示为0和1，这两个数字是数字逻辑中的基本元素。

数字逻辑研究的范围包括数制、逻辑运算、逻辑代数、逻辑函数、数字逻辑电路等。

2. 基本概念在数字逻辑中，有几个基本概念是必须要了解的，包括数制、位权、数字编码、二进制加法和减法、二进制码等。

其中，数制是指用来表示数字的一组符号和表示方法，位权是指数字中各个位上的数值和位置的关系，数字编码是把数字用一定的代码表示出来，二进制加法和减法是对二进制数字进行加减运算。

3. 逻辑门逻辑门是数字逻辑的基本构件，它用来实现逻辑运算功能。

常见的逻辑门包括与门、或门、非门、异或门和与非门等。

这些逻辑门可以根据输入信号的不同，输出不同的逻辑运算结果。

逻辑门是数字逻辑电路的核心部件，它可以实现各种逻辑功能。

4. 布尔代数布尔代数是逻辑代数的一种，它是一种用来表示逻辑运算的代数系统。

在布尔代数中，逻辑运算可以用加法、乘法和求反运算来表示，这些运算具有一些特定的性质，比如交换律、结合律、分配律等。

布尔代数是数字逻辑的数学基础，它可以用来描述和分析各种逻辑函数和逻辑运算。

5. 逻辑功能在数字逻辑中，逻辑功能是指逻辑门实现的具体功能。

常见的逻辑功能包括与运算、或运算、非运算、异或运算等。

这些逻辑功能可以根据实际需求进行组合和变换，从而实现复杂的逻辑运算。

6. 数字逻辑电路数字逻辑电路是数字逻辑的物理实现，它由逻辑门和其他逻辑功能部件组成。

数字逻辑电路可以用来实现各种逻辑运算、逻辑函数和逻辑功能，它是数字系统中的核心部件。

7. 存储器存储器是一种用来存储信息的设备，它可以用来保存数字信息、程序信息和数据信息等。

在数字逻辑中，存储器通常是由触发器组成的，它可以存储和传输数字信号。

8. 计数器和触发器计数器是一种用来计数和累加的设备，它可以用来实现各种计数功能和定时功能。

数字逻辑处理数字信号的逻辑数字逻辑是一种在计算机或数字设备中，处理、存储、传递和转换数字信息的电子技术。

信号是用数字来表示的各种事物的运动状态和关系。

由于采用了二进制的表示形式，所以也称为数字信号。

信号可以用不同的表示方式，例如数值、字母或文字等，但是数字化后的每一种表示都具有相同的性质，例如不能再进行“或”运算，不能出现奇偶次序错误，没有时间含义，可以用来表示具有非负值的信息等。

因此数字信号可以方便地表示、存储和传输。

在线性时不变系统中，信号的表示不会随时间而变化，例如普通交流电压，其波形不会随着交流电流大小的改变而发生变化。

但是随着工程实际问题复杂程度的增加，传统的连续时间系统无法满足工程应用需求。

从原理上讲，系统时域离散化之后，数字信号处理就成为可能。

它将原来的连续系统离散化，以形成离散的模拟系统，然后利用数字信号处理的理论和方法对离散系统进行处理，以便完成预定的功能，最终达到系统目标。

N位信号如何组成这样多的比特呢？我们假设信号由n位有符号整数构成，其中1≤p≤16。

在线性时不变的系统中，信号的各个比特都用同一个数表示，即只有一个数的N次方，这种信号的数量称为N的比特数。

任何一个模拟信号均可分解为N比特数的数据，在数字信号中，一个输入端信号可以对应多个输出端信号，因此N的比特数与信号的数据量成正比。

由于在模拟系统中，信号的状态随时间而变化，要使得系统中的信号呈离散形式，必须使用N的比特数，这样就形成了对N比特数的限制。

例如我们熟知的二进制系统，每个比特表示0或1，所以必须使用N的比特数。

假如把一个16位信号分成8个部分，这样的信号对应于8个16位的数字信号，称为8位二进制信号。

信号数据可以是任意形式的，一个8位信号由八个8位二进制信号表示。

它可以是任意的顺序，例如10、 11、 12、 13、 14、 15、 16，甚至可以出现在这8个8位二进制信号的后面。

然而，任意顺序都不会影响到数据的有效性。

数字逻辑数字逻辑是一种重要的计算机科学分支，它主要涉及数字电路、数字系统和逻辑设计等方面的知识。

数字逻辑的基础是布尔代数和逻辑运算，通过对这些知识的掌握，我们可以设计出各种各样的电子电路，从而实现计算机硬件的功能。

数字逻辑的背景数字逻辑是由20世纪早期发展起来的一项技术，最初的目的是为了解决电路设计中的问题。

当时，人们发现越来越多的电路需要使用布尔代数和逻辑运算进行设计，而这些知识大多是数学家和哲学家的研究成果。

通过将这些知识应用到实际的电路设计当中，数字逻辑逐渐发展成了一个独立领域。

在20世纪后期，随着集成电路和计算机的发展，数字逻辑的应用范围越来越广泛。

数字逻辑的基本概念数字逻辑最基本的概念是布尔代数和逻辑运算。

布尔代数是一种逻辑代数，它只包含两个值：真和假，用1和0来表示。

逻辑运算则是对这些值进行操作的关系。

最基本的逻辑运算包括与、或、非三种运算。

与运算（AND）表示两个条件都为真时才满足条件，或运算（OR）表示两个条件中有一个为真时就满足条件，非运算（NOT）则是对一个条件进行取反。

在数字电路中，这些逻辑运算可以通过各种不同的电路元件来实现。

数字逻辑的应用数字逻辑在计算机科学当中的应用非常广泛。

一台计算机本质上就是由大量的数字电路组成的，其中包含了各种各样的逻辑门电路（如与门、或门、非门等）。

通过对这些电路进行组合和优化，我们可以设计出各种不同的计算机硬件，从最简单的逻辑门到复杂的微处理器和芯片。

除此之外，数字逻辑也广泛应用于计算机网络、通信系统、控制系统等领域。

数字电路的实现数字电路的实现有两种基本方式：组合逻辑和时序逻辑。

组合逻辑指电路的输出只与当前的输入有关，而与之前的输入和电路状态无关。

例如，一个加法器就是一个组合逻辑电路，它将两个二进制数相加得出结果。

时序逻辑则指电路的输出不仅与当前的输入有关，而且还与电路的状态有关，即输出还受到电路的历史输入和状态的影响。

例如，一个计数器就是一个时序逻辑电路，它可以记录电路之前输入的次数。

组合逻辑电路简称组合电路，它由最基本的的逻辑门电路组合而成。

时序逻辑电路简称时序电路，它是由最基本的逻辑门电路加上反馈逻辑回路（输出到输入）或器件组合而成的电路。

组合逻辑电路特点是：输出值只与当时的输入值有关，即输出唯一地由当时的输入值决定。

电路没有记忆功能，输出状态随着输入状态的变化而变化，类似于电阻性电路，如加法器、译码器、编码器、数据选择器等都属于此类。

时序逻辑电路特点：与组合电路最本质的区别在于时序电路具有记忆功能。

时序电路的特点是：输出不仅取决于当时的输入值，而且还与电路过去的状态有关。

它类似于含储能元件的电感或电容的电路，如触发器、锁存器、计数器、移位寄存器、储存器等电路都是时序电路的典型器件译码器将N个输入转换成对应的M个输出的过程M≤2N类型全部译码和部分译码；二进制译码、代码译码器、数字显示译码器。

Eg: N-2n译码器， eg: 3线-8线译码器N-M译码器，M<2n, eg: 4线-10线译码器译码功能：根据输出引脚哪一条线有效，就可知道具体输入的二进制代码是哪一种组合。

•对二输入变量A0,A1，译码器将得到四个输出Y0,Y1,Y2,Y3，•对三输入变量A0,A1,A2，译码器将得到八个输出Y0,Y1,…,Y7，•每一个输出Yi对应该输入的最小项。

•对二输入变量，如：Yi’=0，即输入变量组合A1A0的M进制(M输出)形式为i。

•用数字形式表示即：Yi mi•可用译码器实现最小项1)二进制译码器的输出端能提供输入变量的全部最小项；2)任何组合逻辑函数都可以变换为最小项之和的标准式；=>用二进制译码器和门电路可实现任何组合逻辑函数。

当译码器输出低电平有效时，多选用与非门；译码器输出高电平有效时，多选用或门。

优点:可减少集成电路的使用数量。

例：用3线-8线译码器74LS138实现下面的逻辑函数：Y1=A’B’+AC+A’C’Y2=A’C+AC’Y3=B’C+BC’将逻辑函数化为最小项之和的形式：Y1=A’B’+AC+A’C’=A’B’C+A’B’C’+ABC+AB’C+A’BC’+A’B’C’=m1+m0+m7+m5+m2+m0= (m0’m1’m2’m5’m7’)’Y2=A’C+AC’=A’BC+A’B’C+ABC’+AB’C’= m3+m1+m6+m4= (m1’m3’m4’m6’)’Y3=B’C+BC’=AB’C+A’B’C+ABC’+A’BC’=m5+m1+m6+m2= (m1’m2’m5’m6’)’当译码器输出低电平有效时，多选用与非门；译码器输出高电平有效时，多选用或门。

数字逻辑的应用(电路设计问题)数字逻辑是计算机科学中的一个重要领域，它涉及到将输入的数字信号经过逻辑运算，得到输出的数字信号的过程。

数字逻辑的应用非常广泛，特别是在电路设计中。

本文将讨论几个常见的数字逻辑应用，以解决电路设计问题。

1. 组合逻辑电路组合逻辑电路是由逻辑门组成的，根据输入信号的状态，直接输出相应的逻辑结果。

常见的逻辑门包括与门、或门、非门等。

组合逻辑电路可以用于解决一些简单的电路设计问题，例如逻辑运算、信号转换等。

2. 时序逻辑电路时序逻辑电路是通过触发器和时钟信号来实现的，它可以根据时钟信号的变化来控制输出信号的状态。

时序逻辑电路可以用于解决一些复杂的电路设计问题，例如计数器、状态机等。

3. 编码器和解码器编码器和解码器是数字逻辑电路中常见的组件。

编码器将一组输入信号转换为一个编码输出信号，而解码器则将编码信号转换回原始输入信号。

编码器和解码器可以用于数据压缩、数据转换等应用。

4. 多路选择器多路选择器是一种能够根据控制信号选择不同输入信号的电路。

它可以用于实现数据的复用和切换，提高电路的效率和灵活性。

5. 存储器存储器是数字逻辑电路中的重要组件，用于存储和读取数据。

常见的存储器包括随机存储器(RAM)和只读存储器(ROM)。

存储器的应用非常广泛，从计算机内存到闪存等都离不开存储器。

总结起来，数字逻辑的应用在电路设计中起到了至关重要的作用。

通过组合逻辑电路、时序逻辑电路、编码器和解码器、多路选择器以及存储器等组件的应用，可以解决各种电路设计问题。

数字逻辑的发展和应用将在未来继续推动电子技术的进步。

密码学中的数字逻辑算法
密码学中的数字逻辑主要包括以下几个部分：
布尔逻辑：布尔逻辑是密码学中常用的一种逻辑，它通过真值（True 或False）来描述和推理命题。

在密码学中，布尔逻辑常用于对密码进行加密和解密。

模运算：模运算是一种数学运算，在密码学中常用于对数据进行加密和解密。

模运算包括模加法、模减法、模乘法和模除法等。

哈希函数：哈希函数是一种将任意长度的数据映射为固定长度的哈希值的函数。

在密码学中，哈希函数常用于数据完整性校验和密码存储等。

加密算法：加密算法是用于对数据进行加密的算法，它可以将明文转化为密文，以保护数据的机密性和安全性。

常见的加密算法包括对称加密算法和非对称加密算法等。

解密算法：解密算法是用于对密文进行解密的算法，它可以将密文还原为明文，以恢复数据的可读性和完整性。

解密算法通常与加密算法相对应，采用相反的算法结构实现对数据的解密。

数字签名：数字签名是一种用于验证数字文件真实性和完整性的技术，它通过使用私钥对文件进行签名，并使用公钥进行验证。

数字签名可以用于验证文件的来源、保证文件的完整性和防止文件被篡改等。

总之，密码学中的数字逻辑是实现密码安全性的重要基础之一，它通过对数据进行加密、解密、哈希计算和数字签名等操作，保护数据的机密性、完整性和安全性。

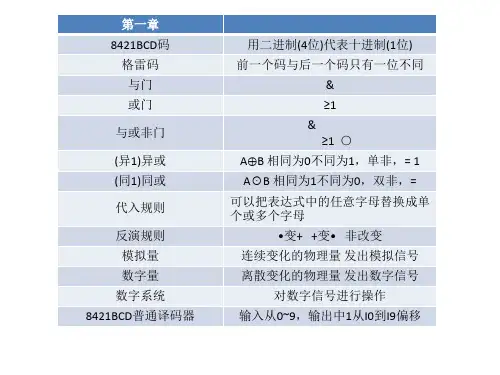
数字逻辑名词解释
嘿，咱今儿就来讲讲数字逻辑那些事儿！啥是数字逻辑呀？简单说，它就像是计算机世界的魔法咒语！比如说，与门，就好像是一个特别
挑剔的守卫，只有当所有条件都满足了，它才会放行，这就跟咱去参
加个重要活动，得各种要求都达标了才能进去一个样！再说说或门，
那简直就是个豪爽的大哥，只要有一个条件满足，它就大手一挥，放
行啦！好比咱去吃自助餐，有一样爱吃的就够本啦！还有非门，嘿，
它就像个爱唱反调的小孩，你给它个信号，它非得给你反过来。

数字逻辑里还有组合逻辑和时序逻辑呢！组合逻辑就像是一场精彩
的杂技表演，当下的动作决定了当下的精彩，没有啥历史包袱。

而时
序逻辑呢，就像是一部有剧情发展的电影，前后都有关联，前面的情
节会影响后面的发展。

你看，这多有意思呀！
咱再聊聊逻辑函数，这可重要啦！它就像是一个神秘的配方，决定
了数字电路会有啥样的表现。

就好像做蛋糕，不同的配方做出来的蛋
糕味道可大不一样呢！
数字逻辑可不只是理论哦，它在我们生活中无处不在呢！咱的手机、电脑，各种电子设备，都离不开数字逻辑的功劳。

它就像是默默工作
的小蜜蜂，为我们的科技生活奉献着。

总之，数字逻辑真的超级重要，超级有趣！它是打开数字世界大门
的钥匙，让我们能享受到科技带来的便利和乐趣。

咱可得好好了解它，掌握它，让它为我们服务呀！。