【机械工程】提高弯曲梁强度的措施.pptx
- 格式:pptx
- 大小:3.95 MB
- 文档页数:8

§7-5 提高弯曲强度的措施如前所述,弯曲正应力是影响弯曲强度的主要因素。
根据弯曲正应力的强度条件][max max σσ≤=zW M (a ) 上式可以改写成内力的形式][][max σz W M M =≤ (b ) (b )式的左侧是构件受到的最大弯矩,(b )式的右侧是构件所能承受的许用弯矩。
由(a )和(b )两式可以看出,提高弯曲强度的措施主要是从三方面考虑:减小最大弯矩、提高抗弯截面系数和提高材料的力学性能。
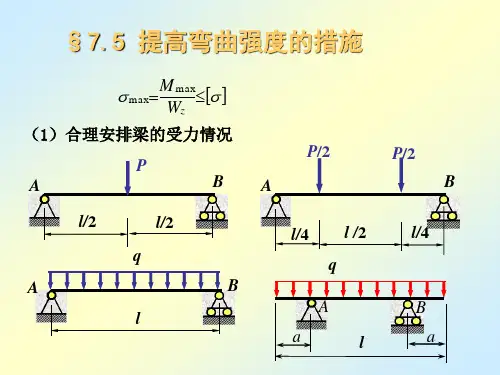
1.减小最大弯矩1)改变加载的位置或加载方式首先,可以通过改变加载位置或加载方式达到减小最大弯矩的目的。
如当集中力作用在简支梁跨度中间时(6-13a ),其最大弯矩为Pl 41;当载荷的作用点移到梁的一侧,如距左侧l 61处(图6-13b ),则最大弯矩变为Pl 365,是原最大弯矩的倍。
当载荷的位置不能改变时,可以把集中力分散成较小的力,或者改变成分布载荷,从而减小最大弯矩。
例如利用副梁把作用于跨中的集中力分散为两个集中力(图6-13c ),而使最大弯矩降低为56.0Pl 81。
利用副梁来达到分散载荷,减小最大弯矩是工程中经常采用的方法。
2)改变支座的位置其次,可以通过改变支座的位置来减小最大弯矩。
例如图6-14a 所示受均布载荷的简支梁,22max 125.081ql ql M ==。
若将两端支座各向里移动 (图6-14b ),则最大弯矩减小为l 2.02401ql ,22max 025.0401ql ql M ==只及前者的51。
图6-15a 所示门式起重机的大梁,图6-15b 所示锅炉筒体等,其支承点略向2.提高抗弯截面系数中间移动,都是通过合理布置支座位置,以减小 的工程实例。
1在截面积高。
例如对截maxM )选用合理的截面形状A 相同的条件下,抗弯截面系数 W 愈大,则梁的承载能力就愈面高度b 的矩形截面梁,梁竖放时h 大于宽度216bh W =;而梁平放时,1226hb W =。

提高梁弯曲强度的主要途径
梁作为结构构件,具有抗弯能力,是许多工程结构中不可或缺的.由于具有抗弯性能,因而控制梁弯曲强度很重要.怎样提高梁弯曲强度,是经常被建议的一个问题.梁弯曲强度的提高是为了满足工程需求.
首先,应从梁的本身材料开始,选择多性能优良的材料,这样增加结构整体特性.其次,应根据实际情况,合理设计结构,减小面积,减少自重.此外,要根据实际需要,合理选择衬垫,凹槽,强化等,使梁具有更高的弯曲强度.另外,还应在设计和施工中,采取抗震计算,根据分析结果,进行严格的抗震设计,从而满足结构物抗震性能要求.
此外,通过完善施工技术,良好的质量保证检测,使梁具有更佳的弯曲强度,并建立完善的抗震设计标准体系,提高抗震设计水平.
总之,提高梁弯曲强度的主要途径主要有材料、减少面积、衬垫加强、抗震计算、施工技术及质量保证等.不仅需要在设计中进行科学严谨的设计,还应重视施工中质量保证与抗震计算,认真考虑使未来的工程结构更加可靠和稳健.。


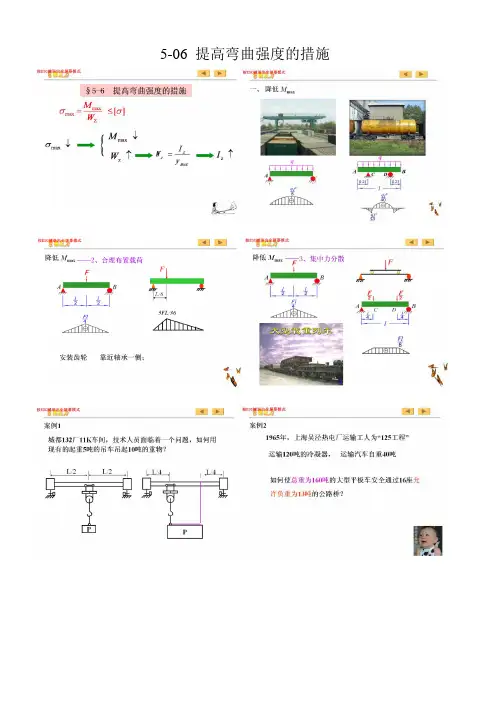
5-06 提高弯曲强度的措施
工字型比矩形好,矩形比圆形好!
要求y拉小于y压,所以中性轴偏向于抗拉一侧。
回忆:
切应力计算公式:与剪力大小成正比,与以外的面积对中性轴的静矩成正比,b为欲求切应力截面尺寸的宽度。
工字型、圆形、矩形、T形截面:切应力沿高度的变化规律,最大值?
采用什么办法提高梁的弯曲强度?
1、分散载荷;
2、合理截面:细长、截面的大部分分布在远离中性轴的区域;
3、衡量合理截面的指标:抗弯截面系数和横截面的比值,商值越大越合理;
4、等强度:各个面上的最远的点同时达到许用应力。

提高梁弯曲强度的主要措施弯曲正应力是控制抗弯强度的主要因素。
因此,讨论提高梁抗弯强度的措施,应以弯曲正应力强度条件为主要依据。
由]σ[σmax max ≤=zW M 可以看出,为了提高梁的强度,可以从以下三方面考虑。
(1) 合理安排梁的支座和载荷从正应力强度条件可以看出,在抗弯截面模量z W 不变的情况下,M max 越小,梁的承载能力越高。
因此,应合理地安排梁的支承及加载方式,以降低最大弯矩值。
例如图1(a)所示简支梁,受均布载荷q 作用,梁的最大弯矩为281ql M max =。
图1 简支梁如果将梁两端的铰支座各向内移动0.2l ,如图1(b)所示,则最大弯矩变为2401ql M max =,仅为前者的1/5。
由此可见,在可能的条件下,适当地调整梁的支座位置,可以降低最大弯矩值,提高梁的承载能力。
例如,门式起重机的大梁图2(a),锅炉筒体图2(b)等,就是采用上述措施,以达到提高强度,节省材料的目的。
图2 合理安排梁的支座和载荷(2) 采用合理的截面形状由正应力强度条件可知,梁的抗弯能力还取决于抗弯截面系数W Z 。
为提高梁的抗弯强度,应找到一个合理的截面以达到既提高强度,又节省材料的目的。
比值A W z 可作为衡量截面是否合理的尺度,AW z 值越大,截面越趋于合理。
例如图3中所示的尺寸及材料完全相同的两个矩形截面悬臂梁,由于安放位置不同,抗弯能力也不同。
竖放时662h bh bh A W z == 平放时 662b bh hb A W z == 当h>b 时,竖放时的A W z 大于平放时的AW z ,因此,矩形截面梁竖放比平放更为合理。
在房屋建筑中,矩形截面梁几乎都是竖放的,道理就在于此。
图3矩形梁的不同放置在讨论截面的合理形状时,还应考虑材料的特性。
对于抗拉和抗压强度相等的材料,如各种钢材,宜采用对称于中性轴的截面,如圆形、矩形和工字形等。
这种横截面上、下边缘最大拉应力和最大压应力数值相同,可同时达到许用应力值。



7-6 提高弯曲强度的措施梁的设计既要保证其具有足够的强度,在荷载作用下能安全的工作,又要节约材料,减轻自重,使其经济合理。
一般情况下,梁的弯曲强度是由正应力控制的,弯曲正应力强度条件max max z []M W σσ=≤是梁弯曲强度计算的主要依据。
要提高梁的强度应从以下几个方面入手:一、采用合理的截面形状1、根据W z /A 的比值选择截面梁能承受的弯矩与抗弯截面系数W z 成正比,而用料的多少又与截面面积A 成正比,所以W z /A 的比值越大越合理。
对截面高度相同而形状不同的截面,可用W z /A 的比值来比较:① 高为h 宽为b 的矩形截面2160.1676bh W h h A bh === ② 直径为h 的圆形截面32320.12584h W h h A h ππ===③ 高为h 的槽形及工字形截面 (0.27~0.31)W h A =可见,槽形及工字形截面最合理,矩形截面次之,圆形截面最差。
这一结论也可用正应力的分布规律得到解释:当距中性轴最远处应力达到相应许用应力时,中性轴上(或附近)的应力分别为零(或较小),这部分材料没有充分发挥作用。
故应把这部分材料移至远离中性轴的位置。
为了充分发挥材料的潜力应将截面面积布置得离中性轴远些为好。
所以,工程上常常采用工字形、环形、箱形截面等截面形式。
2、根据材料的力学特性选择截面对于用抗拉和抗压强度相同的塑性材料制成的梁,宜选用对称于中性轴的截面,如工字形、矩形和圆环形截面。
y 1y 2-max图7-27对于由脆性材料制成的梁,由于抗拉强度小于抗压强度,宜采用中性轴不是对称轴的截面,且应使中性轴靠近强度较低的一侧,如铸铁等脆性材料制成的梁常采用T 形和箱形截面(如图7-27),并使y 1和y 2之比满足下式:+max 11max 22/[]/[]z z My I y My I y σσσσ+--=== 即:截面受拉、受压边缘到的距离与材料的抗拉、抗压许用应力成正比,这样,截面上的最大拉应力和最大压应力同时达到许用应力。