人教版初中数学第十一章三角形知识点复习过程
- 格式:doc
- 大小:135.00 KB
- 文档页数:15


初二数学第十一章第1节全等三角形人教新课标版一、学习目标:1. 通过实例理解全等图形的概念和特征,并能找出全等图形。
2. 能叙述全等三角形的定义及相关概念,并能找出两个全等三角形的对应边和对应角。
3. 掌握全等三角形的性质,会利用全等三角形的性质进行简单的推理和计算,解决一些实际问题。
二、重点、难点:重点是全等三角形的概念,难点是全等三角形的对应顶点要对应写,对应关系要明确。
三、考点分析:本讲所涉及的考点是全等三角形的概念与全等三角形的性质。
在这里,全等三角形的概念属于了解范畴,而全等三角形的性质属于掌握范畴,对其性质还要求会运用。
这两个知识点不会单独出大题,只会以小题的形式出现,或在大题中用到。
所以,大家只要在掌握各概念性质的基础上弄清对应关系即可。
1. 全等三角形的基本概念:(1)全等图形的定义:能够完全重合的两个图形叫做全等图形。
(2)全等三角形的定义:能够完全重合的两个三角形叫做全等三角形。
重合的顶点叫做对应顶点。
重合的边叫做对应边。
重合的角叫做对应角。
(3)全等三角形的表示方法:△ABC≌△A’B’C’(如图1)A’B C ’图12. 全等三角形的性质:(1)全等三角形的对应边相等;(2)全等三角形的对应角相等。
知识点一:全等三角形的基本概念例1. 下列说法正确的有()①用一张底片冲洗出来的10张一寸照片是全等图形②我国国旗上的4颗小五角星是全等图形③所有的正方形是全等图形④全等图形的面积一定相等A. 1个B. 2个C. 3个D. 4个思路分析:1)题意分析:本题主要考查全等图形定义中对“能够完全重合”的理解。
2)解题思路:根据全等图形的定义:“能够完全重合的两个图形叫做全等图形。
”来判断题目中每一句话中所谈到的图形是否能完全重合。
解答过程:用一张底片冲洗出来的10张一寸照片的形状和大小完全相同,它们是全等图形,所以①正确;我国国旗上的四颗小五角星的形状和大小也完全相同,它们也是全等图形;所以②正确;所有的正方形只是形状相同,但大小不一定相同,所以它们不是全等图形,故③不正确;全等图形的形状和大小完全相同,所以面积一定相等,所以④正确。
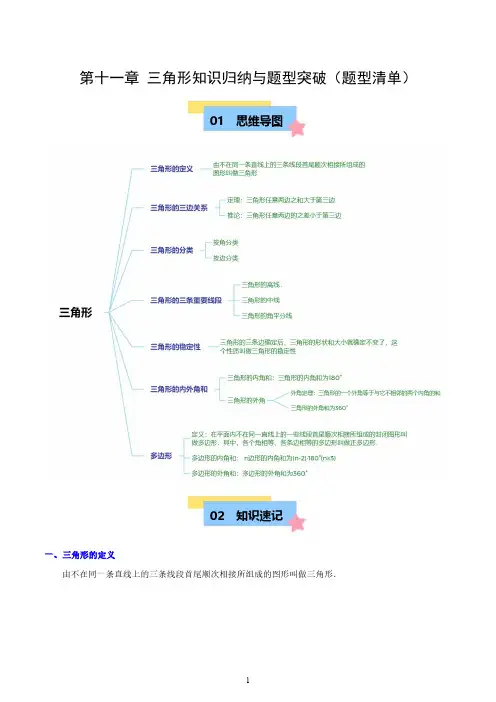
第十一章三角形知识归纳与题型突破(题型清单)01思维导图02知识速记一、三角形的定义由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.要点诠释:(1)三角形的基本元素:①三角形的边:即组成三角形的线段;②三角形的角:即相邻两边所组成的角叫做三角形的内角,简称三角形的角;③三角形的顶点:即相邻两边的公共端点.(2)三角形的定义中的三个要求:“不在同一条直线上”、“三条线段”、“首尾顺次相接”.(3)三角形的表示:三角形用符号“△”表示,顶点为A 、B 、C 的三角形记作“△ABC ”,读作“三角形ABC ”,注意单独的△没有意义;△ABC 的三边可以用大写字母AB 、BC 、AC 来表示,也可以用小写字母a 、b 、c 来表示,边BC 用a 表示,边AC 、AB 分别用b 、c 表示.二、三角形的三边关系定理:三角形任意两边之和大于第三边.推论:三角形任意两边的之差小于第三边.要点诠释:(1)理论依据:两点之间线段最短.(2)三边关系的应用:判断三条线段能否组成三角形,若两条较短的线段长之和大于最长线段的长,则这三条线段可以组成三角形;反之,则不能组成三角形.当已知三角形两边长,可求第三边长的取值范围.(3)证明线段之间的不等关系.三、三角形的分类1.按角分类:⎧⎪⎧⎨⎨⎪⎩⎩直角三角形三角形 锐角三角形斜三角形 钝角三角形要点诠释:①锐角三角形:三个内角都是锐角的三角形;②钝角三角形:有一个内角为钝角的三角形.2.按边分类:⎧⎪⎧⎨⎨⎪⎩⎩不等边三角形三角形 底边和腰不相等的等腰三角形等腰三角形 等边三角形要点诠释:①不等边三角形:三边都不相等的三角形;②等腰三角形:有两条边相等的三角形叫做等腰三角形,相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫顶角,腰与底边夹角叫做底角;③等边三角形:三边都相等的三角形.四、三角形的三条重要线段三角形的高、中线和角平分线是三角形中三条重要的线段,它们提供了重要的线段或角的关系,为我们以后深入研究三角形的一些特征起着很大的帮助作用,因此,我们需要从不同的角度弄清这三条线段,列表如下:线段名称三角形的高三角形的中线三角形的角平分线文字语言从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段.三角形中,连接一个顶点和它对边中点的线段.三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段.图形语言作图语言过点A 作AD ⊥BC 于点D .取BC 边的中点D ,连接AD .作∠BAC 的平分线AD ,交BC 于点D .标示图形符号语言1.AD 是△ABC 的高.2.AD 是△ABC 中BC 边上的高.3.AD ⊥BC 于点D .4.∠ADC =90°,∠ADB =90°.1.AD 是△ABC 的中线.2.AD 是△ABC 中BC 边上的中线.3.BD =DC =12BC 4.点D 是BC 边的中点.1.AD 是△ABC 的角平分线.2.AD 平分∠BAC ,交BC 于点D .3.∠1=∠2=12∠BAC .(或∠ADC=∠ADB=90°)推理语言因为AD是△ABC的高,所以AD⊥BC.(或∠ADB=∠ADC=90°)因为AD是△ABC的中线,所以BD=DC=12BC.因为AD平分∠BAC,所以∠1=∠2=12∠BAC.用途举例1.线段垂直.2.角度相等.1.线段相等.2.面积相等.角度相等.注意事项1.与边的垂线不同.2.不一定在三角形内.—与角的平分线不同.重要特征三角形的三条高(或它们的延长线)交于一点.一个三角形有三条中线,它们交于三角形内一点.一个三角形有三条角平分线,它们交于三角形内一点.五、三角形的稳定性三角形的三条边确定后,三角形的形状和大小就确定不变了,这个性质叫做三角形的稳定性.要点诠释:(1)三角形的形状固定是指三角形的三个内角不会改变,大小固定指三条边长不改变.(2)三角形的稳定性在生产和生活中很有用.例如,房屋的人字梁具有三角形的结构,它就坚固而稳定;在栅栏门上斜着钉一条(或两条)木板,构成一个三角形,就可以使栅栏门不变形.大桥钢架、输电线支架都采用三角形结构,也是这个道理.(3)四边形没有稳定性,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.四边形的不稳定性也有广泛应用,如活动挂架,伸缩尺.有时我们又要克服四边形的不稳定性,如在门框未安好之前,先在门框上斜着钉一根木板,使它不变形.六、三角形的内角和三角形内角和定理:三角形的内角和为180°.要点诠释:应用三角形内角和定理可以解决以下三类问题:①在三角形中已知任意两个角的度数可以求出第三个角的度数;②已知三角形三个内角的关系,可以求出其内角的度数;③求一个三角形中各角之间的关系.七、三角形的外角1.定义:三角形的一边与另一边的延长线组成的角叫做三角形的外角.如图,∠ACD是△ABC的一个外角.要点诠释:(1)外角的特征:①顶点在三角形的一个顶点上;②一条边是三角形的一边;③另一条边是三角形某条边的延长线.(2)三角形每个顶点处有两个外角,它们是对顶角.所以三角形共有六个外角,通常每个顶点处取一个外角,因此,我们常说三角形有三个外角.2.性质:(1)三角形的一个外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于任意一个与它不相邻的内角.要点诠释:三角形内角和定理和三角形外角的性质是求角度及与角有关的推理论证明经常使用的理论依据.另外,在证角的不等关系时也常想到外角的性质.3.三角形的外角和:三角形的外角和等于360°.要点诠释:因为三角形的每个外角与它相邻的内角是邻补角,由三角形的内角和是180°,可推出三角形的三个外角和是360°.八、多边形的概念1.定义:在平面内不在同一直线上的一些线段首尾顺次相接所组成的封闭图形叫做多边形.其中,各个角相等、各条边相等的多边形叫做正多边形.2.相关概念:边:组成多边形的各条线段叫做多边形的边.顶点:每相邻两条边的公共端点叫做多边形的顶点.内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角.外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.3.多边形的分类:画出多边形的任何一边所在的直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形,如果整个多边形不在直线的同一侧,这个多边形叫凹多边形.如图:要点诠释:(1)正多边形必须同时满足“各边相等”,“各角相等”两个条件,二者缺一不可;(2)过n 边形的一个顶点可以引(n -3)条对角线,n 边形对角线的条数为(3)2n n -;(3)过n 边形的一个顶点的对角线可以把n 边形分成(n -2)个三角形.九、多边形内角和n 边形的内角和为(n -2)·180°(n ≥3).要点诠释:(1)内角和公式的应用:①已知多边形的边数,求其内角和;②已知多边形内角和求其边数;(2)正多边形的每个内角都相等,都等于(2)180n n- °;十、多边形的外角和多边形的外角和为360°.要点诠释:(1)在一个多边形的每个顶点处各取一个外角,这些外角的和叫做多边形的外角和.n 边形的外角和恒等于360°,它与边数的多少无关;(2)正n 边形的每个内角都相等,所以它的每个外角都相等,都等于360n°;(3)多边形的外角和为360°的作用是:①已知各相等外角度数求多边形边数;②已知多边形边数求各相等外角的度数.凸多边形凹多边形03题型归纳题型一三角形的稳定性例题:(23-24七年级下·陕西咸阳·阶段练习)如图,墙上置物架的底侧一般会各设计一根斜杆,与水平和竖直方向的支架构成三角形,这是利用三角形的()A.全等性B.对称性C.稳定性D.灵活性巩固训练1.(23-24八年级上·云南昆明·期末)我国建造的港珠澳大桥全长55公里,集桥、岛、隧于一体,是世界最长的跨海大桥.如图,这是港珠澳大桥的斜拉索,它能拉住桥面,并将桥面向下的力通过钢索传给索塔,确保桥面的稳定性和安全性.那么港珠澳大桥斜拉索建设运用的数学原理是()A.三角形的不稳定性B.三角形的稳定性C.四边形的不稳定性D.四边形的稳定性3.(23-24七年级下·黑龙江哈尔滨·期中)如图,松花江大桥的钢架结构采用三角形的形状,这其中运用的数学道理是.4.(23-24七年级下·全国·假期作业)如图,建高楼常需要用塔吊来吊建筑材料,而塔吊的上部是三角形结构,这是因为三角形具有.题型二判断三边是否能构成三角形例题:(23-24七年级下·江苏盐城·期末)下列每组数分别表示3根小木棒的长度(单位:cm),其中能搭成三角形的是()A.4,5,10B.5,5,10C.5,8,10D.5,10,15巩固训练1.(23-24七年级下·海南儋州·期末)下列长度的三条线段中,能构成三角形的是()A.1,3,5B.2,4,6C.1,2,3D.3,4,52.(23-24七年级下·河北邢台·阶段练习)甲同学对下列三角形的边长分别进行标注,那么他标注错误的是()A.B.C.D.3.(2024·河北邯郸·二模)将一根吸管按如图所示的位置摆放在单位长度为1的数轴(不完整)上,吸管左-”处,右端对应数轴上的“5”处.若将该吸管剪成三段围成三角形,第一刀剪在数轴上的端对应数轴上的“8“5-”处,则第二刀可以剪在()A.“4-”处B.“3-”处C.“1-”处D.“2”处题型三已知三角形的两边长,求第三边的取值范围两边长分别为4与5,第三边的长为奇数,则第三边的长的例题:(23-24七年级下·重庆·期末)已知ABC最大值为.巩固训练1.(23-24七年级下·江苏无锡·期末)已知三角形的两边长为3和4,则第三条边长可以为.(请写出一个符合条件的答案)2.(23-24七年级下·黑龙江大庆·期中)一个三角形的两边长为2和6,第三边为奇数,则这个三角形的周长为.3.(23-24七年级下·内蒙古包头·期中)一个三角形的两边长分别为5和7,若x 为最长边且为整数,则此三角形的周长为.题型四判断是否三角形的高线例题:下列各图中,正确画出AC 边上的高的是()A .B .C .D .巩固训练1.下面四个图形中,线段BD 是ABC 的高的图形是()A .B .C .D .2.(2023秋·甘肃庆阳·八年级统考期末)如图,在ABC 中,A ∠是钝角,下列图中作BC 边上的高线,正确的是()A .B .C .D .3.如图,AD BC ⊥,EC BC ⊥,CF AB ⊥,点D ,C ,F 是垂足,下列说法错误的是()A .ABD △中,AD 是BD 边上的高B .ABD △中,EC 是BD 边上的高C .CEB 中,EC 是BC 边上的高D .CEB 中,FC 是BE 边上的高题型五根据三角形的中线求面积例题:(2023春·广东茂名·七年级校考阶段练习)如图,ABC 的面积为20,点D ,E ,F 分别为BC AD CE,,的中点,则阴影部分BFC △的面积为()A .4B .5C .6D .10巩固训练1.(2023春·山西太原·七年级山西大附中校考期中)如图,AD BE 、是ABC 的中线,则下列结论中,正确的个数有()(1)AOE COE S S = ;(2)AOB EODC S S = 四边形;(3)2BOC COE S S = ;(4)4ABC BOC S S = .A .1个B .2个C .3个D .4个2.(2023春·江苏扬州·七年级校联考阶段练习)如图,BD 是ABC 的中线,点E 、F 分别为BD CE 、的中点,若AEF △的面积为22cm ,则ABC 的面积是________2cm .3.(2023春·江苏南京·七年级校考阶段练习)如图,且满足13AE AD =,13AF AC =题型六与平行线有关的三角形内角和问题例题:(23-24七年级下·上海虹口·期中)如图,已知AB ED ∥,80EDC ∠=︒,53ECD ∠=︒,105B ∠=︒,那么ACB =∠.巩固训练1.(23-24七年级下·陕西渭南·期中)如图,在三角形ABC 中,点D ,H ,E 分别是边AB ,BC ,CA 上的点,连接DE ,DH ,F 为DH 上一点,连接EF ,若12180∠+∠=︒,365B ∠=∠=︒,52C ∠=︒.则FEC ∠的度数为︒.2.(23-24七年级下·陕西咸阳·期中)如图,AN 平分BAM ∠,BM 平分ABN ∠,AN BM ⊥于点C ,25MBN ∠=︒,则下列说法:①90BCN ∠=︒;②AM BN ;③50DAM ∠=︒;④60MAN ∠=︒,其中正确的是.(填序号)3.(23-24七年级下·上海浦东新·期中)如图,将一副直角三角板放在同一条直线AB 上,其中3045OMN OCD ∠=︒∠=︒,.将三角尺OCD 绕点O 以每秒10︒的速度顺时针方向旋转一周,设旋转的时间为t 秒.在旋转的过程中,边CD 恰好与边MN 平行,t 的值为.题型七与角平分线有关的三角形内角和问题例题:(23-24七年级下·江苏南京·期末)如图,在ABC 中,AD 平分BAC ∠,过点A 作EF BC ∥.若40EAB ∠=︒,80C ∠=︒,则ADC ∠=.巩固训练1.(23-24七年级下·上海浦东新·阶段练习)如图,在ABC 中,125BDC ∠=︒,如果ABC ∠与ACB ∠的平分线交于点D ,那么A ∠=度.2.(23-24七年级下·辽宁大连·期中)如图,在ABC 中,BD CD 、分别平分,ABC ACB BG CG ∠∠、、分别平分三角形的两个外角,48EBC FCB G ∠∠∠=︒、,则D ∠=︒.3.(23-24七年级下·湖南衡阳·期末)如图,在ABC 中,30B ∠=︒,70C ∠=︒,AE 平分BAC ∠,AD BC ⊥于点D .(1)求BAE ∠的度数.(2)求EAD ∠的度数.题型八三角形的外角的定义及性质例题:(23-24七年级下·四川乐山·期末)如图,在ABC 中,点D 在BC 的延长线上,70A ∠=︒,120ACD ∠=︒,则B ∠=︒.巩固训练1.(23-24七年级下·浙江杭州·阶段练习)如图,已知直线12l l ∥,154∠=︒,2100∠=︒,则A ∠=度.2.(23-24七年级下·江苏淮安·期末)如图,ABC 的两个外角的平分线交于点P .若64BPC ∠=︒,则A ∠=.3.(23-24七年级下·江西南昌·期末)已知直线12l l ∥,将含30︒角的直角三角板按如图所示摆放.若2140∠=︒,则1∠=.题型九多边形的内角和与外角和例题:(23-24七年级下·江苏镇江·期末)足球的表面是由12个正五边形和20个正六边形组成的.如图,将足球上的一个正六边形和它相邻的一个正五边形展开放平,则图中的ABC ∠=.巩固训练1.(23-24九年级下·重庆开州·阶段练习)如图,3∠和4∠是四边形ABCD 的外角,若1120∠=︒,275∠=︒,则34∠+∠=.2.(23-24八年级下·江西萍乡·期末)一个多边形的内角和是它的外角和的1.5倍,则这个多边形的边数为.3.(23-24七年级下·河南驻马店·阶段练习)如图,已知59MON ∠=︒,正五边形ABCDE 的顶点A 、B 在射线OM 上,顶点E 在射线ON 上,则NED ∠的度数为.题型十在网格中画三角形的中线、高线及求三角形的面积例题:(2023春·黑龙江哈尔滨·七年级哈尔滨市第六十九中学校校考期中)下图为79⨯的网格,每一小格均为正方形,已知ABC .(1)画出ABC 中BC 边上的中线AD ;(2)画出ABC 中AB 边上的高CE .(3)直接写出ABC 的面积为_________.巩固训练1.(2023春·黑龙江哈尔滨·七年级哈尔滨市第四十七中学校考期中)如图所示方格纸中,每个小正方形的边长均为1,点A ,点B ,点C 在小正方形的顶点上.(1)画出ABC 中边BC 上的高AD ;(2)画出ABC 中边AB 上的中线CE ;(3)直接写出ACE △的面积为______.2.(23-24七年级下·江苏连云港·阶段练习)如图,在方格纸内将ABC 水平向右平移4个单位得到A B C ''' .(1)画出A B C ''' ;(2)若连接AA ',BB ',则这两条线段之间的关系是_________;(3)画出AB 边上的中线CD ;(利用网格点和直尺画图)(4)图中能使ABC PBC S S =△△的格点P 有_________个(点P 异于点A ).3.(23-24七年级下·江苏扬州·阶段练习)如图,方格纸中每个小正方形边长均为1,在方格纸内将ABC 的点C 平移至点C '得到A B C ''' .(1)画出A B C ''' ;(2)线段AC 和A C ''的关系是_______.(3)借助方格画出AB 边上的中线CD 和高CE ;(4)四边形ACC A ''面积为_______.第十一章三角形知识归纳与题型突破(题型清单)01思维导图02知识速记一、三角形的定义由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.要点诠释:(1)三角形的基本元素:①三角形的边:即组成三角形的线段;②三角形的角:即相邻两边所组成的角叫做三角形的内角,简称三角形的角;③三角形的顶点:即相邻两边的公共端点.(2)三角形的定义中的三个要求:“不在同一条直线上”、“三条线段”、“首尾顺次相接”.(3)三角形的表示:三角形用符号“△”表示,顶点为A 、B 、C 的三角形记作“△ABC ”,读作“三角形ABC ”,注意单独的△没有意义;△ABC 的三边可以用大写字母AB 、BC 、AC 来表示,也可以用小写字母a 、b 、c 来表示,边BC 用a 表示,边AC 、AB 分别用b 、c 表示.二、三角形的三边关系定理:三角形任意两边之和大于第三边.推论:三角形任意两边的之差小于第三边.要点诠释:(1)理论依据:两点之间线段最短.(2)三边关系的应用:判断三条线段能否组成三角形,若两条较短的线段长之和大于最长线段的长,则这三条线段可以组成三角形;反之,则不能组成三角形.当已知三角形两边长,可求第三边长的取值范围.(3)证明线段之间的不等关系.三、三角形的分类1.按角分类:⎧⎪⎧⎨⎨⎪⎩⎩直角三角形三角形 锐角三角形斜三角形 钝角三角形要点诠释:①锐角三角形:三个内角都是锐角的三角形;②钝角三角形:有一个内角为钝角的三角形.2.按边分类:⎧⎪⎧⎨⎨⎪⎩⎩不等边三角形三角形 底边和腰不相等的等腰三角形等腰三角形 等边三角形要点诠释:①不等边三角形:三边都不相等的三角形;②等腰三角形:有两条边相等的三角形叫做等腰三角形,相等的两边都叫做腰,另外一边叫做底边,两腰的夹角叫顶角,腰与底边夹角叫做底角;③等边三角形:三边都相等的三角形.四、三角形的三条重要线段三角形的高、中线和角平分线是三角形中三条重要的线段,它们提供了重要的线段或角的关系,为我们以后深入研究三角形的一些特征起着很大的帮助作用,因此,我们需要从不同的角度弄清这三条线段,列表如下:线段名称三角形的高三角形的中线三角形的角平分线文字语言从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段.三角形中,连接一个顶点和它对边中点的线段.三角形一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段.图形语言作图语言过点A 作AD ⊥BC 于点D .取BC 边的中点D ,连接AD .作∠BAC 的平分线AD ,交BC 于点D .标示图形符号语言1.AD 是△ABC 的高.2.AD 是△ABC 中BC 边上的高.3.AD ⊥BC 于点D .4.∠ADC =90°,∠ADB =90°.1.AD 是△ABC 的中线.2.AD 是△ABC 中BC 边上的中线.3.BD =DC =12BC 4.点D 是BC 边的中点.1.AD 是△ABC 的角平分线.2.AD 平分∠BAC ,交BC 于点D .3.∠1=∠2=12∠BAC .(或∠ADC=∠ADB=90°)推理语言因为AD是△ABC的高,所以AD⊥BC.(或∠ADB=∠ADC=90°)因为AD是△ABC的中线,所以BD=DC=12BC.因为AD平分∠BAC,所以∠1=∠2=12∠BAC.用途举例1.线段垂直.2.角度相等.1.线段相等.2.面积相等.角度相等.注意事项1.与边的垂线不同.2.不一定在三角形内.—与角的平分线不同.重要特征三角形的三条高(或它们的延长线)交于一点.一个三角形有三条中线,它们交于三角形内一点.一个三角形有三条角平分线,它们交于三角形内一点.五、三角形的稳定性三角形的三条边确定后,三角形的形状和大小就确定不变了,这个性质叫做三角形的稳定性.要点诠释:(1)三角形的形状固定是指三角形的三个内角不会改变,大小固定指三条边长不改变.(2)三角形的稳定性在生产和生活中很有用.例如,房屋的人字梁具有三角形的结构,它就坚固而稳定;在栅栏门上斜着钉一条(或两条)木板,构成一个三角形,就可以使栅栏门不变形.大桥钢架、输电线支架都采用三角形结构,也是这个道理.(3)四边形没有稳定性,也就是说,四边形的四条边长确定后,不能确定它的形状,它的各个角的大小可以改变.四边形的不稳定性也有广泛应用,如活动挂架,伸缩尺.有时我们又要克服四边形的不稳定性,如在门框未安好之前,先在门框上斜着钉一根木板,使它不变形.六、三角形的内角和三角形内角和定理:三角形的内角和为180°.要点诠释:应用三角形内角和定理可以解决以下三类问题:①在三角形中已知任意两个角的度数可以求出第三个角的度数;②已知三角形三个内角的关系,可以求出其内角的度数;③求一个三角形中各角之间的关系.七、三角形的外角1.定义:三角形的一边与另一边的延长线组成的角叫做三角形的外角.如图,∠ACD是△ABC的一个外角.要点诠释:(1)外角的特征:①顶点在三角形的一个顶点上;②一条边是三角形的一边;③另一条边是三角形某条边的延长线.(2)三角形每个顶点处有两个外角,它们是对顶角.所以三角形共有六个外角,通常每个顶点处取一个外角,因此,我们常说三角形有三个外角.2.性质:(1)三角形的一个外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于任意一个与它不相邻的内角.要点诠释:三角形内角和定理和三角形外角的性质是求角度及与角有关的推理论证明经常使用的理论依据.另外,在证角的不等关系时也常想到外角的性质.3.三角形的外角和:三角形的外角和等于360°.要点诠释:因为三角形的每个外角与它相邻的内角是邻补角,由三角形的内角和是180°,可推出三角形的三个外角和是360°.八、多边形的概念1.定义:在平面内不在同一直线上的一些线段首尾顺次相接所组成的封闭图形叫做多边形.其中,各个角相等、各条边相等的多边形叫做正多边形.2.相关概念:边:组成多边形的各条线段叫做多边形的边.顶点:每相邻两条边的公共端点叫做多边形的顶点.内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角.外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角.对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.3.多边形的分类:画出多边形的任何一边所在的直线,如果整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形,如果整个多边形不在直线的同一侧,这个多边形叫凹多边形.如图:要点诠释:(1)正多边形必须同时满足“各边相等”,“各角相等”两个条件,二者缺一不可;(2)过n 边形的一个顶点可以引(n -3)条对角线,n 边形对角线的条数为(3)2n n -;(3)过n 边形的一个顶点的对角线可以把n 边形分成(n -2)个三角形.九、多边形内角和n 边形的内角和为(n -2)·180°(n ≥3).要点诠释:(1)内角和公式的应用:①已知多边形的边数,求其内角和;②已知多边形内角和求其边数;(2)正多边形的每个内角都相等,都等于(2)180n n- °;十、多边形的外角和多边形的外角和为360°.要点诠释:(1)在一个多边形的每个顶点处各取一个外角,这些外角的和叫做多边形的外角和.n 边形的外角和恒等于360°,它与边数的多少无关;(2)正n 边形的每个内角都相等,所以它的每个外角都相等,都等于360n°;(3)多边形的外角和为360°的作用是:①已知各相等外角度数求多边形边数;②已知多边形边数求各相等外角的度数.凸多边形凹多边形03题型归纳题型一三角形的稳定性例题:(23-24七年级下·陕西咸阳·阶段练习)如图,墙上置物架的底侧一般会各设计一根斜杆,与水平和竖直方向的支架构成三角形,这是利用三角形的()A.全等性B.对称性C.稳定性D.灵活性【答案】C【分析】本题主要考查了三角形具有稳定性,根据三角形具有稳定性,即可进行解答.【详解】解:墙上置物架的底侧一般会各设计一根斜杆,与水平和竖直方向的支架构成三角形,这是利用三角形的稳定性,故选;C.巩固训练1.(23-24八年级上·云南昆明·期末)我国建造的港珠澳大桥全长55公里,集桥、岛、隧于一体,是世界最长的跨海大桥.如图,这是港珠澳大桥的斜拉索,它能拉住桥面,并将桥面向下的力通过钢索传给索塔,确保桥面的稳定性和安全性.那么港珠澳大桥斜拉索建设运用的数学原理是()A.三角形的不稳定性B.三角形的稳定性C.四边形的不稳定性D.四边形的稳定性【答案】B【分析】本题主要考查了三角形的特性,解题的关键是熟练掌握三角形的稳定性;根据三角形的稳定性进行解答即可.。

第十一章三角形
11.1 与三角形有关的线段【高、中线(重心)、角平分线】
两边之差<第三边<两边之和。
按边分类、三角形的稳定性。
11.2 与三角形有关的角
三角形内角和定理:三角形三个内角的和等于180º。
直角三角形的两个锐角互余。
有两个角互余的三角形是直角三角形。
推论:三角形的外角等于与它不相邻的两个内角的和。
备注:推论和定理一样,可以作为进一步推理的依据。
11.3 多边形及其内角和
多边形:在平面内,由一些线段首尾顺次相接组成的封闭式图形。
对角线:连接多边形不相邻的两个顶点的线段。
正多边形:各个角都相等,各条边都相等的多边形。
n边形内角和等于(n-2)×180º。
多边形的外角和等于360º。
作者留言:
非常感谢!您浏览到此文档。
为了提高文档质量,欢迎您点赞或留言告诉我文档的不足之处,以便于对该文档进行完善优化,在此本人深表感谢!祝您天天快乐!
良好的学习态度能够更好的提高学习能力。
良好的学习态度应该包括:
1、主动维持学习的兴趣,不断提升学习能力。
2、合理安排学习的时间。
3、诚挚尊重学习的对象,整合知识点。
4、信任自己的学习能力,制定学习复习计划。
5、做题的时候要学会反思、归类、整理出对应的解题思路。
因此,良好的学习态度的养成,应该从养成良好的学习习惯开始。
无论是初学者,还是学有所成者,都应该有一个良好的学习态度,都应该有一个良好的学习习惯。



新人教版八年级数学知识点总结第十一章三角形一、知识框架:二、知识概念:1.三角形:①概念:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.②相关的名词:三角形的角(内角)、边、顶点、记法、读法。
③三角形的分类:两种分类方法(边、角)2.三边关系(性质):三角形任意两边的和大于第三边,任意两边的差小于第三边.(重点)数学表达式:3.高:①概念:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高.②作法:③性质:④垂心:4.中线:①概念:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.②作法:③性质:④重心:5.角平分线:①概念:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.②作法:③性质:④内心:补充:三角形的内心、外心、垂心、重心、旁心。
6.三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性.7.三角形的内角和定理:①内容:三角形的内角和为180°②证明:(掌握证明的过程即可)③应用:8.直角三角形:①概念:②性质:③判定:9.三角形的外角:①概念:②性质:10.三角形的外角和定理:①内容:②证明:(掌握证明的过程即可)③应用:11.多边形:①概念:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.②相关的名词:多边形的角(内角)、边、顶点。
12.多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.13.多边形的对角线:①概念:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.②条数公式:14.正多边形:①概念:在平面内,各个角都相等,各条边都相等的多边形叫正多边形.②性质:③判定:15.多边形内角和:①公式:n边形的内角和等于(2)n-·180°n-·180°。
即:W=(2)②推理过程:16.多边形的外角和:①内容:多边形的外角和为360°.②证明:(掌握证明的过程即可)。

第十一章三角形、知识框架:二、知识概念:1. 三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形2. 三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边3. 高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高•4•中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线5. 角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.6. 三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性.7. 多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形8. 多边形的内角:多边形相邻两边组成的角叫做它的内角9. 多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角10. 多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.11. 正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形12. 平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面,13. 公式与性质:⑴三角形的内角和:三角形的内角和为180 °⑵三角形外角的性质:性质1 :三角形的一个外角等于和它不相邻的两个内角的和性质2 :三角形的一个外角大于任何一个和它不相邻的内角⑶多边形内角和公式:n边形的内角和等于(n-2)• 180°⑷多边形的外角和:多边形的外角和为360° .⑸多边形对角线的条数:①从n边形的一个顶点出发可以引(n-3)条对角线,把多边形分成(n -2)个三角形.②n边形共有血勺条对角线.。

八年级数学上册知识点总结1第十一章 三角形知识点总结11.1 与三角形有关的线段 第1课时 三角形的边 1. 三角形的概念由不在同一条直线上的 相接所组成的图形叫做三角形。
2.三角形按边分类3. 三角形三边的关系(重点)三角形的 。
三角形的 。
用数学表达式表达就是:记三角形三边长分别是a ,b ,c ,则 或 。
已知三角形两边的长度分别为a ,b ,求第三边长度的范围:|a -b |<c <a +b 要求会的题型: ①数三角形的个数方法:分类,不要重复或者多余。
②给出三条线段的长度或者三条线段的比值,要求判断这三条线段能否组成三角形 方法:最小边+较小边>最大边 不用比较三遍,只需比较一遍即可 ③给出多条线段的长度,要求从中选择三条线段能够组成三角形方法:从所给线段的最大边入手,依次寻找较小边和最小边;直到找完为止,注意不要找重,也不要漏掉。
④已知三角形两边的长度分别为a ,b ,求第三边长度的范围 方法:第三边长度的范围:|a -b |<c <a +b⑤给出等腰三角形的两边长度,要求等腰三角形的底边和腰的长方法:因为不知道这两边哪条边是底边,哪条边是腰,所以要分类讨论,讨论完后要写“综上”,将上面讨论的结果做个总结。
第2课时 三角形的高、中线与角平分线 1. 三角形的高从△ABC 的顶点向它的对边BC 所在的直线 ,垂足为D ,那么线段AD 叫做△ABC 的边BC 上的高。
三角形的三条高的交于一点,这一点叫做 。
2. 三角形的中线连接△ABC 的顶点A 和它所对的对边BC 的 D ,所得的线段AD 叫做△ABC 的边BC 上的中线。
三角形三条中线的交于一点,这一点叫做 。
三角形的中线可以将三角形分为 的两个小三角形。
3. 三角形的角平分线∠A 的平分线与对边BC 交于点D ,那么线段AD 叫做三角形的角平分线。
要区分三角形的“角平分线”与“角的平分线”,其区别是:三角形的角平分线是条 ;角的平分线是条 。
初二数学第十一章全等三角形综合复习人教新课标版一、学习目标:1. 复习全等形与全等三角形的概念、全等三角形的判定定理,以及角平分线的作图方法和角平分线的性质等知识,建立知识系统;2. 使学生总结寻找全等三角形及其全等条件的方法、归纳常见辅助线的作法,使学生掌握分析问题的方法,提升解题能力。
二、重点、难点:重点:将所学知识科学地组织起来,将其纳入已有的知识结构中。
难点:提升分析问题、解决问题的能力。
三、考点分析:全等三角形是初中几何的重要内容,也是数学中最基础的知识,是研究平面几何的重要工具。
近几年的中考数学试题中,经常将全等与其他知识结合在一起,考查学生综合运用数学知识解决问题的能力,形式多种多样,为全等这一传统的话题增添了新颖的味道。
1. 全等三角形的概念及性质;2. 三角形全等的判定;3. 角平分线的性质及判定。
知识点一:证明三角形全等的思路通过对问题的分析,将解决的问题归结到证明某两个三角形的全等后,采用哪个全等判定定理加以证明,可以按下图思路进行分析:⎧→⎧⎪⎪→⎨⎪⎪⎪→⎩⎪⎪→→⎧⎪⎪→⎧⎪⎪⎨⎨⎪→⎨⎪⎪⎪⎪⎪→⎩⎩⎪⎪→⎧⎪⎨→⎪⎩⎪⎩SAS SSS HL AAS SAS ASA AAS ASA AAS 找夹角已知两边找第三边找直角边为角的对边找任一角找夹角的另一边已知一边一角边为角的邻边找夹边的另一角找边的对角找夹边已知两角找任一对边 切记:“有三个角对应相等”和“有两边及其中一边的对角对应相等”的两个三角形不一定全等。
例1. 如图,,,,A F E B 四点共线,AC CE ⊥,BD DF ⊥,AE BF =,AC BD =。
求证:ACF BDE ∆≅∆。
思路分析:从结论ACF BDE ∆≅∆入手,全等条件只有AC BD =;由A E B F =两边同时减去EF 得到AF BE =,又得到一个全等条件。
还缺少一个全等条件,可以是CF DE =,也可以是A B ∠=∠。
由条件AC CE ⊥,BD DF ⊥可得90ACE BDF ∠=∠=,再加上AE BF =,AC BD =,可以证明ACE BDF ∆≅∆,从而得到A B ∠=∠。
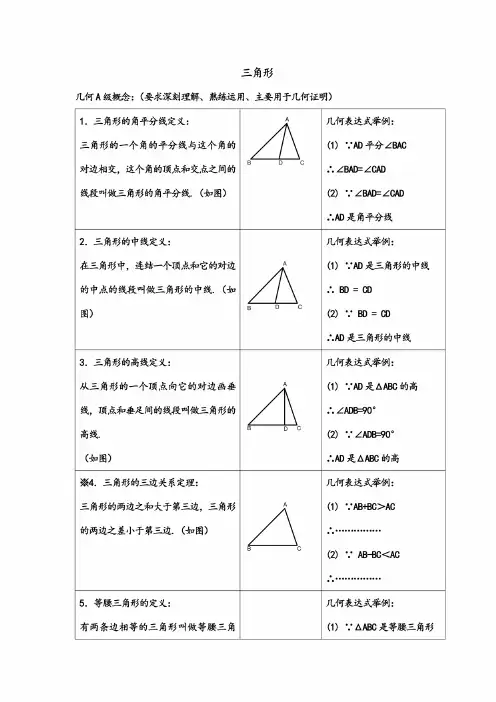
三角形几何A级概念:(要求深刻理解、熟练运用、主要用于几何■证明)1.三角形的角平分线定义:三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.(如图)A△B D C几何表达式举例:(1)河平分NBAC.•.ZBAD=ZCAD(2)VZBAD^ZCAD...AD是角平分线2.三角形的中线定义:在三角形中,连结一个顶点和它的对边的中点的线段叫做三角形的中线.(如图)AzA B D C几何表达式举例:(1)•.•AD是三角形的中线BD=CD⑵V BD=CD.•.AD是三角形的中线3.三角形的高线定义:从三角形的一个顶点向它的对边画垂线,顶点和垂足间的线段叫做三角形的高线.(如图)AA B D C几何表达式举例:(1)...AD是AABC的高ZADB^O0(2)•.NADB力0°AAD是△A BC的高^4.三角形的三边关系定理:三角形的两边之和大于第三边,三角形的两边之差小于第三边.(如图)AzA B C几何表达式举例:(1)VAB+eC>AC•••(2)V AB-BC<AC•••5.等腰三角形的定义:有两条边相等的三角形叫做等腰三角几何表达式举例:(1)•.•△ABC是等腰三角形形.(如图)AA AB=AC(2)VAB=ACB C.•.△ABC是等腰三角形6.等边三角形的定义:有三条边相等的三角形叫做等边三角形.(如图)A△几何表达式举例:(1)WABC是等边三角形.•.AB=BC=ACB C(2)•.•AB=BC=AC.•.△ABC是等边三角形7.三角形的内角和定理及推论:(1)三角形的内角和180°;(如图)⑵直角三角形的两个锐角互余;(如图)⑶三角形的一个外角等于和它不相邻的两个内角的和;(如图)浓⑷三角形的一个外角大于任何一个和它不相邻的内角.A A 几何表达式举例:(1)•:N A+N B+N 0=180°•••⑵V ZC=90°:.ZA+ZB=90°⑶V ZACD=ZA+ZBB c c B r-------c-----D(1)(2)(3)(4)••⑷ZACD>ZA••8.直角三角形的定义:有一个角是直角的三角形叫直角三角形.(如图)A[X几何表达式举例:(1)V ZC=90°.•.△ABC是直角三角形C B⑵•「△ABC是直角三角形A ZC=90°9.等腰直角三角形的定义:几何表达式举例:两条直角边相等的直角三角形叫等腰直角三角形.(如图)A(1)V ZC=90°CA=CB.•.△ABC是等腰直角三角形⑵V AABC是等腰直角三角形A ZC=90°CA=CB10.全等三角形的性质:(1)全等三角形的对应边相等;(如图)(2)全等三角形的对应角相等.(如图)A E二4R C f G 几何表达式举例:(1)VAABC^AEFGAB=EF.....⑵VAABC^AEFG .•.ZA=ZE.....11.全等三角形的判定:“SAS""ASA""AAS”"SSS""HL".(如图)A E△△B C f G(1)(2)A EK KC B G F(3)几何表达式举例:(1)V AB=EFV ZB=ZF又BC=FG.-.AABC^AEFG⑵.............⑶在Rt AABC和RtAEFG中V AB=EF又AC=EG.•.RtAABC^RtAEFG12.角平分线的性质定理及逆定理:(1)在角平分线上的点到角的两边距离相等;(如图)(2)到角的两边距离相等的点在角几何表达式举例:(1)V0C平分NA0B 又VCD±0A CE±0B CD=CE系:a2+b2=c2,那么这个三角形是直角三角形.(如图)19.Rt△斜边中线定理及逆定理:(1)直角三角形中,斜边上的中线是斜边的一半;(如图)⑵如果三角形一边上的中线是这边的一半,那么这个三角形是直角三角形.(如图)AkC B几何表达式举例:•.•△ABC是直角三角形•..D是AB的中点.•.CD=2AB(2)VCD=AD=BD.•.△ABC是直角三角形几何B级概念:(要求理解、会讲、会用,主要用于填空和选择题)一基本概念:三角形、不等边三角形、锐角三角形、钝角三角形、三角形的外角、全等三角形、角平分线的集合定义、原命题、逆命题、逆定理、尺规作图、辅助线、线段垂直平分线的集合定义、轴对称的定义、轴对称图形的定义、勾股数.二常识:1.三角形中,第三边长的判断:另两边之差V第三边V另两边之和.2.三角形中,有三条角平分线、三条中线、三条高线,它们都分别交于一点,其中前两个交点都在三角形内,而第三个交点可在三角形内,三角形上,三角形外.注意:三角形的角平分线、中线、高线都是线段.3.如图,三角形中,有一个重要的面积等式,即:若CD±AB,BE±CA,则CD«AB=BE-CA.4.三角形能否成立的条件是:最长边V另两边之和.X5.直角三角形能否成立的条件是:最长边的平方等于另两边的平方和.B C6.分别含30°、45°、60°的直角三角形是特殊的直角三角形.7.如图,双垂图形中,有两个重要的性质,即:a△C B(1)AC•CB=CD•AB;(2)Z1=ZB,N2=NA.8.三角形中,最多有一个内角是钝角,但最少有两个外角是钝角.9.全等三角形中,重合的点是对应顶点,对应顶点所对的角是对应角,对应角所对的边是对应边.10.等边三角形是特殊的等腰三角形.11.几何习题中,“文字叙述题"需要自己画图,写已知、求证、证明.12.符合“AAA”“SSA“条件的三角形不能判定全等.13.几何习题经常用四种方法进行分析:(1)分析综合法;(2)方程分析法;(3)代入分析法;(4)图形观察法.14.几何基本作图分为:(1)作线段等于已知线段;(2)作角等于已知角;(3)作已知角的平分线;(4)过已知点作已知直线的垂线;(5)作线段的中垂线;(6)过已知点作已知直线的平行线.15.会用尺规完成“SAS”、“ASA"、“AAS"、“SSS"、“HL”、“等腰三角形”、“等边三角形”、“等腰直角三角形"的作图.16.作图题在分析过程中,首先要画出草图并标出字母,然后确定先画什么,后画什么;注意:每步作图都应该是几何基本作图.17.几何画图的类型:(1)估画图;(2)工具画图;(3)尺规画图.湘8.几何重要图形和辅助线:(1)选取和作辅助线的原则:①构造特殊图形,使可用的定理增加;②一举多得;③聚合题目中的分散条件,转移线段,转移角;④作辅助线必须符合几何基本作图.(2)已知角平分线.(若BD是角平分线)①在BA 上截取BE=BC 构造全等,转移线段和角;AC角形.②过D 点作DE/7BC 交AB 于E,构造等腰三B (5)其它作等边三角形ABC 一边的平行线DE,构造新的等边三角形;②作CE/7AB,转移角;③延长BD 与AC 交于E, 不规则图形转化为规则图。
人教版八年级数学上册第11章三角形知识点总结复习第11章三角形知识点总结复习1、三角形的概念由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
组成三角形的线段叫做三角形的边;相邻两边的公共端点叫做三角形的顶点;相邻两边所组成的角叫做三角形的内角,简称三角形的角。
2、三角形中的主要线段(1)三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点间的线段叫做三角形的角平分线。
(2)在三角形中,连接一个顶点和它对边的中点的线段叫做三角形的中线。
(3)从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高)。
3、三角形的稳定性三角形的形状是固定的,三角形的这个性质叫做三角形的稳定性。
三角形的这个性质在生产生活中应用很广,需要稳定的东西一般都制成三角形的形状。
4、三角形的特性与表示三角形有下面三个特性:(1)三角形有三条线段(2)三条线段不在同一直线上三角形是封闭图形(3)首尾顺次相接三角形用符号“?”表示,顶点是A、B、C的三角形记作“?ABC”,读作“三角形ABC”。
5、三角形的分类三角形按边的关系分类如下:不等边三角形三角形底和腰不相等的等腰三角形等腰三角形等边三角形三角形按角的关系分类如下:直角三角形(有一个角为直角的三角形)三角形锐角三角形(三个角都是锐角的三角形)斜三角形钝角三角形(有一个角为钝角的三角形)把边和角联系在一起,我们又有一种特殊的三角形:等腰直角三角形。
它是两条直角边相等的直角三角形。
6、三角形的三边关系定理及推论(1)三角形三边关系定理:三角形的两边之和大于第三边。
推论:三角形的两边之差小于第三边。
(2)三角形三边关系定理及推论的作用:①判断三条已知线段能否组成三角形②当已知两边时,可确定第三边的范围。
③证明线段不等关系。
7、三角形的角关系三角形的内角和定理:三角形三个内角和等于180°。
推论:①直角三角形的两个锐角互余。
人教版八年级数学上册第十一章三角形知识点复习巩固一、思维导图二、知识点复习1. 三角形的三边关系:三角形的两边之和大于第三边,两边之差小于第三边.2. 三角形的分类3. 三角形的高、中线与角平分线高:顶点与对边垂足间的线段,三条高或其延长线相交于一点,如图 .中线:顶点与对边中点间的线段,三条中线相交于一点(重心),如图②.角平分线:三条角平分线相交于一点,如图③.4. 三角形的内角和与外角(1)三角形的内角和等于180°;(2)三角形的一个外角等于与它不相邻的两个内角的和;(3)三角形的一个外角大于和它不相邻的任何一个内角.5. 多边形及其内角和在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.正多边形的各个角都相等,各条边都相等的多边形.n 边形内角和等于(n -2)×180 °(n ≥3的整数)n 边形的外角和等于360°.正多边形的每个内角的度数是 正多边形的每个外角的度数是(2)180,n n -⨯︒360.n︒三、知识点巩固练习知识点1 三角形的三边关系1.下列长度的三条线段中,能组成三角形的是()A 4 cm,5 cm,9 cmB 8 cm,8 cm,15 cmC5 cm,5 cm,10 cm D 6 cm,7 cm,14 cm2.(泰州中考)已知三角形两边的长分别为1,5,第三边长为整数,则第三边的长为___________知识点2 三角形的重要线段3.如图,在△ABC中,∠C=90°,D,E为AC上的两点,且AE=DE,BD平分∠EBC,则下列说法不正确的是()A.BC是△ABE的高B.BE是△ABD的中线C.BD是△EBC的角平分线D.∠ABE=∠EBD=∠DBC4.如图,BD是△ABC的中线,AB=8,BC=6,△ABD和△BCD的周长的差是________.5.如图,△ABC的边BC上的高为AF,中线为AD,AC边上的高为BG,已知AF=6,BC=10,BG=5(1)求△ABC的面积;(2)求AC的长(3)说明△ABC和△ACD的面积关系知识点3 三角形的内角和与外角和6.如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD=()A.145B.150°C.155°D.1607.如图,在△ABC中,点D在BA的延长线上,DE∥BC.如果∠BAC=65°,∠C=30°,那么∠BDE的度数是_______.8.如图,在△ABC与△DBE中,AC∥DE,点B,C,E在同一直线上,AC,BD相交于点F.若∠BDE=85°,∠BAC=55°,∠ABD:∠DBE=3:4,求∠DBE的度数知识点4 多边形的内角和与外角和9.一个正多边形的边长为2,每个外角都为60°,则这个多边形的周长是()A.8B.12C.16D.1810.如图,小明将几块六边形纸片分别剪掉了一部分(虚线部分),得到了一个新多边形.若新多边形的内角和为540°,则对应的是下列图形()A. B. C. D.参考答案1.B2.53.D4.25.解:(1)S △ABC BC·AF=106=30.(2)AC=12(3)S △ABC =2S △ACD6.B7.958.解:∠DBE=409.B10.C。
人教版八年级数学上册知识点整理(完整版)第十一章三角形一、三角形的有关概念(一)三角形:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
(二)基本元素1、三个顶点:点A、点B、点C2、三个内角:∠A、∠B、∠C3、三条边(1)表示方法①线段AB、AC、BC②a(∠A所对的边BC用a表示)、b、c(2)三角形的三边关系(依据:两点之间线段最短)①三角形两边之和大于第三边,数学语言:a+b>c,a+c>b,b+c>a。
;②三角形两边之差小于第三边,数学语言:a−b<c,a−c<b,b−c<a。
③判断三条线段能否组成三角形,只需判断“两条较短的线段之和大于第三条”即可。
4、三角形的表示方法:顶点是A、B、C的三角形,记作∆ABC,读作“三角形ABC”。
(三)三角形的稳定性:三角形三条边的长度确定之后,三角形的形状就唯一确定了。
二、三角形的分类(一)按边分类1、三边都不相等的三角形2、等腰三角形(1)概念:有两条边相等的三角形叫做等腰三角形,其中相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
(2)等边三角形:三边都相等的三角形叫做等边三角形(特殊的等腰三角形)。
(二)按角分类1、锐角三角形:三个内角都是锐角。
2、直角三角形:有一个内角是直角的三角形。
3、钝角三角形:有一个内角是钝角的三角形。
三、与三角形有关的线段(一)三角形的高1、定义:从三角形的一个顶点向它所对的边所在直线画垂线,顶点和垂足之间的线段叫做三角形的这条边上的高。
从∠ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做∠ABC 的边BC上的高,记作AD∠BC于点D。
3、几何语言(1)AD是三角形的边BC上的高。
(2)AD⊥BC于点D。
4、三角形三条高的位置(1)锐角三角形:三条高及其交点都在三角形内部。
(2)直角三角形:有两条高与两条直角边重合,斜边上的高在三角形内部,三条高交于三角形的直角顶点。
初中数学(人教版)八年级上知识点最全总结第十一章全等三角形一.知识框架二.知识概念1. 全等三角形:两个三角形的形状、大小、都一样时,其中一个可以经过平移、旋转、对称等运动(或称变换)使之与另一个重合,这两个三角形称为全等三角形。
2 .全等三角形的性质:全等三角形的对应角相等、对应边相等。
3. 三角形全等的判定公理及推论有:(1 )“ 边角边” 简称“SAS”(2 )“ 角边角” 简称“ASA”(3 )“ 边边边” 简称“SSS”(4 )“ 角角边” 简称“AAS”(5 )斜边和直角边相等的两直角三角形(HL )。
4. 角平分线推论:角的内部到角的两边的距离相等的点在叫的平分线上。
5. 证明两三角形全等或利用它证明线段或角的相等的基本方法步骤:①、确定已知条件(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形、等所隐含的边角关系),②、回顾三角形判定,搞清我们还需要什么,③、正确地书写证明格式( 顺序和对应关系从已知推导出要证明的问题). 在学习三角形的全等时,教师应该从实际生活中的图形出发,引出全等图形进而引出全等三角形。
通过直观的理解和比较发现全等三角形的奥妙之处。
在经历三角形的角平分线、中线等探索中激发学生的集合思维,启发他们的灵感,使学生体会到集合的真正魅力。
第十二章轴对称一.知识框架二.知识概念1. 对称轴:如果一个图形沿某条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形;这条直线叫做对称轴。
2. 性质:(1 )轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线。
(2 )角平分线上的点到角两边距离相等。
(3 )线段垂直平分线上的任意一点到线段两个端点的距离相等。
(4 )与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
(5 )轴对称图形上对应线段相等、对应角相等。
3. 等腰三角形的性质:等腰三角形的两个底角相等,(等边对等角)4. 等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合,简称为“三线合一”。