广东省小学200米环形跑道(含直跑道)示意图
- 格式:doc
- 大小:1.16 MB
- 文档页数:1

第10讲环形跑道1.环形跑道——追及问题。
同时同地同向而行,甲、乙双方在同一环形跑道,以不同的速度,乙何时能够追上甲。
(甲的速度<乙的速度)等量关系:追上1次,甲所用时间=乙所用时间;甲的路程+1个环形跑道的长度=乙的路程。
追上n次,甲所用时间=乙所用时间;甲的路程+n个环形跑道的长度=乙的路程。
2.环形跑道——相遇问题。
同时同地相向而行,甲、乙双方在同一环形跑道,以一定的速度,甲、乙双方何时相遇。
(甲、乙速度可以相同,也可以不同)等量关系:相遇1次,甲所用时间=乙所用时间;甲的路程+乙的路程=1个环形跑道的长度。
相遇n次,甲所用时间=乙所用时间;甲的路程+乙的路程=n个环形跑道的长度。
3.经典公式。
路程=速度×时间同时同地出发:反向每相遇一次,合走一圈路程和=速度和×相遇时间同向每追上一次,多走一圈路程差=速度差×追及时间第一,环形跑道问题中,对速度、时间、路程之间关系的处理;第二,多次追及、相遇问题的处理;第三,不同地点出发问题的处理;第四,利用线段图加强对问题的理解。
例1.一个圆形跑道的周长是500米,两个学生同时同地背向而行,黄英每分钟走66米,欣欣每分钟走59米,经过几分钟才能相遇?考点:环形跑道相遇问题分析:此题属于环形跑道问题中的相遇问题,同时同地背向而行,也可以理解为她们二人在一条长为500米的线段两端,相向而行,用路程除以她们的速度之和就是所需要的时间。
解答:500÷(66+59)=4(秒)点评:考察环形跑道的相遇问题,关键是知道两个学生的时间是一致的例2.小张和小玉各以一定的速度,在周长为500米的环形跑道上跑步,小玉的速度是200米/分。
(1)小张和小玉同时同地出发,反向跑步,1分钟后两人第一次相遇,小张的速度是多少米/分?(2)小张和小玉同时同地出发,同一方向跑步,小张跑多少圈后才能再次遇上小玉?考点:环形跑道的多次相遇问题分析:(1)小张和小玉同时同地,反向跑步,用路程除以时间,就是他们二人的速度之和,再减去小玉的速度就是小张的速度。

运动场地划线 The manuscript was revised on the evening of 2021第一章400米环形塑胶跑道田径场4×100米接力赛的画法400米环形4×100米接力赛跑的起跑线和各接力区的位置与画法,400米环形4×100米接力赛跑全程分道跑进,所以各分道起跑线的位置和画法和400米赛跑的相同。
4×100米接力赛跑时,每条分道上要画三个接力区。
规则规定:每个接力区的长度为20米。
在各个接力区后10米处再画一条“预跑”线,表示接棒运动员可从这条线内起跑,但是传、接棒必须在20米的接力区内进行和完成。
各接力区位置的分布情况如下o第一接力区在第二分界线附近,第二接力区在第三分界线附近,第三接力区在第四分界线向后的地方。
从起跑线至第一接力区“预跑”线为80米,从第一接力区的“项跑”线至第一接力区后沿为10米;从第一接力区前沿至第二接力区“须跑”线为70米;从第二接力区“顶跑”线至第二接力区后沿为10米(第一道的第二接力区“预跑”线至第三分界线的距离为20米分界线至第二接力区前沿为10米),从第二接力区前沿至第三接力区“预跑”线的距离为70米,从第三接力区“预跑”线至第三接力区后沿为10米,至第四分界线的距离为34.04米;从第三接力区前沿至第四分界线距离为4.04米,至终点线90米。
?图28是标准400米环形(分道宽1.25米)上4×l00米接力赛跑各接力区的位置和有关距离的示意图。
上一页:下一页:4*100米接力起跑为400米起跑线,首先在跑道上计算出100米,200米,300米分道起跑线位置,在起跑线的前后各10米画出前后沿,在4*200米,4*400米接力为第一圈和第二圈的第一弯道末端抢道标志线前为完全分道跑。
在4*200米,4*400米接力起跑线为(400米起跑线+800米起跑线),在4*200米,接力第1接力区中线为(800米起跑线+200米起跑),接力区为前后各10米在4*200米第2接力区和4*400米第1接力区中线为800米起跑线,前后各10米为接力区,在4*200米第3接力区同4*100米第2接力区的第1道同。

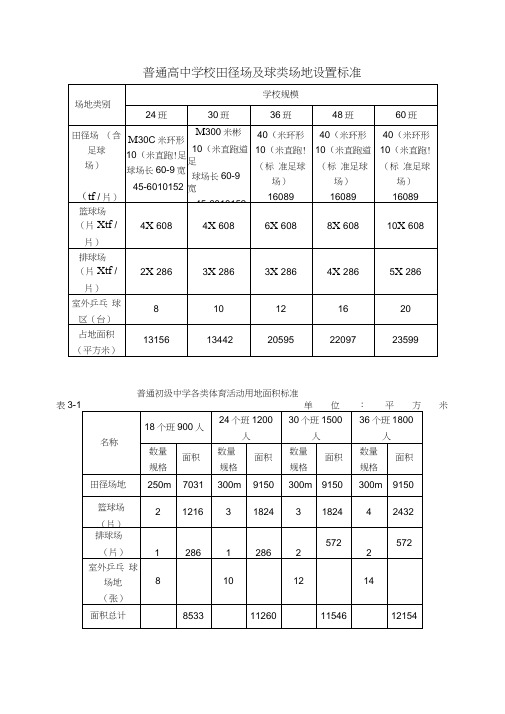
中小学运动场地基本
标准
-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
中小学运动场地基本标准
一、小学场地标准:
二、初中场地标准:
三、工作要求:
1、直跑道设置:300米以上的环形田径场应设置包括110米的直跑道;200米的环形田径场应至少设置60米的直跑道,条件允许的应有100米直跑道。
2、环形跑道设置:环形田径场跑道内应有至少6条分跑道,跑道的内外道沿必须是水泥道沿(严禁用砖代替),跑道地面应用白灰、炉渣、土进行搅拌,用压路机压制而成。
3、弧形场地设置:环形田径场两端的弧形场地内一端要设置一个沙坑(长5米、宽3米、助跑跑道长25-45米,也可在其它地方设置)沙坑需用砖砌,水泥粉制,另一端需设置一个标准的铅球场地。
4、不规则场地:环形田径场因受到地理环境限制达不到标准的,需因地制宜规划相应的不规则的环形田径场,但跑道的内外道沿、跑道内地面应按照以上要求执行。
5、篮球、排球场地:因受地理环境限制,不能另选地方设置的,可在环形田径场内设置,场地必须硬化,每个场地的间隔距离为3米以上,场地的线条要用白漆涂画清晰。
6、器械体操区:学校可根据场地条件在环形田径场地外的适当位置集中进行配备安置。
7、运动场围墙:需用水泥沙浆粉刷涂白,需在围墙上安排运动图标和标语。
8、绿化美化:运动场地其余未进行硬化的地面,要统一规划进行草坪绿化。
教育局体卫站
二〇一三年二月二十日。


广东省教育厅关于印发《广东省义务教育标准化学校标准》的通知粤教基〔2013〕17号各地级以上市人民政府,各县(市、区)人民政府,省政府各部门、各直属机构:经省人民政府同意,现将《广东省义务教育标准化学校标准》印发给你们,请认真贯彻执行。
附件: 广东省义务教育标准化学校标准广东省教育厅2013 年8月19日附件广东省义务教育标准化学校标准第一章总则第一条为规范我省义务教育学校办学行为,全面推进素质教育,促进义务教育均衡优质标准化发展,高水平、高质量普及九年义务教育,推进教育强省建设,根据《中华人民共和国义务教育法》和国家有关教育法律法规、标准,结合我省实际,制定本标准。
第二条本标准适用于我省义务教育普通中小学校,包括非完全小学、完全小学(含教学点)、初级中学和九年制学校。
义务教育阶段特殊教育学校标准另行规定。
—1—第二章办学条件第三条学校有独立的校园。
学校生均用地面积,小学(含九年制学校小学阶段,下同)不低于18 m2,初中(含九年制学2 2校中学阶段,下同)不低于23 m 。
市中心城区小学不低于9.4 m,2初中不低于10.1 m。
第四条学校布局、选址、规划设计、建筑标准等符合国家《中小学校设计规范》(GB 50099—2011)的要求,确保学生和教职工安全。
学校严禁建设在地震、地质塌裂、暗河、洪涝等自然灾害及人为风险高的地段和污染超标的地段。
校园及校内建筑与污染源的距离应符合对各类污染源实施控制的国家现行有关标准的规定。
高压电线、长输天然气管道、输油管道严禁穿越或跨越学校;当在学校周边敷设时,安全防护距离及防护措施应符合相关规定。
学校内不得有宗教活动场所。
学校周边环境应有利于学生的身心健康。
不得与市场、医院太平间、易燃易爆危险品仓库、加油站为邻。
校园周边200 米范围内不得有游戏机室、歌舞厅、桌球室、网吧等经营性场所。
教学区的环境噪声应符合《民用建筑隔声设计规范》(GB 50118—2010)的要求。
环形跑道问题教学目标1、掌握如下两个关系:(1)环形跑道问题同一地点出发,如果是相向而行,则每合走一圈相遇一次(2)环形跑道问题同一地点出发,如果是同向而行,则每追上一圈相遇一次2、遇见多人多次相遇、追及能够借助线段图进行分析3、用比例解、数论等知识解环形跑道问题知识精讲本讲中的行程问题是特殊场地行程问题之一。
是多人(一般至少两人)多次相遇或追及的过程解决多人多次相遇与追击问题的关键是看我们是否能够准确的对题目中所描述的每一个行程状态作出正确合理的线段图进行分析。
一、在做出线段图后,反复的在每一段路程上利用:路程和=相遇时间×速度和路程差=追及时间×速度差二、解环形跑道问题的一般方法:环形跑道问题,从同一地点出发,如果是相向而行,则每合走一圈相遇一次;如果是同向而行,则每追上一圈相遇一次.这个等量关系往往成为我们解决问题的关键。
环线型同一出发点直径两端同向:路程差nS nS+0.5S 相对(反向):路程和nS nS-0.5S模块一、常规的环形跑道问题【例 1】一个圆形操场跑道的周长是500米,两个学生同时同地背向而行.黄莺每分钟走66米,麻雀每分钟走59米.经过几分钟才能相遇?【巩固】周老师和王老师沿着学校的环形林荫道散步,王老师每分钟走55米,周老师每分钟走65米。
已知林荫道周长是480米,他们从同一地点同时背向而行。
在他们第10次相遇后,王老师再走米就回到出发点。
【例 2】上海小学有一长300米长的环形跑道,小亚和小胖同时从起跑线起跑,小亚每秒钟跑6米,小胖每秒钟跑4米,(1)小亚第一次追上小胖时两人各跑了多少米?(2)小亚第二次追上小胖两人各跑了多少圈?【巩固】小张和小王各以一定速度,在周长为500米的环形跑道上跑步.小王的速度是200米/分.⑴小张和小王同时从同一地点出发,反向跑步,1分钟后两人第一次相遇,小张的速度是多少米/分?⑵小张和小王同时从同一点出发,同一方向跑步,小张跑多少圈后才能第一次追上小王?【巩固】一条环形跑道长400米,甲骑自行车每分钟骑450米,乙跑步每分钟250米,两人同时从同地同向出发,经过多少分钟两人相遇?【巩固】小新和正南在操场上比赛跑步,小新每分钟跑250米,正南每分钟跑210米,一圈跑道长800米,他们同时从起跑点出发,那么小新第三次超过正南需要多少分钟?【巩固】幸福村小学有一条200米长的环形跑道,冬冬和晶晶同时从起跑线起跑,冬冬每秒钟跑6米,晶晶每秒钟跑4米,问冬冬第一次追上晶晶时两人各跑了多少米,第2次追上晶晶时两人各跑了多少圈?【巩固】小明和小刚清晨来到学校操场练习跑步,学校操场是400米的环形跑道,小刚对小明说:“咱们比比看谁跑的快”,于是两人同时同向起跑,结果10分钟后小明第一次从背后追上小刚,同学们一定知道谁跑得快了,小明的速度是每分钟跑140米,那么如果小明第3次从背后追上小刚时,小刚一共跑了米.【巩固】如图1,有一条长方形跑道,甲从A点出发,乙从C点同时出发,都按顺时针方向奔跑,甲每秒跑5米,乙每秒跑4.5米。
什么是环形跑道问题?环形跑道问题,从同一地点出发,如果是相向而行,则每合走一圈相遇一次;如果是同向而行,则每追上一圈相遇一次.这个等量关系往往成为我们解决问题的关键。
环形跑道问题的等量关系环形跑道:同相向而行的等量关系:乙程-甲程=跑道长,背向而行的等量关系:乙程+甲程=跑道长。
环形跑道问题的例题讲解经典环形跑道问题例题详解环形跑道问题乙两车同时从同一点出发,沿周长6千米的圆形跑道以相反的方向行驶.甲车每小时行驶65千米,乙车每小时行驶55千米.一旦两车迎面相遇,则乙车立刻调头;一旦甲车从后面追上乙车,则甲车立刻调头,那么两车出发后第11次相遇的地点距离点有多少米?(每一次甲车追上乙车也看作一次相遇)解析:第一次是一个相遇过程,相遇时间为:6÷(65+55)=0.05 小时,相遇地点距离A点:55×0.05=2.75千米.然后乙车调头,成为追及过程,追及时间为:6÷(65-55)=0.6 小时,乙车在此过程中走的路程为:55×0.6=33 千米,即5圈又3千米,那么这时距离A点3-2.75=0.25 千米.此时甲车调头,又成为相遇过程,同样方法可计算出相遇地点距离A点0.25+2.75=3千米,然后乙车掉头,成为追及过程,根据上面的计算,乙车又要走5圈又3千米,所以此时两车又重新回到了A点,并且行驶的方向与最开始相同.所以,每4次相遇为一个周期,而11÷4=2…3,所以第11次相遇的地点与第3次相遇的地点是相同的,与A点的距离是3000米.圆形跑道问题例题解析有一个圆形跑道周长是600米,甲在乙前面240米处, 两人同时沿顺时针方向跑.已知甲每分钟跑120米,乙每分钟跑100米,问几分钟后甲追上乙?如果追上后继续跑,问多少分钟后,甲第二次追上乙?240÷(120-100)=12600÷(120-100)=30根据这个算式可以套用类型公式。