初中数学九年级24.1.2垂径定理导学案(一)

人教版数学九年级上册《24.1.2垂直于弦的直径》教学设计1一. 教材分析《24.1.2垂直于弦的直径》是人教版数学九年级上册的一节重要内容。

本节内容主要介绍了垂径定理及其应用。

教材通过实例引导学生探究圆中垂直于弦的直径的性质，并运用这一性质解决一些实际问题。

本节内容既是前面所学知识的延续，也为后续学习圆的性质和圆的方程打下基础。

二. 学情分析九年级的学生已经学习了平面几何的基本知识，对图形的性质和变换有一定的了解。

但是，他们对圆的性质和应用的理解还不够深入。

因此，在教学过程中，教师需要从学生的实际出发，逐步引导学生理解和掌握垂径定理，并能够运用这一定理解决实际问题。

三. 教学目标1.让学生理解垂径定理的内容，并能够运用垂径定理解决一些实际问题。

2.培养学生的逻辑思维能力和解决问题的能力。

3.激发学生对数学的兴趣，提高他们的数学素养。

四. 教学重难点1.重难点：垂径定理的理解和运用。

2.难点：如何引导学生从实际问题中发现垂径定理的规律，并能够一般性地表述这一规律。

五. 教学方法1.采用问题驱动的教学方法，引导学生通过观察、思考、讨论、总结等方式发现和理解垂径定理。

2.运用多媒体辅助教学，通过动画演示和实例分析，帮助学生直观地理解垂径定理。

3.采用分组合作学习的方式，让学生在合作中发现问题、解决问题，培养他们的团队协作能力。

六. 教学准备1.准备相关的教学多媒体课件和教学素材。

2.准备一些实际问题，用于引导学生运用垂径定理解决实际问题。

3.准备一些练习题，用于巩固所学知识。

七. 教学过程1.导入（5分钟）通过一个实际问题，引导学生思考圆中垂直于弦的直径的性质。

例如，在一个圆形水池中，有一根绳子绕着水面漂浮，绳子的两端分别固定在圆形水池的两侧，求绳子的中点与水池中心的距离。

2.呈现（10分钟）通过多媒体展示垂径定理的证明过程，让学生直观地理解垂径定理。

同时，引导学生观察和思考垂径定理的适用范围和条件。

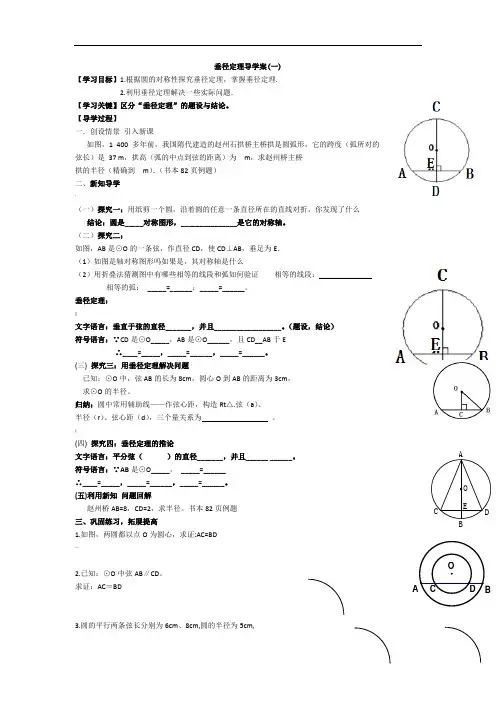
C BD O A 垂径定理导学案(一)【学习目标】1.根据圆的对称性探究垂径定理，掌握垂径定理.2.利用垂径定理解决一些实际问题．【学习关键】区分“垂径定理”的题设与结论。

【导学过程】一．创设情景 引入新课如图，1 400 多年前，我国隋代建造的赵州石拱桥主桥拱是圆弧形，它的跨度（弧所对的弦长）是 37 m ，拱高（弧的中点到弦的距离）为 m ，求赵州桥主桥拱的半径（精确到 m ）．（书本82页例题）二、新知导学'（一）探究一：用纸剪一个圆，沿着圆的任意一条直径所在的直线对折，你发现了什么 结论：圆是_____对称图形，_______________是它的对称轴。

（二）探究二：如图，AB 是⊙O 的一条弦，作直径CD ，使CD ⊥AB ，垂足为E ．（1）如图是轴对称图形吗如果是，其对称轴是什么（2）用折叠法猜测图中有哪些相等的线段和弧如何验证 相等的线段：______________ 相等的弧： _____=______；_____=______。

垂径定理：|文字语言：垂直于弦的直径_______，并且__________________。

（题设，结论）符号语言：∵CD 是⊙O_____，AB 是⊙O______，且CD__AB 于E∴____=_____，_____=______，_____=______。

(三) 探究三：用垂径定理解决问题已知：⊙O 中，弦AB 的长为8cm ，圆心O 到AB 的距离为3cm ，求⊙O 的半径。

归纳：圆中常用辅助线——作弦心距，构造Rt △.弦（a ）、半径（r ）、弦心距（d ），三个量关系为 。

|(四) 探究四：垂径定理的推论文字语言：平分弦（ ）的直径_______，并且______ ______。

符号语言：∵AB 是⊙O_____， _____=______∴____=_____，_____=______，_____=______。

(五)利用新知 问题回解赵州桥AB=8，CD=2，求半径。

人教版数学九年级上册24.1.2《垂径定理》教学设计2一. 教材分析《垂径定理》是人教版数学九年级上册第24章第1节的内容，本节课主要介绍圆中的垂径定理。

垂径定理是指：圆中，如果一条直线垂直于直径，那么这条直线平分这条直径，并且平分直径所对的圆周角。

教材通过生活中的实例引入垂径定理的概念，然后通过证明和应用来巩固这个定理。

二. 学情分析学生在学习本节课之前，已经掌握了圆的基本概念和性质，如圆的周长、直径、半径等。

同时，学生也掌握了平行线和相交线的性质。

但是，学生对于圆中的垂径定理可能比较难以理解和证明，因此需要通过生活中的实例和图形的直观展示，帮助学生理解和掌握这个定理。

三. 教学目标1.知识与技能：让学生理解和掌握圆中的垂径定理，能够运用垂径定理解决相关问题。

2.过程与方法：通过观察、操作、证明等过程，培养学生的几何思维和解决问题的能力。

3.情感态度与价值观：激发学生对数学的兴趣，培养学生的团队合作意识。

四. 教学重难点1.教学重点：理解和掌握垂径定理，能够运用垂径定理解决相关问题。

2.教学难点：垂径定理的证明和运用。

五. 教学方法1.情境教学法：通过生活中的实例引入垂径定理，激发学生的学习兴趣。

2.演示法：通过图形的直观展示，帮助学生理解和证明垂径定理。

3.问题驱动法：通过提出问题和解决问题，引导学生主动探索和学习。

4.小组合作学习：鼓励学生分组讨论和合作，培养学生的团队合作意识。

六. 教学准备1.教具准备：多媒体教学设备、圆规、直尺、黑板等。

2.教学素材：教材、课件、练习题等。

七. 教学过程1.导入（5分钟）通过展示生活中的实例，如自行车轮子、时钟等，引导学生观察和思考圆中的垂径定理。

让学生感受到数学与生活的紧密联系，激发学生的学习兴趣。

2.呈现（10分钟）展示垂径定理的定义和性质，通过图形的直观展示，让学生理解和掌握垂径定理。

同时，引导学生思考如何证明这个定理。

3.操练（10分钟）让学生分组讨论和合作，尝试证明垂径定理。

《24.1.2垂直于弦的直径》导学案课题垂直于弦的直径数学年级九年级上册知识目标1.掌握垂径定理及其推导过程。

2. 利用垂径定理解决圆的一般问题。

重点难点重点：垂径定理及其运用难点：垂径定理及其运用教学过程知识链接什么是轴对称图形？我们学过哪些轴对称图形？圆也是轴对称图形吗？怎样验证一个图形是轴对称图形，是否圆也具有轴对称的性质呢？今天这节课我们一起来探索相关知识，板书课题。

合作探究活动一、拿出一张圆形纸片，沿着圆的任意一条直径对折，重复做几次，你发现了什么？结论：圆是轴对称图形。

有无数条对称轴，任何一条直径所在的直线都是它的对称轴．活动二、如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．你能发现图中有那些相等的线段和弧？为什么？结论：AE=BE,即直径CD平分弦AB,并且平分弧AB、弧ADB,即=,=.试一试证明你的发现！已知：在⊙O中，CD是直径，AB是弦CD⊥AB，垂足为E．求证：AE＝BE，证明：连结OA、OB，则OA＝OB．∵垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴又是⊙O的对称轴．∴当把圆沿着直径CD折叠时，CD两侧的两个半圆重合，A点和B点重合，AE和BE重合，、分别和、重合．∴AE＝BE，你能用文字语言、符号语言归纳出上述结论吗？（1）垂径定理：（2）符号语言：∵AB是⊙O的又∵CDAB⊥∴DECE= = ； =_________我们把这个定理分成几个结论分别有：①CD是直径、AB是弦，②CD⊥AB③AE＝BE④=⑤我们知道①②可以推出结论③④⑤，那么如果交换符号结论是否有更多的结论成立？试一试：例如：①直径过圆心③平分弦推出②垂直于弦④平分弦所对优弧⑤平分弦所对的劣弧证明这个结论。

（这个证明方法类似上面的证法，教师点评）形成推论1：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．为什么强调这里的弦不是直径？一个圆的任意两条直径总是互相平分，但它们不一定互相垂直．因此这里的弦如果是直径，结论不一定成立．类比推论1你可以写出相应的命题吗?相信自己是最棒的!小组之间讨论，最后教师归纳总结：垂径定理及推论小结：垂径定理的几个基本图形，教师展示ppt，垂径定理中出现的常见三角形，用于计算：在a，d，r，h中，已知其中任意两个量，可以求出其它两个量．例、我是赵州桥，我历史悠久，是世界上现存最早、保存最好的巨大石拱桥。

24.1.2垂直于弦的直径（1） 班级： 姓名：学习目标：1.通过画图和观察，发现垂径定理，了解垂径定理的证明方法，会简单运用垂径定理.2.培养合情推理能力，发展空间观念.学习重点和难点：1. 重点：垂径定理。

2．难点：垂径定理的证明。

一、自主学习1.:垂径定理：垂直于弦的直径平分 ，平分这条弦所对的几何语言：∵AB 为⊙O 的直径 ，AB ⊥CD∴DP= , =⋂　DB ，=⋂　DA （垂径定理）二、巩固训练1．下列说法正确的是( )A ．垂直于弦的直线平分弦所对的两条弧B ．平分弦的直径垂直于弦C ．垂直于直径的直线平分这条直径D ．弦的垂直平分线经过圆心 2．如图，AB 是⊙O 的直径，CD 为弦，CD ⊥AB 于点E ，则下列结论中不成立是( )A.AC ︵＝AD ︵B.BC ︵＝BD ︵C ．OE ＝BED ．CE ＝DE3. 如图，AB 是⊙O 的直径，AB ⊥CD ，则CE= ，⋂AC = .（第3题） （第4题） （第5题）4.如图，OC ⊥AB 于点C ，AC=3，则BC= ，AB= .5.如图，在⊙O 中，半径r ＝10，弦AB ＝12，M 是弦AB 上的动点，则线段OM 长的最小值是( )A ．10B ．16C ．6D ．86.一辆装满货物，宽为2.4米的卡车，欲通过如图所示的隧道，则卡车的外形高必须低于( )A ．4.1米B ．4.0米C ．3.9米D ．3.8米7.在⊙O 中，弦AB 的长为16cm ，圆的半径是10cm ，求圆心O 到AB 的距离。

解：连接AO ，作OE ⊥AB 于E∵OE 经过⊙O 的圆心，OE ⊥AB ∴AE= = cm （ ）在Rt △AOE 中，∵OE 2= （ ）∴OE= = 答：OE 的长为ABCO.8.证明：重直于弦的直径平分弦.已知：如图，CD 是⊙O 的直径，CD ⊥AB. 求证：AE=BE.证明：连结OA ，OB.9. 如图，已知在⊙O 中，（1）弦AB 的长为8厘米，圆心O 到AB 的距离为3厘米，求⊙O 的半径（2）弦AB 的长为6厘米，⊙O 的半径为5厘米，求圆心O 到AB 的距离（3）⊙O 的半径为10厘米，圆心O 到AB 的距离为6厘米，求弦AB 的长拓展延伸：好山好水好绍兴，石拱桥在绍兴处处可见，小明要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥，现测得桥下水面AB 宽度16 m 时，拱顶高出水平面4 m ，货船宽12 m ，船舱顶部为矩形并高出水面3 m.(1)请你帮助小明求此圆弧形拱桥的半径．(2)小明在解决这个问题时遇到困难，请你判断一下，此货船能顺利通过这座拱桥吗？说说你的理由．E ADC BO.。

人教版数学九年级上册24.1.2《垂径定理》说课稿1一. 教材分析《垂径定理》是人教版数学九年级上册第24章圆的一部分，它是圆的性质中的重要定理之一。

本节课的主要内容是引导学生探究并证明圆中垂径定理，即圆中垂直于弦的直径平分弦，并且平分弦所对的弧。

这个定理在解决圆的相关问题时具有重要作用，为学生进一步学习圆的性质和圆的方程打下基础。

二. 学情分析九年级的学生已经学习了平面几何的基本知识，对图形的性质和证明有一定的理解。

他们对圆的概念和性质有一定的了解，但可能对垂径定理的理解还不够深入。

在学习本节课时，学生需要通过观察、思考、探究、证明等过程，理解和掌握垂径定理。

三. 说教学目标1.知识与技能目标：学生能够理解垂径定理的内容，并能够运用垂径定理解决相关问题。

2.过程与方法目标：学生通过观察、思考、探究、证明等过程，培养逻辑思维能力和解决问题的能力。

3.情感态度与价值观目标：学生通过对垂径定理的学习，增强对数学的兴趣和自信心，培养坚持不懈、严谨治学的态度。

四. 说教学重难点1.教学重点：学生能够理解并掌握垂径定理的内容。

2.教学难点：学生能够通过证明过程，理解并掌握垂径定理的证明方法。

五. 说教学方法与手段1.教学方法：采用问题驱动的教学方法，引导学生观察、思考、探究、证明。

2.教学手段：利用多媒体演示和实物模型，帮助学生直观地理解垂径定理。

六. 说教学过程1.导入：通过展示一些与圆相关的实际问题，引发学生对圆的性质的思考，激发学生的学习兴趣。

2.新课引入：介绍垂径定理的概念，引导学生观察和思考垂径定理的性质。

3.探究与证明：学生分组进行探究，通过观察、实验、推理等方法，引导学生自己发现并证明垂径定理。

4.讲解与解释：教师对学生的探究结果进行讲解和解释，帮助学生理解和掌握垂径定理。

5.练习与巩固：学生进行一些相关的练习题，巩固对垂径定理的理解和运用。

6.总结与拓展：学生总结垂径定理的内容和证明方法，并进行一些拓展问题的讨论。

24.1.2 垂径定理（1）教学目标：1、使学生通过观看实验明白得圆的轴对称性；2、把握垂径定理，明白得垂径定理的推证进程；重点：明白得圆的轴对称性难点：垂径定理的推证进程教学进程一、知识频道（交流与发觉）1创设情境观看赵州桥及所给数据，你能求出赵州桥拱的半径吗？这需要用到一个重要的定理：垂径定理2想一想1）若是一个图形沿着一条直线折叠，直线的两旁的部份能够相互重合，那么那个图形叫做________；这条直线叫做________．2）等腰三角形是轴对称图形吗？答：3 试一试用纸剪一个圆，沿着圆的任意一条直径对折，重复做几回，你发觉了什么？答：4 悟一悟：“圆”是不是轴对称图形？它的对称轴是什么？答：例已知：在⊙O中，CD是直径，AB是弦，CD⊥AB，垂足为E．求证：AE=EB，= ，=C O A B M N 证明：连结OA ，OB ，那么OA=OB ．又CD ⊥AB ，∴直线CD 是等腰△OAB 的对称轴，又是 ⊙O 的对称轴．因此沿着直径CD 折叠时，CD 双侧的两个半圆重合，A 点和B 点重合，AE 和BE 重合，、 别离和 、 重合． 因此， 从而取得圆的一条重要性质．5总一总：垂径定理垂直于弦的直径平分这条 ，而且平分弦所对的两条 。

反过来取得推论：平分弦（不是直径）的直径垂直于 ，而且平分弦所对的 。

二 、 方式频道1、以下命题错误的选项是（ ）A 垂直于弦的直径平分这条弦B 弦的中垂线必通过圆心C 平分弧的直径平分这条弧所对的弦D 平分弦的直径平分这条弦所对的弧二、如图，在⊙O 中（填写你以为正确的结论）①假设MN ⊥AB ，垂足为C ，MN 为直径，那么 , ,②假设AC ＝BC,MN 为直径,A B 不是直经，那么 ， ，．三、利用垂径定明白得决问题 例1：如图7-10，已知在⊙O 中，弦AB 的长为8cm ，圆心O 到AB 的距离为3cm.求⊙O 的半径分析：要求⊙O 的半径，连结OA ，只要求出OA 的长就能够够了，因为已知条件点O 到AB 的距离为3cm ，因此作OE ⊥AB 于E ，由 定理解：连结OA ，作OE ⊥AB ，垂足为E∵OE⊥AB，∴（）．∵AB=8cm，∴AE=又∵OE=3cm，在Rt△AOE中,OA=因此⊙O的半径为．。

垂直于弦的直径一、课题引入：问题 ：你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为 m, 拱高(弧的中点到弦的距离)为，你能求出赵洲桥主桥拱的半径吗？二、学习内容：1. 不借助任何工具，你能找到圆形纸片的圆心吗?2.结合图形，说说你寻找圆形纸片的圆心的依据？3.合作探索活动：（1）如图，CD 是⊙O 的弦，画直径AB ⊥CD ，垂足为P ，将圆形纸片沿AB 对折．（2）你发现了什么？①如图，它是轴对称图形吗？如果是，它的对称轴是什么？②你能发现图中有哪些相等的线段和弧？为什么？③从而你能得到哪些结论？4．得出垂径定理5．注意：①条件中的“弦”可以是直径；②结论中的“平分弧”指平分弦所对的劣弧、优弧．6．给出几何语言．7. 求出赵洲桥主桥拱的半径． D C OA B8.典型例题：例1． 如图，以O 为圆心的两个同心圆中，大圆的弦AB 交小圆于点C 、D ，AC 与BD 相等吗？为什么？例2．如图，已知：在⊙O 中，弦AB 的长为8，圆心O 到AB 的距离为3．⑴求的半径；⑵若点P 是AB 上的一动点，试求OP 的范围．三、知识梳理1．圆是图形，是它的对称轴．2．垂径定理及其推论以及它们的应用．①垂径定理：②垂径定理的推论： 3. 注意：事实上据垂径定理与推论可知：对于一个圆和一条直线来说，如果具备：①②③④⑤那么，由五个条件中的任何两个条件都可以推出其他三个结论．4．解决有关弦的问题，经常是过圆心作弦的垂线，或连接圆心和弦的中点，连结OA BP半径等辅助线，为应用垂径定理和勾股定理创造条件．四、达标检测如图，∠C=90°，⊙C与AB相交于点D，AC=5，CB=12，求AD的长．。

永宁中学九年级数学（上）导学案备课组长：教研组长：教科室：课题垂径定理第 1 课时共3 课时设计人唐伟文学习目标：1、探究垂径定理及推论； 2、会用符号语言描述垂径定理。

学习重点：探究垂径定理及推论、学习过程：一、知识点回顾（知识准备）：圆的对称性：二、探究新知：如图：AB是圆形纸片的一条弦，作直径CD，使CD⊥AB，垂足为E。

沿CD对折纸片，发现：①这个图形是对称图形吗②图中有哪些相等的线段和弧请说明理由。

③你能用一句话概括这些结论吗垂直于弦的直径______________________________(垂径定理)④你能用符号语言表达这个结论吗符号语言：∵CD为⊙O的直径，且CD⊥AB于E∴_____________，__________________，________________⑤由对折以上纸片我们还进一步发现：平分弦（不是直径）的直径__________于弦，并_________弦所对的两条弧(垂径定理推论)符号语言：∵CD为⊙O的直径，且AE = BE∴_____________，__________________，_______________三、教师引导：垂径定理的题设和结论关系较复杂，从以上探究我们可进一步将其并归结为：一条直线（1）过圆心；（2）垂直于弦；（3）平分弦；（4）平分弦所对的优弧；（5）平分弦所对的劣弧。

垂径定理就是满足条件（1）、（2）而推出其他结论；推论是满足条件（1）、（3）而推出其他结论。

四、归纳小结：梳理本节所学知识点五、检测与反馈：1、判断下列图形，是否能使用垂径定理(a)AB⊥CD于E (b)E是AB中点 (c)OC⊥AB于E (d)OE⊥AB于E2、如图，AB为⊙O的直径，且AB⊥CD于E。

请用符号语言描述垂径定理及其推论。

A OBCDEO BA CEODCBAEODCBAEOBA E1。

24.1.2 垂直于弦的直径（垂径定理第一课时）【学习目标】1.根据圆的对称性探究垂径定理，掌握垂径定理.2.利用垂径定理解决一些实际问题．【导学过程】一．自主学习（一）回顾复习：（独立完成下列各题）1.如图：AB是⊙O______；CD是⊙O______；⊙O中优弧有__________；劣弧有__________。

2.在___圆或____圆中，能够____________叫等弧。

（二）自主探究（一）自主探究一：用纸剪一个圆，沿着圆的任意一条直径所在的直线对折，你发现了什么？结论：圆是_____对称图形，_______________是它的对称轴。

（二）自主探究二：如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为M．（1）如图是轴对称图形吗？如果是，其对称轴是什么？（2）你能发现图中有哪些相等的线段和弧？为什么？相等的线段：______________相等的弧： _____=______；_____=______。

二、合作交流（一）你还能用其他的方法给出证明吗？垂径定理：文字叙述是：垂直于弦的直径_______，并且__________________。

符号语言：∵CD是⊙O_____，AB是⊙O______，且CD__AB于M∴____=_____，_____=______，_____=______。

(二)合作探究二：用垂径定理解决问题已知：⊙O的直径为10cm，圆心O到AB的距离为3cm，求：弦AB的长。

归纳：圆中常用辅助线——作弦心距（圆心到弦的距离），构造Rt△.弦（a）半径（r）弦心距（d），三个量关系为。

简“半径半弦弦心距”。

（三）巩固练习1．已知：AB为⊙O的直径，弦CD⊥AB，垂足为E，则BC =____，AC =____ ；CE=______2.已知：AB为⊙O的弦，AB=24cm, 圆心O到AB的距离为5cm, 求⊙O的直径3.已知：⊙O的直径AB=20cm，∠B=30°,求：弦BC的长三、展示提升：（1）如图，两圆都以点O为圆心，求证:AC=BD（2）圆中有两条互相平行的弦长分别为6cm、8cm,圆的半径为5cm, 求平行两弦之间的距离四、盘点收获OBCA。

班级： 姓名:编号： 课题24.1.2垂直于弦的直径 课型新授 主备 审核 目标导航 1.理解圆的轴对称性，掌握垂径定理； 2.学会运用垂径定理解决一些有关证明、计算问题；3.了解弓形高、弦心距等概念.【温故知新】1.轴对称图形,轴对称图形的性质。

2.勾股定理求线段长；3.弦、直径、等弧的概念。

【自主学习】活动1:剪一个圆形纸片，沿着它的任意一条直径对折，重复做几次，你发现了什么？由此你得出什么结论？【合作探究】活动2:请继续利用手中的圆形纸片，画一画:(1) 在圆上任意画一条弦AB ；(2) 过圆心O 作弦AB 的垂线，垂足为E.交⊙O 于C ，D 两点。

观察思考：图中有哪些相等关系？如何证明你的猜想？相等的线段： ；相等的弧： .【初步应用】例1：如图(1)，弦AB 的长为8cm ，圆心O 到AB 的距离为3cm.则⊙O 的半径为 cm 。

变式1：如图，已知⊙O 的半径是5cm,弦AB=8 cm ， 则圆心O 到AB 的距离是 cm 。

变式2： 已知⊙O 的半径是5cm ，圆心到弦的距离是3 cm ，则弦AB 的长为 cm 。

变式3：如图(2)，OD ⊥AB 于点E,与⊙O 交于点D,已知AB=8,DE=2，圆是 图形， 是圆的对称轴. 垂径定理：图1 图2则⊙O的半径是。

【方法归纳】例2：如图3，赵州桥是我国隋代建造的石拱桥，距今约有1400年的历史，是我国古代人民勤劳和智慧的结晶.它的主桥拱是圆弧形，它的跨度（弧所对的弦长）为37m，拱高（弧的中点到弦的距离）为7.23m，求赵州桥主桥拱的半径（结果保留小数点后一位）.【能力提升】1、如图，在半径为13的⊙O中，OC垂直弦AB于点D，交⊙O于点C，AB=24，则CD的长是_____．2、如图，点A，B是⊙O上两点，AB=10，点P是⊙O上的动点（P与A，B不重合），连接AP，PB，过点O分别作OE⊥AP于E，OF⊥PB于F，则EF=_____ 。

24.1.2垂直于弦的直径学习目标：理解圆的轴对称性；掌握垂径定理及其推论；学会运用垂径定理及其推论解决一些有关证明、计算。

自主学习： 1.回顾：（1）圆的集合定义；（2）连结圆上任意两点的线段叫圆的______，圆上两点间的部分叫做_______，在同圆或等圆中，能够互相重合的弧叫做。

2．阅读教材82页有关“赵州桥”问题，思考能用学习过的知识解决吗？ 3. 阅读教材81页“探究”内容，自己动手操作： 按下面的步骤做一做：（如图1）第一步，在一张纸上任意画一个⊙O ，沿圆周将圆剪下，作⊙O 的一条弦AB ；第二步，作直径CD,使CD ⊥AB ，垂足为E ； 第三步，将⊙O 沿着直径折叠. 你发现了什么？ 归纳：（1）图1是对称图形，对称轴是.（2）相等的线段有，相等的弧有. 合作探究：探究一：用纸剪一个圆形纸片，沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得到什么结论？结论：圆是____________，任何一条是圆的对称轴。

探究二：已知：如图1，在⊙O 中，CD 为直径，AB 为弦，且CD ⊥AB 垂足为E ，求证：AE=BE ，=，=结论（垂径定理）。

符号语言： ∵，， ∴，，探究三：如图2，⊙O 中，AB 是弦，CD 是直径，AB ，CD 交于点E ，且AE=BE. （1）CD ⊥AB 吗？为什么？（2）还有其他结论成立吗？（3）如图3，若弦AB 过圆心O ，上述结论还成立吗？推论：平分弦（）的直径垂直于弦， 并且 符号语言∵，∴，，综合：对于一个圆和一条直线来说，如果一条直线具备①经过圆心，②垂直于弦，③平分弦（不是直径），④平分弦所对的优弧，⑤平分弦所对的劣弧，五个条件中的任何两个，那么也就具备了其他三个。

AC BCAD BD图1C DD 图2 图3例1 辨析题：下列各图，能否得到AE=BE 的结论？为什么？例2 （1）已知：如图4，在⊙O 中，弦AB=8，O 到AB 的距离等于3，则⊙O 的半径为； （2）已知：如图4，若半径OA=10，弦心距OE=6，则弦AB 的长为；（3）已知：如图5，若弦AB=8cm ，直径CD ⊥AB 于E ，DE=2cm ，则⊙O 的半径为例3（1）已知，如图6，若以O 为圆心作一个⊙O 的同心圆，交大圆的弦AB 于C ，D 两点，求证：AC=BD（2）已知，如图7，⊙O 的两条弦AB ∥CD，求证:=例4 教材例题怎样求赵州桥主桥拱半径？(1) （2） （3） （4） （5）AC BD 图4图5 图7（1）辅助线的常用作法：连半径，过圆心向弦作垂线段。

九年级（上）数学导学案24.1.2 垂直与弦的直径导学目标：知识技能：探索圆的对称性，进而得到垂直于弦的直径所具有的性质。

数学思考:体会在圆的问题中半径是第一重要元素。

解决问题:能够利用垂直于弦的直径的性质解决相关实际问题。

情感态度:发现生活中圆的美，激发学生学习的兴趣，让学生体验到圆来源于生活并为生活服务．导学重难点：1. 重点：垂直于弦的直径所具有的性质以及证明。

2. 难点：利用垂直于弦的直径的性质解决实际问题。

导学过程：一、创设情境，引入新知你知道赵州桥吗？它是1300多年前我国隋代建造的石拱桥，它的主桥拱是圆弧形，它的跨度为37.4m，拱高7.2m,你能求出赵州桥主桥拱的半径吗？二、自主学习，探究新知阅读课本Ｐ80---P81思考下列问题：1.通过对折圆，圆是轴对称图形吗？如果是，它的对称轴是什么？你能找到多少条对称轴？2.教材80页思考？从图中找到哪些相等的线段和弧？为什么？3.由垂径垂直弦可以得到什么结论？（垂径定理）4.由直径平分弦又得到了什么推论？三、合作交流，感悟新知四、反思建构,融汇新知垂径定理：垂直于弦的直径弦，并且平分垂径定理推论：平分弦（不是直径）的直径于弦，并且五、当堂检测，巩固新知一、教材P82练习二、选择1．如图1，如果AB为⊙O的直径，弦CD⊥AB，垂足为E，那么下列结论中，•错误的是（）．A．CE=DE B．BC = BD C．∠BAC=∠BAD D．AC>AD(图1) (图2) (图3) （图4）2．如图2，⊙O的直径为10，圆心O到弦AB的距离OM的长为3，则弦AB的长是（）A．4 B．6C．7 D．83．如图3，已知⊙O的半径为5mm，弦AB=8mm，则圆心O到AB的距离是（）A．1mm B．2mmm C．3mm D．4mm4．如图4，OE⊥AB、OF⊥CD，如果OE=OF，那么_______（只需写一个正确的结论）三、填空1．P为⊙O内一点，OP=3cm，⊙O半径为5cm，则经过P点的最短弦长为________；•最长弦长为_______．2.如图，以O为圆心的两个同心圆中，小圆的弦AB的延长线交大圆于点C，若AB=3，BC=1，则圆环的面积最接近的整数是.。

新人教版义务教育教科书九年级上册24.1.2《垂直于弦的直径》导学案一、学习目标:1、理解圆的轴对称性，掌握垂径定理及其推论。

2、学会运用垂径定理及其推论解决计算，证明和作图问题。

二、预习内容（自学课本81页至83页）复习：1、什么叫做轴对称图形？把一个平面图形沿一条直线______，直线两旁的部分能够互相_________，这个图形就叫做轴对称图形。

圆是轴对称图形吗？对称轴是什么？2、什么叫等弧？在同圆或等圆中，能够互相______的弧叫做等弧。

三、探究学习活动一：自主探究把一个圆沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得到什么结论？结论：圆是___________图形，_________________________是它的对称轴．活动二：小组合作交流（要求：小组每个成员积极发言，记录员填写，每组派一名同学汇报）1、做一做：在⊙O上作的一条弦AB，做直径CD，使CD⊥AB，垂足为E．（1）这个图形是轴对称图形吗？如果是，它的对称轴是什么？答：_______________________________________________________（2）你能发现图中有那些相等的线段和弧？为什么？答：相等的线段：______=_____相等的弧：______=______________=________证明：（方法1）如图，连接OA、OB ，则OA=OB在Rt△OAE和Rt△OBE中，（方法2）：连接OA、OB ，则OA=___∴△OAB是______三角形∴Rt△OAE≌Rt△OBE（）又AB CD∴AE= ∴AE =____(等腰三角形“三线合一”) ∴点和点关于CD对称∵⊙O关于CD对称∴当圆沿着直线CD对折时，点A与点B重合,弧AC与BC重合，AD与CD重合．∴，，2、进一步，我们还可以得到垂径定理推论：四、巩固测评1、2、3题（看课件直接说出答案）4、如图，在⊙O 中，弦AB 的长为8cm ，圆心O 到AB 的距离为3cm ，求⊙O 的半径．5、如图，CD 是⊙O 的直径，弦AB ⊥CD 于E ，CE=1，AB=10，求半径的长6、赵州桥的桥拱是圆弧形，它的跨度（弧所对的弦的长）为37.4m ，拱高（弧的中点到弦的距离）为7.2m ，你能求出赵州桥的主桥拱的半径吗？五、学习心得 _ _____________________________________________________________________________． · OAB EC DO。