当前位置：文档之家 › 生活中的圆周运动l—火车转弯

生活中的圆周运动l—火车转弯

  • 格式：ppt
  • 大小：724.50 KB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

《生活中的圆周运动》 圆盘 圆锥 火车转弯 拱形桥

《生活中的圆周运动》 圆盘 圆锥 火车转弯 拱形桥
第五章第7节 第五章第 节
生 活 中 的 圆 周 运 动
致远新校区高一物理组 2012、2、29 、 、
课前温习5分 课堂幸福 分 课前温习 分，课堂幸福45分 物体要受到指向圆心的合力称为： 物体要受到指向圆心的合力称为：向心力 向心力的特点
方向：总是指向圆心 变力 变力) 方向：总是指向圆心(变力 大小： 大小：
v 2π 2 2 r F = ma = mω = m = mω r = m（ ） =⋯ v 向 向 r T
v2 Fn = m The most important r 2
汽车转弯
受力分析 FN Ff mg
2
O提供向心力 FfFfv F =m 向 r
2000kg 质 量 为 m=2000kg 的 汽 车 ， 在 一 段 半 径 在 20m 的圆弧行水平弯道上行驶， R=20m 的圆弧行水平弯道上行驶 ， 已知弯道 路面和汽车轮胎之间的最大静摩擦力 72mg, 则汽车拐弯时的最大速度是多少？ F=0.72mg, 则汽车拐弯时的最大速度是多少？ 10m/s m/s） （g取10m/s）
圆周运动解题思路
1、确定研究对象。WHO 确定研究对象。 2、确定圆周运动的轨道平面.圆心位置.半径WHAT 确定圆周运动的轨道平面.圆心位置.半径WHAT 3、受力分析.WHY 受力分析. 4、运用平行四边形定则或正交分解法求出向心力 F。 5、根据向心力公式，选择一种形式列方程求解。 根据向心力公式，选择一种形式列方程求解。
火车转弯
1、火车做匀速直线运动和匀速转弯 运动状态是否相同？ 运动状态是否相同？
轮缘
铁轨 (轨距) 轨距)
2、火车在转弯时，若内外轨是相平的，铁 火车在转弯时，若内外轨是相平的， 轨如何对火车提供水平方向的向心力？ 轨如何对火车提供水平方向的向心力？ F

生活中的圆周运动ppt课件

生活中的圆周运动ppt课件

指向圆心的力 背向圆心的力=向心力
G FN
2
m r
FN
移项： FN
G m 2
r
G
C、汽车对桥面的压力小于汽车的重力
FN
D、汽车对桥面的压力大于汽车的重力
拱形桥原理：
FN
FN
v2 Gm
r
G
例3：质量为25kg 的小孩坐在秋千板上，小孩离系绳子的横梁2.5m。如果秋千板 摆到最低点时，小孩运动速度的大小是 5 m/s，她对秋千板的压力是多大?
解： 小孩到最低点时可按凹形桥模型处理，受力分析如 图所示。
外侧轨道与轮之间有弹力
2.速度过小时： 内侧轨道与轮之间有弹力
Fn
r
θ
G
L hθ
为什么桥不做成平的呢？
二、汽车过拱形桥
拱形桥
（凸形桥）
水平桥 凹形桥
二、汽车过拱形桥 问题1：汽车静止在桥上与通过平桥时，受力怎样？
F压＝FN＝mg
二、汽车过拱形桥
问题2：汽车过拱形桥时，在最高点时，车对凸桥的压力又怎样？
N
v2
F外轨 Fn m r
外轨
G
一、火车转弯 问题2：如何设计可以克服上述缺点？
θ
F合
O
mg
θ
问题3：若不受侧向轨道的弹力，谁充当向心力?
Fn=mgtanθ
火车转弯规定临界速度: v临界 gr tan
一、火车转弯 如果火车在转弯处的速度大于规定速度，会对哪个轨道有挤压？如果小 于呢？
N
1.速度过大时：
第六单元 圆周运动
6.4 生活中的圆周运动
课堂导入 弯道处，发现内、外道的高度略有不同，你能说说为什么吗？
一、火车转弯 火车转弯是什么力提供向心力？

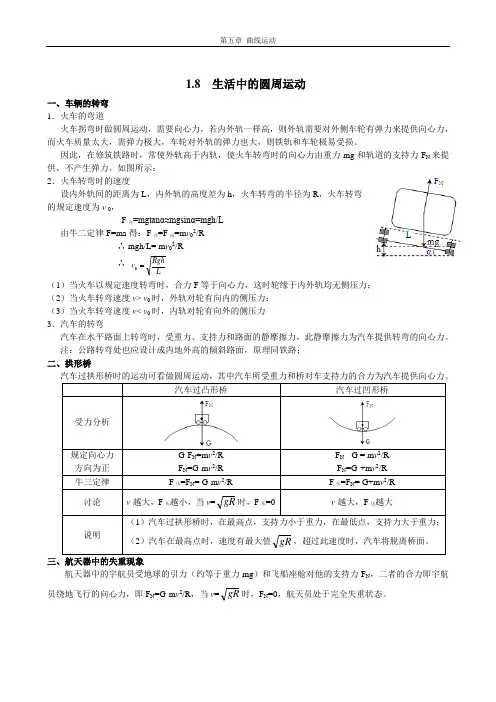
1.8生活中的圆周运动

1.8生活中的圆周运动

1.8 生活中的圆周运动一、车辆的转弯1．火车的弯道火车拐弯时做圆周运动，需要向心力，若内外轨一样高，则外轨需要对外侧车轮有弹力来提供向心力，而火车质量太大，需弹力极大，车轮对外轨的弹力也大，则铁轨和车轮极易受损。

因此，在修筑铁路时，常使外轨高于内轨，使火车转弯时的向心力由重力mg 和轨道的支持力F N 来提供，不产生弹力。

如图所示：2．火车转弯时的速度设内外轨间的距离为L ，内外轨的高度差为h ，火车转弯的半径为R ，火车转弯的规定速度为v 0，F 合=mgtanα≈mgsinα=mgh/L由牛二定律F=ma 得：F 合=F 向=m v 02/R∴ mgh/L= m v 02/R∴ LRgh v 0 （1）当火车以规定速度转弯时，合力F 等于向心力，这时轮缘于内外轨均无侧压力；（2）当火车转弯速度v > v 0时，外轨对轮有向内的侧压力；（3）当火车转弯速度v < v 0时，内轨对轮有向外的侧压力3．汽车的转弯汽车在水平路面上转弯时，受重力、支持力和路面的静摩擦力，此静摩擦力为汽车提供转弯的向心力。

注：公路转弯处也应设计成内地外高的倾斜路面，原理同铁路；二、拱形桥航天器中的宇航员受地球的引力（约等于重力mg ）和飞船座舱对他的支持力F N ，二者的合力即宇航员绕地飞行的向心力，即F N =G-m v 2/R ，当v =gR 时，F N =0，航天员处于完全失重状态。

四、离心运动做匀速圆周运动的物体，在所受合力突然消失或者不足以提供所需的向心力的情况下，就会逐渐远离圆心，这种运动叫做离心运动。

离心运动的条件：F合<F向注：离心运动的物体做以沿抛出点切线方向的初速度做直线运动或抛体运动。

针对练习1．一辆汽车匀速通过半径为R的圆弧形拱形桥，关于汽车的受力情况，下列说法中正确的是（）A. 汽车对路面的压力大小不变，总是等于汽车的重力B. 汽车对路面的压力大小不断发生变化，总是小于汽车所受的重力C. 汽车的牵引力不发生变化D. 汽车的牵引力逐渐变小2．下列关于离心现象的说法正确的是（）A. 当物体所受的离心力大于向心力时产生离心现象B. 做匀速圆周运动的物体，当它所受一切力都突然消失时，它将做背离圆心的圆周运动C. 做匀速圆周运动的物体，当它所受一切力都突然消失时，它将沿切线做直线运动D. 做匀速圆周运动的物体，当它所受一切力都突然消失时，它将做曲线运动3．质量为m的小球，用一条绳子系在竖直平面内做圆周运动，小球到达最高点时的速度为v，到达最低点时的速度变为24vgR ，则两位置处绳子所受的张力之差是（）A. 6mgB. 5mgC. 4mgD.2mg4．水平转盘上放以小木块，当转速为60r/min时，木块离轴8cm，且恰好与转盘无相对运动，当转速增加到120r/min时，为保证木块相对转盘无滑动，则木块应放在离轴cm处。

《生活中的圆周运动》圆周运动PPT课件

《生活中的圆周运动》圆周运动PPT课件

由时公对式桥面m恰vr2无 m压g力 43时m,g由得公r式=40
20 m/s,故B正确。
m
m,当汽车通过拱桥顶点 v12 =mg得v1= gr =
r
【素养训练】 1.飞机俯冲拉起时,飞行员处于超重状态,此时座位对 飞行员的支持力大于所受的重力,这种现象叫过荷。过 荷过重会造成飞行员大脑贫血,四肢沉重,暂时失明,甚 至昏厥。受过专门训练的空军飞行员最多可承受9倍重 力的支持力影响。g取10 m/s2,则当飞机在竖直平面上
2.汽车通过凹形桥的最低点时的情况: 如图所示,汽车在竖直方向受到重力mg和桥的支持力FN 的作用,此二力的合力提供汽车做圆周运动的向心力, 有
FN-mg= m v2 桥由面牛对顿车 第的 三r 支 定持 律力 可知FN=,m汽g+车m对vr桥2 面的压力大小为
F′N=FN=mg+
,方向竖直向下。
(2)如果在弯道处使外轨略高于内轨,如图乙所示,火车 转弯时铁轨对火车的支持力FN的方向不再是竖直的,而 是指向斜向弯道的内侧,它与重力的合力指向圆心,为 火车转弯提供了全部或部分向心力,减轻了轮缘与外轨 的挤压。
2.火车转弯时的规定速度:
(1)相关物理量:若火车转弯时的向心力完全由重力mg 和支持力FN的合力提供,设内、外轨间的距离为L,两轨 高度差为h,火车转弯半径为R,火车的质量为m。
半径R=3 280 m,时速v=144 km/h= (1)临界状态:小球在最高点时,轻杆弹力或轨道压力为
m v2
125 m。选项C正确。 如图所示,细绳系的小球或在轨道内侧的小球做圆周运动。
由公式
得r=40 m,当汽车通过拱桥顶点
R
,代入数值得R=
生活中有很多现象与物理知识有关,下列现象中与离心运动无关的是 ( )

生活中的圆周运动(课件)高一物理(人教版2019必修第二册)

生活中的圆周运动(课件)高一物理(人教版2019必修第二册)




>
典例解析
【例题3】质量为m的小球由轻绳a和b分别系于一轻质细杆的B点和A点，如图所示，绳
a与水平方向成θ角，绳b在水平方向且长为l。当轻杆绕轴AB以角速度ω匀速转动时，
小球在水平面内做匀速圆周运动，则下列说法正确的是（ C ）
A．a绳的张力可能为零 B．a绳的张力随角速度的增大而增大
C．当角速度 >
1、定义：做圆周运动的物体，在受到的合外力突然消失或者不足以提
供做圆周运动所需要的向心力的情况下，将远离圆心运动，我们把这种
运动称为离心运动。这种现象称为离心现象。
2、条件：
0 ≤F合＜mω2r
四、离心运动
3.离心运动的应用
离
心
甩
干
离
心
抛
掷
离
心
脱
水
离
心
分
离
四、离心运动
4.离心运动的防止
（1）车辆拐弯
= . /
三、航天器中的失重现象
以绕地球做匀速圆周运动的宇宙飞船为例，当飞船距地面高度为100 〜 200 km 时，
它的轨道半径近似等于地球半径R，航天员受到的地球引力近似等于他在地面受到的
重力mg。
r≈R
三、航天器中的失重现象

对飞船： =

=


对飞船内的航天员： − =

，b绳将出现弹力

D．若b绳突然被剪断，则a绳的弹力一定发生变化
【解析】A．由于小球m的重力不为零，a绳的张力不可能为零，b绳的张力可能为零，故
A错误；B．由于a绳的张力在竖直方向的分力等于重力，角θ不变，所以a绳张力不变，b

火车转弯问题 ppt课件

火车转弯问题 ppt课件

用夸张方法画 出轮子位置：
外
G
分开的！
F外
内
8
（2）若内外Biblioteka 道一样高，有什么不妥？F向
m
v2 r
火车质量很大，若仅靠外轨 道对它的压力提供向心力， 则轨道很容易变形（压坏）！
N
外
F外
内
9
G
2、做成“外高内低”的倾斜状态，能更好地保 护轨道。
请大概标出火车圆周运动的圆心O的位置！
圆心O
外 内
10
3、火车在外高内低的轨道转弯时，
v2
f静 m r
22
俯视图
v
f静
例１：在一段半径为R的圆形水平轨道上，已知 路面对汽车轮胎的最大静摩擦力是车重的μ倍 （μ＜1），求汽车拐弯时的安全速度是多大？
v gR
mg m v2
r
23
f
m
ax
m
v2 r
f静
m
v2 r
可知:在弯道半径一定时,汽车速度 越大,所需要的向心力越大，
若汽车速度过大，所需要的向心力过大， 最大静摩擦力不足以提供向心力,即:
外
内
速度过小，靠内轨道
16
（3）当速度小于这一理想值时（ grtan），
轮缘与内轨还是外轨间有相互挤压？
N
mgtan mv2
r
外
F内
内FNG
v grtan 内轨道对轮缘产G生压力 17
小结：火车在外高内低的轨道转弯时，若： 轮缘与内、外轨道之间均无挤压
v grtan 外轨道对轮缘产生压力
v grtan 内轨道对轮缘产生压力
综上所述，为保护轨道，火车转弯时的速度应 尽可能控制在___________左右！

《生活中的圆周运动》课件

《生活中的圆周运动》课件
(3)若 Fn<mrω2或Fn<mrv2，则外力不足以将物体拉回到原轨道上，而做离心 运动，即“需要”大于“提供”或“提供不足”。
(4)若 Fn＝0，则物体做直线运动。
如图所示，当外界提供的向心力 F＝mrω2 时，小球恰好在Ⅲ轨道上 做匀速圆周运动。下列关于小球运动的说法中正确的是( )
A．当外界提供的向心力突然消失时，小球将沿Ⅰ轨道运动，这种运动不叫 离心运动
[变式训练] 1．(多选)(2016·连云港高一检测)铁路转弯处的弯道半径 r 是根据地形决定的。 弯道处要求外轨比内轨高，其内外轨高度差 h 的设计不仅与 r 有关，还与火车在 弯道上的行驶速率 v 有关。下列说法正确的是( ) A．v 一定时，r 越小则要求 h 越大 B．v 一定时，r 越大则要求 h 越大 C．r 一定时，v 越小则要求 h 越大 D．r 一定时，v 越大则要求 h 越大
解析： 摩托车只受重力、地面支持力和地面的摩擦力作用，没有离心力， 选项 A 错误；摩托车正常转弯时可看作是做匀速圆周运动，所受的合力等于向心 力，如果向外滑动，说明提供的向心力即合力小于需要的向心力，选项 B 正确； 摩托车将沿曲线做离心运动，选项 C、D 错误。
答案： B
3．速度与轨道压力的关系 (1)当火车行驶速度 v 等于规定速度 v0 时，所需向心力仅由重力和弹力的合力 提供，此时内外轨道对火车无挤压作用。 (2)当火车行驶速度 v>v0 时，外轨道对轮缘有侧压力。 (3)当火车行驶速度 v<v0 时，内轨道对轮缘有侧压力。
铁路在弯道处的内外轨道高度是不同的，已知内外轨道平面与水平 面的夹角为 θ，如图所示，弯道处的圆弧半径为 R，若质量为 m 的火车转弯时速 度等于 gRtan θ，则( )

高一物理《生活中的圆周运动》知识点总结

高一物理《生活中的圆周运动》知识点总结

高一物理《生活中的圆周运动》知识点总结
一、火车转弯
1．如果铁路弯道的内外轨一样高，火车转弯时，由外轨对轮缘的弹力提供向心力．
2．铁路弯道的特点
(1)弯道处外轨略高于内轨．
(2)火车转弯时铁轨对火车的支持力不是竖直向上的，而是斜向弯道的内侧．支持力与重力的合力指向圆心．
二、汽车过拱形桥 v 2v 2三、航天器中的失重现象
1．向心力分析：航天员受到的地球引力与座舱对他的支持力的合力提供向心力，由牛顿第
二定律得：mg －F N ＝m v 2R ，所以F N ＝m (g －v 2
R
)． 2．完全失重状态：当v ＝Rg 时座舱对航天员的支持力F N ＝0，航天员处于完全失重状态．
四、离心运动
1．定义：做圆周运动的物体沿切线方向飞出或做逐渐远离圆心的运动．
2．原因：提供向心力的合力突然消失或合力不足以提供所需的向心力．
3．离心运动的应用和防止
(1)应用：离心干燥器；洗衣机的脱水筒；离心制管技术；分离血浆和红细胞的离心机．
(2)防止：转动的砂轮、飞轮的转速不能太高；在公路弯道，车辆不允许超过规定的速度．。

6.4生活中的圆周运动

6.4生活中的圆周运动

Fn
mg
m v2 R
v
gR
FN
Ff
O
mg
思考：如果汽车转弯的速度过大，会发生什么？
当汽车转弯时,存在一个安全通过的最大速度,如果超过了这个速度,汽 车将发生侧滑现象。
改进措施: (1)增大转弯半径 (2)增加路面的粗糙程度 (3)最重要的一点：应该减速慢行!
三、拱形桥
拱形桥 （凸形桥）
水平桥 凹形桥
FN
FN ＝mg－m
v2
R
mg
当 FN = 0 时，汽车脱离桥面，做平抛运动，汽车及其中的物体处
于完全失重状态。
mg＝m
v2
R
临界速度
FN＝0 时，汽车 的速度为多大？
汽车过凹形桥时，在最低点时，车对凹形桥的压力又怎样？
FN－mg＝m
v2 R
FN ＝mg + m
v2 R
F压＝FN ＝mg + m
v2 R
6.4 生活中的圆周运动
问题1： 在铁路弯道处，
内、外轨道的高度 一样吗？
问题2： 火车在弯道处
行驶时，速度有 要求吗？
一、火车转弯
（1）火车内外轨高度相同
FN
F G
火车转弯时，外侧车轮的轮缘挤压外轨，使外轨发生弹性形变， 外轨对轮缘的弹力是火车转弯所需向心力的主要来源。
由于火车质量太大，因此需要很大的向心力，靠这种方法得到向 心力，不仅铁轨和车轮极易受损，还可能使火车侧翻.
O
F合 = mω2r， 物体做匀速圆周运动 1、定义：做匀速圆周运动的物体，在所受合力突然消失，或者不足 以提供圆周运动所需的向心力时，做逐渐远离圆心的运动，这种运动 叫做离心运动.
2、条件： 0 ≤F合＜mω2r

火车转弯问题

火车转弯问题

内轨道就 要来帮助
三、拱形桥
根据牛顿第二定律
F向=G
FN= G
FN=m mV2
知
（ 1 ）汽车对桥的压力FN´= FN
O
（２）汽车的速度越大
汽车对桥的压力越小
（３）当汽车的速度增大到V= gR 时,压力为零。
V R
汽车开始做平抛运动．
质量为m的汽车以速度V通过半径为R的凹型桥。它经桥的最
生活中的圆周运动
高一 杨菊霞
本节课要解决的主要问题：
1、正确认识向心力的来源 实例分析：圆锥摆；摩托车在桶内做匀速圆周运 动；其他 2、铁路的弯道 3、拱形桥问题
一、分析向心力的来源
请分析以下圆周运动物体的受力，圆心位置。

请分析以下圆周运动的向心力的来源。
二、铁路的弯道
（1）若火车转弯处内外轨无高度差
F合

F合=Fn
mg
tan

mv
2 0
R mv 2
若v>v0时：则 mg tan R
即：mg tan F mv 2
R
Lh
mg
外轨道就 要来帮助
若v<v0时：则
即：mg tan

F

mv 2
R
设计铁路：
当θ很小时 tan sin
mg
h

mv
2 0
LR
即火车转弯的规定速度
v0= Rgh L
低点时对桥的压力为多大？比汽车的重量大还是小？速度越
大压力越大还是越小？
O
根据牛顿第二定律
F向=F1
F1 =m
G =m V2 V2 +Ｇ R
R
R

6.4 生活中的圆周运动(教学设计)高一物理(人教版2019必修第二册)

6.4 生活中的圆周运动(教学设计)高一物理(人教版2019必修第二册)

第4节生活中的圆周运动教学设计思考与讨论：在铁路弯道处，稍微留意一下，就能发现内、外轨道的高度略有不同。

你能解释其中的原因吗？观察与思考：观看视频，思考行驶中的火车为什么会发生脱轨事故呢？一、火车转弯(一)车轮构造思考与讨论：(1)火车转弯时可看做匀速圆周运动，如果火车内外轨道一样高。

火车受哪些力？谁充当向心力？靠这种办法得到的向心力缺点是什么？(2)如果火车外轨道比内轨道高。

火车可以不受轨道侧向的弹力F吗？(3)若不受侧向轨道的弹力，谁充当向心力？是沿哪个方向？(二)临界速度思考与计算：质量为m的火车转弯时，做匀速圆周运动的轨道半径为r，轨道的倾角为θ，求火车速度多大时对轨道无侧向压力。

深度拓展：质量为m的火车转弯时，做匀速圆周运动的轨道半径为r，轨道宽L，高度差为h，求火车速度多大时对轨道侧向无压力。

(图中θ很小）思考与讨论：(1)如果火车在转弯处的速度大于规定速度，会对哪个轨道有挤压？如果小于呢？(2)通过以上学习，你是否可以解释转弯处内外轨高度不同和火车脱轨的原因吗？【要点总结】=√rgtanθ；(1)火车转弯规定临界速度:v临界(2)火车转弯速度大于规定临界速度时：外侧轨道与轮之间有弹力；(3)火车转弯速度小于规定临界速度时：内侧轨道与轮之间有弹力。

思考与讨论：高速公路转弯处和场地自行车比赛的赛道，路面往往有一定的倾斜度，说说这样设计是什么原因？原因分析： (1)水平路面转弯①向心力：自行车侧向所受的静摩擦力。

r v mF f 2=②临界速度：rv mmg 2=μgr v μ=⇒(2)外高内低路面转弯①向心力：重力和支持力的合力。

r v mmg F n 2tan ==θ②临界速度：θtan gr v =二、汽车过拱形桥思考与讨论：公路上的拱形桥是常见的，为什么拱形桥比凹形桥更普遍呢？(一)凹形桥思考与计算：质量为m的汽车在拱形桥上以速度v行驶，若桥面的圆弧半径为R，当汽车通过桥的最低点时，试画出汽车受力分析图，哪些力提供了向心力？桥对汽车的支持力多大？(二)拱形桥质量为m的汽车在拱形桥上以速度v行驶，若桥面的圆弧半径为R，当汽车通过桥的最高点时，试画出汽车受力分析图，哪些力提供了向心力？桥对汽车的支持力多大？思考与讨论：（最高点）（1）当v=0 时，F N等于多少？（2）当v增大时，F N如何变化？（3）当F N =0时，v等于多少？（4）当v≥√gr时，汽车将做何种运动？（5）此时人和座位之间是否有压力存在？思考与讨论:地球可以看做一个巨大的拱形桥，桥面的半径就是地球的半径。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
可-以- 解出,当 v＝ Rg 时座
舱对人说的出支你持的力想F法支=0，人 处于失重状态
三航天器中的失重现象.
一、离心运动
1、离心运动：
做匀速圆周运动的 物体，在所受合力突然 消失，或者不足以提供 圆周运动所需的向心力 的情况下，就做逐渐远 离圆心的运动。这种运 动叫做离心运动。
2、物体作离心运动的条件：
F合 0或F合 mr 2
二、离心运动 应用
1、离心干燥器的金属网笼
利用离心运动把附着在物
体上的水分甩掉的装置
解释：
当网笼转得比较慢时，
水滴跟物体的附着力F 足以
ν
提供所需的向心力F 使水滴 做圆周运动。当网笼转得比 较快时，附着力 F 不足以提
F<mrω 2 F
o
供所需的向心力 F，于是水
解： 根据牛顿第二定律
F向=F1
G =m
V2 R
R
F1
=m
V2 R
+Ｇ
由上式和牛顿第三定律可知
O
F1
V
（ 1 ）汽车对桥的压力F1´= F1
G
（２）汽车的速度越大
汽车对桥的压力越大
思考：汽车不在拱形桥的最高点或最 低点时，它的运动能用上面的方法求 解吗？
mgcosθ－FN=maN 所以FN=mgcosθ－maN 桥面支持力与夹角θ、车 速v都有关。
内筒与洗衣机的脱水筒相 似，里面加入白砂糖，加热使 糖熔化成糖汁。内筒高速旋转， 黏稠的糖汁就做离心运动，从 内筒壁的小孔飞散出去，成为 丝状到达温度较低的外筒，并 迅速冷却凝固，变得纤细雪白， 像一团团棉花。
？问题一：
要使原来作圆周运动的物体作离心运动，该怎么办？
A、提高转速，使所需向心力增大到大于物体所受合外力。
弯，弯道的倾角为θ，半径为r，则
汽车完全不靠摩擦力转弯的速率 是?
（
设内外轨间的距离为L，内 外轨的高度差为h，火车转
弯的半径为R，则火车转
弯的规定速度为v0 ?
F合=mgtanα≈mgsinα=mgh/L
由牛顿第二定律得：
F合=man 所以mgh/L=m
v0 2 R
（图）
即火车转弯的规定速度v0= Rgh
A
B
巩固应用
例、长为0.6m的轻杆OA(不计质量),A端 插个质量为2.0kg的物体,在竖直平面内 绕O点做圆周运动,当球达到最高点的速 度分别为3m/s, 6 m/s,2m/s时,求杆对球 的作用力各为多少?
A
O
巩固应用
例、如图所示，质量为m的小球，用长 为L的细绳，悬于光滑斜面上的0点，小 球在这个倾角为θ的光滑斜面上做圆周 运动，若小球在最高点和最低点的速率 分别是vl和v2，则绳在这两个位置时的 张力大小分别是多大?
L
二、拱型桥
FN
根据牛顿第二定律
F向=G
FN=m
V2 R
FN= G
mV2
R
G
由上式和牛顿第三定律可知
（ 1 ）汽车对桥的压力
V R
（３）当汽车的速度增大到V= gR 时,压力为零。
汽车开始做平抛运动．
质量为m的汽车以速度V通过半径为R的凹型桥。它经桥 的最低点时对桥的压力为多大？比汽车的重量大还是小？ 速度越大压力越大还是越小？
巩固应用
例、绳系着装水的桶，在竖直平面内做圆 周 运 动 ， 水 的 质 量 m=0.5kg ， 绳 长 =40cm. 求
（1）桶在最高点水不流出的最小速率？ （2）水在最高点速率=3m/s时水对桶底的 压力？(g取10m/s2)
巩固应用：
例、质量为1kg的小球沿半径为20cm的圆环在竖直 平面内做圆周运动，如图所示，求 （1）小球在圆环的最高点A不掉下来的最小速度 是多少？此时小球的向心加速度是多少？ （2）若小球仍用以上的速度经过圆环的最高点A， 当它运动到圆环的最低点B时，对圆环的压力是多 少？此时小球的向心加速度是多少？
滴做离心运动，穿过网孔，
飞到网笼外面。
2、洗衣机的脱水筒 3、用离心机把体温计的 水银柱甩回玻璃泡内
当离心机转得比较慢时， 缩口的阻力 F 足以提供所需 的向心力，缩口上方的水银 柱做圆周运动。当离心机转 得相当快时，阻力 F 不足以 提供所需的向心力，水银柱 做离心运动而进入玻璃泡内。
4、制作“棉花”糖的原理：
B、作匀速圆周运动的物体，在所受合外力突然 消失时，将沿圆周切线方向离开圆心 C、作匀速圆周运动的物体，它自己会产生一个 向心力，维持其作圆周运动
D、作离心运动的物体，是因为受到离心力作用 的缘故
２、为了防止汽车在水平路面上转弯时出现“打滑” 的现象，可以：( D )
a、增大汽车转弯时的速度 b、减小汽车转弯时的速度
B、减小合外力或使其消失
三、离心运动的防止：
1、在水平公路上行驶的汽
车转弯时 在水平公路上行驶的汽车，转
弯时所需的向心力是由车轮与路
面的静摩擦力提供的。如果转弯
时速度过大，所需向心力F大于 最大静摩擦力Fmax，汽车将做
υ
F<m
υ2
r
离心运动而造成交通事故。因此，
F
汽车
在公路弯道处，车辆行驶不允许
（
一辆汽车匀速率通过半径为R的圆弧
拱形路面，关于汽车的受力情况，下 列说法正确的是（BD） A．汽车对路面的压力大小不变，总 是等于汽车的重力 B．汽车对路面的压力大小不断发生 变化，总是小于汽车所受重力
C．汽车的牵引力不发生变化 D．汽车的牵引力逐渐变小
思考与讨论- 由请大F压家＝G阅－m读vR2 课＝m本( g－5v8R2面)
在水平铁路转弯处，往往使外轨 略高于内轨，这是为了( ACD ) A．减轻火车轮子挤压外轨 B．减轻火车轮子挤压内轨 C．使火车车身倾斜，利用重力 和支持力的合力提供转弯所需向 心力
D．限制火车向外脱轨
思考
在高速公路的拐弯处，路 面造得外高内低是什么原 因？
（第11题）
如图所示，汽车在倾斜的弯道上拐
过山车
(1）凸形桥半径为R，汽车在顶端的最大速 度是多少？
(2）长为R的轻绳一端系一小球在竖直平面 内做圆周运动，它在最高点的最小速度是 多少？
（3）如果上题改成长为R的轻杆一端 系一小球在竖直平面内做圆周运动，它在 最高点的最小速度是多少？当球在最高点 速度为 1 2 Rg 时，求杆对球的作用力， 当小球在最高点速度2 0.5 Rg 时，求杆 对球的作用力。
超过规定的速度。
2、高速转动的砂轮、飞轮等
？问题二：
要防止离心现象发生，该怎么办？
A、减小物体运动的速度，使物体作圆周运动 时所需的向心力减小
B、增大合外力，使其达到物体作圆周运动时 所需的向心力
巩固练习：
1、下列说法正确的是 ( B )
A、作匀速圆周运动的物体，在所受合外力突然消 失时，将沿圆周半径方向离开圆心
根据牛顿第二定律 V2
F=mg tan α= m R V= Rg tanα V ＞ Rg tanα 外轨对外轮缘有弹力
V＜ Rg tanα 内轨对内轮缘有弹力
N
F
α
α
G
小结：水平面内的圆周运动，轨迹 在水平面内，向心力也一定在水平 面内。
向心力是按效果命名的力，任何一 个或几个力的合力，只要它的作用 效果是使物体产生向心加速度，它 就是物体所受的向心力。
生活中的圆周运动
火车车轮的结构特点：
一、铁路的弯道
火车转弯（内外轨道等高）
N
向左转
G
（1） 火车转弯处内外轨无高度差
外轨对轮缘的弹力F就是使火车转弯 的向心力
向左转 根据牛顿第二定律F=m V2 可知
R 火车质量很大 外轨对轮缘的弹力很大
外轨和外轮之间的磨损大， 铁轨容易受到损坏
N
G
F
（2 ）转弯处外轨高于内轨
c、增大汽车与路面间的摩擦 d、减小汽车与路面间的摩擦
A、a、b
B、a、c
C、b、d
D、b、c
3、下列说法中错误的有：（ B ）
A、提高洗衣机脱水筒的转速，可以使衣服甩得更干
B、转动带有雨水的雨伞，水滴将沿圆周半径方向离开圆心
C、为了防止发生事故，高速转动的砂轮、飞轮等不能超过 允许的最大转速
D、离心水泵利用了离心运动的原理