鄂南高中华师一附中黄石二中荆州中学襄阳四中襄阳五中孝感高中黄冈中学2019届高三第一次联考理科综合试题

鄂南高中、华师一附中、黄冈中学、黄石二中、荆州中学、襄阳四中、襄阳五中、孝感高中湖北省八校2019届高三第一次联考考试时间：2019年12月16日下午15：00—17：00试卷满分：150分注意事项：1．答卷前，考生务必将自己的姓名，准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上指定位置．2．选择题每小题选出答案后，用2B铅笔将答题卡上对应题目的答案标号涂黑，如要改动，用豫皮擦干净后。

再选涂其它答案标号，答在试题卷上无效．3．非选择题用0．5毫米的黑色墨水签字笔答在答题卡上每题对应的答题区域内，答在试题卷上无效．第一部分：听力（共两节，满分30分）做题时，先将答案划在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题l.5分，满分7.5分）听下面五段对话。

每段对话后有一小题，从题中所给的A、B、C三个选项中选出最佳选项，并在答题卡上将该项涂黑。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt?A．￡19.15. B．￡9.15. C．￡9.18.答案是B。

1．How much should the woman pay for the car?A．200 dollars．B．180 dollars．C．150 dollars．2．What's the most probable relationship between the two speakers?A．Boss and secretary．B．Nurse and patient C．Interviewer and interviewee．3．Where is the woman's mother now?A．At home．B．In hospital．C．In operation．4．What do you judge from what the man says?A．The man is anxious to begin his studies．B．The man regrets that he was not a good student．C．The man thinks study is not important.5．Why would the woman rather stay at the hotel?A．It costs less money．B．It saves much labor．C．It feels more comfortable．第二节（共15小题；每小题 1.5分，满分22.5分）听下面5段对话或独白。

湖北省八校（鄂南高中.黄石二中.华师一附中.黄冈中学.荆州中学.孝感中学.襄阳四中.襄阳五中）2019届高三第二次联合考试数学（理科）试题一、选择题（本大题共12小题，共60.0分）1. 设集合A ={y|y =2x ,x ∈R}，B ={x|y =√1−x,x ∈R}，则A ∩B =( )A. {1}B. (0,+∞)C. (0,1)D. (0,1]【答案】D【解析】解：A ={y|y >0}，B ={x|x ≤1}； ∴A ∩B =(0,1]． 故选：D ．可解出集合A ，B ，然后进行交集的运算即可．考查描述法、区间的定义，指数函数的值域，以及交集的运算．2. 若复数z 满足2+zi =z −2i(i 为虚数单位)，z −为z 的共轭复数，则|z −+1|=( )A. √5B. 2C. √3D. 3【答案】A【解析】解：由2+zi =z −2i ，得(1−i)z =2+2i ，则z =2+2i 1−i=2(1+i)2(1−i)(1+i)=2i ，∴z −+1=1−2i ，则|z −+1|=√5． 故选：A ．把已知等式变形，利用复数代数形式的乘除运算化简，结合复数模的公式求解． 本题考查复数代数形式的乘除运算，考查复数模的求法，是基础题．3. 在矩形ABCD 中，AB =4，AD =3，若向该矩形内随机投一点P ，那么使得△ABP与△ADP 的面积都不小于2的概率为( )A. 14B. 13 C. 47 D. 49【答案】D【解析】，解：由题意知本题是一个几何概型的概率， 以AB 为底边，要使面积不小于2， 由于S △ABP =12AB ×h =2h ，则三角形的高要h ≥1，同样，P 点到AD 的距离要不小于43，满足条件的P 的区域如图，其表示的区域为图中阴影部分，它的面积是整个矩形面积的(4−43)(3−1)=163，∴使得△ABP与△ADP的面积都不小于2的概率为：1634×3=49；故选：D．本题是一个几何概型的概率，以AB为底边，要使面积不小于2，则三角形的高要h≥1，得到两个三角形的高即为P点到AB和AD的距离，得到对应区域，利用面积比求概率．本题给出几何概型，明确满足条件的区域，利用面积比求概率是关键．4.已知函数f(x)=(x−1)(ax+b)为偶函数，且在(0,+∞)上单调递减，则f(3−x)<0的解集为()A. (2,4)B. (−∞,2)∪(4,+∞)C. (−1,1)D. (−∞,−1)∪(1,+∞)【答案】B【解析】解：∵f(x)=ax2+(b−a)x−b为偶函数，所以b−a=0，即b=a，∴f(x)= ax2−a，由f(x)在(0,+∞)上单调递减，所以a<0，∴f(3−x)=a(3−x)2−a<0，可化为(3−x)2−1>0，即x2−6x+8>0，解得x<2或x>4故选：B．根据f(x)为偶函数，可得b=a；根据f(x)在(0,+∞)上递减得a<0；然后解一元二次不等式可得．本题考查了奇偶性与单调性得综合，属中档题．5.已知双曲线x2a −y22−a2=1的离心率为√2，则a的值为()A. 1B. −2C. 1或−2D. −1【答案】C【解析】解：双曲线x2a −y22−a2=1的离心率为√2，实轴在x轴上，可得e2=2−a2+aa=2，解得a=1或−2．故选：C．直接利用双曲线的标准方程以及离心率转化求解即可．本题考查双曲线的简单性质的应用，考查计算能力．6.等比数列的前n项和，前2n项和，前3n项的和分别为A，B，C，则()A. A+B=CB. B2=ACC. (A+B)−C=B2D. A2+B2=A(B+C)【答案】D【解析】解：由题意可得：S n=A，S2n=B，S3n=C．由等比数列的性质可得：S2n−S nS n =q n，S3n−S2n S2n− S n=q n，所以B−AA =C−BB−A，所以整理可得：A2+B2=A(B+C)．故选：D．利用等比数列的性质可得S2n−S nS n =q n,S3n−S2nS2n−S n=q n，所以B−AA=C−BB−A，进行整理可得答案．解决此类问题的关键是熟练掌握等比数列的有关性质，并且进行正确的运算，一般以选择题的形式出现．7.执行如图所示的程序框图，若输入m=0，n=2，输出的x=1.75，则空白判断框内应填的条件可能是()A. |m−n|<1B. |m−n|<0.5C. |m−n|<0.2D. |m−n|<0.1【答案】B【解析】解：模拟执行如图所示的程序框图知，输入m=0，n=2，x=1，满足12−3<0，m=1，不满足判断框内的条件，x=1.5，满足1.52−3<0，m=1.5，不满足判断框内的条件，x=1.75，不满足1.752−3<0，n=1.75，由题意，应该满足判断框内的条件，输出x=1.75，此时，m=1.5，n=1.75，则空白判断框内应填的条件为|m−n|<0.5．故选：B．模拟执行如图所示的程序框图，即可得出空白判断框内应填的条件是什么．本题考查了算法与程序语言的应用问题，是基础题．8.将函数f(x)=2sin(2x+π3)图象上的每个点的横坐标缩短为原来的一半，纵坐标不变，再将所得图象向左平移π12个单位得到函数g(x)的图象，在g(x)图象的所有对称轴中，离原点最近的对称轴方程为()A. x=−π24B. x=π4C. x=5π24D. x=π12【答案】A【解析】解：将函数f(x)=2sin(2x+π3)图象上的每个点的横坐标缩短为原来的一半，纵坐标不变，得到y=2sin(4x+π3)，再将所得图象向左平移π12个单位得到函数g(x)的图象，得到g(x)=2sin[4(x+π12)+π3]=2sin(4x+2π3)，由4x+2π3=π2+kπ，k∈Z，得x=14kπ−π24，k∈Z，当k=0时，离原点最近的对称轴方程为x=−π24，故选：A．根据三角函数的图象关系求出g(x)的解析式，结合对称轴方程进行求解即可．本题主要考查三角函数的图象和性质，根据条件求出g(x)的解析式，结合对称轴方程是解决本题的关键．9.在(1+x)2+(1+x)3+⋯+(1+x)9的展开式中，含x2项的系数是()A. 119B. 120C. 121D. 720【答案】B【解析】解：在(1+x)2+(1+x)3+⋯+(1+x)9的展开式中，含x2项的系数为C22+C32+ C42+⋯+C92=C103=120，故选：B．利用二项展开式的通项公式求得含x2项的系数，再利用二项式系数的性质化简得到结果．本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．10.我国古代数学名著《九章算术》记载：“刍甍者，下有袤有广，而上有袤无丈.刍，草也；甍，屋盖也.”翻译为：“底面有长有宽为矩形，顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”如图，为一刍甍的三视图，其中正视图为等腰梯形，侧视图为等腰三角形.则它的体积为()A. 1603B. 160 C. 2563D. 64【答案】A【解析】解：作出几何体的直观图如图所示：沿上棱两端向底面作垂面，且使垂面与上棱垂直，则将几何体分成两个四棱锥和1个直三棱柱，则三棱柱的体积V1=12×4×4×4=32，四棱锥的体积V2=13×2×4×4×1=323，由三视图可知两个四棱锥大小相等，∴V=V1+2V2=1603．故选：A．作出几何体的直观图，将几何体分解成两个四棱锥和一个三棱柱计算体积．本题考查的知识点是由三视图求体积和表面积，其中分析出几何体的形状是解答的关键．11.已知椭圆C：x24+y23=1，直线l：x=4与x轴相交于点E，过椭圆右焦点F的直线与椭圆相交于A，B两点，点C在直线l上，则“BC//x轴”是“直线AC过线段EF中点”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】解：设直线AC与x轴的交点为点N，过点A作AD⊥l，点D是垂足．因为点F是椭圆的右焦点，直线l是右准线，BC//x轴，即BC⊥l，根据椭圆几何性质，得AFAD =BFBC═e(e是椭圆的离心率)．∵AD//FE//BC．∴ENAD =CNCA═BFAB，FNBC=AFAB，即EN═AD⋅BFAB =e⋅AD⋅BCAB=AF⋅BCAB=FN．∴N为EF的中点，即直线AC经过线段EF的中点N，即充分性成立，当直线AB斜率为0时，则BC与x轴重合，此时BC//x轴不成立，则“BC//x轴”是“直线AC过线段EF中点”的充分不必要条件，故选：A．根据充分条件和必要条件的定义，结合直线和椭圆的位置关系进行判断即可．本题主要考查充分条件和必要条件的判断，结合直线和椭圆的位置关系，综合性较强，有一定的难度．12. 下列命题为真命题的个数是( )①ln3<√3ln2； ②lnπ<√πe ； ③2√15<15； ④3eln2<4√2A. 1B. 2C. 3D. 4【答案】C【解析】解：构造函数f(x)=lnx x，导数为f′(x)=1−lnx x 2，当0<x <e 时，f′(x)>0，f(x)递增，x >e 时，f′(x)<0，f(x)递减，可得x =e 处f(x)取得最大值1e ， ln3<√3ln2⇔2ln √3<√3ln2⇔ln √3√3<ln22，由√3<2<e可得f(√3)<f(2)，故①正确； lnπ<√πe ⇔ln √π√π<ln √e √e，由√e <√π<e ，可得f(√e)<f(√π)，故②错误； 2√15<15⇔ln22<ln √15√15，由e −2<√15−2，可得f(2)<f(√15)，故③正确； 3eln2<4√2⇔ln88<√22e<1e ，由f(x)的最大值为1e ，故④正确．故选：C ． 构造函数f(x)=lnx x，求得导数，以及单调性和最值，作出图象，对照选项一一判断即可得到所求答案．本题考查数的大小比较，注意运用构造函数，以及导数的运用：求单调性和最值，考查化简运算能力，属于中档题．二、填空题（本大题共4小题，共20.0分）13. 平面向量a ⃗ 与b ⃗ 的夹角为45∘，a ⃗ =(1,−1)，|b ⃗ |=1，则|a ⃗ +2b ⃗ |=______． 【答案】√10【解析】解：∵a ⃗ 与b ⃗ 的夹角为45∘，且|a ⃗ |=√2，|b ⃗ |=1；∴(a ⃗ +2b ⃗ )2=a ⃗ 2+4a ⃗ ⋅b ⃗ +4b ⃗ 2=2+4+4=10；∴|a ⃗ +2b ⃗ |=√10．故答案为：√10．根据a ⃗ ,b ⃗ 的夹角为45∘，|b ⃗ |=1，并求得|a ⃗ |=√2，从而可求出(a ⃗ +2b ⃗ )2的值，进而得出|a ⃗ +2b ⃗ |的值．考查向量数量积的运算及计算公式，根据向量坐标可求向量长度．14. 已知实数x ，y 满足约束条件{x −y +2≥0x +y +k ≥0x ≤1，且z =x +2y 的最小值为3，则常数k =______． 【答案】−2【解析】解：作出实数x ，y 满足足约束条件{x −y +2≥0x +y +k ≥0x ≤1对应的平面区域，z =x +2y 的最小值为3，平移直线z =x +2y ，由图象可知当直线z =x +2y ，经过点A ，{x =1x+2y=3可得A(1,1)，A(1,1)代入x +y +k =0， 可得k =−2． 故答案为：−2．作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z 的最大值． 本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．15. 考虑函数y =e x 与函数y =lnx 的图象关系，计算：∫ln e 21xdx =______．【答案】e 2+1【解析】解：如下图所示，由于函数y =lnx 与函数y =e x 互为反函数，两个函数的图象关于直线y =x 对称， 结合图象可知，图中两个阴影部分区域的面积相等，所以，∫ln e 21xdx =∫(20e 2−e x )dx =(e 2x −e x )|02=e 2+1． 答案为：e 2+1．作出函数y =lnx 、y =e x 以及直线y =x 的图象，利用函数y =lnx 与函数y =e x 的图象关于直线y =x 对称，利用对称性得出∫ln e 21xdx =∫(20e 2−e x )dx ，利用定积分公式进行计算可得出答案．本题考查定积分的计算，解决本题的关键在于利用函数图象的对称性进行转化，考查计算能力与推理能力，属于中等题．16. 如图所示，在平面四边形ABCD 中，若AD =2，CD =4，△ABC 为正三角形，则△BCD 面积的最大值为______．【答案】4+4√3【解析】解：设∠ADC =α，∠ACD =β，由余弦定理得：AC 2=42+22−2×4×2cosα=20−16cosα， ∴cosβ=AC 2+128AC，又由正弦定理可得ADsinβ=ACsinα，则sinβ=2sinαAC，∴S △BCD =12BC ⋅CD ⋅sin(β+π3)=2BC(12sinβ+√32cosβ)=2BC ⋅(12⋅2sinαAC+√32⋅AC 2+128AC)=4sin(α−π3)+4√3，故△BCD 面积的最大值为4+4√3， 故答案为：4+4√3运用余弦定理，表示出AC ，进而用三角函数表示出S △BCD ．本题考查三角形的面积的最值的求法，注意运用正弦定理，余弦定理和面积公式，属于中档题．三、解答题（本大题共7小题，共82.0分）17. 若数列{a n }的前n 项和为S n ，首项a 1>0且2S n =a n 2+a n (n ∈N ∗)．(1)求数列{a n }的通项公式； (2)若a n >0(n ∈N ∗)，令b n =1an (a n +2)，求数列{b n }的前n 项和T n ．【答案】解：(1)当n =1时，2a 1=2S 1=a 12+a 1，则a 1=1； 当n ≥2时，a n =S n −S n−1=a n 2+a n2−a n−12+a n−12，即(a n +a n−1)(a n −a n−1−1)=0，可得a n =−a n−1或a n −a n−1=1， 可得a n =(−1)n−1或a n =n ； (2)由a n >0，则a n =n ，b n =1an (a n+2)=1n(n+2)=12(1n −1n+2)， 即有前n 项和T n =12(1−13+12−14+13−15+⋯+1n−1−1n+1+1n −1n+2) =12(1+12−1n+1−1n+2)=34−2n+32(n+1)(n+2)．【解析】(1)由数列的递推式：当n =1时，a 1=S 1；当n ≥2时，a n =S n −S n−1，化简计算可得所求通项公式； (2)求得b n =1a n (a n +2)=1n(n+2)=12(1n−1n+2)，再由数列的裂项相消求和，化简可得所求和．本题考查数列的通项公式的求法，注意运用数列递推式，考查数列的裂项相消求和，化简整理的运算能力，属于基础题．18. 如图，四边形ABCD 与BDEF 均为菱形，FA =FC ，且∠DAB =∠DBF =60∘．(1)求证：AC ⊥平面BDEF ；(2)求直线AD 与平面ABF 所成角的正弦值．【答案】证明：(1)设AC 与BD 相交于点O ，连接FO ， ∵四边形ABCD 为菱形，∴AC ⊥BD ，且O 为AC 中点， ∵FA =FC ，∴AC ⊥FO ，又FO ∩BD =O ，∴AC ⊥平面BDEF.…………………(5分) 解：(2)连接DF ，∵四边形BDEF 为菱形，且∠DBF =60∘， ∴△DBF 为等边三角形，∵O 为BD 中点，∴FO ⊥BD ，又AC ⊥FO ，∴FO ⊥平面ABCD ．∵OA ，OB ，OF 两两垂直，∴建立空间直角坐标系O −xyz ，如图所示，………(7分) 设AB =2，∵四边形ABCD 为菱形，∠DAB =60∘，∴BD =2，AC =2√3． ∵△DBF 为等边三角形，∴OF =√3．∴A(√3,0,0)，B(0,1，0)，D(0,−1,0)，F(0,0，√3)，∴AD ⃗⃗⃗⃗⃗ =(−√3,−1,0)，AF ⃗⃗⃗⃗⃗ =(−√3,0,√3)，AB ⃗⃗⃗⃗⃗ =(−√3,1，0)． 设平面ABF 的法向量为n⃗ =(x,y ，z)， 则{AF ⃗⃗⃗⃗⃗ ⋅n ⃗ =−√3x +√3z =0AB ⃗⃗⃗⃗⃗ ⋅n ⃗ =−√3x +y =0，取x =1，得n ⃗ =(1,√3,1)． 设直线AD 与平面ABF 所成角为θ，………(10分) 则直线AD 与平面ABF 所成角的正弦值为： sinθ=|cos <AD ⃗⃗⃗⃗⃗ ,n ⃗ >|=|AD ⃗⃗⃗⃗⃗⃗ ⋅n ⃗ ||AD ⃗⃗⃗⃗⃗⃗ |⋅|n ⃗ |=√155.…………………(12分) 【解析】(1)设AC 与BD 相交于点O ，连接FO ，推导出AC ⊥BD ，AC ⊥FO ，由此能证明AC ⊥平面BDEF ．(2)连接DF ，推导出△DBF 为等边三角形，从而FO ⊥BD ，AC ⊥FO ，进而FO ⊥平面ABCD.由OA ，OB ，OF 两两垂直，建立空间直角坐标系O −xyz ，利用向量法能求出直线AD 与平面ABF 所成角的正弦值．本题考查线面垂直的证明，考查线面角的正弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查空间想象能力、运算求解能力，考查化归与转化思想、数形结合思想，是中档题．19. 某市政府为了节约生活用电，计划在本市试行居民生活用电定额管理，即确定一户居民月用电量标准a ，用电量不超过a 的部分按平价收费，超出a 的部分按议价收费.为此，政府调查了100户居民的月平均用电量(单位：度)，以[160,180)，[180,200)，[200,220)，[220,240)，[240,260)，[260.280),[280,300)分组的频率分布直方图如图所示．(1)根据频率分布直方图的数据，求直方图中x 的值并估计该市每户居民月平均用电量μ的值；(2)用频率估计概率，利用(1)的结果，假设该市每户居民月平均用电量X 服从正态分布N(μ,σ2)(═)估计该市居民月平均用电量介于μ～240度之间的概率；(═)利用(═)的结论，从该市所有居民中随机抽取3户，记月平均用电量介于μ～240度之间的户数为ξ，求ξ的分布列及数学期望E(ξ)．【答案】解：(1)由(0.002+0.0095+0.011+0.0125+x +0.005+0.0025)×20=1， 得x =0.0075，------------(2分)∴μ=170×0.04+190×0.19+210×0.22+230×0.25+250×0.15+270×0.1+290×0.05=225.6.…………………(4分)(2)(═)P(225.6<X <240)=12[1−2P(X >240)]=15.-----------------(6分)(═)∵ξ～B(3,15)，∴P(Y =i)=C 3i(15)i (45)3−i ，i =0，1，2，3.-------(8分)∴ξ的分布列为：ξ 0123P6412548125121251125-----------------(10分)∴E(Y)=3×15=35.…………………………(12分)【解析】(1)由(0.002+0.0095+0.011+0.0125+x +0.005+0.0025)×20=1，求出x =0.0075，由此能估计该市每户居民月平均用电量μ的值．(2)(═)P(225.6<X <240)=12[1−2P(X >240)]，由此能求出结果．(═)∵ξ～B(3,15)，∴P(Y =i)=C 3i(15)i (45)3−i ，i =0，1，2，3，由此能求出ξ的分布列及数学期望E(ξ)．本题考查频率、平均数、概率、离散型随机变量的分布列、数学期望的求法，考查频率分布直方图、二项分布的性质等基础知识，考查运算求解能力，是中档题．20. 如图，圆O ：x 2+y 2=4，A(2,0)，B(−2,0)，D 为圆O 上任意一点，过D 作圆O 的切线分别交直线x =2和x =−2于E ，F 两点，连AF ，BE 交于点G ，若点G 形成的轨迹为曲线C ．(1)记AF ，BE 斜率分别为k 1，k 2，求k 1⋅k 2的值并求曲线C 的方程；(2)设直线l ：y =x +m(m ≠0)与曲线C 有两个不同的交点P ，Q ，与直线x =2交于点S ，与直线y =−1交于点T ，求△OPQ 的面积与△OST 面积的比值λ的最大值及取得最大值时m 的值． 【答案】解：(1)设D(x 0,y 0)，(y 0≠0)，易知过D 点的切线方程为x 0x +y 0y =4，其中x 02+y 02=4，则E(2,4−2x 0y 0)，F(−2,4+2x 0y 0)，∴k 1k 2=4−2x 0y 04⋅4+2x 0y 0−4=16−4x 02−16y 02=−4y 0216y 02=−14 设G(x,y)，由k 1k 2=−14， ∴yx−2⋅yx+2=−14， ∴x 24+y 2=1，(y ≠0)故曲线C 的方程为x 24+y 2=1(y ≠0)(2){x 2+4y 2=4y=x+m，消y 可得5x 2+8mx +4m 2−4=0， 设P(x 1,y 1)，Q(x 2,y 2)，则x 1+x 2=−85m ，x 1x 2=4m 2−45由△=64m 2−20(4m 2−4)>0得−5<m <√5且m ≠0且m ≠±2 ∴|PQ|=√1+k 2⋅√(x 1+x 2)2−4x 1x 2=√2⋅√(−85m)2−4×4m 2−45=4√25√5−m 2，∵与直线x =2交于点S ，与直线y =−1交于点T ， ∴S(2,2+m)，T(−m −1,−1)∴|ST|=√(3+m)2+(3+m)2=√2(3+m)， ∴λ=S OPQ S △OST =|PQ||ST|=45√5−m 2(3+m)2，令3+m =t ，t ∈(3−√5,3+√5)且t ≠1，3，5 则λ=45√−t 2+6t−4t 2=45√−4t 2+6t−1=45√−(1t−34)2+54，当1t =34，即t =43，m =−53时，λ取得最大值2√55．【解析】(1)设D(x 0,y 0)，(y 0≠0)，易知过D 点的切线方程为x 0x +y 0y =4，根据斜率公式，即可得出．(2)直线方程与椭圆方程联立化为：5x 2+8mx +4m 2−4=0，设P(x 1,y 1)，Q(x 2,y 2)，由△>0可得m 的范围，再求得|ST|，通过换元利用二次函数的单调性即可得出 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长公式、三角形面积计算公式、二次函数的单调性，考查了推理能力与计算能力，属于中档题．21. 已知函数f(x)=(1+ax 2)e x −1．(1)当a ≥0时，讨论函数f(x)的单调性； (2)求函数f(x)在区间[0,1]上零点的个数．【答案】解：(1)f′(x)=(ax 2+2ax +1)e x ……………(1分) 当a =0时，f′(x)=e x ≥0，此时f(x)在R 单调递增； ……………(2分) 当a >0时，△=4a 2−4a ，①当0<a ≤1时，△≤0，ax 2+2ax +1≥0恒成立， ∴f′(x)≥0，此时f(x)在R 单调递增；……(3分)②当a >1时，令f′(x)=0，解得：x 1=−1−√1−1a ，x 2=−1+√1−1a ，x ，f′(x)，f(x)的变化如下：即f(x)在(−∞,−1−√1−1a )和(−1+√1−1a ,+∞)上单调递增；在(−1−√1−1a ,−1+√1−1a )上单调递减； ……(5分)综上：当0≤a ≤1时，f(x)在R 单调递增；当a >1时，f(x)在(−∞,−1−√1−1a )和(−1+√1−1a ,+∞)上单调递增；在(−1−√1−1a ,−1+√1−1a )上单调递减；…………………(6分) (2)由(1)知，当0≤a ≤1时，f(x)在[0,1]单调递增，f(0)=0，此时f(x)在区间[0,1]上有一个零点；当a >1时，−1−√1−1a <0且−1+√1−1a<0，∴f(x)在[0,1]单调递增；f(0)=0，此时f(x)在区间[0,1]上有一个零点； 当a <0时，令f′(x)=0，故x =−1+√1−1a >0(负值舍去)①当−1+√1−1a ≥1即−13≤a <0时，f(x)在[0,1]单调递增，f(0)=0，此时f(x)在区间[0,1]上有一个零点； ②当−1+√1−1a<1即a <−13时，若f(1)>0即1e −1<a <−13时，f(x)在[0,−1+√1−1a )单调递增，在[−1+√1−1a ,1]单调递减，f(0)=0，此时f(x)在区间[0,1]上有一个零点；若f(1)≤0即a ≤1e −1时，f(x)在[0,−1+√1−1a )单调递增，在[−1+√1−1a ,1]单调递减，f(0)=0，此时f(x)在区间[0,1]上有零点x =0和在区间[−1+√1−1a ,1]有一个零点共两个零点；综上：当a ≤1e −1时，f(x)在区间[0,1]上有2个零点；当a >1e −1时，f(x)在区间[0,1]上有1个零点.…………………(12分)【解析】(1)求出函数的导数，通过讨论a 的范围，求出函数的单调区间即可； (2)通过讨论a 的范围，求出函数f(x)在[0,1]的单调性，从而判断函数的零点个数． 本题考查了函数的单调性，最值问题，考查导数的应用以及分类讨论思想，转化思想，是一道综合题．22. 已知直线l 的参数方程为{x =−√22ty =a +√22t(t 为参数，a ∈R)，曲线C 的极坐标方程为ρsin 2θ=4cosθ．(1)分别将直线l 的参数方程和曲线C 的极坐标方程化为直角坐标方程； (2)若直线l 经过点(0,1)，求直线l 被曲线C 截得线段的长． 【答案】解：(1)∵直线l 的参数方程为{x =−√22ty =a +√22t (t 为参数，a ∈R)， ∴直线l 的方程为y =−x +a ，即x +y −a =0，…………………(2分) ∵曲线C 的极坐标方程为ρsin 2θ=4cosθ，∴ρ2sin 2θ=4ρcosθ， ∴曲线C 的直角坐标方程为y 2=4x.……………(5分)(2)∵直线l 的参数方程{x =−√22ty =a +√22t(t 为参数，a ∈R) 过(0,1)，∴a =1，将直线l 的参数方程{x =−√22ty =a +√22t(t 为参数，a ∈R)代入y 2=4x ， 得t 2+6√2t +2=0， t 1+t 2=−6√2，t 1t 2=2， 由直线参数方程的几何意义可知，|AB|=|t 1−t 2|=√(t 1+t 2)2−4t 1t 2=√72−8=8.…………………(10分)【解析】(1)直线l 的参数方程消去参数，能求出直线l 的直角坐标方程；曲线C 的极坐标方程化为ρ2sin 2θ=4ρcosθ，由此能求出曲线C 的直角坐标方程．(2)由直线l 的参数方程过(0,1)，得到a =1，将直线l 的参数方程代入y 2=4x ，得t 2+6√2t +2=0，由此能求出|AB|．本题考查直线和曲线的直角坐标方程的求法，考查弦长的求法，考查直角坐方程、极坐标方程、参数方程的互化等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．23. 已知函数f(x)=|2x −4|+|x +1|，x ∈R ．(1)解不等式f(x)≤9；(2)若方程f(x)=−x 2+a 在区间[0,2]有解，求实数a 的取值范围． 【答案】解：(1)f(x)≤9可化为|2x −4|+|x +1|≤9， 故{3x −3≤9x>2，或{5−x ≤9−1≤x≤2，或{−3x +3≤9x<−1；…(2分) 解得：2<x ≤4，或−1≤x ≤2，或−2≤x <−1； …(4分) 不等式的解集为[−2,4]；…(5分)(2)由题意：f(x)=−x 2+a ⇔a =x 2−x +5，x ∈[0,2]．故方程f(x)=−x 2+a 在区间[0,2]有解⇔函数y =a 和函数y =x 2−x +5，图象在区间[0,2]上有交点∵当x ∈[0,2]时，y =x 2−x +5∈[194,7]∴，实数a 的取值范围是[194,7]…………………(10分)【解析】(1)通过讨论x 的范围得到关于x 的不等式组，解出即可；(2)根据题意，原问题可以等价函数y =a 和函数y =x 2−x +5图象在区间[0,2]上有交点，结合二次函数的性质分析函数y =x 2−x +5的值域，即可得答案．本题考查绝对值不等式的性质以及应用，注意零点分段讨论法的应用，属于中档题．。

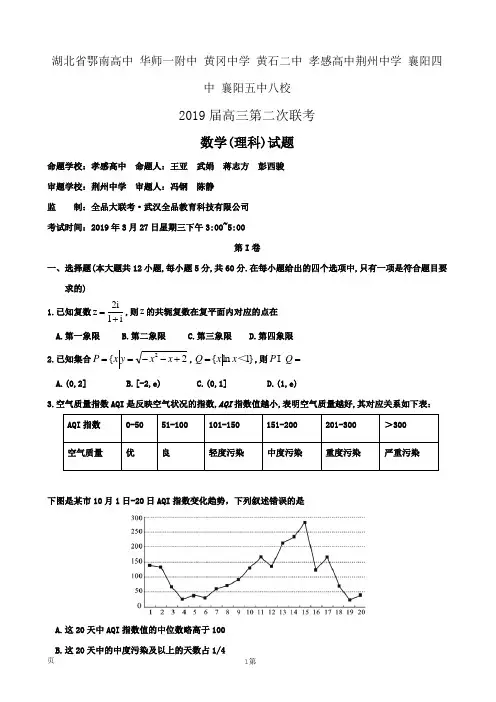
湖北省鄂南高中 华师一附中 黄冈中学 黄石二中 孝感高中荆州中学 襄阳四中 襄阳五中八校2019届高三第二次联考数学(理科)试题命题学校：孝感高中 命题人：王亚 武娟 蒋志方 彭西骏 审题学校：荆州中学 审题人：冯钢 陈静 监 制：全品大联考·武汉全品教育科技有限公司 考试时间：2019年3月27日星期三下午3:00~5:00第I 卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知复数i1i 2z +=,则z 的共轭复数在复平面内对应的点在A.第一象限B.第二象限C.第三象限D.第四象限 2.已知集合2{2+--==x x y x P ,}1ln {＜x x Q =,则=Q PA.(0,2]B.[-2,e)C.(0,1]D.(1,e)3.空气质量指数AQI 是反映空气状况的指数,AQI 指数值越小,表明空气质量越好,其对应关系如下表：下图是某市10月1日-20日AQI 指数变化趋势，下列叙述错误的是A. 这20天中AQI 指数值的中位数略高于100B. 这20天中的中度污染及以上的天数占1/4C. 该市10月的前半个月的空气质量越来越好D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好4.若等差数列{a n }的公差为-2,a 5是a 2与a 6的等比中项,则该数列的前n 项和Sn 取得最大值时,n 的值等于 A.4 B.5 C.6 D.75.将5个人从左至右排成一行,最左端只能排成甲或乙,最右端不能排甲,则不同的排法共有 A.36种 B.42种 C.48种 D.60种6.在△ABC 中,AD 为BC 边上的中线,且ED AE =,若AC u AB EB +=λ,则=uλA.-3B.31- C.3 D.317.“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一副“勾股圆方图”，用数形结合的方法给出了勾股定理的详细证明.如下图所示的“勾股圆方图”中，四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形，若直角三角形中较小的锐角6πα=，现在向该正方形区域内随机地投掷一枚飞镖，飞镖落在小正方形内的概率是A.23-1 B.23 C.43-4 D.438.函数])0,2[)(cos (sin cos 2)(π-∈+=x x x x x f 的最大值为A.2-1 B.1 C.2 D.21+9.已知抛物线)0(22＞p px y =的焦点为F ,过F 的直线l 交抛物线于B A ,两点(点A 在第一象限),若直线l 的倾斜角为32π,则=BFAFA.31 B.52 C.21 D.3210.如图,某多面体的三视图中正视图、侧视图和俯视图的外轮廓分别为直角三角形、直角梯形和直角三角形，则该多面体的各条棱中，最长的棱的长度为A.22B.10C.32D.1311.已知双曲线)0,(12222＞b a by ax =-的左、右顶点分别为B A ,,右焦点为F ,过点F 且垂直于x 轴的直线l 交双曲线于N M ,2点,P 为直线l 上的一点，当APB ∆的外接圆面积达到最小值时,点P 恰好在M (或N )处,则双曲线的离心率为A.2B.3C.2D.512.已知函数⎪⎩⎪⎨⎧--≥+=0),1ln(20,121)(2＜x x x x x f ,若函数kx x f x g -=)()(有且只有2个零点,则实数k 的取值范围为A.(0,2)B.(0,12)C.(2,+∞)D.(12,2)第II 卷二、填空题(本大题共4小题,每小题5分,共20分,把正确答案填在答题卡)13. 若y x ,满足⎪⎩⎪⎨⎧≥+≥≤322y x x y x ,则y x 2+的最小值为_____.14. 已知函数13)1()(23+--+=ax x a x x f ,若)(x f 在1=x 处取得极值,则曲线)(x f y =在点(0,f (0))处的切线方程为____.15. 已知数列{a n }满足a n =2a n-1+2n-1(n ∈N*,n ≥2),若a 4=65,则a 1=____.16. 设),0(4)4(ln )(),(2222R b a bba b a b a ∈+-+-=＞ϕ,当b a ,变化时),(b a ϕ的最小值为_____.三、解答题(本大题分为必考题和选做题两部分共70分)17．(12分)在△ABC 中,角A,B,C 的对边分别是a,b,c ，且向量m =(2a-c ,b )与向量n =(cos C ,cos B )共线。

湖北省黄冈中学、华师一附中、襄阳四中、襄阳五中、荆州中学等八校2019届高三第二次联考数学（文）试题考试时间：2019年3月27日下午15:00—17:00★祝考试顺利★注意事项：1.答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2.选择题的作答:每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

3.填空题和解答题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

4.选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。

答案写在答题卡上对应的答题区域内，写在试卷、草稿纸和答题卡上的非答题区域均无效。

5.考试结束后，请将答题卡上交。

第I 卷一、选择题:本题共12小题,每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的. 1.)300cos(0-的值 A. 21- B.23- C. 23 D. 212.已知复数),9R y x yi x z ∈+=，若i yix i+=++142，则||z = A.{0} B.{1}C. φD.10 3.已知集合 A={2<)5(log <2+x x }，B={x x y y -+-=11|}，则=B AA. {0}B. {1}C. φD. {-1<<4|x x -}4.用反证法证明命题：“0>ca bc ab 0,>,,,++++∈c b a R c b a ，则 a>0，b>0，c>0”时应假设为A. a ，b ，c 均不为正数B. a ，b ，c 至少有一个正数C. a ，b ，c 不全为正数D. a ，b ，c 至多有一个正数5.设a ，b 是单位向量，且a,b 的夹角为60°，则c=3a + b 的模为 A.13 B. 13 C. 4 D. 166.设m l ,表示两条不同的直线，βα,表示两个不同的平面，Q 表示一个点，给出下列四个命题，其中正确的命题是 ①lQ l a Q ∈⇒⊂∈α,②ββ∈⇒⊂=l m Q m l ,③αα⊂⇒∈∈⊂m a Q m Q l m l ,,,//④βαββαβα∈⊥∈∈=⊥l l Q Q m ,,,且,A.①②B.②③C.②③D.③④7.函数x x x x x f cos sin 2sin cos )(22--= (其中]2,0[π∈x ）的值域是A. [-1,1]B. [2-,2] C . [2-,1] D. [-1,2]8.已知三棱锥的三视图如图所示，且各顶点在同一球面上，则该球体的表面积是A.π12B. π10C. π8D.π69.已知 a = ln2,b = log 23，c = log 58,则 a ，b ，c 的大小关系是 A. a 〈c 〈b B. a 〈b 〈c C. c 〈a 〈b D. c 〈b 〈a 10.在△ABC 中，AC=2，BC=22，则∠B 的取值范围是 A.4B <0π≤B.6B <0π≤^C. 4B <0π≤或0<B 43≤π D.6B <0π≤或ππ<B 65≤ 11.两个好朋友小聪和小明，在同一天小聪从深圳到黄石，中午到武汉站的时间为13:30,然后再乘坐城 际铁路到黄石，中间有1小时在武汉站候车室休息。

湖北省鄂南高中华师一附中黄冈中学黄石二中荆州中学孝感高中襄阳四中襄阳五中八校2019届高三第二次联考理科综合试题命题学校：襄阳四中命题人：徐曙光王琴王洪升曹静张华马宁莎审题学校：荆州中学审题人：黎莉孔鹏珂毛建明顾琼刘俊华鄢先军监制：全品大联考·武汉全品教育科技有限公司考试时间：2019年3月28日上午9：00—11：30★祝考试顺利★注意事项：1．答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

4．选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。

答案写在答题卡上对应的答题区域内，写在试卷、草稿纸和答题卡上的非答题区域均无效。

5．考试结束后，请将本试卷和答题卡一并上交。

可能用到的相对原子质量：H—1 C—12 Si—28 C1—35.5 P—31 Cu—64 一、选择题：本题共13小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列有关细胞的组成、结构与功能的叙述，不正确的是A．草履虫等个体较大的细胞有两个细胞核，保证了正常的核质比B．哺乳动物成熟的红细胞没有细胞核，利于血红蛋白携带氧C．神经细胞有许多突起，利于接受刺激产生兴奋并传导兴奋D．线粒体内膜上的蛋白质只有有氧呼吸相关的酶，利于有氧呼吸高效进行2．下列四种现象，不能用右图表示的是A．在温度和pH适宜的条件下，酶促反应速率随底物浓度的变化B．在气候条件适宜的情况下，弃耕农田物种丰富度随时间的变化C．在质量浓度为0.3g／mL的蔗糖溶液中，紫色洋葱鳞片叶外表皮细胞吸水能力随时间的变化D．植物横放于地，其水平方向的根近地一侧生长素浓度随时间的变化(虚线表示对根生长既不促进也不抑制的生长素浓度)3．下列有关生物学研究方法的叙述，不正确的是A．通过显微镜观察并绘制细胞结构图片属于构建物理模型B．运用假说—演绎法验证的实验结果不一定与演绎推理的结论相符C．生命系统的不同层次都可从系统的组成、结构和功能等方面进行研究D．荧光标记法和同位素标记法都可用于追踪物质的运行和变化规律4．下表是探究两种植物根部竞争和茎叶竞争对植物生长影响的实验结果。

鄂南高中华师一附中黄冈中学黄石二中湖北省八校荆州中学孝感高中襄阳四中襄阳五中英语试题命题学校：黄冈中学命题人：方方冯静审题学校：荆州中学审题人：赖锋利王芳监制：大联考·武汉教育科技有限公司考试时间：2019年3月28日下午15：00—17：00★祝考试顺利★注意事项：1. 答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2. 选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

3. 非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

4. 考试结束后，请将答题卡上交。

第一部分听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt?A. £19.15.B. £9. 18.C. £9.15.答案是C。

1. What will the speakers do?A. Catch a flight.B. Pick up their son.C. Deal with an accident.2. How does the man feel about Lila?A. Bored.B. Scared.C. Excited.3. How did the woman get to Baltimore?A. By train.B. By bus.C. By taxi.4. Where is the man going tomorrow?A. To the school.B. To the beach.C. To the cinema.5. What does the woman mainly talk about?A. Buying a good bike.B. Learning how to drive.C. Paying attention to safety.第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

2019届高三第二次联考文科综合试题12.某商品的需求曲线与供给曲线如图5所示，其中E点为供求平衡点，P2为均衡价格。

不考虑其他因素，可推断出下列结论①国家为保护农民生产积极性，可将农产品最低保护价定在巧处②国家为保障民生，可将基本品种食盐的最高限制价定在P2处③当价格处于P1时，该商品生产者获利增加，其互补品需求量降低④当价格处于P0时，该商品市场实现供求平衡，其生产者不赚不亏A.①②B.①④C.②③D.③④13. 2018年9月13日，经济日报刊发了题为《对“私营经济离场论”这类蛊惑人心的奇葩论调应高度警惕——“两个毫不动摇”任何时候都不能偏废》的文章。

其经济学依据是①公有制经济和非公有制经济都是我国经济社会发展的重要基础②非公有制经济能支撑经济增长，更加适应先进生产力发展要求③公有制经济和非公有制经济都是社会主义经济的重要组成部分④发展非公有制经济是坚持和完善我国基本经济制度的必然要求A.①③B.①④C.②③D_②④14.党的十九大提出：“中国特色社会主义进入新时代，我国社会主要矛盾已经转化为人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾。

”这个关于新的社会主要矛盾的科学判断，具有十分重要的理论价值和现实意义。

要解决好新的社会主要矛盾，必须①实施精准扶贫政策，坚决打赢脱贫攻坚战，实现城乡一体化发展②实施积极的货币政策，适度降低增值税税率，减轻企业税收负担③坚持“绿水青山就是金山银山”的理念，走生态优先绿色发展之路④着力解决社会生产落后的问题，满足人民日益增长的物质文化需要A.①③B.①④C.②③D.②④15.2018年以来，我国出台多项扩大进口的政策措施，一方面满足国内不断升级的消费需求，将促进我国经济实现高质量发展;另一方面，为其他贸易伙伴提供更多机会，会对各国经济贸易的增长产生拉动作用。

扩大进口的政策措施对我国经济发展的积极影响有①有利于我国对外贸易平衡发展，吸引更多外商投资②有利于“倒逼”国内企业提升管理水平，提高竞争力③有利于带动其他国家经济发展，构建人类命运共同体④为我国发展更髙层次的开放型经济创造良好国际环境A.①②B.③④C.①③D.②④16.“人不以规矩则废，党不以规矩则乱”，党员干部讲规矩要做到“心有所畏、言有所戒、行有所止”，下列体现“心有所畏”的是①把严守政治纪律和政治规矩摆在重要位置，坚决维护纪律②党员干部要始终牢记权力是人民赋予的，牢记公权为民③增强对各类谣言具备明辨是非的能力、不予传播的自律④要带头做好表率，自觉抵制不良风气，厉行勤俭节约A.①②B.①③C.②④D.③④17.习近平总书记指出：“我国法治建设的成就，归结起来就是开辟了中国特色社会主义法治道路。

2019届湖北省八校（鄂南高中.黄石二中.华师一附中.黄冈中学.荆州中学.孝感中学.襄阳四中.襄阳五中）高三第二次联合考试数学（理）一、单选题1．设集合，，则A．B．C．D．【答案】D【解析】：化简集合，根据交集的定义计算【详解】：因为集合，化简，所以，故选D．【点睛】：研究集合问题，一定要抓住元素，看元素应满足的属性．研究两集合的关系时，关键是将两集合的关系转化为元素间的关系，本题实质求满足属于集合且属于集合的元素的集合．2．若复数z满足为虚数单位，为z的共轭复数，则A．B．2 C．D．3【答案】A【解析】分析：把已知等式变形，利用复数代数形式的乘除运算化简，结合复数模的公式求解.详解：由，得，则，，则，故选A.点睛：复数是高考中的必考知识，主要考查复数的概念及复数的运算．要注意对实部、虚部的理解，掌握纯虚数、共轭复数这些重要概念，复数的运算主要考查除法运算，通过分母实数化转化为复数的乘法，运算时特别要注意多项式相乘后的化简，防止简单问题出错，造成不必要的失分.3．在矩形ABCD中，，，若向该矩形内随机投一点P，那么使得与的面积都不小于2的概率为A．B．C．D．【答案】D【解析】，由题意知本题是一个几何概型的概率，以AB为底边，要使面积不小于2，由于，则三角形的高要h⩾1,同样,P点到AD的距离要不小于，满足条件的P的区域如图，其表示的区域为图中阴影部分,它的面积是，∴使得△ABP与△ADP的面积都不小于2的概率为：.故选D.4．已知函数为偶函数，且在上单调递减，则的解集为A．B．C．D．【答案】B【解析】根据函数奇偶性的定义，求出a，b的关系，结合函数的单调性判断a的符号，然后根据不等式的解法进行求解即可．【详解】∵f（x）=（x-1）（ax+b）=ax2+（b-a）x-b为偶函数，∴f（-x）=f（x），则ax2-（b-a）x-b=ax2+（b-a）x-b，即-（b-a）=b-a，得b-a=0，得b=a，则f（x）=ax2-a=a（x2-1），若f（x）在（0，+∞）单调递减，则a＜0，由f（3-x）＜0得a[（3-x）2-1）]＜0，即（3-x）2-1＞0，得x＞4或x＜2，即不等式的解集为（-∞，2）∪（4，+∞），故选B．【点睛】本题主要考查不等式的求解，根据函数奇偶性的性质求出a，b的关系是解决本题的关键．5．已知双曲线的离心率为，则a的值为A．1 B．C．1或D．【答案】C【解析】分析：可用排除法，验证与是否符合题意即可得结果.详解：可用排除法，当时，化为，离心率为，符合题意；当时，化为，离心率为，符合题意,的值为，故选C.点睛：用特例代替题设所给的一般性条件，得出特殊结论，然后对各个选项进行检验，从而做出正确的判断，这种方法叫做特殊法. 若结果为定值，则可采用此法. 特殊法是“小题小做”的重要策略，排除法解答选择题是高中数学一种常见的解题思路和方法，这种方法即可以提高做题速度和效率.6．等比数列的前n项和，前2n项和，前3n项的和分别为A，B，C，则A．B．C．D．【答案】D【解析】分析：由等比数列的性质，可知其第一个项和，第二个项和，第三个项和仍然构成等比数列，化简即可得结果.详解：由等比数列的性质可知，等比数列的第一个项和，第二个项和，第三个项和仍然构成等比数列，则有构成等比数列，，即，，故选D.点睛：本题考查了等比数列的性质，考查了等比数列前项和，意在考查灵活运用所学知识解决问题的能力，是基础题.7．执行如图所示的程序框图，若输入，，输出的，则空白判断框内应填的条件可能是A．B．C．D．【答案】B【解析】分析：将题中所给的程序框图模拟运行，逐步运算，结合题的条件，明确循环几次，到什么程度就会结束，从而利用相关的条件，得到其满足的式子，从而求得结果. 详解：当第一次执行，，，返回；第二次执行，，，，返回；第三次执行，，，，要输出x，故满足判断框，此时，故选B.点睛：该题考查的是有关程序框图的问题，涉及到的知识点是补全程序框图，在解题的过程中，注意对框图进行模拟运行，结合题的条件，求得结果.8．将函数图象上的每个点的横坐标缩短为原来的一半，纵坐标不变，再将所得图象向左平移个单位得到函数的图象，在图象的所有对称轴中，离原点最近的对称轴方程为A．B．C．D．【答案】A【解析】分析：根据平移变换可得，根据放缩变换可得函数的解析式，结合对称轴方程求解即可.详解：将函数的图象上的每个点的横坐标缩短为原来的一半，纵坐标不变，得到，再将所得图象向左平移个单位得到函数的图象，即，由，得，当时，离原点最近的对称轴方程为，故选A.点睛：本题主要考查三角函数的图象与性质，属于中档题.由函数可求得函数的周期为；由可得对称轴方程；由可得对称中心横坐标. 9．在的展开式中，含项的系数是A．119 B．120 C．121 D．720【答案】B【解析】分析：展开式中含项的系数是，利用组合数的运行性质计算即可.详解：的展开式中，含项的系数是，故选B.点睛：本题主要考查二项展开式定理的通项与系数以及组合式的性质，属于简单题. 二项展开式定理的问题也是高考命题热点之一，关于二项式定理的命题方向比较明确，主要从以下几个方面命题：（1）考查二项展开式的通项公式；（可以考查某一项，也可考查某一项的系数）（2）考查各项系数和和各项的二项式系数和；（3）二项展开式定理的应用.10．我国古代数学名著九章算术记载：“刍甍者，下有袤有广，而上有袤无丈刍，草也；甍，屋盖也”翻译为：“底面有长有宽为矩形，顶部只有长没有宽为一条棱刍甍字面意思为茅草屋顶”如图，为一刍甍的三视图，其中正视图为等腰梯形，侧视图为等腰三角形则它的体积为A．B．160 C．D．64【答案】A【解析】分析：由三视图可知该刍甍是一个组合体，它由成一个直三棱柱和两个全等的四棱锥组成，根据三视图中的数据可得其体积.详解：由三视图可知该刍甍是一个组合体，它由成一个直三棱柱和两个全等的四棱锥组成，根据三视图中的数据，求出棱锥与棱柱的体积相加即可，，故选A.点睛：本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力，属于难题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响，对简单组合体三视图问题，先看俯视图确定底面的形状，根据正视图和侧视图，确定组合体的形状.11．已知椭圆C：，直线l：与x轴相交于点E，过椭圆右焦点F的直线与椭圆相交于A，B两点，点C在直线l上，则“轴”是“直线AC过线段EF中点”的A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】分析：若轴，不妨设与轴交于点，过作交直线于点，由平行线的性质结合椭圆第二定义可得，进而可得结果.详解：若轴，不妨设与轴交于点，过作交直线于点，则：，两次相除得：，又由第二定义可得，为的中点，反之，直线过线段中点，直线斜率为零，则与重合，所以“轴”是“直线过线段中点”的充分不必要条件，故选A.点睛：判断充要条件应注意：首先弄清条件和结论分别是什么，然后直接依据定义、定理、性质尝试.对于带有否定性的命题或比较难判断的命题，除借助集合思想化抽象为直观外，还可利用原命题和逆否命题、逆命题和否命题的等价性，转化为判断它的等价命题；对于范围问题也可以转化为包含关系来处理.12．下列命题为真命题的个数是；；；A．1 B．2 C．3 D．4【答案】C【解析】本题首先可以构造函数，然后通过导数计算出函数的单调性以及最值，然后通过对①②③④四组数字进行适当的变形，通过函数的单调性即可比较出大小。

湖北省黄冈中学、华师一附中、襄阳四中、襄阳五中、荆州中学等八校2019届高三生物第二次联考试题一、选择题：本题共13小题，每小题6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.下列有关细胞的组成、结构与功能的叙述，不正确的是A.草履虫等个体较大的细胞有两个细胞核，保证了正常的核质比B.哺乳动物成熟的红细胞没有细胞核，利于血红蛋白携带氧C.神经细胞有许多突起，利于接受刺激产生兴奋并传导兴奋D.线粒体内膜上的蛋白质只有有氧呼吸相关的酶，利于有氧呼吸高效进行2.下列四种现象，不能用右图表示的是A.在温度和pH适宜的条件下，酶促反应速率随底物浓度的变化B.在气候条件适宜的情况下，弃耕农田物种丰富度随时间的变化C.在质量浓度为0.3g/mL的蔗糖溶液中，紫色洋葱鳞片叶外表皮细胞吸水能力随时间的变化D.植物横放于地，其水平方向的根近地一侧生长素浓度随时间的变化（虚线表示对根生长既不促进也不抑制的生长素浓度）3.下列有关生物学研究方法的叙述，不正确的是A.通过显微镜观察并绘制细胞结构图片属于构建物理模型B.运用假说一演绎法验证的实验结果不一定与演绎推理的结论相符C.生命系统的不同层次都可从系统的组成、结构和功能等方面进行研究D.荧光标记法和同位素标记法都可用于追踪物质的运行和变化规律4.下表是探究两种植物根部竞争和茎叶竞争对植物生长影响的实验结果。

表中单株干重的百分比表示在无关变量相同且适宜的情况下，每组单株干重占单独种植时干重的百分比。

下列分析错误的是A.甲组和乙组均为对照组B.Z和W要求选择同种生长发育状况相同的植株C.植物受土壤资源限制的程度比受光资源限制的程度更高D.植物根茎叶竞争时干重的总降低程度接近于根部和茎叶单独竞争时干重下降程度的乘积5.下列有关遗传和变异的叙述，不正确的是A.某DNA病毒把病毒外壳蛋白基因插入到受体细胞染色体DNA上属于基因重组B.一对夫妇中只有一方患线粒体肌病(线粒体DNA缺陷导致），子女表现为全部正常或全部患该病C.皱粒豌豆的染色体DNA中插入了一段外来的DNA序列，导致编码淀粉分支酶的基因结构改变属于基因突变D.控制人类单基因遗传病的基因遗传都遵循分离定律，控制多基因遗传病的基因遗传都遵循自由组合定律6.下列有关信息传递的叙述，正确的是A. T2噬菌体的遗传信息传递可以在肺炎双球菌的核糖体上进行B.激素和神经递质都是通过与靶细胞细胞膜上的受体结合来传递信息C.在没有受到抗原刺激的情况下，少数B细胞经淋巴因子作用后就可开始增殖、分化D.利用昆虫信息素诱捕或警示有害动物，降低害虫种群密度，属于生物防治29.(10分）科学家以真核生物绿藻为材料，研究不同波长的光对植物光合速率的影响。

2018-2019学年湖北省黄冈中学、华师一附中、襄阳四中、襄阳五中、荆州中学等八校高三（下）第二次联考数学试卷（文科）一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）cos（﹣300°）等于（）A．﹣B．﹣C．D．2．（5分）已知复数z＝x+yi（x，y∈R），若，则|z|＝（）A．{0}B．{1}C．∅D．3．（5分）已知集合A＝{x|0＜log2（x+5）＜2}，B＝{}，则A∩B＝（）A．{0}B．{1}C．∅D．{x|﹣4＜x＜﹣1} 4．（5分）用反证法证明命题：“a，b，c∈R，a+b+c＞0，ab+bc+ca＞0，则a＞0，b＞0，c＞0”时应假设为（）A．a，b，c均不为正数B．a，b，c至少有一个正数C．a，b，c不全为正数D．a，b，c至多有一个正数5．（5分）设，是单位向量，且，的夹角为60°，则＝3+的模为（）A．B．13C．4D．166．（5分）设l，m表示两条不同的直线，α，β表示两个不同的平面，Q表示一个点，给出下列四个命题，其中正确的命题是（）①Q∈α，l⊂α⇒Q∈l②l∩m＝Q，m⊂β⇒l∈β③l∥m，l⊂α，Q∈m，Q∈α⇒m⊂α④α⊥β，且α∪β＝m，Q∈β，Q∈l，l⊥α∈βA．①②B．②③C．②③D．③④7．（5分）函数f（x）＝cos2x﹣sin2x﹣2sin x cos x（其中）的值域是（）A．[﹣1，1]B．[，]C．[，1]D．[﹣1，] 8．（5分）已知三棱锥的三视图如图所示，且各顶点在同一球面上，则该球体的表面积是（）A．12πB．10πC．8πD．6π9．（5分）已知a＝ln2，b＝log23，c＝log58，则a，b，c的大小关系是（）A．a＜c＜b B．a＜b＜c C．c＜a＜b D．c＜b＜a10．（5分）在△ABC中，AC＝，BC＝，则∠B的取值范围是（）A．B．^C．或D．或11．（5分）两个好朋友小聪和小明，在同一天小聪从深圳到黄石，中午到武汉站的时间为13：30，然后再乘坐城际铁路到黄石，中间有1小时在武汉站候车室休息．小明从沌口开发区坐出租车到武汉站，小明到达武汉站的时间为14：00〜15：00之间任一时刻到达，然后乘坐发车时间为15：30的高铁到北京，那么两个好朋友能够在武汉站会面的概率是（）A．B．C．D．12．（5分）已知双曲线（a＞b＞0）的左焦点为F，过原点直线与双曲线相交于A，B两点，已知|AB|＝20，|AF|＝16，且cos，则双曲线的离心率（）A．5B．3C．2D．二、填空题：本题共4小题，每小题5分，共20分．13．（5分）某高中对学生春节期间观看亚洲杯的调查，该校高一有800人，高二有900人，高三有1300人，现采用分层抽样随机抽取60人，则高三年级应抽取人．14．（5分）在直角△AOB中，∠AOB＝90°，，OC平分∠AOB且与AB相交于C，则在上的投影为．15．（5分）已知抛物线方程为x2＝12y，过抛物线的焦点作倾斜角为60°的直线与抛物线相交于A，B两点，则|AB|＝．16．（5分）已知函数，给出下列命题，其中正确命题的序号是．（1）x1，x2是f（x）＝3的两个不相等的根，则；（2）是函数f（x）的对称中心；（3）也是函数的对称中心；（4）是函数f（x）的对称轴．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤.17．（12分）设数列{a n}的前n项和为S n，且，在正项等比数列{b n}中，b3＝a2，b4＝a4．求（1）{a n}和{b n}的通项公式；（2）设c n＝令T n＝c1+c2+…+c n，求T10．18．（12分）如图：正三棱柱ABC﹣A1B1C1中BC＝2，CC1＝2，点P在平面ABB1A1中，且PA1＝PB1＝（1）求证：PC1⊥AB；（2）求三棱锥P﹣A1B1C的体积19．（12分）某公司准备加大对一项产品的科技改造，经过充分的市场调研与模拟，得到x，y之间的一组数，其中x单位：百万元）是科技改造的总投入，y（单位：百万元）是改造后的额外收益．其中是对当地GDP的增长贡献值．（1）若从五组数据中任取两组，求至少有一组满足G（x，y）≥25的概率；（2）对于表中数据，甲、乙两个同学给出的拟合直线方程为：l1：y＝2x+1，，试用最小二乘法判断哪条直线的拟合程度更好．（附；Q越小拟合度越好．）20．（12分）已知椭圆（a＞b＞0）的离心率是椭圆上三个不同的点，F为其右焦点，且|AF|，|BF|，|CF|成等差数列（1）求椭圆的方程；（2）求m+p的值；（3）若线段AC的垂直平分线与x轴交点为D，求直线BD的斜率k．21．（12分）已知函数f（x）＝lnx+ax2+bx．（1）函数f（x）在（1，f（1））点的切线l方程为2x+y＝0，求a，b的值，并求函数f （x）的最大值；（2）当a＝0，b＝l且t∈（0，+∞），关于x的方程tf（x）＝x2有唯一实数解，求实数t的值．请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题计分．[选修4一4：坐标系与参数方程]22．（10分）在极坐标系中，已知直线l：p（cosθ+sinθ）＝2与曲线C：C：p＝4cosθ．（1）若直线l与曲线C有两个交点A，B，求|AB|；（2）若点P是曲线上与A，B相异的任一点，求△PAB面积的最大值．[选修4一5：不等式选讲]23．（1）已知函数f（x）＝|x﹣2a|+|x+b|（a＞0，b＞0）的最小值为2，求a与b的关系；（2）若a，b满足（1）中的条件，求9a+3b的最小值．2018-2019学年湖北省黄冈中学、华师一附中、襄阳四中、襄阳五中、荆州中学等八校高三（下）第二次联考数学试卷（文科）参考答案与试题解析一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）cos（﹣300°）等于（）A．﹣B．﹣C．D．【分析】利用三角函数关系式与诱导公式即可求得cos（﹣3000）的值．【解答】解：∵cos（﹣300°）＝cos（﹣360°+60°）＝cos60°＝．故选：C．【点评】本题考查运用诱导公式化简求值，属于基础题．2．（5分）已知复数z＝x+yi（x，y∈R），若，则|z|＝（）A．{0}B．{1}C．∅D．【分析】把已知等式变形，利用复数代数形式的乘除运算化简，再由复数相等的条件求得x，y值，代入复数模的计算公式求解．【解答】解：∵，∴2+4i＝（1+i）（x+yi）＝（x﹣y）+（x+y）i，则，即x＝3，y＝1．∵z＝x+yi，∴|z|＝．故选：D．【点评】本题考查复数代数形式的乘除运算，考查复数相等的条件及复数模的求法，是基础题．3．（5分）已知集合A＝{x|0＜log2（x+5）＜2}，B＝{}，则A∩B＝（）A．{0}B．{1}C．∅D．{x|﹣4＜x＜﹣1}【分析】分别求出集合A，B，由此能求出A∩B．【解答】解：∵集合A＝{x|0＜log2（x+5）＜2}＝{x|﹣4＜x＜﹣1}，B＝{}＝{y|y＝0}，∴A∩B＝∅．故选：C．【点评】本题考查交集的求法，考查交集定义、不等式的性质等基础知识，考查运算求解能力，是基础题．4．（5分）用反证法证明命题：“a，b，c∈R，a+b+c＞0，ab+bc+ca＞0，则a＞0，b＞0，c＞0”时应假设为（）A．a，b，c均不为正数B．a，b，c至少有一个正数C．a，b，c不全为正数D．a，b，c至多有一个正数【分析】由于用反证法证明命题时，应先假设命题的否定成立【解答】解：∵用反证法证明命题时，应先假设命题的否定成立，而“a＞0，b＞0，c＞0”的否定为：“a，b，c不全为正数”，故选：C．【点评】本题主要考查用命题的否定，反证法证明数学命题的方法和步骤，把要证的结论进行否定，得到要证的结论的反面，是解题的突破口，属于基础题．5．（5分）设，是单位向量，且，的夹角为60°，则＝3+的模为（）A．B．13C．4D．16【分析】根据条件即可得出，从而可求出，进而可得出的模．【解答】解：∵；∴；∴．故选：A．【点评】考查单位向量的概念，向量夹角的定义，以及向量数量积的运算及计算公式，向量长度的求法．6．（5分）设l，m表示两条不同的直线，α，β表示两个不同的平面，Q表示一个点，给出下列四个命题，其中正确的命题是（）①Q∈α，l⊂α⇒Q∈l②l∩m＝Q，m⊂β⇒l∈β③l∥m，l⊂α，Q∈m，Q∈α⇒m⊂α④α⊥β，且α∪β＝m，Q∈β，Q∈l，l⊥α∈βA．①②B．②③C．②③D．③④【分析】根据空间点，线面之间的位置关系进行判断即可．【解答】解：①Q∈α，l⊂α，则Q∈l不一定成立，故①错误，排除A，②l∩m＝Q，m⊂β，则l∈β不一定成立，只有两个不同的点同时在平面β内才成立，故②错误，排除B，C，③l∥m，l⊂α，Q∈m，Q∈α⇒m⊂α，正确④α⊥β，且α∪β＝m，Q∈β，Q∈l，l⊥α∈β，正确故选：D．【点评】本题主要考查命题的真假判断，涉及空间点，线面位置关系的判断，结合定义和性质是解决本题的关键．7．（5分）函数f（x）＝cos2x﹣sin2x﹣2sin x cos x（其中）的值域是（）A．[﹣1，1]B．[，]C．[，1]D．[﹣1，]【分析】利用三角恒等变换化简f（x）的解析式，再利用余弦函数的定义域和值域求得f （x）的值域．【解答】解：函数f（x）＝cos2x﹣sin2x﹣2sin x cos x＝cos2x﹣sin2x＝cos（2x+），∵，∴2x+∈[，]，∴cos（2x+）∈[﹣1，]，故f（x）∈[﹣，1]，故选：C．【点评】本题主要考查三角恒等变换，余弦函数的定义域和值域，属于基础题．8．（5分）已知三棱锥的三视图如图所示，且各顶点在同一球面上，则该球体的表面积是（）A．12πB．10πC．8πD．6π【分析】根据题意把该三棱锥放入长方体中，知三棱锥的外接球即为长方体的外接球，求出外接球的表面积．【解答】解：根据三视图知，把该三棱锥放入长宽高分别为2、、的长方体中，如图所示；则三棱锥的外接球即为长方体的外接球，所以外接球的直径满足（2R）2＝PC2＝22++＝12，所以外接球的表面积是4πR2＝12π．故选：A．【点评】本题考查了三视图与直观图的关系，也考查了空间想象能力与转化能力，是基础题．9．（5分）已知a＝ln2，b＝log23，c＝log58，则a，b，c的大小关系是（）A．a＜c＜b B．a＜b＜c C．c＜a＜b D．c＜b＜a【分析】容易得出，从而得出a，b，c的大小关系．【解答】解：∵，；∴a＜c＜b．故选：A．【点评】考查对数函数的单调性，以及对数的运算．10．（5分）在△ABC中，AC＝，BC＝，则∠B的取值范围是（）A．B．^C．或D．或【分析】设AB＝x（），利用余弦定理建立cos B关于x的函数，从而求出B的范围．【解答】解：设AB＝x，则，由余弦定理可得，＝，根据余弦函数的性质可知，．故选：B．【点评】本题考查余弦定理的应用，属于中档题目．11．（5分）两个好朋友小聪和小明，在同一天小聪从深圳到黄石，中午到武汉站的时间为13：30，然后再乘坐城际铁路到黄石，中间有1小时在武汉站候车室休息．小明从沌口开发区坐出租车到武汉站，小明到达武汉站的时间为14：00〜15：00之间任一时刻到达，然后乘坐发车时间为15：30的高铁到北京，那么两个好朋友能够在武汉站会面的概率是（）A．B．C．D．【分析】由题意知本题是一个几何概型，以面积为测度，根据面积之比得到概率．【解答】解：由题意知本题是一个几何概型，且于小明到达的时间有关，∵试验发生包含的所有事件对应的测度为14：00﹣15：00＝60分钟，其中能够在武汉站会面的测度为14：00﹣14：30＝30分钟∴两人能够会面的概率p＝＝，故选：D．【点评】本题主要考查几何概型的概率的计算，利用面积为测度是解决本题的关键．12．（5分）已知双曲线（a＞b＞0）的左焦点为F，过原点直线与双曲线相交于A，B两点，已知|AB|＝20，|AF|＝16，且cos，则双曲线的离心率（）A．5B．3C．2D．【分析】在△AFB中，由余弦定理可得|AF|2＝|AB|2+|BF|2﹣2|AB||BF|cos∠ABF，即可得到|BF|，设F′为双曲线的右焦点，连接BF′，AF′．根据对称性可得四边形AFBF′是矩形．即可得到a，c，进而求得离心率．【解答】解：在△AFB中，|AB|＝20，|AF|＝16，且cos，由余弦定理可得|AF|2＝|AB|2+|BF|2﹣2|AB||BF|cos∠ABF，从而可得（|BF|﹣12）2＝0，解得|BF|＝12．设F′为双曲线的右焦点，连接BF′，AF′．根据对称性可得四边形AFBF′是矩形．∴|BF′|＝16，|FF′|＝10．∴2a＝|16﹣12|，2c＝20，解得a＝2，c＝10．∴e＝＝5．故选：A．【点评】熟练掌握余弦定理、双曲线的定义、对称性、离心率、矩形的性质等基础知识是解题的关键．二、填空题：本题共4小题，每小题5分，共20分．13．（5分）某高中对学生春节期间观看亚洲杯的调查，该校高一有800人，高二有900人，高三有1300人，现采用分层抽样随机抽取60人，则高三年级应抽取26人．【分析】利用分层抽样的性质直接求解．【解答】解：某高中对学生春节期间观看亚洲杯的调查，该校高一有800人，高二有900人，高三有1300人，现采用分层抽样随机抽取60人，则高三年级应抽取：60×＝26．故答案为：26．【点评】本题考查高三应抽取人数的求法，考查分层抽样的性质等基础知识，考查运算求解能力，是基础题．14．（5分）在直角△AOB 中，∠AOB ＝90°，，OC 平分∠AOB 且与AB 相交于C ，则在上的投影为．【分析】如图距离直角坐标系，求出C 的坐标，利用向量的数量积求解即可． 【解答】解：在直角△AOB 中，∠AOB ＝90°，如图：建立直角坐标系，，OC 平分∠AOB 且与AB 相交于C ，可得A （1，0），B （0，2），AB 的方程为：2x +y ＝2，则C （，），则在上的投影为：＝＝．故答案为：．【点评】本题考查向量的数量积的应用，求解C 的坐标是解题的关键．15．（5分）已知抛物线方程为x 2＝12y ，过抛物线的焦点作倾斜角为60°的直线与抛物线相交于A ，B 两点，则|AB |＝ 12+6 ．【分析】直线l 的方程与抛物线方程联立得关于x 的一元二次方程，可得x 1+x 2值，再根据抛物线定义即可求得弦长．【解答】解：抛物线方程为x 2＝12y ，可得焦点坐标（0，3），由题意得：直线l 的方程为y ＝x +3，代入x 2＝12y ，得：x 2﹣12x ﹣36＝0．设点A （x 1，y 1），B （x 2，y 2），则：x 1+x 2＝12，由抛物线定义得：弦长|AB |＝x 1+x 2+p ＝12+6．故答案为：12+6．【点评】本题考查直线与圆锥曲线的综合问题，考查抛物线的性质与方程，属中档题．16．（5分）已知函数，给出下列命题，其中正确命题的序号是（1）（2）（3）．（1）x1，x2是f（x）＝3的两个不相等的根，则；（2）是函数f（x）的对称中心；（3）也是函数的对称中心；（4）是函数f（x）的对称轴．【分析】（1）根据正切函数的周期性进行判断（2）根据正切函数的对称中心即可判断（2）（3）（4）正切函数不存在对称轴【解答】解：（1）函数的最小正周期T＝，若x1，x2是f（x）＝3的两个不相等的根，则x1﹣x2＝，k≠0，则成立；（2）由2x+＝，得x＝﹣，即函数的对称中心为（﹣，0），k∈Z，当k＝0时，是函数f（x）的对称中心；故（2）正确，（3）由（2）知是函数的对称中心，故（3）正确；（4）f（x）只有对称中心，没有对称轴，即是函数f（x）的对称轴错误，故正确的是（1）（2）（3），故答案为：（1）（2）（3）【点评】本题主要考查与正切函数有关的命题的真假判断，结合正切函数的周期性以及对称性是解决本题的关键．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤.17．（12分）设数列{a n}的前n项和为S n，且，在正项等比数列{b n}中，b3＝a2，b4＝a4．求（1）{a n}和{b n}的通项公式；（2）设c n＝令T n＝c1+c2+…+c n，求T10．，计算可得所【分析】（1）由数列的递推式：n＝1时，a1＝S1；n≥2时，a n＝S n﹣S n﹣1求{a n}的通项公式，再由等比数列的通项公式可得所求；（2）由题意可得T10＝（a1+a3+a5+a7+a9）+（b2+b4+b6+b8+b10），计算可得所求和．【解答】解：（1）数列{a n}的前n项和为S n，且，可得n＝1时，a1＝S1＝3；n≥2时，a n＝S n﹣S n＝n2+n+1﹣（n﹣1）2﹣（n﹣1）﹣1＝2n，﹣1则a n＝；在正项等比数列{b n}中，b3＝a2，b4＝a4．可得b3＝a2＝4，b4＝a4＝8，可得公比q＝2，首项b1＝1，则b n＝2n﹣1；（2）c n＝，可得T10＝（a1+a3+a5+a7+a9）+（b2+b4+b6+b8+b10）＝（3+6+10+14+18）+（2+8+32+128+512）＝733．【点评】本题考查数列的递推式的运用，以及等比数列的通项公式，考查数列的求和方法：分组求和，化简运算能力，属于中档题．18．（12分）如图：正三棱柱ABC﹣A1B1C1中BC＝2，CC1＝2，点P在平面ABB1A1中，且PA1＝PB1＝（1）求证：PC1⊥AB；（2）求三棱锥P﹣A1B1C的体积【分析】（1）设A1B1的中点为D，连接PD与DC1，由已知可得PD⊥A1B1，同理DC1⊥A1B1，由线面垂直的判定可得A1B1⊥平面PDC1，得到A1B1⊥PC1．则PC1⊥AB；（2）由已知直接利用等积法求三棱锥P﹣A1B1C的体积．【解答】（1）证明：设A1B1的中点为D，连接PD与DC1，∵PA1＝PB1，∴PD⊥A1B1，同理DC1⊥A1B1，又PD∩DC1＝D，∴A1B1⊥平面PDC1，∴A1B1⊥PC1．又∵AB∥A1B1，∴PC1⊥AB；（2）解：∵△A1B1C1为正三角形，边长为2，PA1＝PB1＝．∴＝．【点评】本题考查空间中直线与直线、直线与平面位置关系的判定及其应用，考查空间想象能力与思维能力，训练了利用等积法求多面体的体积，是中档题．19．（12分）某公司准备加大对一项产品的科技改造，经过充分的市场调研与模拟，得到x，y之间的一组数，其中x单位：百万元）是科技改造的总投入，y（单位：百万元）是改造后的额外收益．其中是对当地GDP的增长贡献值．（1）若从五组数据中任取两组，求至少有一组满足G（x，y）≥25的概率；（2）对于表中数据，甲、乙两个同学给出的拟合直线方程为：l1：y＝2x+1，，试用最小二乘法判断哪条直线的拟合程度更好．（附；Q越小拟合度越好．）【分析】（1）由题知后两组数据满足条件，从五组数据中任意取出两组有10种情况，满足条件有后面两组，有一且满足条件的有2×3＝6种，两组均可有1种，共7种情况，由此能求出至少有一组满足G（x，y）≥25的概率．．（2）列表格求出Q1＜Q2，从而直线L1拟合度更好．【解答】解：（1）由题知后两组数据满足条件：从五组数据中任意取出两组有10种情况，（如ABCDE中取出两个有AB，AC，AD，AE，BC，BD，BE，CD，CE，DE，共10种），满足条件有后面两组，有一且满足条件的有2×3＝6种，（如AD，BD，CD《AE，BE，CE），两组均可有1种，（如DE），共7种情况，故至少有一组满足G（x，y）≥25的概率P＝．（2）如表格：＝4，＝17.5，Q1＜Q2，∴直线L1拟合度更好．【点评】本题考查概率的求法，考查最小二乘法的应用，考查古典概型、列举法等基础知识，考查运算求解能力，是基础题．20．（12分）已知椭圆（a＞b＞0）的离心率是椭圆上三个不同的点，F为其右焦点，且|AF|，|BF|，|CF|成等差数列（1）求椭圆的方程；（2）求m+p的值；（3）若线段AC的垂直平分线与x轴交点为D，求直线BD的斜率k．【分析】（1）根据椭圆的离心率公式和点在椭圆上，即可求出椭圆的方程，（2）由椭圆的第二定义，结合|AF|，|BF|，|CF|成等差数列，即可求出m+n＝6，（3）利用点差法求出直线AC的斜率，可得直线AC的方程，即可求出点D的坐标，可得直线BD的斜率k．【解答】解：（1）∵e＝＝，∴a＝2c，b＝c，将点B代入可得+＝1，∴+＝1，解得c＝2，∴椭圆的方程为+＝1．（2）由椭圆的第二定义|BF|＝ed＝e（﹣x0）＝a﹣3e，同理可得|AF|＝a﹣me，|BF|＝a﹣pe，∵|AF|，|BF|，|CF|成等差数列，∴m+p＝6．（3）∵+＝1，+＝1，两式相减可得（m+p）（m﹣p）＝﹣（n+q）（n﹣q），∴k AC＝＝﹣，∴AC的中垂线为y﹣＝（n+q）（x﹣3），令y＝0可得x＝，∴D（，0）为定点，∴k BD＝﹣．【点评】本题考查了椭圆的方程的求法，椭圆的性质，点差法，考查了运算能力和转化能力，属于中档题．21．（12分）已知函数f（x）＝lnx+ax2+bx．（1）函数f（x）在（1，f（1））点的切线l方程为2x+y＝0，求a，b的值，并求函数f （x）的最大值；（2）当a＝0，b＝l且t∈（0，+∞），关于x的方程tf（x）＝x2有唯一实数解，求实数t的值．【分析】（1）求得f（x）的导数，可得切线的斜率，由已知切线方程可得a，b；进而得到f（x）的单调性和极值、最值；（2）当a＝0时，方程tf（x）＝x2即x2﹣tx﹣tlnx＝0，令g（x）＝x2﹣tx﹣tlnx，对其进行求导，利用导数来函数的单调性和最值，解方程可得所求值．【解答】解：（1）函数f（x）＝lnx+ax2+bx的导数为f′（x）＝+2ax+b，在（1，f（1））点的切线斜率为k＝1+2a+b，由题意可得1+2a+b＝﹣2，且a+b＝﹣2，可得a＝b＝﹣1，f（x）＝lnx﹣x2﹣x的导数为f′（x）＝﹣2x﹣1，由f′（x）＝0，可得x＝（﹣1舍去），当0＜x＜时，f′（x）＞0，f（x）递增；x＞时，f′（x）＜0，f（x）递减，可得x＝处，f（x）取得极大值，且为最大值﹣ln2﹣；（2）a＝0，b＝1时，方程tf（x）＝x2即x2﹣tx﹣tlnx＝0，设g（x）＝x2﹣tx﹣tlnx，解g′（x）＝2x﹣t﹣＝0，得x1＝（x1＜0舍去），x2＝，可得g（x）在x∈（0，x2）单调增加，在x∈（x2，+∞）单调减少，最大值为g（x2），因为tf（x）＝x2有唯一实数解，g（x）有唯一零点，所以g（x2）＝0，由即，得x2+2lnx2﹣1＝0，因为h（x）＝x+lnx﹣1单调递增，且h（1）＝0，所以x2＝1，从而t＝1．【点评】此题考查利用导数来研究函数的切线，最值和函数的单调性，考查构造函数法和方程思想，此题是一道中档题．请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题计分．[选修4一4：坐标系与参数方程]22．（10分）在极坐标系中，已知直线l：p（cosθ+sinθ）＝2与曲线C：C：p＝4cosθ．（1）若直线l与曲线C有两个交点A，B，求|AB|；（2）若点P是曲线上与A，B相异的任一点，求△PAB面积的最大值．【分析】（1）直接利用x＝ρcosθ，y＝ρsinθ及x2+y2＝ρ2即可化极坐标方程为直角坐标方程，求出圆心坐标为（2，0），半径为2，可得直线过圆心，得|AB|＝2r＝4；（2）令∠PAB＝θ，（θ∈（0，）），代入三角形面积公式，由正弦函数的值域求解．【解答】解：（1）由l：ρ（cosθ+sinθ）＝2，得x+y＝2．由C：ρ＝4cosθ，得ρ2＝4ρcosθ，得x2+y2﹣4x＝0，即（x﹣2）2+y2＝4．∴圆心坐标为（2，0），半径为2．∵直线过圆心，∴|AB|＝2r＝4；（2）令∠PAB＝θ，（θ∈（0，）），则．当时取最大值．【点评】本题考查简单曲线的极坐标方程，考查极坐标化直角坐标，是基础题．[选修4一5：不等式选讲]23．（1）已知函数f（x）＝|x﹣2a|+|x+b|（a＞0，b＞0）的最小值为2，求a与b的关系；（2）若a，b满足（1）中的条件，求9a+3b的最小值．【分析】（1）利用绝对值不等式的性质进行求解即可，（2）利用基本不等式的性质进行转化求解．【解答】解：（1）f（x）＝|x﹣2a|+|x+b|≥|x﹣2a﹣（x+b）|＝|2a+b|，即f（x）的最小值为|2a+b|，若f（x）的最小值为2，∴|2a+b|＝2，∵a＞0，b＞0∴2a+b＝2．（2）若a，b满足（1）中的条件，则2a+b＝2．则9a+3b≥2＝2＝2＝6，当且仅当2a＝b＝1，即a＝，b＝1时取等号即.9a+3b的最小值为6．【点评】本题主要考查函数最值的应用，结合绝对值不等式的性质以及利用基本不等式的性质是解决本题的关键．。

鄂南高中华师一附中黄冈中学黄石二中荆州中学孝感高中襄阳四中襄阳五中2019届高三第一次联考命题学校：鄂南高中命题人：朱锐、吴芳、江向东、李慕云、李萍审题人：朱锐、吴芳、江向东、李慕云、李萍注意事项：1．答卷前，考生务必将自己的班级、姓名、考号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效。

3．回答主观题时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，将答题卡交回。

第Ⅰ卷阅读题一、现代文阅读（35分）（一）阅读下面的文字，完成1-3题。

（9分，每小题3分）中国古代文学数千年的历史不仅产生了经典，而且产生了多种丰富的经典类型，各经典类型之间并不都处于平行并列的层次，互有交叉。

作为研究者，重要的是努力还原这种类型形态上的固有丰富性。

“六艺”本身虽然主要并不作为文学经典来看待，但在正统的文学观念看来，所有的文学作品却都要在“道文合一”的意义上回溯于它并以它为评价的标准。

因此，从文学经典的类型这个角度看，“六艺”具有确定无疑的“大经典”地位，其他与之相比只能是“小经典”。

就文学经典来说，以秦汉文和《过秦论》为例，秦汉文是大经典，《过秦论》则是秦汉文中的小经典。

不同的时代审美风尚不同，对文学作品的接受也有差异，所以每一个朝代人们心目中的经典也都会发生一些变化或调整。

先秦人虽然未必有像我们现在这样明确的文学经典，但对《诗经》等典籍显然极为熟悉，成为教育和训练外交辞令的一项重要内容。

如“赋诗言志”“断章取义”等等，如果在外交场合运用得当可收“不战而屈人之兵”之效。

汉代人的文学经典是诗骚赋，司马相如的赋尤被推崇。

六朝人的文学经典除诗赋外，更开始了一个骈体文的繁盛时代。

到了宋代，随着承续韩柳的欧苏王曾等的古文影响日益扩大，一些古文经典的地位也逐渐得到确认和凸显。

隋唐以后，随着科举制度的确立，围绕着科举考试科目也产生了策论、经义等供举子临摹、学习的经典范文。

鄂南高中 华师一附中 黄冈中学 黄石二中湖北省八校荆州中学 孝感高中 襄阳四中 襄阳五中2019届高三第二次联考 数学（理科）试题一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知复数z 满足21iz i=+，那么z 的共轭复数在复平面上对应的点位于 ( ) A. 第一象限 B. 第二象限C. 第三象限D. 第四象限【答案】D 【解析】试题分析：因为22(1)11(1)(1)i i i z i i i i -===++-+,所以1z i =-，所以z 的共轭复数在复平面上对应的点位于第四象限，故选D.考点：1.复数的运算；2.复数的几何意义.2.已知集合{|P x y ==，{|ln 1}Q x x =<，则P Q =I A. (0,2] B. [2,e)- C. (0,1] D. (1,e)【答案】C 【解析】由题意知，集合P 表示函数y =的定义域，由220x x --+≥，即220x x +-≤，(1)(2)0x x -+≤，解得21x -≤≤，所以[2,1]P =-.由ln 1x <，得0e x <<，所以(0,e)Q =，所以(0,1]P Q ⋂=，故选C.3.空气质量指数AQI 是反映空气质量状况的指数，AQI 指数值越小，表明空气质量越好，其对应关系如表：如图是某市10月1日-20日AQI指数变化趋势：下列叙述错误的是（）A. 这20天中AQI指数值的中位数略高于100B. 这20天中的中度污染及以上的天数占1 4C. 该市10月的前半个月的空气质量越来越好D. 总体来说，该市10月上旬的空气质量比中旬的空气质量好【答案】C【解析】【分析】根据所给图象，结合中位数的定义、AQI指数与污染程度的关系以及古典概型概率公式，对四个选项逐一判断即可.【详解】对A，因为第10天与第11天AQI指数值都略高100，所以中位数略高于100，正确；对B，中度污染及以上的有第11，13，14，15，17天，共5天占14，正确；对C，由图知，前半个月中，前4天的空气质量越来越好，后11天该市的空气质量越来越差，错误；对D，由图知，10月上旬大部分AQI指数在100以下，10月中旬大部分AQI指数在100以上，所以正确，故选C.【点睛】与实际应用相结合的题型也是高考命题的动向，这类问题的特点是通过现实生活的事例考查书本知识，解决这类问题的关键是耐心读题、仔细理解题，只有吃透题意，才能将实际问题转化为数学模型进行解答.4.若等差数列{}n a的公差为-2，且5a是2a与6a的等比中项，则该数列的前n项和n S取最大值时，n的值等于（）A. 4B. 5C. 6D. 7【答案】C 【解析】 【分析】计算得到132n a n =-，610a =>，710a =-<，得到答案.【详解】5a 是2a 与6a 的等比中项，故2526a a a =⋅，即()()()21118210a a a -=--，解得111a =.故132n a n =-，610a =>，710a =-<，故6S 最大. 故选：C .【点睛】本题考查了等差数列，等比数列的综合应用，确定数列的正负分界点是解题的关键.5.将5个人从左至右排成一行，最左端只能排甲或乙，最右端不能排甲，则不同的排法共有( ) A. 36种 B. 42种C. 48种D. 60种【答案】B 【解析】 【分析】根据题意，可分为两种情况讨论：①甲在最左端，将剩余的4人全排列；②乙在最左端，分析可得此时的排法数目，由分类计数原理，即可求解．【详解】根据题意，最左端只能拍甲或乙，可分为两种情况讨论：①甲在最左端，将剩余的4人全排列，共有4424A =种不同的排法；②乙在最左端，甲不能在最右端，有3种情况，将剩余的3人全排列，安排好在剩余的三个位置上，此时共有33318A =种不同的排法，由分类计数原理，可得共有241842+=种不同的排法，故选B ．【点睛】本题主要考查了排列、组合的综合应用，其中解答中注意优先元素受到的限制条件，合理分类求解是解答的关键，着重考查了推理与运算能力，属于中档试题．6.在ABC V 中，AD 为BC 边上的中线，且AE ED =u u u r u u u r，若EB AB AC λμ=+u u u ru u u ru u u r，则λμ=（ ） A. -3 B. 13-C. 3D.13【答案】A 【解析】 【分析】化简得到3144 EB AB AC =-uu u r u u u r u u u r，计算得到答案.【详解】()11312444EB EA AB AD AB AB AC AB AB AC AB ACλμ=+=-+=-++=-=+ u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r，故34λ=，14μ=-，故3λμ=-.故选：A.【点睛】本题考查了向量基本定理的应用，意在考查学生的应用能力.7.“勾股定理”在西方被称为“毕达哥拉斯定理”，三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”，用形数结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中，四个相同的直角三角形与中间的小正方形拼成一个大正方形，若直角三角形中较小的锐角6πα=，现在向大正方形区域内随机地投掷一枚飞镖，飞镖落在小正方形内的概率是（）A.34B.32C.434D.312-【答案】D【解析】设大正方形边长为1,则小正方形面积为11331412222-⨯⨯⨯=- ,因此所求概率为23132112=-选D.8.函数()2cos(sin cos),02f x x x x xπ⎛⎫⎡⎤=+∈-⎪⎢⎥⎣⎦⎝⎭的最大值为（）A. 12B. 1C. 2D. 12+【答案】C【解析】【分析】化简得到()2214f x xπ⎛⎫=++⎪⎝⎭，432,44xπππ⎡⎤+∈-⎢⎥⎣⎦，计算得到答案.【详解】()2cos (sin cos )sin 2cos 21214f x x x x x x x π⎛⎫=+=++=++ ⎪⎝⎭，,02x ⎡⎤∈-⎢⎥⎣⎦π，则432,44x πππ⎡⎤+∈-⎢⎥⎣⎦，故()()max 02f x f ==.故选：C .【点睛】本题考查了三角函数的最值，意在考查学生的计算能力和转化能力.9.已知抛物线22(0)y px p =>的焦点为F ，过F 的直线l 交抛物线于A ，B 两点（点A 在第一象限），若直线l 的倾斜角为23π，则||||AF BF 等于（ ）A.13 B.25C.12D.23【答案】A 【解析】 【分析】如图所示，作辅助线，计算23AF p =，2BF p =，得到答案. 【详解】如图所示：过点A 作准线的垂线与过F 点x 轴的垂线交于点M ，过点B 作准线的垂线与过F 点x轴的垂线交于点N . 直线l 的倾斜角为23π，则6AFM π∠=，则AMF ∆中，12AM AF =， 故12CM AC AM AF AF p =+=+=，故23AF p =，同理可得：2BF p =. 故||1||3AF BF =. 故选：A .【点睛】本题考查了抛物线中线段的比例关系，意在考查学生的计算能力和转化能力.10. 如图，某多面体的三视图中正视图、侧视图和俯视图的外轮廓分别为直角三角形、直角梯形和直角三角形，则该多面体的各条棱中，最长的棱的长度为（）A. 22B. 10C. 3D. 13【答案】C【解析】DE=+=C．【详解】试题分析：由题意得，该多面体为如下几何体，最长的棱长为8423考点：空间几何体三视图．11.已知双曲线22221(0,0)x y a b a b-=>>的左、右顶点分别为,A B ，右焦点为F .过点F 且垂直于x 轴的直线l交双曲线于,M N 两点，P 为直线l 上一点，当APB ∠最大时，点P 恰好在M （或N ）处.则双曲线的离心率为（ ） 23 C. 2 5【答案】A 【解析】当过,A B 的圆与直线l 相切于P 点时，直线上其它点都在圆外，此时APB ∠最大，由切割线定理得2222||||||()()FP FB FA c a c a c a b ==-+=-=，点P 恰好在M 处，所以||FM b =，由双曲线通径公式可得可知2||b FM a =， 所以2,,1b bb a b a a=∴==，所以双曲线的离心率为212b e a ⎛⎫=+= ⎪⎝⎭.本题选择A 选项.点睛：双曲线的离心率是双曲线最重要的几何性质，求双曲线的离心率(或离心率的取值范围)，常见有两种方法：①求出a ，c ，代入公式c e a=； ②只需要根据一个条件得到关于a ，b ，c 的齐次式，结合b 2＝c 2－a 2转化为a ，c 的齐次式，然后等式(不等式)两边分别除以a 或a 2转化为关于e 的方程(不等式)，解方程(不等式)即可得e (e 的取值范围)．12.已知函数0()2ln(1),0x f x x x =⎪--<⎩…，若函数()()g x f x kx =-有且只有两个零点，则实数k 的取值范围为（ ） A. （0,2） B. 10,2⎛⎫ ⎪⎝⎭C. (2,)+∞D. 1,22⎛⎫⎪⎝⎭【答案】D 【解析】 【分析】求导得到函数的单调性，画出函数图像，计算斜率范围，根据图像得到答案. 【详解】当0x ≥时，()f x =2241y x -=的一部分， 渐近线为12y x =，斜率为12；当0x <时，()2ln(1)f x x =--，()2'01f x x=>-，函数单调递增. 画出图像， 如图所示：当0x <时， ()2'1f x x =-，故()'02f =，根据图像知：122k <<. 故选：D .【点睛】本题考查了函数零点个数问题，画出函数图像是解题的关键.二、填空题（把正确答案填在答题卡上）13.若x ，y 满足223x y x x y ≤⎧⎪≥⎨⎪+≥⎩，则2x y +的最小值为________.【答案】5 【解析】 【分析】先作出可行域，再做直线1:2l y x =-，平移l ，找到使直线在y 轴上截距最小的点，代入即得。

湖北省鄂南高中 华师一附中 黄冈中学 黄石二中 孝感高中荆州中学 襄阳四中 襄阳五中八校2019届高三第二次联考数学(理科)试题注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔在答题卡上填写自己的准考证号、姓名、试室号和座位号。

用2B 型铅笔把答题卡上试室号、座位号对应的信息点涂黑。

2．选择题每小题选出答案后，用2B 型铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡整洁。

考试结束后，将试卷和答题卡一并交回。

第I 卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知复数i1i2z +=,则z 的共轭复数在复平面内对应的点在 A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.已知集合2{2+--==x x y x P ,}1ln {＜x x Q =,则=Q P A.(0,2] B.[-2,e) C.(0,1] D.(1,e)3.空气质量指数AQI 是反映空气状况的指数,AQI 指数值越小,表明空气质量越好,其对应关系如下表： AQI 指数 0-50 51-100 101-150 151-200 201-300 ＞300 空气质量优良轻度污染中度污染重度污染严重污染下图是某市10月1日-20日AQI 指数变化趋势，下列叙述错误的是A. 这20天中AQI 指数值的中位数略高于100B. 这20天中的中度污染及以上的天数占1/4C. 该市10月的前半个月的空气质量越来越好D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好4.若等差数列{a n }的公差为-2,a 5是a 2与a 6的等比中项,则该数列的前n 项和Sn 取得最大值时,n 的值等于A.4B.5C.6D.75.将5个人从左至右排成一行,最左端只能排成甲或乙,最右端不能排甲,则不同的排法共有 A.36种 B.42种 C.48种 D.60种6.在△ABC 中,AD 为BC 边上的中线,且ED AE =,若AC u AB EB +=λ,则=uλA.-3B.31-C.3D.31 7.“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一副“勾股圆方图”，用数形结合的方法给出了勾股定理的详细证明.如下图所示的“勾股圆方图”中，四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形，若直角三角形中较小的锐角6πα=，现在向该正方形区域内随机地投掷一枚飞镖，飞镖落在小正方形内的概率是 A.23-1 B.23 C.43-4 D.43 8.函数])0,2[)(cos (sin cos 2)(π-∈+=x x x x x f 的最大值为A.2-1B.1C.2D.21+9.已知抛物线)0(22＞p px y =的焦点为F ,过F 的直线l 交抛物线于B A ,两点(点A 在第一象限),若直线l 的倾斜角为32π,则=BFAF A.31 B.52 C.21 D.3210.如图,某多面体的三视图中正视图、侧视图和俯视图的外轮廓分别为直角三角形、直角梯形和直角三角形，则该多面体的各条棱中，最长的棱的长度为 A.22 B.10 C.32 D.1311.已知双曲线)0,(12222＞b a by a x =-的左、右顶点分别为B A ,,右焦点为F ,过点F 且垂直于x 轴的直线l 交双曲线于N M ,2点,P 为直线l 上的一点，当APB ∆的外接圆面积达到最小值时,点P 恰好在M (或N )处,则双曲线的离心率为 A.2 B.3 C.2 D.512.已知函数⎪⎩⎪⎨⎧--≥+=0),1ln(20,121)(2＜x x x x x f ,若函数kx x f x g -=)()(有且只有2个零点,则实数k 的取值范围为A.(0,2)B.(0,12)C.(2,+∞)D.(12,2)第II 卷二、填空题(本大题共4小题,每小题5分,共20分,把正确答案填在答题卡)13. 若y x ,满足⎪⎩⎪⎨⎧≥+≥≤322y x x y x ,则y x 2+的最小值为_____.14. 已知函数13)1()(23+--+=ax x a x x f ,若)(x f 在1=x 处取得极值,则曲线)(x f y =在点(0,f (0))处的切线方程为____.15. 已知数列{a n }满足a n =2a n-1+2n-1(n ∈N*,n ≥2),若a 4=65,则a 1=____.16. 设),0(4)4(ln )(),(2222R b a b b a b a b a ∈+-+-=＞ϕ,当b a ,变化时),(b a ϕ的最小值为_____.三、解答题(本大题分为必考题和选做题两部分共70分)17．(12分)在△ABC 中,角A,B,C 的对边分别是a,b,c ，且向量m =(2a-c ,b )与向量n =(cos C ,cos B )共线。

湖北省黄冈中学、华师一附中、襄阳四中、襄阳五中、荆州中学等八校2019届高三第二次联考英语试题考试时间：2019年3月28日下午15:00—17:0★祝考试顺利★注意事项：1.答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2.选择题的作答:每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

4.考试结束后，请将答题卡上交。

第一部分听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题;每小题1.5分，满分7. 5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例：How much is the shirt?A. £19.15.B. £9. 18.C. £9.15.答案是C。

1. What will the speakers do?A. Catch a flight.B. Pick up their son.C. Deal with an accident.2. How does the man feel about Lila?A. Bored.B. Scared.C. Excited.3. How did the woman get to Baltimore?A. By train.B. By bus.C. By taxi.4.Where is the man going tomorrow?A. To the school.B. To the beach.C. To the cinema.5.What does the woman mainly talk about?A.Buying a good bike.B.Learning how to drive.C.Paying attention to safety.第二节（共15小题;每小题1.5分，满分22. 5分）听下面5段对话或独白。

湖北省八校（鄂南高中.黄石二中.华师一附中.黄冈中学.荆州中学.孝感中学.襄阳四中.襄阳五中）2019届高三第二次联合考试数学（理科）试题一、选择题（本大题共12小题，共60.0分）1.设集合，，则A. B. C. D.【答案】D【解析】【分析】：化简集合，根据交集的定义计算．【详解】：因为集合，化简，所以，故选D．【点睛】：研究集合问题，一定要抓住元素，看元素应满足的属性．研究两集合的关系时，关键是将两集合的关系转化为元素间的关系，本题实质求满足属于集合且属于集合的元素的集合．2.若复数z满足为虚数单位，为z的共轭复数，则A. B. 2 C. D. 3【答案】A【解析】分析：把已知等式变形，利用复数代数形式的乘除运算化简，结合复数模的公式求解.详解：由，得，则，，则，故选A.点睛：复数是高考中的必考知识，主要考查复数的概念及复数的运算．要注意对实部、虚部的理解，掌握纯虚数、共轭复数这些重要概念，复数的运算主要考查除法运算，通过分母实数化转化为复数的乘法，运算时特别要注意多项式相乘后的化简，防止简单问题出错，造成不必要的失分.3.在矩形ABCD中，，，若向该矩形内随机投一点P，那么使得与的面积都不小于2的概率为A. B. C. D.【答案】D【解析】，由题意知本题是一个几何概型的概率，以AB为底边，要使面积不小于2，由于，则三角形的高要h⩾1,同样,P点到AD的距离要不小于，满足条件的P的区域如图，其表示的区域为图中阴影部分,它的面积是，∴使得△ABP与△ADP的面积都不小于2的概率为：.故选D.4.已知函数为偶函数，且在上单调递减，则的解集为A. B.C. D.【答案】B【解析】【分析】根据函数奇偶性的定义，求出a，b的关系，结合函数的单调性判断a的符号，然后根据不等式的解法进行求解即可．【详解】∵f（x）=（x-1）（ax+b）=ax2+（b-a）x-b为偶函数，∴f（-x）=f（x），则ax2-（b-a）x-b=ax2+（b-a）x-b，即-（b-a）=b-a，得b-a=0，得b=a，则f（x）=ax2-a=a（x2-1），若f（x）在（0，+∞）单调递减，则a＜0，由f（3-x）＜0得a[（3-x）2-1）]＜0，即（3-x）2-1＞0，得x＞4或x＜2，即不等式的解集为（-∞，2）∪（4，+∞），故选B．【点睛】本题主要考查不等式的求解，根据函数奇偶性的性质求出a，b的关系是解决本题的关键．5.已知双曲线的离心率为，则a的值为A. 1B.C. 1或D.【答案】C【解析】分析：可用排除法，验证与是否符合题意即可得结果.详解：可用排除法，当时，化为，离心率为，符合题意；当时，化为，离心率为，符合题意,的值为，故选C.点睛：用特例代替题设所给的一般性条件，得出特殊结论，然后对各个选项进行检验，从而做出正确的判断，这种方法叫做特殊法. 若结果为定值，则可采用此法. 特殊法是“小题小做”的重要策略，排除法解答选择题是高中数学一种常见的解题思路和方法，这种方法即可以提高做题速度和效率.6.等比数列的前n项和，前2n项和，前3n项的和分别为A，B，C，则A. B.C. D.【答案】D【解析】分析：由等比数列的性质，可知其第一个项和，第二个项和，第三个项和仍然构成等比数列，化简即可得结果.详解：由等比数列的性质可知，等比数列的第一个项和，第二个项和，第三个项和仍然构成等比数列，则有构成等比数列，，即，，故选D.点睛：本题考查了等比数列的性质，考查了等比数列前项和，意在考查灵活运用所学知识解决问题的能力，是基础题.7.执行如图所示的程序框图，若输入，，输出的，则空白判断框内应填的条件可能是A. B. C. D.【答案】B【解析】分析：将题中所给的程序框图模拟运行，逐步运算，结合题的条件，明确循环几次，到什么程度就会结束，从而利用相关的条件，得到其满足的式子，从而求得结果.详解：当第一次执行，，，返回；第二次执行，，，，返回；第三次执行，，，，要输出x，故满足判断框，此时，故选B.点睛：该题考查的是有关程序框图的问题，涉及到的知识点是补全程序框图，在解题的过程中，注意对框图进行模拟运行，结合题的条件，求得结果.8.将函数图象上的每个点的横坐标缩短为原来的一半，纵坐标不变，再将所得图象向左平移个单位得到函数的图象，在图象的所有对称轴中，离原点最近的对称轴方程为A. B. C. D.【答案】A【解析】分析：根据平移变换可得，根据放缩变换可得函数的解析式，结合对称轴方程求解即可. 详解：将函数的图象上的每个点的横坐标缩短为原来的一半，纵坐标不变，得到，再将所得图象向左平移个单位得到函数的图象，即，由，得，当时，离原点最近的对称轴方程为，故选A.点睛：本题主要考查三角函数的图象与性质，属于中档题.由函数可求得函数的周期为；由可得对称轴方程；由可得对称中心横坐标.9.在的展开式中，含项的系数是A. 119B. 120C. 121D. 720【答案】B【解析】分析：展开式中含项的系数是，利用组合数的运行性质计算即可.详解：的展开式中，含项的系数是，故选B.点睛：本题主要考查二项展开式定理的通项与系数以及组合式的性质，属于简单题. 二项展开式定理的问题也是高考命题热点之一，关于二项式定理的命题方向比较明确，主要从以下几个方面命题：（1）考查二项展开式的通项公式；（可以考查某一项，也可考查某一项的系数）（2）考查各项系数和和各项的二项式系数和；（3）二项展开式定理的应用.10.我国古代数学名著九章算术记载：“刍甍者，下有袤有广，而上有袤无丈刍，草也；甍，屋盖也”翻译为：“底面有长有宽为矩形，顶部只有长没有宽为一条棱刍甍字面意思为茅草屋顶”如图，为一刍甍的三视图，其中正视图为等腰梯形，侧视图为等腰三角形则它的体积为A. B. 160 C. D. 64【答案】A【解析】分析：由三视图可知该刍甍是一个组合体，它由成一个直三棱柱和两个全等的四棱锥组成，根据三视图中的数据可得其体积.详解：由三视图可知该刍甍是一个组合体，它由成一个直三棱柱和两个全等的四棱锥组成，根据三视图中的数据，求出棱锥与棱柱的体积相加即可，，故选A.点睛：本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力，属于难题.三视图问题是考查学生空间想象能力最常见题型，也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键，不但要注意三视图的三要素“高平齐，长对正，宽相等”，还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响，对简单组合体三视图问题，先看俯视图确定底面的形状，根据正视图和侧视图，确定组合体的形状.11.已知椭圆C：，直线l：与x轴相交于点E，过椭圆右焦点F的直线与椭圆相交于A，B两点，点C在直线l上，则“轴”是“直线AC过线段EF中点”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】分析：若轴，不妨设与轴交于点，过作交直线于点，由平行线的性质结合椭圆第二定义可得，进而可得结果.详解：若轴，不妨设与轴交于点，过作交直线于点，则：，两次相除得：，又由第二定义可得，为的中点，反之，直线过线段中点，直线斜率为零，则与重合，所以“轴”是“直线过线段中点”的充分不必要条件，故选A.点睛：判断充要条件应注意：首先弄清条件和结论分别是什么，然后直接依据定义、定理、性质尝试.对于带有否定性的命题或比较难判断的命题，除借助集合思想化抽象为直观外，还可利用原命题和逆否命题、逆命题和否命题的等价性，转化为判断它的等价命题；对于范围问题也可以转化为包含关系来处理.12.下列命题为真命题的个数是；；；A. 1B. 2C. 3D. 4【答案】C【解析】【分析】本题首先可以构造函数，然后通过导数计算出函数的单调性以及最值，然后通过对①②③④四组数字进行适当的变形，通过函数的单调性即可比较出大小。