范式补充练习题

Normalization Questions and AnswersDatabase Systems,CSCI4380-01Sibel AdalıOctober28,2002Question1Suppose you are given a relation R=(A,B,C,D,E)with the following functional dependencies:{CE→D,D→B,C→A}.a.Find all candidate keys.b.Identify the best normal form that R satisfies(1NF,2NF,3NF,or BCNF).c.If the relation is not in BCNF,decompose it until it becomes BCNF.At each step,identify a new relation,decompose and re-compute the keys and the normal forms they satisfy.Answer.a.The only key is{C,E}b.The relation is in1NFc.Decompose into R1=(A,C)and R2=(B,C,D,E).R1is in BCNF,R2is in2NF.Decompose R2 into,R21=(C,D,E)and R22=(B,D).Both relations are in BCNF.Question2Suppose you are given a relation R=(A,B,C,D,E)with the following functional de-pendencies:{BC→ADE,D→B}.a.Find all candidate keys.b.Identify the best normal form that R satisfies(1NF,2NF,3NF,or BCNF).c.If the relation is not in BCNF,decompose it until it becomes BCNF.At each step,identify a new relation,decompose and re-compute the keys and the normal forms they satisfy.Answer.a.The keys are{B,C}and{C,D}b.The relation is in3NFc.It cannot be put into BCNF,even if I remove D and put into a relation of the form(B,C,D)(I need C for the functional dependency),the resulting relation would not be in BCNF.Question3Suppose you are given a relation R=(A,B,C,D,E)with the following functional de-pendencies:BD→E,A→C.a.Show that the decomposition into R1=(A,B,C)and R2=(D,E)is lossy.You can show using any method.My suggestion is to show how spurious tuples result from this decomposition with respect to the table below:A B C D E12345183441b.Find a single dependency from a single attribute X to another attribute Y such that when you add the dependency X→Y to the above dependencies,the decomposition in part a is no longer lossy.Answer.a.If we were to decompose the relations into:A B C 123 183D E 45 44and then join the two(in this case with a cartesian product),we would get:A B C D E12345183451234418344Tuples2and3are not in the original relation.Hence,this decomposition is lossy.b.This decomposition cannot be made lossless.The problem is there is no longer a way to make sure BD→E holds across two relations since they do not share any attributes.However,a lossy decomposition of the form(A,B,C),(C,D,E)can be made lossless by adding an FD B→C. Question4You are given the following set of functional dependencies for a relation R(A,B,C,D,E,F), F={AB→C,DC→AE,E→F}.a.What are the keys of this relation?b.Is this relation in BCNF?If not,explain why by showing one violation.c.Is the decomposition(A,B,C,D)(B,C,D,E,F)a dependency preserving decomposition?If not, explain briefly.Answer.a.What are the keys of this relation?{A,B,D}and{B,C,D}.b.Is this relation in BCNF?If not,explain why by showing one violation.No,all functional dependencies are actually violating this.No dependency contains a superkey on its left side.c.Is the decomposition(A,B,C,D)(B,C,D,E,F)a dependency preserving decomposition?If not, explain briefly.Yes,AB→C and DC→A are preserved in thefirst relation.DC→E and E→F are preserved in the second relation.Question5You are given the below functional dependencies for relation R(A,B,C,D,E),F= {AB→C,AB→D,D→A,BC→D,BC→E}.a.Is this relation is in BCNF?If not,show all dependencies that violate it.b.Is this relation in3NF?If not,show all dependencies that violate it.2c.Is the following dependency implied by the above set of dependencies?If so,show how using the Amstrong’s Axioms given in the book(p.362-363):ABC→AEAnswer.Keys for the relation:{A,B},{B,D},{B,C}.a.Not in BCNF since D→A does have a superkey on the left hand side.b.In3NF since in D→A,A is part of a key.c.BC→E(given)ABC→AE by the augmentation rule.Question6You are given the table below for a relation R(A,B,C,D,E).You do not know the functional dependencies for this relation.This question is independent of Question2above.A B C D E’a’1221’s1’’a’’e’2364’e2’’b’’a’1991’b5’’c’’b’2132’z8’’d’Suppose this relation is decomposed into the following two tables:R1(A,B,C,D)and R2(A,C,E). Is this decomposition lossless?Explain your reasoning.Answer.R1A B C D ’a’1221’s1’’e’2364’e2’’a’1991’b5’’b’2132’z8’R2A C E’a’1’a’’e’4’b’’a’1’c’’b’2’d’R1 R2A B C D E’a’1221’s1’’a’’e’2364’e2’’b’’a’1991’b5’’c’’b’2132’z8’’d’’a’1221’s1’’a’’a’1991’b5’’c’Since the last two rows are not in the original relation,then this decomposition is lossy.Question7You are given the below set of functional dependencies for a relation R(A,B,C,D,E,F,G), F={AD→BF,CD→EGC,BD→F,E→D,F→C,D→F}.a.Find the minimal cover for the above set of functional dependencies using the algorithm described in class.Give sufficient detail to show your reasoning,but be succinct.You do not have to list all the cases you test/consider for the algorithm.Show all steps where you make changes to the above set in detail.ing the functional dependencies that you computed in step a,find the keys for this relation. Is it in BCNF?Explain your reasoning.c.Suppose we decompose the above relation into the following two relations:R1(A,B,C,D,E)R2(A,D,F,G)Use the functional dependencies in the minimal cover.For each relation,write down the functional dependencies that fall within that relation(you can decompose a dependency of the form AD→BF into two i.e.AD→B and AD→F when computing this).3Using these functional dependencies,determine if this decomposition is lossless and/or dependency preserving.Explain your reasoning.Answers.a.Step1.{AD→B,AD→F,CD→E,CD→G,CD→C,BD→F,E→D,F→C,D→F}Step2.removeCD→C,AD→F,and BD→F.{AD→B,CD→E,CD→G,F→C,D→F,E→D}Step3.remove D from CD→E and CD→G{AD→B,D→E,D→G,F→C,D→F,E→D}Finally recombine{AD→B,D→EGF,F→C,E→D}.b.Keys:{A,D},{A,E}.Not in BCNF since the last three functional dependencies do not have a superkey on the left hand side.c.R1(A,B,C,D,E)Dependencies:AD→B,D→E,E→D R2(A,D,F,G)Dependencies:D→GF.Not functional dependency preserving,the dependency F→C is not preserved.head(R1)∩head(R2)={A,D}R1:AD→ABCDE is not true since C is not implied by A,DR2:AD→ADF G is true since this is implied by D→GF as follows:AD→AD inclusion rule,since D→GF,use set accumulation rule,AD→ADGF.Hence,thisis a lossless decomposition.Question8You are given the following set F of functional dependencies for a relation R(A,B,C,D,E,F): F={ABC→D,ABD→E,CD→F,CDF→B,BF→D}.a.Find all keys of R based on these functional dependencies.b.Is this relation in Boyce-Codd Normal Form?Is it3NF?Explain your answers.c.Can the set F be simplified(by removing functional dependencies or by removing attributes from the left hand side of functional dependencies)without changing the closure of F(i.e.F+)? Hint.Consider the steps of the minimal cover algorithm.Do any of them apply to this functional dependency?Answer.a.Keys:{A,B,C}and{A,C,D}b.It is not in BCNF.Counterexample ABD→E and ABD is not a superkey.It is not in3NF.Counterexample ABD→E,and ABD is not a superkey and E is not prime attribute(part of a key).c.Let F’be obtained by replacing CDF→B with CD→B.According to F and F’,CD+={C,D,B,F}.Hence,we can remove F from this functional dependency without changing the meaning of the system.Question9Consider relation R(X,Y,Z).Relation R currently has three tuples:(6,4,2),(6,6, 8)and(6,4,8).Which of the following three functional dependencies can you infer do not holdfor relation R?Explain your answer.Y→X4Z→YXY→ZAnswer.Thefirst functional dependency holds,but the rest do not hold.The second and third tuples both have8for Z but different values of Y.Thefirst and third tuples both have6and4for X and Y but different values for Z.Question10Consider the relation R(V,W,X,Y,Z)with functional dependencies{Z→Y,Y→Z,X→Y,X→V,V W→X}.a)List the possible keys for relation R based on the functional dependencies above.b)Show the closure for attribute X given the functional dependencies above.c)Suppose that relation R is decomposed into two relations,R1(V,W,X)and R2(X,Y,Z).Is this decomposition a lossless decomposition?Explain your answer.Answer.a.{V,W},{X,W}b.X+={X,V,Y,Z}c.Yes it is lossless.To be lossless the attributes in common between the two relations must functionally determine all the attributes in one of the two relations.The only attribute in common is X and it functionally determines all the attributes in R2.Question11Given relation R(W,X,Y,Z)and set of functional dependencies F={X→W,W Z→XY,Y→W XZ}.Compute the minimal cover for F.Answer.Step1:X→W,W Z→X,W Z→Y,Y→W,Y→X,Y→ZStep2:Don’t need W Z→X,since W Z→Y and Y→XDon’t need Y→W,since Y→X and X→WThis leaves{X→W W Z→Y,Y→X,Y→Z}Step3:Only need to consider W Z→Y.Can’t eliminate W or Z.So nothing is eliminated.Step4:{X→W W Z→Y,Y→XZ}is the minimal coverQuestion12Given relation R(W,X,Y,Z)and set of functional dependencies G={Z→W,Y→XZ,XW→Y},where G is a minimal cover:a)Decompose R into a set of relations in Third Normal Form.b)Is your decomposition in part a)also in Boyce Codd Normal Form?Explain your answer. Answer.a.Possible keys:{Y},{X,Z},{W,X}R1=(Z,W),R2=(X,Y,Z),R3=(X,Y,W)b.Yes.In each of the three relations,the left side of the funcational dependencies that apply are superkeys for the relation.Hence,all three relations satisfy the definition of BCNF.Question13Consider a relation named EMP DEPT with attributes:ENAME,SSN,BDATE, ADDRESS,DNUMBER,DNAME,and DMGRSSN.Consider also the set G of functional depen-dencies for EMP DEPT:5G={SSN→ENAME BDAT E ADDRESS DNUMBER,DNUMBER→DNAME,DMGRSSM}.a)Calculate the closures SSN+and DNAME+with respect to G.b)Is the set of functional dependences G minimal?If not,find a minimal set of functional depen-dencies that is equivalent to G.c)List an update anomaly that can occur for relation EMP DEPT.d)List an insertion anomaly that can occur for relation EMP DEPT.e)List a deletion anomaly that can occur for relation EMP DEPT.Answer.a)SSN+={SSN,ENAME,BDAT E,ADDRESS,DNUMBER,DNAME,DMGRSSN}DNAME+={DNAME}b)It is minimal.c)Since every member of a department has a reference to the manager of that department(i.e., Dmgrssn),when the department manager changes this reference must be changed multiple places.This leads to the possibility of an inconsistency in the database if they are not all changed.d)You cannot enter data about a department until you have employees for the department.e)If you delete the last employee for a department,you lose all information about the department. Question14You are given the following functional dependencies for the”EMPLOYEE”relation. Explain whether the relation”EMPLOYEE”is BCNF and3NF?Database:EMPLOYEE(ssn,first-name,last-name,address,date-joined,supervisor-ssn) DEPARTMENT(dept-no,name,manager-ssn)WORKS-IN(employee-ssn,dept-no)INVENTORY(dept-no,item-id,quantity)ITEMS(item-id,item-name,type)Foreign keys:1.EMPLOYEE.supervisor-ssn and WORKS-IN.employee-ssn point to EMPLOYEE.ssn.2.WORKS-IN.dept-no and INVENTORY.dept-no point to DEPARTMENT.dept-no.3.INVENTORY.item-id points to ITEMS.item-id.{ssn→supervisor−ssn,ssn→first−name,ssn→last−name,ssn→date−joined,ssn→address,address→ssn}.Answer.In BCNF,since ssn and address are both keys of EMPLOYEE.6。

示例2：我认为是别人请彭天锡到家唱戏。原因是他唱戏妙天下，多扮演丑净，角色扮演惟妙惟肖，让人如临其境。（言之有理即可）
【解析】本题考查对重点句子的理解。可以认为是彭天锡请人教他唱戏，花尽家财。根据第一段中的“然出出皆有传头，未尝一字杜撰”“到余家串戏五六十场，而穷其技不尽”可知他表演技艺多端，惟妙惟肖，形神兼具。由此可推知他必定是请了很多人教他唱戏，才有了如此水平。也可以认为是别人请彭天锡唱戏，花尽家财。根据第二段中的“天锡多扮丑净，千古之奸雄佞幸，经天锡之心肝而愈狠，借天锡之面目而愈刁，出天锡之口角而愈险。设身处地，恐纣之恶不如是之甚也。皱眉视眼，实实腹中有剑，笑里有刀，鬼气杀机，阴森可畏”可知其唱戏妙天下，多扮演丑净，角色扮演惟妙惟肖，让人如临其境。人们欣赏他的技艺，于是就会多次请他来唱戏，花尽了家财。言之有理即可。
范式进入官场当了郡功曹。后来元伯生了重病，元伯快死时，叹气道：“真遗憾，没看见我的生死至交！”不久元伯就死了。范式忽然梦中遇见元伯向他喊道：“巨卿，我在某天已经死了，要在某个时候下葬，永远回到地下了。你没有忘记我，但我们地下人间，大概（我们）再也不能相见了！”范式恍然之间醒了，又悲又叹，眼泪都流下来了，就把情况全部告诉了太守，请求去奔丧。太守虽然心里不相信，但是不愿意违背他对友情的感情，答应了范式的请求。范式穿上会见朋友才穿的衣服，在元伯下葬那天，骑马飞奔赶去送葬。还没等他赶到，下葬的队伍就已经出发了，棺材抬到墓穴旁边后，将要安放到墓穴里，可灵柩却无论如何也放不下去。元伯的母亲抚着棺木说：“元伯，你难道还在盼望什么吗？”于是放下灵柩，不多会儿，果然看见有人驾着素车、骑着白马哭号着赶来。元伯的母亲望着说：“这一定是范巨卿。”范巨卿到了之后，轻敲着棺木说：“你去吧，元伯！死和生是不同的道路，从此永别了。”参加下葬仪式的有一千多人，全都为此流下眼泪。范式趁势牵着绳子在前拉着，灵柩在这时才能向前。范式最后留下来住宿在坟墓旁边，在坟旁栽下树木，之后才离开。

的真值为 0 。 （3）设p,q均为命题，在 p与q不能同时为真 条件下，p与q的
排斥或也可以写成p与q的相容或。
（4）公式(pq)与(pq) (pq) 共同的成真赋值为 01,10 （5）设A为任意的公式，B为重言式，则AB的类型为 重言式
5
第五章 作业
补充填空题： (1) x yF(x,y)的前束范式为 xyF(x,y) 。 (2)由量词分配等值式,x(A(x)B(x)) xA(x) xB(x) (3)缩小量词的辖域，x(F(x)B) xF(x) B (4)公式((xG(x) x F(x)) yG(y)) x F(x)的类型为 永真式 。
(4)设p,q为真命题，r,s为假命题，则复合命题
(pr)(qs)的真值为 0 。
(5)矛盾式的主析取范式为 0 。 (6)设公式A含命题变项p,q,r,又已知A的主合取范式为
M0M2M3M5，_则A的主析取范式为 m1 m4 m6 m7
4
第一章作业
补充：填空题 （1）公式(pq) (pq) 的成真赋值为 01, 10 。 （2）设p,r为真命题，q,s为假命题，则复合命题 (pq) (r s)
(3)在一阶逻辑中，将命题符号化时，若没有指明个体域，则 使用_全总 个体域。
(4)设A为任意的一阶逻辑公式，若A中 不含自由出现的个体变 项 ，则称A为封闭的公式。
2
第三章 作业
补充填空题： (1)(AB)B A 为拒取式推理定律。 (2)(AB)B A 为析取三段论推理定律。
(3)(AB)(BC) A C 为假言三段论推理定
1
第四章 作业
补充填空
(1)设F(x): x具有性质F，G(x)：x具有性质G。命题“有的x既
有性质F又有性质G”的符号化形式为 x(F(x)G(x))

关系范式练习题关系范式是数据库设计中的重要概念，它帮助我们规范化数据模型，减少数据冗余，提高数据库的性能和可维护性。

在本篇文章中，我们将通过练习题来巩固和应用关系范式的知识。

题目一：学生选课系统假设我们有一个学生选课系统，其中包含以下几个关系：学生(Student)：学号，姓名，性别，年龄，专业课程(Course)：课程编号，课程名称，学分选课(Selection)：学号，课程编号请按照关系范式的要求对上述关系进行规范化处理。

解答：1.首先，我们观察到学生关系中有学号、姓名、性别、年龄、专业五个属性。

这些属性都关于学生本身，不存在部分依赖关系，所以该关系已经符合第一范式(1NF)。

2.接下来，我们看到课程关系中有课程编号、课程名称、学分三个属性。

这些属性也不存在部分依赖关系，所以该关系也符合第一范式(1NF)。

3.最后，我们观察到选课关系中有学号、课程编号两个属性。

这个关系存在一个主键依赖：学号加上课程编号能唯一确定选课关系。

因此，选课关系符合第二范式(2NF)。

综上所述，学生关系、课程关系和选课关系分别符合第一范式和第二范式。

题目二：学生社团管理系统假设我们有一个学生社团管理系统，其中包含以下几个关系：学生(Student)：学号，姓名，性别，年龄，专业社团(Club)：社团编号，社团名称，指导老师参加(Join)：学号，社团编号，加入时间请按照关系范式的要求对上述关系进行规范化处理。

解答：1.首先，我们观察到学生关系中有学号、姓名、性别、年龄、专业五个属性。

这些属性都关于学生本身，不存在部分依赖关系，所以该关系已经符合第一范式(1NF)。

2.然后，我们看到社团关系中有社团编号、社团名称、指导老师三个属性。

这些属性也不存在部分依赖关系，所以该关系也符合第一范式(1NF)。

3.接下来，我们观察到参加关系中有学号、社团编号、加入时间三个属性。

该关系存在一个主键依赖：学号加上社团编号能唯一确定参加关系。

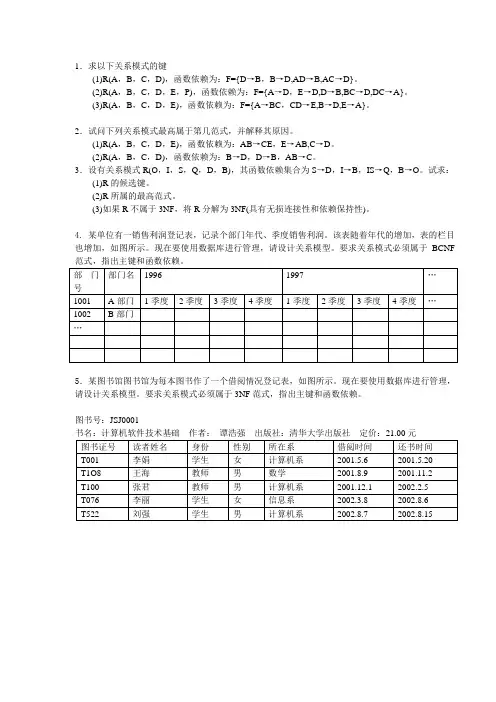
1．求以下关系模式的键
(1)R(A，B，C，D)，函数依赖为：F={D→B，B→D,AD→B,AC→D}。

(2)R(A，B，C，D，E，P)，函数依赖为：F={A→D，E→D,D→B,BC→D,DC→A}。

(3)R(A，B，C，D，E)，函数依赖为：F={A→BC，CD→E,B→D,E→A}。

2．试问下列关系模式最高属于第几范式，并解释其原因。

(1)R(A，B，C，D，E)，函数依赖为：AB→CE，E→AB,C→D。

(2)R(A，B，C，D)，函数依赖为：B→D，D→B，AB→C。

3．设有关系模式R(O，I，S，Q，D，B)，其函数依赖集合为S→D，I→B，IS→Q，B→O。

试求：
(1)R的候选键。

(2)R所属的最高范式。

(3)如果R不属于3NF，将R分解为3NF(具有无损连接性和依赖保持性)。

4.某单位有一销售利润登记表，记录个部门年代、季度销售利润。

该表随着年代的增加，表的栏目也增加，如图所示。

现在要使用数据库进行管理，请设计关系模型。

要求关系模式必须属于BCNF 范式，指出主键和函数依赖。

5．某图书馆图书馆为每本图书作了一个借阅情况登记表，如图所示。

现在要使用数据库进行管理，请设计关系模型。

要求关系模式必须属于3NF范式，指出主键和函数依赖。

图书号：JSJ0001。

3NF（每个非主属性既不部分也不传递函数依赖于码） 消除主属性对码的部分和传递函数依赖
↓ BCNF （每个决定因素都包含码）
2024/8/7
数据库技术及应用
9
（课程号，课程名） （任课教师） （学号，姓名，性别）
（学号,任课教师，成绩） （课程号，任课教师）。
2024/8/7
数据库技术及应用
4
练习： 设有一个记录学生毕业设计情况的关系模式： R(学号，学生名，班级，教师号，教师名，职称，毕业设计题目，成绩) 如果规定：每名学生只有一位毕业设计指导教师，每位教师可指导多名学生； 学生的毕业设计题目可能重复。 (1)根据上述规定，写出模式R的基本FD和关键码。 (2)R最高属于几范式。 (3)将R规范到3NF。
（3）从实际出发：
1）要能够查询到学生所在的学院。
3NF
（学号，姓名，性别） （学院，院长）
（学号，姓名，性别，学院） （学院，院长）
2024/8/7
数据库技术及应用
3
2NF 2)要能够反映出学生选课这个关系。
（学号，姓名，性别）
（课程名，课程号）
（学号，课程号，成绩）
（成绩）
BCNF
3)要能够查询出学生的某门课程被哪位任课教师所教的信息。
2024/8/7
数据库技术及应用
6
温故知新：数据库设计的基本步骤
数据库设计的过程(六个阶段)
需求分析； 概念结构设计； 逻辑结构设计; 数据库物理设计； 数据库实施; 数据库运行和维护。
2024/8/7
数据库技术及应用
7
规范化理论的作用：改造关系模式，通过分解关
系模式来消除其中不合适的问题，以解决删除异常、 更新异常、插入异常和数据冗余问题。

范式练习题一、选择题1. 范式的概念最早由哪位学者提出？A. 托马斯·库恩B. 卡尔·波普尔C. 弗朗西斯·培根D. 伊曼努尔·康德2. 范式转换通常伴随着哪些特征？A. 科学共同体的分裂B. 新理论的快速接受C. 旧理论的完全废弃D. 科学实践的连续性3. 以下哪项不是范式转换的特点？A. 科学革命B. 理论的非连续性C. 旧范式的完全取代D. 科学知识的累积4. 托马斯·库恩认为科学发展的主要模式是什么？A. 逻辑实证主义B. 范式转换C. 科学方法论D. 科学哲学二、填空题5. 范式是科学共同体成员共同接受的______、______和______的集合。

6. 范式转换通常发生在______和______之间，这种转换并非平滑过渡，而是伴随着激烈的争论和冲突。

7. 范式转换后，新的范式会取代旧的范式，成为新的______和______的基础。

三、判断题8. 范式转换是科学发展中不可避免的现象。

（对/错）9. 范式转换意味着科学知识的彻底断裂。

（对/错）10. 范式的概念只适用于自然科学领域。

（对/错）四、简答题11. 描述范式转换的过程，并说明其对科学发展的意义。

12. 讨论范式转换与科学革命之间的关系。

五、论述题13. 根据托马斯·库恩的观点，分析范式转换对科学实践和科学理论的影响。

14. 探讨范式转换在现代科学发展中的作用及其对科学哲学的启示。

六、案例分析题15. 以某个科学领域的范式转换为例，分析其对科学发展的影响，并讨论这一转换对其他科学领域可能产生的影响。

以上题目旨在帮助学习者理解范式和范式转换的概念，以及它们在科学发展中的作用。

通过这些练习，学习者可以更深入地了解科学哲学和科学史的相关知识。

工程数学练习题一、 判断题1． 若A 为集合，则A Φ={ф} （ ） 2． 设A ，B 为集合。

若B ≠ф，则A —B ⊂A 。

（ ） 3． 若R 为集合A 上的反对称关系，则R 2亦然。

（ ） 4． 若R 1，R 2为集合A 上的相容关系，则R1·R2亦然。

（ ） 5． 若g ·f 为内射且f 为满射，则g 为内射。

（ ）6． 若f:X →Y 且A ，B ⊆Y ，则f -1[A ⋂B ]=f -1[A] ⋂f -1[B] （ ） 7． 若P 为命题变元，则P ∧—P 为主合取范式。

（ ） 8． 若P ，Q 为命题变元，则（P Q ） （-P Q ）为可满足的。

（ ） 9． 简单无向图的邻接矩阵是一个对角线元素全为“0”的0-1矩阵。

（ ） 10．若V 为有向图G 的结点集，则∑∑∈-∈-=Vv Vv v G d v G d )()(。

（ ）11．π是无理数，并且如果3是无理数，则2也是无理数。

（ ） 12．只有6能2整除，6才能被4整除。

（ ） 13．用真值表判断下列公式类型1）)(r q p p ∨∨→ （ ） 2）q p p 7)7(→→ （ ） 3）r r q ∧→)(7 （ ） 4）)77()(p q q p →→→ （ ） 5）)77()(q p r p ∧↔∧ （ ） 6）)())()((r p r q q p →→→∧→ （ ） 7）)()(s r q p ↔↔→ （ ） 14．判断下述命题的真假1）)()()(C A B A C B A ⨯=⨯ （ ） 2）)()()(C A B A C B A ⨯⨯=⨯⨯ （ ） 3）存在集合A 使得A A A ⨯⊆ （ ） 4）)()()(A A P A P A P ⨯=⨯⨯ （ ）二、单项选择题1．1、一个连通的无向图G ，如果它的所有结点的度数都是偶数，那么它具有一条 （ ） A 、汉密尔顿回路 B 、欧拉回路 C 、汉密尔顿通路D 、初级回路2、设G 是连通简单平面图，G 中有11个顶点5个面，则G 中的边是（ ） A 、10 B 、12 C 、16 D 、143、设i 是虚数，·是复数乘法运算，则G=（{}+--i i ,,1,1·）是群，下列是G 的子群是（ ）A 、（{},1·）B 、（{},1-·）C 、（{},i ·）D 、（{},i -·）4、设Z 为整数集，A 为集合，A 的幂集为P （A ），+、－、／为数的加、减、除运算， 为集合的交运算，下列系统中是代数系统的有（ ）A 、（Z , + , /）B 、（Z , /）C 、（z , －, /）D 、（P （A ）, ）5、设A=（1,2,3），A 上二元关系R 的关系图如下： R 具有的性质是 （ ）A 、自反性B 、对称性C 、传递性D 、反自反性 6、设A=|a,b,c|A 上二元关系R=|〈a,a 〉〈b,b 〉〈a,c 〉|，则关系R 的对称闭包S （R ）是（ ） A 、R I A B 、R C 、R |〈c,a 〉| D 、R I A 7、设X=|a,b,c|,1X 上恒等关系，要使1X |〈a,b 〉,〈b,c 〉,〈c,a 〉, 〈b,a 〉| R 为X 上的等价关系，R 应取 （ ） A 、|〈c,a 〉, 〈a,c 〉| B 、|〈c,b 〉, 〈b,a 〉| C 、|〈c,a 〉, 〈b,a 〉| D 、|〈a,c 〉, 〈c,b 〉| 8、下列式子正确的是（ ）A 、Ø∈ØB 、Ø⊆ØC 、|Ø|⊆ ØD 、|Ø|∈Ø9、若P:他聪明:Q:他用功:则“他虽聪明，但不用功”，可符号化为 （ ） A 、PVQ B 、PA|Q C 、P ΓQ D 、PV –Q10、以下命题公式中，为永假式的是 （ ） A 、p →（pVqVr ） B 、（p →Γp ）→Γp C 、|（q →p ）∧pD 、|(pV Γp) →（p ∧Γp ）11、M 未知时，求Q 2的置信区间，应选择统计量为（ ） A ．)1,0(/～N nQ M x -B ．)1(/--n ～t nS M xC ．)1,0(～N QMx - D ．)1(122--n ～n x Q12、)3)(2)(1()(+++=S S S SS F 不解析点有（ ）个。

范式练习题（打印版）### 范式练习题（打印版）一、选择题1. 范式是指：- A. 一种科学理论- B. 一个研究领域的基本假设和方法论- C. 一种科学实践- D. 一种科学实验2. 下列哪一项不是范式转换的特征？- A. 出现新的研究问题- B. 旧范式下的问题得到解决- C. 科学共同体的分裂- D. 旧范式下的概念和理论被重新解释3. 托马斯·库恩认为，科学发展的主要动力是：- A. 科学实验- B. 范式转换- C. 科学理论的完善- D. 科学方法的改进二、填空题1. 科学革命通常伴随着_______，它标志着一个旧范式的终结和新范式的开始。

2. 范式转换的过程中，科学家们可能会经历_______，即对旧范式的质疑和对新范式的探索。

3. 托马斯·库恩在他的著作《科学革命的结构》中提出了_______的概念，对科学发展的理论做出了重要贡献。

三、简答题1. 请简述范式转换对科学发展的意义。

2. 描述一下托马斯·库恩对科学发展阶段的划分，并解释每个阶段的特点。

四、论述题1. 论述范式转换过程中可能出现的科学共同体的分裂现象，并分析其对科学发展的影响。

参考答案一、选择题1. B2. B3. B二、填空题1. 范式转换2. 危机3. 范式三、简答题1. 范式转换是科学发展的重要阶段，它标志着科学从一种理论体系向另一种理论体系的转变。

这个过程通常伴随着科学共同体对现有理论和方法的质疑，以及对新理论和方法的探索。

范式转换不仅能够解决旧范式下无法解释的问题，而且能够为科学研究提供新的视野和方法，从而推动科学的进步。

2. 托马斯·库恩将科学发展划分为三个阶段：常规科学、危机和科学革命。

常规科学阶段是指在某个范式的指导下，科学家们通过积累和验证知识来解决研究问题。

危机阶段是指当常规科学中出现无法用现有范式解释的问题时，科学家们开始对现有范式产生质疑。

科学革命阶段是指新的范式取代旧的范式，从而解决危机阶段中的问题，为科学发展带来新的活力。

数理逻辑部分综合练习一、单项选择题1．设P：我将去打球，Q：我有时间．命题“我将去打球，仅当我有时间时”符号化为( )．A．P∨⌝P⌝Q→ B．QP→ C．QP↔ D．Q 2．命题公式P?Q的合取范式是 ( )．A．P?Q B．（P?Q）?（P?Q）C．P?Q D．?（?P??Q）3．命题公式)⌝的析取范式是( )．P→(QA．Q⌝ D．QP∨P⌝∨P⌝⌝ C．Q∧ B QP∧4．下列公式成立的为( )．A．?P??Q ? P?Q B．P??Q ? ?P?QC．Q?P ? P D．?P?(P?Q)?Q5．下列公式 ( )为重言式．A．?P??Q?P?Q B．(Q?(P?Q)) ?(?Q?(P?Q))C．(P?(?Q?P))?(?P?(P?Q)) D．(?P?(P?Q)) ?Q6．设A（x）：x是人，B（x）：x是学生，则命题“不是所有人都是学生”可符号化为（）．A．(∀x)(A(x)?B(x)) B．?(∃x)(A(x)?B(x))C．?(?x)(A(x)?B(x)) D．?(∃x)(A(x)??B(x))7．设A（x）：x是人，B（x）：x是工人，则命题“有人是工人”可符号化为（）．A．(?x)(A(x)?B(x)) B．(?x)(A(x)?B(x))C．?(?x)(A(x)?B(x)) D．?(?x)(A(x)??B(x))8．表达式))yQyRxzx∀∨∀中x∧∃xP→((,)(y))(zQ((z),∀的辖域是( )．A．P(x, y) B．P(x, y)?Q(z) C．R(x, y) D．P(x, y)?R(x, y) 9．在谓词公式(?x)(A(x)→B(x)?C(x，y))中，（）．A．x，y都是约束变元 B．x，y都是自由变元C．x是约束变元，y都是自由变元 D．x是自由变元，y都是约束变元补充题：设个体域为自然数集合，下列公式中是真命题的为 ( )A．)1∃∀y+yx(=xy⋅(=∃∀yxx B．)0C．)yxyx=+∃∀(y2yxyx=⋅∃ D．)∀(x二、填空题1．命题公式()→∨的真值是．P Q P2．设P：他生病了，Q：他出差了．R：我同意他不参加学习. 则命题“如果他生病或出差了，我就同意他不参加学习”符号化的结果为．3．含有三个命题变项P，Q，R的命题公式P?Q的主析取范式是．4．设个体域D＝{a, b},那么谓词公式)xA∀∨x∃消去量词后的等值式)yB((y为．5．设个体域D＝{1, 2, 3}，A(x)为“x小于3”，则谓词公式(?x)A(x) 的真值为．6．谓词命题公式(?x)((A(x)?B(x)) ?C(y))中的自由变元为 .三、公式翻译题1．请将语句“今天是天晴”翻译成命题公式．2．请将语句“小王去旅游，小李也去旅游．”翻译成命题公式．3．请将语句“他去旅游，仅当他有时间．”翻译成命题公式．4．请将语句“所有人都努力工作．”翻译成谓词公式．四、判断说明题（判断下列各题，并说明理由．）1．命题公式P P⌝∧的真值是1．2．命题公式?P∧(P??Q)∨P为永真式．3．下面的推理是否正确，请给予说明．五．计算题1．求P?Q?R的析取范式，合取范式、主析取范式，主合取范式．2．设谓词公式()((,)()(,,))()(,)∃→∀∧∀．x P x y z Q y x z y R y z（1）试写出量词的辖域；（2）指出该公式的自由变元和约束变元．3．设个体域为D={a1, a2}，求谓词公式?y?xP(x,y)消去量词后的等值式．六、证明题1．试证明命题公式 (P?(Q??R))??P?Q与?（P??Q）等价．2．试证明(?x)(P(x)?R(x))?(?x)P(x)?(?x)R(x)．。

专题十三仿用、变换句式——2023届高考语文二轮复习专题练习（含答案）专题十三仿用、变换句式1.我国的传统节日是民族之根，每一个节日都有其典型特征和节日内涵。

请从元宵节、端午节、重阳节等传统节日中任选两个仿写，结构与示例一致。

示例：清明节——暮春三月，梨花微雨，清扫祭台怀亲人。

2.请仿照下面这首《自由的风》，以“自由的雨”或“自由的云”为题写一首小诗，格式不必完全一致。

自由的风你从梦中苏醒/在清晨的蓝天下散步你穿过树林/树木为你歌唱你踏过溪流/流水为你鼓掌3.请根据文意续写两个句子,保持与前文结构上的一致。

孟子，你为了拯救天下苍生，历寒暑，驱车马，宣仁政，置安危荣辱于度外。

贫贱不能动摇你坚定的意志，纵使两袖清风，你仍然胸怀一腔浩气；富贵____，____，____；威武____，____，____。

你是天地间独一无二的伟丈夫！4.家风是给家人树立的价值准则，良好的家风培育美好的种子。

请根据横批，利用所给材料组成三副关于家风的对联，要求用完材料。

横批：勤劳致富勤俭持家耕读传家材料：独长偏生莫奢华尚勤俭败由奢穷在惰丹桂有根创业艰难成由勤俭守成不易黄金无种诗书门第富在辛劳种田人家（1）勤劳致富______________________________________（2）勤俭持家______________________________________（3）耕读传家_____________________________________5.以“小说《三体》”为主语，把下面三个短句改写成一个长句，可适当增减词语，但不能改变原意。

①小说《三体》被普遍认为是中国科幻文学的里程碑之作。

②刘慈欣是小说《三体》的作者。

③小说《三体》获得世界科幻文学界最高奖项“雨果奖”。

6.将下面的长单句改写成两个前后衔接的短句，其中一个是主动句，一个是被动句，不得改变原意。

南京鼓楼医院日前向世人公布的新近发现的记录了1937年至1941年鲍恩典经历的南京大屠杀的日记再一次揭穿了日本某些政客认为不存在南京大屠杀的谎言。

主范式 习题
一、 本章的主要内容及要求 1． 基本内容 等值式与等值演算 基本的等值式（16 组，24 个公式） 主析取与主合取范式 联结词完备集
2. 要求 深刻理解等值式的概念 牢记基本等值式的名称及它们的内容 了解简单析取式、简单合取式、析取范式、合取范式 的概念 深刻理解极小项、极大项的概念、名称及下角标与成 真、成假赋值的关系，并理解简单合取式与极小项的 关系 熟练掌握求主范式的方法（等值演算、真值表等） 会用公式的主范式求公式的成真、成假赋值及判断公 式的类型、简单应用 会将任何公式化成任何联结词完备集中的公式
④ A (pqrsu)(pqrsu) 结论：由④可知，A 的成真赋值为 00110 与 11001，因而
派孙、李去（赵、钱、周不去）或派赵、钱、周 去（孙、李不去）
A 的演算过程
A (pq)((qr)(qr))
(su)(u(pq))
（1） 若赵去，钱也去. （2） 李、周两人中必至少有一人去 （3） 钱、孙两人中去仅去一人. （4） 孙、李两人同去或同不去. （5） 若周去，则赵、钱也去.
用等值演算法分析该公司如何选派他们出国？ 解此类问题的步骤应为：
○1 将简单命题符号化 ○2 写出各复合命题 ○3 写出由②中复合命题组成的合取式 ○4 将③中公式化成析取式（最好是主析取范 式）
解 （1）为真，这是显然的
（2）为假. 注意, 任何公式与它的主范式是等值的，显 然重言式不能与 0 等值。重言式的主合取范式不含 极大项，因而主合取范式为 1.
（3）的分析类似于（2），矛盾式的主析取范式为 0. （4）为假，因为{, }不是完备集，比如矛盾式(pq)q
不能化成{, }中的公式. （5）为真，注意{, , }的子集{, }为完备集.

1．假设某企业集团数据库中有一关系模式R如下：R（商店编号，商品编号，商品库存数量，部门编号，负责人）如果规定：（1）每个商店的每种商品只在该商店的一个部门销售；（2）每个商店的每个部门只有一个负责人；（3）每个商店的每种商品只有一个库存数量。

试分析：（1）根据上述规定，写出关系模式R的基本函数依赖；（2）指出该关系模式R的候选码（3）指出该关系模式R的范式级别，为什么？若R不是3NF，将R分解为3NF。

（1）函数依赖如下：（商店编号，商品编号）部门编号，（商店编号，部门编号）负责人，（商店编号，商品编号）商品库存数量（2）R的候选码是（商店编号，商品编号）。

由（商店编号，商品编号）商店编号（自反律）及（商店编号，商品编号）部门编号（已知）⇒（商店编号，商品编号）（商店编号，部门编号）（合并）又有（商店编号，部门编号）负责人⇒（商店编号，商品编号）负责人（传递）由，，得（商店编号，商品编号）（商店编号，商品编号，商品库存数量，部门编号，负责人），根据关键字的定义，可得R的候选码是（商店编号，商品编号）。

（3）因为R中存在非主属性“负责人”对候选码（商店编号，商品编号）的传递函数依赖，所以R属于2NF，不属于3NF。

（4）将R分解成R1（商店编号，商品编号，商品库存数量，部门编号），R2（商店编号，部门编号，负责人）则R1，R2均为3NF。

2．建立一个描述学生情况的数据库：一个系有若干学生，但一个学生只属于一个系；一个系只有一名负责人；一个学生可以选修多门课程，每门课程有若干学生选修；每个学生学习每一门课程有一个成绩；学生（用学号SNO描述）；系（用系名SDEPT描述）；系负责人（用其姓名MN描述）；课程（用课程名CNAME描述）；成绩（G）；假定建立了如下关系模式S(SNO, SEDPT, MN, CNAME, G)试分析：（4）指出该关系模式中的函数依赖（5）指出该关系模式的范式级别（要求按照各范式定义简要分析）按3NF的定义将其分解为3NF，要求无损联结并保持函数依赖（要求解题过程）（1）函数依赖如下：SNO SDEPT，SDEPT MN，（SNO，CNAME）G（2）该关系属于1NF，因为首先该关系中每一个属性都不可再分，所以属于1NF；其次，该关系的候选码为（SNO，CNAME），非主属性为SDEPT，MN，G，存在非主属性对码的部分依赖（SNO SDEPT ，SDEPT部分依赖于码），所以不属于2NF。

§1.4 命题公式的范式习题1.41. 下列命题公式哪些是析取范式哪些是合取范式？ （1）)()(r q q p ∧∨⌝∧⌝ （2）)()(q p q p ∨⌝∧⌝∨ （3）q r p ∨⌝∧⌝)( （4）q q p ⌝∧∨)( （5）q p ∨⌝ （6）r q p ⌝∧⌝∧⌝ （7）p ⌝ （8）q（9）1（10）0解 是析取范式的有：(1)、(3)、（5）、（6）、(7)、 (8)、（9）、（10）；是合取范式有：（2）、（4）、（5）、（6）、(7)、 (8)、（9）、（10）。

2. 在下列由3个命题变元r q p 、、组成的命题公式中，指出哪些是标准析取范式哪些是标准合取范式？ （1）)()(r q p r q p ∧∧⌝∨∧⌝∧⌝ （2）)()(r q p r q p ∨∨⌝∧⌝∨⌝∨ （3）q r q p ∨⌝∧⌝∧⌝)( （4）)()()(r q r p q p ∨∧⌝∨⌝∧∨ （5）r q p ⌝∨∨⌝ （6）r q p ⌝∧⌝∧⌝（7）1（8）0解 是标准析取范式的有：（1）、（6）、（8）；是标准合取范式的有：（2）、（5）、（7）。

3. 找出一个只含命题变元p 、q 和r 的命题公式，当p 和q 为真而r 为假时命题公式为真，否则为假。

解 r q p ⌝∧∧。

4. 找出一个只含命题变元p 、q 和r 的命题公式，在p 、q 和r 中恰有两个为假时命题公式为真，否则为假。

解 ))()()(r q p r q p r q p ∧⌝∧⌝∨⌝∧∧⌝∨⌝∧⌝∧。

5. 利用等价演算法求下列命题公式的标准析取范式，并求其成真赋值。

（1）)()(p q q p ∨⌝→→⌝（2）r q q p ∧∧→⌝)(（3）)())((r q p r q p ∨∨→∧∨ 解（1） )()(p q q p ∨⌝→→⌝)()(p q q p ∨⌝∨∨⌝= p q q p ∨⌝∨⌝∧⌝=)()()()()()(q p q p q p q p q p ∧∨⌝∧∨⌝∧⌝∨⌝∧∨⌝∧⌝= )()()(q p q p q p ∧∨⌝∧∨⌝∧⌝=除0=p ，1=q 外，其余均为成真赋值。

S中存在传递函数依赖：
Cno→Sdept，Sdept→Sloc ，Cno→Sloc
26
作业
(2)班级关系模式： 关系模式： C(Cno,Cspec,Sdept,Cnum,Cdate) 极小函数依赖集为： C：Cno→Cspec，Cspec→Sdept，Cno→Cnum
Cno→Cdate，(Cspec,Cdate) →Cno
Sno Sname Sage 20 21 22 Sdept 001 002 003 deptID Dname Mname 2001011 李华 2001012 顾芳 2001013 张林
001
002 003
自动化
计算机 管理
张三
李四 王五
13
主码和外码表示了关系之间的联系。
13
课堂练习题：
下列关于关系模式的码的叙述中，哪一条
22
12.已知:关系模式R(U,F)中,U=ABCDEG.
F={BG→C,BD→E,DG→C,ADG→BC,AG→B,B→D}求: (1)R的侯选码(2)R最高满足第几范式 13．设有关系模式R（职工号，项目名，工资，部门名， 部门经理） 如果规定：每个职工可以参加多个项目，各领一份工资； 每个项目只属于一个部门管， 每个部门只有一个经理。 （1）写出该关系模式的函数依赖集合。 （2）判断候选码。 （3）说明不满足2NF的理由，并把R分解为2NF的模式集
平凡函数依赖不反映新的语义，无实际意义和价值； 无特别声明，均讨论有语义价值的非平凡依赖。
5
5
几种函数依赖类型（二）：

在关系模式R(U)中，如果X→Y，并且对于X的任何一 个真子集X’,都有X’ Y, 则称Y完全函数依赖于X， 记作X ｆY,否则称Y部分函数依赖于X，记作X P Y。

中小学文言文阅读理解《范式访友》（含练习题答案）范式访友范式，字巨卿。

少游太学，为诸生，与汝南张劭为友。

劭字元伯。

二人并告归乡里。

式谓元伯曰：“后二年当还，将过拜尊亲，见孺子焉。

”乃共克期日。

后期方至，元伯具以白母，请设馔以候之。

母曰：“二年之别，千里结言，尔何相信之审邪？”对曰：“巨卿信士，必不乖违。

”母曰：“若然，当为尔酝酒。

”至其日，巨卿果到，升堂拜饮，尽欢而别。

【注释】1、太学：汉朝设在京城的最高学府。

2、诸生：求学的人。

3、告：请假，告假。

4、过：探望，拜访。

5、尊亲：指张劭的父母。

6、孺子：小孩子，指张劭的子女。

7、克：约定或限定。

8、具：具体详细。

9、白：告诉。

10、以：后省之把这件事告诉母亲。

11、馔：饮食，食物。

名词。

12、结言：口头答应。

13、审：确定。

14、对：回答。

15、信士：讲信用的人。

16、乖违：违背，此指违约。

17、若：如果。

18、然：这样。

18、酝：酿酒。

19、其日：约定的那天。

【参考译文】范式，字巨卿。

少年时去太学上学，和汝南的张劭是朋友。

张劭字元伯。

后来两人同时请假回故乡。

范式对张劭说：两年以后，我将到你家拜访你的父母，来看你的子女。

就一同约定了时间。

后来约定的时间快到了，张劭把这事详细地告诉了母亲，请母亲准备饮食等待范式到来。

张劭的母亲说：已经分别了两年，相隔千里的约定，你怎么敢相信它确实会来的呢？张劭说：巨卿是讲诚信的人，一定不会(违背诺言。

他母亲说：如果果真如此，我自当为你们酿酒。

到了约定的那一天，范式果然到了。

两人一同喝酒，尽兴后分别。

【启发】甘戊面对船夫的讥讽，没有慌乱，而是耐心地列出各项实例，有理有据地说明“物各有短长”，让船夫哑口无言，认识到自己的浅薄。

“尺有所短，寸有所长”，人都各有长处，也各有短处，彼此都有可取之处。

不能拿己之短比别人之长，妄自菲薄；更不能拿己之长比别人之短，狂妄自大。

要学会取长补短，从各方面来完善自己。

【课后练习】1、解释下列句中划线的词语。

8
DeMorgan Revisited
Recall DeMorgan’s identities:
•Conjunctional negation:
(p1p2…pn) (p1p2…pn)
•Disjunctional negation:
(p1p2…pn) (p1p2…pn)
Since the quantifiers are the same as taking a bunch of AND’s () or OR’s () we have:
•Universal negation:
x P(x ) x P(x )
•Existential negation:
x P(x ) x P(x )
9
谓词公式的前束范式
一个谓词公式，如果量词都在整个式子 的前头，其作用域延伸到整个谓词公式的末
尾，这样的谓词公式叫前束范式。 定理：
任意一个谓词公式，都有一个与之等 价的前束范式。
要求：
能把任意一个谓词公式转化为与之等 价的前束合取（析取）范式。
14
重点与难点
重点：
理解前束范式的意义
难点：
前束范式与主合（析）取ຫໍສະໝຸດ 式的区别15上周习题讲解
P23 (2) C) P23 (8) B) D) P29 (2) P39 (4)
16
课本练习
P18习题（6）
由n个命题变元组成不等价的命题公式的个数为： (A) 2n (B) 2n (C) n2 (D)
24
补充练习
某人说：“我家的每一个成员都是在广州出 生的。”如果他说的话事实上是错的，则 下面哪一条是对的？（ ）
A、他家没有一个成员出生在广州。 B、他家至少有一个成员出生在广州。 C、他不是出生在广州。 D、他家至少有一个成员不是出生在广州。 E、如果他出生在广州，现在他仅是个儿童。