下载文档原格式
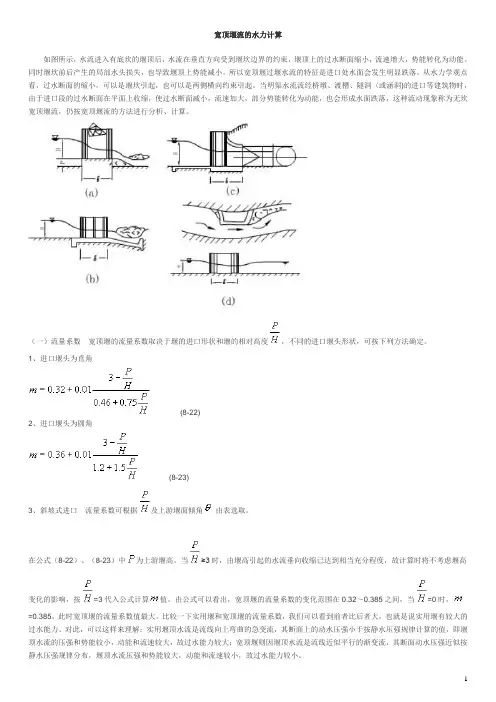
宽顶堰流的水力计算如图所示，水流进入有底坎的堰顶后，水流在垂直方向受到堰坎边界的约束，堰顶上的过水断面缩小，流速增大，势能转化为动能。
同时堰坎前后产生的局部水头损失，也导致堰顶上势能减小。
所以宽顶堰过堰水流的特征是进口处水面会发生明显跌落。
从水力学观点看，过水断面的缩小，可以是堰坎引起，也可以是两侧横向约束引起。
当明渠水流流经桥墩、渡槽、隧洞〈或涵洞)的进口等建筑物时，由于进口段的过水断面在平面上收缩，使过水断面减小，流速加大，部分势能转化为动能，也会形成水面跌落，这种流动现象称为无坎宽顶堰流，仍按宽顶堰流的方法进行分析、计算。
（一）流量系数宽顶堰的流量系数取决于堰的进口形状和堰的相对高度，不同的进口堰头形状，可按下列方法确定。
1、进口堰头为直角(8-22)2、进口堰头为圆角(8-23)3、斜坡式进口流量系数可根据及上游堰面倾角由表选取。
在公式（8-22）、（8-23）中为上游堰高。
当≥3时，由堰高引起的水流垂向收缩已达到相当充分程度，故计算时将不考虑堰高变化的影响，按=3代入公式计算值。
由公式可以看出，宽顶堰的流量系数的变化范围在0.32～0.385之间，当=0时，=0.385，此时宽顶堰的流量系数值最大。
比较一下实用堰和宽顶堰的流量系数，我们可以看到前者比后者大，也就是说实用堰有较大的过水能力。
对此，可以这样来理解：实用堰顶水流是流线向上弯曲的急变流，其断面上的动水压强小于按静水压强规律计算的值，即堰顶水流的压强和势能较小，动能和流速较大，故过水能力较大；宽顶堰则因堰顶水流是流线近似平行的渐变流，其断面动水压强近似按静水压强规律分布，堰顶水流压强和势能较大，动能和流速较小，故过水能力较小。
（二）侧收缩系数宽顶堰的侧收缩系数仍可按公式（8-21）计算。
（三）淹没系数当堰下游水位升高到影响宽顶堰的溢流能力时，就成为淹没出流。
试验表明：当≥0.8时，形成淹没出流。
淹没系数可根据由表查出。
无坎宽顶堰流在计算流量时，仍可使用宽顶堰流的公式。
堰闸出流淹没系数可信度评价作者：李占松师冰雪来源：《科技创新与应用》2016年第26期摘要：堰流和闸孔出流是水利枢纽常见的两种泄流方式。
其出流形式分为自由出流和淹没出流两类。
淹没出流时需要用淹没系数对流量计算公式进行修正。
堰闸泄水建筑物下游通常都存在水跃，淹没出流时下游肯定是淹没式水跃衔接。
淹没水跃由于与完整水跃相比消能不充分，水面波动也明显增强。
在实验确定淹没系数时，水位等的测量精度决定了其可信度。
分析表明，在大淹没度情况下，要得到有价值的淹没系数，实测值误差必须满足非常苛刻的要求。
反之，在测量精度一定的条件下，欲使对淹没系数的研究有价值，必须预先进行可行性评估。
这为该方面研究提供了基本的评价方法。
在泄水建筑物水力计算中，也可作为确定其采信程度的依据。
关键词：水力学；堰流；闸孔出流；淹没系数；可信度1 概述堰流和闸孔出流是水利枢纽中常见的两种泄流方式。
其出流形式又分为自由出流和淹没出流。
泄洪时，常出现大淹没度的情况。
在这种情况下，查取水力学教材[1]或水力计算手册[2]，会存在淹没系数与相关要素对应关系区间偏大的现象，插值计算可能会出现比较大的偏差。
于是，有不少学者对大淹没度的堰闸出流进行研究，试图探讨在这种情况下淹没系数比较准确的规律。
实测时，一方面存在着水面波动引起的测量偏差；另一方面，对应于一定的测量水平存在着计量误差。
两者就构成了实测值与真实值之间的整体误差。
这些都是不可能完全消除的[3][4]。
实际上，堰闸出流形式为淹没出流时，往往都伴随着下游大淹没度的水跃。
水跃消能极不充分，水面波动显著。
分析堰闸出流实测值的误差对淹没系数可信度的影响，具有较大的理论价值和实际意义。
2 堰闸出流计算基本公式堰流计算基本公式为：其中：Q为流量（m）；？滓s为淹没系数；？着1为侧收缩系数；m为流量系数；b为堰的净过流宽度（m）；g为重力加速度，通常取9.8m/s2；H0为堰上作用全水头（m）。
文章主要探讨淹没系数的可信度，为简单计，只考虑无侧向收缩的情况，即侧收缩系数？着1取1.0。
堰闸隧洞的泄流能力计算公式商榷毛昶熙(南京水利科学研究院)摘要泄流能力是决定泄水建筑物尺寸大小的关键性问题，虽有设计手册可供查算，但很多模型试验的结果与设计差距很大。
同样，大孔径隧洞的泄流能力也常发生较大设计误差。
本文从水力学基本原理追索计算公式的合理性，并以模型试验资料验证，说明有些公式应加修正，测流控制断面应加明确，消能流态及其水头损失均应加考虑。
最后还给出了堰闸淹没泄流的流量系数表达式和大孔径隧洞泄洪流量的计算公式。
关键词堰闸隧洞泄流能力流量系数计算公式泄流能力是决定堰闸隧洞等建筑物尺寸大小的一个必备数据，所以在水力学中开展研究也最早，而且计算公式及其实验性流量系数均能从设计手册中查用，似乎已不存在什么问题了。
然而很多模型试验的结果却说明与设计差距很大。
例如50年代治淮工程有不少闸都可省去1～3孔，流量比设计大20%左右，废黄河地涵试验结果比设计大40～50%，可以缩减5孔。
南四湖二级闸134孔可以减为78孔。
就以最近试验的通榆河总渠地涵来说，15孔可省去3孔，对于隧洞泄流能力的试验结果也多超出设计值。
因此仍有必要探明原因改进计算和测流方法。
1 泄流能力的基本公式泄流能力计算均是以能量守恒原理引导的，即沿程取两个控制断面1,2写其能量方程可得α1(V12/2g)+H1=α2(V22/2g)+H2+hf式中势能水头H1、H2是在同一基面上的，两断面间沿程水头损失可表示为若令总水头H0=α1(V12/2g)+H1，则上式可解出下游控制断面的流速为则通过下游控制断面A的流量，考虑其水流收缩时，则为式中流量系数μ=εφ，就定义为收缩系数与流速系数的乘积。
此流量系数μ包含着两断面间沿程水头损失hf，与消能发生关系。
2 堰闸泄流对于宽顶堰(图1)，当其自由泄流时，由于堰顶产生临界水深H2=hc=(2/3)H，宽度b时，由式(3)可得并知流量系数最大值为，对于一般水闸(图2)，因进口翼墙闸墩阻水情况不同，可取0.37[1,2,3]。
堰闸出流淹没系数可信度评价堰流和闸孔出流是水利枢纽常见的两种泄流方式。
其出流形式分为自由出流和淹没出流两类。
淹没出流时需要用淹没系数对流量计算公式进行修正。
堰闸泄水建筑物下游通常都存在水跃，淹没出流时下游肯定是淹没式水跃衔接。
淹没水跃由于与完整水跃相比消能不充分，水面波动也明显增强。
在实验确定淹没系数时，水位等的测量精度决定了其可信度。
分析表明，在大淹没度情况下，要得到有价值的淹没系数，实测值误差必须满足非常苛刻的要求。
反之，在测量精度一定的条件下，欲使对淹没系数的研究有价值，必须预先进行可行性评估。
这为该方面研究提供了基本的评价方法。
在泄水建筑物水力计算中，也可作为确定其采信程度的依据。
标签：水力学；堰流；闸孔出流；淹没系数；可信度1 概述堰流和闸孔出流是水利枢纽中常见的两种泄流方式。
其出流形式又分为自由出流和淹没出流。
泄洪时，常出现大淹没度的情况。
在这种情况下，查取水力学教材[1]或水力计算手册[2]，会存在淹没系数与相关要素对应关系区间偏大的现象，插值计算可能会出现比较大的偏差。
于是，有不少学者对大淹没度的堰闸出流进行研究，试图探讨在这种情况下淹没系数比较准确的规律。
实测时，一方面存在着水面波动引起的测量偏差；另一方面，对应于一定的测量水平存在着计量误差。
两者就构成了实测值与真实值之间的整体误差。
这些都是不可能完全消除的[3][4]。
实际上，堰闸出流形式为淹没出流时，往往都伴随着下游大淹没度的水跃。
水跃消能极不充分，水面波动显著。
分析堰闸出流实测值的误差对淹没系数可信度的影响，具有较大的理论价值和实际意义。
2 堰闸出流计算基本公式堰流计算基本公式为：其中：Q为流量（m）；？滓s为淹没系数；？着1为侧收缩系数；m为流量系数；b为堰的净过流宽度（m）；g为重力加速度，通常取9.8m/s2；H0为堰上作用全水头（m）。
文章主要探讨淹没系数的可信度，为简单计，只考虑无侧向收缩的情况，即侧收缩系数？着1取1.0。
堰闸出流淹没系数可信度评价
堰流和闸孔出流是水利枢纽常见的两种泄流方式。
其出流形式分为自由出流和淹没出流两类。
淹没出流时需要用淹没系数对流量计算公式进行修正。
堰闸泄水建筑物下游通常都存在水跃，淹没出流时下游肯定是淹没式水跃衔接。
淹没水跃由于与完整水跃相比消能不充分，水面波动也明显增强。
在实验确定淹没系数时，水位等的测量精度决定了其可信度。
分析表明，在大淹没度情况下，要得到有价值的淹没系数，实测值误差必须满足非常苛刻的要求。
反之，在测量精度一定的条件下，欲使对淹没系数的研究有价值，必须预先进行可行性评估。
这为该方面研究提供了基本的评价方法。
在泄水建筑物水力计算中，也可作为确定其采信程度的依据。
标签：水力学；堰流；闸孔出流；淹没系数；可信度
1 概述
堰流和闸孔出流是水利枢纽中常见的两种泄流方式。
其出流形式又分为自由出流和淹没出流。
泄洪时，常出现大淹没度的情况。
在这种情况下，查取水力学教材[1]或水力计算手册[2]，会存在淹没系数与相关要素对应关系区间偏大的现象，插值计算可能会出现比较大的偏差。
于是，有不少学者对大淹没度的堰闸出流进行研究，试图探讨在这种情况下淹没系数比较准确的规律。
实测时，一方面存在着水面波动引起的测量偏差；另一方面，对应于一定的测量水平存在着计量误差。
两者就构成了实测值与真实值之间的整体误差。
这些都是不可能完全消除的[3][4]。
实际上，堰闸出流形式为淹没出流时，往往都伴随着下游大淹没度的水跃。
水跃消能极不充分，水面波动显著。
分析堰闸出流实测值的误差对淹没系数可信度的影响，具有较大的理论价值和实际意义。
2 堰闸出流计算基本公式
堰流计算基本公式为：
其中：Q为流量（m）；？滓s为淹没系数；？着1为侧收缩系数；m为流量系数；b为堰的净过流宽度（m）；g为重力加速度，通常取9.8m/s2；H0为堰上作用全水头（m）。
文章主要探讨淹没系数的可信度，为简单计，只考虑无侧向收缩的情况，即侧收缩系数？着1取1.0。
同时，堰前行近流速水头可以忽略，堰上作用全水头H0可以近似取堰上作用水头H。
闸孔出流计算基本公式为：
其中：Q为流量（m）；？滓s为淹没系数；？滋为流量系数；b为堰的净过
流宽度（m）；e为闸门开度（m）；g为重力加速度，通常取9.8m/s2；H0为闸上作用全水头（m）。
闸孔出流计算通常不单独考虑（或忽略）侧向收缩的影响。
并且，闸前行近流速水头往往都可以忽略，闸上作用全水头H0近似取闸上作用水头H。
3 堰闸出流淹没系数可信度评价公式
用符号“？驻”表示某一物理量的绝对误差，用符号“？啄”表示其相对误差，用符号“R”表示其可信度。
并且，绝对误差用实测值减去真实值来定义；相对误差用绝对误差与真实值之比来定义；可信度用实测值与真实值之比来定义。
可信度为1时为绝对可信，越接近于1越可信，越偏离1越不可信。
3.1 堰流淹没系数可信度评价公式
堰流流量计算基本公式实测值形式为：
3.2 闸孔出流淹没系数可信度评价公式
3.3 用直角三角形薄壁堰测流量时的公式简化形式
进行水力学实验时，常见的流量测定方法有多种，如电磁流量计、孔板流量计和直角三角形薄壁堰等。
以直角三角形薄壁堰测流为例。
其最简单的流量计算公式形式为：
Q=1.4Hs2.5 （11）
其中：Hs为直角三角形薄壁堰堰上作用水头，以m计；流量Q单位为m3/s。
不难得出流量与堰上作用水头可信度之间的关系为：
4 堰闸出流淹没系数可信度评价
堰闸出流淹没系数可信度可分别依据（13）式和（14）式进行评价。
上述两式右端各量均为长度量的可信度。
简单计，认为其相对误差可取相同值，其绝对值表示为|？啄L|。
据相对误差和可信度的定义，不难得出两者之间的关系。
如对应于长度量L，关系式为：
R（L）=1+？啄L （15）
在实测量精度一定的情况下，为评价淹没系数最差的可信度，（13）式或（14）式分母各量均取-|？啄L|的相对误差计算可信度，分子取|？啄L|的相对误差计算可信度，可得表1。
反之亦然。
通常情况下，水力学实验控制实测量相对误差小于5%，由表中数据可以看出相对于实测量相对误差5%，淹没系数的相对误差已达22%；如严格控制实测精度至3%，淹没系数的相对误差也有16%。
反之，如欲得到相对误差小于10%的淹没系数值，必须使实测量的相对误差控制在2%以内，这应该是非常苛刻的要求；如欲得到相对误差小于5%的淹没系数值，必须使实测量的相对误差控制在1%以内，在现有的测量条件下这几乎是不可能的。
在大淹没度的情况下，堰闸下游水跃的淹没度很大，水面波动显著；同时，上下游水头差很小。
实测量的相对误差难免有8%～10%之多。
此时推算出的淹没系数相对误差已达49%～61%。
所以，特定条件下研究大淹没度堰闸淹没系数，应客观全面评价其价值，有可能已无实际意义。
5 结束语
堰流和闸孔出流流量系数可信度可分别用（6）式和（10）式进行评价。
如若测量流量用直角三角形薄壁堰，（6）式和（10）式又可分别表示成（13）式和（14）式。
若近似认为各长度量的实测值相对误差相同，则可得淹没系数与各实测量相对误差的对应关系如表1所示。
从表1可以看出，实测量的相对误差对淹没系数的相对误差影响显著。
如欲使淹没系数具有较高的精度，就必须对实测量的精度提出非常苛刻的要求。
在大淹没度情况下，对淹没系数实验研究之前，须进行全局评价并预估其价值，以免结果事倍功半甚至前功尽弃。
参考文献
[1]四川大学水力学与山区河流开发保护国家重点实验室.水力学（上册）[M].北京：高等教育出版社，2016：300-341.
[2]武汉大学水利水电学院水力学流体力学教研室.水力计算手册[M].李炜主编.北京：中国水利水电出版社，2006：82+103.
[3]李占松，朱士江.水流运动的不确定性刍议[A].第七届全国水力学与水利信息学大会论文集（2015水力学与水利信息学进展）[C].武汉：武汉理工大学出版社，2015，10（1）：71-75.
[4]李占松，王艳梅.论流动的恒定性与非恒定性[J].河南科学，2014，3
2（11）：2252-2255.
师冰雪（1991-），女，汉族，河南漯河人，水利水电工程专业硕士研究生。
