北京市朝阳区2013年中考一模数学试题

北京市朝阳区2013年初中毕业考试数学试卷第Ⅰ卷（选择题32分）一、选择题（共8道小题，每小题4分，共32分）下列各题均有四个选项，其中只有一个是符合题意的．请用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑． 1. -7 的相反数是A ． 7B ．－7C ．71 D ．71-2.中国航空母舰“辽宁号”的满载排水量为67500吨。

将数67500用科学记数法表示为A ．0.675×105B ． 6. 75×104C ． 67.5×103D ． 675×1023.把4张形状、质地完全相同的卡片分别写上数字1，2，3，4，再将这些卡片放在一个不透明的盒子里，随机从中抽取1张卡片，则抽取的卡片上的数字为奇数的概率是A ．41 B ．31 C ．21 D ． 14.北京2013年3月的一周中每天最高气温如下：7， 13，15，16，15，17，19，则在这一周中，最高气温的众数和中位数分别是A ．15和15B ．15和16C ． 16和15D ．19和16 5. 如图，已知直线l 1//l 2，∠1=40°，则∠2的度数为A ．30°B ． 40°C ． 50°D ． 60° 6．如图，⊙O 的半径为5，AB 是弦，OC ⊥AB 于点C ，若OC=3，则AB 的长为A ． 3B ． 4C ． 6D ．87．二次函数21(1)32y x =-+的顶点在A．第一象限． B ．第二象限．C ．第象限D ．第象限．8．如图，矩形ABCD的两条对角线相交于点O，∠BOC=120°，AB=3，一动点P以1cm/s的速度延折线OB—BA运动，那么点P的运动时间x（s）与点C、O、P围成的三角形的面积y之间的函数图象为A B C D第Ⅱ卷（共68分）二．填空题（共5道小题，每小题4分，共20分）9. 若-2是方程062=+-mxx的一个根，则m= .10. 分解因式：2218m-=．11．侧面展开图是扇形的几何体是 .12．如图，菱形ABCD的一条对角线BD上一点O，到菱形一边AB的距离为2，那么点O到另外一边BC的距离为_________.13．若关于x的一元二次方程kx2-2x+1 = 0有两个实数根，则k的取值范围是.三．解答题（共9道小题，14题—20题每小题5分，21题6分，22题7分，共48 分）14．（本小题5分）计算：()1-)32(-45in2-82-1︒+s．解：15．（本小题5分）求不等式组()⎪⎩⎪⎨⎧≥-+>-12131325xxx的整数解.解：6如图所示，在△ABC 中，AD ⊥BC 于D ，BE ⊥AC 于E ，AD 与BE 相交于F ，且BF=AC. 求证：DF=DC. 证明：17．列方程或方程组解应用题（本小题5分）动物园的门票售价：成人票每张50元，儿童票每张30元. 某日动物园售出门票700张，共得29000元. 请问当日儿童票售出多少张？解：18．（本小题5分）某学校为了解该校七年级学生的身高情况，抽样调查了部分同学身高，将所得数据处理后，制成扇形统计图和频数分布直方图（部分）如下（每组只含最低值不含最高值，身高单位：cm ，测量时精确到1cm ）：（1）请根据所提供的信息补全频数分布直方图；（2）写出该样本中，七年级学生身高的中位数所在组的范围; ;（3）如果该校七年级共有500名学生，那么估计该校七年级身高在160cm 及160cm 以上的学生共有 人；（4）若该校所在区的七年级学生平均身高为155 cm ，请结合以上信息，对该校七年级学生的身高情况提出一个你的见解./cm165~170cm已知：一次函数2+=x y 与反比例函数xk y =相交于A 、B 两点且A 点的纵坐标为4.（1）求反比例函数的解析式； （2）求△AOB 的面积. 解：20．（本小题5分）如图，AB 为⊙O 的直径，BC 是弦，OE ⊥BC ，垂足为F ，且与⊙O 相交于点E ，连接CE 、AE ，延长OE 到点D ，使∠ODB=∠AEC. (1)求证：BD 是⊙O 的切线； (2)若cosD=54，BC=8,求AB 的长.(1)证明：(2)解：如图，抛物线c xy +-=243与x 轴分别交于点A 、B ，直线2343+-=x y 过点B ，与y 轴交于点E ，并与抛物线c x y +-=243相交于点C ．（1）求抛物线c xy +-=243的解析式；（2）直接写出点C 的坐标；（3）若点M 在线段A B 上以每秒1个单位长度的速度从点A 向点B 运动（不与点A 、B 重合），同时，点N 在射线B C 上以每秒2个单位长度的速度从点B 向点C 运动．设点M 的运动时间为t 秒，请写出M N B △的面积S 与t 的函数关系式，并求出点M 运动多少时间时，M N B △的面积最大，最大面积是多少？解：在矩形ABCD中，AD=4，M是AD的中点，点E是线段AB上一动点，连接EM并延长交线段CD的延长线于点F.（1）如图1，求证：ME=MF；（2）如图2，点G是线段BC上一点，连接GE、GF、GM，若△EGF是等腰直角三角形，∠EGF=90°，求AB的长；（3）如图3，点G是线段BC延长线上一点，连接GE、GF、GM，若△EGF是等边三角形，求AB 的长.北京市朝阳区2013年初中毕业考试数学试卷参考答案及评分标准一、选择题（共8道小题，每小题4分，共32分）二、填空题（共5道小题，每小题4分，共20分）9. －5 10. ）（3)3(2-+a a 11. 圆锥 12. 2 13. k ≤1且k ≠0三、解答题（共9道小题，14题—20题每小题5分，21题6分，22题7分，共48 分） 14．解：原式23222221-⨯-+=.…………………………………………………………………4分.212-=………………………………………………………………………………5分15．解： 523(1)132x x x ->+⎧⎪⎨-≥⎪⎩　①1 ②解① 得 x ＞25. …………………………………………………………………………2分解② 得 x ≤4. ……………………………………………………………………………4分 原不等式组的整数解为3和4. ……………………………………………………………5分16. 证明：∵AD ⊥BC ，∴∠BDF ＝∠ADC ＝90°. ……………………………………………………………………1分 ∴∠A ＋∠C ＝90°.又∵BE ⊥AC ， ∴∠B ＋∠C ＝90°.∴∠B =∠A . …………………………………………………………………………………2分 又∵BF=AC ，…………………………………………………………………………………3分∴△BDF ≌△ADC . …………………………………………………………………………4分 ∴DF =DC . …………………………………………………………………………………5分17．解：设当日儿童票售出x 张，成人票售出y 张. ………………………………………………1分根据题意，得⎨⎧=+=+.290005030,700y x y x ……………………………………………………………………3分 解得⎩⎨⎧==.400,300y x …………………………………………………………………………………4分答：当日儿童票售出300张，成人票售出400张. ……………………………………………5分18. 解：（1）补图（图略）； …………………………………………………………………………2分（2）155—160；…………………………………………………………………………………3分 （3）160 ；………………………………………………………………………………………4分 （4）如：该校七年级多数学生的身高达到或者超过区平均身高. ………………………5分（说明：其他合理解答均可）19．（1）根据题意，得4= x+2，解得x =2.∴A （2，4）. 把A （2，4）代入xk y =，解得8=k . ∴xy 8=. …………………………………………2分（2）当0=y 时，02=+x ，2-=x .∴B （－2，0）. ………………………………………3分 ∴OB ＝2.如图，作AC ⊥x 轴于点C ，∵A （2，4），∴AC ＝4. ∴S △AOB ＝.421=⋅⋅AC OB …………………………5分20．（1）证明：∵∠D ＝∠AEC ，∠AEC ＝∠ABC ，∴∠D ＝∠ABC . ………………………………………………………………………1分 ∵OF ⊥BC ， ∴∠D +∠DBC ＝90°. ∴∠ ABC +∠DBC ＝90°.∴BD 是⊙O 的切线. ……………………………………………………………2分（2）解：如图，连接AC .∵ AB 是⊙O 的直径，∴∠ACB =90°．………………………………………3分 ∵∠ABC =∠D ． ∴cos ∠ABC= cos D =54．即B C A B=54，……………………………………………4分∵BC ＝8，∴AB =10． …………………………………………5分21．解：（1）由2343+-=x y ，当0=y 时，解得2=x . ∴B （2，0）.∵抛物线c x y +-=243经过点B （2，0），∴3=c .∴此抛物线的解析式为3432+-=x y .………………………………………………2分（2）C （1-，49）. ………………………………………………………………………3分（3） 如图，作ND ⊥x 轴于点D ，由2343+-=x y 得E （0，23）. ∴BE=25.由3432+-=x y 得A （－2，0）. ∴AB=4.由题意，得AM =t ，BM =4－t ，BN =2t . 由△BND ∽△BEO ，得BE BN OEDN =.∴56t DN =. ………………………………………4分∴△MNB 的面积S 56)4(2121t t ND BM ⋅-⋅=⋅⋅=.∴t t S 512532+-=.…………………………………5分 即512)2(532+--=t S ，自变量t 的取值范围是0＜t ＜4. t= 2时，512=最大S .…………………………………6分22. （1）证明：在矩形ABCD 中，∠A ＝∠FDM ＝90°.又∵AM ＝DM ，∠AME ＝∠DMF ， ∴△AME ≌△DMF .∴ME =MF . ………………………………………2分 （2）解：如图，过点G 作GH ⊥AD 于点H .∴四边形ABGH 是矩形.∵△EGF 是等腰直角三角形， 由（1）得，ME =MF ， ∴ME =MG ， ∠EMG ＝90°.∴∠AME +∠DMG ＝∠HGM +∠DMG= 90°. ∴∠AME ＝∠HGM . 又∵∠A ＝∠MHG ，∴△AME ≌△HGM . ……………………………3分 ∴AM=HG . ∴AB=HG=AM=21AD=2. ………………………4分（3）解：如图，过点G 作GH ⊥AD ，交AD 的延长线于点H .∴四边形ABGH 是矩形.∵△EGF 是等边三角形，∠MEG ＝60°， 由（1）得，ME =MF ， ∴∠EMG ＝90°.∴∠AME +∠HMG ＝∠AME +∠AEM = 90°. ∴∠AEM ＝∠HMG . 又∵∠A ＝∠AHG ，∴△AEM ∽△HGM . ……………………………5分 ∴EMMG AMGH =.∴tan ∠MEG=EMMG AMGH == tan 60°=3.又∵AM=21AD=2，∴AB=GH=23.…………………………………7分。

新世纪教育网精选资料 版权全部 @新世纪教育网九年级综合水平质量调研数学试卷2013.3学校 ___________________ 班级 _______________姓名 ________________ 学号 _____________考1． 本试卷共 8 页，共五道大题， 25 道小题，满分 120 分，考试时间 120 分钟 .生 2． 在试卷和答题卡上正确填写学校．班级．姓名．学号.须3． 试题答案一律填涂或书写在 答题卡 上，在试卷上作答无效 .知4． 考试结束，请将本试卷和答题卡一并交回.注 意 1 ． 考生要按规定的要求在机读答题卡上作答，题号要对应，填涂要规范.事项 2 ． 考试结束后，试卷和机读答题卡由监考人一并回收.第一卷（机读卷 32 分）一 1.4 的算术平方根是选 A ． 2B ．± 2C ． 16D ．± 16择2. 如图，已知 △ ABC 为直角三角形， ∠ C=90°，若 C题 沿图中虚线剪去∠ C ， 则∠ 1+∠ 2 等于D本 A.90°B. 135 °E12题C. 150 °D. 270 °BA32第 2分题图，3.布袋中装有 1 个红球， 2 个白球， 3 个黑球，它们除颜色外完好同样，从袋中任每 小 意摸出一个球，摸出的球是白球．．的概率是题 A ．1B ．1C ． 1D ．543626分4.某班的 9 名同学的体重分别是（单位：千克）： 61，59， 70，59， 65，67，59，63，57，这组数据的众数和中位数分别是A ． 59，61B ．59，63C ． 59， 65D ． 57，61 5.全世界可被人类利用的淡水总量仅占地球上总水量的 0.00003 ，所以珍惜水、保护 水，是我们每一位公民当仁不让的责任．此中数字 0.00003 用科学记数法表示为A ．3 10 4B ．3 10 5C ．0.310 4D ．0.3 10 56.如图，模块①－⑤均由 4 个棱长为 1 的小正方体构成，模块⑥由 15 个棱长为 1的小正方体构成 .现从模块①－⑤中选出三个放到模块⑥上，使得模块⑥成为一个棱长为 3 的大正方体 . 则以下选择方案中，能够达成任务的为新世纪教育网精选资料版权全部@新世纪教育网一选择题本题32分，每小题4分A．模块②，④，⑤B．模块①，③，⑤C．模块①，②，⑤D．模块③，④，⑤7.如图，两个齐心圆，大圆的弦 AB与小圆相切于点 P，大圆的弦CD经过点 P，且 CD=13， PC=4，则两圆构成的圆环的面积是A．16πB．36πC．52πD．81π第 7题图8. 矩形 ABCD 中，AD8cm， AB 6cm ．动点E从点C开始沿边 CB 向点B以 2cm/s 的速度运动至点 B 停止，动点 F从点 C 同时出发沿边CD 向点 D 以 1cm/s 的速度运动至点D停止．如图可获得矩形CFHE ，设运动时间为 x（单位： s），此时矩形 ABCD 去掉矩形 CFHE 后节余部分的面积为y(单位： cm2) ，则 y 与 x 之间的函数关系用图象表示大概是以下图第 8题图中的注 1．第Ⅱ卷包含 4 道填空和 13 道解答，共 8 . 答前要真，看清目意要求，按要求真作答.事2．答笔迹要工整，画要清楚，卷面要整.3．考生除画能够用笔外，答必用色或黑色笔、珠笔.二填空本共16分，每小4分三解答本第二卷（非机读卷88 分）9.若分式 x 24的 0， x 的．x210.如，点 A、 B 、C是半径6的⊙O上的点，BB 30,AC 的_____________.AOC第 10如，在△ ABC 中， D、 E 分 AB、 AC 上的点， DE∥A 11.BC．若 AD ＝3， DB＝ 5，DE ＝ 1.2， BC＝．D EB C第 1112. 如，在ABC 中，A，ABC 的平分与ACD 的均分交于点A，得 A，11A1=． A1 BC 的均分与A1CD 的均分交于点A2，得A2，⋯⋯，A2009 BC 的均分与A2009CD的均分第 12交于点 A2010，得 A2010，A2010=．13.（本小 5 分）( 3 1)04sin6027题14. （本小题 5 分）共3x1430解不等式组x，并把它的解集表示在数轴上．2x2分，每小题5分15. （本小题 5 分）A D如图， E、F 是平行四边形ABCD 对角线 AC E上两点， BE ∥ DF ，求证：AF CE 。

北京市朝阳区2013年中考数学一模试卷一、选择题（共8道小题，每小题4分，共32分）下列各题均有四个选项，其中只有一个是符合题意的．请用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑．2．（4分）（2013•朝阳区一模）中国航空母舰“辽宁号”的满载排水量为67500吨．将数675003．（4分）（2013•朝阳区一模）把4张形状、质地完全相同的卡片分别写上数字1，2，3，4，再将这些卡片放在一个不透明的盒子里，随机从中抽取1张卡片，则抽取的卡片上的数字为B∴抽取的卡片上的数字为奇数的概率是=4．（4分）（2013•朝阳区一模）北京2013年3月的一周中每天最高气温如下：7，13，15，5．（4分）（2013•朝阳区一模）如图所示，直线l1∥l2，∠1=40°，则∠2为（）6．（4分）（2013•朝阳区一模）如图，⊙O的半径为5，AB为弦，OC⊥AB，垂足为C，若OC=3，则弦AB的长为（）==47．（4分）（2013•朝阳区一模）二次函数y=（x ﹣1）2+3的顶点在（ ）y=8．（4分）（2013•朝阳区一模）如图，矩形ABCD 的两条对角线相交于点O ，∠BOC=120°，AB=3，一动点P 以1cm/s 的速度延折线OB ﹣BA 运动，那么点P 的运动时间x （s ）与点C 、O 、P 围成的三角形的面积y 之间的函数图象为（ ）BAB=•=•二．填空题（共5道小题，每小题4分，共20分）9．（4分）（2013•朝阳区一模）如果2是方程x2﹣mx+6=0的一个根，那么m=5．10．（4分）（2013•朝阳区一模）因式分解：2x2﹣18=2（x+3）（x﹣3）．11．（4分）（2013•朝阳区一模）侧面展开图是矩形的简单几何体是圆柱，棱柱．12．（4分）（2013•朝阳区一模）如图所示，菱形ABCD的一条对角线BD上一点O到菱形一边AB的距离为3，那么O点到另外一边BC的距离为3．13．（4分）（2013•朝阳区一模）若关于x的一元二次方程kx2﹣2x+1=0有实数根，则k的取值范围是k≤1且k≠0．三．解答题（共9道小题，14题-20题每小题5分，21题6分，22题7分，共48分）14．（5分）（2013•朝阳区一模）计算：（1﹣）0+﹣2sin45°﹣（）﹣1．﹣×﹣=﹣15．（5分）（2013•朝阳区一模）求不等式组的整数解．则不等式组16．（5分）（2013•朝阳区一模）如图所示，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，且BF=AC．求证：DF=DC．17．（5分）（2013•朝阳区一模）动物园的门票售价：成人票每张50元，儿童票每张30元．某日动物园售出门票700张，共得29000元．求成人票和儿童票各售出多少张．，解得18．（5分）（2013•朝阳区一模）某学校为了解该校七年级学生的身高情况，抽样调查了部分同学身高，将所得数据处理后，制成扇形统计图和频数分布直方图（部分）如下（每组只含最低值不含最高值，身高单位：cm，测量时精确到1cm）：（1）请根据所提供的信息补全频数分布直方图；（2）写出该样本中，七年级学生身高的中位数所在组的范围；155～160cm；（3）如果该校七年级共有500名学生，那么估计该校七年级身高在160cm及160cm以上的学生共有160人；（4）若该校所在区的七年级学生平均身高为155cm，请结合以上信息，对该校七年级学生的身高情况提出一个你的见解．19．（5分）（2013•朝阳区一模）已知：一次函数y=x+2与反比例函数y=相交于A、B两点且A点的纵坐标为4．（1）求反比例函数的解析式；（2）求△AOB的面积．y=得，y=组成方程组得，，，×4+20．（5分）（2013•朝阳区一模）如图，AB为⊙O的直径，BC是弦，OE⊥BC，垂足为F，且与⊙O相交于点E，连接CE、AE，延长OE到点D，使∠ODB=∠AEC．（1）求证：BD是⊙O的切线；（2）若cosD=，BC=8，求AB的长．都对BF=CF=ABC=，=521．（6分）（2013•朝阳区一模）如图，抛物线y=﹣x2+c与x轴分别交于点A、B，直线y=﹣x+过点B，与y轴交于点E，并与抛物线y=﹣x2+c相交于点C．（1）求抛物线y=﹣x2+c的解析式；（2）直接写出点C的坐标；（3）若点M在线段AB上以每秒1个单位长度的速度从点A向点B运动（不与点A、B 重合），同时，点N在射线BC上以每秒2个单位长度的速度从点B向点C运动．设点M 的运动时间为t秒，请写出△MNB的面积S与t的函数关系式，并求出点M运动多少时间时，△MNB的面积最大，最大面积是多少？=x+过点﹣）联立抛物线及直线解析式可得：或，，）BE==EBO=，EBO==（×t=t t=（（．﹣t最大面积是22．（7分）（2013•朝阳区一模）在矩形ABCD中，AD=4，M是AD的中点，点E是线段AB上一动点，连接EM并延长交线段CD的延长线于点F．（1）如图1，求证：ME=MF；（2）如图2，点G是线段BC上一点，连接GE、GF、GM，若△EGF是等腰直角三角形，∠EGF=90°，求AB的长；（3）如图3，点G是线段BC延长线上一点，连接GE、GF、GM，若△EGF是等边三角形，则AB=2．=cot60，== HG=AM=2=cot60===AM=2 AB=HG=2．。

2013年北京市朝阳区高考数学一模试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.1．（5分）（2013•朝阳区一模）i为虚数单位，复数的虚部是（）A．B．C．D．考点：复数的基本概念；复数代数形式的乘除运算．专题：计算题．分析：利用复数的除法法则，把分子、分母分别乘以分母的共轭复数即可得出．解答：解：复数==的虚部是．故选A．点评：熟练掌握复数的运算法则和共轭复数是解题的关键．2．（5分）（2013•朝阳区一模）已知集合M={x|﹣2＜x＜3}，N={x|lg（x+2）≥0}，则M∩N=（）A．（﹣2，+∞）B．（﹣2，3）C．（﹣2，﹣1]D．[﹣1，3）考点：交集及其运算．专题：函数的性质及应用．分析：解对数不等式可以求出集合N，进而根据集合交集及其运算，求出M∩N．解答：解：∵N={x|lg（x+2）≥0}=[﹣1，+∞），集合M={x|﹣2＜x＜3}，则M∩N=[﹣1，3）故选D．点评：本题考查的知识点是对数不等式的解法，集合的交集及其运算，其中解不等式求出集合N是解答本题的关键．3．（5分）（2013•朝阳区一模）已知向量，．若，则实数m的值为（）A．﹣3 B．C．D．考点：平行向量与共线向量；平面向量的坐标运算．专题：平面向量及应用．分析：先求得得==（3，1），再由，则这两个向量的坐标对应成比例，解方程求得实数m的值．解答：解：由题意可得==（3，1），若，则这两个向量的坐标对应成比例，即，解得m=﹣3，故选A．点评：本题主要考查两个向量共线的性质，两个向量坐标形式的运算，属于中档题．4．（5分）（2013•朝阳区一模）在极坐标系中，直线与曲线ρ=2cosθ相交于A，B两点，O为极点，则∠AOB的大小为（）A．B．C．D．考点：点的极坐标和直角坐标的互化．专题：直线与圆．分析：把极坐标方程化为直角坐标方程，求出AC，DC的值，可得∠AOC的值，从而得到∠AOB=2∠AOC 的值．解答：解：直线ρcosθ=即x=，曲线ρ=2cosθ即ρ2=2ρcosθ，即（x﹣1）2+y2=1，表示以C（1，0）为圆心，以1为半径的圆．如图．Rt△ADC中，∵cos∠ACO==，∴∠ACO=，在△AOC中，AC=OC，∴∠AOC=，∴∠AOB=2∠AOC=，故选C．点评：本题考查把极坐标方程化为直角坐标方程的方法，直线和圆的位置关系，求出∠ACO是解题的关键．5．（5分）（2013•朝阳区一模）在下列命题中，①“”是“sinα=1”的充要条件；②的展开式中的常数项为2；③设随机变量ξ～N（0，1），若P（ξ≥1）=p，则．其中所有正确命题的序号是（）A．②B．③C．②③D．①③考点：命题的真假判断与应用．专题：计算题．分析：①利用特殊值α=，判断出为假命题．②利用二项展开式的通项公式求出第r+1项，令x的指数为0得常数项．③根据随机变量ξ～N（0，1），正态曲线关于x=0对称，得到对称区间对应的概率相等，根据大于1的概率得到小于﹣1的概率，根据对称轴一侧的区间的概率是，得到结果．解答：解：①是假命题．α=，是能推得sinα=1，反之，sinα=1，α可以为或其他数值．②：的通项为T r+1=C（）r=2r﹣4C4r x12﹣4r令12﹣4r=0得r=3∴展开式的常数项为T4=C43=2；正确；③：∵随机变量ξ～N（0，1），∴正态曲线关于x=0对称，∵P（ξ≥1）=p，∴P（ξ＜﹣1）=p，∴P（﹣1＜ξ＜0）=﹣p，正确．故选C．点评：本题考查命题真假的判断，考查了充要条件、二项式定理、正态分布等知识．6．（5分）（2013•朝阳区一模）某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为（）A．4B．C．D．8考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：三视图复原的几何体是长方体的三分之二，依据三视图的数据，得出长方体长、宽、高，即可求出几何体的体积．解答：解：三视图复原的几何体是长方体，长方体长、宽、高分别是：2，2，3，所以这个几何体的体积是2×2×3=12，长方体被一个平面所截，得到的几何体的是长方体的三分之二，如图所示，则这个几何体的体积为12×=8．故选D．点评：此题考查了由三视图判断几何体，考查三视图的读图能力，计算能力，空间想象能力，本题是基础题，常考题型．7．（5分）（2013•朝阳区一模）抛物线y2=2px（p＞0）的焦点为F，已知点A，B为抛物线上的两个动点，且满足∠AFB=120°．过弦AB的中点M作抛物线准线的垂线MN，垂足为N，则的最大值为（）A．B．1C．D．2考点：抛物线的简单性质．专题：计算题；圆锥曲线的定义、性质与方程．分析：设|AF|=a，|BF|=b，连接AF、BF．由抛物线定义得2|MN|=a+b，由余弦定理可得|AB|2=（a+b）2﹣ab，进而根据基本不等式，求得|AB|的取值范围，从而得到本题答案．解答：解：设|AF|=a，|BF|=b，连接AF、BF由抛物线定义，得|AF|=|AQ|，|BF|=|BP|在梯形ABPQ中，2|MN|=|AQ|+|BP|=a+b．由余弦定理得，|AB|2=a2+b2﹣2abcos120°=a2+b2+ab配方得，|AB|2=（a+b）2﹣ab，又∵ab≤（）2，∴（a+b）2﹣ab≥（a+b）2﹣（a+b）2=（a+b）2得到|AB|≥（a+b）．所以≤=，即的最大值为．故选：A点评：本题在抛物线中，利用定义和余弦定理求的最大值，着重考查抛物线的定义和简单几何性质、基本不等式求最值和余弦定理的应用等知识，属于中档题．8．（5分）（2013•朝阳区一模）已知函数f（x）=2x+1，x∈N*．若，使f（x0）+f（x0+1）+…+f（x0+n）=63成立，则称（x0，n）为函数f（x）的一个“生成点”．函数f（x）的“生成点”共有（）A．1个B．2个C．3个D．4个考点：函数的值；数列的求和．专题：压轴题；新定义．分析：由f（x0）+f（x0+1）+…+f（x0+n）=63，得（2x0+1）+[2（x0+1）+1]+…+[2（x0+n）+1]=63，化简可得（n+1）（2x0+n+1）=63，由，得或，解出即可．解答：解：由f（x0）+f（x0+1）+…+f（x0+n）=63，得（2x0+1）+[2（x0+1）+1]+…+[2（x0+n）+1]=63所以2（n+1）x0+2（1+2+…n）+（n+1）=63，即（n+1）（2x0+n+1）=63，由，得或，解得或，所以函数f（x）的“生成点”为（1，6），（9，2）．故选B．点评：本题考查数列求和及函数求值，考查学生对问题的阅读理解能力解决问题的能力．二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上.9．（5分）（2013•朝阳区一模）在等比数列{a n}中，2a3﹣a2a4=0，则a3=2，{b n}为等差数列，且b3=a3，则数列{b n}的前5项和等于10．考点：等比数列的通项公式；等比数列的前n项和．专题：等差数列与等比数列．分析：由题意可得a2a4=，代入已知可解得a3=2，进而可得b3=a3=2，代入等差数列的求和公式可得S5==，计算即可．解答：解：由等比数列的性质可得a2a4=，代入可得2a3﹣=0，解得a3=2，或a3=0（舍去）；故b3=a3=2，由等差数列的求和公式和性质可得：数列{b n}的前5项和S5===5×2=10故答案为：2；10点评：本题考查等比数列和等差数列的性质和求和公式，属基础题．10．（5分）（2013•朝阳区一模）在△ABC中，a，b，c分别为角A，B，C所对的边．已知角A为锐角，且b=3asinB，则tanA=．考点：正弦定理．专题：解三角形．分析：由条件，利用正弦定理可得sinB=3sinAsinB，求得sinA的值，再由同角三角函数的基本关系求得tanA的值．解答：解：在△ABC中，角A为锐角，且b=3asinB，由正弦定理可得sinB=3sinAsinB，∵sinA≠0，故sinA=，∴cosA==tanA==，故答案为．点评：本题主要考查正弦定理，同角三角函数的基本关系，属于中档题．11．（5分）（2013•朝阳区一模）执行如图所示的程序框图，输出的结果S=20．考点：程序框图．分析：题目首先给累加变量S和循环变量i赋值，S=0，i=0．先执行一次运算S=S+2i﹣1，然后判断i≥6是否成立，不成立继续执行i=i+2，S=S+2i﹣1，成立时结束循环，输出S．解答：解：框图首先给累加变量S和循环变量i赋值，S=0，i=0．执行S=0+2×0﹣1=﹣1；判断0≥6不成立，执行i=0+2=2，S=﹣1+2×2﹣1=2；判断2≥6不成立，执行i=2+2=4，S=2+2×4﹣1=9；判断4≥6不成立，执行i=4+2=6，S=9+2×6﹣1=20；判断6≥6成立，跳出循环，输出S的值为20．故答案为20．点评：本题考查了程序框图，考查了直到型结构，直到型结构是先执行后判断，不满足条件执行循环，满足条件跳出循环，算法结束，是基础题．12．（5分）（2013•朝阳区一模）如图，圆O是△ABC的外接圆，过点C作圆O的切线交BA的延长线于点D．若，AB=AC=2，则线段AD的长是1；圆O的半径是2．考点：与圆有关的比例线段．专题：选作题．分析：①由切割线定理得CD2=DA•DB，即可得出DA；②由余弦定理可得∠DCA，利用弦切角定理可得∠ABC=∠DCA，再利用正弦定理得即可．解答：解：①∵CD是⊙O的切线，由切割线定理得CD2=DA•DB，CD=，DB=DA+AB=DA+2，∴，又DA＞0，解得DA=1．②在△ACD中，由余弦定理可得cos∠ACD===，∵0＜∠ACD＜π，∴．根据弦切角定理可得∠ABC=∠DCA=．由正弦定理可得==4，∴R=2．故答案分别为1，2．点评：熟练掌握切割线定理、弦切角定理、正弦定理、余弦定理是解题的关键．13．（5分）（2013•朝阳区一模）函数f（x）是定义在R上的偶函数，且满足f（x+2）=f（x）．当x∈[0，1]时，f（x）=2x．若在区间[﹣2，3]上方程ax+2a﹣f（x）=0恰有四个不相等的实数根，则实数a的取值范围是．考点：根的存在性及根的个数判断．专题：函数的性质及应用．分析：问题等价于在区间[﹣2，3]上函数f（x）与y=a（x+2）的图象有四个不同的交点，由函数的性质可作出它们的图象，由斜率公式可得边界，进而可得答案．解答：解：在区间[﹣2，3]上方程ax+2a﹣f（x）=0恰有四个不相等的实数根，等价于在区间[﹣2，3]上函数f（x）与y=a（x+2）的图象有四个不同的交点，由f（x+2）=f（x）可得函数的周期为2，且为偶函数，函数y=a（x+2）的图象为过定点（﹣2，0）且斜率为a的直线，作出它们的图象可得：由图图可知，当直线介于CB和CA之间符合题意，而由斜率公式可得k CB==，k CA==，故实数a的取值范围是：，故答案为：点评：不本题考查方程根的存在性及个数的判断，数形结合是解决问题的关键，属中档题．14．（5分）（2013•朝阳区一模）在平面直角坐标系xOy中，已知点A是半圆x2﹣4x+y2=0（2≤x≤4）上的一个动点，点C在线段OA的延长线上．当时，则点C的纵坐标的取值范围是[﹣5，5]．考点：平面向量数量积的运算．专题：压轴题；平面向量及应用．分析：设点C（a，b），由题意可得=λ，且λ＞0，当点A在点M（2，2）时，由=20，且a=b，解得b的值．当点A在点N（2，﹣2）时，由=20，且a=﹣b，解得b的值，从而求得C的纵坐标的取值范围．解答：解：半圆x2﹣4x+y2=0（2≤x≤4）即（x﹣2）2+y2=4 （2≤x≤4），设点C（a，b），由于与的方向相同，故=λ，且λ＞0，当点A在点M（2，2）时，=2a+2b=20，且a=b，解得b=5．当点A在点N（2，﹣2）时，=2a+（﹣2b）=20，且a=﹣b，解得b=﹣5．综上可得，则点C的纵坐标的取值范围是[﹣5，5]，故答案为[﹣5，5]．点评：本题主要考查两个向量共线的性质，两个向量坐标形式的运算，体现了数形结合与分类讨论的数学思想，属于中档题三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程.15．（13分）（2013•朝阳区一模）已知函数（ω＞0）的最小正周期为π．（Ⅰ）求ω的值及函数f（x）的单调递增区间；（Ⅱ）当时，求函数f（x）的取值范围．考点：二倍角的余弦；两角和与差的正弦函数；二倍角的正弦；正弦函数的单调性．专题：三角函数的图像与性质．分析：（Ⅰ）利用两角和的正弦公式，二倍角公式化简函数f（x）的解析式为，由此求得它的最小正周期．令，求得x的范围，即可得到函数f（x）的单调递增区间．（Ⅱ）因为，根据正弦函数的定义域和值域求得函数f（x）的取值范围．解答：解：（Ⅰ）==．…（4分）因为f（x）最小正周期为π，所以ω=2．…（6分）所以．由，k∈Z，得．所以函数f（x）的单调递增区间为[]，k∈Z．…（8分）（Ⅱ）因为，所以，…（10分）所以．…（12分）所以函数f（x）在上的取值范围是[]．…（13分）点评：本题主要考查两角和的正弦公式，二倍角公式，正弦函数的单调性和周期性，正弦函数的定义域和值域，属于中档题．16．（13分）（2013•朝阳区一模）盒子中装有四张大小形状均相同的卡片，卡片上分别标有数字﹣1，0，1，2．称“从盒中随机抽取一张，记下卡片上的数字后并放回”为一次试验（设每次试验的结果互不影响）．（Ⅰ）在一次试验中，求卡片上的数字为正数的概率；（Ⅱ）在四次试验中，求至少有两次卡片上的数字都为正数的概率；（Ⅲ）在两次试验中，记卡片上的数字分别为ξ，η，试求随机变量X=ξ•η的分布列与数学期望EX．考点：离散型随机变量及其分布列；离散型随机变量的期望与方差．专题：概率与统计．分析：（Ⅰ）根据古典概型概率计算公式求解：P（A）=；（Ⅱ）设事件B：在四次试验中，至少有两次卡片上的数字都为正数，则P（B）=1﹣P（），根据独立重复试验中某事件发生k次的概率计算公式即可求得；（Ⅲ）由题意可知ξ，η的可能取值为﹣1，0，1，2，从而随机变量X的可能取值为﹣2，﹣1，0，1，2，4．根据古典概型该类计算公式求得X取各值时的概率即可写出分布列，利用期望公式即可求得期望值；解答：解：（Ⅰ）设事件A：在一次试验中，卡片上的数字为正数，则．答：在一次试验中，卡片上的数字为正数的概率是．（Ⅱ）设事件B：在四次试验中，至少有两次卡片上的数字都为正数．由（Ⅰ）可知在一次试验中，卡片上的数字为正数的概率是．所以．答：在四次试验中，至少有两次卡片上的数字都为正数的概率为．（Ⅲ）由题意可知，ξ，η的可能取值为﹣1，0，1，2，所以随机变量X的可能取值为﹣2，﹣1，0，1，2，4．；；；；；．所以随机变量X的分布列为X ﹣2 ﹣1 0 1 2 4P所以．点评：本题考查离散型随机变量的分布列及期望，考查古典概型概率计算公式，考查学生对问题的阅读理解能力．17．（14分）（2013•朝阳区一模）如图，在四棱锥P﹣ABCD中，平面PAC⊥平面ABCD，且PA⊥AC，PA=AD=2．四边形ABCD满足BC∥AD，AB⊥AD，AB=BC=1．点E，F分别为侧棱PB，PC上的点，且．（Ⅰ）求证：EF∥平面PAD；（Ⅱ）当时，求异面直线BF与CD所成角的余弦值；（Ⅲ）是否存在实数λ，使得平面AFD⊥平面PCD？若存在，试求出λ的值；若不存在，请说明理由．考点：直线与平面平行的判定；异面直线及其所成的角；平面与平面垂直的判定．专题：计算题；空间位置关系与距离；空间角．分析：（Ⅰ）由==λ可知，EF∥BC，依题意，可求得EF∥AD，再利用线面平行的判断定理即可证得结论；（Ⅱ）可证得PA，AB，AD两两垂直，以之为轴建立空间直角坐标系，可求得与的坐标，利用向量的数量积即可求得异面直线BF与CD所成角的余弦值；（Ⅲ）设F（x0，y0，z0），则=（x0，y0，z0﹣2），=（1，1，﹣2），由=λ，可求得F（λ，λ，2﹣2λ），再设出平面AFD的一个法向量为n1=（x1，y1，z1），平面PCD的一个法向量为n2=（x2，y2，z2），可求得这两个法向量的坐标，利用n1•n2=0，即可求得λ的值．解答：证明：（Ⅰ）由已知，==λ，所以EF∥BC．因为BC∥AD，所以EF∥AD．而EF⊄平面PAD，AD⊂平面PAD，所以EF∥平面PAD．…（4分）（Ⅱ）因为平面ABCD⊥平面PAC，平面ABCD∩平面PAC=AC，且PA⊥AC，所以PA⊥平面ABCD．所以PA⊥AB，PA⊥AD．又因为AB⊥AD，所以PA，AB，AD两两垂直．…（5分）如图所示，建立空间直角坐标系，因为AB=BC=1，PA=AD=2，所以A（0，0，0），B（1，0，0），C（1，1，0），D（0，2，0），P（0，0，2）．当λ=时，F为PC中点，所以F（，，1），所以=（﹣，，1），=（﹣1，1，0）．设异面直线BF与CD所成的角为θ，所以cosθ=|cos＜，＞|==，所以异面直线BF与CD所成角的余弦值为．…（9分）（Ⅲ）设F（x0，y0，z0），则=（x0，y0，z0﹣2），=（1，1，﹣2）．由已知=λ，所以（x0，y0，z0﹣2）=λ（1，1，﹣2），所以，∴=（λ，λ，2﹣2λ）．设平面AFD的一个法向量为n1=（x1，y1，z1），因为=（0，2，0），所以即，令z1=λ，得n1=（2λ﹣2，0，λ）．设平面PCD的一个法向量为n2=（x2，y2，z2），因为=（0，2，﹣2），=（﹣1，1，0），所以即令x2=1，则n2=（1，1，1）．若平面AFD⊥平面PCD，则n1•n2=0，所以（2λ﹣2）+λ=0，解得．所以当λ=时，平面AFD⊥平面PCD．…（14分）点评：本题考查直线与平面的平行，考查异面直线所成的角，考查面面垂直，突出考查空间直角坐标系在证明与计算中的应用．属于中档题．18．（13分）（2013•朝阳区一模）已知函数f（x）=x2﹣（a+2）x+alnx+2a+2，其中a≤2．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）若函数f（x）在（0，2]上有且只有一个零点，求实数a的取值范围．考点：利用导数研究函数的单调性；函数的零点．专题：导数的综合应用．分析：（I）先求函数的定义域再求函数的导数，当导数大于0时函数单调递增，当导数小于0时单调递减．（II）此题考查的是函数的零点存在问题．在解答的过程当中要先结合函数f（x）在区间（0，2]内有且只有一个零点的条件，结合（I）中确定函数的增减区间，求出函数的极小值和极大值，再转化出不等关系，利用此不等关系即可获得问题的解答．解答：解：（I）函数定义域为x＞0，且f′（x）=2x﹣（a+2）+=…（2分）①当a≤0，即时，令f'（x）＜0，得0＜x＜1，函数f（x）的单调递减区间为（0，1），令f'（x）＞0，得x＞1，函数f（x）的单调递增区间为（1，+∞）．②当，即0＜a＜2时，令f'（x）＞0，得或x＞1，函数f（x）的单调递增区间为，（1，+∞）．令f'（x）＜0，得，函数f（x）的单调递减区间为．③当，即a=2时，f'（x）≥0恒成立，函数f（x）的单调递增区间为（0，+∞）．…（7分）（Ⅱ）①当a≤0时，由（Ⅰ）可知，函数f（x）的单调递减区间为（0，1），f（x）在（1，2]单调递增．所以f（x）在（0，2]上的最小值为f（1）=a+1，由于，要使f（x）在（0，2]上有且只有一个零点，需满足f（1）=0或解得a=﹣1或a＜﹣．②当0＜a≤2时，由（Ⅰ）可知，（ⅰ）当a=2时，函数f（x）在（0，2]上单调递增；且，所以f（x）在（0，2]上有且只有一个零点．（ⅱ）当0＜a＜2时，函数f（x）在上单调递减，在（1，2]上单调递增；又因为f（1）=a+1＞0，所以当时，总有f（x）＞0．因为e＜1＜a+2，所以f（e）=e[e﹣（a+2）]+（alne+2a+2）＜0．所以在区间（0，）内必有零点．又因为f（x）在（0，）内单调递增，从而当0＜a≤2时，f（x）在（0，2]上有且只有一个零点．综上所述，0＜a≤2或a＜﹣或a=﹣1时，f（x）在（0，2]上有且只有一个零点．…（13分）点评：此题考查的是利用导数研究函数的单调性，函数的零点存在问题．在解答的过程当中充分体现了等价转化的思想，以及零点定理的相关知识．值得同学们体会反思．19．（14分）（2013•朝阳区一模）已知中心在原点，焦点在x轴上的椭圆C过点，离心率为，点A为其右顶点．过点B（1，0）作直线l与椭圆C相交于E，F两点，直线AE，AF与直线x=3分别交于点M，N．（Ⅰ）求椭圆C的方程；（Ⅱ）求的取值范围．考平面向量数量积的运算；椭圆的标准方程．点：圆锥曲线的定义、性质与方程．专题：分析：（Ⅰ）设椭圆的方程为，依题意可得a、b、c的方程组，解之可得方程；（Ⅱ）由（Ⅰ）可知点A的坐标为（2，0）．（1）当直线l的斜率不存在时，不妨设点E在x轴上方，可得；（2）当直线l的斜率存在时，写直线的方程，联立方程组，消y并整理得（4k2+1）x2﹣8k2x+4k2﹣4=0．进而由根与系数的关系表示出向量的数量积为，由k 的范围可得其范围，综合可得．解答：解：（Ⅰ）由题意，设椭圆的方程为，依题意得解之可得a2=4，b2=1．所以椭圆C的方程为．…（4分）（Ⅱ）由（Ⅰ）可知点A的坐标为（2，0）．（1）当直线l的斜率不存在时，不妨设点E在x轴上方，易得，，所以．…（6分）（2）当直线l的斜率存在时，由题意可设直线l的方程为y=k（x﹣1），显然k=0时，不符合题意．由消y并整理得（4k2+1）x2﹣8k2x+4k2﹣4=0．设E（x1，y1），F（x2，y2），则．直线AE，AF的方程分别为：，令x=3，则．所以，．…（10分） 所以======．…（12分）因为k 2＞0，所以16k 2+4＞4，所以，即．综上所述，的取值范围是．…（14分）点评： 本题考查平面向量数量积的运算，涉及椭圆的标准方程，以及直线与椭圆的位置关系的应用，属中档题．20．（13分）（2013•朝阳区一模）设τ=（x 1，x 2，…，x 10）是数1，2，3，4，5，6，7，8，9，10的任意一个全排列，定义，其中x 11=x 1．（Ⅰ）若τ=（10，9，8，7，6，5，4，3，2，1），求S （τ）的值；（Ⅱ）求S （τ）的最大值；（Ⅲ）求使S （τ）达到最大值的所有排列τ的个数．考点： 排列及排列数公式；数列的求和．专题： 等差数列与等比数列；概率与统计．分析：（Ⅰ）依题意，τ=（x 1，x 2，…，x 10）=（10，9，8，7，6，5，4，3，2，1），代入S （τ）=|2x k﹣3x k+1|计算即可求得S（τ）的值；（Ⅱ）可求得数10，9，8，7，6，5，4，3，2，1的2倍与3倍，从而可求得其中较大的十个数之和与较小的十个数之和的差，从而可得S（τ）的最大值；（Ⅲ）利用数1，2，3，4所产生的8个数都是较小的数，而数7，8，9，10所产生的8个数都是较大的数，从而使S（τ）取最大值的排列中，必须保证数1，2，3，4互不相邻，数7，8，9，10也互不相邻；而数5和6既不能排在7，8，9，10之一的后面，又不能排在1，2，3，4之一的前面，利用排列组合知识即可求得答案．解答：解：（Ⅰ）∵τ=（10，9，8，7，6，5，4，3，2，1），x11=x1，依题意，S（τ）=|2x k﹣3x k+1|，∴S（T）=|2x k﹣3x k+1|=7+6+5+4+3+2+1+0+1+28=57，．…（3分）（Ⅱ）数10，9，8，7，6，5，4，3，2，1的2倍与3倍分别如下：20，18，16，14，12，10，8，6，4，2，30，27，24，21，18，15，12，9，6，3其中较大的十个数之和与较小的十个数之和的差为203﹣72=131，所以S（τ）≤131．对于排列τ0=（1，5，6，7，2，8，3，9，4，10），此时S（τ0）=131，所以S（τ）的最大值为131．…（8分）（Ⅲ）由于数1，2，3，4所产生的8个数都是较小的数，而数7，8，9，10所产生的8个数都是较大的数，所以使S（τ）取最大值的排列中，必须保证数1，2，3，4互不相邻，数7，8，9，10也互不相邻；而数5和6既不能排在7，8，9，10之一的后面，又不能排在1，2，3，4之一的前面．设x1=1，并参照下面的符号排列1△○□△○□△○□△○其中2，3，4任意填入3个□中，有6种不同的填法；7，8，9，10任意填入4个圆圈○中，共有24种不同的填法；5填入4个△之一中，有4种不同的填法；6填入4个△中，且当与5在同一个△时，既可以在5之前又可在5之后，共有5种不同的填法，所以当x1=1时，使S （τ）达到最大值的所有排列τ的个数为6×24×4×5=2880，由轮换性知，使S（τ）达到最大值的所有排列τ的个数为28800．…（13分）点评：本题考查排列及排列数公式，考查抽象思维与综合分析能力，考查运算能力，属于难题．。

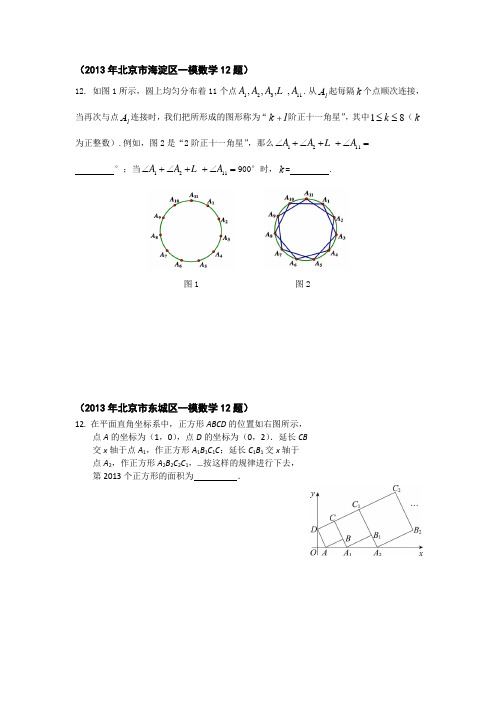
12. 如图1所示，圆上均匀分布着11个点12311,,,,A A A A .从A 1起每隔k 个点顺次连接，当再次与点A 1连接时，我们把所形成的图形称为“k +1阶正十一角星”，其中18k ≤≤（k 为正整数）.例如，图2是“2阶正十一角星”，那么1211A A A ∠+∠++∠=°；当1211A A A ∠+∠++∠=900°时，k = .图1 图2（2013年北京市东城区一模数学12题）12. 在平面直角坐标系中，正方形ABCD 的位置如右图所示，点A 的坐标为（1，0），点D 的坐标为（0，2）．延长CB 交x 轴于点A 1，作正方形A 1B 1C 1C ；延长C 1B 1交x 轴于 点A 2，作正方形A 2B 2C 2C 1，…按这样的规律进行下去，第2013个正方形的面积为 ．12．在平面直角坐标系xOy中，有一只电子青蛙在点A(1,0)处．第一次，它从点A先向右跳跃1个单位，再向上跳跃1个单位到达点A1；第二次，它从点A1先向左跳跃2个单位，再向下跳跃2个单位到达点A2；第三次，它从点A2先向右跳跃3个单位，再向上跳跃3个单位到达点A3；第四次，它从点A3先向左跳跃4个单位，再向下跳跃4个单位到达点A4；……依此规律进行，点A6的坐标为；若点A n的坐标为（2013，2012），则n= ．（ 2013年北京市朝阳区一模数学12题）12. 在平面直角坐标系xOy中，动点P从原点O出发，每次向上平移1个单位长度或向右平移2个单位长度，在上一次平移的基础上进行下一次平移．例如第1次平移后可能到达的点是（0，1）、（2，0），第2次平移后可能到达的点是（0，2）、（2，1）、（4，0），第3次平移后可能到达的点是（0，3）、（2，2）、（4，1）、（6，0），依此类推……．我们记第1次平移后可能到达的所有点的横、纵坐标之和为l1，l1=3；第2次平移后可能到达的所有点的横、纵坐标之和为l2，l2=9；第3次平移后可能到达的所有点的横、纵坐标之和为l3，l3=18；按照这样的规律，l4= ；l n= (用含n的式子表示，n是正整数)．12．我们把函数图象与x 轴交点的横坐标称为这个函数的零点.如函数12+=x y 的图象与x 轴交点的坐标为（21-，0），所以该函数的零点是-（1）函数542-+=x x y 的零点是 ； （2）如图，将边长为1的正方形ABCD 放置在平面直角坐标系xOy 中，且顶点A 在x 轴上.若正方形ABCD 沿x 轴正方向滚动，即先以顶点A 为中心顺时针旋转，当顶点B 落在x 轴上时，再以顶点B 为中心顺时针旋转，如此继续.顶点D 的轨迹是一函数的图象，则该函数在其两个相邻零点间的图象与x 轴所围区域的面积为 .（ 2013年北京市石景山区一模数学12题）12．将全体正整数排成一个三角形数阵：1 2 3 4 5 6 7 8 9 10． ． ． ． ． ． ．按照以上排列的规律，第5行从左到右的第3个数为_______；第n 行（n ≥3）从左到右的第3个数为 ．（用含n 的代数式表示）12．如图，在△ABC 中，AB =AC =2，点P 在BC 上．若点P 为BC 的中点，则2m AP BP PC =+⋅的值为 ；若BC 边上有100个不同的点P 1，P 2，…，P 100，且m i =AP i 2+BP i ⋅P i C （i =1,2，…，100），则m =m 1+m 2+…+m 100 的值为 ．（ 2013年北京市顺义区一模数学12题）12．如图，边长为1的菱形ABCD 中，60DAB ∠=°，则菱形ABCD 的面积是 ，连结对角线AC ，以AC 为边作第二个菱形11ACC D ，使160D AC ∠=°；连结1AC ，再以1AC 为边作第三个菱形122AC C D ，使2160D AC ∠=°；……，按此规律所作的第n 个菱形的面积为___________．PCB AC 1D 1D 2C 2DA B图BA第12题图D 15D 2 D 3 D 4D 0C12．定义一种对正整数n 的“F 运算”：①当n 为奇数时，结果为31n +；②当n 为偶数时，结果为k n 2（其中k 是使得k n2为奇数的正整数），并且运算重复进行.例如，取6n =，则：12363105F F F −−−→−−−→−−−→① ②②第次第次第次……，若1n =，则第2次“F 运算”的结果是 ；若13n =，则第2013次“F 运算”的结果是 .（ 2013年北京市大兴区一模数学12题）12．如图，正方形ABCD 边长为2cm ，动点P 从A 点出发，沿正方形的边按逆时针方向运动，当它的运动路程为2013cm 时，线段PA 的长为______cm ；当点P 第n 次（n 为正整数）到达点D 时，点P 的运动路程为______cm(用含n 的代数式表示)．（ 2013年北京市怀柔区一模数学12题）12. 如图，△ABC 是一个边长为2的等边三角形，AD 0⊥BC，垂足为点D 0．过点D 0作D 0D 1⊥AB，垂足为点D 1；再过点D 1作D 1D 2⊥AD 0，垂足为点D 2；又过点D 2作D 2D 3⊥AB，垂足为点D 3；……；这样一直作下去，得到一组线段：D 0D 1，D 1D 2，D 2D 3，……，则线段D 1D 2的长为 ，线段D n-1D n 的长为 （n 为正整数）．12．观察下列等式：第1个等式：⎪⎭⎫ ⎝⎛-⨯=⨯=311213111a ； 第2个等式：⎪⎭⎫ ⎝⎛-⨯=⨯=5131215312a ； 第3个等式：⎪⎭⎫ ⎝⎛-⨯=⨯=7151217513a ； 第4个等式：⎪⎭⎫⎝⎛-⨯=⨯=9171219714a ； ………………………………请解答下列问题：（1）按以上规律列出第5个等式：a 5 = = ； （2）求a 1 + a 2 + a 3 + a 4 + … + a 100的值为（ 2013年北京市平谷区一模数学12题）12．如图1、图2、图3，在ABC △中，分别以AB AC 、为边，向ABC △外作正三角形，正四边形，正五边形，BE CD 、相交于点O ．如图4，AB AD 、是以AB 为边向ABC △外所作正n 边形的一组邻边；AC AE 、是以AC 为边向ABC △外所作正n (n 为正整数)边形的一组邻边．BE CD 、的延长相交于点O ．图1中BOC ∠= ；图4中BOC ∠= （用含n 的式子表示）．12．如图，在平面直角坐标系xOy 中，点0M 的坐标为(1,0)，将线段0OM 绕原点O 沿逆时针方向旋转45︒，再将其延 长到1M ，使得001OM M M ⊥，得到线段1OM ；又将线段 1OM 绕原点O 沿逆时针方向旋转45︒，再将其延长到2M ，使得112OM M M ⊥，得到线段2OM ，如此下去，得到线 段3OM ，4OM ,，则点1M 的坐标是 ，点M 5的坐标是 ；若把点)(n n n y x M ，（n 是自然数）的横坐标n x ，纵坐 标n y 都取绝对值后得到的新坐标(),n n x y 称之为点n M 的绝对坐标， 则点83n M +的绝对坐标是 （用含n 的代数式表示）．（ 2013年北京市房山区一模数学12题）12．如图，在平面直角坐标系中，以原点O4，…，同心圆与直线y x =和y x =-分别交于1A ，2A ，3A ，4A ，…，则点31A 的坐标是 ．12．观察下面一列数的规律并填空：0，3，8，15，24，…，则它的第2013个数是 .第n个数是_________ ．。

2013年北京市各区中考一模试题汇编之--------图形操作题2013年海淀一模22.问题：如图1，a 、b 、c 、d 是同一平面内的一组等距平行线（相邻平行线间的距离为1）.画出一个正方形A B C D ，使它的顶点A 、B 、C 、D 分别在直线a 、b 、d 、c 上，并计算它的边长.图1 图2小明的思考过程：他利用图1中的等距平行线构造了33⨯的正方形网格，得到了辅助正方形E F G H ，如图2所示, 再分别找到它的四条边的三等分点A 、B 、C 、D ，就可以画出一个满足题目要求的正方形.请回答：图2中正方形A B C D 的边长为 . 请参考小明的方法，解决下列问题：（1）请在图3的菱形网格（最小的菱形有一个内角为60︒，边长为1）中，画出一个等边△A B C ，使它的顶点A 、B 、C 落在格点上，且分别在直线a 、b 、c 上；（3）如图4，1l 、2l 、3l 是同一平面内的三条平行线，1l 、2l 之间的距离是215，2l 、3l 之间的距离是2110，等边△A B C 的三个顶点分别在1l 、2l 、3l 上，直接写出△A B C 的边长.图3 图42013年西城一模22．先阅读材料，再解答问题：小明同学在学习与圆有关的角时了解到：在同圆或等圆中，同弧（或等弧）所对的圆周角相等．如图，点A、B、C、D均为⊙O上的点，则有∠C=∠D．小明还发现，若点E在⊙O外，且与点D在直线AB同侧，则有∠D>∠E．请你参考小明得出的结论，解答下列问题：(1) 如图1，在平面直角坐标系xOy中，点A的坐标为(0,7)，点B的坐标为(0,3)，点C的坐标为(3,0)．①在图1中作出△ABC的外接圆（保留必要的作图痕迹，不写作法）；②若在x轴的正半轴上有一点D，且∠ACB =∠ADB，则点D的坐标为；(2) 如图2，在平面直角坐标系xOy中，点A的坐标为(0,m)，点B的坐标为(0,n)，其中m>n>0．点P为x轴正半轴上的一个动点，当∠APB达到最大时，直接写出此时点P的坐标．2013年东城一模22. 如图，在菱形纸片ABCD中，AB=4cm，∠ABC=120°，按下列步骤进行裁剪和拼图：第一步：如图1，在线段AD上任意取一点E，沿EB，EC剪下一个三角形纸片EBC(余下部分不再使用)；第二步：如图2，沿三角形EBC的中位线GH将纸片剪成两部分，并在线段GH上任意取一点M，线段BC上任意取一点N，沿MN将梯形纸片GBCH剪成两部分；第三步：如图3，将MN左侧纸片绕G点按顺时针方向旋转180°，使线段GB与GE重合，将MN右侧纸片绕H点按逆时针方向旋转180°，使线段HC与HE重合，再与三角形纸片EGH拼成一个与三角形纸片EBC面积相等的四边形纸片．(注：裁剪和拼图过程均无缝且不重叠)（1）请你在图3中画出拼接成的四边形；（2）直接写出拼成的四边形纸片周长的最小值为________cm，最大值为________cm．2013年朝阳一模22.（本小题7分）在矩形ABCD中，AD=4，M是AD的中点，点E是线段AB上一动点，连接EM并延长交线段CD的延长线于点F.（1）如图1，求证：ME=MF；（2）如图2，点G是线段BC上一点，连接GE、GF、GM，若△EGF是等腰直角三角形，∠EGF=90°，求AB的长；（3）如图3，点G是线段BC延长线上一点，连接GE、GF、GM，若△EGF是等边三角形，求AB的长.22．问题解决：已知：如图，D 为AB 上一动点，分别过点A 、B 作AB CA ⊥于点A ，AB EB ⊥于点B ，联结CD 、DE .（1）请问：点D 满足什么条件时，DE CD +的值最小？（2）若8=AB ，4=AC ，2=BE ，设x AD =.用含x 的代数式表示DE CD +的长（直接写出结果）. 拓展应用：参考上述问题解决的方法，请构造图形， 并求出代数式()22144x x ++-+的最小值.2013年门头沟一模22．操作与探究：在平面直角坐标系xOy 中，点P 从原点O 出发，且点P 只能每次向上平移2个单位长度或向右平移1个单位长度． （1）实验操作：在平面直角坐标系xOy 中，点P 从原点O 出发， 平移1次后可能到达的点的坐标是(0,2)，(1,0)；点P 从原点O 出发，平移2次后可能到达的点的坐标是(0,4)，(1,2)，(2,0)；点P 从原点O 出发，平移3次后可能到达的点的坐标是 ； （2）观察发现：任一次平移，点P 可能到达的点在我们学过的一种函数的图象上，如：平移1次后在函数22+-=x y的图象上；平移2次后在函数42+-=x y的图象上，…．若点P 平移5次后可能到达的点恰好在直线3yx=上，则点P 的坐标是 ；（3）探究运用：点P 从原点O 出发经过n 次平移后，到达直线x y =上的点Q ，且平移的路径长不小于30，不超过32，求点Q 的坐标．AB CDExO1y122．如图1，在四边形A B C D中，A B C D、分别是B C A D、的中点，连结E F=，E F并延长，分别与B A C D∠=∠（不需证明）．、的延长线交于点M N、，则B M E C N E小明的思路是：在图1中，连结B D，取B D的中点H，连结H E H F、，根据三角形中位线定理和平行线性质，可证得B M E C N E∠=∠．问题：如图2，在A B C、、分别是B C A D △中，A C A B>，D点在A C上，A B C D=，E F的中点，连结E F并延长，与B A的延长线交于点G，若60E F C∠=°，连结G D，判断△的形状并证明．A G D2013年房山一模22.已知，矩形纸片ABCD中，AB=8cm，AD=6cm，按下列步骤进行操作：如图①，在线段AD上任意取一点E，沿EB，EC剪下一个三角形纸片EBC(余下部分不再使用)；如图②，沿三角形EBC的中位线GH将纸片剪成两部分，并在线段GH上任意取一点M，线段BC上任意取一点N，沿MN将梯形纸片GBCH剪成两部分；如图③，将MN左侧纸片绕G点按顺时针方向旋转180°，使线段GB与GE 重合，将MN右侧纸片绕H点按逆时针方向旋转180°，使线段HC与HE重合，拼成一个与三角形纸片EBC面积相等的四边形纸片． (注：裁剪和拼图过程均无缝且不重叠)（1）通过操作，最后拼成的四边形为（2）拼成的这个四边形的周长的最小值为_______________________________cm,最大值为___________________________cm．22. 如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形A B C D 的边长为2，E 是A D 的中点，沿C E 将菱形A B C D 剪成①、②两部分，用这两部分可以分别拼成直角三角形、等腰梯形、矩形，要求所拼成图形的顶点均落在格点上．（1）在下面的菱形斜网格中画出示意图；（2）若所拼成的直角三角形、等腰梯形、矩形的面积分别记为S 1、S 2、S 3，周长分别记为l 1、l 2、3l ，判断所拼成的三种图形的面积、周长的大小关系（用“=”、“＞”、“＜”、“≤）：面积关系是 ； 周长关系是 ．2013年延庆一模22. 操作与探究：（本题满分5分）阅读下面材料：将正方形ABCD （如图1）作如下划分：第1次划分：分别联结正方形ABCD 对边的中点（如图2），得线段HF 和EG ，它们交于点M ，此时图2中共有5个正方形；第2次划分：将图2左上角正方形AEMH 按上述方法再作划分，得图3，则图3中共有_______个正方形；若每次都把左上角的正方形依次划分下去，则第100次划分后，图中共有_______个正方形；继续划分下去，能否将正方形ABCD 划分成有2013个正方形的图形？需说明理由.图3图2图1MFGHEMFGHEABABABDCCDCD第22题图（矩形）（等腰梯形）（直角三角形）E DCBA ②①第22题图图①图②图③CB EC BE G HM NC BE G HM N A D22．如图,长方形纸片ABCD 中,AB ＝8cm ,AD ＝6cm ,按下列步骤进行裁剪和拼图:第一步:如图①,在线段AD 上任意取一点E ,沿EB ,EC 剪下一个三角形纸片EBC (余下部分不再使用)；第二步:如图②,沿三角形EBC 的中位线GH 将纸片剪成两部分,并在线段GH 上任意取一点M ,线段BC 上任意取一点N ,沿MN 将梯形纸片GBCH 剪成两部分；第三步:如图③,将MN 左侧纸片绕G 点按顺时针方向旋转180︒,使线段GB 与GE 重合,将MN 右侧纸片绕H 点按逆时针方向旋转180︒,使线段HC 与HE 重合,拼成一个与三角形纸片EBC 面积相等的四边形纸片.(注:裁剪和拼图过程均无缝且不重叠). （1）所拼成的四边形是什么特殊四边形？（2）拼成的这个四边形纸片的周长的最小值是多少?22．操作与探究：如图，在平面直角坐标系xOy 中，已知点0M 的坐标为（1,0）．将线段0OM绕原点O 沿逆时针方向旋转45，再将其延长到1M ，使得01OMMM ⊥，得到线段1OM ；又将线段1OM绕原点O 沿逆时针方向旋转45，再将其延长到2M ，使得112OMMM ⊥，得到线段2OM，如此下去，得到线段3OM ，4OM，…，n OM ．（1）写出点M 5的坐标； （2）求56O M M △的周长；（3）我们规定：把点)(n n n y x M ，（=n 0,1,2,3…）的横坐标n x ，纵坐标n y 都取绝对值后得到的新坐标()n ny x,称之为点nM的“绝对坐标”．根据图中点n M的分布规律，请写出点n M 的“绝对坐标”．2013年燕山一模22．阅读下列材料：问题：如图⑴，已知正方形ABCD 中，E 、F 分别是BC 、CD 边上的点，且 ∠EAF ＝45°． 判断线段BE 、EF 、FD 之间的数量关系，并说明理由．小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△DAF 绕点A 顺时针旋转90°，得到△BAH ，然后通过证明三角形全M 5M 4M 3M 2M 1O M 0-55-55 y x等可得出结论．请你参考小明同学的思路，解决下列问题：⑴ 图⑴中线段BE 、EF 、FD 之间的数量关系是；⑵ 如图⑵，已知正方形ABCD 边长为5，E 、F 分别是BC 、CD 边上的点，且∠EAF ＝45°，AG ⊥EF 于点G ，则AG 的长为 ，△EFC 的周长为 ； ⑶ 如图⑶，已知△AEF 中，∠EAF ＝45°，AG ⊥EF 于点G ，且EG ＝2，GF ＝3，则△AEF 的面积为 ． 是 ．2013年大兴一模22.分别以△ABC 的边AC 与边BC 为边，向△ABC 外作正方形ACD 1E 1和正方形BCD 2E 2，连结D 1D 2.(1)如图1，过点C 作直线HG 垂直于直线AB 于点H ，交D 1D 2于点G ．试探究线段GD 1与线段GD 2的数量关系，并加以证明．（2）如图2，CF 为AB 边中线，试探究线段CF 与线段D 1D 2的数量关系，并加以证明．2013年昌平一模图⑴ 图⑵ 图⑶FA EBCDGG E AFAEBC FDH 图2D 2D 1E 2E 1FCBA22. （1）人教版八年级数学下册92页第14题是这样叙述的：如图1，□ABCD 中，过对角线BD 上一点P 作EF ∥BC ，HG ∥AB ，图中哪两个平行四边形的面积相等？为什么？ 根据习题背景，写出面积相等的一对平行四边形的名称为 和 ； （2）如图2，点P 为□ABCD 内一点，过点P 分别作AD 、AB 的平行线分别交□ABCD的四边于点E 、F 、G 、H . 已知S □BHPE = 3，S □PFDG = 5，则P A C S ∆= ； （3）如图3，若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH （不重复、无缝隙）.已知①②③④四个平行四边形面积的和为14，四边形ABCD 的面积为11，则菱形EFGH 的周长为 ．图2图3图1⑤④③②①H PA BGEH DF C ABGEP DF C HGFE DCBA2013年怀柔一模22. 理解与应用：我们把对称中心重合、四边分别平行的两个正方形之间的部分叫“方形环”，易知方形环四周的宽度相等．．．．. 一条直线l 与方形环的边线有四个交点M 、'M 、'N 、N ．小明在探究线段'MM 与N N ' 的数量关系时，从点'M 、'N 向对边作垂线段E M '、F N '，利用三角形全等、相似及锐角三角函数等相关知识解决了问题．请你参考小明的思路解答下列问题：(1)直线l 与方形环的对边相交时（22题图1），直线l 分别交AD 、D A ''、C B ''、BC 于M 、'M 、'N 、N ，小明发现'MM 与N N '相等，请你帮他说明理由；(2)直线l 与方形环的邻边相交时（22题图2），l 分别交AD 、D A ''、C D ''、DC 于M 、'M 、'N 、N ，l 与DC 的夹角为α，请直接写出NN MM ''的值（用含α的三角函数表示）.MACD'N B'C E'B 'M 'A 'D NFl (α222题图'N A CDE BM N'A 'D F'M 'C 'B l122题图。

2013圆一模汇总燕山如图，△ABC 中，AC ＝B C 错误！未找到引用源。

错误！未找到引用源。

．以B C 为直径作⊙O 交错误！未找到引用源。

于点错误！未找到引用源。

，交错误！未找到引用源。

于点G ．作直线错误！未找到引用源。

交AC 错误！未找到引用源。

于点错误！未找到引用源。

，交错误！未找到引用源。

的延长线于点错误！未找到引用源。

．⑴求证：直线EF 是错误！未找到引用源。

的切线； ⑵若BC ＝6，AB ＝43，求DE 的长． 延庆如图，AB 是⊙O 的直径，AC 和BD 是它的两条切线，CO 平分∠ACD ．（1）求证：CD 是⊙O 的切线； （2）若AC=2，BD=3，求AB 的长． 通州已知：如图，AB 是⊙O 的直径，AC 是弦．过点A 作∠BAC 的角平分线，交⊙O 于点D ，过点D 作AC 的垂线，交AC 的延长线于点E ．（1）求证：直线ED 是⊙O 的切线；OFEBADCGEA BC DOEO FO 的值．（2）连接EO，交AD于点F，若5AC=3AB，求昌平如图，四边形ABCD 是⊙O 的内接正方形，延长AB 到E ，使BE =AB ，连接CE . （1）求证：直线CE 是⊙O 的切线；（2）连接OE 交BC 于点F ，若OF =2 , 求EF 的长.EDC BAO F通州已知：如图，AB 是⊙O 的直径，AC 是弦．过点A 作∠BAC 的角平分线，交⊙O 于点D ，过点D 作AC 的垂线，交AC 的延长线于点E ．（1）求证：直线ED 是⊙O 的切线； （2）连接EO ，交AD 于点F ，若5AC =3AB ，求EO FO的值．顺义如图，已知ABC △，以AC 为直径的O 交AB 于点D ，点E 为 AD 的中点，连结CE 交AB 于点F ，且BF BC =.（1）判断直线BC 与⊙O 的位置关系，并证明你的结论； （2）若O 的半为2,3cos 5B =,求CE 的长.EA BC DOF OEDC BACBE AOD 石景山如图，BD 为⊙O 的直径，AB =AC ，AD 交B C 于点E ，AE =1，ED =2. (1)求证：∠ABC =∠ADB ； (2)求AB 的长；(3)延长DB 到F ，使得BF =BO ，连接FA ，试判断直线FA 与⊙O 的 位置关系，并说明理由． 平谷如图，AB 是O ⊙的直径，点C 在O ⊙上，CAB ∠的平分线交O ⊙于点D ，过点D 作AC 的垂线交AC 的延长线于点E ，连接BC 交AD 于点F .（1）求证：ED 是O ⊙的切线； （2）若108AB AD ==，，求CF 的长. 密云如图，PA PB 、分别与O 相切于点A B 、，点M 在PB 上，且//OM AP ，MN AP ⊥，垂足为N ． （1）求证：=OM AN（2）若O 的半径=3R ，=9PA，求OM 的长．已知：如图，AB 是⊙O 的直径，AC 是⊙O 的弦，M 为AB 上一点，过点M 作DM ⊥AB ，交弦AC 于点E ，交⊙O 于点F ，且DC ＝DE ．（1）求证：DC 是⊙O 的切线；（2）如果DM ＝15，CE ＝10，5cos 13AEM ∠=，求⊙O 半径的长．怀柔如图，已知AB 是⊙O 的直径，点C 在⊙O 上，过点C 的直线与AB 的延长线交于点P ，AC=PC ， ∠COB=2∠PCB.（1）求证：PC 是⊙O 的切线；（2）点M 是弧AB 的中点，CM 交AB 于点N ，若AB=4，求MN ·MC 的值. 丰台已知：如图，在Rt △ABC 中，∠ABC =90°，以AB 为直径的⊙O 交AC 于点D ，E 是BC 的中点，连结DE ． （1）求证：DE 与⊙O 相切； （2）连结OE ，若cos ∠BAD =35，BE =143，求OE 的长．OE MF DC BACEOB AD已知：如图，过正方形ABCD 的顶点B 作直线BE 平行于对角线AC ，AE=AC （E ，C 均在AB 的同侧）. 求证：∠CAE=2∠BAE . 东城如图，C 是以AB 为直径的⊙O 上一点，过O 作OE ⊥AC 于点E ，过点A 作⊙O 的切线 交OE 的延长线于点F ，连结CF 并延长交BA 的延长线于点P . （1）求证：PC 是⊙O 的切线.（2）若AB =4，AP ∶PC =1∶2，求CF 的长. 朝阳如图，⊙O 是△ABC 是的外接圆，BC 为⊙O 直径，作∠CAD =∠B ，且点D 在BC 的延长线上． (1)求证：直线AD 是⊙O 的切线； (2)若sin ∠CAD =24，⊙O 的半径为8，求CD 长．DABC OPO C BAI海淀已知：如图，在△ABC 中，AB AC =．以AB 为直径的⊙O 交BC 于点D ，过点D 作DE ⊥AC 于点E . (1)求证：DE 与⊙O 相切；(2)延长DE 交BA 的延长线于点F .若6AB =，sin B =5,5求线段AF 的长.西城如图，在△ABC 中，AB=AC ，以AC 为直径作⊙O 交BC 于点D ，过点D 作FE ⊥AB 于点E ，交AC 的延长线于点F ．(1) 求证：EF 与⊙O 相切；(2) 若AE=6，sin ∠CFD=35，求EB 的长．。

2013年北京市各城区中考一模代数综合题23题汇总1、(2013年一模门头沟)23．已知关于x 的一元二次方程21(2)2602x m x m +-+-=．（1）求证：无论m 取任何实数，方程都有两个实数根； （2） 当<3m 时，关于x 的二次函数21(2)262y x m x m =+-+-的图象与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，且2AB =3OC ，求m 的值；2、（2013年一模丰台）23．二次函数2y x bx c =++的图象如图所示，其顶点坐标为M (1,-4)． （1）求二次函数的解析式；（2）将二次函数的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合新图象回答：当直线y x n =+与这个新图象有两个公共点时，求n 的取值范围．（3）在（2）的条件下，过点C 作直线l ∥x 轴，将二次函数图象在y 轴左侧的部分沿直线l 翻折，二次函数图象的其余部分保持不变，得到一个新的图象，记为G ．请你结合图象回答：当直线13y x b =+与图象G 只有一个公共点时，b 的取值范围．3、（2013年一模平谷）23. 已知关于m 的一元二次方程221x mx +-=0. （1）判定方程根的情况；（2）设m 为整数，方程的两个根都大于1-且小于32，当方程的两个根均为有理数时，求m 的值．4、（2013年顺义一模）23．已知关于x 的方程2(32)220mx m x m -+++= （1）求证：无论m 取任何实数时，方程恒有实数根.（2）若关于x 的二次函数2(32)22y mx m x m =-+++的图象与x 轴两个交点的横坐标均为正整数，且m 为整数，求抛物线的解析式.5、（2013年石景山一模）23. 如图，直线33y x =-+交x 轴于A 点，交y 轴于B 点，过A 、B 两点的抛物线1C 交x 轴于另一点M （-3,0）. (1)求抛物线1C 的解析式；(2)直接写出抛物线1C 关于y 轴的对称图形2C 的解析式； (3)如果点'A 是点A 关于原点的对称点，点D 是图形2C 的顶点，那么在x 轴上是否存在点P ，使得△PAD 与△'A BO是相似三角形？若存在，求出符合条件的P 点坐标；若不存在，请说明理由.6、（2013年海淀一模）23.在平面直角坐标系xOy 中，抛物线22y mx mx n =-+与x 轴交于A 、B 两点，点A 的坐标为(2,0)-．（1）求B 点坐标； （2）直线y =12x +4m +n 经过点B . ①求直线和抛物线的解析式；②点P 在抛物线上，过点P 作y 轴的垂线l ，垂足为(0,)D d ．将抛物线在直线l 上方的部分沿直线l 翻折，图象的其余部分保持不变，得到一个新图象G ．请结合图象回答：当图象G 与直线y =12x +4m +n 只有两个公共点时，d 的取值范围是 ．7、（2013年西城一模）23．已知关于x 的一元二次方程22(4)0x a x a +++=．(1) 求证：无论a 为任何实数，此方程总有两个不相等的实数根； (2) 抛物线21:2(4)C y x a x a =+++与x 轴的一个交点的横坐标为2a，其中0a ≠，将抛物线1C 向右平移14个单位，再向上平移18个单位，得到抛物线2C ．求抛物线2C 的解析式； (3) 点A (m ,n )和B (n ,m )都在(2)中抛物线C 2上，且A 、B 两点不重合，求代数式33222m mn n -+的值．8、（2013年通州一模）23. 已知二次函数()2214y x k x k =-++的图象与x 轴分别交于点()1,0A x 、()2,0B x ，且32-<1x <12-． （1）求k 的取值范围；（2）设二次函数()2214y x k x k =-++的图象与y 轴交于点M ，若OM OB =，求二次函数的表达式；（3）在(2)的条件下，若点N 是x 轴上的一点，以N 、A 、M 为顶点作平行四边形，该平行四边形的第四个顶点F 在二次函数()2214y x k x k =-++的图象上，请直接写出满足上述条件的平行四边形的面积.9、（2013年东城一模）23. 已知关于x 的一元二次方程x 2＋(m ＋3)x ＋m ＋1＝0． （1）求证：无论m 取何值，原方程总有两个不相等的实数根； （2）当m 为何整数时，原方程的根也是整数．10、（2013年朝阳一模） 23．二次函数2134y x x n =++-的图象与x 轴只有一个交点；另一个二次函数2222(1)46y nx m x m m =--+-+的图象与x 轴交于两点，这两个交点的横坐标都是整数，且m 是小于5的整数． 求（1）n 的值；（2）二次函数2222(1)46y nx m x m m =--+-+的图象与x 轴交点的坐标．11、（2013年密云一模）2312、（2013年延庆一模）24. （本题满分7分）如图，已知平面直角坐标系xOy ，抛物线y＝－x 2＋bx ＋c 过点A(4,0)、B(1,3) .（1）求该抛物线的解析式，并写出该抛物线的对称轴和顶点坐标； （2）记该抛物线的对称轴为直线l ，设抛物线上的点P(m,n)在第四象限，点P 关于直线l 的对称点为E ，点E 关于y 轴的对称点为F ，若四边形OAPF 的面积为20，求m 、n 的值.13、（2013年房山一模）23.已知，抛物线2y x bx c =-++，当1＜x ＜5时，y 值为正；当x ＜1或x ＞5时，y 值为负. （1）求抛物线的解析式.（2）若直线y kx b =+（k ≠0）与抛物线交于点A （32，m ）和B （4，n ），求直线的解析式. （3）设平行于y 轴的直线x=t 和x=t+2分别交线段AB 于E 、F ，交二次函数于H 、G. ①求t 的取值范围②是否存在适当的t 值，使得EFGH 是平行四边形？若存在，求出t 值；若不存在，请说明理由.14、（2013年昌平一模）23. 已知抛物线22y x kx k =-+-+．（1）求证：无论k 为任何实数，该抛物线与x 轴都有两个交点； （2）在抛物线上有一点P （m ，n ），n <0，OP =103，且线段OP与x 轴正半轴所夹锐角的正弦值为45，求该抛物线的解析式；（3）将（2）中的抛物线x 轴上方的部分沿x 轴翻折，与原图象的另一部分组成一个新的图形M ，当直线y x b =-+与图形M 有四个交点时，求b 的取值范围.15、（2013年怀柔一模）23． 已知关于x 的方程03)13(2=+++x k kx ． （1）求证：无论k 取任何实数时，方程总有实数根;（2）若二次函数3)13(2+++=x k kx y 的图象与x 轴两个交点的横坐标均为整数，且k 为正整数，求k 值;（3）在（2）的条件下，设抛物线的顶点为M，直线y=－2x＋9与y轴交于点C，与直线OM交于点D．现将抛物线平移，保持顶点在直线OD上．若平移的抛物线与射线CD（含端点C）只有一个公共点，求它的顶点横坐标的值或取值范围.16、（2013年大兴一模）23．如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N．其顶点为D．（1）抛物线及直线AC的函数关系式；（2）设点M（3，m），求使MN+MD的值最小时m的值；（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由.。