高考数学真题汇编7 立体几何 理( 解析版)

专题07 立体几何综合问题【题型解读】▶▶题型一 空间点、线、面的位置关系及空间角的计算(1)空间点、线、面的位置关系通常考查平行、垂直关系的证明，一般出现在解答题的第(1)问，解答题的第(2)问常考查求空间角，求空间角一般都可以建立空间直角坐标系，用空间向量的坐标运算求解．(2)利用向量求空间角的步骤：第一步：建立空间直角坐标系；第二步：确定点的坐标；第三步：求向量(直线的方向向量、平面的法向量)坐标；第四步：计算向量的夹角(或函数值)；第五步：将向量夹角转化为所求的空间角；第六步：反思回顾．查看关键点、易错点和答题规范．【例1】 (2019·河南郑州高三联考)在如图所示的多面体中，四边形ABCD 是平行四边形，四边形BDEF是矩形，ED ⊥平面ABCD ，∠ABD ＝π6，AB ＝2AD . (1)求证：平面BDEF ⊥平面ADE ；(2)若ED ＝BD ，求直线AF 与平面AEC 所成角的正弦值．【答案】见解析【解析】(1)在△ABD 中，∠ABD ＝π6，AB ＝2AD ，由余弦定理，得BD ＝3AD ，从而BD 2＋AD 2＝AB 2，所以△ABD 为直角三角形且∠ADB ＝90°，故BD ⊥AD .因为DE ⊥平面ABCD ，BD ⊂平面ABCD ，所以DE ⊥BD .又AD ∩DE ＝D ，所以BD ⊥平面ADE .因为BD ⊂平面BDEF ，所以平面BDEF ⊥平面ADE .(2)由(1)可得，在Rt △ABD 中，∠BAD ＝π3，BD ＝3AD ， 又由ED ＝BD ，设AD ＝1，则BD ＝ED ＝ 3.因为DE ⊥平面ABCD ，BD ⊥AD ，所以可以点D 为坐标原点，DA ，DB ，DE 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，如图所示．则A (1,0,0)，C (－1，3，0)，E (0,0，3)，F (0，3，3)．所以AE →＝(－1,0，3)，AC →＝(－2，3，0)．设平面AEC 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧ n ·A E →＝0，n ·A C →＝0，即⎩⎨⎧ －x ＋3z ＝0，－2x ＋3y ＝0，令z ＝1，得n ＝(3，2,1)为平面AEC 的一个法向量．因为A F →＝(－1，3，3)， 所以cos 〈n ，A F →〉＝n ·A F →|n |·|A F →|＝4214， 所以直线AF 与平面AEC 所成角的正弦值为4214. 【素养解读】本例问题(1)证明两平面垂直，考查了逻辑推理的核心素养；问题(2)计算线面所成的角时，考查了直观想象和数学运算的核心素养．【突破训练1】 (2018·北京卷)如图，在三棱柱ABC －A 1B 1C 1中，CC 1⊥平面ABC ，D ，E ，F ，G 分别为AA 1，AC ，A 1C 1，BB 1的中点，AB ＝BC ＝ 5 ，AC ＝AA 1＝2.(1)求证：AC ⊥平面BEF ；(2)求二面角B －CD －C 1的余弦值；(3)证明：直线FG 与平面BCD 相交．【答案】见解析【解析】(1)证明：在三棱柱ABC －A 1B 1C 1中，因为CC 1⊥平面ABC ，所以四边形A 1ACC 1为矩形．又E ，F 分别为AC ，A 1C 1的中点，所以AC ⊥EF .因为AB ＝BC .所以AC ⊥BE ，所以AC ⊥平面BEF .(2)由(1)知AC ⊥EF ，AC ⊥BE ，EF ∥CC 1.又CC 1⊥平面ABC ，所以EF ⊥平面ABC .因为BE ⊂平面ABC ，所以EF ⊥BE .如图建立空间直角坐称系Exyz .由题意得B (0,2,0)，C (－1,0,0)，D (1,0,1)，F (0,0,2)，G (0,2,1)．所以CD →＝(2,0,1)，C B →＝(1,2,0)，设平面BCD 的法向量为n ＝(a ，b ，c )，所以⎩⎪⎨⎪⎧ n ·C D →＝0，n ·C B →＝0，所以⎩⎪⎨⎪⎧ 2a ＋c ＝0，a ＋2b ＝0.令a ＝2，则b ＝－1，c ＝－4，所以平面BCD 的法向量n ＝(2，－1，－4)，又因为平面CDC 1的法向量为E B →＝(0,2,0)，所以cos 〈n ，E B →〉＝n ·E B→|n ||EB →|＝－2121. 由图可得二面角B －CD －C 1为钝二面角，所以二面角B －CD －C 1的余弦值为－2121. (3)证明：平面BCD 的法向量为n ＝(2，－1，－4)，因为G (0,2,1)，F (0，0,2)，所以G F →＝(0，－2,1)，所以n ·G F →＝－2，所以n 与G F →不垂直，所以GF 与平面BCD 不平行且不在平面BCD 内，所以GF 与平面BCD 相交． ▶▶题型二 平面图形折叠成空间几何体的问题1．先将平面图形折叠成空间几何体，再以其为载体研究其中的线、面间的位置关系与计算有关的几何量是近几年高考考查立体几何的一类重要考向，它很好地将平面图形拓展成空间图形，同时也为空间立体图形向平面图形转化提供了具体形象的途径，是高考深层次上考查空间想象能力的主要方向．2．(1)解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量．一般情况下，长度是不变量，而位置关系往往会发生变化，抓住不变量是解决问题的突破口．(2)在解决问题时，要综合考虑折叠前后的图形，既要分析折叠后的图形，也要分析折叠前的图形．(3)解决翻折问题的答题步骤第一步：确定折叠前后的各量之间的关系，搞清折叠前后的变化量和不变量；第二步：在折叠后的图形中确定线和面的位置关系，明确需要用到的线面；第三步：利用判定定理或性质定理进行证明．【例2】 (2018·全国卷Ⅰ)如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把△DFC 折起，使点C 到达点P 的位置，且PF ⊥BF .(1)证明：平面PEF ⊥平面ABFD ；(2)求DP 与平面ABFD 所成角的正弦值．【答案】见解析【解析】(1)证明：由已知可得，BF ⊥PF ，BF ⊥EF ，所以BF ⊥平面PEF .又BF ⊂平面ABFD ，所以平面PEF ⊥平面ABFD .(2)作PH ⊥EF ，垂足为H .由(1)得，PH ⊥平面ABFD .以H 为坐标原点，HF →的方向为y 轴正方向，|B F →|为单位长，建立如图所示的空间直角坐标系Hxyz .由(1)可得，DE ⊥PE .又DP ＝2，DE ＝1，所以PE ＝ 3.又PF ＝1，EF ＝2，故PE ⊥PF .可得PH ＝32，EH ＝32. 则H (0,0,0)，P ⎝ ⎛⎭⎪⎫0，0，32，D ⎝ ⎛⎭⎪⎫－1，－32，0，D P →＝⎝ ⎛⎭⎪⎫1，32，32，H P →＝⎝ ⎛⎭⎪⎫0，0，32为平面ABFD 的法向量．设DP 与平面ABFD 所成角为θ，则sin θ＝⎪⎪⎪⎪⎪⎪⎪⎪H P →·D P →|H P →|·|DP →|＝ 34 3＝34. 所以DP 与平面ABFD 所成角的正弦值为34. 【素养解读】本例在证明或计算过程中都要考虑图形翻折前后的变化，因此综合考查了逻辑推理、数学运算、直观想象、数学建模的核心素养．【突破训练2】 如图1，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝π2，AB ＝BC ＝1，AD ＝2，E 是AD 的中点，O 是AC 与BE 的交点，将△ABE 沿BE 折起到△A 1BE 的位置，如图2.(1)证明：CD ⊥平面A 1OC ；(2)若平面A 1BE ⊥平面BCDE ，求平面A 1BC 与平面A 1CD 所成锐二面角的余弦值．【答案】见解析【解析】(1)证明：在题图1中，因为AB ＝BC ＝1，AD ＝2，E 是AD 的中点∠BAD ＝π2，所以BE ⊥AC .即在题图2中，BE ⊥OA 1，BE ⊥OC ，从而BE ⊥平面A 1OC .又CD ∥BE ，所以CD ⊥平面A 1OC .(2)由已知，平面A 1BE ⊥平面BCDE ，又由(1)知，BE ⊥OA 1，BE ⊥OC .所以∠A 1OC 为二面角A 1－BE －C 的平面角，所以∠A 1OC ＝π2. 如图，以O 为原点，OB →，OC →，OA 1→分别为x 轴、y 轴、z 轴正方向建立空间直角坐标系，因为A 1B ＝A 1E ＝BC ＝ED ＝1，BC ∥ED ，所以B ⎝ ⎛⎭⎪⎫22，0，0，E ⎝ ⎛⎭⎪⎫－22，0，0，A 1⎝ ⎛⎭⎪⎫0，0，22，C ⎝ ⎛⎭⎪⎫0，22，0， 得BC →＝⎝ ⎛⎭⎪⎫－22，22，0，A 1C →＝⎝ ⎛⎭⎪⎫0，22，－22， CD →＝BE →＝(－2，0,0)．设平面A 1BC 的一个法向量n 1＝(x 1，y 1，z 1)，平面A 1CD 的一个法向量n 2＝(x 2，y 2，z 2)，平面A 1BC 与平面A 1CD 的夹角为θ，则⎩⎪⎨⎪⎧ n 1·BC →＝0，n 1·A 1C →＝0，得⎩⎪⎨⎪⎧ －x 1＋y 1＝0，y 1－z 1＝0，取n 1＝(1,1,1)； 由⎩⎪⎨⎪⎧ n 2·CD →＝0，n 2·A 1C →＝0，得⎩⎪⎨⎪⎧x 2＝0，y 2－z 2＝0，取n 2＝(0,1,1)， 从而cos θ＝|cos 〈n 1，n 2〉|＝23×2＝63， 即平面A 1BC 与平面A 1CD 所成锐二面角的余弦值为63. ▶▶题型三 线、面位置关系中的探索性问题是否存在某点或某参数，使得某种线、面位置关系成立问题，是近几年高考命题的热点，常以解答题中最后一问的形式出现，解决这类问题的基本思路类似于反证法，即“在假设存在的前提下通过推理论证，如果能找到符合要求的点(或其他的问题)，就肯定这个结论，如果在推理论证中出现矛盾，就说明假设不成立，从而否定这个结论”．【例3】 (2018·全国卷Ⅱ)如图，在三棱锥P －ABC 中，AB ＝BC ＝2 2 ，PA ＝PB ＝PC ＝AC ＝4，O 为AC 的中点．(1)证明：PO ⊥平面ABC ； (2)若点M 在棱BC 上，且二面角M －PA －C 为30°，求PC 与平面PAM 所成角的正弦值．【答案】见解析【解析】(1)证明：因为AP ＝CP ＝AC ＝4，O 为AC 的中点，所以OP ⊥AC ，且OP ＝2 3.连接OB ，因为AB ＝BC ＝22AC ，所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB ＝12AC ＝2. 由OP 2＋OB 2＝PB 2知PO ⊥OB .由OP ⊥OB ，OP ⊥AC 知PO ⊥平面ABC .(2)如图，以O 为坐标原点，OB →的方向为x 轴正方向，建立空间直角坐标系Oxyz .则O (0,0,0)，B (2,0,0)，A (0，－2,0)，C (0,2,0)，P (0,0,23)，A P →＝(0,2,23)，取平面PAC 的一个法向量O B →＝(2,0,0)．设M (a,2－a,0)(0<a ≤2)，则A M →＝(a,4－a,0)．设平面PAM 的法向量为n ＝(x ，y ，z )． 由A P →·n ＝0，A M →·n ＝0得⎩⎨⎧ 2y ＋23z ＝0，ax ＋(4－a)y ＝0，可取n ＝(3(a －4)，3a ，－a )， 所以cos 〈O B →，n 〉＝23(a －4)23(a －4)2＋3a 2＋a2.由已知得|cos 〈O B →，n 〉|＝32. 所以23|a －4|23(a －4)2＋3a 2＋a2＝32.解得a ＝－4(舍去)，a ＝43. 所以n ＝⎝ ⎛⎭⎪⎫－833，433，－43.又P C →＝(0,2，－23)， 所以cos 〈P C →，n 〉＝34.所以PC 与平面PAM 所成角的正弦值为34. 【素养解读】本例问题(1)中证明线面垂直直接考查了逻辑推理的核心素养；问题(2)中要探求点M 的位置，要求较高，它既考查了直观想象的核心素养，又考查了数学建模的核心素养．【突破训练3】 如图，在直三棱柱ABC －A 1B 1C 1中，平面A 1BC ⊥侧面ABB 1A 1，且AA 1＝AB ＝2. (1)求证：AB ⊥BC ；(2)若直线AC 与平面A 1BC 所成的角为π6，请问在线段A 1C 上是否存在点E ，使得二面角A －BE －C 的大小为2π3，请说明理由．【答案】见解析【解析】(1)证明：连接AB 1交A 1B 于点D ，因为AA 1＝AB ，所以AD ⊥A 1B ，又平面A 1BC ⊥侧面ABB 1A 1，平面A 1BC ⊂平面ABB 1A 1＝A 1B ，所以AD ⊥平面A 1BC ，BC ⊂平面A 1BC ，所以AD ⊥BC .因为三棱柱ABC －A 1B 1C 1是直三棱柱，所以AA 1⊥底面ABC ，所以AA 1⊥BC ，又AA 1∩AD ＝A ，所以BC ⊥侧面ABB 1A 1，所以BC ⊥AB . (2)由(1)得AD ⊥平面A 1BC ，所以∠ACD 是直线AC 与平面A 1BC 所成的角，即∠ACD ＝π6，又AD ＝2，所以AC ＝22，假设存在适合条件的点E ，建立如图所示空间直角坐标系Axyz ，设A 1E →＝λA 1C →(0≤λ≤1)，则B (2，2，0)，B 1(2，2，2)，由A 1(0,0,2)，C (0,22，0)，得E (0,22λ，2－2λ)，设平面EAB 的一个法向量m ＝(x ，y ，z )， 由⎩⎪⎨⎪⎧m ·AE →＝0，m ·AB →＝0，得⎩⎨⎧ 22λy ＋(2－2λ)z ＝0，2x ＋2y ＝0， 所以可取m ＝(1－λ，λ－1，2λ)， 由(1)知AB 1⊥平面A 1BC ，所以平面CEB 的一个法向量n ＝(1,1，2)， 所以12＝⎪⎪⎪⎪⎪⎪cos 2π3＝cos 〈m ，n 〉＝m·n |m ||n |＝2λ22(λ－1)2＋2λ2，解得λ＝12，故点E 为线段A 1C 中点时，二面角A －BE －C 的大小为2π3.。

2013年全国高考理科数学试题分类汇编7：立体几何一、选择题1 ．（2013年高考新课标1（理））如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为（ ）A ．35003cm πB ．38663cm πC ．313723cm πD ．320483cm π【答案】A2 ．（2013年普通高等学校招生统一考试广东省数学（理）卷（纯WORD 版））设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是（ ）A ．若αβ⊥,m α⊂,n β⊂,则m n ⊥B ．若//αβ,m α⊂,n β⊂,则//m nC ．若m n ⊥,m α⊂,n β⊂,则αβ⊥D ．若m α⊥,//m n ,//n β,则αβ⊥【答案】D3 ．（2013年上海市春季高考数学试卷(含答案)）若两个球的表面积之比为1:4,则这两个球的体积之比为（ ）A ．1:2B ．1:4C ．1:8D ．1:16【答案】C4 ．（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））已知正四棱柱1111ABCD A B C D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于（ ）A ．23B ．3C ．3D ．13【答案】A5 ．（2013年高考新课标1（理））某几何体的三视图如图所示,则该几何体的体积为（ ）A ．168π+B ．88π+C ．1616π+D ．816π+【答案】A6 ．（2013年高考湖北卷（理））一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有（ ）A ．1243V V V V <<< B．1324V V V V <<<C ．2134V V V V <<<D ．2314V V V V <<<【答案】C7 ．（2013年高考湖南卷（理））已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能．．．等于 （ ）A ．1B C ．2D ．2【答案】C8 ．（2013年普通高等学校招生统一考试广东省数学（理）卷（纯WORD 版））某四棱台的三视图如图所示,则该四棱台的体积是（ ）A ．4B ．143C ．163D ．6【答案】B9 ．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））已知n m ,为异面直线,⊥m 平面α,⊥n 平面β.直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则 （ ）A ．βα//,且α//lB ．βα⊥,且β⊥lC ．α与β相交,且交线垂直于lD ．α与β相交,且交线平行于l【答案】D10．（2013年普通高等学校招生统一考试山东数学（理）试题（含答案））已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为（ ）A ．512πB ．3πC ．4πD ．6π【答案】B11．（2013年普通高等学校招生统一考试重庆数学（理）试题（含答案））某几何体的三视图如题()5图所示,则该几何体的体积为 （ ）A ．5603B ．5803C ．200D ．240正视图俯视图侧视图第5题图【答案】C12．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））已知三棱柱111ABC A B C -的6个顶点都在球O 的球面上,若34AB AC ==，,AB AC ⊥,112AA =,则球O 的半径为（ ）A ．2B ．C ．132D ．【答案】C13．（2013年高考江西卷（理））如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD ,正方体的六个面所在的平面与直线CE,EF 相交的平面个数分别记为,m n ,那么m n +=（ ）A ．8B ．9C ．10D ．11【答案】A14．（2013年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为（ ）A ．B ．C ．D ．【答案】A15．（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））在下列命题中,不是公理．．的是 （ ）A ．平行于同一个平面的两个平面相互平行B ．过不在同一条直线上的三点,有且只有一个平面C ．如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D ．如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线 【答案】A 16．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））在空间中,过点A 作平面π的垂线,垂足为B ,记)(A f B π=.设βα,是两个不同的平面,对空间任意一点P ,)]([)],([21P f f Q P f f Q βααβ==,恒有21PQ PQ =,则（ ）A ．平面α与平面β垂直B ．平面α与平面β所成的(锐)二面角为045C ．平面α与平面β平行D ．平面α与平面β所成的(锐)二面角为060【答案】A 17．（2013年高考四川卷（理））一个几何体的三视图如图所示,则该几何体的直观图可以是【答案】D 二、填空题18．（2013年高考上海卷（理））在xOy 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y = 和1y =-围成的封闭图形记为D,如图中阴影部分.记D 绕y轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48ππ,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________【答案】2216ππ+.19．（2013年高考陕西卷（理））某几何体的三视图如图所示, 则其体积为___3π_____.【答案】3π 20．（2013年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））已知圆O 和圆K 是球O的大圆和小圆,其公共弦长等于球O 的半径,32OK =,且圆O 与圆K 所在的平面所成的一个二面角为60 ,则球O 的表面积等于______.【答案】16π21．（2013年高考北京卷（理））如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E上,点P 到直线CC 1的距离的最小值为__________.【答案】522．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））如图,在三棱柱ABC C B A -111中,F E D ，，分别是1AA AC AB ，，的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.【答案】1:2423．（2013年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________2cm .【答案】2424．（2013年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））如图,正方体1111ABCD A BC D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S.则下列命题正确的是__①②③⑤___(写出所有正确命题的编号).①当102CQ <<时,S 为四边形;②当12CQ =时,S 为等腰梯形;③当34CQ =时,S 与11C D 的交点R 满足1113C R =;④当314CQ <<时,S 为六边形;⑤当1CQ =时,S的面积为2. 【答案】①②③⑤A BCAD EF BC25．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））某几何体的三视图如图所示,则该几何体的体积是____________.【答案】1616π-26．（2013年普通高等学校招生统一考试福建数学（理）试题（纯WORD 版））已知某一多面体内接于一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________【答案】12π27．（2013年上海市春季高考数学试卷(含答案)）在如图所示的正方体1111ABCD A BC D -中,异面直线1A B 与1B C 所成角的大小为_______【答案】3π三、解答题28．（2013年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））如图,AB 是圆的直径,PA 垂直圆所在的平面,C 是圆上的点.(I)求证:PAC PBC ⊥平面平面；(II)2.AB AC PA C PB A ===--若，1，1，求证：二面角的余弦值D 1 C 1 B 1A 1D C AB【答案】（I ）证明：由AB 是圆O 的直径，得BC AC ⊥。

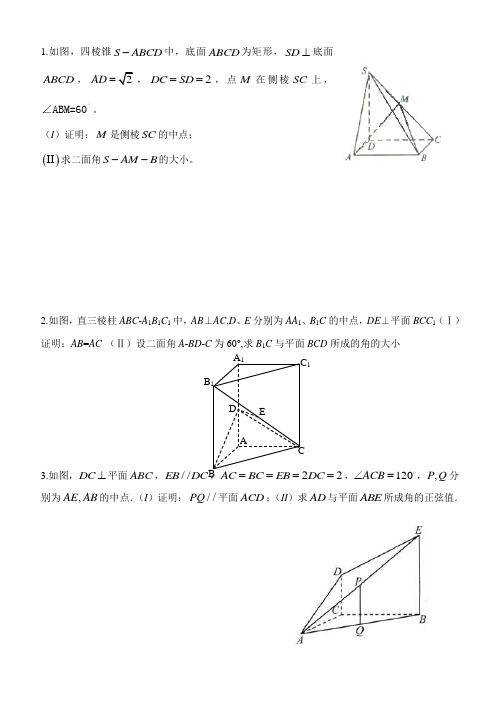
资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载高考立体几何大题及答案(理)地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容1.如图，四棱锥中，底面为矩形，底面，，，点在侧棱上，。

（I）证明：是侧棱的中点；求二面角的大小。

2.如图，直三棱柱ABC-A1B1C1中，AB⊥AC,D、E分别为AA1、B1C的中点，DE⊥平面BCC1（Ⅰ）证明：AB=AC （Ⅱ）设二面角A-BACBA1B1C1DED-C为60°,求B1C与平面BCD所成的角的大小3.如图，平面，，，，分别为的中点．（I）证明：平面；（II）求与平面所成角的正弦值．4.如图，四棱锥的底面是正方形，，点E在棱PB上.（Ⅰ）求证：平面；（Ⅱ）当且E为PB的中点时，求AE与平面PDB所成的角的大小.5.如图，在四棱锥中，底面是矩形，平面，，．以的中点为球心、为直径的球面交于点．（1）求证：平面⊥平面；（2）求直线与平面所成的角；（3）求点到平面的距离．6.如图，正方形所在平面与平面四边形所在平面互相垂直，△是等腰直角三角形，（I）求证：；（II）设线段、的中点分别为、，求证：∥（III）求二面角的大小。

7.如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD,SD ＝AD＝a,点E是SD上的点，且DE＝a(0<≦1). (Ⅰ)求证：对任意的（0、1），都有AC⊥BE:(Ⅱ)若二面角C-AE-D的大小为600C，求的值。

8.如图3，在正三棱柱中，AB=4, ,点D是BC的中点，点E 在AC上，且DEE.（Ⅰ）证明：平面平面; （Ⅱ）求直线AD 和平面所成角的正弦值。

9.如图，正方形所在平面与平面四边形所在平面互相垂直，△是等腰直角三角形，（I）求证：；（II）设线段、的中点分别为、，求证：∥（III）求二面角的大小。

2013年高考解析分类汇编7：立体几何一、选择题1 ．（2013年高考重庆卷（文8））某几何体的三视图如题(8)所示,则该几何体的表面积为（）A．180B．200C．220D．240【答案】D【解析】本题考查三视图以及空间几何体的表面积公式。

由三视图可知该几何体是个四棱柱。

棱柱的底面为等腰梯形，高为10.等腰梯形的上底为2，下底为8，高为4，腰长为5。

所以梯形的面积为284202+⨯=，梯形的周长为282520++⨯=。

所以四棱柱的表面积为2022010240⨯+⨯=，选D.2 ．（2013年高考课标Ⅱ卷（文9））一个四面体的顶点在空间直角坐标系O xyz-中的坐标分别是(1,0,1)，(1,1,0)，(0,1,1)，(0,0,0)，画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到正视图可以为（）(A) (B) (C) (D)【答案】A【解析】在空间直角坐标系中，先画出四面体O ABC-的直观图，以zOx平面为投影面，则得到正视图(坐标系中红色部分),所以选A.3 ．（2013年高考课标Ⅰ卷（文11））某几何函数的三视图如图所示,则该几何的体积为（ ）A ．168π+B ．88π+C ．1616π+D ．816π+ 【答案】A【解析】由三视图可知，该几何体的下部分是平放的半个圆柱，圆柱的底面半径为2,圆柱的高为4。

上部分是个长方体，长方体的棱长分别为2,2,4.所以半圆柱的体积为212482ππ⨯⨯⨯=，正方体的体积为22416⨯⨯=，所以该几何体的体积为168π+，选A.4 ．（2013年高考大纲卷（文11））已知正四棱锥1111112,ABCD A B C D AA AB CD BDC -=中，则与平面所成角的正弦值等于（ ）A ．23B．3C．3D ．13【答案】A【解析】如图，因为BD ⊥平面ACC 1A 1，所以平面ACC 1A 1⊥平面BDC 1，在Rt △CC 1O 中，过C 作CH ⊥C 1O 于H ，连结DH ，则∠CDH 即为所求，令a AB =，显然2223a CH a ⨯===，所以223sin 3a CDH a ∠==，故选A.5 ．（2013年高考四川卷（文2））一个几何体的三视图如图所示,则该几何体可以是 （ ）A ．棱柱B ．棱台C ．圆柱D ．圆台【答案】D【解析】由三视图可知，该几何体为圆台. 6 ．（2013年高考浙江卷（文5））已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是（ ）A ．108cm 3B ．100 cm 3C ．92cm 3D ．84cm 3【答案】B【解析】此图的直观图是一个底面边长为6和3，高为6的长方体截去一个角，对应三棱锥的的三条侧棱上分别为3,4,4.如图。

三观一统2020年高中数学十年高考真题精解（全国卷I）专题7 立体几何（理）十年树木，百年树人，十年磨一剑。

本专辑按照最新2020年考纲，对近十年高考真题精挑细选，去伪存真，挑选符合最新考纲要求的真题，按照考点/考向同类归纳，难度分层精析，对全国卷Ⅰ具有重要的应试性和导向性。

三观指的观三题（观母题、观平行题、观扇形题），一统指的是统一考点/考向，并对十年真题进行标灰（调整不考或低频考点标灰色）。

（一）2020考纲（二）本节考向题型研究汇总一、考向题型研究一：空间几何体之三视图（2018新课标I卷T7理科）某圆柱的高为2，底面周长为16，其三视图如右图．圆柱表面上的点在正视图上的对应点为，圆柱表面上的点在左视图上的对应点为，则在此圆柱侧面上，从到的路径中，最短路径的长度为A. 2√17B. 2√5C. 3D. 2【答案】B【解析】分析：首先根据题中所给的三视图，得到点M和点N在圆柱上所处的位置，点M在上底面上，点N在下底面上，并且将圆柱的侧面展开图平铺，点M、N在其四分之一的矩形的对角线的端点处，根据平面上两点间直线段最短，利用勾股定理，求得结果.详解：根据圆柱的三视图以及其本身的特征，可以确定点M和点N分别在以圆柱的高为长方形的宽，圆柱底面圆周长的四分之一为长的长方形的对角线的端点处，所以所求的最短路径的长度为√42+22=2√5，故选B.点睛：该题考查的是有关几何体的表面上两点之间的最短距离的求解问题，在解题的过程中，需要明确两个点在几何体上所处的位置，再利用平面上两点间直线段最短，所以处理方法就是将面切开平铺，利用平面图形的相关特征求得结果.（2016新课标I卷T6理科）如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是（A）17π（B）18π（C）20π（D）28π【答案】A【解析】原立体图如图所示：是一个球被切掉左上角的后的三视图表面积是的球面面积和三个扇形面积之和故选A ．（2015新课标I 卷T11理科）圆柱被一个平面截去一部分后与半球（半径为r ）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20π，则r=（ ）18782271=42+32=1784S πππ⨯⨯⨯⨯（A ）1 （B ）2 （C ）4 （D ）8 【答案】B【解析】由正视图和俯视图知，该几何体是半球与半个圆柱的组合体，圆柱的半径与球的半径都为r ，圆柱的高为2r ，其表面积为22142222r r r r r r πππ⨯+⨯++⨯=2254r r π+=16 + 20π，解得r=2，故选B.【点睛】简单几何体的三视图；球的表面积公式、圆柱的测面积公式(2013新课标Ⅰ卷T8理科)某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π 【答案】A【解析】由三视图可知该几何体为半圆柱上放一个长方体，由图中数据可知圆柱底面半径r ＝2，长为4，在长方体中，长为4，宽为2，高为2，所以几何体的体积为πr 2×4×12＋4×2×2＝8π＋16.故选A.（2017新课标I卷T7理科）某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，这些梯形的面积之和为（）A．10 B．12 C．14 D．16【答案】B【分析】由三视图可得直观图，由图形可知该立体图中只有两个相同的梯形的面，根据梯形的面积公式计算即可【解析】解：由三视图可画出直观图，该立体图中只有两个相同的梯形的面，S梯形=×2×（2+4）=6，∴这些梯形的面积之和为6×2=12，故选：B．【点睛】本题考查了体积计算公式，考查了推理能力与计算能力，属于中档题（2015新课标I 卷T11文科）圆柱被一个平面截去一部分后与半球（半径为)r 组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为1620π+，则(r = )A ．1B ．2C ．4D ．8【答案】A【解析】解：由几何体三视图中的正视图和俯视图可知， 截圆柱的平面过圆柱的轴线， 该几何体是一个半球拼接半个圆柱，∴其表面积为：22222111142222542222r r r r r r r r r πππππ⨯+⨯+⨯⨯+⨯+⨯=+， 又Q 该几何体的表面积为1620π+， 22541620r r ππ∴+=+，解得2r =，故选：B ．(2014新课标Ⅰ卷T12理科)如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（）A．6C．4【答案】B【分析】画出图形，结合三视图的数据求出棱长，推出结果即可【解析】解：几何体的直观图如图：AB=4，BD=4，C到BD的中点的距离为：4，∴．AC==6，AD=4，显然AC最长．长为6．故选：B．【点睛】本题考查三视图求解几何体的棱长，考查计算能力(2013新课标I 卷T11文科)某几何体的三视图如图所示，则该几何体的体积为( )．A ．π816+B ．π88+C ．π1616+D ．π168+【答案】A【解析】该几何体为一个半圆柱与一个长方体组成的一个组合体． V 半圆柱＝12π×22×4＝8π， V 长方体＝4×2×2＝16.所以所求体积为16＋8π.故选A.（2012新课标I 卷T7文科）如图，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（A ）6 （B ）9 （C ）12（D）18【答案】B【解析】由三视图知，其对应几何体为三棱锥，其底面为一边长为6，这边上高为3，棱锥的高为3，故其体积为1163332⨯⨯⨯⨯=9，故选B.（2011新课标I卷T8文科）在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为（）A．B．C．D．【答案】D【分析】由俯视图和正视图可以得到几何体是一个简单的组合体，是由一个三棱锥和被轴截面截开的半个圆锥组成，根据组合体的结构特征，得到组合体的侧视图．【解析】解：由俯视图和正视图可以得到几何体是一个简单的组合体，是由一个三棱锥和被轴截面截开的半个圆锥组成，∴侧视图是一个中间有分界线的三角形，故选：D．【点睛】本题考查简单空间图形的三视图，考查由三视图看出原几何图形，再得到余下的三视图，本题是一个基础题．空间几何体的三视图与直观图1．空间几何体的三视图（1）三视图的概念①光线从几何体的前面向后面正投影，得到的投影图叫做几何体的正视图;②光线从几何体的左面向右面正投影，得到的投影图叫做几何体的侧视图;③光线从几何体的上面向下面正投影，得到的投影图叫做几何体的俯视图.几何体的正视图、侧视图和俯视图统称为几何体的三视图.如图.（2）三视图的画法规则①排列规则：一般地，侧视图在正视图的右边，俯视图在正视图的下边.如下图：②画法规则ⅰ)正视图与俯视图的长度一致，即“长对正”；ⅱ)侧视图和正视图的高度一致，即“高平齐”；ⅲ)俯视图与侧视图的宽度一致，即“宽相等”.③线条的规则ⅰ)能看见的轮廓线用实线表示；ⅱ)不能看见的轮廓线用虚线表示.（3）常见几何体的三视图2．空间几何体的直观图（1）斜二测画法及其规则对于平面多边形，我们常用斜二测画法画它们的直观图.斜二测画法是一种特殊的画直观图的方法，其画法规则是：①在已知图形中取互相垂直的x轴和y轴，两轴相交于点O.画直观图时，把它们画成对应的x′轴和y′轴，两轴相交于点O′，且使∠x′O′y′=45°(或135°)，它们确定的平面表示水平面.②已知图形中平行于x轴或y轴的线段，在直观图中分别画成平行于x′轴或y′轴的线段.③已知图形中平行于x 轴的线段，在直观图中保持原长度不变，平行于y 轴的线段，长度为原来的一半.（2）用斜二测画法画空间几何体的直观图的步骤①在已知图形所在的空间中取水平平面，作互相垂直的轴Ox ，Oy ，再作Oz 轴使∠xOz =90°，且∠yOz =90°. ②画直观图时，把它们画成对应的轴O ′x ′，O ′y ′，O ′z ′，使∠x ′O ′y ′=45°(或135°)，∠x ′O ′z ′=90°，x ′O ′y ′所确定的平面表示水平平面.③已知图形中，平行于x 轴、y 轴或z 轴的线段，在直观图中分别画成平行于x ′轴、y ′轴或z ′轴的线段，并使它们和所画坐标轴的位置关系与已知图形中相应线段和原坐标轴的位置关系相同.④已知图形中平行于x 轴或z 轴的线段，在直观图中保持长度不变，平行于y 轴的线段，长度变为原来的一半.⑤画图完成以后，擦去作为辅助线的坐标轴，就得到了空间图形的直观图. （3）直观图的面积与原图面积之间的关系①原图形与直观图的面积比为SS ='4倍. 3.空间几何体的三视图问题的常见类型及解题策略：(1)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．(2)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线，不能看到的部分用虚线表示．(3)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合.4.空间几何体结构特征的判断技巧：紧扣结构特征是判断的关键，熟悉空间几何体的结构特征，依据条件构建几何模型，在条件不变的情况下，变换模型中的线面关系增加线、面等基本元素，然后再依据题意判定通过反例对结构特征进行辨析，即要说明一个命题是错误的，只要举出一个反例即可5.由三视图还原直观图的方法还原后的几何体一般为较熟悉的柱、锥、台、球的组合体注意图中实线、虚线，实际是原几何体中的可视线与被遮挡线想象原图形，并画出草图后进行三视图还原，把握三视图和几何体之间的关系，与所给三视图比较，通过调查准备画出几何体6.常见三视图对应的几何体：三视图为三个三角形，对应三棱锥三视图为两个三角形，一个四边形，对应四棱锥三视图为两个三角形，一个圆，对应圆锥三视图为一个三角形，两个四边形，对应三棱柱三视图为两个四边形，一个圆，对应圆柱5.具体方法可采用垂线法或者削体法二、考向题型研究二：空间几何体之外接球、内接球(2013新课标I 卷T15文科)已知H 是球O 的直径AB 上一点，2:1:=HB AH ，⊥AB 平面α，H 为垂足，α截球O 所得截面的面积为π，则球O 的表面积为 ．【答案】9π2【解析】如图， 设球O 的半径为R ， 则AH ＝23R ， OH ＝3R . 又∵π·EH 2＝π，∴EH ＝1.∵在Rt △OEH 中，R 2＝22+13R ⎛⎫⎪⎝⎭，∴R 2＝98.∴S 球＝4πR 2＝9π2（2019新课标I 卷T12理科）．已知三棱锥P -ABC 的四个顶点在球O 的球面上，PA =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，PB 的中点，∠CEF =90°，则球O 的体积为A ．B ．C ． D【答案】D【分析】先证得PB ⊥平面PAC ，再求得PA PB PC ===从而得P ABC -为正方体一部分，进而知正方体的体对角线即为球直径，从而得解.【解析】解法一:,PA PB PC ABC ==∆Q 为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别为PA 、AB 中点，//EF PB ∴，EF AC ∴⊥，又EF CE ⊥，,CE AC C EF =∴⊥I 平面PAC ，PB ⊥平面PAC ，PAB PA PB PC ∴∠=90︒,∴===，P ABC ∴-为正方体一部分，2R ==34433R V R =∴=π==π，故选D ．解法二:设2PA PB PC x ===，,E F 分别为,PA AB 中点，//EF PB ∴，且12EF PB x ==，ABC ∆Q 为边长为2的等边三角形，CF ∴=90CEF ∠=︒1,2CE AE PA x ∴=== AEC ∆中余弦定理()2243cos 22x x EAC x+--∠=⨯⨯，作PD AC ⊥于D ，PA PC =Q ，D Q 为AC 中点，1cos 2AD EAC PA x ∠==，2243142x x x x+-+∴=，22121222x x x ∴+=∴==，PA PB PC ∴===又===2AB BC AC ，,,PA PB PC ∴两两垂直，2R ∴==2R ∴=，344338V R ∴=π=π⨯=，故选D. 【点睛】本题考查学生空间想象能力，补体法解决外接球问题．可通过线面垂直定理，得到三棱两两互相垂直关系，快速得到侧棱长，进而补体成正方体解决．（2017新课标I 卷T16文科）已知三棱锥S ﹣ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径．若平面SCA ⊥平面SCB ，SA=AC ，SB=BC ，三棱锥S ﹣ABC 的体积为9，则球O 的表面积为 ． 【答案】36π【解析】解：三棱锥S ﹣ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径，若平面SCA ⊥平面SCB ，SA=AC ，SB=BC ，三棱锥S ﹣ABC 的体积为9，可知三角形SBC 与三角形SAC 都是等腰直角三角形，设球的半径为r ， 可得，解得r=3．球O 的表面积为：4πr 2=36π． 故答案为：36π．【点睛】本题考查球的內接体，三棱锥的体积以及球的表面积的求法，考查空间想象能力以及计算能力．（2012新课标I 卷T8文科）平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π 【答案】B【解析】设球的半径为R ，由球的截面性质得R ==所有球的体积343V R π== （2011新课标I 卷T15理科）已知矩形ABCD 的顶点都在半径为4的球O 的球面上，且AB=6，BC=2，则棱锥O ﹣ABCD 的体积为 ．【答案】8【分析】由题意求出矩形的对角线的长，结合球的半径，球心到矩形的距离，满足勾股定理，求出棱锥的高，即可求出棱锥的体积． 【解析】解：矩形的对角线的长为：，所以球心到矩形的距离为：=2，所以棱锥O ﹣ABCD 的体积为：=8．故答案为：8【点睛】本题是基础题，考查球内几何体的体积的计算，考查计算能力，空间想象能力，常考题型．（2017新课标I卷T16理科）如图，圆形纸片的圆心为O，半径为5cm，该纸片上的等边三角形ABC 的中心为O．D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形．沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥．当△ABC的边长变化时，所得三棱锥体积（单位：cm3）的最大值为．【答案】4cm3．【分析】法一：由题，连接OD，交BC于点G，由题意得OD⊥BC，OG=BC，设OG=x，则BC=2 x，DG=5﹣x，三棱锥的高h=，求出S△ABC=3，V==，令f（x）=25x4﹣10x5，x∈（0，），f′（x）=100x3﹣50x4，f（x）≤f（2）=80，由此能求出体积最大值．法二：设正三角形的边长为x，则OG=，FG=SG=5﹣，SO=h===，由此能示出三棱锥的体积的最大值．【解析】解法一：由题意，连接OD，交BC于点G，由题意得OD⊥BC，OG=BC，即OG的长度与BC的长度成正比，设OG=x，则BC=2x，DG=5﹣x，三棱锥的高h===，=3，则V===，令f（x）=25x4﹣10x5，x∈（0，），f′（x）=100x3﹣50x4，令f′（x）≥0，即x4﹣2x3≤0，解得x≤2，则f（x）≤f（2）=80，∴V≤=4cm3，∴体积最大值为4cm3．故答案为：4cm3．解法二：如图，设正三角形的边长为x，则OG=，∴FG=SG=5﹣，SO=h===，∴三棱锥的体积V===，令b（x）=5x4﹣，则，令b'（x）=0，则4x3﹣=0，解得x=4，∴（cm3）．故答案为：4cm3．【点睛】本题考查三棱锥的体积的最大值的求法，考查空间中线线、线面、面面间的位置关系、函数性质、导数等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，是中档题．1．球的表面积和体积公式设球的半径为R ，它的体积与表面积都由半径R 唯一确定，是以R 为自变量的函数，其表面积公式为24πR ，即球的表面积等于它的大圆面积的4倍；其体积公式为34π3R . 2．球的切、接问题（常见结论）（1）若正方体的棱长为a ，则正方体的内切球半径是12a ；与正方体．外接球球心是正方体的中心内切球球心是正方体的中心与各条棱相切的求，球心是正方体的中心（2）若长方体的长、宽、高分别为a，b，h球心是体对角线的交点（3）若正四面体的棱长为a；a．与正四面体所有棱相切的球的半径是4球心是正四面体的中心（4）球与圆柱的底面和侧面均相切，则球的直径等于圆柱的高，也等于圆柱底面圆的直径．（5）球与圆台的底面与侧面均相切，则球的直径等于圆台的高．综上，可以认为，外接球的球心在空间几何体底面的外接圆的圆心的竖直线上3、球的表面积和体积确定一个球的条件是球心和球的半径，已知球的半径可以利用公式求球的表面积和体积；反之，已知球的体积或表面积也可以求其半径.球与几种特殊几何体的关系：(1)长方体内接于球，则球的直径是长方体的体对角线长；(2)正四面体的外接球与内切球的球心重合，且半径之比为3∶1；(3)直棱柱的外接球：找出直棱柱的外接圆柱，圆柱的外接球就是所求直棱柱的外接球.特别地，直三棱柱的外接球的球心是上、下底面三角形外心连线的中点；(4)球与圆柱的底面和侧面均相切，则球的直径等于圆柱的高，也等于圆柱底面圆的直径；(5)球与圆台的底面和侧面均相切，则球的直径等于圆台的高．与球有关的实际应用题一般涉及水的容积问题，解题的关键是明确球的体积与水的容积之间的关系，正确建立等量关系.有关球的截面问题，常画出过球心的截面圆，将空间几何问题转化为平面中圆的有关问题解决.球心到截面的距离d与球的半径R及截面圆的半径r之间满足关系式：d=.5.柱体的外接球问题，其解题关键是在于确定球心在多面体中的位置，找到球的半径或者直径与多面体相关元素之间的关系，结合原有多面体的特性求出球的半径，然后再利用球的表面积和体积公式进行正确计算，常见的方法是将多面体还原成正方体和长方体中再去求解6.椎体的外接球问题的关键是确定球心位置：将椎体还原或者补形为正方体或者长方体，进而确定球心椎体的外接球的球心一定在过底面的外心与底面垂直的直线上球心到各顶点的距离都相等球心一定在外接球的直径上三、考向题型研究三：空间几何体的体积（2018新课标I卷T12理科）已知正方体的棱长为1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为A. 3√34B. 2√33C. 3√24D. √32【答案】A【解析】分析：首先利用正方体的棱是3组每组有互相平行的4条棱，所以与12条棱所成角相等，只需与从同一个顶点出发的三条棱所成角相等即可，从而判断出面的位置，截正方体所得的截面为一个正六边形，且边长是面的对角线的一半，应用面积公式求得结果.详解：根据相互平行的直线与平面所成的角是相等的，所以在正方体ABCD −A 1B 1C 1D 1中，平面AB 1D 1与线AA 1,A 1B 1,A 1D 1所成的角是相等的，所以平面AB 1D 1与正方体的每条棱所在的直线所成角都是相等的， 同理平面C 1BD 也满足与正方体的每条棱所在的直线所成角都是相等， 要求截面面积最大，则截面的位置为夹在两个面AB 1D 1与C 1BD 中间的，且过棱的中点的正六边形，且边长为√22，所以其面积为S =6×√34⋅(√22)2=3√34，故选A.【点睛】该题考查的是有关平面被正方体所截得的截面多边形的面积问题，首要任务是需要先确定截面的位置，之后需要从题的条件中找寻相关的字眼，从而得到其为过六条棱的中点的正六边形，利用六边形的面积的求法，应用相关的公式求得结果.(2013新课标Ⅰ卷T6理科)如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器的厚度，则球的体积为( )．A ．500π3cm 3B ．866π3cm 3C ．1372π3cm 3D ．2048π3cm 3【答案】A【解析】设球半径为R ，由题可知R ，R －2，正方体棱长一半可构成直角三角形，即△OBA 为直角三角形，如图．BC ＝2，BA ＝4，OB ＝R －2，OA ＝R ， 由R 2＝(R －2)2＋42，得R ＝5，所以球的体积为34500π5π33(cm 3)，故选A.(2013新课标I 卷T19文科)如图，三棱柱ABC －A 1B 1C 1中，CA ＝CB ，AB ＝AA 1，∠BAA 1＝60°. (1)证明：AB ⊥A 1C ；(2)若AB ＝CB ＝2，A 1C ，求三棱柱ABC －A 1B 1C 1的体积．【答案】答案见解析【解析】(1)证明：取AB 的中点O ，连结OC ，OA 1，A 1B . 因为CA ＝CB ， 所以OC ⊥AB .由于AB ＝AA 1，∠BAA 1＝60°， 故△AA 1B 为等边三角形， 所以OA 1⊥AB .因为OC ∩OA 1＝O ，所以 AB ⊥平面OA 1C . 又A 1C ⊂平面OA 1C ，故AB ⊥A 1C .(2)解：由题设知△ABC 与△AA 1B 都是边长为2的等边三角形， 所以OC ＝OA 1＝3.又A 1C ＝6，则A 1C 2＝OC 2＋21OA ， 故OA 1⊥OC .因为OC ∩AB ＝O ，所以OA 1⊥平面ABC ，OA 1为三棱柱ABC －A 1B 1C 1的高． 又△ABC 的面积S △ABC ＝3，故三棱柱ABC －A 1B 1C 1的体积V ＝S △ABC ×OA 1＝3.（2012新课标I 卷T19文科）如图，三棱柱111ABC A B C -中，侧棱垂直底面， ∠ACB =90°，AC =BC =12AA 1，D 是棱AA 1的中点。

专题7 立体几何（2）立体几何大题：10年10考，每年1题．第1小题多为证明垂直问题，第2小题多为体积计算问题（2014年是求高）．1．（2019年）如图，直四棱柱ABCD﹣A1B1C1D1的底面是菱形，AA1＝4，AB＝2，∠BAD＝60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求点C到平面C1DE的距离．【解析】（1）连结B1C，ME，∵M，E分别是BB1，BC的中点，∴ME∥B1C，又N为A1D的中点，∴ND＝12A1D，由题设知A1B1//DC，∴B1C//A1D，∴ME//ND，∴四边形MNDE是平行四边形，∴MN∥ED，又MN⊄平面C1DE，∴MN∥平面C1DE．（2）过C作C1E的垂线，垂足为H，由已知可得DE⊥BC，DE⊥C1C，∴DE⊥平面C1CE，故DE⊥CH，∴CH⊥平面C1DE，故CH的长即为C到时平面C1DE的距离，由已知可得CE＝1，CC1＝4，∴C1E，故CH，∴点C 到平面C 1DE ． 2．（2018年）如图，在平行四边形ABCM 中，AB ＝AC ＝3，∠ACM ＝90°，以AC 为折痕将△ACM 折起，使点M 到达点D 的位置，且AB ⊥DA ． （1）证明：平面ACD ⊥平面ABC ；（2）Q 为线段AD 上一点，P 为线段BC 上一点，且BP ＝DQ ＝23DA ，求三棱锥Q ﹣ABP 的体积．【解析】（1）∵在平行四边形ABCM 中，∠ACM ＝90°，∴AB ⊥AC ， 又AB ⊥DA ．且AD ∩AC ＝A ， ∴AB ⊥面ADC ，∵AB ⊂面ABC ， ∴平面ACD ⊥平面ABC ；（2）∵AB ＝AC ＝3，∠ACM ＝90°，∴AD ＝AM ＝∴BP ＝DQ ＝23DA ＝ 由（1）得DC ⊥AB ，又DC ⊥CA ，∴DC ⊥面ABC ，∴三棱锥Q ﹣ABP 的体积V ＝11DC 33S ∆ABP ⨯ ＝C 121DC 333S ∆AB ⨯⨯＝12113333323⨯⨯⨯⨯⨯⨯＝1． 3．（2017年）如图，在四棱锥P ﹣ABCD 中，AB ∥CD ，且∠BAP ＝∠CDP ＝90°． （1）证明：平面PAB ⊥平面PAD ；（2）若PA ＝PD ＝AB ＝DC ，∠APD ＝90°，且四棱锥P ﹣ABCD 的体积为83，求该四棱锥的侧面积．【解析】（1）∵在四棱锥P ﹣ABCD 中，∠BAP ＝∠CDP ＝90°， ∴AB ⊥PA ，CD ⊥PD ， 又AB ∥CD ，∴AB ⊥PD ， ∵PA ∩PD ＝P ，∴AB ⊥平面PAD ， ∵AB ⊂平面PAB ，∴平面PAB ⊥平面PAD ．（2）设PA ＝PD ＝AB ＝DC ＝a ，取AD 中点O ，连结PO ， ∵PA ＝PD ＝AB ＝DC ，∠APD ＝90°，平面PAB ⊥平面PAD ，∴PO ⊥底面ABCD ，且AD ，PO ＝2a ， ∵四棱锥P ﹣ABCD 的体积为83， 由AB ⊥平面PAD ，得AB ⊥AD ，∴V P ﹣ABCD ＝CD 13S AB ⨯⨯PO 四边形＝1D 3⨯AB⨯A ⨯PO ＝132a a ⨯⨯＝313a ＝83， 解得a ＝2，∴PA ＝PD ＝AB ＝DC ＝2，AD ＝BC ＝PO ，∴PB ＝PC∴该四棱锥的侧面积：S 侧＝S △PAD +S △PAB +S △PDC +S △PBC＝1D 2⨯PA⨯P +12⨯PA⨯AB +1D DC 2⨯P ⨯+1C 2⨯B＝11112222222222⨯⨯+⨯⨯+⨯⨯+⨯＝6+4．（2016年）如图，已知正三棱锥P﹣ABC的侧面是直角三角形，PA＝6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连接PE并延长交AB于点G．（1）证明：G是AB的中点；（2）在图中作出点E在平面PAC内的正投影F（说明作法及理由），并求四面体PDEF的体积．【解析】（1）∵P﹣ABC为正三棱锥，且D为顶点P在平面ABC内的正投影，∴PD⊥平面ABC，则PD⊥AB，又E为D在平面PAB内的正投影，∴DE⊥面PAB，则DE⊥AB，∵PD∩DE＝D，∴AB⊥平面PDE，连接PE并延长交AB于点G，则AB⊥PG，又PA＝PB，∴G是AB的中点；（2）在平面PAB内，过点E作PB的平行线交PA于点F，F即为E在平面PAC内的正投影．∵正三棱锥P﹣ABC的侧面是直角三角形，∴PB⊥PA，PB⊥PC，又EF∥PB，所以EF⊥PA，EF⊥PC，因此EF⊥平面PAC，即点F为E在平面PAC内的正投影．连结CG，因为P在平面ABC内的正投影为D，所以D是正三角形ABC的中心．由（1）知，G 是AB 的中点，所以D 在CG 上，故CD ＝23CG ． 由题设可得PC ⊥平面PAB ，DE ⊥平面PAB ，所以DE ∥PC ，因此PE ＝23PG ，DE ＝13PC ．由已知，正三棱锥的侧面是直角三角形且PA ＝6，可得DE ＝2，PG ＝PE ＝ 在等腰直角三角形EFP 中，可得EF ＝PF ＝2． 所以四面体PDEF 的体积V ＝13×DE ×S △PEF ＝13×2×12×2×2＝43．5．（2015年）如图，四边形ABCD 为菱形，G 为AC 与BD 的交点，BE ⊥平面ABCD ． （1）证明：平面AEC ⊥平面BED ；（2）若∠ABC ＝120°，AE ⊥EC ，三棱锥E ﹣ACD【解析】（1）∵四边形ABCD 为菱形， ∴AC ⊥BD ， ∵BE ⊥平面ABCD ， ∴AC ⊥BE ， 则AC ⊥平面BED ， ∵AC ⊂平面AEC ， ∴平面AEC ⊥平面BED ；（2）设AB ＝x ，在菱形ABCD 中，由∠ABC ＝120°，得AG ＝GC ，GB ＝GD ＝2x，∵BE ⊥平面ABCD ，∴BE ⊥BG ，则△EBG 为直角三角形，∴EG ＝12AC ＝AG ＝2x ，则BE x ，∵三棱锥E ﹣ACD 的体积V ＝11C GD 32⨯A ⨯⨯BE 3x 解得x ＝2，即AB ＝2， ∵∠ABC ＝120°，∴AC 2＝AB 2+BC 2﹣2AB •BC cos ABC ＝4+4﹣2×1222⎛⎫⨯⨯-⎪⎝⎭＝12，即AC ＝在三个直角三角形EBA ，EBD ，EBC 中，斜边AE ＝EC ＝ED ， ∵AE ⊥EC ，∴△EAC 为等腰三角形， 则AE 2+EC 2＝AC 2＝12， 即2AE 2＝12， ∴AE 2＝6，则AE ，∴从而得AE ＝EC ＝ED ，∴△EAC 的面积S ＝11C 22⨯EA⨯E =3， 在等腰三角形EAD 中，过E 作EF ⊥AD 于F ，则AE ，AF ＝1D 2A ＝1212⨯=，则EF =∴△EAD 的面积和△ECD 的面积均为S ＝122⨯故该三棱锥的侧面积为3+6．（2014年）如图，三棱柱ABC﹣A1B1C1中，侧面BB1C1C为菱形，B1C的中点为O，且AO⊥平面BB1C1C．（1）证明：B1C⊥AB；（2）若AC⊥AB1，∠CBB1＝60°，BC＝1，求三棱柱ABC﹣A1B1C1的高．【解析】（1）连接BC1，则O为B1C与BC1的交点，∵侧面BB1C1C为菱形，∴BC1⊥B1C，∵AO⊥平面BB1C1C，∴AO⊥B1C，∵AO∩BC1＝O，∴B1C⊥平面ABO，∵AB⊂平面ABO，∴B1C⊥AB；（2）作OD⊥BC，垂足为D，连接AD，作OH⊥AD，垂足为H，∵BC⊥AO，BC⊥OD，AO∩OD＝O，∴BC⊥平面AOD，∴OH⊥BC，∵OH⊥AD，BC∩AD＝D，∴OH⊥平面ABC，∵∠CBB1＝60°，∴△CBB1为等边三角形，∵BC＝1，∴OD∵AC ⊥AB 1，∴OA ＝12B 1C ＝12，由OH •AD ＝OD •OA ，可得AD ，∴OH ＝14，∵O 为B 1C 的中点，∴B 1到平面ABC ，∴三棱柱ABC ﹣A 1B 1C 1的高7．7．（2013年）如图，三棱柱ABC ﹣A 1B 1C 1中，CA ＝CB ，AB ＝AA 1，∠BAA 1＝60° （1）证明：AB ⊥A 1C ； （2）若AB ＝CB ＝2，A 1C ＝，求三棱柱ABC ﹣A 1B 1C 1的体积．【解析】（1）如图，取AB 的中点O ，连结OC ，OA 1，A 1B ． 因为CA ＝CB ，所以OC ⊥AB ．由于AB ＝AA 1，160∠BAA =，故△AA 1B 为等边三角形， 所以OA 1⊥AB ．因为OC ∩OA 1＝O ，所以AB ⊥平面OA 1C ． 又A 1C ⊂平面OA 1C ，故AB ⊥A 1C ；（2）由题设知△ABC 与△AA 1B 都是边长为2的等边三角形，所以1C O =OA =．又1C A =，则22211C C A =O +OA ，故OA 1⊥OC ．因为OC ∩AB ＝O ，所以OA 1⊥平面ABC ，OA 1为三棱柱ABC ﹣A 1B 1C 1的高．又△ABC 的面积C S ∆AB故三棱柱ABC ﹣A 1B 1C 1的体积C 1V 3S ∆AB =⨯OA ==．8．（2012年）如图，三棱柱ABC ﹣A 1B 1C 1中，侧棱垂直底面，∠ACB ＝90°，AC ＝BC ＝12AA 1，D 是棱AA 1的中点．（1）证明：平面BDC 1⊥平面BDC（2）平面BDC 1分此棱柱为两部分，求这两部分体积的比．【解析】（1）由题意知BC ⊥CC 1，BC ⊥AC ，CC 1∩AC ＝C ， ∴BC ⊥平面ACC 1A 1，又DC 1⊂平面ACC 1A 1， ∴DC 1⊥BC ．由题设知∠A 1DC 1＝∠ADC ＝45°，∴∠CDC 1＝90°，即DC 1⊥DC ，又DC ∩BC ＝C ， ∴DC 1⊥平面BDC ，又DC 1⊂平面BDC 1， ∴平面BDC 1⊥平面BDC ；（2）设棱锥B ﹣DACC 1的体积为V 1，AC ＝1，由题意得V 1＝1121132+⨯⨯⨯＝12，又三棱柱ABC ﹣A 1B 1C 1的体积V ＝1， ∴（V ﹣V 1）：V 1＝1：1，∴平面BDC1分此棱柱两部分体积的比为1：1．9．（2011年）如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形．∠DAB＝60°，AB＝2AD，PD⊥底面ABCD．（1）证明：PA⊥BD；（2）设PD＝AD＝1，求棱锥D﹣PBC的高．【解析】（1）因为∠DAB＝60°，AB＝2AD，由余弦定理得BD D，从而BD2+AD2＝AB2，故BD⊥AD，又PD⊥底面ABCD，可得BD⊥PD，所以BD⊥平面PAD．故PA⊥BD．（2）解：作DE⊥PB于E，已知PD⊥底面ABCD，则PD⊥BC，由（1）知，BD⊥AD，又BC∥AD，∴BC⊥BD．故BC⊥平面PBD，BC⊥DE，则DE⊥平面PBC．由题设知PD＝1，则BD，PB＝2．根据DE•PB＝PD•BD，得DE即棱锥D﹣PBC10．（2010年）如图，已知四棱锥P﹣ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高．（1）证明：平面PAC⊥平面PBD；（2）若AB，∠APB＝∠ADB＝60°，求四棱锥P﹣ABCD的体积．。

立体几何立体几何是高考数学的必考内容，在大题中一般分两问，第一问考查空间直线与平面的位置关系证明；第二问考查空间角、空间距离等的求解。

考题难度中等，常结合空间向量知识进行考查。

2024年高考有很大可能延续往年的出题方式。

题型一：空间异面直线夹角的求解1(2023·上海长宁·统考一模)如图，在三棱锥A-BCD中，平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)求证：AO⊥CD；(2)若BD⊥DC,BD=DC,AO=BO，求异面直线BC与AD所成的角的大小.【思路分析】(1)利用面面垂直的性质、线面垂直的性质推理即得.(2)分别取AB,AC的中点M,N，利用几何法求出异面直线BC与AD所成的角.【规范解答】(1)在三棱锥A-BCD中，由AB=AD,O为BD的中点，得AO⊥BD，而平面ABD⊥平面BCD，平面ABD∩平面BCD=BD，AO⊂平面ABD，因此AO⊥平面BCD，又CD⊂平面BCD，所以AO⊥CD.(2)分别取AB,AC的中点M,N，连接OM,ON,MN，于是MN⎳BC,OM⎳AD，则∠OMN是异面直线BC与AD所成的角或其补角，由(1)知，AO ⊥BD ，又AO =BO ，AB =AD ，则∠ADB =∠ABD =π4，于是∠BAD =π2，令AB =AD =2，则DC =BD =22，又BD ⊥DC ，则有BC =BD 2+DC 2=4，OC =DC 2+OD 2=10，又AO ⊥平面BCD ，OC ⊂平面BCD ，则AO ⊥OC ，AO =2，AC =AO 2+OC 2=23，由M ,N 分别为AB ,AC 的中点，得MN =12BC =2,OM =12AD =1,ON =12AC =3，显然MN 2=4=OM 2+ON 2，即有∠MON =π2，cos ∠OMN =OM MN =12，则∠OMN =π3，所以异面直线BC 与AD 所成的角的大小π3.1、求异面直线所成角一般步骤：(1)平移：选择适当的点，线段的中点或端点，平移异面直线中的一条或两条成为相交直线．(2)证明：证明所作的角是异面直线所成的角．(3)寻找：在立体图形中，寻找或作出含有此角的三角形，并解之．(4)取舍：因为异面直线所成角θ的取值范围是0,π2，所以所作的角为钝角时，应取它的补角作为异面直线所成的角．2、可通过多种方法平移产生，主要有三种方法：(1)直接平移法(可利用图中已有的平行线)；(2)中位线平移法；(3)补形平移法(在已知图形中，补作一个相同的几何体，以便找到平行线)．3、异面直线所成角：若n 1 ,n 2分别为直线l 1,l 2的方向向量，θ为直线l 1,l 2的夹角，则cos θ=cos <n 1 ,n 2 > =n 1 ⋅n 2n 1 n 2.1(2023·江西萍乡·高三统考期中)如图，在正四棱台ABCD -A 1B 1C 1D 1中，E ,F 分别是BB 1,CD 的中点.(1)证明：EF ⎳平面AB1C 1D ；(2)若AB =2A 1B 1，且正四棱台的侧面积为9，其内切球半径为22，O 为ABCD 的中心，求异面直线OB 1与CC 1所成角的余弦值.【答案】(1)证明见解析；(2)45【分析】(1)根据中位线定理，结合线面平行判定定理以及面面平行判定定理，利用面面平行的性质，可得答案；(2)根据题意，结合正四棱台的几何性质，求得各棱长，利用线线角的定义，可得答案.【解析】(1)取CC 1中点G ，连接GE ,GF ，如下图：在梯形BB 1C 1C 中，E ,G 分别为BB 1,CC 1的中点，则EG ⎳B 1C 1，同理可得FG ⎳C 1D ，因为EG ⊄平面AB 1C 1D ，B 1C 1⊂平面AB 1C 1D ，所以EG ⎳平面AB 1C 1D ，同理可得GF ⎳平面AB 1C 1D ，因为EG ∩FG =G ，EG ,FG ⊆平面EFG ，所以平面EFG ⎳平面AB 1C 1D ，又因为EF ⊆平面EFG ，所以EF ⎳平面AB 1C 1D ；(2)连接AC ,BD ，则AC ∩BD =O ，连接A 1O ,A 1C 1,B 1O ,在平面BB 1C 1C 中，作B 1N ⊥BC 交BC 于N ，在平面BB 1D 1D 中，作B 1M ⊥BD 交BD 于M ，连接MN ，如下图：因为AB =2A 1B 1，则OC =A 1C 1，且OC ⎳A 1C 1，所以A 1C 1CO 为平行四边形，则A 1O ⎳CC 1，且A 1O =CC 1，所以∠A 1OB 1为异面直线OB 1与CC 1所成角或其补角，同理可得：B 1D 1DO 为平行四边形，则B 1O =D 1D ，在正四棱台ABCD -A 1B 1C 1D 1中，易知对角面BB 1D 1D ⊥底面ABCD ，因为平面ABCD ∩平面BB 1D 1D =BD ，且B 1M ⊥BD ，B 1M ⊂平面BB 1D 1D ，所以B 1M ⊥平面ABCD ，由内切球的半径为22，则B 1M =2，在等腰梯形BB 1C 1C 中，BC =2B 1C 1且B 1N ⊥BC ，易知BN =14BC ，同理可得BM =14BD ，在△BCD 中，BN BC=BM BD =14，则MN =14CD ，设正方形ABCD 的边长为4x x >0 ，则正方形A 1B 1C 1D 1的边长为2x ，MN =x ，由正四棱台的侧面积为9，则等腰梯形BB 1C 1C 的面积S =94，因为B 1M ⊥平面ABCD ，MN ⊂平面ABCD ，所以B 1M ⊥MN ，在Rt △B 1MN ，B 1N =B 1M 2+MN 2=2+x 2，可得S =12⋅B 1N ⋅B 1C 1+BC ，则94=12×2+x 2×4x +2x ，解得x =12，所以BC =2，B 1C 1=1，BN =14BC =12，B 1N =32，则A 1B 1=1，在Rt △BB 1N 中，BB 1=B 1N 2+BN 2=102，则CC 1=DD 1=102，所以在△A 1OB 1中，则cos ∠A 1OB 1=A 1O 2+B 1O 2-A 1B 212⋅A 1O ⋅B 1O=1022+102 2-12×102×102=45，所以异面直线OB 1与CC 1所成角的余弦值为45.2(2023·辽宁丹东·统考二模)如图，平行六面体ABCD -A 1B 1C 1D 1的所有棱长都相等，平面CDD 1C 1⊥平面ABCD ，AD ⊥DC ，二面角D 1-AD -C 的大小为120°，E 为棱C 1D 1的中点．(1)证明：CD ⊥AE ；(2)点F 在棱CC 1上，AE ⎳平面BDF ，求直线AE 与DF 所成角的余弦值．【答案】(1)证明见解析；(2)37【分析】(1)根据面面垂直可得线面垂直进而得线线垂直，由二面角定义可得∠D 1DC =120°，进而根据中点得线线垂直即可求；(2)由线面平行的性质可得线线平行，由线线角的几何法可利用三角形的边角关系求解，或者建立空间直角坐标系，利用向量的夹角即可求解.【解析】(1)因为平面CDD 1C 1⊥平面ABCD ，且两平面交线为DC ,AD ⊥DC ，AD ⊂平面ABCD , 所以AD ⊥平面CDD 1C 1，所以AD ⊥D 1D ,AD ⊥DC ，∠D 1DC 是二面角D 1-AD -C 的平面角，故∠D 1DC =120°．连接DE ，E 为棱C 1D 1的中点，则DE ⊥C 1D 1,C 1D 1⎳CD ，从而DE ⊥CD ．又AD ⊥CD ，DE ∩AD =D ，DE ,AD ⊂平面AED ，所以CD ⊥平面AED ，ED ⊂平面AED ,因此CD ⊥AE ．(2)解法1：设AB =2，则DE =D 1D 2-12D 1C 1 2=3，所以CE =AE =AD 2+DE 2=7．连AC 交BD 于点O ，连接CE 交DF 于点G ，连OG ．因为AE ⎳平面BDF ，AE ⊂平面AEC ,平面AEC ∩平面BDF =OG ，所以AE ∥OG ，因为O 为AC 中点，所以G 为CE 中点，故OG =12AE =72．且直线OG 与DF 所成角等于直线AE 与DF 所成角．在Rt △EDC 中，DG =12CE =72，因为OD =2，所以cos ∠OGD =722+72 2-(2)22×72×72=37．因此直线AE 与DF 所成角的余弦值为37．解法2；设AB =2，则DE =D 1D 2-12D 1C 1 2=3，所以CE =AE =AD 2+DE 2=7．取DC 中点为G ，连接EG 交DF 于点H ，则EG =DD 1=2．连接AG 交BD 于点I ，连HI ，因为AE ⎳平面BDF ，AE ⊂平面AGE ，平面AGE ∩平面BDF =IH ，所以AE ∥IH ．HI 与DH 所成角等于直线AE 与DF 所成角．正方形ABCD 中，GI =13AG ，DI =13DB =223，所以GH =13EG ，故HI =13AE =73．在△DHG 中，GH =13EG =23，GD =1，∠EGD =60°，由余弦定理DH =1+49-1×23=73．在△DHI 中，cos ∠DHI =732+73 2-223 22×73×73=37．因此直线AE 与DF 所成角的余弦值为37．解法3:由(1)知DE ⊥平面ABCD ，以D 为坐标原点，DA为x 轴正方向，DA为2个单位长，建立如图所示的空间直角坐标系D -xyz ．由(1)知DE =3，得A 2,0,0 ,B 2,2,0 ,C 0,2,0 ,E (0,0,3)，C 1(0,1,3)．则CC 1=(0,-1,3)，DC =(0,2,0)，AE =(-2,0,3)，DB =(2,2,0)．由CF =tCC 1 0≤t ≤1 ，得DF =DC +CF =(0,2-t ,3t )．因为AE ⎳平面BDF ，所以存在唯一的λ，μ∈R ，使得AE =λDB +μDF=λ2,2,0 +μ(0,2-t ,3t )=2λ,2λ+2μ-tμ,3μt ，故2λ=-2,2λ+2μ-tμ=0,3μt =3，解得t =23，从而DF =0,43,233 ．所以直线AE 与DF 所成角的余弦值为cos AE ,DF =AE ⋅DF|AE ||DF |=37．题型二：空间直线与平面夹角的求解2(2024·安徽合肥·统考一模)如图，三棱柱ABC -A 1B 1C 1中，四边形ACC 1A 1,BCC 1B 1均为正方形，D ,E 分别是棱AB ,A 1B 1的中点，N 为C 1E 上一点.(1)证明：BN ⎳平面A 1DC ；(2)若AB =AC ,C 1E =3C 1N，求直线DN 与平面A 1DC 所成角的正弦值.【思路分析】(1)连接BE ,BC 1,DE ,则有平面BEC 1⎳平面A 1DC ，可得BN ⎳平面A 1DC ；(2)建立空间直角坐标系，利用空间向量进行计算即可.【规范解答】(1)连接BE ,BC 1,DE .因为AB ⎳A 1B 1，且AB =A 1B 1，又D ,E 分别是棱AB ,A 1B 1的中点，所以BD ⎳A 1E ，且BD =A 1E ，所以四边形BDA 1E 为平行四边形，所以A 1D ⎳EB ，又A 1D ⊂平面A 1DC ,EB ⊄平面A 1DC ，所以EB ⎳平面A 1DC ，因为DE ⎳BB 1⎳CC 1，且DE =BB 1=CC 1，所以四边形DCC 1E 为平行四边形，所以C 1E ⎳CD ，又CD ⊂平面A 1DC ,C 1E ⊄平面A 1DC ，所以C 1E ⎳平面A 1DC ，因为C 1E ∩EB =E ,C 1E ,EB ⊂平面BEC 1，所以平面BEC 1⎳平面A 1DC ，因为BN ⊂平面BEC 1，所以BN ⎳平面A 1DC .(2)四边形ACC 1A 1,BCC 1B 1均为正方形，所以CC 1⊥AC ,CC 1⊥BC ，所以CC 1⊥平面ABC .因为DE ⎳CC 1，所以DE ⊥平面ABC ，从而DE ⊥DB ,DE ⊥DC .又AB =AC ，所以△ABC 为等边三角形.因为D 是棱AB 的中点，所以CD ⊥DB ，即DB ,DC ,DE 两两垂直.以D 为原点，DB ,DC ,DE 所在直线为x ,y ,z 轴，建立如图所示的空间直角坐标系D -xyz .设AB =23，则D 0,0,0 ,E 0,0,23 ,C 0,3,0 ,C 10,3,23 ,A 1-3,0,23 ，所以DC =0,3,0 ,DA 1=-3,0,23 .设n=x ,y ,z 为平面A 1DC 的法向量，则n ⋅DC=0n ⋅DA 1 =0，即3y =0-3x +23z =0 ，可取n=2,0,1 .因为C 1E =3C 1N ，所以N 0,2,23 ,DN =0,2,23 .设直线DN 与平面A 1DC 所成角为θ，则sin θ=|cos ‹n ,DN ›|=|n ⋅DN ||n |⋅|DN |=235×4=1510，即直线DN 与平面A 1DC 所成角正弦值为1510.1、垂线法求线面角(也称直接法)：(1)先确定斜线与平面，找到线面的交点B 为斜足；找线在面外的一点A ，过点A 向平面α做垂线，确定垂足O ；(2)连结斜足与垂足为斜线AB 在面α上的投影；投影BO 与斜线AB 之间的夹角为线面角；(3)把投影BO 与斜线AB 归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。

高中数学《立体几何》大题及答案解析( 理)1.（ 2009 全国卷Ⅰ）如图，四棱锥S ABCD 中，底面 ABCD 为矩形， SD底面ABCD，AD2 ，DCo SD 2 ，点 M 在侧棱 SC 上，∠ABM=60。

（I ）证明：M是侧棱SC的中点；求二面角 S AM B 的大小。

2.（ 2009 全国卷Ⅱ）如图，直三棱柱DE ⊥平面 BCC 1（Ⅰ）证明： AB=AC 的角的大小ABC-A 1B1C1中， AB ⊥ AC,D 、E 分别为 AA 1、 B1C 的中点，（Ⅱ）设二面角A-BD-C 为 60°,求 B 1C 与平面 BCD 所成A 1 C1B1D EACB3. （ 2009浙江卷）如图，DC平面ABC，EB / / DC，AC BC EB 2DC 2 ，ACB 120o， P,Q 分别为 AE , AB 的中点．（I）证明： PQ / / 平面ACD；（II）求AD与平面 ABE 所成角的正弦值．4.（ 2009 北京卷）如图，四棱锥P ABCD 的底面是正方形，PD 底面 ABCD ，点E在棱PB上.（Ⅰ）求证：平面AEC 平面 PDB ；（Ⅱ）当 PD2AB 且E为PB的中点时，求 AE 与平面 PDB 所成的角的大小.5.（ 2009 江西卷）如图，在四棱锥P ABCD 中，底面 ABCD 是矩形， PA平面ABCD，PA AD 4 ， AB 2 ．以 BD 的中点 O 为球心、 BD 为直径的球面交PD 于点 M ．（1）求证：平面ABM⊥平面PCD；（2）求直线PC与平面ABM所成的角；（3）求点O到平面ABM的距离．PMA DOBC6（. 2009 四川卷）如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△ ABE 是等腰直角三角形，AB AE , FA FE , AEF 45 （I）求证： EF 平面 BCE ；（ II ）设线段 CD 、 AE 的中点分别为 P 、 M ，求证： PM ∥平面BCE （ III ）求二面角 F BD A 的大小。

高考真题分类汇编：立体几何一、选择题1.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）()A 6 ()B 9 ()C 12 ()D 18【答案】B【解析】由三视图可知，该几何体是三棱锥，底面是俯视图，高为3，所以几何体的体积为93362131=⨯⨯⨯⨯=V ,选B. 2.已知矩形ABCD ，AB=1，BC=2。

将△沿矩形的对角线BD 所在的直线进行翻折，在翻折过程中。

A.存在某个位置，使得直线AC 与直线BD 垂直.B.存在某个位置，使得直线AB 与直线CD 垂直.C.存在某个位置，使得直线AD 与直线BC 垂直.D.对任意位置，三对直线“AC 与BD ”，“AB 与CD ”，“AD 与BC ”均不垂直 【答案】C【解析】最简单的方法是取一长方形动手按照其要求进行翻着，观察在翻着过程，即可知选项C 是正确的．3.已知三棱锥S ABC -的所有顶点都在球O 的求面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =；则此棱锥的体积为（ ）()A 26 ()B 36 ()C 23 ()D 22【答案】A【解析】ABC ∆的外接圆的半径3r =点O 到面ABC 的距离226d R r =-=SC 为球O 的直径⇒点S 到面ABC的距离为23d =此棱锥的体积为112336ABC V S d ∆=⨯==另：123ABC V S R ∆<⨯=排除,,B C D ,选A. 4.下列命题正确的是（ ）A 、若两条直线和同一个平面所成的角相等，则这两条直线平行B 、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C 、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D 、若两个平面都垂直于第三个平面，则这两个平面平行【答案】C【解析】A.两直线可能平行，相交，异面故A 不正确；B.两平面平行或相交；C.正确；D.这两个平面平行或相交.5.如图，半径为R 的半球O 的底面圆O 在平面α内，过点O 作平面α的垂线交半球面于点A ，过圆O 的直径CD 作平面α成45角的平面与半球面相交，所得交线上到平面α的距离最大的点为B ，该交线上的一点P 满足60BOP ∠=，则A 、P 两点间的球面距离为（ ）A 、R、4R π C 、R 、3R π【答案】A【解析】根据题意，易知平面AOB ⊥平面CBD,BOP AOB AOP ∠⋅∠=∠∴cos cos cos422122=⋅=,42arccos =∠∴AOP ，由弧长公式易得，A 、P 两点间的球面距离为arccos4R . 6.如图，在空间直角坐标系中有直三棱柱111ABC A B C -，12CA CC CB ==，则直线1BC 与直线1AB 夹角的余弦值为（ ）A.55 B.53C. 255 D. 35【答案】A.【解析】设a CB =||，则a CC CA 2||||1==，),2,0(),0,2,0(),,0,0(),0,0,2(11a a B a C a B a A ，),2,0(),,2,2(11a a BC a a a AB -=-=∴，55||||,cos 111111=⋅>=<∴BC AB BC AB BC AB ，故选A. 7.某几何体的正视图和侧视图均如图1所示，则该几何体的俯视图不可能是【答案】D【解析】本题是组合体的三视图问题，由几何体的正视图和侧视图均如图1所示知，原图下面图为圆柱或直四棱柱，上面是圆柱或直四棱柱或下底是直角的三棱柱，Ａ，Ｂ，Ｃ都可能是该几何体的俯视图，Ｄ不可能是该几何体的俯视图，因为它的正视图上面应为如图的矩形.【点评】本题主要考查空间几何体的三视图，考查空间想象能力.是近年高考中的热点题型. 8.已知某几何体的三视图如图所示，则该几何体的体积为A ．8π3B ．3πC ．10π3D ．6π 【答案】B【解析】显然有三视图我们易知原几何体为 一个圆柱体的一部分，并且有正视图知是一个1/2的圆柱体，底面圆的半径为1，圆柱体的高为6，则知所求几何体体积为原体积的一半为3π.选B.9.某几何体的三视图如图所示，它的体积为A ．12π B.45π C.57π D.81π 【答案】C【解析】该几何体的上部是一个圆锥，下部是一个圆柱，根据三视图中的数量关系，可得πππ57533-53312222=⨯⨯+⨯⨯⨯=+=圆柱圆锥V V V ．故选C ．10.一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是 A.球 B.三棱柱 C.正方形 D.圆柱 【答案】D.【命题立意】本题考查了空间几何体的形状和三视图的概念，以及考生的空间想象能力，难度一般.【解析】球的三视图全是圆；如图正方体截出的三棱锥三视图全是等腰直角三角形；正方体三视图都是正方形.可以排除ABC ，故选Ｄ．11.设四面体的六条棱的长分别为1，1，1，1，2和a ，且长为a 的棱与长为2的棱异面，则a 的取值范围是（A ）(0,2) （B ）(0,3) （C ）(1,2) （D ）(1,3) 【答案】A【解析】因为22211)22(12=-=-=BE 则BE BF <，222=<=BE BF AB ，选A ，12.某三棱锥的三视图如图所示，该三梭锥的表面积是（ ）A. 28+65B. 30+65C. 56+ 125D. 60+125【答案】B【解析】从所给的三视图可以得到该几何体为三棱锥，如图所示，图中蓝色数字所表示的为直接从题目所给三视图中读出的长度，黑色数字代表通过勾股定理的计算得到的边长。