2010-2012年中考数学分析

九年级数学试卷分析九年级数学试卷分析一、各题分值：本次考试满分120分，共26道题，答题时间120分钟。

其中选择题16道，共42分，填空题4道，共12分，解答题6道，共66分。

各知识点在试题中的分布如下：二、学生答题情况分析：从考场答题情况看：学生做这套题的时间比较充分，能留出一定时间进行检查。

从判卷情况来看：在选择题部分，5,8,12,15,16错的较多。

填空题部分，17,20题错的较多，在以后的专题训练中，可以加大规律探索题的训练。

17题说明学生对基本概念的掌握不够扎实。

21题计算题在第二问分式的化简上问题较多，主要问题在于：1.不化简，直接代入求值。

2.在化简时进行了去分母。

22题主要问题在于：1.第一问k的值不求数。

2.第二问关系式中带k。

3.第三问中列为等式。

23.问题在于：1.第二问不写猜想结果。

2.在第二问证全等时对于等角的证明。

24题问题在于：第二大问的第二小问对于答题情况的说明不够明确。

25题的问题在于：1.第一问求a+b得值做的非常不好，说明学生在抛物线的平移部分掌握不好。

2.第二问第一小问不求顶点坐标。

3.最后一问求出m的值后不会舍。

26题的问题在于：1.扇形面积公式掌握不准。

2.在证明相似时，对应条件不会找。

三：试卷优点：1.试卷对知识点的考察明确，基础。

有利于双基的考察。

2.2.紧密联系2015年中考卷及2016中考考试说明的题型示例，有指导性。

3.题型选择全面，考察的有针对性。

四：试题缺点和错误：本次考试作为摸底考试试题，很好的针对了现有学生的特点和水平。

五：下次命题应出哪些考点及建议：1.注重题目考察知识点的综合性。

2.函数部分的考察可以考察一次函数与反比例函数或者是一次函数与二次函数的结合。

3.几何综合题可适当的增大难度。

模拟考试数学试卷分析为了对初三的第二轮复习进行有效检验，也为下一轮复习进行“查缺补漏”。

我们学校初三学生进行徐州市二模考试。

二模是一个定位考，是考生们中考前的一次模拟测试。

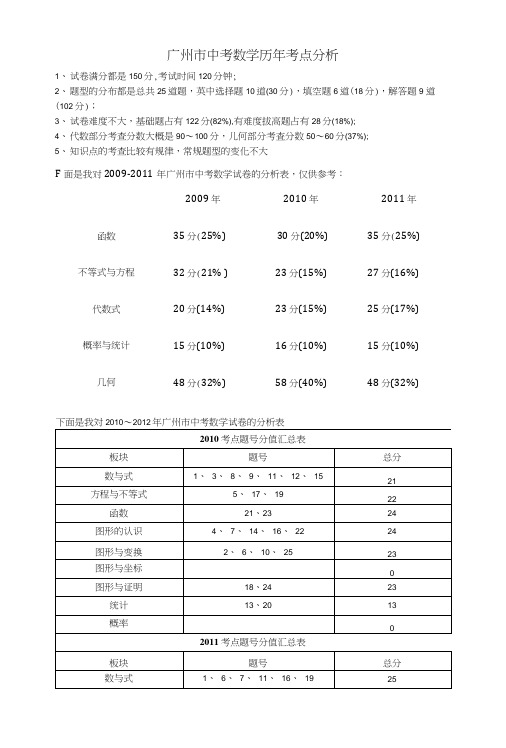
广州市中考数学历年考点分析
1、试卷满分都是150分,考试时间120分钟;
2、题型的分布都是总共25道题，英中选择题10道(30分)，填空题6道(18分)，解答题9 道(102分)；
3、试卷难度不大，基础题占有122分(82%),有难度拔高题占有28分(18%);
4、代数部分考查分数大概是90〜100分，儿何部分考査分数50〜60分(37%);
5、知识点的考查比较有规律，常规题型的变化不大
F面是我对2009-2011年广州市中考数学试卷的分析表，仅供参考：
2009 年2010 年2011 年函数35 分(25%)30 分(20%)35 分(25%)不等式与方程32 分(21% )23 分(15%)27 分(16%)代数式20 分(14%)23 分(15%)25 分(17%)
概率与统计15 分(10%)16 分(10%)15 分(10%)几何48 分(32%)58 分(40%)48 分(32%)
下面是我対2010〜2012年广州市中考数学试卷的分析表
各模块近三年考查分析。

北京市初中数学专题知识点I、数与代数部分:一、数与式：1、实数：1）实数的有关概念；常考点：倒数、相反数、绝对值(选择第1题，必考题4分) 2）科学记数法表示一个数(选择题第二题，必考4分)3）实数的运算法则：混合运算（解答题13题，必考4分）4）实数非负性应用：3、整式： 1）整式的概念和简单运算、化简求值（解答题5分）2）利用提公因式法、公式法进行因式分解（选择填空必考题4分）4、分式：化简求值、计算（解答题）、分式求取值范围（一般为填空题）（易错点：分母不为0）5、二次根式：求取值范围、化简运算（填空、解答题4分）二、方程与不等式：1、解分式方程（易错点：注意验根）、一元二次方程（常考解答题）2、解不等式、解集的数轴表示、解不等式组解集（常考解答题）3、解方程组、列方程（组）解应用题（若为分式方程仍勿忘检验）（必考解答题）4、一元二次方程根的判别式三、函数及其图像1、平面直角坐标系与函数1）函数自变量取值范围，并会求函数值；2）坐标系内点的特征；3）能结合图像对简单实际问题中的函数关系进行分析（选择8题）2、一次函数（通常与反比例函数相结合，以解答题形式出现。

）3、反比例函数4、二次函数（必考解答题，基本在24题出现，通常是求解析式以及与特殊几何图形综合，动态探究等，有时也在选择题第八题中出现。

）II、空间与图形一、图形的认识1、立体图形、视图和展开图（不是常考题型，但是如果出现则以选择题形式出现）2、线段、射线、直线（其中垂直平分线、线段中点性质及应用常在解答题中出现，两点间线段最短常用于解决路径最短的问题）3、角与角分线（解答题）4、相交线与平行线5、三角形（三角形的内角和、外角和、三边关系常以选择题形式出现，而三角形中位线的性质应用又是解答题中常用的添加辅助线的方法，其中有关三角形全等的性质、判定是必考解答题，三角形运动、折叠、旋转、平移（全等变换）、拼接等又是探究问题中的重要考点之一）6、等腰三角形与直角三角形（该考点常与四边形与圆相结合在解答题中出现，而与函数综合形成代数几何综合题，也是必考的解答题）7、多边形：内角和公式、外角和定理（选择题）8、四边形（特殊的平行四边形：性质、判定、以及与轴对称、旋转、平移和函数等结合应用以动点问题、面积问题及相关函数解析式问题出现，同时，梯形问题是中考中的必考解答题，而与四边形有关的图形探究题又是最后一道解答题25题的通常考察形式。

2012年中考数学试卷分析分值分析：选择题6题，4分/题，难度系数A级，预防粗心，共24分；填空12题，4分/题，共48分，第18题难度Ｂ＋，正确率为５０％；计算题19题，10分；解方程20题，10分；21题解直角三角形，10分；22题一次函数的实际应用10分，23题简单的几何证明和计算１０分；２４题函数和平面直角坐标系的混合运用，难度系数Ｃ，１２分；２５题第一问较简单，难度系数Ａ，第２问难度系数Ｃ，第３问难度系数Ｃ＋，共１４分。

知识点分析：１、单项式和多项式，初一上册内容；２、概率和统计，中位数、众数和平均数；３、解不等式，解集的确定；４、二次根式、分母有理化、化简和求值；５、轴对称图形和中心对称图形；６圆与圆的位置关系；７、计算，求绝对值；８、因式分解－提取公因式法；９、函数的增减性；１０、解根式方程；１１、一元二次方程根的情况；１２、函数的平移；１３、概率的计算；１４、频率分布和统计；１５、向量的计算－三角形法则和平行四边形法则；１６、相似三角形性质的运用；１７、正三角形多心合一的问题及应用；１８、平移和翻折的运用（画图能力）；１９、计算，细心，难度系数Ａ－；２０、解方程，难度系数Ａ；２１题解直角三角形的运用，建立直角三角形，难度系数Ａ＋；２２、应用题或一次函数的运用，难度系数Ａ＋；２３、三角形一边平行线、比例线段的运用和平心四边形，几何部分，难度系数B；24、函数。

平面直角坐标系和锐角三角比的综合运用，难度系数不是很大，但是因涉及知识点和计算较多，故定为B+或C，25、圆的综合运用，往往会和相似三角形混合运用，但是今年没有涉及到，圆的比重增加；分数占比：初一上118分，初一下20分，初二上20分，初二下30分，初三上32分，初三下30分；难易比例为：2:8做试卷要求：1-6必须全部正确；12-17全部正确，18题正确率50%，19-23全部正确，24，前两问，25题第一问，只要准确率保证，学员基本能考到130分。

聊城市2012年中考数学试题及试卷分析聊城市中考数学阅卷评价组聊城市2012年中考数学试题以《义务教育数学课程标准》及《聊城市2012年高中招生考试说明》的内容、范围、要求为依据。

依照“有利于推进课堂教学改革，培养学生的综合能力、创新精神与实践能力；有利于减轻学生课业负担，促进学生生动、活泼主动的学习；有利于高中中专学校选拔素质较高，能力较强的新生”的指导思想。

从我市的教学实际和学生的实际出发，立足于学生发展的需要，注重考察学生的教学基础知识、基本技能、基本能力和基本思想方法，思维能力，空间观念及利用教学知识分析和解决简单实际问题的能力。

坚持以能力立意，注重了时代性，应用性，探究性，综合性和教育性的考察。

为我市进一步推进新课改作出了正确的导向。

一﹑考试形式及试卷结构考试采用闭卷笔试形式，全卷满分120分，考试时间120分钟。

试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷为选择题共12个小题，满分36分；第Ⅱ卷为非选择题，包括填空题5个，共15分，解答题8个，共69分。

从试题结构及呈现形式上看，以考察学生的基础知识掌握程度和推理运算能力为主，以知识立意的同时更加注重能力立意，实际应用及动手能力的考察，体现了稳中求新和考查学生的基本数学素养的素质教育要求，试题难度适中，合乎选拔性考试命题的要求，同时也考察了学生为进一步学习高中课程的主干基础知识。

二﹑主要知识点分布三﹑试题的主要特点1.关注双基教学，重视课本作用本卷全面考察了学生对基础知识、基本思想方法的理解和运用。

试题大部分来源于教材，但又高于教材。

题目知识覆盖面广，求新求活，很好的考察了学生的数学基本素养。

注重对基础知识基本能力，基本的思想方法理解和运用是数学教学的主要内容。

也为下一步教学，进一步指明了方向。

2.贴进生活，重视应用能力的培养数学课程标准明确提出：要培养学生的应用意识，使学生认识到现实生活中，蕴含着大量的数学信息，数学在现实世界中有着广泛的应用，面对实际问题能主动尝试，从数学的角度寻求解决问题的策略。

2012年全国中考数学试题分类解析汇编(159套63专题）专题58：开放探究型问题一、选择题二、填空题1. （2012陕西省3分）在同一平面直角坐标系中，若一个反比例函数的图象与一次函数y=2x+6-的图象无．公共点，则这个反比例函数的表达式是 ▲ （只写出符合条件的一个即可）． 【答案】5y x=（答案不唯一）。

【考点】开放型问题，反比例函数与一次函数的交点问题，一元二次方程根与系数的关系。

【分析】设反比例函数的解析式为：k y x =， 联立y=2x+6-和k y x=，得k 2x+6x -=，即22x 6x+k 0-= ∵一次函数y=2x+6-与反比例函数k y x= 图象无公共点， ∴△＜0，即268k 0<--（），解得k ＞92。

∴只要选择一个大于92的k 值即可。

如k=5，这个反比例函数的表达式是5y x=（答案不唯一）。

2. （2012广东湛江4分） 请写出一个二元一次方程组 ▲ ，使它的解是x=2y=1⎧⎨-⎩． 【答案】x+y=1x+2y=0⎧⎨⎩（答案不唯一）。

【考点】二元一次方程的解。

【分析】根据二元一次方程解的定义，围绕x=2y=1⎧⎨-⎩列一组等式，例如： 由x ＋y=2＋（－1）=1得方程x ＋y=1；由x －y=2－（－1）=3得方程x －y=3；由x ＋2y=2＋2（－1）=0得方程x ＋2y=0；由2x ＋y=4＋（－1）=3得方程2x ＋y=3；等等，任取两个组成方程组即可，如x+y=1x+2y=0⎧⎨⎩（答案不唯一）。

3. （2012广东梅州3分）春蕾数学兴趣小组用一块正方形木板在阳光做投影实验，这块正方形木板在地面上形成的投影是可能是▲ （写出符合题意的两个图形即可）【答案】正方形、菱形（答案不唯一）。

【考点】平行投影。

【分析】根据平行投影的特点：在同一时刻，平行物体的投影仍旧平行。

所以，在同一时刻，这块正方形木板在地面上形成的投影是平行四边形或特殊的平行四边形，例如，正方形、菱形（答案不唯一）。

对于贵州省黔南州近三年中考数学的几点认识摘要：中考作为具有终结性和选拔性双重功能的考试，是义务教育阶段教学成果反馈的重要环节，各地区的中学对于中考的分析都非常的重视，本文就贵州省黔南州近三年中考数学作了一些研究，阐述了作者对中考数学的一点认识。

关键词：黔南州中考数学近三年一、近三年贵州省黔南州中考数学试题分析中考作为具有终结性和选拔性双重功能的考试，是义务教育阶段教学成果反馈的重要环节。

从贵州省黔南州2011年、2012年和2013年近三年的中考试卷来看，试题的设置严格按照《全日制义务教育数学课程标准（实验稿）》和当年的《黔南州中考说明——数学》的要求命制，试卷较好地诠释了数学课程标准的基本要求，充分体现了新课程理念关于考试评价提出的指导性、基础性、全面性、科学性、主体性的命题原则。

近三年来贵州省黔南州中考数学试卷从整体上来看是“稳中求变、变中求新”趋势，体现了“重视基础、突出能力、关注探究、联系实际、促进发展”的指导思想。

试题结构合理、情景素材真实，试卷主要题型分有：选择题、填空题和解答题三种题型，各大题的分值相对稳定，难易比例合理。

（具体参看附表）试卷在题目设计上每年都有区别，特别是2013年的贵州省黔南州中考数学试卷在前两年的基础上有了一个较大的调整，整套试卷总题数上增加了一道选择题，而整套试卷题目的设计层次分明、坡度递进，是一套结构合理、试题新颖、与实际生活联系紧密的试卷。

下面就从几个方面来分析研究近三年的贵州省黔南州中考数学试卷的结构特点。

（一）试题的基本结构2011、2012这两年整个试卷题量均为三大题25小题，2013年增加一题总题量为三大题26小题；满分都是150分，考试时间均为2个小时。

容易题、中档题、难题分值比例约为：2011年6∶7∶2；2012年7∶7∶1；2013年6∶7∶2，其中“数与式”约占42%，“空间与图形”约占38%，“概率与统计”约占20%。

这三年的试题结构基本保持一致，难易分配比例差别不大，难点分散，每一大类题型的最后两题在同类题型中都较难，特别是解答题最后两道题的最后一问都属于具有选拔作用的问题。

2012年全国中考数学试题分类解析汇编(159套63专题）专题54：图形的旋转变换一、选择题1. （2012天津市3分）将下列图形绕其对角线的交点逆时针旋转900，所得图形一定与原图形重合的是【 】（A ）平行四边形 （B ）矩形 （C ）菱形 （D ）正方形 【答案】D 。

【考点】旋转对称图形【分析】根据旋转对称图形的性质，可得出四边形需要满足的条件：此四边形的对角线互相垂直、平分且相等，则这个四边形是正方形。

故选D 。

2. （2012广东佛山3分）如图，把一个斜边长为2且含有300角的直角三角板ABC 绕直角顶点C 顺时针旋转900到△A 1B 1C ，则在旋转过程中这个三角板扫过的图形的面积是【 】A ．πB ．．3+42π．11124π【答案】D 。

【考点】旋转的性质，勾股定理，等边三角形的性质，扇形面积。

【分析】因为旋转过程中这个三角板扫过的图形的面积分为三部分扇形ACA 1、 BCD 和△ACD 计算即可：在△ABC 中，∠ACB=90°，∠BAC=30°，AB=2，∴BC=12AB=1，∠B=90°－∠BAC=60°。

∴AC =∴AB C 1S B C A C 22∆=⨯⨯=设点B 扫过的路线与AB 的交点为D ，连接CD ， ∵BC=DC，∴△BCD 是等边三角形。

∴BD=CD=1。

∴点D 是AB 的中点。

∴AC D AB C 11S S 2224∆∆==⨯=S 。

∴1AC D AC A BC D ABC S S S ∆∆=++扇形扇形的面扫过积26013113603604464124ππππ⨯⨯=+=++=+故选D 。

3. （2012广东汕头4分）如图，将△ABC 绕着点C 顺时针旋转50°后得到△A′B′C′．若∠A=40°．∠B′=110°，则∠BCA′的度数是【 】A ．110° B．80° C．40° D．30° 【答案】B 。

2012年北京中考数学第24题:旋转与轴对称变换、四边形内角和24．在ABC △中，BA BC BAC =∠=α，，M 是AC 的中点，P 是线段BM 上的动点，将线段PA 绕点P 顺时针旋转2α得到线段PQ 。

（1） 若α=60︒且点P 与点M 重合（如图1），线段CQ 的延长线交射线BM 于点D ，请补全图形，并写出CDB ∠的度数；（2） 在图2中，点P 不与点B M ，重合，线段CQ 的延长线与射线BM 交于点D ，猜想CDB ∠的大小（用含α的代数式表示），并加以证明；（3） 对于适当大小的α，当点P 在线段BM 上运动到某一位置（不与点B ，M 重合）时，能使得线段CQ 的延长线与射线BM 交于点D ，且PQ QD =，请直接写出α的范围。

(2)连接PC 、AD ，易证APD CPD ≅V V∴AP=PC ∠ADB=∠CDB ∠P AD=∠PCD 又∵PQ =P A ∴PQ =PC ，∠ADC =2∠CDB ，∠PQC =∠PCD =∠P AD 所以∠P AD +∠PQD =∠PQC +∠PQD =180°所以∠APQ +∠ADC =360°－(∠P AD +∠PQD )=180°2α-∴∠ADC =180°－∠APQ =1802α-∴2∠CDB =1802α-∴∠CDB =90α- （3）∠CDB =90α-且PQ =QD ∴∠P AD =∠PCQ =∠PQC =2∠CDB =1802α-∵点P 不与点B 、M 重合 ∴∠BAD >∠P AD >∠MAD所以21802ααα>︒->∴4560α︒<<︒心得体会：由等腰三角形与底边中线应想到轴对称。

此题可设∠PAC=β，可得∠CPQ=2（900－β）-2α 进而求得∠PCQ=α+β，∠ACD=α=∠BAC,所以AB ∥CD ， 所以∠CDB =∠ABD=90α- D 图1B Q AM (P )M A Q B 图2P。