工程力学(单辉祖)合肥工业大学精品讲义03平面一般力系(复习)
- 格式:ppt
- 大小:1.30 MB
- 文档页数:12

工程力学课后习题答案单辉祖著工程力学课后习题答案(单辉祖著)在学习工程力学这门课程时,课后习题的练习与答案的参考对于巩固知识、加深理解起着至关重要的作用。
单辉祖所著的《工程力学》一书,以其严谨的逻辑和丰富的内容,成为众多学子学习工程力学的重要教材。
下面,我们将为您详细呈现这本教材的课后习题答案。
首先,让我们来谈谈第一章的习题。
在这部分中,主要涉及到静力学的基本概念和受力分析。
例如,有一道题是关于一个简单的支架结构,要求画出其受力图。
对于这道题,我们需要明确各个构件之间的连接方式,判断是固定铰支座、活动铰支座还是其他约束类型,然后根据力的平衡条件,准确地画出每个构件所受到的力。
答案中,我们清晰地标注了各个力的大小、方向和作用点,并且通过合理的布局,使受力图易于理解。
第二章的习题重点围绕平面汇交力系和平面力偶系展开。
其中,有一道计算题要求计算多个力在某一点的合力。
在解答这道题时,我们首先将每个力分解为水平和垂直方向的分力,然后分别计算水平和垂直方向上的合力,最后通过勾股定理求出总的合力大小和方向。
答案的给出过程中,每一步的计算都有详细的说明,让学习者能够清晰地看到解题的思路和方法。
第三章的内容是平面任意力系。
这一章的习题难度有所增加,涉及到力系的简化、平衡方程的应用等。
比如,有一道题是求解一个复杂结构在给定载荷下的支座反力。
解题时,我们先对力系进行简化,找到主矢和主矩,然后根据平衡方程列出方程组,通过求解方程组得到支座反力的大小和方向。
答案中不仅给出了最终的结果,还展示了求解方程组的具体步骤和计算过程,方便学习者对照检查自己的解题过程。
第四章是空间力系。
这部分的习题对于空间想象力和数学运算能力有一定的要求。
例如,有一道题要求计算空间力在坐标轴上的投影以及对某点的矩。
在解答时,我们需要运用空间直角坐标系的知识,通过三角函数等方法求出投影的大小,再根据矩的定义计算出对某点的矩。
答案中会详细说明投影和矩的计算过程,并且配以适当的图示,帮助学习者更好地理解空间力系的概念。
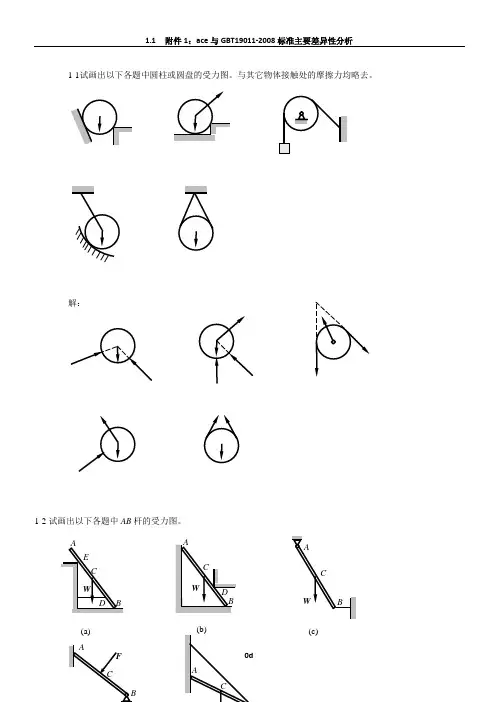
1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2试画出以下各题中AB杆的受力图。
A(BF((W(AW(F(F(F(FW(AW(F(c)(a)解:1-3试画出以下各题中AB 梁的受力图。
解:(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)FWA1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(d)D(e)F Bx(a)(b)(c)(d)(e)W(f)(a)D(b)B(c)BF DF CBF ABF BC1-5 试画出以下各题中指定物体的受力图。
(a) 结点A,结点B;(b) 圆柱A和B及整体;(c) 半拱AB,半拱BC及整体;(d) 杠杆AB,切刀CEF及整体;(e) 秤杆AB,秤盘架BCD及整体。
解:(a)(b)(c)(c)(d)ATFBAF(b)D(e)(d)(e)2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445N ,F 2=535N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:’CBF 1F12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)211 1.1222D A D D A F F FF F BC AB AC F FF F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN ,如图所示。




2-2解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)211 1.1222D A D D A F F FF F BC AB AC F FF F F =====∴===2-4解:(1) 研究AB ,受力分析并画受力图:(2) 画封闭的力三角形:相似关系:B A F F FCDE cde CD CE ED∆≈∆∴== 几何尺寸:11 22CE BD CD ED =====F FDF F AF DFF BF A dce12010 22010.4 45arctan 18.4B A o oCE F F kNCDED F F kN CDCECD α=⨯=⨯==⨯===-=2-6解:(1) 取DE 为研究对象,DE 为二力杆;F D = F E(2) 取ABC 为研究对象,受力分析并画受力图;画封闭的力三角形:'15166.7 23A D E F F F F N ===⨯= 2-7解:(1)取铰链B 为研究对象,AB 、BC 均为二力杆,画受力图和封闭力三角形;1BC F =(2) 取铰链C 为研究对象,BC 、CD 均为二力杆,画受力图和封闭力三角形;22cos30o CB F F F ==由前二式可得:F FF F BCF AB F 1 CF CDF 2F CB F CD12122210.61 1.63BC CB F F F F or F F ==∴===2-9 解:(1) 取整体为研究对象,受力分析,AB 、AB 、AD 均为二力杆,画受力图,得到一个空间汇交力系;(2) 列平衡方程:0 cos 45 cos 4500 cos 6000 sin 60sin 45sin 450o o x AC AB o yAD o o o zAD AC AB F F F F F F FF F F =⨯-⨯==-==--=∑∑∑解得:2 1.2 0.735 4AD AC AB AD F F kN F F F kN ===== AB 、AC 杆受拉,AD 杆受压。



1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2试画出以下各题中AB杆的受力图。
A(BF((W(AW(F(F(F(FW(AW(F(c)(a)解:1-3试画出以下各题中AB 梁的受力图。
解:(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)FWA1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(d)D(e)F Bx(a)(b)(c)(d)(e)W(f)(a)D(b)B(c)BF DF CBF ABF BC1-5 试画出以下各题中指定物体的受力图。
(a) 结点A,结点B;(b) 圆柱A和B及整体;(c) 半拱AB,半拱BC及整体;(d) 杠杆AB,切刀CEF及整体;(e) 秤杆AB,秤盘架BCD及整体。
解:(a)(b)(c)(c)(d)ATFBAF(b)D(e)(d)(e)2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445N ,F 2=535N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:’CBF 1F12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)211 1.1222D A D D A F F FF F BC AB AC F FF F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ,力的大小等于20KN ,如图所示。
